Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In recent years, the view that the functional and structural systems of the brain can be modeled as complex networks has motivated a large amount of research on the application of graph theoretical concepts to brain network analysis [3, 9].

The standard brain network model consists of a set of nodes, which represent a partitioning of the cortex and of other gray matter structures. These nodes are connected via a set of edges, or links, that represent structural and/or functional connections between gray matter partition units. Such a graph model of the brain’s network organization can be constructed from a variety of imaging modalities such as structural MRI, diffusion MRI, functional MRI, or EEG/MEG. In this framework, a characterization of the organization of the different computational nodes and the functional or structural interaction between them is achieved via graph theoretical analysis [3, 9].

In this standard view of the brain network, a natural emphasis is placed on the nodes of the graph, which represent the computational units of the brain. While most graph theoretical measures do take edges into account, their ultimate goal is to describe the relationship between the computational centers, i.e. the nodes of the graph. The relationship between the edges themselves is often overlooked.

Yet, the study of the brain warrants a deeper investigation into the connections themselves. In our paper, we focus on structural connectivity networks derived from diffusion MRI data. In such networks, the graph edges represent white matter tracts. There is an extensive body of literature that implicates white matter tracts in a variety of psychiatric disorders such as schizophrenia, autism (and many others), where the tracts are seen not only as ‘wires’ that link computational nodes that may be lesioned in some way, but are also seen as lesion sites themselves, as revealed, for example, by changes in DTI measures such as FA, Trace etc. (see e.g. [6] for a review of DTI findings in schizophrenia).

The motivation behind our paper is thus to introduce a novel formalism for brain network analysis that shifts the emphasis from the nodes, which are typically gray matter structures, to edges, which are typically white matter structures (at least in the type of structural networks under consideration in this paper). Referring to the standard brain network graph as the Primal graph, we introduce (a type of) a Dual graph whose nodes correspond to the edges in the Primal graph. In the graph theory community, different authors have given to this construct several alternative names: the line graph, the edge-to-vertex dual, the interchange graph, the adjoint graph, and others (e.g. [4, 8]). Here, we use interchangeably the names dual graph and line graph for this construct which we describe in further detail below. It has previously been used in brain network analysis for wavelet smoothing of connectivity [5], but not explicitly as a descriptor of the organization of connections (to the extent of our knowledge).

1.1 Scalar vs. Vector Weights in Brain Network Analysis

In standard brain network analysis, the edges in the Primal graph may have a scalar weight associated with them in order to reflect connectivity strength, measured for example as functional or structural correlation between connected gray matter regions, or as mean track FA in structural networks based on diffusion MRI [3, 9]. While graph theoretic measures for networks with scalar weights are well-known and widely used [9], it is not clear how these measures can be extended to the case of vector-weighted networks. In fact, the analysis of vector weighted networks is still an open problem. Meanwhile, the ever-increasing abundance of measurements on white matter tracts in neuroscientific applications highlights further the need to remove the restriction to single scalar connection weights in traditional network analysis.

In this paper, we propose a two-step solution to this problem. First, we introduce a transformation from the Primal graph to a Dual graph, such that weights on edges in the Primal graph become feature vectors on nodes in the Dual graph. Then, we introduce a metric on vector weights associated to nodes in dual space. The Dual graph can then be analysed via standard graph measures, modified to take into account the metric on feature vectors associated with each node. With this approach, we achieve a solution to the vector weights problem while incorporating it into a novel graph formalism, which allows to stress novel aspects of network connectivity.

To summarize, working in the dual space makes it possible to explicitly model relations between connections in the Primal graph. Furthermore, these connections can now be characterized by a vector of relevant features as opposed to single scalar features. We test our approach on a small population study on schizophrenia, where we show that the dual graph can improve the separation between schizophrenia patients and normal controls. Of course, the goal of this study is certainly not to make clinical claims regarding schizophrenia. As a first study based on this novel methodology, with a small population sample, it is inherently preliminary and limited, and its purpose is to only illustrate the method and show how it could be applied in a future clinical study.

2 The Model

Before describing the dual graph model, we first formalize the notions of feature vectors and distances between them. We then incorporate these concepts into our novel dual graph formalism, which is designed to facilitate the analysis of network relations between connections associated with feature vectors.

2.1 Feature Vectors in Product Spaces

Consider the simple case of two feature vectors \((x_{1},y_{1})\) and \((x_{2},y_{2})\). If R x and R y are 2 metric spaces and \(x_{1},x_{2} \in R_{x}\) and \(y_{1},y_{2} \in R_{y}\), then the metric for the product space R x × R y is given by

$$\displaystyle{ d^{2}((x_{ 1},y_{1}),(x_{2},y_{2})) = d^{2}(x_{ 1},x_{2}) + d^{2}(y_{ 1},y_{2}). }$$
(1)

Please see [2] for details. This result can be used to formulate geodesic distances between two feature vectors.

In general, we will be working with m feature vectors \(\mathbf{f}_{i} = (x_{i1},x_{i2}\ldots,x_{in}),\ i \in [1.. m]\), each with n features. As a first step in computing (1), we need to define the metrics of each individual feature space. We can endow each of the feature metric spaces with either an Euclidean or a Riemannian metric. In the Euclidean case, the metric is simply \(d(x_{i1},x_{j1}) =\vert x_{i1} - x_{j1}\vert\). In the Riemannian case, one possible metric is \(d(x_{i1},x_{j1}) =\log (t(x_{i1})/t(x_{j1}))\), where \(t: R_{1} \rightarrow \mathbb{R}_{+}\bigcup \{0\} \equiv \mathbb{R}_{0+}\) is a mapping of the feature value from its native space to the space of non-negative real numbers.

In this article, we use feature vectors with three features: \(x_{\mathit{FA}},x_{\mathit{Tr}},x_{\mathit{Disp}}\), which are the mean values of FA, Trace and Dispersion, respectively, computed over each track. Dispersion is a measure of track geometry introduced in [10, 11]. The values of all these three features range from 0 to some maximum value. In the case of FA, this maximum value is 1. In the case of Trace, it is three times the maximum value of the diffusion coefficient of free water at normal body temperature, i.e. 0.009 s/mm2. In the case of Dispersion, the maximum value is π radians. Thus, for these three features we define \(t(x) = x/(x^{\mathit{max}} - x)\) where x max is the maximum possible value for each feature, as given above.

These metrics, together with (1) allow us to define geodesic distance measures on the product space of our feature vectors \(\mathbf{f}_{i} = (x_{\mathit{iFA}},x_{\mathit{iTr}},x_{\mathit{iDisp}})\):

$$\displaystyle{ d_{R}(\mathbf{f}_{i},\mathbf{f}_{j}) = \sqrt{log\left (\frac{t(x_{\mathit{iFA } } )} {t(x_{\mathit{jFA}})}\right )^{2} + log\left (\frac{t(x_{\mathit{iTr}})} {t(x_{\mathit{jTr}})}\right )^{2} + log\left (\frac{t(x_{\mathit{iDisp}})} {t(x_{\mathit{jDisp}})}\right )^{2}} }$$
(2)

for the Riemannian case, or

$$\displaystyle{ d_{E}(\mathbf{f}_{i},\mathbf{f}_{j}) = \sqrt{\vert x_{\mathit{iFA } } - x_{\mathit{jFA } } \vert ^{2 } +\vert x_{\mathit{iTr } } - x_{\mathit{jTr } } \vert ^{2 } +\vert x_{\mathit{iDisp } } - x_{\mathit{jDisp } } \vert ^{2}} }$$
(3)

for the Euclidean case. Note that these distances could also be used to compute other operations on the space F of feature vectors, for example the mean of a set of feature vectors \(\{\mathbf{f}_{1},\ \ldots \,\mathbf{f}_{m}\}\), which can be defined as

$$\displaystyle{ \min _{\mathbf{\bar{f}}\in F}\sum _{i=1}^{m}d(\mathbf{\bar{f}},\mathbf{f}_{ i}), }$$
(4)

where d can be one of d R or d E as defined above. However, in the present paper, we only focus on distance.

2.2 The Dual Graph

A network is represented as a graph G = { V, E} where V is a set of vertices that are pairwise joined by a set of edges E. Our model is based on the concept of the line graph, borrowed from graph theory, which defines a dual form of the graph G [4, 8] and which we will denote as D(G). Given a graph G, its line graph D(G) is formed by interchanging the roles of V and E. In other words, the line graph D(G) = { V D, E D} has a one-to-one correspondence between its vertex set V D and the edge set E of G. Furthermore, two vertices in D(G) are connected if and only if the corresponding edges in G share a common endpoint (vertex). More formally,

$$\displaystyle\begin{array}{rcl} E_{D}& =& \{\ \{(v_{1},v),(v,v_{2})\}\ \ \vert \\ & &\quad \{v,v_{1},v_{2}\} \in V, \\ & & \quad (v_{1},v) \in E,(v,v_{2}) \in E\ \}.{}\end{array}$$
(5)

The transformation of the Primal graph G to the Dual graph D(G) entails that each vertex of degree k in G results in \(k(k - 1)/2\) edges in D(G). Isolated nodes in G, i.e. nodes of degree 0, are not represented in D(G).

Figure 1 shows a simple example of a graph and its corresponding line graph.

Fig. 1
figure 1

A simple example of a graph G and it’s corresponding dual graph D(G)

Full size image

3 Experimental Methods

These theoretical tools are combined in a set of experiments designed to illustrate their application to neuroscientific studies. To this end, we performed a small scale population study on schizophrenia, where we computed the three features for a set of connections in each participant. We then used the above distance measures in computing the standard network measure of global efficiency on the dual graph [9]. This dual approach reveals between-group network differences that are not detected with a standard analysis on the Primal graph. The efficiency measure was picked as an example, others are possible as well.

3.1 Subjects and Data Acquisition

Our subject population consists of 14 adult male healthy control subjects and ten adult male chronic schizophrenia patients. In each subject, diffusion MRI data was acquired on a GE Signa HDxt 3.0T scanner using an echo planar imaging sequence with a double echo option, an 8 Channel coil and ASSET with a SENSE-factor of 2. The acquisition consisted of 51 directions with b = 900 s/mm2, and eight images with b = 0 s/mm2, with scan parameters TR = 17,000 ms, TE = 78 ms, FOV = 24 cm, 144 ×144 encoding steps, 1.7 mm slice thickness. Eighty five axial slices covering the whole brain were acquired. Structural MR T1 images at 1 mm resolution were acquired as well.

3.2 Network Construction and Analysis

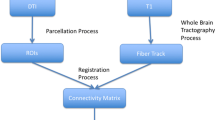
In each subject, we computed whole-brain tractography with the filtered tractography method of [7], followed by a standard FreeSurfer parcellation of the cortex (http://surfer.nmr.mgh.harvard.edu), which was then registered to the subject’s diffusion MRI space, specifically to the unweighted b0 volume. From the whole-brain tractography we extracted all existing connections between pairs of FreeSurfer-defined cortical areas. As the number of fibers per connection varies across subjects, we selected those connections that have at least 30 fibers in every subject. There were 218 such connections. Based on them, we constructed a structural network graph, our Primal graph G, a schematic view of which is shown in Fig. 2. By working with only these 218 connections, we ensure to have the same network representation in all 24 subjects. In this manner, the structural network topology is not a source of variability, and will not affect the observed between-group differences.

Fig. 2
figure 2

An illustration of our structural network consisting of 218 connections, shown over a translucent rendering of the brain surface

Full size image

In each subject, we computed the mean values for FA and Trace along each of these 218 connections. Additionally, we applied the method of [10] to compute mean fiber dispersion over each fiber bundle, using a spatial scale parameter S = 8. 5 mm. We then computed D(G), the Dual graph of our Primal brain network graph G, as described previously in Sect. 2.2. Each node in the Dual graph represents one of the 218 connections and is associated with a feature vector of three elements, i.e. the mean values of FA, Trace and Dispersion.

Using the distance measures defined in Sect. 2.1, we then computed the global efficiency measure on the dual graph using the implementation available in the Brain Connectivity Toolbox [9]. The global efficiency of a graph is a network theoretic measure commonly used in brain network analysis, defined as the average inverse shortest path length in the network [9]. In the case of our dual graph, path length between nodes translates to similarity between feature vectors. We chose global efficiency as one possible network measure that can be used to compare graphs. Of course, many other measures are available, and a future study should investigate several different network measures, not only one. Here, we restrict ourselves to one measure for brevity of exposition. Also, we note that previous network analysis studies have shown global efficiency in functional networks to be abnormal in schizophrenia [1]. Thus, we chose the global network efficiency as an example measure to compare the primal graph vs. the dual graph approach in a population study in schizophrenia, with results presented next in Sect. 4.

4 Results

It is important to remember that the goal of our experiments is not to make clinical claims of significance in schizophrenia, but rather to simply illustrate the behavior of our method and to suggest ways in which it could be used in the future. At this stage, we only use a small population sample, and all our clinical findings remain preliminary.

We compared global network efficiency between our groups of schizophrenia patients and control subjects in a series of experiments, where the efficiency measure was computed on the Dual graph using either the Riemannian distance measure (2) or the Euclidean distance measure (3). We performed these comparisons using the full feature vectors. In addition, to explore the performance of single features in isolation, we considered modified feature vectors containing only one feature. The global efficiency measure computed with individual features on the Dual graph was also compared to the efficiency measure computed in the Primal graph, where the feature under consideration was used as weight in a classical weighted graph computation [9]. The results of all these experiments, in the form of p-values, are summarized in Table 1. We note that network efficiency in functional connectivity has previously been shown to be abnormal in schizophrenia [1]. Broadly, our results seem to fall in line with this finding.

Table 1 p-Values for the global network efficiency comparison between our schizophrenia and controls groups
Full size table

5 Discussion

We wish to re-emphasize that the main conclusions to be drawn from our results do not rest in the specific p-values. Even when the p-value drops below the standard threshold of 0.05, it is still difficult to make claims of clinical significance given the small size of the subject population. Rather, we would like to steer the reader’s attention to the overall pattern of the p-value change. First, we note that the choice of Euclidean vs. Riemannian distance measure may or may not influence the comparison result. When the comparison is made with the full feature vector with three features, the p-value drops to a nearly significant level when choosing the Riemannian metric over the Euclidean.

Second, our experiments demonstrate that working with the Dual graph, as opposed to the Primal graph, comes with a ‘dual’ benefit. First, we are no longer restricted to single scalar features (weights), we can now work with feature vectors—the equivalent of vector-valued edge weights in the Primal graph. Second, even when using single scalar features, the dual graph formalism appears to allow for a better discrimination between the control and schizophrenia groups. An exact mathematical derivation of why this may be the case is the topic of future work. At this point, we will point to the fact that in the Primal weighted graph, a path length is a sum of edge weights. In contrast, in the Dual graph formalism, a path length is the sum of distances between features. Thus, in some sense, the Dual graph represents a differential form of the Primal graph. Thus, in the case of the Dual graph, increased efficiency embodies the notion that along a path, connections have a smaller variation between their feature vectors, possibly denoting reduced local ‘specialization’. In other words, increased efficiency implies that connections along a path are more homogeneous in terms of their feature vectors. If some of these features carry functional information (not in our present paper, but in our future work), then changes in such similarity could be important to reveal how functional and structural connection properties change together in a disease. Of course, a full theoretical analysis of the Dual graph measures is necessary, as well as an extended analysis of their implications. This will be done in future work.

We believe that this novel Dual graph formalism holds great promise for highlighting the importance of connections in brain network analysis. In terms of relevance to brain disorders such as schizophrenia, where white matter abnormalities are known to be important, the Dual graph approach is expected to reveal a novel view on the organization and distribution of white matter abnormalities in the brain, in a manner that cannot be directly accessed with traditional track-based studies, or with the traditional Primal graph approach to brain network analysis.

The present paper was aimed at introducing and illustrating the main concepts. Future work can proceed in several different directions. First, we showed how a distance measure between feature vectors can be used to compute a length-based network measure, namely efficiency. Other network measures, such as clustering and centrality need to be explored as well. Second, in this paper we worked with up to three features per connection. Future work will surely explore a wider variety of connection features, not all of which need to be tied to DTI. Additionally, we kept network topology constant across subjects in the present work, in order to limit potential sources of variability. Future work needs to relax this constraint. In order to do this, however, first we must understand the effect of thresholding the network structure. In the present work, our network consisted of connections with at least 30 fibers in every subject. Future work needs to investigate how robust are the results relative to variation in this threshold value. In addition to answering all these methodological questions, the method’s performance in clinical studies needs to also be further explored, in carefully designed studies with a larger population size.