Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The Global Geodetic Observing System (GGOS) (Plag and Pearlman 2009) of the International Association of Geodesy (IAG) established during its Planning Meeting 2010 (February 1–3, Miami/Florida, USA) the GGOS Theme 1: Unified Height System. The main purpose is to provide a global gravity field-related vertical reference system that (1) supports a highly-precise (at cm-level) combination of physical and geometric heights worldwide, (2) allows the unification of all existing local height datums, and (3) guarantees vertical coordinates with global consistency (the same accuracy everywhere) and long-term stability (the same order of accuracy at any time) (Kutterer et~al. 2012). Activities to be undertaken under the umbrella of the GGOS Theme 1 are understood as the continuation of the work started by the 2007–2011 IAG Inter-Commission Project 1.2 Vertical Reference Frames (IAG ICP1.2, Ihde 2007). The main result of the IAG ICP1.2 is the document Conventions for the Definition and Realisation of a Conventional Vertical Reference System—CVRS (Ihde et~al. 2007). These conventions describe the fundamentals to be taken into consideration for the establishment of a vertical reference system fulfilling the requirements outlined by GGOS. According to CVRS and Kutterer et~al. (2012), the global vertical datum shall correspond to a level surface of the Earth’s gravity field with a given potential value W 0 = const. and, consequently, a formal recommendation about the W 0 value to be adopted is a main objective of GGOS Theme 1 (cf. GGOS 2020 Action Plans 2011–2015, unpublished). The agreed value of W 0 must also be promoted as a defining parameter for a new reference ellipsoid and as a reference value for the estimation of the constant L G , which is necessary for the transformation between Terrestrial Time (TT) and Geocentric Coordinate Time (GCT) (Petit and Luzum 2010).

It is well-known that any W 0 value can be arbitrarily appointed for the determination of vertical coordinates (e.g., Heck and Rummel 1990; Heck 2004). However, the establishment of a vertical reference system with global consistency demands that the selected W 0 value be realisable with high-precision at any time and at any place around the world. With this, the real problem is not the selection of the value W 0, but its realisation, i.e., the estimation of the position and geometry of the equipotential surface that W 0 is defining, namely the geoid. To get correspondence between W 0 and the global geoid, it is necessary that both be estimated from the same geodetic observations and that they be consistent with other defining parameters of geometric and physical models of the Earth. Consequently, like any reference system, W 0 should be based on some adopted conventions, which guarantee its uniqueness, reliability and repeatability. Otherwise there would be as many W 0 reference values (i.e., global zero-height surfaces) as there are groups evaluating it.

The responsibility of outlining the necessary standards and conventions for the determination and realisation of a reference W 0 value was given to the Working Group on Vertical Datum Standardisation. It was established for a period of 4 years (2011–2015) as a common initiative of GGOS Theme 1, IAG Commissions 1 (Reference Frames) and 2 (Gravity Field), and the International Gravity Field Service (IGFS). According to IAG nomenclature (Drewes et~al. 2012), it is called Joint Working Group JWG 0.1.1. The first activities faced by JWG 0.1.1 concentrate on (1) making an inventory about the published W 0 computations to identify methodologies, conventions, standards, and models presently applied (cf. Sánchez 2012) and (2) bringing together the different groups working on the determination of a global W 0 in order to coordinate these individual initiatives for a unified computation. Once these aims are achieved, the next steps relate to the preparation of a proposal for a formal IAG/GGOS convention about W 0 and to provide a roadmap for the usage of W 0 in the unification (linkage) of the local height systems into the global datum. This paper discusses the first W 0 estimations performed in the frame of this JWG 0.1.1.

2 Empirical Determination of W 0

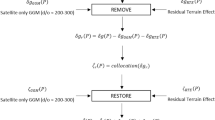
The empirical estimation of W 0 is strongly related to the concept of “geoid”. The most accepted definition of this is understood to be the equipotential surface coinciding, in the sense of the least squares, with the mean sea surface at rest worldwide (Gauss 1876, p. 32). Since this “ideal” cannot be satisfied, the realisation of this definition has been refined over time depending on the geodetic observations and analysis strategies available for geoid modelling (e.g., Mather 1978; Heck and Rummel 1990; Heck 2004). In particular, Mather (1978), based on the availability of satellite altimetry techniques and the possibility to estimate the dynamic ocean topography (DOT), indicates that the geoid represents that level surface with respect to the average of the DOT is zero when sampled over all oceans (S), i.e.,

$$ {\displaystyle \underset{S}{\int } {\it DOT}^2\mathrm{d}s}\kern0.5em =\kern0.5em \min $$
(1)

The DOT at any point j(φ,λ,h) located at the sea surface can be written as:

$$ {\it DOT}_j\kern0.5em =\kern0.5em \left[{h}_S-{r}_j-{N}_j\right]=\frac{W_0\kern0.5em -\kern0.5em {W}_j}{\gamma_j} $$
(2)

Here, (φ,λ,h) are the ellipsoidal coordinates latitude, longitude and height of j, h S is the height of the satellite with respect to a reference ellipsoid; r j is the range measurement representing the distance between the satellite and j; and N j , γ j and W j denote geoid undulation, normal gravity and gravity potential at j. To satisfy Eq. (2) it is assumed that γ j is computed from the same ellipsoid to which h S and N j are referred. In this way, for consistency, it is expected that the values N j (φ,λ), defined geometrically, describe the equipotential surface defined by W 0 (cf. Sánchez 2012). According to this, the minimum condition in Eq. (1) can be re-written as (cf. Sacerdorte and Sansò 2001):

$$ \begin{array}{l}\frac{\partial }{\partial {W}_0}{\displaystyle \underset{S}{\int } {\it DOT}^2\;\mathrm{d}s}\kern0.5em =\kern0.5em \frac{\partial }{\partial {W}_0}{\displaystyle \underset{S}{\int }{\left[\frac{W_0-{W}_j}{\gamma_j}\right]}^2}\mathrm{d}s\kern0.5em =\kern0.5em 0\kern0.62em ;\kern0.5em \\[10pt] {}{W}_0\kern0.5em =\kern0.5em \frac{{\displaystyle \underset{S}{\int}\frac{W_j}{\gamma_j^2}\;\mathrm{d}s}}{{\displaystyle \underset{S}{\int}\frac{1}{\gamma_j^2}\;\mathrm{d}s}}\end{array} $$
(3)

Equation (3) is, in general, the basic approach most applied during the last two decades for the empirical estimation of a global W 0 value (e.g., Burša et~al. 2002; Sánchez 2007; Dayoub et~al. 2012). The geometry of the sea surface is assumed to be described by the coordinates contained in a mean sea surface model (MSS) and the potential values W j are derived from a global gravitational model (GGM) expressed normally as a spherical harmonic expansion (e.g., Heiskanen and Moritz 1967, p. 57).

Dayoub et~al. (2012) propose the reduction of the sea surface heights by an oceanographic mean dynamic topography model (MDT) in order to get a level surface closer to the geoid, i.e.,

$$ {N}_j\left(\varphi, \lambda \right)\kern0.5em =\kern0.5em {h}_j\left(\varphi, \lambda \right)- {\it MDT}_j\left(\varphi, \lambda \right) $$
(4)

Basically, DOT and MDT are representing the same, but, in this context, the first one is derived from satellite altimetry in combination with a gravimetric geoid, and the second one is obtained from ocean circulation analysis. Hence, the MDT model is independent of pre-given gravimetric geoid models. Dayoub et~al. (2012) base their computations on the ECCO2 model (Menemenlis et~al. 2008).

Another approach applied presently for the estimation of a global W 0 is the solution of the geodetic boundary value problem. In this case, an additional unknown (ΔW 0 = W 0 −U 0) representing the difference between the Earth’s gravity potential W 0 and the normal potential U 0 introduced for the linearization of the boundary conditions is included in the observation equations (e.g., Sacerdote and Sansò 2004), Heck and Rummel 1990). As U 0 is known, the determination of ΔW 0 allows the estimation of W 0. In general, the observables building the boundary conditions (i.e., geopotential numbers and physical heights used for the estimation of gravity anomalies) refer to different vertical datums, and therefore, there shall be as many ΔW 0 unknowns as existing i datums: (ΔW i0  = W i0  − U 0) (e.g., Rummel and Teunissen 1988; Heck and Rummel 1990; Sacerdorte and Sansò 2004). According to this, the geodetic boundary value problem in linear and spherical approximation can be formulated as:

$$ {\nabla}^2T\kern0.5em =\kern0.5em 0,\kern1em \mathrm{outside}\kern0.5em \varSigma $$
(5a)
$$ -\frac{\partial T}{\partial r}-\frac{2}{R}T\kern0.5em =\kern0.5em {g}_j-\frac{2}{R}\Delta {W}_0^i,\kern0.5em \mathrm{on}\kern0.5em \varSigma $$
(5b)
$$ T\to 0,\kern0.5em \mathrm{at}\kern0.5em \infty $$
(5c)

Σ is the boundary surface, T is the anomalous potential, and function g j represents the observational data included in the boundary conditions. The multiple vertical datum dependence in (5b) can be avoided if the boundary conditions are given as a function of only one kind of data (j = 1), depending on only one vertical datum (i = 1). For instance, taking into consideration only ocean areas and by applying exclusively satellite altimetry data and satellite-only global gravity models, there will be only one ΔW i0  (i = 1) and the W 0 obtained can be thus conventionally assumed as the global reference level (Sánchez 2008). In this case, g j in Eq. (5b) corresponds to the gravity disturbance at the sea surface:

$$ \delta {g}_P\kern0.5em =\kern0.5em {g}_P\kern0.5em -\kern0.5em {\gamma}_P $$
(6)

Some empirical evaluations of this approach utilize as input data sea surface heights of a MSS model (assumed as the geometrical representation of the boundary surface Σ) and gravity disturbances derived from a GGM in combination with the normal gravity of the GRS80 ellipsoid (e.g. Sánchez 2008; Čunderlík and Mikula 2009). In particular, Čunderlík and Mikula (2009) extend the computations to land areas, where the geometry of the boundary surface is represented by means of an SRTM model (specifically the SRTM_PLUS V1.0, Becker and Sandwel 2003). Nevertheless, ΔW 0 takes different values depending on the continent, and consequently, authors recommend adoption of a value computed over the ocean areas only.

3 Current W 0 Estimates

At present, there are four groups working on the estimation of a global W 0 value (local estimations, i.e., based on data distributed within limited geographical areas have not been considered). The group with the largest experience, called in the following the Prague Group, started this kind of computations in the early 1990s (e.g., Burša et~al. 1992, 1997). Then, in the first decade of the 2000s, some related computations were published by the Munich Group (e.g., Sánchez 2007, 2008), and the Bratislava Group (e.g., Čunderlík et~al. 2008; Čunderlík and Mikula 2009). Finally, the most recent contribution to the global W 0 estimation was produced by the Latakia(/Newcastle) Group (e.g., Dayoub 2010; Dayoub et~al. 2012).

The four groups apply in general different methodologies and different input models of the sea surface and the Earth’s gravity field. The Prague Group (e.g., Burša et~al. 2007a) and the Latakia Group (e.g., Dayoub et~al. 2012) solve Eq. (3) using an equal-area weighting function for the estimation of the averaged potential value. The Bratislava Group (e.g., Čunderlík and Mikula 2009) and the Munich Group (e.g., Sánchez 2008) prefer the solution of the geodetic boundary value problem (Eq. 5). The computations of the Bratislava Group are based on the boundary element method, while the computations of the Munich Group are based on an analytical solution of the boundary value problem. Furthermore, the Prague Group uses its own sea surface models, derived from TOPEX/Poseidon and Jason 1 data (e.g., Burša et~al. 1998, 2001, 2002, 2007a), while the other groups (e.g., Čunderlík et~al. 2008; Čunderlík and Mikula 2009; Sánchez 2007, 2009; Dayoub et~al. 2012) also apply models already published by other specialists, such as CLS01 (Hernandes and Schaeffer 2001), KMS04 (Andersen et~al. 2006) or DNSC08 (Andersen and Knudsen 2009). Further analyses (e.g., Burša et~al. 2007a; Sánchez 2007; Dayoub et~al. 2012) are also devoted to estimating time variations of W 0 (by taking into consideration yearly sea surface models) and to identifying the dependence of the W 0 estimation on the GGM spectral resolution, the MSS spatial resolution, and the MSS latitude coverage. As expected, this mixture of strategies, MSS and GGM models produces different W 0 values, which are very similar (Fig. 1), but with discrepancies larger than the expected realisation accuracy, i.e., >1 m2 s−2 (∼10 cm).

At present, the most commonly accepted W 0 value is that included in the IERS Conventions (W 0 = 62,636,856.0 ± 0.5 m2 s−2, Petit and Luzum 2010, Table 1.1). The objective there is not to provide a vertical reference level but to explain the value assigned to the constant L G (=W 0/c 2) (Resolution B1.9 of the XXIV General Assembly of the International Astronomical Union, 2000). This W 0 value was recommended by Groten (2004) as the “best estimate” available at that time and its computation is explained by Burša et~al. (1999).

Before this kind of computations could be performed, the procedure to obtain a global W 0 value was the determination of a reference ellipsoid and to assume W 0 = U 0 by definition. U 0 corresponds to the normal potential at the surface of the reference (biaxial geocentric) ellipsoid and can be computed from the ellipsoid parameters, e.g., Somigliana theory (cf. Heiskanen and Moritz 1967, p. 67). Today, the GRS80 ellipsoid is used (Moritz 2000).

4 Towards a Unified W 0 Estimation

In the frame of JWG 0.1.1, it was agreed by the four groups to perform a new W 0 computation applying their own methodologies, but introducing the same input models in order to identify possible inconsistencies between the individual procedures. The MSS’s selected at this first step are MSS_CNES_CLS11 (Schaeffer et~al. 2012) and DTU10 (Andersen 2010). With respect to the reference time period adopted in the computation of each model, it is assumed that the corresponding sea surface heights are given at epoch 1996.0 in the CLS11 model and at epoch 2001.0 in the DTU10 model. The Latakia and Munich Groups referred the data to the mean tide system, while the Bratislava Group used the tide-free system. The Prague Group continues working with its own MSSs, but in this study, only Jason 1 data are considered. The usage of data referring to different tide systems shall not influence the obtained W 0 values, as already demonstrated by Burša et~al. (1999) and Dayoub et~al. (2012).

Fig. 1
figure 1

Examples of W 0 values computed after the publication of the GRS80 ellipsoid. The values included in the IERS conventions are also represented. The value 62,636,000 m2 s−2 must be added. Credits for GGMs applied in the different computations: EGM96 (Lemoine et~al. 1998), EIGEN-GC03 (Förste et~al. 2005), EGM2008 (Pavlis et~al. 2012)

Full size image

The four groups utilised the GGMs EGM2008 (Pavlis et~al. 2012), EIGEN-6C (Förste et~al. 2011) and GOCO03S (Mayer-Gürr et~al. 2012), which were evaluated considering degree/order up to 250 and the complete expansion, i.e., EGM2008 up to 2160 and EIGEN-6C up to 1420. The GGMs were referenced to epoch 1996.0 when using the CLS11 model and to epoch 2001.0 for the DTU10 model. In addition, their coefficient C 2,0 was transformed to the same tide system in which the MSS were represented.

Results show that the higher degree coefficients of the GGM do not influence the global estimation of W 0: from n = 10 to n = 20 W 0 changes by −1.46 m2 s−2, from n = 20 to n = 30 it varies −0.52 m2 s−2. In general, when the retained harmonic degree n grows, the difference between the corresponding W 0 values decreases. Nevertheless, up to n =120 the variation of W 0 is smaller than 0.001 m2 s−2. This proves that the dependence of W 0 on the harmonics n > 120 is negligible (Fig. 2).

Fig. 2
figure 2

W 0 dependence on the GGM’s harmonic degree n (GGM: EGM2008, MSS: CLS11). Value 62,636,800 m2 s−2 should be added

Full size image
Fig. 3
figure 3

W 0 dependence on the MSS latitudinal coverage. Estimates applying CLS11 and DTU10 in combination with GOCO03S, EIGEN-6C and EGM-2008. Value 62,636,800 m2 s−2 should be added

Full size image

The choice of GGM has insignificant effects on W 0 causing maximum differences of about 0.04 m2 s−2 in the final estimates (Fig. 3). The effects of the MSS are, by contrast, larger. The comparison between the W 0 values obtained after applying CLS11 and DTU10 reveals a constant offset of 0.30 m2 s−2. This can be understood as a difference of about 3 cm in the mean height of the models. In fact, after comparing both MSS models, positive differences larger than +10 cm in the Indian Ocean and the western equatorial part of the Pacific Ocean as well as negative differences less than −5 cm in the Tasman Sea and the Antarctic Ocean are found. The mean value of these discrepancies is +3.0 cm with a standard deviation ±7.3 cm. This could be attributable to differences in the processing of the altimetry data as well as in the corrections applied to each model; for more details about the computation of these models see: Andersen (2010) and Schaeffer et~al. (2012). In addition, as mentioned above, it is assumed that CLS11 refers to epoch 1996.0 and DTU10 to 2001.0, so it would be necessary to refer both sets of sea surface heights to the same epoch. To investigate this issue, a common date at 2005.0 was adopted; and results from both models were shifted to this date using the value of dW 0 /dt = −0.027 m2 s−2 year−1 from Dayoub et~al. (2012). Results show that the offset is reduced by almost 0.2 m2 s−2 (Fig. 4).

Fig. 4
figure 4

W 0 estimates after adding the oceanographic mean dynamic topography model ECCO2 to the sea surfaces models CLS11 and DTU10. (a) CLS11 at 1996.0 and DTU10 at 2001.0. (b) CLS11 and DTU10 at 2005.0. Value 62,636,800 m2 s−2 should be added

Full size image

The estimate also strongly depends on the latitudinal limits covered by the MSS. If the area is increased from φ = 60°N/S to φ = 80°N/S, W 0 changes by more than 1 m2 s−2 (cf. Sánchez 2007; Dayoub et~al. 2012). If the same experiment is done varying the limits from φ = 50°N/S to φ = 84°N/S, it is evident that the largest influence on W 0 from the data coverage is happening between φ = 50°N/S and φ = 70°N/S, while after φ = 70°N/S the change becomes less noticeable (Fig. 4). Following Dayoub et~al. (2012), the sea surface heights included in the models CLS11 and DTU10 were reduced by the MDT values of the ECCO2 model (Menemenlis et~al. 2008). This considerably decreases the W 0 dependence on the latitudinal coverage (Fig. 4).

Table 1 Summary of the W 0 estimates delivered by the four groups working on the W 0 determination in the frame of the JWG 0.1.1
Full size table

Concluding Remarks and Outlook

The W 0 estimations obtained by the four groups in this first attempt are very similar (Table 1), especially those values based on the same models and the same latitudinal coverage (cf. estimations of the Bratislava, Latakia and Munich groups). However, there are discrepancies of about 0.5 m2 s−2, which can be caused by the usage of different MSS models (cf. values of the Prague Group with the others in Table 1). To evaluate if these differences are significant, the next step is to perform a formal error propagation analysis that allows us to establish the uncertainty in W 0. In parallel, it is necessary to start selecting some conventions for a formal recommendation on W 0. To do this, some open questions that need to be answered first are listed in the following:

  • The Gaussian definition for the geoid is based on the sea surface sampled globally. At present, we are restricted to the range of the satellite altimetry measurements (i.e. φ = ∼82°N/S). Under this perspective—should the polar regions be integrated in the W 0 computation?

  • The sea surface should be quasi-stationary, i.e., it should not show any significant temporal variations detectable in the satellite altimetry data. Normally, most of these effects (tides, sea state bias, etc.) are reduced, but how should the seasonal variations be considered, especially those generated by the sea ice cycle and glaciations and melting effects in the polar regions?

  • The precision of the satellite altimetry data degrades in coastal areas. Should they be excluded from the global W 0 computation? If not, how can their reliability be improved?

  • The continental surfaces can be considered, together with the sea surface, as a part of the known boundary surface in the solution of the geodetic boundary value problem. Can the existing topography surface models refine/improve the W 0 computation?

  • Since both the Earth’s surface and gravity field vary with time, should W 0 also be defined to vary with time? Which strategy should be followed to estimate the variation of W 0 through time? How should the reference epoch be appointed and how often should the datum be updated?

  • Which tide system should be selected for the W 0 realisation?

Independently of the answers to these questions, it is clear that the potential value U 0 of the GRS80 ellipsoid and the W 0 value included in the IERS conventions differ considerably from the recent W 0 computations: the former corresponds to an equipotential surface located about 67 cm beneath the sea surface scanned by satellite altimetry, while the latter is located about 17 cm lower. Although any of these values could be introduced as a vertical reference level (as could any other value), the reliability of their realisation cannot be guaranteed, since the most recent geodetic models describing the geometry and physics of the Earth yield other values. In this respect, the need to provide a new “better estimate” of W 0 is urgent.