Feed-Forward Control Designs

Abstract

In contrast to Chap. 6 on feedback control, this chapter is focused on feed-forward control design. These designs focus on either gust load or maneuver load alleviation, respectively. The first section presents a convex synthesis of a conceptual, triggered finite-impulse response (FIR) gust load alleviation system, while the second section develops a maneuver load alleviation system for lateral command response based on convex synthesis. The last section focuses on a full-information $\fancyscript{H}_{\infty }$-design for maneuver loads alleviation for the longitudinal direction.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Gust Loads Alleviation System Via Convex Optimization

T. Haniš and M. Hromčík

The potential advantages of blended wing body (BWB) aircrafts in terms of fuel efficiency are opposed by technical challenges such as the alleviation of gust loads. Due to low wing loading, gusts generally have a more severe impact on BWB aircraft than on conventional aircraft wing tube aircraft. This section presents the design and optimization of a gust load alleviation system (GLAS) for a large BWB airliner. Numerical simulations are performed with an aeroelastic model of the initial aircraft model created within the NACRE project including GLAS in order to compute time series of modal displacements for deriving equivalent static load cases which are used for resizing of the aircraft structure. This design is carried out in this section is carried out for the 750-passenger NACRE BWB aircraft predesign model. The same methodology has been shown and carried out on the ACFA BWB configuration in [22].

Remark: Note that the scope of the $\fancyscript{L}_{\infty }$-optimization of gust load alleviation in this context can only be utilized to verify feasibility of a GLAS for the given aircraft. The resulting controller is not directly applicable for implementation on an aircraft—this requires certification criteria such as the CS-25 “continuous turbulence design criteria” to be carefully addressed which is out of scope in this design and in the context of the ACFA 2020 project in general.

1.1 Introduction

The coupled aeroelastic/flight mechanic BWB model used for this investigation is parameterized in Mach, dynamic pressure, fuel mass, and center of gravity (CG) position. The CG variation is achieved by fuel redistribution which is important on a BWB airplane for trim without too large control surface deflections in order to achieve optimum cruise performance. For some fuel configurations the BWB airliner is statically unstable, thus requiring artificial stabilization. The BWB airliner is controlled/stabilized by an underlying feedback control system using trailing edge flaps (see Chap. 6 for details on feedback control laws design). The elevators and spoilers on the upper side of the wings are used for feed-forward control. On each wing, the three inner spoilers are actuated simultaneously, and the three outer spoilers are actuated simultaneously as well. The control commands by the feed-forward GLAS are added to the commands computed by feedback flight control laws. Taking into account maneuver load alleviation, gust loads become the dominant sizing factor. For efficient gust load alleviation, the weighted $\fancyscript{L}_{\infty }$ norm of the responses of wing bending and torsion moment need to be minimized for gusts of different scale lengths throughout the whole flight envelope while not exceeding maximum and minimum load factors. The worst-case gust length of a particular flight condition will be taken into account, but augmentation of the optimization for more gust lengths and operating points is straightforward.

Fig. 7.1

GLAS setup

1.2 Gust Load Alleviation System Design

The GLAS (see Fig. 7.1) is based on a triggered feed-forward control system for attenuation of aircraft excitation $\mathbf d (t)$ by exogenous disturbance signal $w(t)$, in our case wind gust of $1 - \cos$ shape. Design of the wind gust detection system itself, the trigger, is not treated here. It is assumed that it is possible to estimate an upcoming wind gust and its direction with a certain time delay needed for estimation. The reference signal $\alpha _\mathrm {wind}$ is then the triggering signal used as input for the GLAS feed-forward controller $H(s)$ and it is considered as a unit step signal. The GLAS $H(s)$ can be realized as a FIR shaping input (step) command $\alpha _\mathrm {wind}$ and producing control signals $\mathbf u _\mathrm {GLAS}$, or as a memory storing device containing the control signals sequences $\mathbf u _\mathrm {GLAS}$ and putting them out once triggered by $\alpha _\mathrm {wind}$. The effect of $\mathbf u _\mathrm {GLAS}$ on $\mathbf e (t)$ is expressed as a response of the transfer function $G_\mathrm{c}(s)$, the so-called Secondary Control Path (SCP). Considering a model of the aircraft linearized in a certain trim point, the error signal $\mathbf e (t)$ is just the sum of aircraft response $\mathbf d (t)$ to wind gust disturbance $w(t)$ and response of the aircraft to the GLAS control command $\mathbf u _\mathrm {GLAS}$. The error signal $\mathbf e (t)$ contains the wing bending and torsion moments and shear forces at wing cuts, as well as the incremental load factor $\Delta n_z(t)$. The design objective is to choose $H(s)$ in order to minimize the $\fancyscript{L}_{\infty }$ norm of a criterion based on forces and moments as will be explained later, keep $\Delta n_z(t)$ within certain limits (for passenger safety), and at the same time remain within various limits for the $\fancyscript{L}_{\infty }$ norm of $\mathbf u _\mathrm {GLAS}(t)$, that is, considering the saturation of control surfaces. The control surfaces used for the GLAS are the elevator $u_\mathrm {Elevator}$ and the spoilers $u_\mathrm {Spoiler}$. The vector of control commands $\mathbf u _\mathrm {GLAS}(t)$ thus can be written as:

$$\begin{aligned} \mathbf u _\mathrm {GLAS}(t) = \left[ u_\mathrm {Elevator}(t),\ u_\mathrm {Spoiler}(t) \right] ^\mathrm {T}\end{aligned}$$

(7.1)

where $u_\mathrm {Elevator}$ is elevator control command and $u_\mathrm {Spoiler}$ denotes spoilers command.

1.3 Convex Synthesis

The convex synthesis approach is exploited to design the control law. This methodology described by [2, 4], can easily address both time- and frequency-domain criterions and constraints. A nice overview and aircraft control specific designs can be found in [7].

The generalized plant in Fig. 7.2 is considered. Therein, system $P$ represents the controlled plant, $K$ is the feedback control law and $H$ is the feed-forward control system. The signals $w$ and $z$ are exogenous input signals and controlled (criterion) output signals, respectively. Signals $u_\mathrm {FF}$ and $u_\mathrm {FB}$ are input signals actuated by feed-forward and feedback control systems. The signals $y$ and $u_\mathrm {ref}$ are the measurable output signals and the reference signal for the feed-forward control system, respectively.

Fig. 7.2

Convex synthesis design plant

The convex synthesis methodology can be applied for both feedback and feed-forward control system design. Nevertheless, only the feed-forward control system design will be addressed in this section. The feedback control law $K$ in Fig. 7.2 is considered as a fixed control law. The parameterization of the discrete-time feed-forward controller $H(z)$ is affine in the weights $\theta _i$,

$$\begin{aligned} H(z)=\sum ^{n}_{i=1} \theta _{i} \cdot H_{i}(z), \end{aligned}$$

(7.2)

where the transfer functions $H_{i}(z)$ are a priori fixed basis functions and scalars, $\theta _{i}$ for $i \ge 1$ are the decision variables of the optimization problem. The exogenous input signal $w(t)$ is considered as one case of a 1 $-\cos$-shaped gust (plotted in Fig. 7.3). The result of the optimization will be the FIR filter $H(z)$ (decision variables $\theta _{i}$ define the coefficients of such FIR filter), therefore the reference input signal $u_\mathrm {ref}$ is considered as a discrete unit pulse at time $t = 0$ as plotted in Fig. 7.4. The time-domain response of the feed-forward-controlled closed-loop system can be expressed by (7.3) in an affine form,

Fig. 7.3

Considered wind gust profile

Fig. 7.4

Reference input signal

$$\begin{aligned} z(t)=\theta _{0} \cdot z_{0}(t) + \sum ^{n}_{i=1} \theta _{i} \cdot z_{i}(t), \end{aligned}$$

(7.3)

where $z_{0}(t)$ is the response of the feed-forward-controlled closed-loop system for disturbance signal $w(t)$ (according to (7.4), plotted in Fig. 7.5). In this case the coefficient $\theta _{0}$ is equal to one. The second term corresponds to the response of closed-loop system (defined by (7.5), plotted in Figs. 7.6 and 7.7) for reference signal $u_\mathrm {ref}$ (in this case a discrete unit pulse) shaped by particular basis function $H_i(z)$ which are chosen to be unit delays so that $H(z)$ becomes a FIR filter by design.

Fig. 7.5

Mx response to wind gust input

$$\begin{aligned} Z_{0}(z)= P(z) W(z) \end{aligned}$$

(7.4)

$$\begin{aligned} Z_{i}(s)= P(z) H_{i}(z) U(z). \end{aligned}$$

(7.5)

Fig. 7.6

Mx responses to the Spoiler input

Fig. 7.7

Mx responses to the Elevator input

The correspondence between the time-domain and the $z$-domain is defined by

$$\begin{aligned} z_{i}(t)=Z^{-1} \left\{ Z_{i}(z)\right\} . \end{aligned}$$

(7.6)

Finally, the convex optimization task can be defined as a linear program with criteria expressed as:

$$\begin{aligned} \min _{\theta } c^\mathrm {T}\theta , \end{aligned}$$

(7.7)

and constraints:

$$\begin{aligned} A \theta \le b \end{aligned}$$

(7.8)

The criterion as well as constraints will be explained in detail in Sect. 7.1.4.

1.4 Formulation of the Optimization Problem

With sizing gusts of different lengths from $30\,\text {ft}$ ($9.14\,\text {m}$) to $500\,\text {ft}$ ($152.4\,\text {m}$) starting at time $t=0$ it was sufficient to fulfill the following constraints within a time interval $[0; t_\mathrm {end} 10\,\text {s}]$ since oscillations excited by gusts sufficiently diminish after that amount of time. First, only one length of a sizing wind gust case is considered to keep the definition simple and clear. The maximum and minimum control surface deflections need to be bounded by:

$$\begin{aligned} u_\mathrm {Elevator}(n)\ \le \ u_\mathrm {ElevatorMax},\quad \forall n \in \left[ 0;t_\mathrm {end} F_\mathrm {s}\right] \end{aligned}$$

(7.9)

$$\begin{aligned} u_\mathrm {Elevator}(n)\ \ge \ u_\mathrm {ElevatorMin},\quad \forall n \in \left[ 0;t_\mathrm {end} F_\mathrm {s}\right] \end{aligned}$$

(7.10)

$$\begin{aligned} u_\mathrm {Spoiler}(n)\ \le \ u_\mathrm {SpoilerMax},\quad \forall n \in \left[ 0;t_\mathrm {end} F_\mathrm {s}\right] \end{aligned}$$

(7.11)

$$\begin{aligned} u_\mathrm {Spoiler}(n)\ \ge \ u_\mathrm {SpoilerMin},\quad \forall n \in \left[ 0;t_\mathrm {end} F_\mathrm {s}\right] . \end{aligned}$$

(7.12)

With subscript $\mathrm {Max}$ denoting maximum allowed deflection of the respective control surface, and subscript $\mathrm {Min}$ denoting prescribed minimum allowed deflection of the respective control surface (maximal negative deflection). Control surface deflection rate ${\mathrm {d}u}/{\mathrm {d}t}$ needs to be limited because the available actuators’ energy is finite. Thereby, $F_\mathrm {s}$ is the sampling frequency, and $T_\mathrm {s} = {1}/{F_\mathrm {s}}$ denotes the sampling time of the discrete-time controller. Then rate limits of control surfaces are defined by:

$$\begin{aligned} \frac{u_\mathrm {Elevator}(n) - u_\mathrm {Elevator}(n-1)}{T_\mathrm {s}}\ \le \ \frac{\mathrm {d}u}{\mathrm {d}t}_{\mathrm {ElevatorMax}}, \quad \forall n \in \left[ 1;t_\mathrm {end} F_\mathrm {s}\right] \end{aligned}$$

(7.13)

$$\begin{aligned} \frac{u_\mathrm {Elevator}(n) - u_\mathrm {Elevator}(n-1)}{T_\mathrm {s}}\ \ge \ \frac{\mathrm {d}u}{\mathrm {d}t}_{\mathrm {ElevatorMin}}, \quad \forall n \in \left[ 1;t_\mathrm {end} F_\mathrm {s}\right] \end{aligned}$$

(7.14)

$$\begin{aligned} \frac{u_\mathrm {Spoiler}(n) - u_\mathrm {Spoiler}(n-1)}{T_\mathrm {s}}\ \le \ \frac{\mathrm {d}u}{\mathrm {d}t}_\mathrm {SpoilerMax}, \quad \forall n \in \left[ 1;t_\mathrm {end} F_\mathrm {s}\right] \end{aligned}$$

(7.15)

$$\begin{aligned} \frac{u_\mathrm {Spoiler}(n) - u_\mathrm {Spoiler}(n-1)}{T_\mathrm {s}}\ \ge \ \frac{\mathrm {d}u}{\mathrm {d}t}_\mathrm {SpoilerMin}, \quad \forall n \in \left[ 1;t_\mathrm {end} F_\mathrm {s}\right] \end{aligned}$$

(7.16)

For passenger safety, the maximum and the minimum load factors need to be bounded as well.

$$\begin{aligned} n_z(n)\ \le \ 2.5, \quad \forall n \in \left[ 0;t_\mathrm {end} F_\mathrm {s}\right] \end{aligned}$$

(7.17)

$$\begin{aligned} n_z(n)\ \ge \ 1, \quad \forall n \in \left[ 0;t_\mathrm {end} F_\mathrm {s}\right] . \end{aligned}$$

(7.18)

The cost function $J$ is defined as a function of the vector of control commands $\mathbf u _\mathrm {GLAS}(n)$ with tuning parameters $a_1, a_2, a_3$ and $b_1, b_2, b_3$. Considering that positive as well as negative peak forces and moments need to be reduced in magnitude, the cost function $J$ can by divided into two parts:

$$\begin{aligned} J_\mathrm {max}&= \max _{n\in \left[ 0,\ t_\mathrm {end} F_\mathrm {s} \right] } \left[ a_1\cdot \left( \sum ^{n}_{i=0} f^\mathrm {Gust}_{z}(i)\cdot w(n-i) + \sum ^{n}_{i=0} f^\mathrm {Elevator}_{z}(i) \cdot u_\mathrm {Elevator}(n-i)\right. \right. \nonumber \\&\qquad \qquad \qquad \qquad \qquad \quad \left. {} + \sum ^{n}_{i=0} f^\mathrm {Spoiler}_{z}(i) \cdot u_\mathrm {Spoiler}(n-i) \right) \nonumber \\&\qquad \qquad \qquad \qquad {} +a_2\cdot \left( \sum ^{n}_{i=0} m^\mathrm {Gust}_{x}(i)\cdot w(n-i) + \sum ^{n}_{i=0} m^\mathrm {Elevator}_{x}(i) \cdot u_\mathrm {Elevator}(n-i) \right. \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \left. {} + \sum ^{n}_{i=0} m^\mathrm {Spoiler}_{x}(i) \cdot u_\mathrm {Spoiler}(n-i) \right) \nonumber \\&\qquad \qquad \qquad \qquad {} +a_3\cdot \left( \sum ^{n}_{i=0} m^\mathrm {Gust}_{y}(i)\cdot w(n-i) + \sum ^{n}_{i=0} m^\mathrm {Elevator}_{y}(i) \cdot u_\mathrm {Elevator}(n-i) \right. \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \left. \left. {} + \sum ^{n}_{i=0} m^\mathrm {Spoiler}_{y}(i) \cdot u_\mathrm {Spoiler}(n-i) \right) \right] \end{aligned}$$

(7.19)

$$\begin{aligned} J_\mathrm {min}&= \min _{n\in \left[ 0,\ t_\mathrm {end} F_\mathrm {s} \right] }\left[ b_1\cdot \left( \sum ^{n}_{i=0} f^\mathrm {Gust}_{z}(i)\cdot w(n-i) + \sum ^{n}_{i=0} f^\mathrm {Elevator}_{z}(i) \cdot u_\mathrm {Elevator}(n-i)\right. \right. \nonumber \\&\qquad \qquad \qquad \qquad \qquad \quad \left. {} + \sum ^{n}_{i=0} f^\mathrm {Spoiler}_{z}(i) \cdot u_\mathrm {Spoiler}(n-i) \right) \nonumber \\&\qquad \qquad \qquad \qquad {} +b_2\cdot \left( \sum ^{n}_{i=0} m^\mathrm {Gust}_{x}(i)\cdot w(n-i) + \sum ^{n}_{i=0} m^\mathrm {Elevator}_{x}(i) \cdot u_\mathrm {Elevator}(n-i) \right. \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \left. {} + \sum ^{n}_{i=0} m^\mathrm {Spoiler}_{x}(i) \cdot u_\mathrm {Spoiler}(n-i) \right) \nonumber \\&\qquad \qquad \qquad \qquad {} +b_3\cdot \left( \sum ^{n}_{i=0} m^\mathrm {Gust}_{y}(i)\cdot w(n-i) + \sum ^{n}_{i=0} m^\mathrm {Elevator}_{y}(i) \cdot u_\mathrm {Elevator}(n-i) \right. \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \left. \left. {} + \sum ^{n}_{i=0} m^\mathrm {Spoiler}_{y}(i) \cdot u_\mathrm {Spoiler}(n-i) \right) \right] . \end{aligned}$$

(7.20)

Finally an overall criterion is defined as:

$$\begin{aligned} J = J_\mathrm {max} - J_\mathrm {min}. \end{aligned}$$

(7.21)

Thereby, $w(n)$ is the discrete-time gust excitation and $f^\mathrm {Gust}_z(i)$, $f^\mathrm {Elevator}_z(i)$, $f^\mathrm {Spoiler}_z(i)$ denote the $i$th sample of impulse responses of the linearized aircraft model to gust excitation, elevators inputs, and spoilers inputs, respectively. At selected wing cut, the respective $i$th sample of pulse responses for torsion moment are $m^\mathrm {Gust}_y(i)$, $m^\mathrm {Elevator}_y(i)$, $m^\mathrm {Spoiler}_y(i)$, and for bending moment $m^\mathrm {Gust}_x(i)$, $m^\mathrm {Elevator}_x(i)$, $m^\mathrm {Spoiler}_x(i)$. The static shear force, torsion moment, and bending moment for $1\,\text {g}$ level flight are not considered in this design.

The optimization problem can thus be formulated as:

$$\begin{aligned} \min _{u_\mathrm {Elevator},\ u_\mathrm {Spoiler}} J \end{aligned}$$

(7.22)

with constraints expressed by (7.9)–(7.18).

Fig. 7.8

Spoiler deflection signal

Fig. 7.9

Elevator deflection signal

Fig. 7.10

Spoiler deflection signal rate

Fig. 7.11

Elevator deflection rate

Fig. 7.12

Wing bending moment attenuation

Fig. 7.13

Wing torsional moment attenuation

Fig. 7.14

Vertical acceleration at the center of gravity

1.5 Gust Load Alleviation System: Results

Simulations of the resulting feed-forward control system are presented in this section. The deflections of spoilers and elevator commanded by the triggered GLAS are plotted in Figs. 7.8 and 7.9. One can see that maximal and minimal deflection constraints of each control surface are fulfilled.

Similarly, requirements for deflection rates of spoilers as well as elevators (plotted in Figs. 7.10 and 7.11) are taken into account during the optimization and fulfilled by the resulting control law. One can see that the deflection rate constraints are the limiting factor of the resulting control law and limit achievable control performance. The dynamic aircraft wing bending moment was reduced by more than 50$\,\%$ in the sense of the $\fancyscript{L}_{\infty }$ norm. The resulting structural load alleviation performance in wing bending is plotted in Fig. 7.12.

Similarly, the dynamic wing torsion moment was reduced by more than 60$\,\%$ in the $\fancyscript{L}_{\infty }$ norm sense. The resulting structural load alleviation performance in wing torsion is plotted in Fig. 7.13. Eventually the vertical acceleration response is presented in Fig. 7.14. One can see that also the constraints for vertical acceleration are fulfilled.

2 Lateral Maneuver Loads Alleviation System Via Convex Optimization

A. Schirrer and M. Kozek

In this section, a maneuver load alleviation system is designed for the ACFA BWB configuration by a convex synthesis approach. The feed-forward design can directly be cast into a convex optimization problem and is thus efficiently solvable. Its development is based on the multi-model feed-forward design developed for the NACRE BWB 750-passenger aircraft model, published in [16].

2.1 Design Goals and Problem Definition

The control goals related to Maneuver loads alleviation are most effectively addressed via a dynamic pilot command preshaper (feed-forward control law) once the closed-loop system is designed and conditioned (robustified) sufficiently well. The closed-loop plants obtained by earlier control designs are then utilized as design plants for the feed-forward design. This control design stage has the following goals:

• Given a step input roll angle reference signal, drive the system such that a decoupled roll maneuver with the given end angle is flown.

• Mach and dynamic pressure are assumed measurable and available for controller scheduling. The design task will be reduced to designs for fixed values of the Mach and dynamic pressure parameters and the same set of basis functions will be used across all designs so that only numerator coefficients need to be scheduled/interpolated a posteriori.

• The CG and Fuel parameters are considered unknown during operation and thus the controller should yield satisfactory responses for all CG/Fuel cases.

• The following requirements on the response shape must be fulfilled robustly:

  • Average static gain (DC gain) from roll reference to roll angle equal to 1 over all CG/Fuel cases.

  • Fulfill roll rise time requirement to $95\,\%$ rise level in 7 s.

  • No or minimal overshoot (less than $1\,\%$) in the roll reference response.

  • Decoupling: restrict side-slip response $\beta$ to $\pm 10\,\text {mrad}$ for a $1\,\text {rad}$ roll step.

  • For a 60° roll step, all rate and deflection bounds of the control surfaces have to hold. The deflection bounds for Flap 5 (outer aileron) are reduced to $50\,\%$ in order to retain controllability for the One-Engine-Inoperable case.

• The sizing loads with respect to the roll maneuver (that is, the maximum total loads occurring in a shaped 60° roll maneuver over all parameter cases) should be minimized.

2.2 Methodology

2.2.1 Linear Matrix Inequalities (LMIs)

An Linear Matrix Inequality (LMI) problem is a convex optimization problem commonly used in control design (see [3]) as:

$$\begin{aligned} \inf _\mathbf{x }{\left( \mathbf c ^\mathrm {T}\mathbf x \right) } \end{aligned}$$

(7.23)

$$\begin{aligned} \text{ s.t. }\ \ \mathbf F (\mathbf x ) = \mathbf F _0 + \sum _{i=1}^{n}{x_i \mathbf F _i} \succeq 0. \end{aligned}$$

(7.24)

The matrices $\mathbf F _i = \mathbf F _i^\mathrm {T}\in \mathbb {R}^{n \times n}$ are symmetric and fixed, $\mathbf x = [x_1, \ldots , x_n]^\mathrm {T}$ are the decision variables, and $\mathbf c ^\mathrm {T}$ is the cost vector. The constraint $\mathbf F (\mathbf x ) \succeq 0$ means that the matrix $\mathbf F (\mathbf x )$ be positive-semidefinite, that is, that it possesses only non-negative eigenvalues.

2.2.2 Convex Control Design

With a plant transfer function (or, time-domain response signals) parameterized in affine form,

$$\begin{aligned} \mathbf G (s)&= \mathbf G _0(s) + \sum _{i}\mathbf{G _i(s) \theta _i}, \end{aligned}$$

(7.25)

as in the case of a feed-forward design or the Youla-parameterized convex feedback control design, important time- and frequency-domain requirements can be stated as linear programing (LP), quadratic programing (QP), or Linear Matrix Inequality (LMI) constraints (convex in the parameters $\varvec{\uptheta }$), see [6]. Similarly, by bounding a constraint by an additional free variable instead of a constant, any such constraint can be turned into an objective. Then, the bounding variable itself is considered as the minimizing objective.

2.2.2.1 Time-Domain: Single-Input Single-Output (SISO) $\fancyscript{L}_{\infty }$ Bounds

A central benefit of convex synthesis methods is the direct incorporation of time-domain constraints and objectives, which enables template-based step-response shaping. Closed-loop time-domain responses are affine in $\varvec{\uptheta }$:

$$\begin{aligned} z(t)&= \fancyscript{L}^{-1}\left\{ \mathbf Z (s)\right\} = z_0(t) + \sum _{i=1}^{n}{z_i(t)\theta _i}. \end{aligned}$$

(7.26)

To constrain a time-domain response $z(t)$ by given lower and upper time-domain bounds $z_\mathrm {L}(t_k) < z(t_k) < z_\mathrm {U}(t_k)$, $t_k \in \{t_1, \ldots , t_N\}$, the expansion into the affine form yields two linear programing (LP)-type constraints for each $t_k$:

$$\begin{aligned} \left[ \begin{array}{ccc}-z_1(t_k),&\ldots ,&-z_n(t_k)\end{array}\right] \varvec{\uptheta }&< z_0(t_k) - z_\mathrm {L}(t_k),\end{aligned}$$

(7.27)

$$\begin{aligned} \left[ \begin{array}{ccc}\ \ z_1(t_k),&\ldots ,&\ \ z_n(t_k)\end{array}\right] \varvec{\uptheta }&< z_\mathrm {U}(t_k) - z_0(t_k). \end{aligned}$$

(7.28)

Note that (7.27)–(7.28) also represent two (scalar) LMI constraints and can directly be included in an LMI problem.

2.2.2.2 Frequency-Domain: Multi-input Multi-output (MIMO) $\fancyscript{H}_{\infty }$ Bound

The constraint $\left\| \mathbf G \right\| _\infty < x$ can be discretized for a stable $\mathbf G ({j}\omega )$ at a frequency grid $\omega _k \in \{\omega _1,\ldots ,\omega _N\}$ via $N$ constraints $\bar{\sigma }(\mathbf G ({j}\omega _k)) < x$. These can be translated into (real-valued) LMI constraints:

$$\begin{aligned} \left. \left[ \begin{array}{cccc}x\mathrm{I}&{}\mathrm{Re }(\mathbf G )&{}\mathbf 0 &{}\mathrm{Im }(\mathbf G )\\ &{}x\mathrm{I}&{}\mathrm{Im }(\mathbf G ^{\mathrm {H}})&{}\mathbf 0 \\ &{}&{}x\mathrm{I}&{}\mathrm{Re }(\mathbf G )\\ \mathrm {sym.}&{}&{}&{}x\mathrm{I}\end{array}\right] \,\right| _{{j}\omega _k}&\succ 0, \end{aligned}$$

(7.29)

where $\mathrm{Re }(\cdot )$, $\mathrm{Im }(\cdot )$, and $(\cdot )^{\mathrm {H}}$ indicate the real part, imaginary part, and the Hermitian transpose, respectively. This LMI is affine in the parameters (see [6, 15]). Note that this constraint asserts $\mathbf G$ stable a priori and is thus not applicable to enforce stability of $\mathbf G$.

2.2.2.3 Frequency-Domain: MIMO $\fancyscript{H}_{2}$ Bound

The $\fancyscript{H}_{2}$ norm of a stable, strictly proper linear dynamic system $\mathbf G ({j}\omega )$ is

$$\begin{aligned} \left\| \mathbf G ({j}\omega )\right\| _2 = h&= \sqrt{\frac{1}{2\uppi } \int \limits _{-\infty }^{\infty }{\text {tr}{\left[ \left( \mathbf G ({j}\omega )\right) ^{\mathrm {H}}\left( \mathbf G ({j}\omega )\right) \right] }\mathrm {d}\omega }}. \end{aligned}$$

(7.30)

For a sufficiently fine and broad finite frequency gridding, (7.30) can be approximated by the Riemann sum

$$\begin{aligned} h&\cong \widetilde{h} = \sqrt{\frac{1}{\uppi } \sum _{k=1}^{N}{\text {tr}{\left[ \left( \mathbf G ({j}\omega _k)\right) ^{\mathrm {H}}\left( \mathbf G ({j}\omega _k)\right) \right] }(\omega _{k+1}-\omega _k)}}. \end{aligned}$$

(7.31)

This $\fancyscript{H}_{2}$ norm approximation can be expanded to a (convex) quadratic form for $\mathbf G$ affine in $\varvec{\uptheta }$ ($\beta \in \mathbb {R}$, $\varvec{\upgamma } = [\gamma _1, \ldots , \gamma _n]^\mathrm {T}\in \mathbb {R}^n$, $\varvec{\Gamma } = [\Gamma _{i,j}] \in \mathbb {R}^{n \times n}$):

$$\begin{aligned} \mathbf G ({j}\omega _k)&= \mathbf G _k = {\widetilde{{\varvec{G}}}}_k + \sum _{i=1}^{n}\mathbf{G _{ki}\theta _{i}},\end{aligned}$$

(7.32)

$$\begin{aligned} {\widetilde{h}}^{2}&= \frac{1}{\uppi }\left( \beta + \varvec{\upgamma }^\mathrm {T}\varvec{\uptheta } + \varvec{\uptheta }^\mathrm {T}\varvec{\Gamma } \varvec{\uptheta }\right) , \end{aligned}$$

(7.33)

$$\begin{aligned} \beta = \sum _{k=1}^{N}{\text {tr}{\left[ {\widetilde{\mathbf{G }}_k}^{\mathrm {H}}\widetilde{\mathbf{G }}_k\right] }},\quad \gamma _i = \sum _{k=1}^{N}{2\mathrm{Re }\left\{ \text {tr}{\left[ {\widetilde{\mathbf{G }}_k}^{\mathrm {H}}\mathbf G _{ki}\right] }\right\} }, \end{aligned}$$

$$\begin{aligned} \Gamma _{i,j} = \sum _{k=1}^{N}{\mathrm{Re }\left\{ \text {tr}{\left[ \mathbf{G _{ki}}^{\mathrm {H}}\mathbf G _{kj}\right] }\right\} }. \end{aligned}$$

Note that only real terms remain due to the properties of the trace and the Hermitian transpose. The matrix $\varvec{\Gamma }$ is positive (semi-)definite, making the function $\widetilde{h}^2(\varvec{\uptheta })$ convex, and $\varvec{\Gamma }$ can be decomposed into its Cholesky factors $\varvec{\Gamma } = \mathbf L ^\mathrm {T}\mathbf L$. Then, an LMI constraint equivalent to $\tilde{h}^2 < x$ ($x \in \mathbb {R}^{+}$) is given as (see [17])

(7.34)

Note that this constraint is of fixed size ($(n+1) \times (n+1)$) with respect to the frequency grid size $N$, which allows to use high approximation precision by a fine grid in the precalculation of $\beta$, $\varvec{\upgamma }$, and $\varvec{\Gamma }$.

2.2.2.4 Adaptive Constraint Refinement

The optimization problem size is primarily determined by the number of basis functions (and thereby weighting parameters) and by the number of gridpoints in time or frequency at which point-wise constraints (or objectives) are defined. An adaptive grid refinement procedure has thus been implemented for high computational efficiency:

• 1. Start with coarse design grids.

• 2. Formulate and solve optimization problem (7.23)–(7.24) for the current design grids.

• 3. Validate the solution on fine validation grids.

• 4. Pick, per violated objective/constraint, at most $n_\mathrm {add}$ points that are most violated (and mutually sufficiently spaced) and add them to the design grids.

• 5. If no violations: done. Else: return to step (2).

2.3 Control Design

2.3.1 Reference Control Law Design

To formulate the load minimization criterion, a reference control law is necessary to obtain an initial feed-forward law that shapes the response to approximately fulfill the posed requirements. This task has been helped by the sensible shaping of the closed loop in the initial control design (by partial eigenstructure assignment, see Sect. 6.2). The dominant rigid-body (RB) poles already partially fulfill the response shape requirements.

Fig. 7.15

Two interconnection architectures of a (possibly scheduled) feed-forward controller $\mathbf Q$ with feedback-controlled plant $\mathbf P$, a only directly affects the control input $u$, whereas b also modifies the measured signals fed to the feedback controller $K$

Figure 7.15 depicts a simple interconnection of the feed-forward controller $\mathbf K _{\mathrm {f{}f}}$ and the closed-loop plant. Thereby $\mathbf r = \begin{bmatrix} r_\phi \\ r_\beta \end{bmatrix}$ is the $(2\times 1)$ reference signal vector. A simple choice of reference control law is obtained as follows:

• Compute the optimal $(2 \times 2)$ static decoupling coefficient matrix $\widetilde{\mathbf{K }}_{{\mathrm {f{}f}}} = \begin{bmatrix}k_{11}&k_{12}\\k_{21}&k_{22}\end{bmatrix}$ that minimizes the following objective function:

  $$\begin{aligned} J = \sum _{j_{\mathrm {CG}}, j_{\mathrm {Fuel}}}{\left\| \mathbf{I }-\mathbf{G }_{{\mathrm {cl}},j_{{\mathrm {CG}}}, j_{{\mathrm {Fuel}}}}({j}0)\widetilde{\mathbf{K }_{{\mathrm {f{}f}}}}\right\| }, \end{aligned}$$

  (7.35)

  where $\mathbf{G }_{{\mathrm {cl}},j_{{\mathrm {CG}}}, j_{{\mathrm {Fuel}}}}$ is the closed-loop transfer function of the aircraft for the parameter cases $j_{{\mathrm {CG}}}$ and $j_{{\mathrm {Fuel}}}$ ($j_{{\mathrm {Mach}}}$ and $j_{{\mathrm {Dyn.Pressure}}}$ are fixed for the studied design) from $\mathbf{u } = \begin{bmatrix}\delta _{\mathrm {Fl34}}\\ \delta _{\mathrm {Ru}}\end{bmatrix}$ to $\mathbf{z } = \begin{bmatrix}\phi \\ \beta \end{bmatrix}$ (see Fig. 7.15). The reference feed-forward law acts only on $\mathbf{u }$, so $\mathbf{Q }_{\mathrm {ref}} = \begin{bmatrix}\mathbf{Q }_{{\mathrm {ref},1}}\\ \mathbf{Q }_{{\mathrm {ref}},1}\end{bmatrix} = \begin{bmatrix}\mathbf{Q }_{{\mathrm {ref}},1}\\ \mathbf{0 }\end{bmatrix}$.

• Add PT1 filters to fulfill control command rate limits in the 60° roll maneuver:

  $$\begin{aligned} \mathbf{Q }_{{\mathrm {ref}},1} = \widetilde{\mathbf{K }_{{\mathrm {f{}f}}}}\begin{bmatrix}\frac{1}{Ts+1}&0\\0&\frac{1}{Ts+1}\end{bmatrix} \end{aligned}$$

  (7.36)

  The time constant was chosen $T = 1\,\text {s}$ which does not violate the rate limits and leads to a rise level of $90 \ldots 95\,\%$ in $7\,\text {s}$ in the roll reference–roll transfer function.

This reference law is used to compute the preliminary sizing total loads and parameter cases for the roll maneuver.

2.3.2 Feed-Forward Design by Convex Optimization

The optimization problem is formulated and solved by the LP/LMI control design optimization framework developed in [15].

The structure depicted in Fig. 7.15 has been utilized to design the feed-forward controller $\mathbf Q (s)$ by convex optimization. The closed-loop is comprised of the aircraft model (plant $\mathbf P$) and the combined control law $\mathbf K$ of stage 1 (initial feedback-controlled plant via partial eigenstructure assignment, see Sect. 6.2) and stage 2 (robust controller obtained by DGK-iteration, see Sect. 6.3).

The feed-forward law has one input (the roll reference $\phi _\mathrm {ref}$) and access to an extended set of nine separate outputs

$$\begin{aligned} \mathbf u _\mathrm {ext} = \begin{bmatrix}\Delta \delta _\mathrm {Fl3},&\Delta \delta _\mathrm {Fl4},&\Delta \delta _\mathrm {Fl5},&\Delta \delta _\mathrm {Ru},&\Delta \beta ,&\Delta \phi ,&\Delta p,&\Delta r,&\Delta Nz_\mathrm {lat.law}\end{bmatrix}^\mathrm {T}\!. \end{aligned}$$

(7.37)

The control law $\mathbf Q$ is obtained as weighted sum of basis functions $\mathbf Q _i(s)$:

$$\begin{aligned} \mathbf Q (s) = \sum _{i=1}^{n_Q}\mathbf{Q _i(s)\theta _i} \end{aligned}$$

(7.38)

This basis is composed of 20 basis functions per SISO channel which were chosen ad hoc as PT1 and PT2 dynamics with their poles evenly distributed in the dynamic range of interest. Note that the same basis is utilized for all feed-forward designs across the parameter range to facilitate a posteriori scheduling on the flight parameters.

The current optimization problem can then be formulated as an LP problem as follows:

$$\begin{aligned} \text{ minimize } \mathbf c ^\mathrm {T}\mathbf x \end{aligned}$$

(7.39)

$$\begin{aligned} \text{ subject } \text{ to } \mathbf A \mathbf x \le \mathbf b \end{aligned}$$

(7.40)

where the cost vector $\mathbf c$ and the constraints are obtained automatically by the optimization framework, based on an adaptive invocation of time-domain constraints and objectives on the closed loop. The vector of decision variables $\mathbf{x }$ contains the feed-forward control law weights $\theta _i$ as well as bound variables to formulate signal or system norm objectives (see Sect. 7.2.2.2).

These objectives and constraints are listed in Table 7.1 and closely related to those listed in Chap. 5. They are defined for each fuel and each CG case (31 cases) in the optimization framework and iteratively added to the actual LP formulation until the full validation on all parameter cases and on a fine time gridding ($T_\mathrm {s} = 0.05\,\text {s}$) is successful for all constraints and objectives. This method has shown to be highly efficient and enables a computationally feasible design for very large constraint sets (of which most constraints are inactive at the optimal solution, but have to be tested).

Table 7.1 Defined objectives and constraints for feed-forward design

The objective formulations are normalized with respect to the initial sizing loads (as obtained from the initial control law) in the following way:

Let $\overline{z}_{jk}$ be the preliminary sizing total load of load $j$ ($j \in \{Fz, Mx, My\}$) at cut $k$ ($k=1,\ldots ,14$). Also, let $z_{0,jk,\mathrm {cfmq}}$ be the corresponding trim (static/$1\,\text {g}$) load at CG case $\mathrm {c}$, fuel case $\mathrm {f}$, Mach case $\mathrm {m}$, and dynamic pressure case $\mathrm {q}$. Then, the allowed lateral dynamic load in this parameter case until sizing is

$$\begin{aligned} z_{\mathrm {dyn,max,}jk,\mathrm {cfmq}} = \left| \overline{z}_{jk}\right| - \left| z_{0,jk,\mathrm {cfmq}}\right| . \end{aligned}$$

(7.41)

This quantity is utilized to scale the objective such that an objective value of $1$ means that the load becomes globally sizing and thus this normalization introduces global information into the local optimization problem. The actual optimization objective is the maximum of all scaled control objectives, so an objective function value of less than $1$ means that the linear validation of the roll maneuver generates total loads which are less than the sizing loads.

2.3.3 Obtaining a Scheduled Control Law Using the Multi-stage Design Procedure

The multi-staged control law design allows one to employ direct a posteriori interpolation methods, specifically tailored to the partial control law at each stage.

In the scope of the lateral ACFA control design, the following interpolation onsets are utilized:

• The 1st-order “stage 1” control law (partial eigenstructure assignment, see Sect. 6.2) is parameterized in Mach number and dynamic pressure. Because of its low dynamic complexity, it can be transformed to a unique controllability companion form and a well-defined element-wise interpolation of the state-space system in this representation can be performed.

• The 30th-order “stage 2” control law (DGK-iteration, see Sect. 6.3) is of low authority and robust against considerable plant dynamics variations. Validation of the fixed control law with plants and the scheduled stage 1 control law across the entire flight envelope shows Robust Stability (RS). However, the added performance in terms of vibration attenuation at the design case at cruise flight conditions becomes marginal or lost as the plant parameters differ too much. This could be repaired by redesigns of the “stage 2” control law in other flight parameter points, but due to the associated effort this is out of scope here. For a posteriori scheduling onsets refer to [14, 15].

• The feed-forward control law developed in this section is robustly designed for a particular Mach and Dynamic Pressure parameter case to provide Robust Performance (RP) for all fuel and CG cases. It turned out that it is necessary to parameterize the feed-forward control law by the Mach and Dynamic Pressure parameters to achieve the demanded high performance. This interpolation can also be done in an a posteriori manner and it is simplified by utilizing the same set of basis functions for all designs. Then, only the optimization variables (the weightings $\theta _i$) need to be interpolated. The optimization problem can directly be extended to consider multiple models with perturbed Mach and Dynamic Pressure parameters, however, increasing the size of the problem. Note also that the feed-forward law cannot destabilize the (linear) aircraft model.

2.4 Validation

The optimization is carried out and yields a dynamic controller $\mathbf Q (s)$ which satisfies all constraints and minimizes the roll maneuver-induced total loads with respect to sizing load levels. As a result, a typical optimization result for loads alleviation is shown in Fig. 7.16 for a representative case in cruise flight conditions and cut moment $My_{13}$. In this maneuver, all constraints (tracking, rise time, settling, undershoot) on the roll response, side-slip decoupling and input magnitudes and rates are satisfied. As an example, the roll response and the demanded template are shown in Fig. 7.17 for the same parameter case.

Fig. 7.16

Typical loads reduction result (selected parameter case at cruise flight conditions at cut $My_{13}$) for an optimal feed-forward controller satisfying all roll maneuver requirements robustly

Fig. 7.17

Typical roll tracking performance for an optimal feed-forward controller (selected parameter case at cruise flight conditions)

Note that this specific formulation of the objective allows uncritical loads to increase in favor of further reduction in the critical load levels, which is correct for the considered global optimization goal.

The final validation over the entire relevant parameter space is shown in Sect. 8.1.4.

3 Maneuver Loads Alleviation System Via $\fancyscript{H}_{\infty }$ Full-Information Feed-Forward Design

C. Westermayer, A. Schirrer and M. Kozek

The design methodology for the feed-forward controller presented in the following is based on the so-called two degree of freedom (2DOF) concept. The fundamentals of this concept can be found in [18, 23], where the separation of feedback and feed-forward controllers is introduced by the use of two stable Youla parameters. While in the literature various approaches based on the 2DOF concept are reported [5, 8, 10, 13], the feed-forward control design approach shown here is based on the findings in [11, 12]. Therein, an $\fancyscript{H}_{\infty }$ full-information approach is presented for both, reference signal tracking and measurable disturbance rejection. The optimization problem is formulated as an LMI optimization problem and its applicability for the linear parameter varying (LPV) case is discussed. This design is carried out for the ACFA BWB configuration for the longitudinal dynamics. It has been developed in detail in [19] and published in [21].

Fig. 7.18

General 2DOF architecture

3.1 Methodology

3.1.1 2DOF Concept and Feed-Forward Design

Starting point of the presented design methodology is based on the fact that the design of feedback and feed-forward controller can be decoupled. This is demonstrated in [9, 12] for the general 2DOF control architecture as shown in Fig. 7.18 (left). Therein, the decoupling is revealed by splitting up the control signal into $\mathbf u = \mathbf K _\mathrm {f{}f}\mathbf r +\mathbf K _\mathrm {fb}\mathbf y$ and rewriting it in terms of two stable Youla parameters for parametrization and a right fractional coprime factorization of the system plant $\mathbf G$.

As indicated in the right diagram of Fig. 7.18, the input to the feedback controller $\mathbf K _{\mathrm {fb}}$ is the difference between the ideal system response provided by the prefilter or feed-forward controller $\mathbf K _\mathrm {f{}f}$ and the real measurements. The only input to $\mathbf K _\mathrm {f{}f}$ is the reference command, while its generated control signal is acting directly on the system $\mathbf G$. The independence of $\mathbf K _\mathrm {f{}f}$ from $\mathbf K _\mathrm {fb}$ enables self-contained focusing on design specifications most relevant for feed-forward control, which in terms of $\fancyscript{H}_{\infty }$ design and according to the Bounded Real Lemma is expressed by a performance path, where $\Vert \mathbf T \Vert _\infty \le \gamma$ is to be minimized. This is indicated in Fig. 7.19 where $\mathbf T _{zr}$ is obtained by a lower Linear Fractional Transformation (LFT) of the augmented plant $\mathbf P$ and the state feedback matrix $\mathbf F$.

Fig. 7.19

Generalized closed loop and optimization transfer function matrix $\mathbf T _\mathrm {zr}$ obtained by a lower LFT

Thereby, the augmented plant $\mathbf P$ has to be built such that the particular design specifications are met. $\mathbf P$ is again an interconnection of the system plant $\mathbf G$, frequency weightings $\mathbf W _{{i}}$ and additionally a reference model $\mathbf T _\mathrm {ref}$ to be tracked. Details on their formulation for the given problem will be presented in Sect. 7.3.3. It is important to note that according to Fig. 7.19 the feedback vector is composed of the state vector $\mathbf x _\mathrm {P}$ and the reference input vector $\mathbf r$. Both are assumed to be known which reasons the name full-information design.

3.1.2 Full-Information LMI Optimization Problem

Before the LMI optimization problem can be formulated, the closed-loop system has to be derived. Therefore, the open-loop representation

$$\begin{aligned} \left[ \begin{array}{c} \dot{\mathbf{x }}_\mathrm {P} \\ \mathbf z \\ \mathbf x _\mathrm {P} \\ \mathbf r \end{array} \right] = \underbrace{\left[ \begin{array}{ccc} \mathbf A _\mathrm {P} &{}\mathbf B _\mathrm {P_1}&{}\mathbf B _\mathrm {P_2}\\ \mathbf C _\mathrm {P_\mathrm {1}} &{}\mathbf D _\mathrm {P_\mathrm {11}}&{}\mathbf D _\mathrm {P_\mathrm {12}}\\ \mathbf I &{}\mathbf 0 &{}\mathbf 0 \\ \mathbf 0 &{}\mathbf I &{}\mathbf 0 \end{array}\right] }_\mathbf{P } \left[ \begin{array}{c} \mathbf x _\mathrm {P} \\ \mathbf r \\ \mathbf u \end{array} \right] \end{aligned}$$

(7.42)

and the full-information control law $\mathbf u =\mathbf F _\mathrm {1}\mathbf x +\mathbf F _\mathrm {2}\mathbf r$ have to be connected, yielding

$$\begin{aligned} \left[ \begin{array}{c} \varvec{\dot{x}}_{\mathrm {P}}\\ \mathbf z \end{array}\right] = \underbrace{\left[ \begin{array}{ccc} \mathbf A _\mathrm {P}+\mathbf B _\mathrm {P_2}\mathbf F _\mathrm {1}&{}\mathbf B _\mathrm {P_1} + \mathbf B _\mathrm {P_2}\mathbf F _\mathrm {2}\\ \mathbf C _\mathrm {P_\mathrm {1}}+\mathbf D _\mathrm {P_\mathrm {12}}\mathbf F _\mathrm {1}&{}\mathbf D _\mathrm {P_\mathrm {11}}+\mathbf D _\mathrm {P_\mathrm {12}}\mathbf F _\mathrm {2} \end{array}\right] }_\mathbf{T } \left[ \begin{array}{c} \mathbf x _{\mathrm {P}}\\ \mathbf r \end{array}\right] , \end{aligned}$$

(7.43)

where the static feedback matrix $\mathbf F =[\mathbf F _\mathrm {1}, \mathbf F _\mathrm {2}]$ was appropriately partitioned. With the closed-loop system defined, the procedure to derive the full-information optimization LMI is equivalent to a pure state feedback design. The finally obtained results are given by the following proposition.

Proposition 7.1

[12] Consider the system (7.43). If there exist matrices $\mathbf F _\mathrm {2}$, $\varvec{\bar{Y}}$ and $\varvec{\bar{Q}}=\varvec{\bar{Q}}^\mathrm {T}$, such that $\varvec{\bar{Q}}>0$ and

$$\begin{aligned} \left[ \begin{array}{ccc} \mathbf A _\mathrm {P}\varvec{\bar{Q}}+\varvec{\bar{Q}}\mathbf A _\mathrm {P}^\mathrm {T}+\mathbf B _\mathrm {P_2}\varvec{\bar{Y}}+\varvec{\bar{Y}}^\mathrm {T}\mathbf B _\mathrm {P_2}^\mathrm {T}&{}\mathbf B _\mathrm {P_1} + \mathbf B _\mathrm {P_2}\mathbf F _\mathrm {2}&{}(\mathbf C _\mathrm {P_\mathrm {1}}\varvec{\bar{Q}}+\mathbf D _\mathrm {P_\mathrm {12}}\varvec{\bar{Y}})^\mathrm {T}\\ (\mathbf B _\mathrm {P_\mathrm {1}}+\mathbf B _\mathrm {P_\mathrm {2}}\mathbf F _\mathrm {2})^\mathrm {T}&{}-\gamma \mathbf I &{}(\mathbf D _\mathrm {P_\mathrm {11}}+\mathbf D _\mathrm {P_\mathrm {12}}\mathbf F _\mathrm {2})^\mathrm {T}\\ \mathbf C _\mathrm {P_\mathrm {1}}\varvec{\bar{Q}}+\mathbf D _\mathrm {P_\mathrm {12}}\varvec{\bar{Y}}&{}\mathbf D _\mathrm {P_\mathrm {11}}+\mathbf D _\mathrm {P_\mathrm {12}}\mathbf F _\mathrm {2}&{}-\gamma \mathbf I \end{array}\right] <0 \end{aligned}$$

(7.44)

hold, then

• 1. the matrix $\mathbf A _\mathrm {P}$ is exponentially stable and

• 2. there exists a scalar $\gamma >0$ such that $||T_{zr}||_\infty < \gamma$ holds.

If a feasible solution is obtained, the optimal $\fancyscript{H}_{\infty }$ static full-information feedback matrix is given by:

$$\begin{aligned} \mathbf F _\mathrm {opt}=[\mathbf Y \mathbf Q ^{-1}, \mathbf F _\mathrm {2}]. \end{aligned}$$

(7.45)

An important fact is that the full-information LMI formulation of Proposition 7.1 can be extended to linear parameter varying systems $\mathbf G (\varvec{\rho })$ with system matrices $\mathbf A _\mathrm {G}(\varvec{\rho }),$ $\mathbf B _\mathrm {G}(\varvec{\rho }),$ $\mathbf C _\mathrm {G}(\varvec{\rho }),$ $\mathbf D _\mathrm {G}(\varvec{\rho })$ depending affinely on the parameter vector $\varvec{\rho }(t)$. However, for the given model of the BWB aircraft, a polytopic representation is not directly available, that is, the system matrices are not described as affine functions of the parameter vector from the outset.

3.1.3 Deriving the Final Feed-Forward Controller $\mathbf K _\mathrm {f{}f}$

The result of the LMI optimization according to Proposition 7.1 is the optimal feedback matrix $\mathbf F _\mathrm {opt}$. In order to obtain the final feed-forward controller $\mathbf K _\mathrm {f{}f}{}$, the output and feed-through matrices $\mathbf C _\mathrm {P_\mathrm {1}}$ and $\mathbf D _\mathrm {P_\mathrm {11}}$, $\mathbf D _\mathrm {P_\mathrm {12}}$ of the augmented plant $\mathbf P$ have to be replaced by [12]

$$\begin{aligned} \mathbf C _\mathrm {P_\mathrm {ff,1}} = \left[ \begin{array}{ccccc} \mathbf E \mathbf C _\mathrm {G}&{}\mathbf 0 &{}\mathbf 0 &{}\mathbf 0 &{}\mathbf 0 \\ \mathbf 0 &{}\mathbf 0 &{}\mathbf 0 &{}\mathbf 0 &{}\mathbf 0 \end{array}\right] ,\quad&\mathbf D _\mathrm {P_\mathrm {ff,11}} = \left[ \begin{array}{c} \mathbf 0 \\ \mathbf 0 \end{array}\right] ,\quad&\mathbf D _\mathrm {P_\mathrm {ff,12}} = \left[ \begin{array}{c} \mathbf E \mathbf D _\mathrm {G}\\ \mathbf I \end{array}\right] \end{aligned}$$

(7.46)

yielding

$$\begin{aligned} \mathbf P _\mathrm {f{}f} = \left[ \begin{array}{ccc} \mathbf A _\mathrm {P}&{}\mathbf B _\mathrm {P_1}&{}\mathbf B _\mathrm {P_2}\\ \mathbf C _\mathrm {P_\mathrm {ff,1}}&{}\mathbf D _\mathrm {P_\mathrm {ff,11}}&{}\mathbf D _\mathrm {P_\mathrm {ff,12}}\\ \mathbf I &{}\mathbf 0 &{}\mathbf 0 \\ \mathbf 0 &{}\mathbf I &{}\mathbf 0 \end{array}\right] . \end{aligned}$$

(7.47)

The index $\mathbf G$ refers to the system plant and the selector matrix $\mathbf E$ is used to select all outputs $\mathbf y$ used by the feedback controller $\mathbf K _\mathrm {fb}$. As evident from Fig. 7.20 the feed-forward controller is the result of the lower LFT

$$\begin{aligned} \mathbf K _\mathrm {f{}f}{}=\fancyscript{F}_{\mathrm {l}}(\mathbf P _\mathrm {f{}f},\mathbf F _\mathrm {opt}). \end{aligned}$$

(7.48)

Fig. 7.20

Modified generalized closed-loop including the optimal solution $\mathbf F _\mathrm {opt}$ (left) and final feed-forward controller $\mathbf K _\mathrm {f{}f}{}$ obtained by a lower LFT (right)

3.2 Design Goals and Problem Definition

The design specifications (as listed in Chap. 5) to be addressed in the feed-forward controller design process are given as follows:

• 1. Track the reference command input given by the vertical acceleration at the CG position $N\!z_{\mathrm {CG}}$. The rise time of $N\!z_{\mathrm {CG}}$ to a unit step command input must be between 3–5 s and no overshoot is tolerated.

• 2. Overshoot of accompanying pitch rate response at the CG position, $q_\mathrm {CG}$, must be lower than 30 %.

• 3. Constrain the demanded control signals by maximum deflection and deflection rate limits according to Table 5.1.

• 4. Minimize maximum structural loads caused by maneuver tracking. As reference maneuvers serve $+1.5$ and $-1.0\,\mathrm {g}$ $N\!z_{\mathrm {CG}}$ reference steps, where $\mathrm {g}=9.81~\mathrm{m/s}^{2}$.

All these specifications have to be fulfilled over the considered flight envelope. The performance of the designed controllers has to be demonstrated together with the feedback control law. Here, the LPV feedback control law from Sect. 6.5 is utilized.

3.3 Control Design

3.3.1 Design Architecture

The first step of the $\fancyscript{H}_{\infty }$ full-information feed-forward design process is to define an appropriate design architecture representing a standard problem formulation in the $\fancyscript{H}_{\infty }$ framework which addresses the essential design specifications. The augmented plant used in this work is shown in Fig. 7.21.

Fig. 7.21

Left augmented plant for feed-forward full-information control design; Right generalized closed loop

The performance weights $\mathbf W _u$, $\mathbf W _{y}$, and $\mathbf W _\mathrm {p}$ have to be appropriately chosen in order to enforce the desired performance during optimization. Details on these choices are given in Sect. 7.3.3.2. The systems $\mathbf G _\mathrm {f{}f}{}$, $\mathbf T _\mathrm {ref}{}$, $\mathbf W _u$, $\mathbf W _{y}$, and $\mathbf W _\mathrm {p}$ are given in state-space representation ($\mathbf A _i$, $\mathbf B _i$, $\mathbf C _i$, $\mathbf D _i$), where the index $i$ is used as placeholder for the aforementioned system names. Interconnecting these systems according to Fig. 7.21 leads to the augmented system $\mathbf P$ in state-space form

$$\begin{aligned} \left[ \begin{array}{c} \varvec{\dot{x}}(t)\\ \mathbf z (t)\\ \mathbf x (t)\\ r(t) \end{array}\right] = \underbrace{\left[ \begin{array}{c|cc} \mathbf A _\mathrm {P} &{}\mathbf B _\mathrm {P_1}&{}\mathbf B _\mathrm {P_2}\\ \hline \mathbf C _\mathrm {P_\mathrm {1}} &{}\mathbf D _\mathrm {P_\mathrm {11}}&{}\mathbf D _\mathrm {P_\mathrm {12}}\\ \mathbf I &{}\mathbf 0 &{}\mathbf 0 \\ \mathbf 0 &{}\mathbf I &{}\mathbf 0 \end{array}\right] }_\mathbf{P } \left[ \begin{array}{c} \mathbf x (t)\\ r(t)\\ \mathbf u (t) \end{array}\right] , \end{aligned}$$

(7.49)

where

$$\begin{aligned} \mathbf A _{\mathrm {P}} = \left[ \begin{array}{ccccc} \mathbf A _{\mathrm {G_{ff}}}&{}\mathbf 0 &{}\mathbf 0 &{}\mathbf 0 &{}\mathbf 0 \\ \mathbf B _{\mathrm {W_y}}\mathbf E _{\mathrm {1}}\mathbf C _{\mathrm {G_{ff}}}&{}\mathbf A _{\mathrm {W_y}}&{}\mathbf 0 &{}\mathbf 0 &{}-\mathbf B _{\mathrm {W_y}}\mathbf C _{\mathrm {T_{ref}}}\\ \mathbf 0 &{}\mathbf 0 &{}\mathbf A _{\mathrm {W_u}}&{}\mathbf 0 &{}\mathbf 0 \\ \mathbf B _{\mathrm {W_p}}\mathbf E _{\mathrm {2}}\mathbf C _{\mathrm {G_{ff}}}&{}\mathbf 0 &{}\mathbf 0 &{}\mathbf A _{\mathrm {W_p}}&{}\mathbf 0 \\ \mathbf 0 &{}\mathbf 0 &{}\mathbf 0 &{}\mathbf 0 &{}\mathbf A _{\mathrm {T_{ref}}}\\ \end{array}\right] , \end{aligned}$$

(7.50)

$$\begin{aligned} \mathbf B _{\mathrm {P_1}} = \left[ \begin{array}{c} \mathbf 0 \\ -\mathbf B _{\mathrm {W_{y}}}\mathbf D _{\mathrm {T_{ref}}}\\ \mathbf 0 \\ \mathbf 0 \\ \mathbf B _{\mathrm {T_{ref}}}\\ \end{array}\right] ,\quad&\mathbf B _{\mathrm {P_2}} = \left[ \begin{array}{c} \mathbf B _{\mathrm {G_{ff}}}\\ \mathbf B _{\mathrm {W_{y}}}\mathbf E _{\mathrm {1}}\mathbf D _{\mathrm {G_{ff}}}\\ \mathbf B _{\mathrm {W_{u}}}\\ \mathbf B _{\mathrm {W_{p}}}\mathbf E _{\mathrm {2}}\mathbf D _{\mathrm {G_{ff}}}\\ \mathbf 0 \\ \end{array}\right] , \end{aligned}$$

(7.51)

$$\begin{aligned} \mathbf C _{\mathrm {P_1}} = \left[ \begin{array}{ccccc} \mathbf D _{\mathrm {W_y}}\mathbf E _{\mathrm {1}}\mathbf C _{\mathrm {G_{ff}}}&{}\mathbf C _{\mathrm {W_y}}&{}\mathbf 0 &{}\mathbf 0 &{}-\mathbf D _{\mathrm {W_y}}\mathbf C _{\mathrm {T_{ref}}}\\ \mathbf 0 &{}\mathbf 0 &{}\mathbf C _{\mathrm {W_u}}&{}\mathbf 0 &{}\mathbf 0 \\ \mathbf D _{\mathrm {W_p}}\mathbf E _{\mathrm {2}}\mathbf C _{\mathrm {G_{ff}}}&{}\mathbf 0 &{}\mathbf 0 &{}\mathbf C _{\mathrm {W_p}}&{}\mathbf 0 \\ \end{array}\right] , \end{aligned}$$

(7.52)

$$\begin{aligned} \mathbf D _{\mathrm {P_{11}}} = \left[ \begin{array}{c} -\mathbf D _{\mathrm {W_{y}}}\mathbf D _{\mathrm {T_{ref}}}\\ \mathbf 0 \\ \mathbf 0 \\ \end{array}\right] , \quad&\mathbf D _{\mathrm {P_{12}}} = \left[ \begin{array}{c} \mathbf D _{\mathrm {W_{y}}}\mathbf E _{\mathrm {1}}\mathbf D _{\mathrm {G_{ff}}}\\ \mathbf D _{\mathrm {W_{u}}}\\ \mathbf D _{\mathrm {W_p}}\mathbf E _{\mathrm {2}}\mathbf D _{\mathrm {G_{ff}}}\\ \end{array}\right] . \end{aligned}$$

(7.53)

Both, the state vector of the augmented plant $\mathbf x$ and the reference input vector $\mathbf r$ are known, forming together the full-information feedback vector. Therefore, the feedback law can be written as $\mathbf u = \mathbf F \mathbf v = \mathbf F _\mathrm {1}\mathbf x + \mathbf F _\mathrm {2}\mathbf r$, with $\mathbf F$ as the static feedback matrix. The generalized closed-loop is shown in the right drawing of Fig. 7.21. Using a lower LFT $\mathbf T =\fancyscript{F}_{\mathrm {l}}(\mathbf P ,\mathbf F )$ leads to the performance transfer paths from $r$ to $z_{\mathrm {y}}$, $\mathbf z _{\mathrm {u}}$ and $\mathbf z _{\mathrm {p}}$ to be minimized:

$$\begin{aligned} \left\| \begin{array}{c} \mathbf T _{\mathrm {z_u,r}}\\ \mathbf T _{\mathrm {z_y,r}}\\ \mathbf T _{\mathrm {z_p,r}} \end{array} \right\| _{\infty } < \gamma . \end{aligned}$$

(7.54)

Due to the resulting complexity originating from the state feedback law, a more detailed decomposition of the single performance transfer paths $\mathbf T _i$ is not considered at this point. Three possible approaches for solving the $\fancyscript{H}_{\infty }$ optimization problem of (7.54) in MATLAB^® are:

• 1. Building the interconnected structure according to Fig. 7.21 and using the function hinfsyn with the method setting ric. Using this setting, the full-information gain matrix is included in the output argument info.

• 2. Instead of the hinfsyn also the function msfsyn can be used. The advantage of this function is that it can be applied to linear parameter varying systems with its parameters varying in a polytope.

• 3. Formulating the appropriate LMIs according to Proposition 7.1 and introducing the system matrices (7.50)–(7.53). The LMIs can be solved using for example the LMI solver mincx of the Robust Control Toolbox of MATLAB^® [1].

The third option has been shown to be more efficient and can also be extended to the LPV design case. With the optimal feedback gain matrix $\mathbf F _\mathrm {opt}$ as the primary optimization result of (7.54), the feed-forward controller $\mathbf K _\mathrm {f{}f}{}$ is obtained as outlined in Sect. 7.3.1.3 by the lower LFT $\mathbf K _\mathrm {f{}f}{}=\fancyscript{F}_{\mathrm {l}} (\mathbf P _\mathrm {f{}f}, \mathbf F _\mathrm {opt})$, where $\mathbf P _\mathrm {f{}f}$ is the modified augmented plant.

3.3.2 Reference Model and Performance Weighting Function Definition

To fulfill the required design specifications, an appropriate reference model as well as a correct shape for the performance weighting functions have to be selected:

Reference model $T_{\mathrm {ref}}$: The reference model selected for the model matching problem must first of all fulfill the requirements concerning rise time, overshoot, and settling time of the controlled variable $N\!z_{\mathrm {CG}}$ to be tracked. Moreover, it is advantageous to incorporate existing actuator dynamics $G_{\mathrm {act}}$ and sensor delays $G_{\mathrm {sen}}$ in the reference model since these dynamics represent hard constraints for the attainable tracking response which cannot be ignored in the design. Therefore, the reference model $T_{\mathrm {ref}}$ consists of three components

$$\begin{aligned} T_{\mathrm {ref}} = G_{\mathrm {sen}} G_{\mathrm {ref}} G_{\mathrm {act}}, \end{aligned}$$

(7.55)

where $G_{\mathrm {sen}}$ is a first-order Padé approximation with 160 ms delay and $G_{\mathrm {act}}$ is the linearized model of the slowest actuator, the combined elevator $EL_\mathrm {t}$:

$$\begin{aligned} G_{\mathrm {sen}} = \frac{(s-12.5)}{(s+12.5)}, \ \ G_{\mathrm {act}} = \frac{7.5}{s^2+3.9s+7.5}. \end{aligned}$$

(7.56)

The reference transfer function is given by a second-order system

$$\begin{aligned} G_{\mathrm {ref}} = \frac{\omega ^2}{s^2+2\zeta \omega s+\omega ^2} \end{aligned}$$

(7.57)

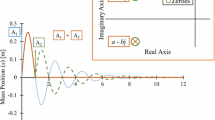
with its parameters set to $\omega =1.5~{{\text {rad}}/{\mathrm{s}}}$ and $\zeta =1$. The corresponding time response of the reference model $T_{\mathrm {ref}}$ is shown in Fig. 7.22 (left).

Fig. 7.22

Left $T_{\mathrm {ref}}$ time response representing an ideal $N\!z_{\mathrm {CG}}$ command response; Right frequency response plot of weighting functions $\mathbf W _{y}$ and $\mathbf W _\mathrm {u_i}$

Command tracking $\mathbf W _{y}$: For command tracking, the difference between the reference model $T_{\mathrm {ref}}$ and the system output to be tracked must be minimized. This can be achieved by a low-pass filter of the form

$$\begin{aligned} \mathbf W _{y}= t_{\mathrm {y1}}\frac{s+t_{\mathrm {y2}}\cdot 10}{s+t_{\mathrm {y2}}\cdot 0.001}, \end{aligned}$$

(7.58)

as shown in Fig. 7.22 (right), with the corresponding tuning parameters $t_{\mathrm {y1}}$ and $t_{\mathrm {y2}}$ appropriately set (see also Sect. 7.3.3.3).

Control energy $\mathbf W _u$: The control energy demanded by the feed-forward controller for reference model tracking can be adjusted by high-pass filters of the form

$$\begin{aligned} \mathbf W _u=\left[ \begin{array}{ccc} t_{\mathrm {u11}}\frac{(s+t_{\mathrm {u21}}\cdot 1)^2}{(s+t_{\mathrm {u21}}\cdot 100)^2} &{} 0 &{} 0 \\ 0 &{} t_{\mathrm {u12}}\frac{(s+t_{\mathrm {u22}}\cdot 1)^2}{(s+t_{\mathrm {u22}}\cdot 100)^2} &{} 0 \\ 0 &{} 0 &{}t_{\mathrm {u13}}\frac{(s+t_{\mathrm {u23}}\cdot 1)^2}{(s+t_{\mathrm {u23}}\cdot 100)^2} \\ \end{array}\right] , \end{aligned}$$

(7.59)

with their general shape shown in Fig. 7.22 (right). The tuning factor $t_{\mathrm {u1i}}$ serves to limit the absolute deflections, while $t_{\mathrm {u2i}}$ is used to constrain the deflection rates. According to the actuator properties, the tuning factor $t_{\mathrm {u2i}}$ is highest for the outmost flap $\mathrm {FL}_\mathrm {3}$. Second-order filters are utilized to ensure a sufficiently steep roll-off and thereby minimize excitation of the aeroelastic modes by the maneuver. This is most important, according to the open-loop analysis in Sect. 5.1.3.2, for the control surfaces at the wing, $\mathrm {FL}_\mathrm {12}$ and $\mathrm {FL}_\mathrm {3}$.

Maneuver loads $\mathbf W _\mathrm {p}$: The maximum Maneuver loads primarily originate from the static content and the first wing bending mode as will be shown below. Therefore, static weighting has shown to be sufficient for the performance outputs:

$$\begin{aligned} \mathbf W _\mathrm {p}=\left[ \begin{array}{ccc} t_{\mathrm {p1}} &{} 0 &{} 0\\ 0 &{} t_{\mathrm {p2}} &{} 0 \\ 0 &{} 0 &{} t_{\mathrm {p3}} \\ \end{array}\right] . \end{aligned}$$

(7.60)

3.3.3 Controller Tuning

With the design architecture according to Sect. 7.3.3.1 and the general shape of corresponding weighting functions as defined in Sect. 7.3.3.2, the subsequent design step is the selection of the tuning factors. This can be carried out either manually or in an automated way as will be presented in the following.

3.3.3.1 Manual Tuning

Manually adjusting the factors of the performance weighting functions (7.58)–(7.60) is not a trivial task when several design specifications have to be considered simultaneously. However, a basic understanding of the tuning possibilities, is similar to the feedback design case, crucial for a successful control design. Exemplarily, $t_{y1}$ is varied to show the effect on tracking performance and $t_\mathrm {p1}$ is varied to evaluate the effect on Maneuver loads control. In Fig. 7.23, the unit step time response of $\mathbf K _\mathrm {f{}f}{}$ from $r$ to $N\!z_{\mathrm {CG}}$, $q_\mathrm {CG}$, and $\eta _\mathrm {EL_t}{}$ is shown. Therefore, $t_{y1}$ was increased stepwise from $t_{y1}=0.01$, where $t_{y1}=1$ represents an optimized setting. In spite of the large tuning parameter variation, the effect on the tracking performance is moderate. Increasing $t_{y1}$ improves tracking performance and also requires faster control inputs. The effect of increased $t_\mathrm {p1}$ is presented in Fig. 7.24. There, Maneuver loads at the wing root $My5$ and at the outer wing $My_\mathrm {12}{}$ are compared. Increasing the weighting on one load output typically leads to reduced Maneuver loads at this and adjacent cut positions, however, this can also cause increased loads at more distant load outputs (waterbed effect). Basically it has been shown that including the wing bending load outputs $My$ also positively affects the vertical force load outputs $F\!z$. In general, a strong relation between load outputs and control energy outputs is evident.

Fig. 7.23

Left unit step time response of $\mathbf K _\mathrm {f{}f}{}$ from $r$ to $N\!z_{\mathrm {CG}}$ and $q_\mathrm {CG}$ for increasing tuning factor $t_{y1}$; Right corresponding $\eta _\mathrm {EL_t}{}$ time response

Fig. 7.24

Left unit step time response of $\mathbf K _\mathrm {f{}f}{}$ from $r$ to $My5$ for increasing tuning factor $t_\mathrm {p1}$; Right corresponding $My_\mathrm {12}{}$ time response

3.3.3.2 Automated Tuning

In order to accelerate the aforementioned tuning parameter selection, an automated approach similar as mentioned in Sect. 6.5.3.3 for feedback control design is described in this section. Therefore, several optimization criteria $c_i$ must be formulated for the design specifications listed in Sect. 7.3.2 mathematically. The following criteria are based on a reference command step $r=1.5$  g, which is a typical validation step to investigate maximum control deflections and rates. For the sake of brevity $y_{\mathrm {1}}(t)=y_{\mathrm {N\!z_{\mathrm {CG}}}}(t)$ and $y_{\mathrm {2}}(t)=y_{\mathrm {q_\mathrm {CG}}}(t)$ are introduced and the reference response for $N\!z_{\mathrm {CG}}$ is denoted by $y_{\mathrm {ref}}$:

• 1. Minimization of the deviation from the $N\!z_{\mathrm {CG}}$ reference model time response:

  $$\begin{aligned} c_1=\sum _{t_{{i}}=1}^{5}(y_{\mathrm {1}}(t_{{i}})-y_{\mathrm {ref}}(t_{{i}}))^2 \end{aligned}$$

  (7.61)

• 2. Limitation of the $q_\mathrm {CG}$ overshoot:

  $$\begin{aligned} c_2={\left\{ \begin{array}{ll} (\frac{\hat{y}_{\mathrm {2}}}{\bar{y}_{\mathrm {2}}})^2-1.3^2, &{} \text {if} \;\frac{\hat{y}_{\mathrm {2}}}{\bar{y}_{\mathrm {2}}} >1.3 \\ 0, &{} \text {otherwise,} \end{array}\right. } \end{aligned}$$

  (7.62)

  where

  $$\begin{aligned} \hat{y}_{\mathrm {2}}=\max _{t<10} y_{\mathrm {2}}(t),\ \bar{y}_{\mathrm {2}}=y_{\mathrm {2}}(t=10) \end{aligned}$$

  (7.63)

  is the maximum and the stationary value of $y_{\mathrm {2}}(t)$, respectively.

• 3. Limitation of the control energy:

  $$\begin{aligned} c_3={\left\{ \begin{array}{ll} (\frac{\hat{\eta }_{{i}}}{\eta _{\mathrm {i,max}}})^2, &{} \text {if}\; \frac{\hat{\eta }_{{i}}}{\eta _{\mathrm {i,max}}} >0.95\\ 0, &{} \text {otherwise,} \end{array}\right. } \end{aligned}$$

  (7.64)
  $$\begin{aligned} c_4={\left\{ \begin{array}{ll} (\frac{\hat{\dot{\eta }}_{{i}}}{\dot{\eta }_{\mathrm {i,max}}})^2, &{} \text {if}\; \frac{\hat{\dot{\eta }}_{{i}}}{\dot{\eta }_{\mathrm {i,max}}} >0.95\\ 0, &{} \text {otherwise,} \end{array}\right. } \end{aligned}$$

  (7.65)

  where

  $$\begin{aligned} \hat{\eta }_{{i}}=\max _{t<10} |\eta _{{i}}(t)|, \ \hat{\dot{\eta }}_{{i}}=\max _{t<10} |\dot{\eta }_{{i}}(t)| \end{aligned}$$

  (7.66)

  is the maximum deflection and deflection rate of the demanded control signal, respectively, while $\eta _{\mathrm {i,max}}$, $\dot{\eta }_{\mathrm {i,max}}$ are specified actuator properties.

• 4. Minimization of Maneuver loads: for maneuver load reduction, a comparative value is necessary. Here, it is obvious to use Maneuver loads obtained with the LPV feedback controller $\hat{M}_{{yi},\mathrm {fb}}$ according to Sect. 6.5 for comparison:

  $$\begin{aligned} c_5=\left( \frac{h_{{i}}\cdot \hat{M}_{{yi},\mathrm {f{}f}}}{\hat{M}_{{yi},\mathrm {fb}}}\right) ^2, \end{aligned}$$

  (7.67)

  where

  $$\begin{aligned} \hat{M}_{{yi},\mathrm {f{}f}}=\max _{t<10} M_{{yi},\mathrm {f{}f}}(t), \ \ \hat{M}_{{yi},\mathrm {fb}}=\max _{t<10} M_{{yi},\mathrm {fb}}(t). \end{aligned}$$

  (7.68)

  The factor $h_{{i}}$ is a weighting factor indicating the impact of the load output in the optimization. Typically, this factor is set to the value $1\le h_{\mathrm {5}} \le 2$ for the load output at the wing root $My_{\mathrm {5}}$ and to the value $0.95\le h_{\mathrm {9,12}} \le 1.2$ for the outer positions $My_{\mathrm {9}}$, $My_{\mathrm {12}}$. The primary goal of the optimization is to reduce loads at the inner wing (cut position 3–7) without increasing the loads at the outer wing.

All these criteria are summed up and form the final cost function to minimize:

$$\begin{aligned} \min _{t_{\mathrm {y1}},t_{\mathrm {u11}},t_{\mathrm {u12}},t_{\mathrm {u13}},t_{\mathrm {p1}},t_{\mathrm {p2}},t_{\mathrm {p3}}}\left\{ \sum _{i=1}^{5}c_i\right\} \end{aligned}$$

(7.69)

The tuning parameters $t_{\mathrm {y2}}, t_{\mathrm {u21}}, t_{\mathrm {u22}}, t_{\mathrm {u23}}$ are not included in the optimization. These are determined a priori and kept constant during the optimization. In order to solve the optimization problem (7.69), again different optimization tools can be applied at this stage. Similar to the feedback design case, a genetic algorithm is utilized (see Sect. 6.5.3.3).

3.3.4 A Posteriori Scheduling

Up to now, only the nominal design case was considered for the feed-forward controller. Now, also the parameter varying case will be investigated. Then, the dynamics of the linear design plant is parameter dependent $\mathbf G _\mathrm {f{}f}{}=\mathbf G _\mathrm {f{}f}{}(\varvec{\rho }(t))$, where $\varvec{\rho }(t)$ represents the flight parameters $\theta _{q}$ and $\theta _\mathrm {Ma}$ as well as the fuel-mass parameter $\theta _\mathrm {fuel}$. The fuel-mass parameter is also taken into consideration since the obtained RP over its parameter range was not satisfactory. The parameter dependency of the plant implies that the augmented plant according to (7.49)–(7.53) is parameter dependent $\mathbf P =\mathbf P (\varvec{\rho }(t))$, with weighting functions $\mathbf W _u$, $\mathbf W _{y}$ and $\mathbf W _\mathrm {p}$ determined as shown in Sect. 7.3.3.3. In order to account for the parameter dependency, an a posteriori scheduling approach due to linear interpolation was considered.

This approach is composed of the following design steps:

• 1. Perform an automated weighting factor optimization according to Sect. 7.3.3.3 on a rough gridding comprising the flight envelope of interest.

• 2. Validate the obtained grid point controllers.

• 3. Design intermediate grid point controllers using weighting functions obtained by linear interpolation of the weighting functions from the rough gridding.

• 4. Perform element-wise linear interpolation of the system matrices $\mathbf A$, $\mathbf B$, $\mathbf C$, $\mathbf D$ from the finely gridded $\mathbf K _\mathrm {f{}f,i}$.

In Fig. 7.25 the $N\!z_{\mathrm {CG}}$ and $q_\mathrm {CG}$ responses of the linearly interpolated controllers $\mathbf K _\mathrm {f{}f,i}$ to a unit reference step are shown exemplarily for the parameters $\theta _{q}=9{,}000$, $\theta _\mathrm {fuel}=91\,$% and $0.82\le \theta _\mathrm {Ma}\le 0.835$. The response hardly changes with varying $\theta _\mathrm {Ma}$ number. In the right plot, the corresponding $\eta _\mathrm {EL_t}{}$ time response is plotted. Strong variations of the control signal for only moderate changes in $\theta _\mathrm {Ma}$ number become evident.

Fig. 7.25

Left unit step response of a posteriori scheduled $\mathbf K _\mathrm {ff}{i}$ from $r$ to $N\!z_{\mathrm {CG}}$ and $q_\mathrm {CG}$ for $0.82\le \theta _\mathrm {Ma}\le 0.835$ and $\theta _{q}=9{,}000$; Right corresponding $\eta _\mathrm {EL_t}{}$ time response

In [19] also an LPV design scheduling approach including the vertex plants in the LMI optimization was applied and verified. Comparing the results of both approaches has shown that a better performance is obtained with the a posteriori scheduling approach for the given application. For that reason this approach was chosen to design the parameter-dependent feed-forward controller over the entire considered operating range. The finally obtained results are presented in the next chapter.

3.4 Validation

This section reports on the validation of the obtained parameter-dependent feed-forward controller $\mathbf K _\mathrm {f{}f}{}(\theta _\mathrm {Ma},\theta _{q},\theta _\mathrm {fuel})$ in order to assess the performance improvement obtained by this prefilter. These results were already presented in [20]. Before considering the obtained results, however, it is important to note that $\mathbf K _\mathrm {f{}f}{}$ is validated together with the LPV feedback controller $\mathbf K _\mathrm {fb}{}$, forming together a 2DOF control architecture according to Fig. 7.18. In order to directly express the obtained performance improvements given by $\mathbf K _\mathrm {f{}f}{}$, again the validation plots show the system response to an $r=1.5$ g reference step command. Moreover, such reference step size also enables to evaluate maximum Maneuver loads as will be shown in the following.

Fig. 7.26

2DOF flight mechanic data time response to $r=1.5\,\text {g}$ reference step command for representative validation models chosen from the parameter envelope

3.4.1 Command Response Behavior and Maneuver Load Reduction

For evaluation of the command response, again essential flight mechanic data $N\!z_{\mathrm {CG}}$, $q_\mathrm {CG}$, $N\!z_\mathrm {f}{}$, and $C^*$ are provided in Fig. 7.26 for a representative set of validation models. The $N\!z_{\mathrm {CG}}$ response has similar characteristics independent of the parameter case and fulfills the requirements concerning rise time and overshoot. A slightly rippled response after $t=3.5~\text {s}$ can be observed for some of the validation models. This can be explained by a higher deviation of the linearized actuator model used for design from the nonlinear model. This deviation is only moderately compensated by the feedback controller and therefore visible in the time response. The $q_\mathrm {CG}$ response is not as pure as the $N\!z_{\mathrm {CG}}$ response, however, also in this case a significant improvement in comparison to feedback control only appears. The maximum overshoot can be reduced significantly and the maximum overshoot requirement of $30\,\%$ is exceeded for a few cases only. The $N\!z_\mathrm {f}{}$ response is hardly different from the $N\!z_{\mathrm {CG}}$ response, while for $C^*$ the spreading effect of $q_\mathrm {CG}$ is visible.

Fig. 7.27

$\mathbf K _\mathrm {f{}f}{}$ control input deflection and deflection rate time responses to $r=1.5\,\text {g}$ reference command step for representative validation models chosen from the parameter envelope

Fig. 7.28

Load output time response comparison of $\mathbf K _\mathrm {fb}{}$ and 2DOF for an $r=1.5$ g reference step command and representative validation models chosen from the parameter envelope

In Fig. 7.27 the demanded control surface deflections $\eta _i$ and deflection rates $\dot{\eta }_i$ of $\mathbf K _\mathrm {f{}f}{}$ are shown for the combined elevator $\mathrm {EL}_\mathrm {t}$, the combined inner flap $\mathrm {FL}_\mathrm {12}$, and the outer flap $\mathrm {FL}_\mathrm {3}$. While the deflection rate signals $\dot{\eta }_i$ are rather similar for the various parameter cases, in the deflection signals $\eta _i$ a broad spreading is visible, indicating the strong variations in low-frequency system dynamics. Both, maximum deflections and deflection rates are well below the given limits for the respective actuators. During design, special attention was paid to keep the necessary deflections for $\mathrm {FL}_\mathrm {12}$ comparatively low, since this flap is mainly used for the roll maneuvers in lateral control. However, only additional tests can ensure that this actuator does not exceed the deflection limits in extremal coordinated turn maneuvers. The deflection of $\mathrm {FL}_\mathrm {3}$ is slightly higher but still below the maximum deflection limits.

Finally, in Fig. 7.28 a comparison of the Maneuver loads time response obtained for $\mathbf K _\mathrm {fb}{}$ only (solid) and for the 2DOF concept (dashed) based on representative load outputs is provided. Thereby, a significant reduction of incremental loads is visible for all outputs, which emphasizes the effectiveness of the chosen control design approach.