Contact Mechanics, Friction and Adhesion with Application to Quasicrystals

Abstract

We discuss the origin of friction and adhesion between hard solids such as quasicrystals. We emphasize the fundamental role of surface roughness in many contact mechanics problems, in particular for friction and adhesion between solid bodies. The most important property of rough surfaces is the surface roughness power spectrum $C(q)$. We present surface roughness power spectra of many surfaces of practical importance, obtained from the surface height profile measured using optical methods and the Atomic Force Microscope. We show how the power spectrum determines the contact area between two solids. We also present applications to contact mechanics and adhesion for rough surfaces, where the power spectrum enters as an important input.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The first sample of a quasicrystal was produced in 1982 [1]. Intensive studies of this class of metallic materials have been conducted since that time. Quasicrystals display a unique combination of physical properties, namely low heat conductivity, relatively high hardness, and (under atmospheric condition) low friction coefficient and low surface energy. These properties make them promising candidates as coatings for, e.g., cookware (see Fig. 13.1), surgical tools and electrical shavers, automotive parts, and for air-space applications.

Fig. 13.1

A stainless steel pan coated by a quasicrystal material. The coating was made using electron beam vapor deposition in vacuum

In this article we present results related to sliding friction, contact mechanics and adhesion. Most of the theory results are very general, and can be applied not only to quasicrystals but also to other materials. In Sect. 13.2 we study how sliding friction depends on the elastic modulus of the solids. In Sect. 13.3 we discuss sliding friction and adhesion for quasicrystals. Section 13.4 presents a general discussion about surface roughness, and in Sects. 13.5 and 13.6 we consider contact mechanics and adhesion. Section 13.7 contains the summary and an outlook.

Fig. 13.2

A particle pulled by a spring (with the velocity $v_0$) in a periodical potential. If the spring $k$ is weak enough or the barrier $U_0$ high enough ($ka^2 \ll U_0$), the particle will perform stick-slip motion. On the other hand, if $ka^2 \gg U_0$ no stick-slip occurs, and the friction force is very small (it will vanish as $v_0\rightarrow 0$)

2 Sliding Friction—Role of Elasticity

Sliding friction for clean solid surfaces, or surfaces separated by a ${\sim }\, 1 \,\mathrm{nm}$ (or less) thick contamination film (boundary lubrication), usually originates from elastic instabilities occurring at the interface [2]. Elastic instabilities occur if the elastic modulus of the solids is low enough or if the lateral corrugation of the interaction potential at the interface is high enough. This is best illustrated by a one dimensional model, see Fig. 13.2. Here a particle is connected to a spring, and the free end of the spring is pulled with some (small) velocity $v_0$. If the spring constant is small enough or the potential well $U_0$ high enough, the particle will perform stick-slip (non-uniform) motion, where during slip the particle moves with a velocity $v(t)$ which is much higher than (and unrelated to) the driving velocity $v_0$. This will result in a large friction force (spring force averaged over time). On the other hand, if the spring is very stiff or the barrier very small, no stick-slip occurs and the velocity of the particle will be of the order of $v_0$, and proportional to $v_0$. In this case the friction force vanishes, at least when $v_0 \rightarrow 0$. In reality, the particle may represent some small group of atoms (block atoms and/or contamination atoms) at the interface, and the spring may represent some effective elastic properties which determine the force necessary to displace the group of atoms relative to the center of mass of the solid walls.

It is important to note that the elastic stiffness of solids depends on the length scale over which they are studied. Thus a solid elastic bar of length $L$ will elongate by a distance proportional to $L$ when exposed to some (fixed) forces $F$ and $-F$ at its two ends. However, since hard solids also tend to have small contact areas (with small average diameter $L$) when squeezed together, this reduces the chances that elastic instabilities will occur at the interface during sliding. Thus, it is clear that hard materials, such as quasicrystals, may exhibit very low friction, in particular since the surfaces will always be incommensurate, thus lowering the barrier $U_0$.

Fig. 13.3

Simulation results for an elastic block sliding on a rigid substrate. The atoms of the bottom surface of the block and of the top surface of the substrate form square lattices which are (nearly) incommensurate. The upper surface of the block is moving with the constant speed $v=0.1$ m/s. Straight line (green): Young modulus $E=10$ GPa, pressure $1$ GPa. Stick and slip (red): Young modulus $E=1$ GPa, pressure $0.1$ GPa. For the softer elastic solid stick-slip occurs at the interface while steady motion occurs for the stiffer block

As illustrations of the discussion above, let us present Molecular Dynamics simulations for an elastic block sliding on a rigid substrate when the wall atoms are (nearly) incommensurate with the substrate atoms. In Fig. 13.3 we show the center-of-mass coordinate of the bottom layer of block atoms as a function of time. Both the sliding layer and the substrate have square lattice structure, but with different lattice spacing to have (nearly) incommensurability (ratio 1.625 close to the golden mean). The upper surface of the block is moving with the constant speed $v=0.1$ m/s. When the elastic stiffness of the block is small, stick-slip occurs (red curve), and the friction coefficient is nonzero. For a stiffer block (green curve), the stick and slip behaviour disappears and the friction coefficient gets negligibly small (below the noise level of the simulations).

Recently, a detailed study was performed of the friction between a Si tip and thin hard coatings [3]. As expected, it was observed that the friction coefficient decreases with increasing elastic modulus of the coating. An extreme case is the friction of diamond against diamond where the friction (when the diamond surfaces are passivated by hydrogen) is extremely small (of the order of 0.01).

3 Application to Quasicrystals

Quasicrystals differ radically from traditional crystalline materials because they have rotational symmetry which is incompatible with periodicity (translational symmetry). Due to the lack of translational symmetry, the plastic deformation properties of quasicrystals fundamentally differ from those of crystals. The plastic yield stress of most metal crystals is relatively low due to small barriers for motion of dislocations. This is not the case in quasicrystals because of the absence of long-range translational symmetry. Consequently, the plastic yield stress is much higher for quasicrystals than for most metallic crystals. Thus, in spite of the fact that quasicrystals only contain metal atoms, they form relatively hard and brittle-like materials. We believe that this is the main reason for the low sliding friction [4, 5] and wear usually observed for quasicrystal materials.

In one set of experiments [6], the adhesion and sliding friction were studied as a sharp tip coated with $\mathrm{W_2C}$ was in contact with a single grain tenfold decagonal $\mathrm{Al}_{72.4}\mathrm{Ni}_{10.4}\mathrm{Co}_{17.2}$ quasicrystals. The coated tip had the radius of curvature ${\sim }\, 100 \,\mathrm{nm}$. For the clean surfaces in ultrahigh vacuum the work of adhesion was found to be ${\approx } \; 0.1 \,\mathrm{eV}/ {\AA }^{2}$, but this value is probably an overestimate of the change in the surface energy $\Delta \gamma = \gamma _1 +\gamma _2 - \gamma _{12}$ since some plastic deformation of the tip-sample contact takes place during rupture of the contact. If the quasicrystal surface is exposed to clean O$_2$ gas, a very thin oxide layer (one or at most two monolayers) is formed on the surface, and the work of adhesion drops to about ${\approx }\; 0.03 \,\mathrm{eV}/{\AA }^{2}$. When the surface is air-oxidized the work of adhesion is only ${\approx }\; 3 \, \mathrm{meV}/{\AA }^{2}$. Similarly, the friction coefficient drops from ${\approx }\; 0.4$ for the clean surface to ${\approx }\; 0.2$ for the surface exposed to O$_2$ and to ${\approx }\; 0.1$ for the air-oxidized surface.

It has been reported that the oxide formed in air on the quasicrystal surface has a thickness of the order of $26 \,{\AA }$ in dry air and $62 \, {\AA }$ in humid air. This is much thicker than the in situ grown oxide (${\approx }\; 6 \,{\AA }$). Thus, the higher friction and work of adhesion on the very thin oxide formed in vacuum could be explained by the more fragile nature of the film that can be partly destroyed by the tip resulting in (weak) cold-welded regions [6]. In addition, the air exposed surface is likely to have a nanometer thick contamination layer consisting of organic molecules, water and other contamination molecules. This layer will also reduce the sliding friction although it may be at least partly removed after repeated sliding over the same surface area.

In another experiment two macroscopic Al$_{70}$Pd$_{21}$Mn$_{9}$ quasicrystals were brought into contact [7]. The crystal surfaces were polished to a mirror finish with $0.25 \,\upmu \mathrm{m}$ diamond pasta. The surface roughness amplitude was not measured but should be of the order of several $10\,\mathrm{nm}$. In this case, even after lateral sliding, no adhesive force could be detected during pull-off. This may seem as a paradox taking into account the relatively large pull-off force measured in [6] when a tip was removed from a quasicrystal. However, the result is easy to understand based on the theoretical results presented in Sect. 13.6. Thus, when two macroscopic solid blocks of hard materials with randomly rough surfaces are brought into contact, the actual contact will only occur in very small, randomly distributed, asperity contact areas. For hard materials with low ductility, such as quasicrystals, a root-mean-square roughness of a few $10 \, \mathrm{nm}$ (as in the present case) is enough to completely remove the (macroscopic) adhesion between the solids for the following reason. Since the asperities have different sizes they will have different amount of elastic deformation, and will act like elastic springs of different sizes. Thus during pull-off the different asperity contact areas will break at different times giving rise to a negligible adhesion even though breaking a single asperity contact region requires a non-negligible force as observed in the tip-substrate experiments reported on in [6]. We point out that a similar effect is observed in silicon wafer bonding (see Sect. 13.4).

For clean surfaces of more ductile metals such as Cu, Au or Al, strong adhesion is usually observed. This is the case even for oxide coated surfaces if sliding occurs before pull-off, as the sliding will break up the oxide coating and result in the formation of cold welded contact areas. During pull-off, because of the high ductility of Cu, Au or Al (and most other metals), “long” metallic bridges may be formed between the solids so that instead of having junctions popping one after another during pull-off, a large number of adhesive junctions may simultaneously impede the surface separation during pull-off (see Fig. 13.4), leading to a large pull-off force.

In [8] sliding friction measurement was performed both for clean surfaces (in ultra high vacuum) and for O$_2$ exposed surfaces and for surfaces oxidized in the air. For clean surfaces the friction coefficient was of order ${\approx }\; 0.6$ which dropped to ${\approx }\; 0.4$ when exposed to O$_2$. The friction coefficient of air exposed surfaces was only ${\approx }\; 0.1$.

4 Surface Roughness

Surface roughness has a huge influence on many important physical phenomena such as contact mechanics, sealing, adhesion and friction. Thus, for example, experiments have shown that already a substrate roughness with a root-mean-square (rms) roughness of order ${\sim }\, 1 \, \upmu \mathrm{m}$ can completely remove the adhesion between a rubber ball and a substrate, while nanoscale roughness will remove the adhesion between most hard solids, e.g., metals and minerals; this is the reason why adhesion is usually not observed in most macroscopic phenomena. Similarly, rubber friction on most surfaces of practical interest, e.g., road surfaces, is mainly due to the pulsating forces which act on the rubber surface as it slides over the substrate asperities.

Fig. 13.4

When two ductile metals, e.g., Au or Al, are separated after being in contact, metallic bridges will occur in many asperity contact areas giving rise to a nonzero pull-off force. For (plastically) harder and more brittle metal because of elastic deformation of the asperities, the asperity contact regions will break one after another during pull-off and no adhesion (or pull-off force) will be observed

Fig. 13.5

a Micrometer sized cantilever beam. b If the beam is too long or too thin the minimum free energy state corresponds to the beam partly bound to the substrate. Surface roughness lowers the binding energy (per unit area) and hence stabilizes the non-bonded state in (a)

Let us illustrate the importance of surface roughness with three modern applications. At present there is a strong effort to produce small mechanical devises, e.g., micromotors. The largest problem in the development of such devices is the adhesion and, during sliding, the friction and wear between the contacting surfaces [9]. As an example, in Fig. 13.5 we show the simplest possible micro device, namely a micrometer cantilever beam. (Suspended micromachined structures such as plates and beams are commonly used in manufacturing of pressure and accelerator sensors.) If the beam is too long or too thin the free beam state in (a) will be unstable, and the bound state in (b) will correspond to the minimum free energy state [10]. Roughly speaking, the state (b) is stable if the binding energy to the substrate is higher than the elastic energy stored in the bent beam. The binding energy to the substrate can be strongly reduced by introducing (or increasing) the surface roughness on the substrate (see Sect. 13.6.1). In addition, if the surfaces are covered by appropriate monolayer films the surfaces can be made hydrophobic thus eliminating the possibility of formation of (water) capillary bridges.

A second application is the formation of hydrophobic coatings on surfaces by creating the appropriate type of surface roughness [11]. This involves copying Nature where many plant surfaces are found to be highly hydrophobic (Fig. 13.6) as a result of the formation of special types of surface roughness (Fig. 13.7). The surface roughness allows air to be trapped between the liquid and the substrate, while the liquid is suspended on the tips of the asperities. Since the area of real liquid-substrate contact is highly reduced, the contact angle of the drop is determined almost solely by the surface tension of the liquid, leading to a very large contact angle. New commercial products based on this “Lotus effect”, such as self-cleaning paints and glass windows, have been produced.

Fig. 13.6

A water droplet on a superhydrophobic surface: The droplet touches the leaf only in a few points and forms a ball. It completely rolls off at the slightest declination. From [11]

Fig. 13.7

A leaf surface with roughness on several length scales optimized (via natural selection) for hydrophobicity and self-cleaning. Through the combination of micro- (cells) and nanostructure (wax crystals) the water contact angle $\theta _0$ is maximized. From [11]

Finally, we discuss the effect of surface roughness on direct wafer bonding [12]. Wafer bonding at room temperature is due to relatively weak interatomic attraction forces, e.g., the van der Waals interaction or hydrogen bonding, giving (for perfectly flat surfaces) an interfacial binding energy of order $6 \, \mathrm{meV}{/}{\AA }^{2}$. The wafer surface roughness is the most critical parameter determining the strength of the wafer bonding. In particular, when the surface roughness exceeds a critical value, the wafers will not bind at all, in agreement with the theory presented in Sect. 13.6.1. Primary grade polished silicon wafer surfaces have rms roughness of order ${\sim }\, 0.1 \, \mathrm{nm}$ when measured over a $10\times 10 \, \upmu \mathrm{m}$ surface area, and such surfaces bind spontaneously. However, when the surface roughness amplitude is of order $1 \, \mathrm{nm}$ the surfaces either bind (slowly) when squeezed together at high enough pressure, or they do not bind at all depending on the detailed nature of the surface roughness power spectra.

Surfaces with “ideal” roughness, e.g., prepared by fracture or by some growth process, have been studied intensively for many years [13–17]. However, much less information has been presented for more common surfaces of engineering interest. In what follows we discuss the nature of the power spectra of some surfaces of practical importance. As illustrations we discuss contact mechanics and adhesion.

4.1 Surface Roughness Power Spectra: Definition and General Properties

The influence of roughness on the adhesion and frictional properties described above is mainly determined by the surface roughness power spectra $C(q)$ defined by [18]

$$\begin{aligned} C(q)= {1\over (2\pi )^2 } \int d^2x \ \langle h(\mathbf{x})h(\mathbf{0})\rangle e^{-i\mathbf{q}\cdot \mathbf{x}}. \end{aligned}$$

(13.1)

Here $h(\mathbf{x})$ is the substrate height measured from the average plane defined so that $\langle h \rangle = 0$. The $\langle \ldots \rangle$ stands for ensemble averaging, or averaging over the surface area (see below). We have assumed that the statistical properties of the substrate are translational invariant and isotropic so that $C(q)$ only depend on the magnitude $q=|\mathbf{q}|$ of the wave vector $\mathbf{q}$. Note that from (13.1) follows

$$ \langle h(\mathbf{x})h(\mathbf{0})\rangle = \int d^2q \ C(q) e^{i\mathbf{q}\cdot \mathbf{x}}, $$

so that the root-mean-square roughness amplitude $\sigma = \langle h^2\rangle ^{1/2}$ is determined by

$$\begin{aligned} \langle h^2 \rangle = \int d^2q \ C(q) = 2\pi \int \limits _0^\infty dq \ q C(q). \end{aligned}$$

(13.2)

In reality, there will always be an upper, $q_1$, and a lower, $q_0$, limit to the $q$-integral in (13.2). Thus, the largest possible wave vector will be of order $2\pi /a$, where $a$ is some lattice constant, and the smallest possible wave vector is of order $2\pi /L$ where $L$ is the linear size of the surface. In general, one may define a root-mean-square roughness amplitude which depends on the range of roughness included in the integration in (13.2):

$$\begin{aligned} \langle h^2 \rangle (q_0,q_1) = 2\pi \int \limits _{q_0}^{q_1} dq \ q C(q). \end{aligned}$$

(13.3)

Fig. 13.8

The surface profile $h(x)$ is decomposed into a top $h_T(x)$ and a bottom $h_B(x)$ profile

For a randomly rough surface, when $h(\mathbf{x})$ are Gaussian random variables, the statistical properties of the surface are completely defined by the power spectra $C(q)$. In this case the height probability distribution

$$P_h = \langle \delta [h-h(\mathbf{x}) ]\rangle $$

will be a Gaussian

$$\begin{aligned} P_h = {1\over ( 2\pi )^{1/2} \sigma } e^{-h^2/ 2 \sigma ^2}. \end{aligned}$$

The height distribution of many natural surfaces, e.g., surfaces prepared by fracture, or surfaces prepared by blasting with small particles (e.g., sand blasting or ion sputtering) are usually nearly Gaussian. On the other hand, rough surfaces, e.g., a surface prepared by fracture, which have been (slightly) polished have a non-symmetric height distribution (i.e., no symmetry as $h \rightarrow -h$) since the asperity tops have been more polished than the bottom of the valleys, and such surfaces (which are of great practical importance—see below) have non-Gaussian height distribution. For such surfaces it is interesting to study the top, $C_T$, and the bottom, $C_B$, power spectra’s defined by

$$\begin{aligned} C_T(q)&= {1\over (2\pi )^2 } \int d^2x \ \langle h_T(\mathbf{x})h_T(\mathbf{0})\rangle e^{-i\mathbf{q}\cdot \mathbf{x}},\end{aligned}$$

(13.4a)

$$\begin{aligned} C_B(q)&= {1\over (2\pi )^2 } \int d^2x \ \langle h_B(\mathbf{x})h_B(\mathbf{0})\rangle e^{-i\mathbf{q}\cdot \mathbf{x}} , \end{aligned}$$

(13.4b)

where $h_T(\mathbf{x}) = h(\mathbf{x})$ for $h > 0$ and zero otherwise, while $h_B(\mathbf{x}) = h(\mathbf{x})$ for $h < 0$ and zero otherwise, see Fig. 13.8. It is easy to show that $C\approx C_T+C_B$. It is also clear by symmetry that for a surface prepared by fracture, $C_T(q)=C_B(q)$, since what is top on one of the cracked block surfaces is the bottom on the other (opposite) crack surface, and vice versa, see Fig. 13.9. However, if the cracked surface is (slightly) polished then, since the polishing will be stronger at the top of the asperities than at the bottom of the valleys [the contact pressure with the polishing object (e.g., sand paper) is highest at the asperity top], $C_B > C_T$. If $n_T$ and $n_B$ are the fraction of the nominal surface area (i.e., the surface area projected on the $xy$-plane) where $h>0$ and $h<0$, respectively, with $n_T+n_B=1$, then we also define $C_T^*(q)= C_T/n_T$ and $C_B^*=C_B/n_B$. In general, $n_T\approx n_B \approx 0.5$ and for surfaces prepared by fracture $n_T=n_B=0.5$. Roughly speaking, $C_T^*$ would be the power spectra which would result if the surface profile in the large valleys (for $h<0$) is replaced by a surface profile with similar short-wavelength roughness as occurs on the large asperities (for $h>0$). A similar statement holds for $C_B^*$.

Fig. 13.9

Rough surfaces prepared by crack propagation have surface roughness with statistical properties which must be invariant under the replacement of $h\rightarrow -h$. This follows from the fact that what is a valley on one of the crack surfaces (say the left) is an asperity with respect to the other crack surface (right). Thus the top and bottom power spectra must obey $C_T(q)=C_B(q)$

Many surfaces tend to be nearly self-affine fractal. A self-affine fractal surface has the property that if part of the surface is magnified, with a magnification which in general is appropriately different in the perpendicular direction to the surface as compared to the lateral directions, then the surface “looks the same”, i.e., the statistical properties of the surface are invariant under the scale transformation. For a self-affine surface the power spectrum has the power-law behavior

$$ C(q) \sim q^{-2(H+1)}, $$

where the Hurst exponent $H$ is related to the fractal dimension $D_\mathrm{f}$ of the surface via $H=3-D_\mathrm{f}$. Of course, for real surfaces this relation only holds in some finite wave vector region $q_0 < q < q_1$, and in a typical case $C(q)$ has the form shown in Fig. 13.10. Note that in many cases there is a roll-off wavelength $q_0$ below which $C(q)$ is approximately constant. We will discuss this point further below.

Finally, note that while the root-mean-square roughness usually is dominated by the longest wavelength surface roughness components, higher order moments of the power spectra such as the average slope or the average surface curvature are dominated by the shortest wavelength components. For example, assuming a self affine fractal surface, (13.3) gives

$$ \langle h^2\rangle (q_0,q_1) \sim \int \limits _{q_0}^{q_1} dq \ q^{-2H-1} \sim q_0^{-2H}-q_1^{-2H} \approx q_0^{-2H} $$

if $q_1/q_0 \gg 1$. However, the average slope and the average curvature have additional factors of $q^2$ and $q^4$, respectively, in the integrand of the $q$-integral, and these quantities are therefore dominated by the large $q$ (i.e., short wavelength) surface roughness components.

Fig. 13.10

Surface roughness power spectra of a surface which is self affine fractal for $q_1>q>q_0$. The long-distance roll-off wave vector $q_0$ and the short distance cut-off wave vector $q_1$ depend on the system under consideration. The slope of the $\mathrm{log} C-\mathrm{log}q$ relation for $q > q_0$ determines the fractal exponent of the surface. The lateral size $L$ of the surface (or of the studied surface region) determines the smallest possible wave vector $q_L=2\pi /L$

4.2 Surface Roughness Power Spectra: Experimental Results

In this section we present power spectra for different surfaces of practical importance. The power spectra have been calculated using (13.1), (13.4a) and (13.4b), where the height profile $h(\mathbf{x})$ has been measured using either an optical method or the Atomic Force Microscope.

Fig. 13.11

The surface roughness power spectra for two freshly cleaved basalt surfaces and a fresh granite surface

4.2.1 Surfaces Produced by Crack Propagation

Figure 13.11 shows the power spectra $C(q)$ for three freshly cleaved stone surfaces, namely a granite and two basalt stone surfaces. Here, and in what follows, we show the power spectra on a log-log scale. Note that the granite and basalt surfaces, in spite of the rather different mineral microstructure (see below), give identical power spectra within the accuracy of the measurement. It has been stated (see, e.g., [19]) that surfaces produced by crack propagation have self affine fractal structure with the universal fractal dimension $D_\mathrm{f} \approx 2.2$. However, our measured $\mathrm{log} C-\mathrm{log} q$ relations are not perfectly straight lines, i.e., the surfaces in the studied length-scale range cannot be accurately described as self affine fractal, and the average slope of the curves in Fig. 13.11 correspond to the fractal dimension $D_\mathrm{f} \approx 2$ rather than $2.2$.

Note the similarity of the power spectra for the basalt and granite surfaces in Fig. 13.11. Granite and basalt both result from magma and have a similar composition, consisting mainly of minerals from the silicate group. However, granite results from magma which is trapped deep in the crust, and it takes very long time to cool down enough to crystallize into solid rock. As a result granite is coarse-textured rock in which individual mineral grains are easily visible. Basalt, on the other hand, results from fast cooling of magma from, e.g., volcanic eruptions, and is therefore fine grained, and it is nearly impossible to see the individual minerals without magnification. In spite of these differences, the surface roughness power spectra of freshly cleaved surfaces are nearly identical. This may indicate some kind of universal power spectrum for surfaces resulting from cleaving of mineral stones of different types.

Note that there is no roll-off region for surfaces produced by fracture (crack propagation), and the surfaces remains fractal-like up to the longest length scale studied, determined by the lateral size $L$ of the surfaces (or of the regions experimentally studied), i.e., with reference to Fig. 13.10, $q_0 = q_L$. One consequence of this is that the rms-roughness amplitude is determined mainly by the $\lambda \sim L$ wavelength fluctuations of the surface height, and will therefore depend on the size $L$ of the surface, and the height distribution $P_h$ obtained for any given realization of the rough surface will not be Gaussian, but will exhibit random fluctuations as compared to other realizations (see Fig. 13.12, which illustrates this point for the three stone surfaces discussed above). However, the ensemble averaged height distribution (not shown) should be Gaussian or nearly Gaussian. Thus, when there is no roll-off region in the measured power spectra, averaging over the surface area is not identical to ensemble averaging. However, when there is a roll-off wave vector $q_0 = 2\pi /\lambda _0$, and if the surface is studied over a region with the lateral size $L\gg \lambda _0$, ensemble averaging and averaging over the surface area $L\times L$ will give identical results for $P_h$, and the rms-roughness amplitude will be independent of $L$ for $L \gg \lambda _0$.

Fig. 13.12

The height distribution $P_h$ for two freshly cleaved (cobble stone) basalt surfaces and a fresh granite surface. Note the random non-Gaussian nature of the height profiles

Fig. 13.13

The surface roughness power spectra $C(q)$ for two freshly cleaved cobble stone (basalt) surfaces, and for a used surface

4.2.2 Polished Crack Surfaces

In the past, cobble stones, made from granite or basalt, were frequently used for road surface pavements. However, these surfaces do not exhibit good frictional properties against rubber. In particular, with increasing time the cobble stone surfaces become polished by the road–tire interaction, which results in a reduced rubber-road friction, even during dry driving conditions. Figure 13.13 illustrates this polishing effect. It shows the power spectrum of a strongly used (basalt) cobble stone, and of two freshly cleaved surfaces (from Fig. 13.11), from the same cobble stone. At long wavelength the power spectrum of the strongly used surface is nearly one decade smaller than that of the freshly prepared surfaces. The effect of the polishing is even better illustrated by calculating the top and bottom power spectra, $C_T^*$ and $C_B^*$, as shown in Fig. 13.14. The top power spectrum is a factor ${\sim }\, 30$ times smaller than the bottom power spectrum for all wave vectors studied. This arises from the higher polishing of the road asperities than of the valleys (the tire–road contact pressure is highest at the road asperities, resulting in the strongest polishing of the asperity tops during breaking on the road). It is important to take this polishing effect into consideration when designing road pavements.

Fig. 13.14

The top $C_\mathrm{T}^*$ and the bottom $C_\mathrm{B}^*$ surface roughness power spectra $C(q)$ for a used cobble stone (basalt) surface

4.2.3 Surfaces with Long-Distance Roll-off

As pointed out above, surfaces prepared by fracture have no natural long-distance cut-off and the rms roughness amplitude increases continuously (without limit) as the probed surface area increases. This is similar to Brownian motion where the mean square displacement increases without limit (as ${\sim }\, t^{1/2}$) as the time $t$ increases. However, most surfaces of engineering interest have a long distance cut-off or roll-off wavelength $\lambda _0$ corresponding to a wave vector $q_0 = 2\pi /\lambda _0$, as shown in Fig. 13.10. For example, if a flat surface is sand blasted for some time the resulting rough surface will have a long distance roll-off length, which increases with the time of sand blasting. Similarly, if atoms or particles are deposited on an initially flat surface the resulting rough surface will have a roll-off wavelength which increases with the deposition time, as has been studied in detail in recent growth models. Another way to produce a surface with a long-distance roll-off wavelength is to prepare the solid from small particles. A nominally flat surface of such a solid has still roughness on length scales shorter than the diameter of the particles, which therefore may act as a long distance roll-off wavelength. We illustrate this here with a solid produced by squeezing together corundum particles at high temperature and pressure (Fig. 13.15), and for a sand paper surface (Fig. 13.17). For both surfaces the height distribution $P_h$ is smooth and nearly Gaussian (see Figs. 13.16 and 13.18), since averaging over a surface area with lateral size $L\gg \lambda _0$ is equivalent to ensemble averaging.

Fig. 13.15

The surface roughness power spectra for a fresh granite surface and a fresh particle-made corundum surface

Fig. 13.16

The height distribution $P_h$ as a function of the height $h$ for a particle-made corundum surface

Fig. 13.17

The surface roughness power spectra $C(q)$ for a sand paper surface. The two curves are based on the height profiles measured with an AFM at two different spatial resolutions over $20\times 20$ and $100\times 100$ $\upmu \mathrm{m}$ square areas

Fig. 13.18

The surface roughness height probability distribution $P_h$ for a sand paper surface. The two curves are based on the height profiles measured with an AFM at two different spatial resolution over $20\times 20$ and $100\times 100$ $\upmu \mathrm{m}$ square areas

The sand paper surface in Fig. 13.17 was studied using the AFM at two different resolutions over square areas $20\times 20$ and $100\times 100 \, \upmu \mathrm{m}$ as indicated by the two different lines in Fig. 13.17. The height distribution $P_h$ (and hence also the rms-roughness amplitude) calculated from these two different measurements over different surface areas, see Fig. 13.18, are nearly identical, as indeed expected when $L$ is larger than the roll-off length $\lambda _0$.

5 Contact Mechanics

Practically all macroscopic bodies have surfaces with roughness on many different length scales. When two bodies with nominally flat surfaces are brought in contact, real (atomic) contact will only occur in small randomly distributed areas, and the area of real contact is usually an extremely small fraction of the nominal contact area. We can visualize the contact regions as small areas where asperities from one solid are squeezed against asperities of the other solid; depending on the conditions the asperities may deform elastically or plastically.

How large is the area of real contact between a solid block and the substrate? This fundamental question has extremely important practical implications. For example, it determines the contact resistivity and the heat transfer between the solids. It is also of direct importance for wear and sliding friction [20], e.g., the rubber friction between a tire and a road surface, and it has a major influence on the adhesive force between two solid blocks in direct contact.

Contact mechanics has a long history. The first study was presented by Hertz [21]. He gave the solution for the frictionless normal contact of two elastic bodies of quadratic profile. He found that the area of real contact $\Delta A$ varies nonlinearly with the load or squeezing force: $\Delta A \propto F_N^{2/3}$. In 1957 Archard [22] applied the Hertz solution to the contact between rough surfaces and showed that for a simple fractal-like model, where small spherical bumps (or asperities) where distributed on top of larger spherical bumps and so on, the area of real contact varies nearly linearly with $F_N$. A similar conclusion was reached by Greenwood [23], Greenwood and Williamson [24], Johnson [25] who again assumed asperities with spherical summit (of identical radius) with a Gaussian distribution of heights, as sketched in Fig. 13.19b. A more general contact mechanics theory has been developed by Bush et al. [26, 27]. They approximated the summit by paraboloids and applied the classical Hertzian solution for their deformation. The height distribution was described by a random process, and they found that at low squeezing force $F_\mathrm{N}$ the area of real contact increases linearly with $F_\mathrm{N}$.

Fig. 13.19

Three models of “rough” surfaces. In case a all the “asperities” are equally high and have identical radius of curvature. In this case, according to the Hertz contact theory, the area of real contact $\Delta A$ between a solid with a flat surface and the shown surface depends non-linearly on the squeezing force (or load) $F_\mathrm{N}$ according to $\Delta A \sim F_\mathrm{N}^{2/3}$. If the asperities have a random distribution of heights as in (b) then, for small $F_\mathrm{N}$, $\Delta A$ is nearly proportional to the squeezing force. If the surface roughness is random with “asperities” of different heights and radius of curvature as in (c), the area of real contact for small $F_\mathrm{N}$ is exactly proportional to the squeezing force

Fig. 13.20

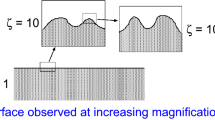
A rubber block (dotted area) in adhesive contact with a hard rough substrate (dashed area). The substrate has roughness on many different length scales and the rubber makes partial contact with the substrate on all length scales. When a contact area is studied at low magnification ($\zeta =1$) it appears as if complete contact occurs in the macro asperity contact regions, but when the magnification is increased it is observed that in reality only partial contact occurs

Figure 13.20 shows the contact between two solids at increasing magnification $\zeta$. At low magnification ($\zeta = 1$) it looks as if complete contact occurs between the solids at many macro asperity contact regions, but when the magnification is increased smaller length scale roughness is detected, and it is observed that only partial contact occurs at the asperities. In fact, if there would be no short distance cut-off the true contact area would vanish. In reality, however, a short distance cut-off will always exist since the shortest possible length is an atomic distance. In many cases the local pressure at asperity contact regions at high magnification will become so high that the material yields plastically before reaching the atomic dimension. In these cases the size of the real contact area will be determined mainly by the yield stress of the solid.

From contact mechanics (see, e.g., [25]) it is known that in the frictionless contact of elastic solids with rough surfaces, the contact stresses depend only upon the shape of the gap between them before loading. Thus, without loss of generality, the actual system may then be replaced by a flat elastic surface [elastic modulus $E$ and Poisson ratio $\nu$, related to the original quantities via $(1-\nu ^2)/E = (1-\nu _1^2)/E_1+(1-\nu _2^2)/E_2$] in contact with a rigid body having a surface roughness profile which results in the same undeformed gap between the surfaces.

One of us (Persson) has recently developed a theory of contact mechanics [28, 29], valid for randomly rough (e.g., self affine fractal) surfaces. In the context of rubber friction, which motivated this theory, mainly elastic deformation occurs. However, the theory can also be applied when both elastic and plastic deformations occur in the contact areas. This case is, of course, relevant to almost all materials other than rubber.

Fig. 13.21

An elastic ball squeezed against a hard, rough, substrate. Left: the system at two different magnifications. Right: the area of contact $A(\lambda )$ on the length scale $\lambda$ is defined as the area of real contact when the surface roughness on shorter length scales than $\lambda$ has been removed

The basic idea behind the new contact theory is that it is very important not to a priori exclude any roughness length scale from the analysis. Thus, if $A(\lambda )$ is the (apparent) area of contact on the length scale $\lambda$ [30] (see Fig. 13.21), then we study the function $P(\zeta )=A(\lambda )/A(L)$ which is the relative fraction of the surface area where contact occurs on the length scale $\lambda =L/\zeta$ (where $\zeta \ge 1$), with $P(1) =1$. Here $A(L)=A_0$ denotes the macroscopic contact area [$L$ is the diameter of the macroscopic contact area so that $A_0\approx L^2$].

Consider the system at the length scale $\lambda =L/\zeta$, where $L$ is the diameter of the nominal contact area. We define $q_L = 2\pi /L$ and write $q=q_L\zeta$. Let $P(\sigma ,\zeta )$ denote the stress distribution in the contact areas under the magnification$\zeta$. The function $P(\sigma ,\zeta )$ satisfies the differential equation (see [28, 29]):

$$\begin{aligned} {\partial P \over \partial \zeta } = f(\zeta ) {\partial ^2 P \over \partial \sigma ^2}, \end{aligned}$$

(13.5)

where $f(\zeta )=G^{\prime }(\zeta )\sigma _0^2$ with

$$\begin{aligned} G(\zeta ) = {\pi \over 4} \left( {E^* \over \sigma _0} \right) ^2 \int \limits _{q_L}^{\zeta q_L} dq \ q^3 C(q), \end{aligned}$$

(13.6)

where $E^*=E/(1-\nu ^2)$.

Equation (13.5) is a diffusion type of equation, where time is replaced by the magnification $\zeta$, and the spatial coordinate with the stress $\sigma$ (and where the “diffusion constant” depends on $\zeta$). Hence, when we study $P(\sigma , \zeta )$ on shorter and shorter length scales (corresponding to increasing $\zeta$), the $P(\sigma ,\zeta )$ function will become broader and broader in $\sigma$-space. We can take into account that detachment actually will occur when the local stress reaches $\sigma = 0$ (we assume no adhesion) via the boundary condition [31]:

$$\begin{aligned} P(0,\zeta )=0. \end{aligned}$$

(13.7)

In order to solve the (13.5) we also need an “initial” condition. This is determined by the pressure distribution at the lowest magnification $\zeta =1$. If we assume a constant pressure $\sigma _0$ in the nominal contact area, then $P(\sigma , 1) = \delta (\sigma -\sigma _0)$.

We assume that only elastic deformation occurs (i.e., the yield stress $\sigma _Y\rightarrow \infty$). In this case

$$ P(\zeta ) = \int \limits _0^\infty d\sigma P(\sigma ,\zeta ). $$

When adhesion is taken into account, tensile stresses can occur at the interface between the two solids, and the boundary condition (13.7) is no longer valid [32, 33], see Sect. 13.6.1. It is straightforward to solve (13.5) with the boundary conditions $P(0,\zeta )=0$ and $P(\infty ,\zeta )=0$ to get

$$\begin{aligned} P(\zeta )= {2\over \pi } \int \limits _0^\infty dx {\mathrm{sin} x \over x} e^{-x^2 G(\zeta )}= \mathrm{erf} \left( {1\over 2 \surd G}\right) . \end{aligned}$$

(13.8)

Note that for small load $\sigma _0$, $G \gg 1$ and in this case (13.8) reduces to $P(\zeta ) \approx P_1(\zeta )$ where

$$\begin{aligned} P_1(\zeta ) = \left[ \pi G(\zeta )\right] ^{-1/2}. \end{aligned}$$

(13.9)

Since $G\sim 1/\sigma _0^2$ it follows that the area of real contact is proportional to the load for small load. Using (13.8) and (13.9) we can write in a general case

$$\begin{aligned} P(\zeta ) = \mathrm{erf} \left( {\surd \pi \over 2} P_1(\zeta )\right) . \end{aligned}$$

(13.10)

Fig. 13.22

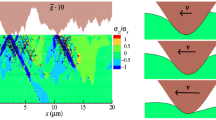
The stress distribution $P(\sigma , \zeta )$ in the contact region between a (rigid) block and an elastic substrate at increasing magnification $\zeta$. a At the lowest (engineering) magnification $\zeta =1$ the substrate surface looks smooth and the block makes (apparent) contact with the substrate in the whole nominal contact area. b, c As the magnification increases, we observe that the area of (apparent) contact decreases, while the stress distribution becomes wider and wider

The physical meaning of (13.5) is as follows: When the system is studied at the lowest magnification $\zeta = 1$ no surface roughness can be observed and the block makes (apparent) contact with the substrate everywhere in the nominal contact area. In this case, if we neglect friction at the interface, the stress at the interface will everywhere equal the applied stress $\sigma _0$, see Fig. 13.22a, so that $P(\sigma , 1) = \delta (\sigma - \sigma _0)$. When we increase the magnification we observe surface roughness with wavelength down to $\lambda = L/\zeta$. In this case one may observe some non-contact regions as shown in Fig. 13.22b. Since the stress must go continuously to zero at the edges of the boundary between the contact and non-contact regions, it follows that the stress distribution $P(\sigma , \zeta )$ will have a tail extending the whole way down to the zero stress as indicated in Fig. 13.22b (right). There will also be a tail toward larger stresses $\sigma > \sigma _0$ because the average stress must be equal to $\sigma _0$. Thus with increasing magnification, the stress distribution will broaden without limit as indicated in Fig. 13.22 (right).

The theory presented above predicts that the area of contact increases linearly with the load for small load. In the standard theory of Greenwood and Williamson [24] this result holds only approximately and a comparison of the prediction of their theory with the present theory is therefore difficult. Bush et al. [26, 27] have developed a more general and accurate contact theory. They assumed that the rough surface consists of a mean plane with hills and valleys randomly distributed on it. The summits of these hills are approximated by paraboloids, the distribution of heights and principal curvatures of which is obtained from the random process theory. This is to be compared with the GW assumption that the caps of the asperities are spherical each having the same mean radius of curvature. As a result of the more random nature of the surface, Bush et al. found that at small load the area of contact depends linearly on the load accordingly to

$$\begin{aligned} {A\over A_0} =\kappa {F_N \over E^*} \left( \int d^2q \ q^2 C(q) \right) ^{-1/2}, \end{aligned}$$

(13.11)

where $\kappa = (2\pi )^{1/2}$. This result is very similar to the prediction of the present theory where, for small load, from (13.6) and (13.9), $A/A_0$ is again given by (13.11) but now with $\kappa = (8/\pi )^{1/2}$. Thus our contact area is a factor of $2/\pi$ smaller than predicted by the theory of Bush et al. Both the theory of Greenwood and Williamson and of Bush et al., assume that the asperity contact regions are independent. However, as discussed in [31], for real surfaces (which always have surface roughness on many different length scales) this will never be the case even at a very low nominal contact pressure. We have argued [31] that this may be the origin of the $2/\pi$-difference between our theory (which assumes roughness on many different length scales) and the result of Bush et al.

The predictions of the theories of Bush et al. [26, 27] and Persson [28, 29] have been compared to numerical calculations (see  [31, 34, 35]). Borri-Brunetto et al. [36] have studied the contact between self affine fractal surfaces using an essentially exact numerical method. They found that the contact area is proportional to the squeezing force for small squeezing forces. Furthermore, it was found that the slope $\alpha (\zeta )$ of the line $A=\alpha (\zeta ) F$ decreased with increasing magnification $\zeta$. This is also predicted by the analytical theory (13.11). In fact, it was found a good agreement between the theory and the computer simulations for the change in the slope with magnification and its dependence on the fractal dimension $D_\mathrm{f}$.

Fig. 13.23

The factor $\kappa$ as a function of Hurst exponent $H$ for self affine fractal surfaces. The two horizontal lines gives the predictions of the theories of Bush et al. (solid line) and Persson (dashed line). From [34]

Hyun et al. have performed a finite-element analysis of contact between elastic self-affine surfaces. The simulations are done for a rough elastic surface contacting a perfectly rigid flat surface. The elastic solid is discretized into blocks and the surface nodes form a square grid. The contact algorithm identifies all nodes on the top surface that attempt to penetrate the flat bottom surface. The total contact area $A$ was obtained by multiplying the number of penetrating nodes by the area of each square associated with each node. As long as the squeezing force is so small that the contact area is below $10\,\%$ of the nominal contact area, i.e., $A/A_0 < 0.1$, the area of real contact is found to be proportional to the squeezing force in accordance with (13.11). In Fig. 13.23 we present the results for the factor $\kappa$ in (13.11) as a function of Hurst exponent $H$ for self affine fractal surfaces. The two horizontal lines gives the predictions of the theories of Bush et al. (solid line) and Persson (dashed line). The agreement with the analytical predictions is quite good considering the ambiguities in discretization of the surface. The algorithm only considers nodal heights and assumes that contact of a node implies contact over the entire corresponding square. This procedure would be accurate if the spacing between nodes where much smaller than the typical size of asperity contacts. However, the majority of the contact area consists of clusters containing only one or a few nodes. Since the number of large clusters grows as $H\rightarrow 1$, this may explain why the numerical results approach Persson’s prediction in this limit.

Hyun et al. also studied the distribution of connected contact regions and the contact morphology. In addition, the interfacial stress distribution was studied and it was found that the stress distribution remained non-zero as the stress $\sigma \rightarrow 0$. This violates the boundary condition (13.7) that $P(\sigma , \zeta )=0$ for $\sigma = 0$. However, it has been shown analytically [31] that for “smooth” surface roughness this latter condition must be satisfied, and we believe that the violation of this boundary condition in the numerical simulations reflects the way the solid was discretized and the way the contact area is defined in the numerical procedure.

Yang et al. [35] have studied contact mechanics using Molecular Dynamics. They also found that the contact area varies linearly with the load for small load, and that the contact area at low magnification is larger than at high magnification (see Fig. 13.24), as predicted by the theory (13.11). The detailed comparison of the simulation results with the theory will be presented elsewhere [35].

Elastic contact theory and numerical simulations show that in the region where the contact area is proportional to the squeezing force, the stress distribution at the interface is independent of the squeezing force. In addition, for an infinite system the distribution of sizes of the contact regions does not depend on the squeezing force (for small squeezing forces). Thus, when the squeezing force increases, new contact regions are formed in such a way that the distribution of contact regions and the pressure distribution remains unchanged. This is the physical origin of Coulombs friction law which states that the friction force is proportional to the normal (or squeezing) force [20], and which usually holds accurately as long as the block-substrate adhesional interaction can be neglected [2].

Fig. 13.24

The contact area between an elastic solid block and a randomly rough hard substrate at high (atomic) magnification (left), and at a lower magnification (right)

6 Adhesion

In this section we discuss adhesion between rough surfaces. We point out that even when the force to separate two solids vanishes, there may still be a finite contact area (at zero load) between two solids as a result of the adhesional interaction between the solids. We also study the adhesion between a thin elastic film and a randomly rough, rigid substrate.

6.1 Adhesion Between Rough Surfaces

A theory of adhesion between an elastic solid and a hard randomly rough substrate must take into account that partial contact may occur between the solids on all length scales. For the case where the substrate surface is self affine fractal theory shows that when the fractal dimension is close to 2, complete contact typically occurs in the macro asperity contact areas (the contact regions observed when the system is studied at a magnification corresponding to the roll-off wavelength $\lambda _0=2\pi /q_0$ of the surface power spectra, see Fig. 13.10), while when the fractal dimension is larger than 2.5, the area of (apparent) contact decreases continuously when the magnification is increased. An important result is that even when the surface roughness is so high that no adhesion can be detected in a pull-off experiment, the area of real contact (when adhesion is included) may still be several times larger than when the adhesion is neglected. Since it is the area of real contact which determines the sliding friction force, the adhesion interaction may strongly affect the friction force even when no adhesion can be detected in a pull-off experiment.

The influence of surface roughness on the adhesion between rubber (or any other elastic solid) and a hard substrates has been studied in a classic paper by Fuller and Tabor [37] (see also [38–44]). They found that already a relative small surface roughness can completely remove the adhesion. In order to understand the experimental data they developed a very simple model based on the assumption of surface roughness on a single length scale. In this model the rough surface is modeled by asperities all of the same radius of curvature and with heights following a Gaussian distribution. The overall contact force was obtained by applying the contact theory of Johnson et al. [45] to each individual asperity. The theory predicts that the pull-off force, expressed as a fraction of the maximum value, depends upon a single parameter, which may be regarded as representing the statistically averaged competition between the compressive forces exerted by the higher asperities trying to prize the surfaces apart and the adhesive forces between the lower asperities trying to hold the surfaces together. This picture of adhesion developed by Tabor and Fuller would be correct if the surfaces had roughness on a single length scale as assumed in their study. However, when roughness occurs on many different length scales, a qualitatively new picture emerges [32, 33], where, e.g., the adhesion force may even vanish (or at least be strongly reduced), if the rough surface can be described as a self affine fractal with fractal dimension $D_\mathrm{f}>2.5$. Even for surfaces with roughness on a single length scale, the formalism used by Fuller and Tabor is only valid at “high” surface roughness, where the area of real contact (and the adhesion force) is very small. The theory presented below is particularly accurate for “small” surface roughness, where the area of real contact equals the nominal contact area.

Fig. 13.25

A rubber surface is “pulled” into a cavity in a hard solid by the rubber-substrate adhesional interaction. The elastic energy stored in the deformation field is of order $E\lambda h^2$

6.1.1 Qualitative Discussion

Let us estimate the energy necessary in order to deform a rubber block so that the rubber fills up a substrate cavity of height $h$ and width $\lambda$. The elastic energy stored in the deformation field in the rubber is given by

$$ U_\mathrm{el} \approx {1\over 2}\int d^3x \ \sigma \epsilon , $$

where the stress $\sigma \approx E \epsilon$, where $E$ is the elastic modulus. The deformation field is mainly localized to a volume ${\sim }\, \lambda ^3$ (see Fig. 13.25) where the strain $\epsilon \approx h/\lambda$. Thus we get $U_\mathrm{el} \approx \lambda ^3 E (h/\lambda )^2 = E \lambda h^2$.

Let us now consider the role of the rubber–substrate adhesion interaction. As shown above, when the rubber deforms and fills out a surface cavity of the substrate, an elastic energy $U_\mathrm{el}\approx E \lambda h^2$ will be stored in the rubber. Now, if this elastic energy is smaller than the gain in adhesion energy $U_\mathrm{ad}\approx \Delta \gamma \lambda ^2$, where $\Delta \gamma =\gamma _1+\gamma _2-\gamma _{12}$ is the change of surface free energy (per unit area) upon contact due to the rubber-substrate interaction (which usually is mainly of the van der Waals type), then (even in the absence of an external load $F_\mathrm{N}$) the rubber will deform spontaneously to fill out the substrate cavities. The condition $U_\mathrm{el} =U_\mathrm{ad}$ gives $h/\lambda \approx (\Delta \gamma /E\lambda )^{1/2}$. For example, for very rough surfaces with $h/\lambda \approx 1$, and with parameters typical for rubber $E=1 \, \mathrm{MPa}$ and $\Delta \gamma = 3 \, \mathrm{meV}/{\AA }^2$, the adhesion interaction will be able to deform the rubber and completely fill out the cavities if $\lambda < 0.1 \, \upmu \mathrm{m}$. For very smooth surfaces $h/\lambda \sim 0.01$ or smaller, so that the rubber will be able to follow the surface roughness profile up to the length scale $\lambda \sim 1 \, \mathrm{mm}$ or longer.

The argument given above shows that for elastic solids with surface roughness on a single length scale $\lambda$, the competition between adhesion and elastic deformation is characterized by the parameter $\theta = Eh^2/\lambda \delta \approx U_\mathrm{el}/U_\mathrm{ad}$, where $h$ is the amplitude of the surface roughness and $\delta = 4(1-\nu ^2)\Delta \gamma /E$the so called adhesion length, $\nu$ being the Poisson ratio of the rubber. The parameter $\theta$ is the ratio between the elastic energy and the surface energy stored at the interface, assuming that complete contact occurs. When $\theta \gg 1$ only partial contact occurs, where the elastic solids make contact only close to the top of the highest asperities, while complete contact occurs when $\theta \ll 1$.

6.1.2 Pull-off Force

Consider a rubber ball (radius $R_0$) in adhesive contact with a perfectly smooth and hard substrate. The elastic deformation of the rubber can be determined by minimizing the total energy which is the sum of the (positive) elastic energy stored in the deformation field in the rubber ball, and the (negative) binding energy between the ball and the substrate at the contact interface. The energy minimization gives the pull-off force [45, 46]

$$\begin{aligned} F_\mathrm{c} = (3\pi /2) R_0 \Delta \gamma . \end{aligned}$$

(13.12)

Consider now the same problems as above, but assume that the substrate surface has roughness described by the function $z=h(\mathbf{x})$. We assume that the surface roughness power spectra has a roll-off wavelength $\lambda _0 = 2\pi /q_0$ (see Fig. 13.10) which is smaller than the diameter of the nominal contact area between the two solids. In this case we can still use the result (13.12), but with $\Delta \gamma$ replaced by $\gamma _\mathrm{eff}$. The effective interfacial energy $\gamma _\mathrm{eff}$ is the change in the interfacial free energy when the elastic solid is brought in contact with the rough substrate. $\gamma _\mathrm{eff}(\zeta )$ depends on the magnification $\zeta$, and the interfacial energy which enters in the rubber ball pull-off experiment is the macroscopic interfacial energy, i.e., $\gamma _\mathrm{eff}(\zeta )$ for $\zeta =1$. If $A_0$ is the nominal contact area and $A_1$ the true atomic contact area, then

$$\begin{aligned} A_0 \gamma _\mathrm{eff}(1) = A_1 \Delta \gamma -U_\mathrm{el}, \end{aligned}$$

(13.13)

where $U_\mathrm{el}$ is the elastic energy stored at the interface as a result of the elastic deformations necessary in order to bring the solids in atomic contact in the area $A_1$.

6.1.3 Stress Probability Distribution

The theory in [32, 33] is based on the contact mechanics formalism described in Sect. 13.4.1. Thus, we focus on the stress probability distribution function $P(\sigma , \zeta )$ which satisfies (13.5):

$$ {\partial P \over \partial \zeta } = f(\zeta ) {\partial ^2 P \over \partial \sigma ^2}. $$

We assume that detachment occurs when the local stress on the length scale $L/\zeta$ reaches $-\sigma _\mathrm{a} (\zeta )$. Thus, the following boundary condition is valid in the present case

$$ P(-\sigma _\mathrm{a}(\zeta ),\zeta )= 0. $$

This boundary condition replaces the condition $P(0,\zeta )=0$ valid in the absence of adhesion (see Sect. 13.4.1).

Let us consider the system on the characteristic length scale $\lambda = L/\zeta$. The quantity $\sigma _\mathrm{a}(\zeta )$ is the stress necessary to induce a detached area of width $\lambda$. This stress can be obtained from the theory of cracks, where for a penny-shaped crack of diameter $\lambda$

$$\begin{aligned} \sigma _\mathrm{a} = \left[ {\pi \gamma _\mathrm{eff}(\zeta ) E \over (1-\nu ^2) \lambda }\right] ^{1/2} = \left[ {\gamma _\mathrm{eff}(\zeta ) E q \over 2 (1-\nu ^2)}\right] ^{1/2}, \end{aligned}$$

(13.14)

where $q=2\pi /\lambda = \zeta q_L$. In [32, 33] we have derived two equations for $\gamma _\mathrm{eff}(\zeta )$ and $P(\zeta )$ which determine how these quantities depend on the magnification $\zeta$; those equations are the basis for the numerical results presented below.

Fig. 13.26

a The macroscopic interfacial energy as a function of the dimensionless surface roughness amplitude $q_0 h_0$. b The normalized area of real contact, $P(\zeta _1)=A(\zeta _1)/A_0$, as a function of $q_0 h_0$. The curves correspond to different adhesion energies: $q_0 \delta = 0.1$, 0.2, 0.4 and 0.8 as indicated. For $H=0.8$ and $q_1/q_0=\zeta _1=100$

6.1.4 Numerical Results

Figure 13.26 shows (a) the effective interfacial energy $\gamma _\mathrm{eff}(\zeta )$ ($\zeta =1$) and (b) the normalized area of real contact, $P(\zeta _1)=A(\zeta _1)/A_0$, as a function of $q_0 h_0$, $h_0$ being the surface r.m.s. roughness and $q_0$ the roll-off wave vector. Results are shown for different adhesion lengths $\delta =4(1-\nu ^2)\Delta \gamma /E$: $q_0 \delta = 0.1$, 0.2, 0.4 and 0.8. We will refer to $\gamma _\mathrm{eff}(1)$ at the magnification $\zeta = 1$ as the macroscopic interfacial free energy which can be deduced from, e.g., the pull off force for a ball according to (13.12). Note that for $q_0\delta =0.4$ and 0.8 the macroscopic interfacial energy first increases with increasing amplitude $h_0$ of the surface roughness, and then decreases. The increase in $\gamma _\mathrm{eff}$ arises from the increase in the surface area. As shown in Fig. 13.26b, for small $h_0$ the two solids are in complete contact, and, as expected, the complete contact remains to higher $h_0$ as $\delta \sim \Delta \gamma /E$ increases. Note also that the contact area is nonzero even when $\gamma _\mathrm{eff}(1)$ is virtually zero: the fact that $\gamma _\mathrm{eff}(1)$ (nearly) vanish does not imply that the contact area vanish (even in the absence of an external load), but imply that the (positive) elastic energy stored at the interface just balance the (negative) adhesion energy from the area of real contact. The stored elastic energy at the interface is given back when removing the block, and when $\gamma _\mathrm{eff} (1) \approx 0$ it is just large enough to break the block-substrate bonding.

6.1.5 Plate Adhesion

In this section we discuss the adhesion of a thin elastic plate to a randomly rough hard substrate. This topic is important for many applications such as thin films used as protective coatings [47], for the manufacturing of multilayered wafer structures [48], or in bio-films for orthopedic implants [49]. The problem under consideration is also of great importance for understanding the adhesion of flies, bugs, and lizards to a rough substrate (see Fig. 13.27), [50, 51] or the adhesive behavior of recently biologically-inspired adhesive films [52].

Fig. 13.27

Insect attachment systems consist of fibers or hair which terminates with leaf-like plates which can easily deform (without storing a lot of elastic energy) to bind strongly even to very rough substrates

Fig. 13.28

a The normalized macroscopic interfacial energy and b the normalized area of real contact, as a function of the dimensionless surface roughness amplitude $q_0h_0$. Thick lines are for the plate case and thin lines are for the semi-infinite solid case. Results are for $H=0.8$ and $q_0d=0.63$, and for two different values of $q_0\delta$

Here we consider in detail the case of a thin plate in partial contact with a hard substrate with a self-affine fractal rough surface. Figure 13.28 (thick lines) shows (a) the macroscopic interfacial energy $\gamma _{eff}\left( 1\right)$, i.e. the effective interfacial energy calculated at the magnification $\zeta =1$, and (b) the normalized area of real contact $P\!\left( \zeta _{1}\right)$ at the maximum magnification $\zeta =\zeta _{1}$, as a function of the dimensionless roughness amplitude $q_{0}h_{0}$. We show results for three different values of $q_{0}\delta$. The results are for $H=0.8$, i.e. $D_{f}=2.2$, and for a dimensionless thickness of the plate equal to $q_{0}d=0.63$. Note that the macroscopic interfacial energy initially increases with the amplitude $h_{0}$ of the rough profile up to a maximum value, and after decreases with $h_{0}$. This is caused by the increase of the real contact area produced by the fine structure of the rough profile. Figure 13.26b shows, indeed, that at small $h_{0}$ the plate adheres in full contact to the substrate, so that an increase of the surface roughness produces a corresponding increases of the area of contact and, hence, of the surface energy. However this is no more true at large $h_{0}$, because of the reduction of the area of real contact. Figure 13.26 also shows that, as expected, the roughness-induced increment of the macroscopic interfacial energy grows by increasing the adhesion length $\delta \sim \Delta \gamma /E$, and that the full contact condition remains to higher amplitude $h_{0}$ as $\delta$ increases.

In Fig. 13.28 we compare the results obtained for the plate case (thick lines) with those of the semi-infinite solid (thin lines). As expected, because of the higher compliance of the plate, both the macroscopic interfacial energy $\gamma _\mathrm{eff}\left( 1\right)$ and the normalized area of real contact $P\!\left( \zeta _{1}\right)$ are larger than for the semi-infinite solid case.

To summarize, at small magnification (long length scales) the plate, because of its higher compliance, is able to adhere in apparent full contact to the long wavelength corrugation of the underlying surface. That is, at length scales longer than the plate thickness, the gain in the adhesion energy upon the contact with the substrate overcomes the repulsive elastic energy produced by the elastic deformations, and the plate is able to fill out the large cavities of the rigid substrate. This produces a larger area of contact and an enhanced capability to adhere to a rough surface in comparison to the semi-infinite elastic solid case. However, at large enough magnification (small length scales) the plate behaves as a semi-infinite solid, and, depending on the roughness statistical properties, the area of true atomic contact may be much smaller than the nominal contact area.

Fig. 13.29

The macroscopic interfacial energy (obtained from the pull-off force) for a smooth rubber surface (ball) in contact with Perspex surface as a function of the roughness (center line average) of the Persplex. Results are shown for a “soft” rubber ($E=0.063 \, \mathrm{MPa}$) and a “hard” rubber ($E=0.487 \, \mathrm{MPa}$). From [40]

6.1.6 Experimental Manifestations

Unfortunately, the surface roughness power spectrum has not been measured for any surface for which adhesion has been studied in detail. Instead only the roughness amplitude (center line average) and the radius of curvature of the largest surface asperities was determined. Nevertheless, the experimental data of Fuller and Tabor [37], Briggs and Briscoe [40] and Fuller and Roberts [41] are in good qualitative agreement with our theoretical results. In Fig. 13.29 we show the macroscopic interfacial energy for “hard” and “soft” rubber in contact with Perspex, as a function the substrate (Perspex) roughness amplitude as obtained by Briggs and Briscoe [40]. It is not possible to compare these results quantitatively with the theory developed above since the power spectrum $C(q)$ was not measured for the Perspex substrate. Even if the surfaces would be self affine fractal as assumed above, not only the surface roughness amplitude will change from one surface to another, but so will the long distance cut off length $\lambda _0$ and hence also the ratio $\zeta _1=q_1/q_0$. In the experiments reported on in [40] the Perspex surfaces where roughened by blasting with fine particles. The roughness could be varied through the choice of the particles and the air pressure.

Fig. 13.30

The pull-off force as a function of the squeeze force or load. For silicon rubber in contact with a smooth glass surface. From [53]

One practical problem is that most rubber materials have a wide distribution of relaxation times, extending to extremely long times. This effect is well known in the context of rubber friction (see Sect. 13.6.1), where measurements of the complex elastic modulus show an extremely wide distribution of relaxation times, resulting in large sliding friction even at very low sliding velocities, $v <10^{-8}$ m/s.

The effect of the stored elastic energy on adhesion has recently been studied using a polyvinylsiloxane rubber block squeezed against a smooth glass surface for a fixed time period before measuring the pull-off force [53]. The square-symbols in Fig. 13.30 show the pull-off force as a function of the squeezing force. For squeezing forces $F_\mathrm{N}>850 \, \mathrm{mN}$ the pull off force decreases. This may be explained by a drastic increase of the elastic energy stored in the rubber because of the strong deformation of the rubber (which remains even when the load is removed as a result of the rubber–glass friction at the interface), see Fig. 13.31 (top). This energy, freed during the process of unloading, will help to break the adhesive bonds at the interface. This effect is even stronger when the surface is structured. Thus, the triangles in the figure shows the pull-off force when the rubber surface is covered by a regular array of rubber cylindrical asperities. In this case the pull-off force drops to nearly zero for $F_\mathrm{N} >700 \, \mathrm{mN}$. Visual inspection shows that in this case the cylindrical asperities at high load bend and make contact with the glass on one side of the cylinder surface, see Fig. 13.31 (bottom). This again stores a lot of elastic energy at the interface which is given back during pull-off, reducing the pull-off force to nearly zero.

Fig. 13.31

Elastic deformation of a rubber block with a smooth surface (top) and a structured surface (bottom). a shows the initial state before applying a squeezing force, and b the new state (without load) after applying (and then removing) a very large squeezing force. In state (b) a lot of elastic energy is stored in the rubber which is “given back” during pull-off resulting in a nearly vanishing pull-off force

6.1.7 The Role of Plastic Yielding on Adhesion

When the local stress in the asperity contact regions between two solids becomes high enough, at least one of the solids yields plastically. This will tend to increase the effective adhesion (or pull-off force) for the following three reasons. First, the area of real contact between the solids will increase as compared to the case where the deformations are purely elastic. Secondly, the amount of stored elastic energy in the contact regions (which is given back during pull-off) will be reduced because of the lowered elastic deformations. Finally, for many materials plastic yielding will strengthen the junctions [54]. For example, most metals are protected by thin oxide layers, and as long as these are intact the main interaction between the surfaces in the contact areas may be of the van der Waals and electrostatic origin. However, when plastic yielding occurs it may break up the oxide films resulting in direct metal-metal contact and the formation of “cold-welded” junctions. When this occurs, because of the high ductility of many metals, during pull-off “long” metallic bridges may be formed between the solids so that instead of having junctions popping one after another during pull-off, a large number of adhesive junctions may simultaneously impede the surface separation during pull-off, leading to a large pull-off force. However, experiment have shown [8] that just squeezing before pull-off will in general only result in very few cold welded junctions, while squeezing and sliding will break up the oxide film, resulting in the formation of many more cold welded contact regions, and will hence result in a much larger pull-off force.

Fig. 13.32

Even the weakest force in Nature of relevance in condensed matters physics, namely the van der Waals force, is relative strong on a macroscopic scale. Thus, for example, if the bond breaking occur uniformly over the contact area as in (b), already a contact area of order $1 \, \mathrm{cm}^2$ can sustain the weight of a car (i.e., a force of order $10^4 \, \mathrm{N}$) [see (a)]. However, on a macroscopic scale the bond-breaking does not usually occur uniformly over the contact area, but by crack propagation, see (c), which drastically reduce the pull-off force. In addition, interfacial surface roughness drastically reduces the pull-off force

6.2 The Adhesion Paradox

The biggest “mystery” related to adhesion is not why it is sometimes observed but rather why it is usually not observed. Thus, even the weakest force in Nature of relevance in condensed matter physics, namely the van der Waals force, is relatively strong on a macroscopic scale. For example, even a contact area of order $1 \, \mathrm{cm}^2$ can sustain the weight of a car (i.e., a force of order $10^4 \, \mathrm{N}$) [see Fig. 13.32a] also when only the van der Waals interaction operates at the interface. [Here we have assumed that the bond breaking occurs uniformly over the contact area as illustrated in Fig. 13.32b.] However, this is never observed in practice and this fact is referred to as the adhesion paradox.

There are several reasons why adhesion is usually not observed between macroscopic bodies. For example, on a macroscopic scale the bond-breaking usually does not occur uniformly as in Fig. 13.32b, but occurs by crack propagation, see Fig. 13.32c. The local stress at the crack tip is much higher than the average stress acting in the contact area, and this drastically reduces the pull-off force. Another reason, already addressed in Sect. 13.6.1, is the influence of surface roughness. Thus, for elastically hard surfaces the true (atomic) contact between the solids at the interface is usually much smaller than the nominal contact area. In addition, the elastic energy stored in the solids in the vicinity of the contact regions is given back during pull-off and helps to break the interfacial bonds between the solids (see Sect. 13.6.1).

It is interesting to note that for very small solid objects, typically of order $100 \, \upmu \mathrm{m}$ or smaller, the bond breaking may occur uniformly over the contact area (no crack propagation) so that adhesion between smooth surfaces of small objects, e.g., in micromechanical applications (MEMS), may be much stronger than for macroscopic bodies, and this fact must be taken into account when designing MEMS [55, 56].

6.3 The Role of Liquids on Adhesion Between Rough Solid Surfaces

As explained in Sect. 13.6.1, surface roughness reduces the adhesion between clean surfaces. First, it lowers the area of real contact. Since the adhesion interaction comes almost entirely from the area where the solids make atomic contact, it is clear that the surface roughness may drastically reduce the adhesion. Secondly, elastic deformation energy is stored in the vicinity of the asperity contact regions. During pull-off the elastic energy is “given back” to the system, usually resulting in a drastic reduction in the effective adhesion and the pull-off force.

Most surfaces have at least nano-scale roughness, and hard solids in the normal atmosphere have at least a monolayer of liquid-like “contamination” molecules, e.g., water and hydrocarbons. Small amount of (wetting) lubricant or contamination liquids between rough solid walls may drastically enhance the adhesion. Thus, for surfaces with nanoscale roughness, a monolayer of a wetting liquid may result in the formation of a large number of nano-bridges between the solids, which increases the pull-off force. This effect is well known experimentally. For example, the adhesion force which can be detected between gauge blocks (steel blocks with very smooth surfaces) is due to the formation of many very small capillary bridges made of water or organic contamination. For thicker lubrication or contamination films the effective adhesion will be more long-ranged but the pull-off force may be smaller. The thickness of the lubricant or contamination layer for which the pull-off force is maximal will in general depend on the nature of the surface roughness, but is likely to be of order the root-mean-square roughness amplitude. In fact, it is an interesting and important problem to find out at exactly what liquid thickness the pull-off force is maximal.

Some insects such as flies or crickets inject a thin layer of a wetting liquid in the contact region between the insect attachment surfaces and the (rough) substrate. The optimum amount of injected liquid will depend on the nature of the substrate roughness, and it is likely that the insect can regulate the amount of injected liquid by a feedback system involving the insect nerve system.

Fig. 13.33

The variation of the average pressure during retraction developed as the block moves a distance of 16 Å away from the substrate. Octane C$_8$H$_{18}$ was used as lubricant. Pull-off (retraction) velocity was $v_\mathrm{z} = 1 \, \mathrm{m/s}$. a For the flat substrate without lubricant. b For the corrugated substrate without lubricant. Curves c–f show results for the corrugated substrate with about 1/8, 1/4, 1/2 and 1 monolayer of octane in the contact region, respectively. For clarity, the curve for the flat substrate (a) is displaced to the right, by $2 \, {\AA }$

Here we consider the adhesion between two solid elastic walls with nanoscale roughness, lubricated by octane [43, 44, 57]. We consider two types of substrates (bottom surface)—flat and nano-corrugated (corrugation amplitude $1 \, \mathrm{nm}$ and wavelength of the corrugation in $x$ and $y$ direction, $4 \ \mathrm{nm}$)—and varied the lubricant coverage from ${\sim }\, 1/8$ to ${\sim }\, 4$ monolayers of octane. The upper surface (the block) is assumed to be atomically smooth but with a uniform cylinder curvature with a radius of curvature $R \approx 100 \, \mathrm{nm}$ (see Fig. 13.35). The results presented here have been obtained using standard molecular dynamics calculations [43].

Fig. 13.34

Snapshot pictures (for three different block positions $d = 0, 3$ and $6 \,{\AA }$) of the lubricant layer during retraction. We only show the lubricant molecules in the central part of the contact area between the block and the substrate surfaces (top view, surfaces parallel to the plane of the image). Octane C$_8$H$_{18}$ was used as lubricant. Pull-off (retraction) velocity was $v_\mathrm{z} = 1 \, \mathrm{m/s}$. For the corrugated substrate with about 1/4 monolayer of octane in the contact region. The circles indicate the position of several asperity tops of the corrugated substrate surface

Figure 13.33 shows the variation of the average pressure during retraction as the block moves a distance of 16 Å away from the substrate. The pull-off (retraction) velocity was $v_z = 1 \, \mathrm{m/s}$. We have varied the lubricant coverage from 0 to 1 monolayer in the contact region. The pull-off force is maximal when the adsorbate coverage is of the order of one monolayer [curve (f)]. However, the pull-off force is still smaller than for a flat substrate without lubricant [curve (a)]. As a function of the octane coverage (for the corrugated substrate) the pull-off force first increases as the coverage increases from zero to ${\sim }\, 1$ monolayer, and then decreases as the coverage is increased beyond monolayer coverage (not shown).

Fig. 13.35

Snapshot pictures (for six different block positions) during retraction. The snapshot pictures show the side view of the central $108 \, {\AA }\times 50 \, {\AA }$ section (in the $xy$-plane) of the contact area. Octane C$_8$H$_{18}$ was used as lubricant. Pull-off (retraction) velocity was $v_\mathrm{z} = 1 \, \mathrm{m/s}$. For the corrugated substrate with about 1/4 monolayer of octane in the contact region

At low octane coverage, the octane molecules located in the substrate corrugation wells during squeezing, are pulled out of the wells during pull-off, forming a network of nano capillary bridges around the substrate nanoasperities, thus increasing the adhesion between two surfaces, see Figs. 13.34 and 13.35. For greater lubricant coverages a single capillary bridge is formed.

Let us discuss the nature of the adhesion for the corrugated substrate, with about 1/4 monolayer of octane in the contact region. Figure 13.34 shows snapshot pictures of the lubricant layer during retraction, as the block moves away from the substrate for three different block positions $d = 0, 3$ and $6 \, {\AA }$. Only the central part of the contact between the block and the substrate is shown, top view, after removing the block and substrate atoms. In the beginning ($d = 0 \, {\AA }$) octane molecules are located in the substrate corrugation wells, or cavities with direct metal–metal contact between the block and the top of the substrate nano asperities (see Fig. 13.35). During retraction ($d = 3 \, {\AA }$) the octane molecules are pulled out of the wells forming an almost symmetric network of nano-bridges around the asperity tops, increasing the adhesion between the two surfaces. This configuration corresponds to the maximal adhesion force, see curve (d) in Fig. 13.33. Thus maximal adhesion is achieved via the formation of many small capillary nano-bridges, involving just a few molecules for each bridge (see Fig. 13.35). Further retraction ($d = 6 \, {\AA }$) results in the collapse of the nano-bridges and the formation of a single “large” capillary bridge in the center of the contact region.

7 Summary and Outlook

We have discussed the origin of friction and adhesion between hard solids such as quasicrystals. However, most of the results presented above are valid for all types of solids. We have emphasized the fundamental role of surface roughness on many contact mechanics problems, in particular for friction and adhesion between solids bodies.

Surface roughness has a huge influence on many common phenomena. It is the main reason for why macroscopic bodies usually do not adhere to each other with any measurable strength. For example, if the floor and the sole of the shoes would be atomically smooth and clean, it would be impossible to walk on the floor! The (nearly) absence of adhesion in most situations is crucial for the function of many man-made constructions.

The surface to volume ratio of solid objects increases as the lateral size of the object decreases. The role of surface roughness becomes therefore more important as the size of objects decreases. The present drive toward the miniaturization of mechanical devices, e.g., MEMS, requires a better understanding of the role of surface roughness on, e.g., contact mechanics and adhesion.

Surface roughness is also of great importance for the function of many biological systems. Thus, flies, bugs, crickets and lizards have developed very soft layers on their attachment organs which allow them to attach and move on both very smooth and rough vertical solid walls, e.g. stone walls or leafs. Another example is non-wetting coatings on plant surfaces based on surface roughness on many different length scales (the so called Lotus effect) [11].

The roughness of surfaces can today be studied strait forwardly using standard equipments based on optical methods and stylus methods, e.g., the atomic force microscope (AFM). These methods cover the whole length scale from atomic dimension to macroscopic distances. Thus, the AFM can probe the surface profile from ${\sim }\, 1 \, \mathrm{nm}$ to $100 \; \upmu \mathrm{m}$ and optical methods from ${\sim }\, 1 \, \upmu \mathrm{m}$ to kilometers. For randomly rough surfaces, the most important quantity which can be deduced from the measured height profile is the surface roughness power spectra. We have shown in this paper how the power spectra determines the contact mechanics and adhesion for solid objects in direct contact. It also govern rubber friction on rough substrates, e.g., tires on a road surfaces, and influence other phenomena of technological importance, e.g., the roughness induced leaking of sealings.

Thus, studies of surface roughness is important not only for understanding many natural and biological phenomena, but also for many technological processes. The present drive toward miniaturization and the design of optimal systems by transfer of ideas from studies on biological systems to materials science (bionics) [11], is likely to accelerate the interest and efforts to study and predict the influence of surface roughness on many phenomena.