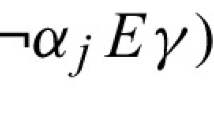Reflections on a Theorem of Henkin

Abstract

The λδ-calculus is the λ-calculus augmented with a discriminator which distinguishes terms. We consider the simply typed λδ-calculus over one atomic type variable augmented additionally with an existential quantifier and a description operator, all of lowest type. First we provide a proof of a folklore result which states that a function in the full type structure of [n] is λδ-definable from the description operator and existential quantifier if and only if it is symmetric, that is, fixed under the group action of the symmetric group of n elements. This proof uses only elementary facts from algebra and a way to reduce arbitrary functions to functions of lowest type via a theorem of Henkin. Then we prove a necessary and sufficient condition for a function on [n] to be λδ-definable without the description operator or existential quantifier, which requires a stronger notion of symmetry.

1 Introduction

Let ℳⁿ be the full type structure over a ground domain of size n. It is folklore that a member of ℳⁿ is symmetric if and only if it is definable in type theory. The origin of this theorem is murky. It is safe to say that it was not known to Newton. Robin Gandy told the senior author that he knew it in the 1940s. It is not unlikely it was known to Church before this. It occurred to the senior author as a student in the 1970s after reading Andrews [1] and Lauchli [5]. There are not many proofs in the literature. A proof appears in Van Benthem [8] in the 1990s, but it is incomplete. A proof follows immediately from an observation due to Leon Henkin [4].

In this note, we intend to do two things. First, we shall generalize the folklore theorem to Church’s λδ-calculus [3] for the ℳⁿ, and also to the “profinite” model which is the “limit” of the ℳⁿ. Second, we shall provide a straightforward proof of the folklore theorem itself using only simple facts about the symmetric group and its action on equivalence relations.

2 Preliminaries

We first do a review of the lambda calculus, simple types, Henkin-style semantics, and extending simple typed lambda calculus to type theory.

2.1 Lambda Calculus

2.1.1 Untyped Lambda Calculus

The untyped lambda calculus serves as the underlying language of our more disciplined systems. We give a quick reminder.

Definition 1

Fix some countable set of variables V={x ₁,x ₂,…}. We define the set of λ-terms, which we denote by Λ inductively:

Variables:

V⊆Λ

Abstraction:

If x∈V and M∈Λ, then

Application:

If M,N∈Λ, then (MN)∈Λ.

We will always identify terms that are the same up to a renaming of bound variables (α equivalence). Moreover, we define a notion of convertibility = _βη formed by the reduction rules

Using this notion of reduction, a term M is in βη normal form if there is no term N such that M→ _βη N.

We write Λ ^∅ for the set of all closed terms, that is, terms with no free variables.

Remark 1

(Notational Conventions for Terms)

We will follow all ordinary conventions when writing terms. When parentheses are omitted, we will associate terms to the left, so that MNP is parsed as (MN)P. The symbol which is “Church’s dot notation” will be used for binders to remind the reader that we are binding in the largest scope possible; so in the x is bound by the λ in both M and N. We write λ-terms with uppercase Latin letters, like F,G,M,N.

What follows are a few useful closed terms that we will use throughout the paper:

2.1.2 Simple Types

Here, we will put a typing discipline on Λ.

Definition 2

On Λ we define the simple typing system in the style of Church, which we notate λ _→. We will have only one type constant, which we denote 0. The set of types, T, is inductively defined as the smallest set containing 0 and closed under arrows, that is, if α and β are types, then α→β is a type. We will use lower case Greek letters at the beginning of the alphabet for types, such as α,β,γ.

For the terms of the system, we mimic what we did the untyped case, but with restrictions. We defined the set Λ _→(α), the set of typed terms of type α, by induction:

Variables:

If x∈V and α is a type, then x ^α∈Λ _→(α).

Abstraction:

If M∈Λ _→(β) and x∈V, then

Application:

If M∈Λ _→(α→β) and N∈Λ _→(α) then

$$MN\in\varLambda_{\to}(\beta) $$

We write $\varLambda_{\to}^{\emptyset}(\alpha)$ for the set of closed terms of type α. We write Λ _→ for ⋃ _α Λ _→(α). Similarly for $\varLambda_{\to }^{\emptyset }$. Instead of writing M∈Λ _→(α), we will usually write M:α, which we read “M has type α” or “M is in α.”

Example 1

The closed terms we had previously defined are all typeable. For example, one can see both True and False have types 0→(0→0).

Definition 3

(Long Normal Form)

We define the long (βη) normal form of a term M:α by induction on the type α. If M:0, then M is in long normal form if and only if it is of the form xM ₁…M _m where each M _i is in long normal form. If M:α→β, then M is in long normal form if M is of the form , where N is in long normal form. Every term has a unique long normal form, which one can obtain by η expansions.

Example 2

The long normal form of the term is

Remark 2

(Notational Conventions for Types)

We will associate types the right to facilitate Currying; therefore α→β→γ is parsed as α→(β→γ). We will tend to not decorate variables with types when it is otherwise deducible from context what type the variable is.

We will use the notation α ⁿ→β to stand for (α→(α→⋯(α→β)⋯)). That is, a term of this type expects n-many inputs of type α and returns an output of type β. Also to improve readability, we will write the type for booleans α→α→α as Bool _α .

2.2 Semantics

In this section, we will define a set-theoretic framework for which we can interpret typed lambda terms. We first give some more general definitions because we will later introduce different semantics.

Definition 4

Suppose we have an indexed family of sets ℳ(α) for each type α. Let ⋅ _α,β be a map from ℳ(α→β)×ℳ(α)→ℳ(β). We say that this is a typed applicative structure if it is extensional; that is, for every f,g∈ℳ(α→β), if we know for every n∈ℳ(α) f⋅ _α,β n=g⋅ _α,β n, then f=g.

Definition 5

Fix a natural number n. We define a model ℳⁿ as follows, by induction on the type α:

That is, we interpret the type 0 to be the set [n], the first n natural numbers, and the type α→β is the function space of objects of type α to objects of type β. Note that this is clearly a typed applicative structure where ⋅ is just function application. This particular typed applicative structure is called the full type structure over [n].

We will write these set-theoretic functions as lowercase Latin letters like f,g,h.

Now that we have a framework which to interpret types, we can make an evaluation of the terms into this framework.

Definition 6

Fix a natural number n and a function φ mapping typed variables x ^α to members of ℳⁿ(α). Then we define the evaluation of term with respect to φ by induction on the term:

2.3 Type Theory

To begin a path from simply typed lambda calculus to a type theory, we need an equality symbol, which we shall call δ. Following the example of Andrews [1], such an addition for all types would lead us to the study of higher order logic. For our purposes, we will just be dealing with first order (classical) logic, and our equality symbol is only for ground type 0.

To add equality, we augment our language with a new constant symbol δ. For the typing rules, we just say that δ is a term of type 0→0→Bool₀, defined by the following axiom:

$$(x=y \implies\delta xy uv = u) \wedge\bigl(\neg(x=y) \implies \delta xyuv = v \bigr) $$

In Statman [7] it was proven that under βη conversion, the equational consequences of this axiom are exactly the same as from these rules:

$$\begin{aligned} \begin{array}{rcl@{\quad}l} \delta MMUV &=& U & \text{(Reflexivity)}\\ \delta MNUU &=& U & \text{(Identity)}\\ \delta XYUV &=& \delta YXVU & \text{(Symmetry)} \\ \delta XYXY &=& Y & \text{(Hypothesis)} \\ P(\delta MN) &=& \delta MN(P\mathbf {True})(P\mathbf {False}) & \text{(Monotonicity)} \\ \delta MN(\delta MNUV)W &=& \delta MNUW &\text{(Stutter)} \\ \delta MNU(\delta MNWV) &=& \delta MNUV &\text{(Stammer)} \end{array} \end{aligned}$$

In the previous section on the untyped lambda calculus, we define closed terms representing the booleans of True and False, as well as And and Not. For first-order type theory we must add a first-order quantifier, ∃:(0→Bool₀)→Bool₀ with the rule

$$\exists M = \begin{cases} \mathbf {True}& \mbox{if } Mn= \textbf{True}\ \mbox{for some } n:0 \\ \mathbf {False}& \mbox{otherwise} \end{cases} $$

and a description operator ι of type (0→Bool₀)→0→0 with the rule

$$\iota M m = \begin{cases} n &\mbox{if } Mn=\textbf{True}\mbox{ and }n\mbox{ is unique such} \\ m & \mbox{otherwise} \end{cases} $$

Also, we can extend our semantics to handle the terms involving δ,∃, and ι in the obvious way; for example, for the equality operator, is the characteristic function of equality. The following shows that the semantics provided by ℳ(n) is sound and complete for βηδ.

Theorem 1

(Soundness and Completeness)

Let M and N be terms of type α.

• 1. (Soundness) If M= _βηδ N, then for every $n\in \mathbb{N}$ and every φ, we have

• 2. (Completeness) If M≠ _βηδ N, then there are some $n\in\mathbb{N}$ and φ such that

Proof

Proof in Statman [7]. □

3 Henkin’s Theorem

We would like to be able to say that every finite function in the above semantics can be represented in some way in the λδ-calculus.

Theorem 2

(Henkin’s Theorem)

Fix an assignment of variables to types φ, a natural number n, and a type α.

• There is a δ _α :0ⁿ→α→α→Bool _α such that for every f,g,h,j∈ℳⁿ(α),

  

• If f∈ℳⁿ(α), then there is F:0ⁿ→α such that

  

Proof

Go by induction on the type α.

If α=0, then define

If f∈ℳⁿ(0), then f∈[n], so f=i for some 1≤i≤n. Then we can just F be the ith projection:

Suppose α=β→γ. We have δ _β and δ _γ , closed terms of types β and γ, respectively, that have the desired property. Enumerate all elements of ℳⁿ(β), {m ₁,m ₂,…,m _k }. By induction hypothesis we know that these are representable; that is, there are closed terms M ₁,…,M _k such that for every i. So define

where $\bar{x}$ is shorthand for x ₁…x _n , and M∧N is And(M)(N). One can easily verify this as desired.

Let f be a function in ℳⁿ(β→γ). Note that f(m _i )∈ℳⁿ(γ) by the definition of the semantics. Therefore, set p _i =f(m _i ). By induction hypothesis, there are closed terms P _i for every 1≤i≤k such that . We define F by doing cases on what our input is:

where “If M then N else P” is “shorthand” for (MN)P. Similarly, this is easily shown to be as claimed. □

The following is an easy corollary to the completeness result stated above and Henkin’s theorem.

Corollary 1

Take M,N:α ₁→α ₂→⋯→α _k →0 with all free variables having type 0. If M≠ _βηδ N, then there are some n and closed terms F _i :0ⁿ→α _i such that

$$M(F_1\bar{x})\cdots(F_k\bar{x}) \neq_{\beta\eta\delta} N(F_1\bar{x})\cdots(F_k\bar{x}) $$

where $\bar{x}$ includes all variables free in both M and N.

Proof

By soundness, for some φ and n, we have . Take $\bar{x}$ to be a sequence of length n of free variables of type 0, containing all the free variables of M and N. Then clearly .

These are set-theoretic functions, therefore there are f ₁∈ℳⁿ(α ₁), …, f _k ∈ℳⁿ(α _k ) such that . By Henkin, all these f _i have closed terms of type 0ⁿ→α _i representing them; denote those closed terms F _i .

Therefore, by completeness, the result follows. □

Consider for each type α the set $\varLambda^{\delta}_{\to }(\alpha)$, that is, the set of terms of $\lambda_{\rightarrow}^{\delta}$ of type α. Define the set 𝒯(α) by

That is, all properly typed terms of type α, modulo βηδ conversion. As a consequence to the above theorem, we have that 𝒯 is an typed applicative structure. For each natural number n, we consider the set of n free variables X:={x ₁,x ₂,…,x _n } of type 0. We can then take the set of all terms M in 𝒯 that are λ-definable from this set (and δ).

This is not necessarily a typed applicative structure. For we may have two terms M ₁ and M ₂ that are not extensionally equal, but are with respect to all terms λ-definable from X∪{δ}. That is, none of the witnesses that M ₁ and M ₂ are different are λ-definable from X∪{δ}. Therefore, we consider only the equivalence classes formed by equality under δ restricted only to the ground set X. So, if we have M ₁ and M ₂ as above, we collapse them. We call the resulting model Gandy hull of X∪{δ} in 𝒯. This is a typed applicative structure, which we will denote by 𝒯ⁿ. For more information on the Gandy hull construction, see [2].

One can see that there is a natural relationship between 𝒯ⁿ and ℳⁿ. There is a natural homomorphism from 𝒯ⁿ to ℳⁿ, which is completely determined by a mapping of X to [n]. Further, we can look at some infinite models. For instance, we can define ℳ^ω to be the full type structure over the natural numbers; so ℳ^ω(0)={1,2,3,…}. We can then take the Gandy hull of {1,2,3,…}∪δ in this model and get a model ℳ.

This model could be obtained another way. Fix a bijection from free variables of type 0 and ω. Then one can build a corresponding homomorphism from 𝒯 to ℳ^ω. The image is exactly ℳ. These models are discussed further in Statman [6].

4 Folklore Theorem

Definition 7

The symmetric group on n elements, which we denote as S _n , is the subset of ℳⁿ(0→0) that are bijections. These form a group with the operation of composition. We call members of the group permutations. We shall use lower case Greek letters in the middle of the alphabet to stand for permutations, for example, π,ρ,σ,τ.

Of course, members of S _n act canonically of type 0 by application. But, we can lift this action to higher types. Consider π∈S _n . We define π _α ∈ℳⁿ(α→α) by induction on α. If α=0, then we just take π ₀(n)=π(n). If α=β→γ, then we define

$$\pi_\alpha(f) = \pi_\gamma\circ f \circ\pi_{\beta}^{-1} $$

Therefore, we have an action of S _n on our entire model ℳⁿ, where π acts on f:α by π _α (f). For this action, we will write π⋅f.

If f∈ℳⁿ, then we denote the stabilizer of f under this action St(f); that is, St(f) is the set of all permutations that fix f.

$$\text {St}(f) := \{ \pi\in S_n \mid\pi\cdot f = f \} $$

We call an f∈ℳⁿ symmetric if St(f)=S _n , that is, f is fixed under the action of all permutations.

Remark 3

We can say that S _n acts on 𝒯ⁿ as well. Any permutation of the free variables elicits an automorphism on the entire set 𝒯ⁿ. The converse, however, is false; there are automorphisms of 𝒯ⁿ that do not come from permutations of the variables. Therefore, when we call F∈𝒯ⁿ symmetric, we mean preserved under all automorphisms, not just the “inner” automorphisms arising from permutations of variables.

Theorem 3

(Folklore Theorem)

f∈ℳⁿ is symmetric if and only if it is λ-definable from δ,ι,∃.

Proof

The right-to-left direction is straightforward. For δ, ι, and ∃ are all symmetric, as are combinators S and K. S and K form a basis for all λ terms, and λ-definable objects are closed under application. Thus, we have that all λ-definable objects are indeed symmetric.

The left-to-right direction will constitute the rest of this section of the paper.

Definition 8

For each function f:0ⁿ→α, we associate a functional f ⁺:(0→0)→α such that

$$f^+\pi= f(\pi1) (\pi2) \ldots(\pi n) $$

A function f is said to be regular if for every g∈ℳⁿ(0→0) where g∉S _n , we have f ⁺ g=g(1).

For the present moment, we will restrict our attention only on functions f:0ⁿ→0.

Remark 4

Note that the action π⋅f in this case is the following:

This and that St(f) is a subgroup implies that π∈St(f) if and only if

Definition 9

Fix an f:0ⁿ→0 regular. We define a relation ∼ _f on S _n by

$$\pi\sim_{f} \sigma\quad{\iff}\quad\pi^{-1} \bigl( f \bigl( \pi(1)\bigr) \ldots\bigl(\pi(n)\bigr) \bigr) = \sigma^{-1} \bigl( f \bigl(\sigma(1)\bigr) \ldots\bigl(\sigma(n)\bigr) \bigr) $$

We restrict this relation to be a right congruence by taking its right congruence hull, which we denote $\sim_{f}^{*}$ and define by

Lemma 1

For f:0ⁿ→0 regular and π∈S _n , the following are equivalent:

• 1. π∈St(f).

• 2. For all ρ∈S _n , we have πρ∼ _f ρ.

• 3. $\pi\sim_{f}^{*} \operatorname {id}$.

Proof

((1) ⇒ (2)). Take π∈St(f). By remark we have

Fix ρ∈S _n . Apply ρ(1),ρ(2),…,ρ(n) to the left:

$$\pi^{-1} \bigl( f\bigl(\pi\rho(1)\bigr)\ldots\bigl(\pi\rho (n)\bigr) \bigr) = f\bigl(\rho(1)\bigr) \ldots\bigl(\rho(n)\bigr) $$

which gives us

$$\rho^{-1}\bigl(\pi^{-1} \bigl( f\bigl(\pi\rho(1)\bigr)\ldots \bigl(\pi\rho(n)\bigr) \bigr)\bigr) = \rho^{-1}\bigl(f\bigl(\rho(1) \bigr) \ldots\bigl(\rho(n)\bigr)\bigr) $$

which implies that πρ∼ _f ρ.

((2) ⇒ (3)). Take ρ∈S _n . We want to show that $\pi\rho^{-1} \sim_{f} \operatorname {id}\rho^{-1}$. The right-hand side is of course just ρ ⁻¹; therefore, this follows immediately from (2).

((3) ⇒ (1)). We want to show that

By extensionality, it suffices to show that the above holds after an arbitrary application. Moreover, let us fix an arbitrary g:0→0 (not necessarily in S _n ). The application of g(1) to the left of both sides, followed by g(2), etc., up to g(n), is an arbitrary application as g is arbitrary; thus, it suffices to show

$$\pi^{-1} \bigl( f\bigl(\pi g(1)\bigr)\ldots\bigl(\pi g(n)\bigr) \bigr) = f\bigl(g(1)\bigr)\ldots\bigl(g(n)\bigr) $$

If g∉S _n , then by regularly of f, both sides are exactly g(1). Otherwise, call ρ:=g is a member of S _n . By (3) (using the right congruence property on ρ ⁻¹), we have that πρ∼ _f ρ. This means that

$$\rho^{-1} \pi^{-1} \bigl( f \pi\bigl(\rho(1)\bigr) \ldots\pi \bigl(\rho(n)\bigr) \bigr) = \rho^{-1} \bigl( f\bigl(\rho(1) \ldots \rho(n) \bigr) \bigr) $$

which is exactly what we wanted. □

From the above one sees that $\sim_{f}^{*}$ partitions S _n into equivalence classes, where St(f) is the class that contains $\operatorname {id}$. All other classes can be written as unions of right cosets of the stabilizer, by property (2).

Let ℬ be the set of equivalence classes. For each B∈ℬ, let χ _B :0ⁿ→Bool₀ denote its characteristic function. That is,

$$\chi_B^+ (\pi) = \begin{cases} \mathbf {True}& \mbox{if }\pi\in B \\ \mathbf {False}& \mbox{otherwise} \end{cases} $$

By the definition of the equivalence relation, if π and σ are in a block B, then π ⁻¹(f ⁺ π)=σ ⁻¹(f ⁺ σ)=:i. So when f is given inputs corresponding to a permutation in B, f is just the ith projection function. Thus, to define f, we need only know which block the given input it in. Therefore, f itself is λδ-definable from the set {χ _B ∣B∈ℬ} via the function

where {B ₁,…B _j }=ℬ, and i _k is the coordinate that f projects on block B _k .

Lemma 2

If f is regular, symmetric of type 0ⁿ→0, then f is λδ-definable.

Proof

Since f is symmetric, by (1), there is only one block of the equivalence class formed by $\sim_{f}^{*}$. Since f is λδ-definable from the set of blocks, we have that f is λδ-definable outright. □

Now, consider arbitrary symmetric f:α ₁→α ₂→⋯→α _k →0. It suffices, given the above, to show that f is definable from regular, symmetric functions of type 0ⁿ→0. Consider the set of lists

For each list L=〈f ₁,…,f _k 〉 in ℒ, we define a function c _L :0ⁿ→0, which we call the Lth coordinate function defined by

where the F _i :0ⁿ→α _i are the terms from Henkin’s theorem corresponding to f _i . Each coordinate function is regular (by the cases defining it) and also symmetric (as f is). So, each c _L is λδ-definable. Thus, we need only show that f is definable from its coordinate functions; f is not definable outright, but we need to use ι and ∃. We begin by the remark that the function alldiff:0ⁿ→Bool₀, which returns True if all the first n inputs are different, and False otherwise is λδ-definable.

Now, we can define f:

Therefore, we have that f is definable if each of the c _L is definable; the c _L are regular functions of type 0ⁿ, which are therefore definable if they are symmetric. It is easy to see that if f is symmetric, then so are its coordinate functions. Therefore, if f is symmetric, then we can substitute the λδ-definition of c _L into each of the c _L above and get a λδ-definition of f (using ∃ and ι).  □

Moreover, we can prove the following strengthening:

Theorem 4

Fix a function f∈ℳⁿ and A⊆ℳⁿ. Then if (⋂ _g∈A St(g))⊆St(f), then f is λδ-definable from functions in A along with ι,∃.

Proof

It is easy to see that St(f)=⋂St(c _L ), where the c _L are the coordinate functions of f; for since f and its coordinate functions are definable from each other, any permutation that fixes f must fix its coordinate functions, and any that fixes all its coordinate functions fixes the function.

Therefore, it suffices that we prove the theorem only for f:0ⁿ→0 and, similarly, assume all g∈A be of type 0ⁿ→0. We suppose that (⋂ _g∈A St(g))⊆St(f). By Lemma 1, since St(g) is exactly the block of the equivalence relation $\sim^{*}_{g}$ containing $\operatorname {id}$, it follows that the set of left cosets of ⋂ _g∈A St(g) is a finer partition of S _n than the set of left cosets of St(f), which are exactly the blocks of $\sim_{f}^{*}$.

Therefore, on any left coset of ⋂ _g∈A St(g) we have that f behaves like a projection operator since the coset is entirely contained in a block of $\sim_{f}^{*}$, which in turn is contained in a block of ∼ _f . Thus, for any permutations π, we can identify the left coset of ⋂ _g∈A St(g) that π is in. f acts uniformly on that block as a projection function, so we can make a definition similar to the above definition of f by its blocks in ∼ _f . □

5 Definability and Symmetry

Let us return our attention to the term model 𝒯, where members are terms with possible free variables among x ₁,x ₂,…. We first state the following result of Lauchli [5].

Proposition 1

(Lauchli)

There is a closed term $F\in\varLambda_{\delta}^{\emptyset}(\alpha)$ if and only if there is an F∈𝒯(α) symmetric (recall: for terms in 𝒯(α), symmetric means fixed under all automorphisms).

Proof

In Lauchli [5], it is stated and proved in terms of intuitionist logic: ⊢ _I α if and only if there is an “invariant” function of type α. □

Theorem 5

Any F∈𝒯 is λδ-definable if and only if it is symmetric.

Proof

It is easy to see that every element of 𝒯 that is λδ-definable is symmetric since it is βηδ equal to a closed term, which is fixed under all automorphisms. We will just prove the converse.

Let F∈𝒯 by symmetric; consider F to be of type α ₁→⋯→α _k →0. Write F as Gx ₁…x _n , where G is closed and free variables of F are among x ₁,…,x _n . By the proposition above, we can get a closed term H:α ₁→⋯→α _k →0, which has the following form in long normal form:

where H′ has type 0 and free variables only among y ₁,…y _k . Consider

$$G\underbrace{H' \ldots H'}_{n\mbox{ times }} $$

This is a term of type α ₁→⋯→α _k →0, which has free variables only among y ₁,…y _k . Thus, the term

is closed.

Recall that F is symmetric. Therefore,

$$F = Gx_1 \ldots x_n =_{\beta\eta\delta} Gy_1 \ldots y_n $$

for any variables y _i :0. Thus, by a substitution, we have that F= _βηδ GY ₁…Y _n for any Y _i :0. Therefore, M= _βηδ F and is closed, thus is a λδ-definition of F. □

Corollary 2

Let h:𝒯→ℳ be defined as x _i ↦i. This is called the canonical homomorphism. A function f∈ℳ is λδ-definable if and only if there is F∈h ⁻¹(f) symmetric.

Proof

Once again the forward direction is straightforward. For the backward direction, we just apply the last theorem. By the last theorem, if F∈h ⁻¹(f) is symmetric, then it is λδ-definable by some closed term G. Since h(G)=f and G is closed, G is also a good λδ-definition for f. □

Definition 10

We call a homomorphism h:𝒯ⁿ→ℳ^m canonical if x _i ↦i for all 1≤i≤m.

We say that an F∈𝒯ⁿ is supersymmetric if for every homomorphism φ:𝒯ⁿ→𝒯ⁿ, φ(F) is symmetric.

Theorem 6

f∈ℳ^m is λδ-definable if and only if there is some n>m and F∈𝒯ⁿ supersymmetric such that for all canonical homomorphisms h:𝒯ⁿ→ℳ^m, we have h(F)=f.

Proof

The left to right direction is trivial since f being λδ-definable gives us a closed term that will satisfy all the requirements.

For the other direction, fix f∈ℳ^m of type α ₁→α ₂→⋯→α _k →0. Suppose that n>m and F∈𝒯ⁿ is supersymmetric where for all homomorphisms h:𝒯ⁿ→ℳ^m, have h(F)=f. Write F=F′x ₁…x _j where F′ is a closed term.

The idea is as follows: we will do induction on the number of free variables on F, j. We will construct a new term M that has j−1 free variables and still has the property that it is supersymmetric and is sent to f under all canonical homomorphisms. At the end of our construction, we will have eliminated all free variables and will have constructed a closed term M that is sent to f under all canonical homomorphisms. But, since M will be closed, M is a λδ-definition for f.

To start the induction, if j=1, then F=F′x ₁. As n>m≥1, we know n>1, so that x _n ≠x ₁. F is supersymmetric, and therefore it is symmetric, so under the automorphism sending x ₁ to x _n , we know F′x ₁=F′x _n . As n>m, we have freedom with our canonical homomorphism to send x _n anywhere; in particular, for any 1≤s≤m, we can define canonical homomorphism h where h(x _n )=s. Therefore, f=F′s for all s. Therefore, we may replace x ₁ in F by anything of type 0, and it would still be sent to f through any canonical homomorphism.

By Lauchli [5], there is a closed term G of type α ₁→⋯α _k →0. We can write F as by doing η expansions. Then, replacing x ₁ to form the term , we have a closed λδ term equal to f.

If j>1, then we wish to eliminate the variable x _j . If j>m, then we already have freedom to send x _j to any number in a canonical homomorphism h. Therefore, for every 1≤s≤m, by picking a canonical homomorphism that sends x _j to s we have

$$f = h\bigl( F' x_1 \ldots x_j\bigr) = F' 1 \ldots n \bigl(h(n+1)\bigr) \ldots\bigl(h(j-1)\bigr) s $$

Since s is unrestricted, we can replace x _j with anything of type 0, and the above is still preserved. In particular, doing an η expansion of F gives us , and then replacing x _j , we get:

M has only j−1 free variables. It remains to show that M is supersymmetric. This, however, is not hard to see. Under the map x _i ↦x ₁ for all 1≤i≤j, we have that, since F is supersymmetric, F′x ₁…x ₁ is symmetric and therefore preserved under all automorphisms. Therefore, for any homomorphism φ:𝒯ⁿ→𝒯ⁿ, we will have φ(M) symmetric since φ(F) was symmetric and M is just F with a free variable replaced by a symmetric term.

If 1<j≤m<n, we have by the symmetry of F by the automorphism switching x _j and x _n that

$$F = F'x_1 \ldots x_{j-1} x_n $$

Now, we have the freedom to send x _n anywhere under any canonical homomorphism, and thus we can repeat what we did above to eliminate x _n . □