Abstract
This is a revised and extended version of an article that encapsulates a key aspect of the “Henkin method” in a general result about the existence of finitely consistent theories satisfying prescribed closure conditions. This principle can be used to give streamlined proofs of completeness for logical systems, in which inductive Henkin-style constructions are replaced by a demonstration that a certain theory “respects” some class of inference rules. The countable version of the principle has a special role and is applied here to omitting-types theorems, and to strong completeness proofs for first-order logic, omega-logic, countable fragments of languages with infinite conjunctions, and a propositional logic with probabilistic modalities. The paper concludes with a topological approach to the countable principle, using the Baire Category Theorem.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
- Deducibility
- Inference
- Finitely consistent
- Maximally consistent
- Countable Henkin Principle
- Lindenbaum’s Lemma
- Completeness
- Omitting types
- Probabilistic modality
- Archimedean inference
- Baire Category Theorem
The Henkin method is the technique for constructing maximally consistent theories satisfying prescribed closure conditions that was introduced by Leon Henkin in his 1947 doctoral dissertation. The method involves building up the desired theory by induction along an enumeration of some relevant class of formulas, with choices being made at each inductive step to include certain formulas, in such a way that when the induction is finished, the theory has the properties desired. The character of this procedure is neatly captured in a phrase of Sacks [20, p. 30], who attributes its importance to the fact that it “takes into account the ultimate consequences of decisions made at intermediate stages of the construction”.
Famously, Henkin used his method to give the first new proof of completeness of first-order logic since the original 1929 proof of Gödel and to prove completeness of a theory of types with respect to “general” models [12, 13]. He obtained the type theory result first and thought it would be of greater interest, as he explained in the remarkable article [16], in which he tells the story of his “accidental” discovery of these completeness proofs while trying to solve a different problem. In fact logicians have paid more attention to the first-order construction, which was eventually adapted to propositional and first-order versions of modal, temporal, intuitionistic and substructural logics. There are now numerous kinds of logical formalism whose model-theoretical analysis owes something of its origin to Henkin’s pioneering ideas.
In the present article the Henkin method is used to derive a general principle about the existence of maximal theories closed under abstract “inference rules”. This principle may then be used to give alternative proofs of completeness theorems, proofs in which the Henkin method is replaced by a demonstration that a certain theory “respects” a certain class of inference rules. This alternative approach is illustrated by a re-working of the completeness and omitting-types theorems for first-order logic and certain fragments of L ∞ω . Some of these involve a countability constraint, and that case of the approach has a particularly direct form that we call the Countable Henkin Principle. It is used to obtain general extension results about the existence of “rich” theories that are closed under countably many inference rules. We apply those extension results to give a proof of strong completeness of a propositional logic with probabilistic modalities, motivated by a recent topological analysis in [17].
The proof of the Countable Henkin Principle itself helps to clarify why some completeness proofs work only under a countability constraint. The essential point is that after building a denumerably long increasing sequence of consistent theories, one must take the union of them to proceed to a further stage. But if the proof theory is non-finitary, the union may not preserve consistency (but only the property of being finitely consistent), and the construction cannot be iterated into the transfinite.
This paper is a revised and extended version of the article [6]. That had a previous revision [8], which added applications to completeness for the Barcan formula in quantified modal logic, and for propositional mono-modal logic with infinitary inference rules. Here those modal applications are replaced by new Sects. 4–7, which include the formulation of the Rich Extension theorems, their alternative topological proof using the Baire Category Theorem, and the discussion of probabilistic modal logic. Also, the Sect. 3.2 on the Omitting-Types Theorem has been rewritten from a more general standpoint, and a new Sect. 3.3 added, which relates this to Henkin’s generalizations of ω-consistency [14] and ω-completeness [15].
1 The Abstract Henkin Principle
Consider a formal language that includes a distinguished formula ⊥ and a unary connective ¬. Think of ⊥ as a constant false sentence, and ¬ as negation. Let Φ be any class of formulas of this language such that ⊥∈Φ and Φ is closed under application of the connective ¬.
Let ⊢ be a subset of 2Φ×Φ, that is, a binary relation from the powerset of Φ to Φ. For Γ⊆Φ and φ∈Φ, write Γ⊢φ if (Γ,φ) belongs to ⊢ and Γ⊬φ otherwise. The relation ⊢ is called a deducibility relation on Φ if it satisfies
-
D1
If Γ⊢φ and Γ⊆Δ, then Δ⊢φ;
-
D2
If φ∈Γ, then Γ⊢φ;
-
D3
If Γ⊢φ and Γ∪{φ}⊢⊥, then Γ⊢⊥;
-
D4
Γ∪{¬φ}⊢⊥ iff Γ⊢φ.
A subset Γ of Φ is called ⊢-consistent if Γ⊬⊥ and finitely ⊢-consistent if each finite subset of Γ is ⊢-consistent in this sense. Γ is maximally ⊢-consistent if it is ⊢-consistent but has no ⊢-consistent proper extension in Φ. Replacing “⊢-consistent” by “finitely ⊢-consistent” in this last definition yields the notion of Γ being maximally finitely ⊢-consistent.
Now from D1 it follows that any ⊢-consistent set is finitely ⊢-consistent. The relation ⊢ is called finitary if, conversely, it satisfies
-
D5
Every finitely ⊢-consistent set is ⊢-consistent, that is, if Γ⊢⊥, then for some finite Γ 0⊆Γ, Γ 0⊢⊥.
If 𝒞 is a collection of finitely ⊢-consistent subsets of Φ that is linearly ordered by set inclusion, that is, Γ⊆Δ or Δ⊆Γ for all Γ,Δ∈𝒞, then the union ⋃𝒞 of 𝒞 is finitely ⊢-consistent. This follows immediately from the fact that any finite subset of ⋃𝒞 is a subset of some Γ∈𝒞. Thus, if
then under the partial ordering of set inclusion P fulfills the hypothesis of Zorn’s Lemma. From the latter we deduce the following:
Lindenbaum’s Lemma
Every finitely ⊢-consistent subset of Φ has a maximally finitely ⊢-consistent extension in Φ.
(Note that this result uses no properties of ⊢ other than the definitions of the concepts referred to in the statement of the lemma.)
An ordered pair (Π,χ) with Π⊆Φ and χ∈Φ will be called an inference in Φ. As motivation, the reader may care to think of Π as a set of “premises” and χ as a “conclusion”, but the notion of inference is quite abstract and applies to any such pair. A set Γ will be said to respect the inference (Π,χ) when
Γ is closed under (Π,χ) if
Γ respects (is closed under) a set ℐ of inferences if it respects (is closed under) each member of ℐ.
The cardinality of a set X will be denoted \(\operatorname{card}X\). If κ is a cardinal number, then X is κ-finite if \(\operatorname{card}X<\kappa\). A κ-finite extension of X is a set of the form X∪Y with Y κ-finite. In other words, a κ-finite extension of X is a set obtained by adding fewer than κ elements to X.
Theorem 1
Let ⊢ be a finitary deducibility relation on Φ. If ℐ is a set of inferences in Φ of cardinality κ, and Γ is a ⊢-consistent subset of Φ such that

then Γ has a maximally ⊢-consistent extension in Φ that is closed under ℐ.
This theorem will be established by first separating out that part of its content that does not involve Lindenbaum’s Lemma. To do this requires a further concept: a set Γ⊆Φ will be said to decide (Π,χ) if
Γ decides a set of inferences if it decides each member of the set.
The following result holds for any deducibility relation.
Lemma 1
-
(1)
If Γ decides (Π,χ) and Γ⊆Δ, then Δ decides (Π,χ).
-
(2)
If Γ decides (Π,χ), then Γ respects (Π,χ).
-
(3)
If Γ is finitely ⊢-consistent, and Γ decides (Π,χ), then Γ is closed under (Π,χ).
-
(4)
If Γ is ⊢-consistent, and Γ respects (Π,χ), then for some ψ∈Φ, Γ∪{ψ} is ⊢-consistent and decides (Π,χ).
Proof
(1) Immediate.
(2) Suppose Γ⊢φ for all φ∈Π. Then if Γ⊬χ, by D2 \(\chi\not\in\varGamma\), so if Γ decides (Π,χ), then ¬ψ∈Γ for some ψ∈Π. But by assumption Γ⊢ψ, and so by D4 Γ∪{¬ψ}⊢⊥, that is, Γ⊢⊥. But then by D1, Γ∪{¬χ}⊢⊥, and so by D4 again, Γ⊢χ. Hence, Γ⊢χ.
(3) Suppose Γ decides (Π,χ), and Π⊆Γ. Then if \(\chi\not\in\varGamma\), then ¬ψ∈Γ for some ψ∈Π⊆Γ. Now by D2, {ψ}⊢ψ, and so by D4, {ψ,¬ψ}⊢⊥. But {ψ,¬ψ}⊆Γ, so then Γ is not finitely ⊢-consistent.
(4) If Γ∪{¬φ} is ⊢-consistent for some φ∈Π, then the result follows with ψ=¬φ. Otherwise, for all φ∈Π, Γ∪{¬φ}⊢⊥, and so by D4, Γ⊢φ. But Γ respects (Π,χ), hence Γ⊢χ. Since Γ⊬⊥, D3 then implies that Γ∪{χ}⊬⊥, so the result follows with ψ=χ. □
Abstract Henkin Principle
Let ⊢ be a finitary deducibility relation on Φ. If ℐ is a set of inferences in Φ of cardinality κ, and Γ is a ⊢-consistent subset of Φ such that

then Γ has a ⊢-consistent extension Δ that decides ℐ.
Note that by applying Lindenbaum’s Lemma to the ⊢-consistent extension Δ given by the conclusion of this result, an extension of Γ is obtained that is maximally ⊢-consistent (since ⊢ is finitary), decides ℐ by Lemma 1(1), and hence is closed under ℐ by Lemma 1(3). This argument proves Theorem 1.
To prove the Abstract Henkin Principle, let {(Π α ,χ α ):α<κ} be an indexing of the members of ℐ by the ordinals less than κ. A sequence {Δ α :α<κ} of extensions of Γ is then defined such that
-
(i)
Δ α is ⊢-consistent;
-
(ii)
Δ γ ⊆Δ α whenever γ<α;
-
(iii)
\(\operatorname{card}(\varDelta _{\alpha}- \varGamma)\leq\alpha\), hence Δ α is a κ-finite extension of Γ;
and such that Δ α+1 decides (Π α ,χ α ). The definition proceeds by transfinite induction on α.
Case 1: If α=0, put Δ α =Γ, so that Δ α is ⊢-consistent by assumption, and \(\operatorname{card}(\varDelta _{\alpha}-\varGamma)=0=\alpha\).
Case 2: Suppose α=β+1, and assume inductively that Δ β has been defined such that (i)–(iii) hold with β in place of α. Then since Δ β is a κ-finite extension of Γ, hypothesis (∗) on Γ implies that Δ β respects (Π β ,χ β ). Hence, by Lemma 1(4), there is a ψ∈Φ such that Δ β ∪{ψ} is ⊢-consistent and decides (Π β ,χ β ). Put Δ α =Δ β ∪{ψ}, so that (i) holds for α. Since Δ β ⊆Δ α , and γ<α iff γ≤β, (ii) follows readily. For (iii), since Δ α −Γ⊆(Δ β −Γ)∪{ψ}, \(\operatorname{card}(\varDelta _{\alpha}-\varGamma)\leq \operatorname{card}(\varDelta _{\beta }-\varGamma )+1\leq\beta+1=\alpha\).
Case 3: Suppose α is a limit ordinal and that for all β<α, Δ β has been defined to satisfy (i)–(iii). Put
Then (ii) is immediate for α. For (i), observe that Δ α is the union of a chain of ⊢-consistent, hence finitely ⊢-consistent, sets Δ β , and so Δ α is finitely ⊢-consistent as in the proof of Lindenbaum’s Lemma. But ⊢ is finitary, so Δ α is then ⊢-consistent. For (iii), observe that
and note that by the inductive hypothesis, if β<α, then \(\operatorname{card}(\varDelta _{\beta}-\varGamma)\leq\beta< \alpha\). Thus, (Δ α −Γ) is the union of a collection of at most \(\operatorname{card}\alpha\) sets, each of which has at most \(\operatorname{card}\alpha\) members. Hence, \(\operatorname{card}(\varDelta _{\alpha}-\varGamma)\leq\operatorname{card}\alpha\leq \alpha\).
This completes the definition of Δ α for all α<κ. Now put Δ=⋃ α<κ Δ α . Then by the argument of Case 3, Δ is a ⊢-consistent extension of Γ. Moreover, for each β<α, Δ β+1 decides (Π β ,χ β ) by Case 2, and so Δ decides (Π β ,χ β ) by Lemma 1(1).
2 The Countable Case
In the proof of the Abstract Henkin Principle, the assumption that ⊢ is finitary is used only in Case 3, and in the final formation of Δ, to show that the union of an increasing sequence of ⊢-consistent sets is ⊢-consistent. But if κ is countable, then Case 3 does not arise. Case 2 is iterated countably many times, and then Δ is constructed as the union of the Δ α . Then if ⊢ is not finitary, Δ may not be ⊢-consistent. However, it will at least be finitely ⊢-consistent, and this gives the following result.
Countable Henkin Principle
Let ⊢ be any deducibility relation on Φ. If ℐ is a countable set of inferences in Φ, and Γ is a ⊢-consistent subset of Φ such that

then Γ has a finitely ⊢-consistent extension that decides ℐ.
The extension of Γ deciding ℐ in this result can be taken to be maximally finitely ⊢-consistent, by applying Lindenbaum’s Lemma and Lemma 1(1). It is also closed under ℐ by Lemma 1(3).
The Countable Henkin Principle will be used below to give proofs of a number of results, including an omitting-types theorem for countable first-order languages, and (strong) completeness theorems for countable fragments of L ∞ω and a probabilistic modal logic. The analysis given here provides one way of “putting one’s finger” on the role of countability restrictions in such applications.
If the ambient formal language has a conjunction connective, allowing the formation of the conjunction ⋀Σ of any finite subset Σ of Φ, then a natural constraint on ⊢ would be to require that for all Γ⊆Φ and all φ∈Φ,
A deducibility relation satisfying this condition will be called conjunctive. Thus, for a conjunctive deducibility relation, hypothesis (∗) in the Countable Henkin Principle can be weakened to

3 Classical Applications
3.1 Completeness for First-Order Logic
Let L be a set of relation, function, and individual-constant symbols, and Γ a set of sentences in the first-order language of L that is consistent under the standard deducibility relation of first-order logic.
The Completeness Theorem asserts that Γ has a model. To prove this, a new language K=L∪C is formed by adding to L a set C of new individual constants of cardinality κ, where κ is the maximum of \(\operatorname{card}\mathsf{L}\) and ℵ0. The usual construction of a model for Γ involves two phases.
Phase 1: Γ is extended by the “Henkin method” to a maximally consistent set Γ ∗ of K-sentences such that for each K-formula φ(x) with at most one variable (x) free,
-
(a)
if ∃xφ∈Γ ∗, then φ(c)∈Γ ∗ for some c∈C.
Phase 2: A model \(\mathfrak{A}^{*}\) is defined based on the quotient set C/∼, where ∼ is the equivalence relation
For each K-formula ψ(x 1,…,x n ), this model satisfies
-
(b)
\(\mathfrak{A}^{*}\models\psi[\mathsf{c}_{1}/{\sim} , \ldots ,\mathsf{c}_{n}/{\sim} ]\) iff ψ(c 1,…,c n )∈Γ ∗.
In particular, \(\mathfrak{A}^{*}\models\sigma\) iff σ∈Γ ∗, where σ is any K-sentence, so since Γ⊆Γ ∗, \(\mathfrak{A}^{*}\models \varGamma\).
The Abstract Henkin Principle of this article may be used to give a succinct development of Phase 1. For this, let Φ be the set of all first-order sentences of K, and ⊢ the standard (finitary) first-order deducibility relation on Φ. Then Γ is ⊢-consistent. The key property of ⊢ that will be used is
-
(c)
if Δ⊢φ(c), and the constant c does not occur in Δ or φ(x), then Δ⊢∀xφ(x).
Now the closure condition (a) on Γ ∗ in Phase 1 is equivalent to
that is, to the closure of Γ ∗ under the inference
Let ℐ be the set of inferences φ
C
for all first-order K-formulas φ with one free variable. The number of such formulas is κ since \(\operatorname{card}\mathsf{K}=\kappa\). Hence,  . Thus, to prove the existence of Γ
∗, it suffices to show that if Δ is a κ-finite subset of Φ, then
. Thus, to prove the existence of Γ
∗, it suffices to show that if Δ is a κ-finite subset of Φ, then

But if \(\operatorname{card} \varDelta <\kappa\), then for any φ, \(\operatorname{card}(\varDelta \cup\{\varphi\})<\kappa\) since κ is infinite. Hence, fewer that κ members of C appear in Δ∪{φ}. But none of these constants appear in Γ. Thus, if
then
and so by (c),
3.2 Omitting Types
Let L be a countable language, and F n the set of all first-order L-formulas all of whose free variables are among x 1,…,x n . A consistent subset of F n will be called an n-type. An L-structure \(\mathfrak{A}\) realises an n-type Σ if there are individuals a 1,…,a n in \(\mathfrak{A}\) such that
\(\mathfrak{A}\) omits Σ if it does not realise Σ. If Γ is a consistent set of L-sentences, then an n-type Σ is isolated over Γ if there is some formula ψ∈F n that is consistent with Γ (i.e. Γ∪{ψ} is consistent) and has
Such a ψ is said to isolate Σ over Γ. This means that Γ∪{ψ}⊬⊥, whereas Γ∪{ψ}⊢φ for all φ∈Σ, that is, Γ∪{ψ} fails to respect the rule (Σ,⊥). Thus, Σ is not isolated over Γ precisely when Γ∪{ψ} does respect the rule (Σ,⊥) for all ψ∈F n .
The basic omitting-types theorem asserts that if a type Σ is not isolated over Γ, then Γ has a (countable) model that omits Σ. This can be proven by a refinement of the proof of the completeness theorem sketched in Sect. 3.1, and the required model is the structure \(\mathfrak{A}^{*}\) given there.
To simplify the exposition, let Σ be a 1-type. Since each individual of \(\mathfrak{A}^{*}\) is of the form c/∼ for some c∈C, to ensure that \(\mathfrak{A}^{*}\) does not realise Σ, it suffices, by clause (b) of the description of \(\mathfrak{A}^{*}\), to show that for each c∈C, there is some formula φ(x 1)∈Σ such that \(\varphi (\mathsf{c})\not\in\varGamma^{*}\). Since \(\bot\not\in\varGamma ^{*}\), this amounts to requiring, for each c∈C, that Γ ∗ be closed under the inference
Lemma 2
For any K-sentence σ, Γ∪{σ} respects Σ c .
Proof
σ may contain members of C other than c. To simplify the notation again, let σ contain just one C-constant d other than c.
Suppose that Γ∪{σ(c,d)}⊢φ(c), and hence Γ⊢σ(c,d)→φ(c) for all φ(x 1)∈Σ. Then as c and d do not occur in Γ, it follows by standard properties of first-order deducibility that for all φ(x 1)∈Σ,
But the formula ∃x 2 σ(x 1,x 2) belongs to F 1, and so since Σ is not isolated over Γ, it follows that ∃x 2 σ(x 1,x 2) is not consistent with Γ. Hence, Γ⊢¬∃x 2 σ(x 1,x 2), and so Γ⊢∀x 1∀x 2¬σ(x 1,x 2). This implies Γ⊢¬σ(c,d), and so Γ∪{σ(c,d)}⊢⊥. □
Now since C is countable, there are countably many rules of the form Σ c . Since the standard deducibility relation of first-order logic is conjunctive, the lemma just proved applies to the Countable Henkin Principle and yields, with Lindenbaum’s Lemma, a maximally ⊢-consistent extension Γ ∗ of Γ that is closed under Σ c for all c∈C. But K is countable since L is countable, and so there are countably many inferences of the form φ C for φ a K-formula with at most one free variable. Hence, if the latter inferences are added to the Σ c , there are still only countably many inferences involved altogether, and so Γ ∗ can be taken to be closed under each φ C as before.
In fact, the whole argument can begin with a countable number of types, not just one. Each type will contribute a countable number of inferences of the form Σ c , and so, since a countable union of countable sets is countable, this will still involve only countably many inferences altogether. Thus, with no extra work, other than these observations about the sizes of sets of inferences, it may be concluded that any countable collection of non-isolated types is simultaneously omitted by some model of Γ.
3.3 C-Completeness and C-Consistency
Let L be a countable language that includes a set C of individual constants. A C -model is any L-structure in which each individual is the interpretation of some constant from C. Thus an L-structure is a C-model iff it omits the 1-type
A set Γ of L-sentences is C -complete if it respects the inference
for all L-formulas φ(x), where we continue to take ⊢ to be the standard first-order deducibility relation. Now Γ⊢∀xφ iff Γ⊢φ since x is not free in Γ, so C-completeness is equivalent to having Γ respect all the inferences ({φ(c):c∈C},φ).
The notion of C-completeness was introduced by Henkin in [15], where he showed that
-
(i)
if Γ is C -complete, then for any sentence σ that is consistent with Γ, there exists a C -model of Γ∪{σ}.
As a preliminary lemma, he proved that if a set of sentences Γ is C-complete, then so is Γ∪{σ} for any sentence σ. This implies that (i) is reducible to the assertion
-
(ii)
every consistent and C -complete set of sentences has a C -model.
Now (ii) can be inferred from the Omitting-Types Theorem, provided that we know that any consistent and C-complete set does not have the type Δ C isolated over it. To prove that, let Γ be consistent and C-complete. Suppose further that there is a formula ψ(x) such that Γ⊢ψ→¬(x=c) for all c∈C. Then Γ⊢∀x(ψ→¬(x=c)), hence Γ⊢ψ(c)→¬(c=c), and so Γ⊢¬ψ(c) for all c∈C. Since Γ is C-complete, this yields Γ⊢¬ψ, so ψ is not consistent with Γ and thus does not isolate Δ C over Γ. The upshot is that Δ C is not isolated over Γ, so there is a model of Γ that omits Δ C and hence is a C-model.
Henkin’s proof of (i) used his general completeness method and applied an earlier result from his paper [14], which states that any strongly C -consistent set of sentences has a \(\sf C\)-model. Here strong C-consistency of Γ can be defined to mean that there is a function assigning to each formula φ(x) with only x free a constant c φ from C such that every sentence of the form
is consistent with Γ. This implies that the set Δ of all sentences of the form φ(c φ )→∀xφ is consistent with Γ, and so Γ∪Δ has a maximally consistent extension Γ ∗. By the nature of Δ, this Γ ∗ is closed under the rules φ C for all φ(x), and the structure \(\mathfrak{A}^{*}\) defined from Γ ∗ as in Sect. 3.1 is a C-model of Γ.
Steven Orey [18] independently proved essentially the same result that a strongly C-consistent set has a C-model, formulating this in the context that C is a collection of constants denoting the natural numbers, in which case a C-model is called an ω-model, and the result provides a completeness theorem for ω-logic, which adds to the standard first-order axiomatization the general rule that
(see [3, Proposition 2.2.13]). Both Henkin and Orey gave examples to show that strong C-consistency of Γ is strictly stronger in general than C -consistency, which itself means that there is no formula φ(x) such that Γ⊢φ(c) for all c∈C and Γ⊢¬∀xφ(x). For ω-logic, this is the notion of ω-consistency introduced by Gödel in proving his incompleteness theorems.
3.4 Completeness for Infinitary Conjunction
The infinitary logic L ∞ω generated by a language L has a proper class of individual variables, and a proper class of formulas obtained by allowing, in addition to ¬φ and ∀vφ, formation of the conjunction ⋀Ψ of any set Ψ of formulas (disjunction being definable by ⋀ and ¬ as usual).
The deducibility relation for infinitary logic has, in addition to the defining properties of deducibility for first-order logic, the axiom schema
and the rule of deduction that if
then
This deducibility relation is not finitary because a set of the form Ψ∪{¬⋀Ψ} will not be ⊢-consistent, but all of its finite subsets could be.
Each formula involved in the following discussion will be assumed to have only a finite number of free variables. This restriction is justified by the fact that it includes all subformulas of infinitary sentences.
A fragment of L ∞ω is a set L A of L ∞ω -formulas that includes all first-order L-formulas and is closed under ¬, ∀, finite conjunctions, subformulas, and substitution for variables of terms each of whose variables appears in L A (cf. [2, p. 84]).
A “weak” completeness theorem [2, Sect. III.4] asserts that if L A is a countable fragment of L ∞ω and Γ is a set of L A -sentences that is consistent, then Γ has a model. To prove this, let C be a denumerable set of new constants, K=L∪C, and K A the set of all formulas obtained from formulas φ∈L A by replacing finitely many free variables by constants c∈C. Then K A is countable and is the smallest fragment of K ∞ω that contains L A . A crucial point to note is that each member of K A contains only finitely many constants from C.
Now let Φ be the (countable) set of sentences in K A , and ⊢ the restriction of the K ∞ω -deducibility relation to Φ. To obtain a Γ-model, Γ is to be extended to a subset Γ ∗ of Φ for which the definition of the model \(\mathfrak{A}^{*}\) can be carried through as for first-order logic and for which the condition
-
(b)
\(\mathfrak{A}^{*}\models\psi[\mathsf{c}_{1}/{\sim} , \ldots, \mathsf{c}_{n}/{\sim} ] \ \mbox{iff}\ \psi(\mathsf{c}_{1}, \ldots\mathsf{c}_{n})\in\varGamma^{*}\)
can be established for each formula ψ(x 1,…,x n ) that belongs to K A . Then \(\mathfrak{A}^{*}\) will be a Γ-model since Γ⊆Γ ∗.
In order for (b) to hold for all K A -formulas, it is sufficient (and necessary) that the following hold.
-
(i)
Γ ∗ is maximally finitely ⊢-consistent: this is sufficient to ensure that \(\mathfrak{A}^{*}\) is well defined; ¬φ∈Γ ∗ iff \(\varphi \not\in\varGamma^{*}\); φ→ψ∈Γ ∗ iff φ∈Γ ∗ implies ψ∈Γ ∗; if ⋀Ψ∈Γ ∗, then φ∈Γ ∗ for all φ∈Γ ∗; and if ∀xφ∈Γ ∗, then φ(c)∈Γ ∗ for all c∈C.
-
(ii)
Γ ∗ is closed under the inference φ C for each K A -formula φ with at most one free variable.
-
(iii)
If ⋀Ψ∈K A , and Ψ⊆Γ ∗, then ⋀Ψ∈Γ ∗, that is, if ⋀Ψ∈K A , then Γ ∗ is closed under the inference (Ψ,⋀Ψ).
Since K A is countable, there are countably many inferences involved in fulfilling (ii) and (iii). Hence, by the Countable Henkin Principle and Lindenbaum’s Lemma, it suffices to show that for all σ∈Φ, Γ∪{σ} respects each such inference. The proof that Γ∪{σ} respects φ C is just as for first-order logic since, as noted above, σ has only finitely many constants from C, whereas Γ has no such constants.
For an inference of the form (Ψ,⋀Ψ), observe that if
then
so
and hence
It is left as an exercise for the reader to formulate and derive an omitting-types theorem for countable fragments of L ∞ω .
4 Richer Extension Theorems
In the application just discussed, a special role was played by maximally finitely consistent sets that are closed under given inference rules. We now study conditions under which every consistent set can be extended to one of these special sets.
Let ℐ be a subset of 2Φ×Φ, that is, a set of inferences. A set Δ of formulas will be called (ℐ,⊢)-rich if
-
Δ is maximally finitely ⊢-consistent, and
-
Δ is closed under ℐ, that is, if (Π,χ)∈ℐ and Π⊆Δ, then χ∈Δ.
So we have already established the following via the Countable Henkin Principle and Lindenbaum’s Lemma:
Theorem 2
(Rich Extension I)
Let ⊢ be a deducibility relation on Φ, and ℐ a countable set of inferences in Φ. If Γ is a ⊢-consistent subset of Φ such that Γ∪Σ respects ℐ for all finite Σ⊆Φ, then Γ has an (ℐ,⊢)-rich extension.
The relation ⊢ will itself be said to respect an inference (Π,χ) if every set of formulas respects (Π,χ) under ⊢, that is, if the condition
holds for every Γ⊆Φ. Also, ⊢ respects ℐ if it respects each member of ℐ. If this is so, then in particular Γ∪Σ will respect ℐ for all ⊢-consistent Γ and all finite Σ⊆Φ. Thus, Theorem 2 gives the following:
Theorem 3
(Rich Extension II)
Let ⊢ be a deducibility relation that respects all members of a countable set ℐ of inferences. Then every ⊢-consistent set of formulas has an (ℐ,⊢)-rich extension.
To refine this result further, we invoke the following property:
- Cut Rule::
-
If Γ⊢φ for all φ∈Π, and Π⊢χ, then Γ⊢χ.
An inference (Π,χ) will be called ⊢-deducible if Π⊢χ. The Cut Rule states that if (Π,χ) is ⊢-deducible, then ⊢ respects it. (The converse is always true: since Π⊢φ for all φ∈Π, if ⊢ respects (Π,χ), then Π⊢χ follows.) Hence, Theorem 3 gives the following:
Theorem 4
(Rich Extension III)
Let ⊢ be a deducibility relation that satisfies the Cut Rule, and let ℐ be a countable set of ⊢-deducible inferences. Then every ⊢-consistent set of formulas has an (ℐ,⊢)-rich extension.
5 Classical Deducibility
D1–D4 provided minimal assumptions from which to derive the Henkin Principle and the Rich Extension theorems. But in what follows additional properties of ⊢ involving an implication connective → will be needed. So from now on we assume that Φ is the class of formulas of some language that includes all the classical truth-functional connectives. We can take ⊥ and → as primitive, and the other connectives ⊤, ¬, ∧, ∨ as defined from them in the usual way.
Consider the following further properties of a relation ⊢ from 2Φ to Φ:
- Assumption Rule::
-
If φ∈Γ or φ is a tautology, then Γ⊢φ.
- Detachment Rule::
-
{φ,φ→ψ}⊢ψ.
- Tautological Rule::
-
If φ is a tautological consequence of Γ, then Γ⊢φ.
- Deduction Rule::
-
Γ∪{φ}⊢ψ implies Γ⊢φ→ψ.
- Implication Rule::
-
Γ⊢ψ implies (φ→Γ)⊢φ→ψ, where
$$(\varphi\to\varGamma)=\{\varphi\to\chi:\chi\in\varGamma\}. $$
Lemma 3
If ⊢ satisfies the Assumption, Detachment and Cut rules, then it satisfies the Tautological Rule.
Proof
From the stated rules it follows that the set {φ:Γ⊢φ} contains all members of Γ and all tautologies, and is closed under Detachment. But by standard theory, any such set contains every tautological consequence of Γ. □
Lemma 4
If ⊢ satisfies the Assumption, Detachment, Cut, and Deduction rules, then it satisfies the Implication Rule and the converse of the Deduction Rule, that is,
Proof
Suppose Γ⊢ψ. Since the Tautological Rule gives
it then follows by the Cut Rule that (φ→Γ)∪{φ}⊢ψ. Hence, by the Deduction Rule, (φ→Γ)⊢φ→ψ, establishing the Implication Rule.
Next, suppose Γ⊢φ→ψ. Now by the Assumption Rule, Γ∪{φ}⊢χ for all χ∈Γ, so this yields Γ∪{φ}⊢φ→ψ by the Cut Rule. But also Γ∪{φ}⊢φ, so the Detachment and Cut rules then give Γ∪{φ}⊢ψ. □
A relation ⊢ satisfying the Assumption, Detachment, Cut, and Deduction rules will be called a classical deducibility relation. Conditions D1–D4 of Sect. 1 can be derived from these rules, as the reader may verify. When ∅⊢φ, where ∅ is the empty set of formulas, we may write ⊢φ and say that φ is ⊢-deducible, Observe that in order for φ to have Γ⊢φ for all Γ (e.g. when φ is a tautology), it is enough by D1 to have ⊢φ.
We note some properties of a maximally finitely ⊢-consistent set Δ that hold when ⊢ is classical. Membership of Δ reflects the properties of the truth-functions, and Δ contains all ⊢-deducible formulas and is closed under the Detachment Rule, that is,
etc. Moreover, a finitely ⊢-consistent set Γ is maximally finitely ⊢-consistent iff it is negation complete in the sense that for all φ∈Φ, either φ∈Γ or ¬φ∈Γ. Such facts can be shown by well-known arguments (or see [6, 8, 9] for details).
6 Probabilistic Modal Logic
The theory of rich sets of formulas will now be applied to a system of propositional logic, originating with Aumann [1], that can express assertions of the type “the probability of φ is at least r”. This assertion will be written symbolically as [r]φ. Here r can be any rational number in the real unit interval [0,1]. The set of all such rationals will be denoted \(\mathbb{Q}^{01}\), and the letters r,s,t,u are reserved to name them. We write \(\mathbb{R}\) as usual for the set of real numbers, and put \(\mathbb {R}^{\geqslant0}=\{x\in\mathbb{R}:x\geqslant0\}\).
The symbol [r] itself is a unary modal connective, reminiscent of the “box” modality □. But those familiar with modal logic may care to note that [r] is not in general a normal modality: the schemes
are not valid in the semantics defined below, unless r=0 or 1. On the other hand,
is always valid, and if a formula φ is valid, then so is [r]φ. The modalities [1] and [0] are both normal, with [0] being of the “Verum” type, that is, [0]φ is valid for every formula φ.
An algebra 𝒜 on a non-empty set X is a non-empty collection of subsets of X that are closed under complements and binary unions. 𝒜 is a σ-algebra if it is also closed under countable unions. Then (X,𝒜) is called a measurable space, and the members of 𝒜 are its measurable sets. A measurable function f:(X,𝒜)→(X′,𝒜′) between measurable spaces is given by a set function f:X→X′ that pulls measurable sets back to measurable sets, that is, f −1(Y)∈𝒜 for all Y∈𝒜′. For this, it suffices that f −1(Y)∈𝒜 for all sets Y in some generating subset of 𝒜′.
A function  on an algebra 𝒜 is finitely additive if μ(Y
1∪Y
2)=μ(Y
1)+μ(Y
2) whenever Y
1 and Y
2 are disjoint members of 𝒜. μ is countably additive if \(\mu(\bigcup_{n} Y_{n})=\sum_{0}^{\infty}\mu(Y_{n})\) whenever {Y
n
∣n<ω} is a sequence of pairwise disjoint members of 𝒜 whose union ⋃
n
Y
n
belongs to 𝒜. A measure is a countably additive function with μ(∅)=0. It is a probability measure if also μ(X)=1.
on an algebra 𝒜 is finitely additive if μ(Y
1∪Y
2)=μ(Y
1)+μ(Y
2) whenever Y
1 and Y
2 are disjoint members of 𝒜. μ is countably additive if \(\mu(\bigcup_{n} Y_{n})=\sum_{0}^{\infty}\mu(Y_{n})\) whenever {Y
n
∣n<ω} is a sequence of pairwise disjoint members of 𝒜 whose union ⋃
n
Y
n
belongs to 𝒜. A measure is a countably additive function with μ(∅)=0. It is a probability measure if also μ(X)=1.
We need the following standard facts about an algebra 𝒜:
-
Any measure μ on 𝒜 is continuous from above, meaning that if Y 0⊇Y 1⊇⋯ is a non-increasing sequence of members of 𝒜 whose intersection belongs to 𝒜, then μ(⋂ n<ω Y n )=lim n→∞ μ(Y n ).
-
A finitely additive
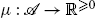 is a measure if it is continuous at ∅, that is, lim
n→∞
μ(Y
n
)=0 for any non-increasing sequence {Y
n
∣n<ω}⊆𝒜 with ⋂
n
Y
n
=∅.
is a measure if it is continuous at ∅, that is, lim
n→∞
μ(Y
n
)=0 for any non-increasing sequence {Y
n
∣n<ω}⊆𝒜 with ⋂
n
Y
n
=∅.
The set of all probability measures on a measurable space (X,𝒜) will be denoted  . It becomes a measurable space itself under the σ-algebra generated by the sets
. It becomes a measurable space itself under the σ-algebra generated by the sets  for all Y∈𝒜 and r∈Q
01.
for all Y∈𝒜 and r∈Q
01.
Now let Φ be the set of formulas generated from a countably infinite set of propositional variables by the classical truth-functional connectives and the modalities [r] for all r∈Q 01. A formula [r 0]⋯[r n−1]φ generated by iterating modalities will be written more briefly as [r 0⋯r n−1]φ. In the case r=0, this is just the formula φ. Notice that Φ is countable since there are countably many variables and Q 01 is countable.
A model ℳ for this language is given by a measurable space (X,𝒜) together with a measurable function f from (X,𝒜) to the space  of probability measures, and a valuation that assigns a measurable set 〚p〛ℳ∈𝒜 to each propositional variable p. We typically write μ
x
for the measure f(x) assigned to x∈X by f. The valuation of variables is extended inductively to all formulas, using the standard Boolean set operations to interpret the truth-functional connectives by
of probability measures, and a valuation that assigns a measurable set 〚p〛ℳ∈𝒜 to each propositional variable p. We typically write μ
x
for the measure f(x) assigned to x∈X by f. The valuation of variables is extended inductively to all formulas, using the standard Boolean set operations to interpret the truth-functional connectives by

and for the modalities putting

The measurability of f ensures that if 〚φ〛ℳ is measurable, then so is 〚[r]φ〛ℳ. Hence, inductively every formula φ is interpreted as a measurable set 〚φ〛ℳ, thought of as the set of points in X that satisfy φ. By writing ℳ,x⊨φ to mean that x∈〚φ〛ℳ, the following properties of satisfaction are obtained:

Satisfaction of a set Γ of formulas is defined by putting ℳ,x⊨Γ iff for all φ∈Γ, ℳ,x⊨φ. A semantic consequence relation is then defined by putting Γ⊨φ iff ℳ,x⊨Γ implies ℳ,x⊨φ for all points x of all models ℳ. In the case that Γ=∅, the relation ∅⊨φ means that φ is valid, that is, satisfied at every point of every model.
A set Γ is unsatisfiable if  for all ℳ and x. This is equivalent to having Γ⊨⊥. The relation ⊨ is not finitary: the set
for all ℳ and x. This is equivalent to having Γ⊨⊥. The relation ⊨ is not finitary: the set
has each of its finite subsets satisfiable but is not itself satisfiable because of the Archimedean property that the real number μ x 〚p〛ℳ cannot be less than s but closer to s than any rational r<s. Thus, Γ s ⊨⊥, but no finite Γ′⊆Γ s has Γ′⊨⊥.
Our objective is to axiomatize the relation ⊨ by constructing an abstract deducibility relation ⊢ and showing that Γ⊢φ iff Γ⊨φ. For this purpose, define an Archimedean inference to be a pair of the form
with s>0. Such an inference is sound for the semantic consequence relation. In the case n=0, the relation
holds just because of the Archimedean property described above, which is independent of the properties of a measure. But when n>0, the proof that

depends on the measure μ x being continuous from above [17].
Notice that the inference (1) is really only of interest when s>0 because any formula of the form [0]φ is valid, hence so is any of the form [r 0⋯r n−10]φ.
Let Ax be the set of all formulas that are instances of the following axioms:
-
A1
[1](φ→ψ)→([r]φ→[r]ψ).
-
A2
[0]⊥.
-
A3
[r]¬φ→¬[s]φ if r+s>1.
-
A4
[r](φ∧ψ)∧[s](φ∧¬ψ)→[r+s]φ if r+s⩽1.
-
A5
¬[r](φ)∧¬[s](ψ)→¬[r+s](φ∨ψ) if r+s⩽1.
These axioms are all valid, and the proof of validity requires only the finite additivity of a probability measure.
Let ℛ be the set of all Archimedean inferences (1). Then ℛ is countable because each such inference ρ is determined by its conclusion formula [r 0⋯r n−1 s]φ and there are only countably many formulas. We will abbreviate this conclusion of ρ to φ ρ (s), suppressing the parameters r 0,…,r n−1, and write each premise correspondingly as φ ρ (r). So ρ takes the form ({φ ρ (r):r<s},φ ρ (s)). Notice that the form of (1) ensures that ℛ is closed under application of the modalities, in the sense that for any u∈Q 01, the pair
is also an Archimedean inference.
Now let ⊢ be the smallest deducibility relation that is classical (i.e. satisfies the Assumption, Detachment, Cut, and Deduction rules) and has the following additional properties:
- Axiom Deducibility::
-
φ∈Ax implies ⊢φ.
- Almost Sure Rule::
-
⊢φ implies ⊢[1]φ.
- Archimedean Rule::
-
{φ ρ (r):r<s}⊢φ ρ (s), for all ρ∈ℛ.
Lemma 5
-
(1)
Monotone Rule: ⊢φ→ψ implies ⊢[r]φ→[r]ψ.
-
(2)
⊢[r]⊤.
-
(3)
⊢[0]φ.
-
(4)
⊢¬[r]⊥, if r>0.
-
(5)
⊢[s]φ→[r]φ, if r<s.
-
(6)
⊢[r]φ→¬[s]ψ, if r+s>1 and ⊢¬(φ∧ψ).
-
(7)
[r]φ∧[s]ψ→[r+s](φ∨ψ), if r+s⩽1 and ⊢¬(φ∧ψ).
-
(8)
⊢φ implies ⊢[r]φ.
-
(9)
⊢[r 0⋯r n−10]φ.
Proof
(Briefly) For (1), from φ→ψ deduce [1](φ→ψ) by the Almost Sure Rule, then apply axiom A1 and the Detachment Rule. (2) comes directly by the Almost Sure Rule. For (3), use the tautology ⊥→φ and apply the Monotone Rule (1) and axiom A2.
(4)–(7) are shown as in Lemmas 4.6 and 4.7 of [10]. (8) follows by the Almost Sure Rule and (5). (9) follows from (3) by repetition of (8). □
Theorem 5
(Soundness)
If Γ⊢φ, then Γ⊨φ.
Proof
The rules defining ⊢ are all satisfied when ⊢ is replaced by ⊨. Since ⊢ is specified to be the smallest relation satisfying these rules, the result follows. □
To prove the converse of this result (strong completeness), a canonical model will be constructed whose points are the (ℛ,⊢)-rich sets of formulas. This requires some proof-theoretic preliminaries concerning the question of when a maximally finitely ⊢-consistent set Δ is closed under the rules from ℛ. For Δ to be closed under a given rule ρ, with conclusion φ ρ (s), it is enough that Δ decides ρ, that is, either φ ρ (s)∈Δ or ¬φ ρ (r)∈Δ for some r<s. By properties of maximally finitely consistent sets, this is equivalent to asking that for some r<s, (¬φ ρ (r)∨φ ρ (s))∈Δ, or equivalently, (φ ρ (r)∧¬φ ρ (s))∉Δ. That provides some motivation for the next result, which uses the full strength of the Archimedean Rule.
Lemma 6
Let Δ be an (ℛ,⊢)-rich set of formulas. For any rule ρ∈ℛ with conclusion φ ρ (s), and any positive t∈Q 01, there exists an r<s with
Proof
Let L={u∈Q 01:[u]φ ρ (s)∈Δ}. Then 0∈L since the formula [0]φ ρ (s) is deducible by Lemma 5(3) and so belongs to Δ. Thus, L is non-empty and must have a supremum l⩽1. Then in general,
For if u⩽l and r<u, there must be a v∈L with r<v. But [v]φ ρ (s)→[r]φ ρ (s) is deducible (Lemma 5(5)) and so belongs to Δ, and this leads to [r]φ ρ (s)∈Δ. Hence, we have {[r]φ ρ (s):r<u}⊆Δ, which by ℛ-closure of Δ implies [u]φ ρ (s)∈Δ, giving (3).
Now take the case l=1. Then [1]φ ρ (s)∈Δ. But [t]¬φ ρ (s)→¬[1]φ ρ (s) is in Δ by axiom A3, so this implies that [t]¬φ ρ (s)∉Δ. Thus, we can pick any r<s and conclude that [t](φ ρ (r)∧¬φ ρ (s))∉Δ with the help of the Monotone Rule.
Alternatively, l<1. In that case, choose a u∈Q 01 with l<u<l+t, and then a v∈Q 01 with u−t⩽v⩽l. Since l<u, [u]φ ρ (s)∉Δ. But Δ is closed under the inference [u]ρ (2), so there is some r<s with [u]φ ρ (r)∉Δ. To complete the lemma, we need to show that it is false that
Now φ ρ (s)→φ ρ (r) is deducible, by Lemma 5(5) and the Monotone Rule. Hence, [v]φ ρ (s)→[v](φ ρ (r)∧φ ρ (s)) is deducible by the Tautological and Monotone rules. But [v]φ ρ (s)∈Δ as v⩽l (3), so this implies
Assume, for contradiction, that (4) is true. Then we must have v+t⩽1 since otherwise by Lemma 5(6), [v](φ ρ (r)∧φ ρ (s))→¬[t](φ ρ (r)∧¬φ ρ (s)) is deducible, which is incompatible with (5) and (4) both holding. But now if v+t⩽1, axiom A4 combines with (5) and (4) to give [v+t]φ ρ (r)∈Δ. Since we already have [u]φ ρ (r)∉Δ, this contradicts the fact that u⩽v+t.
Altogether, we have shown that (4) cannot be true, completing the proof. □
Next, let {ρ 1,…,ρ n ,…} be an enumeration of ℛ with
Fix an (ℛ,⊢)-rich set Δ and a positive t∈Q 01. For each n⩾1, define t n =t/2n. Then by Lemma 6 there exists an r n <s n such that
where ψ n =(φ n (r n )∧¬φ n (s n )).
Lemma 7
For all n⩾1, [t](ψ 1∨⋯∨ψ n )∉Δ.
Proof
Observe that t 1+⋯+t n =∑ i⩽n t/2i<t⩽1.
Now for all i⩽n, [t i ]ψ i ∉Δ by (6), hence ¬[t i ]ψ i ∈Δ. So from axiom A5 we get ¬[t 1+⋯+t n ](⋁ i⩽n ψ i )∈Δ, hence [t 1+⋯+t n ](⋁ i⩽n ψ i )∉Δ. The desired result now follows as ⊢[t](⋁ i⩽n ψ i )→[t 1+⋯+t n ](⋁ i⩽n ψ i ) by Lemma 5(5). □
For any set Γ of formulas, let ⋀ ω Γ be the set of conjunctions of all finite subsets of Γ, that is, ⋀ ω Γ={⋀Σ:Σ⊆Γ and Σ is finite}, and for any r∈Q 01, let
Lemma 8
For any positive t∈Q 01, if [t]⋀ ω Γ can be extended to a (ℛ,⊢)-rich set, then so can Γ.
Proof
Assume that [t]⋀ ω Γ⊆Δ for some (ℛ,⊢)-rich Δ. Let
where the ψ n are obtained from Δ as above and satisfy Lemma 7.
Now if Θ 0 is finitely ⊢-consistent, it must have a maximally finitely ⊢-consistent extension Θ. Then for each n⩾1, the formula ψ n =(φ n (r n )∧¬φ n (s n )) is not in Θ because ¬ψ n ∈Θ. This, as explained above, ensures that ¬φ n (r n )∈Θ or φ n (s n )∈Θ, so Θ decides ρ n and therefore is closed under ρ n . The upshot is that Θ is a maximally finitely ⊢-consistent extension of Γ that is ℛ-closed and hence is (ℛ,⊢)-rich, completing the proof.
So it remains to show that Θ 0 is finitely ⊢-consistent. But if it were not, there would be some finite Σ⊆Γ and some n such that
That would lead to Σ⊢⋁ i⩽n ψ i and hence to ⊢⋀Σ→⋁ i⩽n ψ i . By the Monotone Rule it would follow that ⊢[t]⋀Σ→[t]⋁ i⩽n ψ i . But [t]⋀Σ belongs to Δ by assumption, so this would imply that [t]⋁ i⩽n ψ i ∈Δ, contradicting Lemma 7. □
We are now ready to construct the canonical model, to be denoted ℳ c . Let X c be the set of all (ℛ,⊢)-rich sets of formulas. For each formula φ, let |φ|={Δ∈X c :φ∈Δ}, and put 𝒜 c ={|φ|:φ is a formula}. Then 𝒜 c is an algebra since X−|φ|=|¬φ| and |φ|∪|ψ|=|φ∨ψ|.
For Δ∈X c , define μ Δ :𝒜 c →[0,1] by putting
Thus, the number l defined at the beginning of the proof of Lemma 6 is μ Δ |φ ρ (s)|. In general, we have
For if μ Δ |φ|⩾r, then for any s<r, by definition of μ Δ |φ| as a supremum there is a u>s with [u]φ∈Δ. Hence, [s]φ∈Δ by Lemma 5(5). Thus, {[s]φ:s<r}⊆Δ, implying [r]φ∈Δ because Δ is ℛ-closed. The converse holds by definition.
μ Δ can be shown to be a well-defined finitely additive function as in [10, Theorem 5.4]. By results (3) and (4) of Lemma 5, μ Δ ∅=μ Δ |⊥|=0, and by result (2), μ Δ X c =μ Δ |⊤|=1. Moreover, μ Δ is continuous from above at ∅. To see why, suppose that |φ 0|⊇|φ 1|⊇⋯ is a nested sequence of members of 𝒜 c whose intersection is empty. Then we want to show that lim n→∞ μ Δ |φ n |=0. Now by finite additivity, the number sequence {μ Δ |φ n |:n<ω} is non-increasing. If this sequence did not converge to 0, there would exist a positive rational t with μ Δ |φ n |⩾t for all n. Then if Γ={φ n :n<ω}, then any ψ∈⋀ ω Γ has |ψ|=|φ m | for some m since the |φ n | are nested, hence μ Δ (|ψ|)⩾t, so [t]ψ∈Δ by (7). This shows that [t](⋀ ω Γ) is a subset of Δ. Our Lemma 8 then implies that there is a Θ∈X c with Γ⊆Θ. But then Θ∈⋂ n<ω |φ n |, contradicting the assumption that this intersection is empty. Hence, {μ Δ |φ n |:n<ω} does converge to 0.
Thus, indeed μ
Δ
is continuous from above at ∅ and so is countably additive and a probability measure. Standard measure theory then tells us that it extends uniquely to a probability measure on σ(𝒜
c
), the σ-algebra on X
c
generated by 𝒜
c
. We call this extension μ
Δ
as well. The map Δ↦μ
Δ
from (X
c
,σ(𝒜
c
)) to its space of probability measures  is then a measurable map because each measurable set of the form {μ:μ|φ|⩾r} in the space of measures pulls back along this map to the measurable set |[r]A|∈𝒜
c
, by (7).
is then a measurable map because each measurable set of the form {μ:μ|φ|⩾r} in the space of measures pulls back along this map to the measurable set |[r]A|∈𝒜
c
, by (7).
The model ℳ
c
is now defined on the measurable space (X
c
,σ(𝒜
c
)) by putting  for all propositional variables p.
for all propositional variables p.
Lemma 9
(Truth Lemma)
Every formula
φ
has
 , that is, for all
Δ∈X
c
,
, that is, for all
Δ∈X
c
,

Proof
By induction on the formation of φ, with the base case holding by the definition of  . The cases of the truth-functional connectives are standard, and the case of a formula [r]φ, assuming the result for φ, is given by (7). □
. The cases of the truth-functional connectives are standard, and the case of a formula [r]φ, assuming the result for φ, is given by (7). □
Corollary 1
-
(1)
Every (ℛ,⊢)-rich set Δ is ⊢-deductively closed, that is, Δ⊢φ implies φ∈Δ, and is maximally ⊢-consistent.
-
(2)
A set of formulas is ⊢-consistent iff it has an (ℛ,⊢)-rich extension.
Proof
(1) By the Truth Lemma, every member of Δ is satisfied at the point Δ in ℳ c , that is, ℳ c ,Δ⊨Δ. Thus, if Δ⊢φ, then Δ⊨φ by soundness, hence ℳ c ,Δ⊨φ, and so the Truth Lemma gives φ∈Δ.
It follows that Δ is ⊢-consistent since if Δ⊢⊥, then ⊥∈Δ, which would contradict the finite ⊢-consistency of Δ. But Δ has no proper ⊢-consistent extensions since by the definition of “rich” it has no proper finitely ⊢-consistent extensions.
(2) From left to right holds by Rich Extension Theorem 4. Conversely, if Γ has an (ℛ,⊢)-rich extension Δ, then since ⊥∉Δ, we have Δ⊬⊥ by (1), hence Γ⊬⊥ by D1, so Γ is ⊢-consistent. □
Remark 1
A natural question here is whether this ⊢-deductive closure of a rich set can be shown proof-theoretically, rather than by a model-theoretic detour through the canonical model. A strategy for this is to define the notion of a “theory” as being a set with suitable closure properties, including in this case closure under the Detachment Rule and under ℛ, and then to define a relation Γ⊢+ φ to mean that φ belongs to every theory that includes Γ. In other words, the set {φ:Γ⊢+ φ} is the intersection of all theories that include Γ, and will typically be a theory as well. Thus, if Γ itself is a theory, it will be ⊢+-deductively closed by definition. Moreover, rich sets will be theories, hence a rich set is ⊢+-deductively closed. One then shows that ⊢+ satisfies all the rules that define ⊢, from which it follows that in general Γ⊢φ implies Γ⊢+ φ because ⊢ is specified to be the smallest relation satisfying these rules. Now if Γ is rich and Γ⊢φ, we get Γ⊢+ φ, and hence φ∈Γ because a rich set is ⊢+-deductively closed.
This kind of analysis is applied to modal logic in [9], to dynamic/algorithmic logic in [5], and to coalgebraic logic in [4, 10].
We turn now to our main goal for probabilistic modal logic:
Theorem 6
(Strong Completeness)
-
(1)
Every ⊢-consistent set of formulas is satisfiable.
-
(2)
If Γ⊨φ, then Γ⊢φ.
Proof
(1) and (2) are equivalent. We prove (1) and infer (2).
For (1), if Γ is ⊢-consistent, then by the Rich Extension Theorem 4 there is a Δ∈X c with Γ⊆Δ. By the Truth Lemma 9, ℳ c ,Δ⊨Δ, so Γ is satisfied at Δ in ℳ c . For (2), if Γ⊬φ, then Γ∪{¬φ} is ⊢-consistent by D4, so is satisfiable by (1), implying \(\varGamma\not\models\varphi\). □
Finally on this topic, here are some remarks on the background to the strong completeness result. Heifetz and Mongin [11] gave a finitary axiomatization of the set {φ:∅⊨φ} of valid formulas, using a set of axioms similar to our A1–A5, and a special rule that derives assertions about the probabilities of two finite sets of formulas that are equivalent in a suitable sense. Zhou [21, 22] replaced this rule by the infinitary inference scheme
and showed that the resulting system was equivalent to that of [11]. He also gave an example in [23] to show that the canonical measure associated with a maximally consistent set for this system need not be countably additive.
The present author showed in [10] that the countable additivity of canonical measures follows from the rule
for positive t and countable Γ. This is itself derivable from the rule
by taking φ=⊥ and using ⊢¬[t]⊥ (Lemma 5(4)). For countable Γ, (9) is sound for the present semantics (i.e. is true when ⊢ is replaced by ⊨), as can be shown using continuity of a measure from above [10, Theorem 4.8]. The reference to countability of Γ was required because some of the logics discussed in [10] have uncountably many formulas. In that situation a “rich extension” theorem is not always available, and the analysis of μ Δ given in [10] depended on ⊢ having the Lindenbaum property that every ⊢-consistent set has a maximally ⊢-consistent extension. The semantic consequence relation ⊨ has this property since ⊨-consistency just means satisfiability, and if Γ is satisfied at x in ℳ, then {φ:ℳ,x⊨φ} is a maximally ⊨-consistent set extending Γ. It was shown that ⊨ is characterizable proof-theoretically as the smallest deducibility relation having the Lindenbaum property [10, Theorem 5.17].
The striking insight that the set ℛ of Archimedean inferences suffices to show that μ Δ is countably additive is due to the authors of [17]. Our Lemmas 6–8 are motivated by the Stone duality constructions of Sect. VI of [17] and are intended to give a proof-theoretic manifestation of that insight. Note the equivalence of Lemma 8 and the rule (8) by Corollary 1(2). The countability of the language and of ℛ ensures that the Henkin method can be applied to show that sufficiently many ℛ-rich extensions exist to prove Strong Completeness.
7 The Baire Category Connection
The year after Henkin’s new first-order completeness proof appeared in print, Helena Rasiowa and Roman Sikorski published another proof based on Boolean-algebraic and topological ideas [19]. This introduced what became known as the Rasiowa–Sikorski Lemma, stating that any non-unit element of a Boolean algebra belongs to a prime ideal that preserves countably many prescribed joins. They proved this by using the fact that the Stone space of a Boolean algebra satisfies the Baire Category Theorem: the intersection of countably many open dense sets is dense.
There are intimate relationships between the Rasiowa–Sikorski Lemma, the Baire Category Theorem for certain kinds of spaces, and the Countable Henkin Principle. These are explored in [7]. Here we will illustrate the connection by giving a rapid version of a topological proof of our Rich Extension Theorem 2. As will be evident, this is rather more elaborate than the direct deducibility-theoretic proof.
Let X m be the set of maximally finitely ⊢-consistent sets of subsets of Φ, where ⊢ is a classical deducibility relation. For each φ∈Φ, let |φ| m ={Δ∈X m :φ∈Δ}. The collection {|φ| m :φ∈Φ} is a basis for a compact Hausdorff topology on X m , in which each basic open |φ| m is also closed, because X m −|φ| m =|¬φ| m .
Now let Γ be ⊢-consistent. Define Γ ⊢={φ:Γ⊢φ}, and restrict X m to the set X Γ ={Δ∈X m :Γ ⊢⊆Δ}. Then X Γ =⋂{|φ| m :φ∈Γ ⊢}, so X Γ is a closed subset of X m and hence becomes a compact Hausdorff space itself under the subspace topology. A basis for this subspace topology is {|φ| Γ :φ∈Φ}, where |φ| Γ =|φ| m ∩X Γ ={Δ∈X Γ :φ∈Δ}.
Note that Γ⊆Γ ⊢ by D2. Also, Γ ⊢ is closed under ⊢-deducibility since if Γ ⊢⊢χ, then Γ⊢χ by the Cut Rule. Consequently, Γ ⊢ is ⊢-consistent because Γ is. Therefore, by Lindenbaum’s Lemma, X Γ is non-empty. Moreover, using the Deduction Rule and its converse, we get that in general
Given an inference ρ=(Π,χ), define U ρ ={Δ∈X Γ :Δ is closed under ρ}. Since members of X Γ are negation complete, a given Δ∈X Γ is closed under ρ iff it either contains χ or contains ¬φ for some φ∈Π. Thus,
which shows that U ρ is open, being a union of (basic) open sets.
Lemma 10
If Γ∪{ψ} respects ρ for all ψ∈Φ, then the open set U ρ is dense in the space X Γ .
Proof
Let Γ∪{ψ} respect ρ for all ψ∈Φ. To prove density of U ρ , it suffices to show that any non-empty basic open set |ψ| Γ intersects U ρ . So assume that |ψ| Γ ≠∅.
First, take the case that for some φ∈Π, the set Γ ⊢∪{ψ,¬φ} is ⊢-consistent. Then this set extends by Lindenbaum’s Lemma to a Δ∈X Γ that belongs to |ψ| Γ ∩|¬φ| Γ ⊆|ψ| Γ ∩U ρ , giving the desired result that |ψ| Γ ∩U ρ ≠∅.
The alternative case is that for all φ∈Π, we have Γ ⊢∪{ψ,¬φ}⊢⊥; hence, Γ ⊢∪{ψ}⊢φ by D4, so Γ∪{ψ}⊢φ by (10). But Γ∪{ψ} respects ρ, so then Γ∪{ψ}⊢χ. Hence, (ψ→χ)∈Γ ⊢ by (10).
By assumption there exists some Δ∈|ψ| Γ . Since Γ ⊢⊆Δ, we get (ψ→χ)∈Δ and ψ∈Δ, giving χ∈Δ and thus Δ∈|ψ| Γ ∩|χ| Γ ⊆|ψ| Γ ∩U ρ . So again |ψ| Γ ∩U ρ ≠∅ as required. □
Now to prove the Rich Extension theorem, let ℐ be a countable set of inferences such that Γ∪{ψ} respects ℐ for all ψ∈Φ. Define U ℐ=⋂{U ρ :ρ∈ℐ}. Then U ρ is the set of all (ℐ,⊢)-rich extensions of Γ ⊢. By the lemma just proved, U ℐ is the intersection of countably many open dense subsets of the space X Γ . Hence, U ℐ is dense in X Γ since the Baire Category Theorem holds for any compact Hausdorff space. Since X Γ ≠∅, it follows that U ℐ≠∅. Any member of U ℐ is an (ℐ,⊢)-rich extension of Γ fulfilling Theorem 2.
References
Aumann, R.J.: Interactive epistemology II: Probability. Int. J. Game Theory 28, 301–314 (1999)
Barwise, J.: Admissible Sets and Structures. Springer, Berlin (1975)
Chang, C.C., Keisler, H.J.: Model Theory, 2nd edn. North-Holland, Amsterdam (1977)
Friggens, D., Goldblatt, R.: A modal proof theory for final polynomial coalgebras. Theor. Comput. Sci. 360, 1–22 (2006)
Goldblatt, R.: Axiomatising the Logic of Computer Programming. Lecture Notes in Computer Science, vol. 130. Springer, Berlin (1982)
Goldblatt, R.: An abstract setting for Henkin proofs. Topoi 3, 37–41 (1984)
Goldblatt, R.: On the role of the Baire category theorem and dependent choice in the foundations of logic. J. Symb. Log. 50, 412–422 (1985)
Goldblatt, R.: An abstract setting for Henkin proofs. In: Mathematics of Modality, CSLI Lecture Notes, vol. 43, pp. 191–212. CSLI Publications, Stanford (1993). Expanded version of [6]
Goldblatt, R.: A framework for infinitary modal logic. In: Mathematics of Modality, CSLI Lecture Notes, vol. 43, pp. 213–229. CSLI Publications, Stanford (1993)
Goldblatt, R.: Deduction systems for coalgebras over measurable spaces. J. Log. Comput. 20(5), 1069–1100 (2010). doi:10.1093/logcom/exq029. Cited 12 December 2008
Heifetz, A., Mongin, Ph.: Probability logic for type spaces. Games Econ. Behav. 35, 31–53 (2001)
Henkin, L.: The completeness of the first-order functional calculus. J. Symb. Log. 14, 159–166 (1949)
Henkin, L.: Completeness in the theory of types. J. Symb. Log. 15, 81–91 (1950)
Henkin, L.: A generalisation of the concept of ω-consistency. J. Symb. Log. 19, 183–196 (1954)
Henkin, L.: A generalisation of the concept of ω-completeness. J. Symb. Log. 22, 1–14 (1957)
Henkin, L.: The discovery of my completeness proofs. Bull. Symb. Log. 2(2), 127–158 (1996)
Kozen, D., Larsen, K.G., Mardare, R., Panangaden, P.: Stone duality for Markov processes. In: Proceedings of the 28th Annual ACM/IEEE Symposium on Logic in Computer Science (LICS 2013), pp. 321–330 (2013). Available via doi:10.1109/LICS.2013.38
Orey, S.: ω-consistency and related properties. J. Symb. Log. 21, 246–252 (1956)
Rasiowa, H., Sikorski, R.: A proof of the completeness theorem of Gödel. Fundam. Math. 37, 193–200 (1950)
Sacks, G.E.: Saturated Model Theory. Benjamin, Reading (1972)
Zhou, Ch.: A Complete Deductive System for Probability Logic with Application to Harsanyi Type Spaces. Ph.D. thesis, India University (2007)
Zhou, Ch.: A complete deductive system for probability logic. J. Log. Comput. 19(6), 1427–1454 (2009)
Zhou, Ch.: Intuitive probability logic. In: Ogihara, M., Tarui, J. (eds.) TAMC 2011: Theory and Applications of Models of Computation—8th Annual Conference. Lecture Notes in Computer Science, vol. 6648, pp. 240–251. Springer, Berlin (2011)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2014 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Goldblatt, R. (2014). The Countable Henkin Principle. In: Manzano, M., Sain, I., Alonso, E. (eds) The Life and Work of Leon Henkin. Studies in Universal Logic. Birkhäuser, Cham. https://doi.org/10.1007/978-3-319-09719-0_13
Download citation
DOI: https://doi.org/10.1007/978-3-319-09719-0_13
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-319-09718-3
Online ISBN: 978-3-319-09719-0
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)




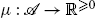 is a measure if it is continuous at ∅, that is, lim
n→∞
μ(Y
n
)=0 for any non-increasing sequence {Y
n
∣n<ω}⊆𝒜 with ⋂
n
Y
n
=∅.
is a measure if it is continuous at ∅, that is, lim
n→∞
μ(Y
n
)=0 for any non-increasing sequence {Y
n
∣n<ω}⊆𝒜 with ⋂
n
Y
n
=∅.