A Numerical Methodology for Resolving Aeroacoustic-Structural Response of Flexible Panel

Abstract

Fluid-structure interaction problem is relevant to the quieting design of flow ducts found in many aeronautic and automotive engineering systems where the thin duct wall panels are directly in contact with a flowing fluid. A change in the flow unsteadiness, and/or in the duct geometry, generates an acoustic wave which may propagate back to the source region and modifies the flow process generating it (i.e. an aeroacoustic process). The unsteady pressure arising from the aeroacoustic processes may excite the flexible panel to vibrate which may in turn modify the source aeroacoustic processes. Evidently there is a strong coupling between the aeroacoustics of the fluid and the structural dynamics of the panel in this scenario. It is necessary to get a thorough understanding of the nonlinear aeroacoustic-structural coupling in the design of effective flow duct noise control. Otherwise, an effective control developed with only one media (fluid or panel) in the consideration may be completely counteracted by the dynamics occurring in another media through the nonlinear coupling. The present paper reports an attempt in developing a time-domain numerical methodology which is able to calculate the nonlinear fluid-structure interaction experienced by a flexible panel in a flow duct and its aeroacoustic-structural response correctly. The developed methodology is firstly verified able to capture the acoustic-structural interaction in the absence of flow where the numerical results agree with theory very well. A uniform mean flow is then allowed to pass through the duct so as to impose an aeroacoustic-structural interaction on the flexible panel. As a result, the nonlinear coupling between the flow aeroacoustics and panel structural dynamics are found completely different from the case without mean flow. A discussion of the new physical behaviors found is given.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The accurate prediction of noise generation by flow induced vibration is an important and challenging task in many engineering problems. It is a major consideration in the quieting design of many applications that involve unsteady flow and flexible structures, such as those found in aircraft, automotive and ventilation systems. For example, people staying indoor are always annoyed by the noise radiation from air-conditioning or ventilation systems. The noise generated by the operations of air-moving machines, or by the turbulent flows in ducts, propagates through the ductworks and radiates from the duct outlets. Besides, the duct walls are commonly constructed from thin metal sheets. They are easily set to vibrate by both turbulent flows and noise. The vibration will generate additional noise to both inside and outside of the ducts [8] which causes more annoyance to people. Usually in such kind of problem, a complex interaction between the flow dynamics, acoustics and structural dynamics is involved. The three dynamical processes affect each other in a coupled manner and the final noise generation is very complicated.

Researchers have attempted different approaches to the study of the dynamics of flow-acoustics-structure interaction problem. Some of them favour their focus on the interaction between flow and structure over the acoustic aspects. Carpenter and Garrad [3] developed a simple model for flow over a compliant surface supported on an elastic foundation for the investigation of different types of flow-induced surface instabilities. Lucey [19] studied the wave-bearing behaviour of a finite flexible plate in a uniform flow. He found that it is possible for the plate to respond at frequencies other than that of the driver in the presence of flow. He assumed an incompressible flow in his study so the relevant acoustic field cannot be resolved. On the other hand, some researchers studied the interaction between an acoustic wave and a vibrating structure. Frendi et al. [10] compared two coupling models of acoustic-structural interaction. He found that the “decoupled model” is more accurate in predicting the panel response and acoustic radiation, and need lower computational cost. Huang [12] studied an idea of duct noise control by installing a flexible panel in an otherwise rigid duct, and provided theoretical solutions of this acoustic-structural interaction problem in frequency domain.

Other researchers are interested in studying the acoustic radiation driven by a fluid-structure interaction. Clark and Frampton [6] demonstrated the importance of including aeroelastic coupling in modelling the structural acoustic response for interior noise control on modern aircraft. Schäfer et al. [21] attempted to solve the fluid-acoustic-structure interaction of a flow past a thin flexible structure fully. They solved the fluid-structure interaction through a numerical coupling of the solutions from a fluid dynamic solver and a structural dynamic solver, and then determined the resultant acoustic field by adding the contributions from the fluid dynamic and structural dynamic solutions. In that way, the acoustic solution was simply treated as a consequence to the fluid-structure interaction but the effect of the acoustics on fluid-structure interaction was omitted.

All the aforementioned studies reveal that the three elemental dynamical processes (i.e. acoustics, flow and structural dynamics) are equally important in literally all fluid-acoustics-structure interaction problems but the current state of effort in resolving their highly coupled interactions is still far from satisfactory. It remains in a stage in which the coupled interaction between any two dynamics (e.g. fluid and structure) are calculated and the solution thus obtained is used to deduce the remaining dynamical process as an effect. In some situations, such effect may be fed back to significantly modify the interactions creating it but the determination of this feed-back process is always lacking. Furthermore, the current approaches usually involve the use of three different solvers for each dynamics. Pairwise dynamical coupling relies on extensive data exchange of three data sets for the calculation of complete interaction. That way would inevitably lead to prohibitively high demands in computational resources, high programming difficulties as well as severe numerical errors arising from data extrapolation involved during the exchanges.

In this light, the goal of the present study is to develop a simple yet accurate numerical methodology that fully accounts for the nonlinear fluid-acoustics-structure interaction encountered in real applications. The development takes the view that typically a fluid-acoustics-structure interaction problem occurs within a domain composed of a compressible fluid and a flexible structure. It is logical to take an approach that calculates the fluid dynamical processes entirely (i.e. fluid dynamics and acoustics) as well as the structural dynamics, and then resolves their coupled interaction. It is more appropriate to describe the fluid-acoustics-structure interaction problem as a aeroacoustic-structural interaction problem. Here we report the formulation of the numerical methodology and demonstrate its capability by solving the aeroacoustic-structural response of a canonical problem that involves an excited panel in a duct carrying a flow.

2 Problem of Interest

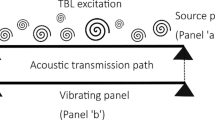
Recently Huang [12] has proposed a concept for low-frequency duct noise control making use of a finite length tensioned flexible panel flush-mounted in an infinite rigid flow duct (Fig. 1). When a plane acoustic wave is propagating through the duct, the panel responds to vibrate and the local distension in the vicinity of the panel thus created renders a local wave propagation speed far less than its isentropic value. The mismatch in the wave speed there leads to reflection and scattering of acoustic wave at the edges of the panel. The extent of reflection and scattering depends on the acoustic-structural interaction occurring with the vibrating panel which eventually results in creates passbands and stopbands for the acoustic transmission.

Fig. 1

Schematic configuration of the problem

We select the cases Huang [12] attempted for the demonstration of the developed numerical methodology. He presented a detailed linear analysis in frequency domain on how various panel parameters (e.g. length, stiffness, structural damping, etc.) influence the acoustic-structural interaction and subsequent transmission loss in the absence of mean flow. His results of the analysis are complete and provide a set of good reference for validating and verifying of the calculation. It is worthwhile to note that Huang and his co-workers [12, 13] have later extended the concept to develop the so-called drum-like silencer configuration by appending a side-branch cavity to the flexible panel. The fluid inside cavity provides additional elastic stiffness to the vibrating panel. In the present paper, the duct side-branch is excluded.

3 Formulation of Numerical Methodology

Schäfer et al. [21] calculated the acoustic field generated from the interaction of a thin flexible panel with a turbulent flow in a semi-open domain in time-domain. They first solved the fluid-structure interaction by coupling, through a parallel data-exchange interface, the solutions obtained from an finite-volume incompressible large-eddy simulation (LES) flow solver and an finite-element structural mechanics solver. Then they summed up the acoustic waves generated respectively from the unsteady flow solution and the panel structural solution using an finite-element acoustic solver. The total acoustic wave is allowed to propagate freely away from the panel. The effect of acoustic wave on the fluid-structure interaction is essentially excluded in the calculation. Such kind of hybrid approach is not appropriate for the present problem of interest. It is because in a flow duct the generated acoustic waves are reflected by the duct walls and mixed with the flow fluctuations. The overall fluctuations may propagate back to the source region and alter the unsteady flow dynamics and the panel structural vibration there. On the other hand, coupling approach described in [21] involves three channels for data exchange with three solvers. It involves many extrapolations of flow and panel vibration data which inevitably leads to substantial loss of useful dynamic data especially those with high-frequencies. Considering all these weaknesses of the hybrid approach, it is proposed to adopt a formulation which tries to maintain the accuracy of individual solvers yet keep the number of data exchange during coupling to minimal.

In order to obtain accurate time-domain solution of the aeroacoustic-structural response of the in-duct flexible panel exposed to flow and acoustic wave, there are three key elements in the numerical methodology. They are (i) the modeling of aeroacoustics of the fluid, (ii) the prediction of the dynamic response of the panel, and (iii) correct coupling strategy for the nonlinear interplay between the fluid aeroacoustics and panel structural dynamics. All of these elements must be included in the formulation of the numerical solver and each one of them must be selected according to the specific configuration considered.

3.1 Aeroacoustic Model

Acoustic motion is just a kind of unsteady flow motions that a fluid medium supports [7]. It is logical to adopt a numerical model for the fluid medium which allows simultaneous calculation of both the acoustic field and the unsteady flow generating it. Otherwise, the inherent nonlinear interaction between these two fields cannot be properly accounted for in the calculation. This capability is particularly important in calculating the present aeroacoustic problem because the acoustic fluctuations experience multiple reflections and scattering inside the duct which may propagate back and alter the unsteady flow dynamics and the panel structural vibration there. This capability is completely missing in the hybrid aeroacoustic models in which the flow solution is used to drive the acoustic field. As such, we adopt an aeroacoustic model based on direct aeroacoustic simulation (DAS) approach [17, 18] in the present study.

The aeroacoustic problem is governed by the two-dimensional compressible Navier-Stokes equations together with ideal gas law for calorically perfect gas. The normalized Navier-Stokes equations without source can be written in the strong conservation form as,

$$ \frac{{\partial \varvec{U}}}{\partial t} + \frac{{\partial \left( {\varvec{F} - \varvec{F}_{v} } \right)}}{\partial x} + \frac{{\partial \left( {\varvec{G} - \varvec{G}_{v} } \right)}}{\partial y} = 0, $$

(1)

where

$$ \begin{aligned} & \varvec{U} = \left[ {\begin{array}{*{20}c} \rho \\ {\rho u} \\ {\rho v} \\ {\rho E} \\ \end{array} } \right],\quad \varvec{F} = \left[ {\begin{array}{*{20}c} {\rho u} \\ {\rho u^{2} + p} \\ {\rho uv} \\ {(\rho E + p)u} \\ \end{array} } \right],\quad \varvec{G} = \left[ {\begin{array}{*{20}c} {\rho v} \\ {\rho uv} \\ {\rho v^{2} + p} \\ {(\rho E + p)v} \\ \end{array} } \right], \\ \varvec{F}_{v} & = \frac{1}{Re}\left[ {\begin{array}{*{20}c} 0 \\ {\tau_{xx} } \\ {\tau_{xy} } \\ {\tau_{xx} u + \tau_{xy} v - q_{x} } \\ \end{array} } \right],\quad \varvec{G}_{v} = \frac{1}{Re}\left[ {\begin{array}{*{20}c} 0 \\ {\tau_{xy} } \\ {\tau_{yy} } \\ {\tau_{xy} u + \tau_{yy} v - q_{y} } \\ \end{array} } \right], \\ \end{aligned} $$

ρ is the density of fluid, u and v are the velocities in x and y direction respectively, t is the time, normal and shear stress $\tau_{xx} = (2/3)\mu \left( {2\partial u/\partial x - \partial v/\partial y} \right),\,\;\tau_{xy} = \mu \left( {2\partial u/\partial y + \partial v/\partial x} \right),\;\;\tau_{yy} = (2/3)\mu \left( {2\partial v/\partial y - \partial u/\partial x} \right)$, total energy $E = p/\rho (\gamma - 1) + (u^{2} + v^{2} )/2$, pressure $p = \rho T/\gamma M^{2}$, heat flux $q_{x} = \left[ {\mu /(\gamma - 1)PrM^{2} } \right]\left( {\partial T/\partial x} \right)\;\,q_{y} = \left[ {\mu /(\gamma - 1)PrM^{2} } \right]\left( {\partial T/\partial y} \right)$, the specific heat ratio $\gamma = 1.4$, Mach number $M = \hat{u}_{0} /\hat{c}_{0}$ where $\hat{u}_{0}$ is the duct mean flow velocity, $\hat{c}_{0} = \sqrt {\gamma \hat{R}\hat{T}_{0} }$, the specific gas constant for air $\hat{R} = 287.058{\kern 1pt} {\text{J}}/({\text{kg}} \cdot {{K}})$, Reynolds number $Re = \hat{\rho }_{0} \hat{c}_{0} \hat{L}_{p} /\hat{\mu }_{0}$, and Prandtl number $Pr = \hat{c}_{p,0} \hat{\mu }_{0} /\hat{k}_{0} = 0.71$.

The DAS solver must be able to accurately calculate the acoustic and flow fluctuations, which exhibit large disparity in their energy and length scales. This poses a strict requirement to the solver of being low dissipation and highly accurate. Conventionally, high order explicit finite difference schemes such as Bogey [2] are adopted in DAS. Recently, the conservation element and solution element (CE/SE) method [5] has been proven to be a viable alternative [18]. This numerical scheme takes an entirely different approach and concept from conventional schemes (e.g., finite-difference). Its numerical framework relies solely on strict conservation of physical laws and emphasis on the unified treatment in both space and time. Lam et al. [18] showed that CE/SE method is capable of resolving the low Mach number interactions between the unsteady flow and acoustic field accurately by calculating the benchmark aeroacoustic problems with increasing complexity. Therefore, the CE/SE based the DAS solver is adopted as the aeroacoustic model in the present study. In this paper, the formulation of the CE/SE method is not given. Its details can be referred to the works of Lam [16].

3.2 Structural Dynamic Model

The dynamic response of the flexible panel can be modeled with the nonlinear Von Karman’s theory for isotropic rectangular elastic plate on Kelvin foundation. The panel is assumed to be of uniform small thickness h _p and initially flat. In the theory the normal displacements of the vibrating panel can reach the order of h _p but the tangential displacements can still be assumed to be negligibly small. Using the same set of reference parameters adopted in the aeroacoustic model, the normalized governing equation for panel displacement $w = \hat{w}/\hat{L}_{p} = w(x,z)$, where z is the direction pointing out of paper in Fig. 1, can be written as,

$$ D\nabla^{4} w - \fancyscript{L}\left( {T_{x} ,T_{y} ,T_{xy} ,w} \right) + \rho_{p} h_{p} \frac{{\partial^{2} w}}{{\partial t^{2} }} + C\frac{\partial w}{\partial t} + Kw = p_{ex} , $$

(2)

where $\fancyscript{L}\left( {T_{x} ,T_{y} ,T_{xy} ,w} \right) = T_{x} [\partial^{2} w/\partial x^{2} ] + T_{y} [\partial^{2} w/\partial y^{2} ] - 2T_{xy} [\partial^{2} w/(\partial x\partial y)],\;\;D = \hat{D}\hat{L}_{p}^{4} /(\hat{\rho }_{0} \hat{u}_{0}^{2} )$ is the flexural rigidity of panel, $\rho_{p} = \hat{\rho }_{p} /\hat{\rho }_{0}$ is the density of panel, $h_{p} = \hat{h}_{p} /\hat{L}_{p}$ is thickness of panel, $C = \hat{C}/(\hat{\rho }_{0} \hat{c}_{0} )$ is the structural damping coefficient, $K_{p} = \hat{K}_{p} \hat{L}_{p} /(\hat{\rho }_{0} \hat{c}_{0} )$ is the stiffness of foundation, $p_{ex} = \hat{p}_{ex} /(\hat{\rho }_{0} \hat{c}_{0}^{2} )$ is the net pressure exerted on the panel surface, $T_{x} = \hat{T}_{x} /(\hat{\rho }_{0} \hat{c}_{0}^{2} \hat{L}_{p} ),\;\;T_{y} = \hat{T}_{y} /(\hat{\rho }_{0} \hat{c}_{0}^{2} \hat{L}_{p} )$ and $T_{xy} = \hat{T}_{xy} /(\hat{\rho }_{0} \hat{c}_{0}^{2} \hat{L}_{p} )$ are the axial stress resultants, and $\nabla^{4} = \partial^{4} /\partial x^{4} + 2\left[ {\partial^{4} /\left( {\partial x^{2} \partial y^{2} } \right)} \right] + \partial^{4} /\partial y^{4}$ is the biharmonic operator.

In his analysis [12], Huang used a membrane model for the structural dynamics of the flexible panel. In order to ensure a consistent comparison with his analytical results, we need to simplify Eq. (2) for the calculation. A membrane can be considered as a very thin (with thickness/span <1/50) elastic panel with no appreciable flexural resistance so D = 0. The panel exterior is freely exposed to ambient air so K = 0. It is further assumed that in-plane shear stress can be ignored because the sideways motion at every point on the membrane is negligible. Consequently the tension is effectively uniform across the panel thickness. With all these assumptions made, the membrane model can describe the thin panel dynamics with small displacements (i.e. $\hat{w}/\hat{h}_{p} \le 0.2$) [4, 20, 23]. For the present study, we further assume no variations of the panel dynamics in $z$-direction so that the panel behaves more or less a quasi one-dimensional flexible beam along $x$-direction. Therefore, $w = w(x),\;\fancyscript{L}\left( {T_{x} ,T_{y} ,T_{xy} ,w} \right) = \fancyscript{L}\left( {T_{x} ,w} \right) = T_{x} [\partial^{2} w/\partial x^{2} ]$, and the panel structural dynamic equation to be solved becomes

$$ \rho_{p} h_{p} \frac{{\partial^{2} w}}{{\partial t^{2} }} + C\frac{\partial w}{\partial t} - T_{x} \frac{{\partial^{2} w}}{{\partial x^{2} }} = p_{ex} . $$

(3)

Note that in this equation the net external pressure should be interpreted as pressure difference across the panel, i.e. $p_{ex} = p_{0} - p$ (Fig. 1).

The panel dynamic equation is solved using the standard finite-difference procedures. The panel is initially discretized into a series of connect linear meshes of size $\Delta x$. All panel mesh points are located below the row of CE/SE solution points just next to boundary of fluid domain (Fig. 2). All spatial derivatives of the panel displacement are approximated using second-order central differences [11] as follows,

$$ \frac{{\partial w^{n,j} }}{\partial x} = w_{x}^{n,j} = \frac{1}{2\Delta x}\left( {w^{n + 1,j} - w^{n - 1,j} } \right), $$

(4)

$$ \frac{{\partial^{2} w^{n,j} }}{{\partial x^{2} }} = w_{xx}^{n,j} = \frac{1}{{\Delta x^{2} }}\left( {w^{n + 1,j} - 2w^{n,j} + w^{n - 1,j} } \right), $$

(5)

where the superscripts j and n indicate the j-th time step and n-th panel mesh point respectively. The second-order spatial derivatives at the two panel edges are given by $w_{xx}^{1,j} = \left( { - 4w^{1,j} + \frac{4}{3}w^{2,j} } \right)/\Delta x^{2}$ and $w_{xx}^{N,j} = \left( { - 4w^{N,j} + \frac{4}{3}w^{N - 1,j} } \right)/\Delta x^{2}$. The time derivatives are calculated using the following approximations, with time step size $\Delta t$,

$$ \frac{{\partial w^{n,j} }}{\partial t} = \dot{w}^{n,j} = \frac{1}{2\Delta t}\left( {w^{n,j + 1} - w^{n,j - 1} } \right), $$

(6)

$$ \frac{{\partial^{2} w^{n,j} }}{{\partial t^{2} }} = {\mathop w\limits^{..}}^{n,j} = \frac{1}{{\Delta t^{2} }}\left( {w^{n,j + 1} - 2w^{n,j} + w^{n,j - 1}} \right), $$

(7)

Fig. 2

Meshes at fluid-panel interface. Dashed line undeflected panel position. Square solution points of boundary cells and ghost cells of CE/SE mesh. Circle panel mesh points

Substituting all these approximations to Eq. (3), the panel displacement is approximated as

$$ w^{n,j + 1} = \frac{{Cw^{n,j - 1} \Delta t - 2\rho_{p} h_{p} \left( {w^{n,j - 1} - 2w^{n,j} } \right) + 2p\Delta t^{2} + 2T_{x} w_{xx}^{n,j} \Delta t^{2} }}{{2\rho_{p} h_{p} + C \Delta t}}. $$

(8)

Therefore, after each time step the dynamics of all panel mesh points $\varvec{W} = [w,\dot{w},\mathop w\limits^{..} ]^{T}$ are readily available.

3.3 Boundary Condition

The boundary conditions for the duct fluid domain are prescribed as follows. Isothermal condition $T_{p} = T_{0}$ is specified on all solid surfaces. Slip boundary condition is applied to all rigid surfaces. For the fluid boundary in contact with the vibrating panel, the tangency condition $(v - \dot{w}) = 0$ and the normal pressure gradient condition $\partial p/\partial y = \rho \mathop w\limits^{..}$ are required to satisfy. Pinned conditions are prescribed at both edges for the flexible panel where the displacement and bending moment are set to zero, i.e. $w^{1,j} = w^{N,j} = w_{xx}^{1,j} = w_{xx}^{N,j} = 0$.

At each time step the fluid domain is deformed by the calculated panel displacement. Usually remeshing (e.g. in So et al. [22]) is applied to the deformed fluid domain so as to eliminate any highly strained mesh where the solution is underresolved. Otherwise the solution accuracy will be seriously deteriorated. In the remeshing procedure all mesh points in the fluid domain are updated so heavy computational resources are required. For the present problem, recognizing the characteristic feature in CE/SE method on how the flow solution is calculated at solution points [16] and the fact that panel displacements are very small compared to panel thickness [12], we can account for the effect of deformation of fluid domain with a much simpler technique that is derived in the spirit of immersed element boundary method [9].

A brief of this simplified technique is given here with the help of the description of the computational domain around a panel mesh point $x^{n}$ illustrated in Fig. 2. In CE/SE method the solution points are not laid on the physical fluid domain boundary. The flow conditions at the boundary there are manifested by placing a mirror ghost cell behind the boundary (e.g. $A_{g}$). Appropriate flow variables are then specified at the ghost cell such that the desired flow conditions at the true panel position are implicitly given by interpolation with the boundary and ghost cells. For the rigid duct boundaries, we set the ghost point transverse velocity $v_{g} = - v_{b}$ for enforcing slip boundary condition. For the vibrating panel surface, we assume that its displacement is smaller than the offset $\delta$ of solution point $A_{b}$ and its velocity in y-direction $v_{g}$ can be approximated as

$$ v_{g} = \dot{w}^{n} + \frac{{\delta + w^{n} }}{{\delta - w^{n} }}\left( {\dot{w}^{n} - v_{b} } \right). $$

(9)

All the flow variables other than $v_{g}$ in the ghost cell are set according to the slip boundary condition procedure of Lam et al. [18]. Certainly we need to pay attention whether our assumption is valid during the course of calculations. For a large displacement (i.e. $w > \delta$), the tangential panel velocity becomes significant and the panel vibration starts to exhibit nonlinear behaviors. In this situation a more elaborated panel structural dynamic model together with a proper remeshing procedure must be used. In all the calculations reported here we found $w/\delta < 68\;\%$ consistently. This observation indicates that our proposed simplified technique works well for the present problem.

3.4 Fluid-Panel Coupling Scheme

When an unsteady flow and an acoustic wave are passing over the flexible panel, the flow pressure fluctuations acting on the panel will force to vibrate. The vibrating panel then modifies the boundary condition of the aeroacoustic flow which has to change as a consequence. The aeroacoustic field and the panel structural response are coupled to each other through the tangency boundary condition (effect of structural response on the unsteady flow) and the normal pressure gradient condition (effect of flow unsteadiness on the structural response). Both physical conditions respectively ensure the continuity of velocity and momentum at the fluid-panel interface in the solution of the problem. Therefore, an coupling scheme that allows seamless coupling of both effects is necessary for the accurate prediction of the flow-panel interaction involved. In addition to achieving the required numerical accuracy, we also want a scheme that is efficient and does not invoke too heavy computational resource requirement for marching the solution. We attempted two schemes for coupling in the present study.

The first scheme we attempted follows the idea of Jaiman et al. [15] which is schematically illustrated in Fig. 3. In this scheme, the panel structural dynamic solution $\varvec{W}_{j - 1}$ available at the end of the $(j - 1)$-th time step is treated as the boundary condition of the fluid domain in contact with the panel for the solver of aeroacoustic model for calculating the new aeroacoustic solution at the j-th time step, i.e. the $\varvec{U}_{j}$. Then the new panel structural response $\varvec{W}_{j}$ is evaluated by solving Eq. (3) with its forcing term, i.e. $p_{ex}$, constructed from the aeroacoustic solution $\varvec{U}_{j}$. Both $\varvec{U}_{j}$ and $W_{j}$ available at the end of the j-th time step are then used as the initial solutions for the $(j + 1)$-th time step and the solution of the problem marches in time afterwards. As such in each time step the update of the panel structural response appears to lag that of aeroacoustic solution. This feature leads to the enforcement of the tangency condition and the normal pressure gradient condition in a staggered manner. Thus the communication between the two solutions is literally one-way so the scheme can be considered to resolve the fluid-panel interaction in a loose coupling sense. The numerical error arising from the delay between the updates of aeroacoustic and structural dynamic solutions can be effectively suppressed with the reduced time step size [15]. Since a small time step size is always needed for the present explicit CE/SE aeroacoustic solver [18], especially in the case with a low Mach number flow, the scheme appears to be a reasonable choice for solving the present problem.

Fig. 3

Calculation procedure of the staggered coupling scheme. AAM aeroacoustical model; SDM structural dynamic model

Another more elaborated scheme we attempted for calculating the fluid-panel coupling follows the idea of Jadic et al. [14] which emphasizes more on the two-way coupling between the aeroacoustic and structural dynamic solutions (Fig. 4). In the calculation at the j-th time step, initial solution estimates, $\varvec{U}_{ie}$ and $\varvec{W}_{ie}$ are firstly evaluated in the same way as described in the loose coupling scheme. The initial estimates are then put into a predictor-corrector procedure in which the errors in the satisfaction of both tangency and normal pressure gradient conditions are minimized in an iterative manner. Essentially, an aeroacoustic solution estimate $\varvec{U}_{k + 1}$ is obtained with an predicted boundary condition $\lambda \varvec{W}_{k} + (1 - \lambda )\varvec{W}_{k - 1}$, where $\lambda$ is the relaxation factor [1]. Then the estimated $\varvec{W}_{k + 1}$ is obtained with an predicted forcing from $\lambda U_{k + 1} + (1 - \lambda )U_{k}$. If the relative errors between the solutions at iterations k and $k + 1$ at all panel mesh points is less than the prescribed precision $\varepsilon$, then the final solutions $\varvec{U}_{j} = \varvec{U}_{k + 1}$ and $\varvec{W}_{j} = \varvec{W}_{k + 1}$ are marched forward to next time step; otherwise the iteration continues until the precision requirement is reached. Since the effects of aeroacoustics on the panel structural dynamics and its vice versa are accounted for in the solution in equal footing, the procedure described leads to a more tightly coupled scheme for resolving the fluid-panel interaction. Nevertheless the computational resources incurred is heavier. In all the calculations reported in the later sections, $\lambda$ is set equal to 0.5 whereas the precision requirement $\varepsilon$ is prescribed to $10^{ - 10}$. The number of iterations in each time step is around 20.

Fig. 4

Calculation procedure of the iterative coupling scheme. AAM aeroacoustical model; SDM structural dynamic model

4 Results and Discussions

Although the numerical methodology developed aims to resolve the nonlinear aeroacoustic-structural interaction between a flexible panel and an incident acoustic wave in the presence of flow, it would be informative to assess how accurate the developed methodology resolves the acoustic-structural response of the panel without flow first. We then proceed to include uniform flows for the study of its capability of resolving the aeroacoustic-structural interaction. We use the same physical parameters as in Huang [12]: duct width $\hat{h} = 100\,{\text{mm}}$, panel length $\hat{L}_{p}$ can be changed, density of panel $\hat{\rho }_{p} = 1000\,{\text{kg/m}}^{3}$ (close to rubber), thickness of panel $\hat{h}_{p} = 0.05\,{\text{mm}}$, tensile force $\hat{T}_{x} = 58.0601\,{\text{N/m}}$ and frequency of incident wave $\hat{f} = 340\,{\text{Hz}}$.

The present computational domain for Huang’s problem is detailed in Fig. 1. In solving the problem, we normalize all the flow and structural variables with the reference parameters, namely, length = panel length $\hat{L}_{p}$, velocity $= \hat{c}_{0} = 340\,{\text{m/s}}$, time $\hat{t}_{0} = \hat{L}_{p} /\hat{c}_{0}$, density $= \hat{\rho }_{0} = 1.225\,{\text{kg/m}}^{ 3}$, and pressure $\hat{\rho }_{0} \hat{c}_{0}^{2}$. Here the variables with a caret “^” denote the quantities with dimensions and subscript “0” means the fluid property in stationary ambient. The duct sections upstream and downstream of the flexible panel is set 36 times of the panel length for ensuring sufficient space for the generated acoustic wave to propagate. In order to avoid the contamination of any erroneous waves reflected from the physical duct inlet and outlet, numerical anechoic termination ($D_{0}$ in Fig. 1) proposed by Lam et al. [17] is attached to the inlet and outlet. It acts to absorb leaving acoustic waves scattered from the vibrating panel. The chosen physical parameter gives $Re = 10^{12}$. Thus the fluid viscosity effect is effectively suppressed and the flow in the calculation is essentially inviscid.

Different meshing on the fluid domain and the panel was attempted for convergence study of the proposed methodology. The mesh used in the calculations for the forthcoming discussions is the largest one that exhibits convergent results. It is defined as follows. The panel mesh size is set to $\Delta x = 0.002$ uniformly. The fluid region above the panel follows the same mesh size along $x$-direction. The mesh size is smoothly increased to $\Delta x = 0.05$ from the panel edges to the duct interior upstream and downstream of the panel over approximately a panel length beyond which $\Delta x$ remains constant on going towards the duct inlet and outlet. A uniform mesh distribution $\Delta y = H/50$ is taken along $y$-direction in all cases.

4.1 Acoustic-Structural Response

As mentioned earlier, the acoustically excited vibration of the flexible panel is able to reflect and scatter the incident acoustic waves. As a result the pressure of the acoustic wave propagating to duct section downstream of the panel is reduced. The reduction of the acoustic pressure is described by the transmission loss TL defined as

$$ {\text{TL}} = 20\mathop {\log }\nolimits_{10} \left( {\frac{{(p_{\text{downstream}} )_{rms} }}{{(p_{\text{incident}} )_{rms} }}} \right), $$

(10)

where subscript rms means the root-mean-squared value. We calculate the TL with different panel lengths $L_{p} /H = 4.3,\;6$ and 8 using both staggered and iterative fluid-panel coupling schemes. No structural damping is assumed. Since the panel length is chosen as the reference length, here we calculate the effects of $L_{p} /H$ variation through modifying the value of duct width H. This is different from the notation adopted in the theory where H is fixed but $L_{p}$ varies. A comparison of the numerical TL with the corresponding theoretical values is given in Table 1. The difference $\Delta {\text{TL}} = {\text{TL}}_{\text{numerical}} - {\text{TL}}_{\text{theoretical}}$ is also provided. In general $\Delta {\text{TL}}$ reduces as $L_{p} /H$ increases. The iterative fluid-panel coupling scheme appears to perform better than the staggered scheme for all cases attempted. The difference in the numerical result is particularly pronounced for a short panel ($L_{p} /H = 4.3$) where the $\Delta {\text{TL}} = 2.2$ db for staggered scheme but $\Delta {\text{TL}} = 0.9$ db for the iterative scheme. All these observations reveal that the iterative coupling scheme is more superior in capturing the fluid-panel interaction. Furthermore a careful check shows that additional time spent in iterative scheme takes approximately 30 % of that used in the staggered scheme. Having compared with the pros and cons of the scheme, we decide to employ the iterative scheme for all subsequent calculations.

Table 1 Transmission loss TL at various $L_{p} /H$

A more elaborated assessment of the numerical methodology with iterative scheme is illustrated in Fig. 5. In this figure the numerical results with panel structural damping are also included. In Huang’s frequency-domain analysis [12], the damping coefficient taken for the n-th structural vibration mode is estimated as

$$ C = \frac{{n\rho_{p} h_{p} \bar{C}}}{{L_{p} }}\sqrt {\frac{{T_{x} }}{{\rho_{p} h_{p} }}} , $$

(11)

where n is the mode number and $\bar{C}$ is a function of material property. For the present time domain analysis, we choose n corresponding to the dominant mode of vibration of undamped panel vibration and $\bar{C} = 0.2$. A summary of the $\Delta {\text{TL}}$ in the figure shows that the largest deviation observed is less than 1 db. It indicates that the present numerical solver is able to capture the acoustic-structural interaction accurately.

Fig. 5

Variation of transmission loss TL with panel length $L_{p} /H$. Line theoretical result with undamped panel [12]; dashed line theoretical result with damped panel; circle numerical result with undamped panel; cross numerical result with damped panel. The table shows $\Delta {\text{TL}}$ at all cases

We can better understand the mechanism of transmission loss through the study of the temporal evolution of the acoustic pressure fluctuations. Take the time-stationary solution for the case with $L_{p} /H = 3.2$ as an example which gives high ${\text{TL}} = 20.9$ in undamped case. Figure 6 illustrates the snapshots of acoustic pressure fluctuations within one period of the acoustic excitation. Figure 6a shows the total acoustic pressure fluctuations $p^{\prime}$. Strong acoustic-structural interaction is evident around in the vicinity of the vibrating panel. Figure 6b shows the propagation of pressure fluctuations $p^{\prime}_{\text{incident}}$ of the incident wave when the flexible panel is absent.

Fig. 6

Snapshots of acoustic pressure fluctuations in one period of incident excitation $(L_{p} /H = 3.2).\;\,t_{0}$ is beginning moment. T is the period of the incident wave. a Total acoustic pressure p′, b incident acoustic wave $p^{\prime}_{\text{incident}}$, c re-radiated wave $p^{\prime}_{{\text{re}}\text{-}\text{{radiated}}}$

In response to the incident excitation the flexible panel re-radiates an acoustic wave $p^{\prime}_{{\text{re}}\text{-}\text{{radiated}}} = p^{\prime} - p^{\prime}_{\text{incident}}$ to both upstream and downstream directions. Upstream of the panel, the re-radiated wave interferes constructively with the incident wave which results in a strong standing wave is created in duct section upstream of the panel (Fig. 6a). Downstream of the panel, the re-radiated wave and the incident wave maintains almost out-of-phase so an effective cancellation is resulted (Fig. 7). This explains why only a weak resultant acoustic wave can be observed in the duct downstream (Fig. 6a) and high TL prevails in this case.

Fig. 7

Variation of the phase difference of between incident wave and re-radiated wave along the duct $(L_{p} /H = 3.2)$

The calculated panel structural response for $L_{p} /H = 5$ and $C = 0$ is illustrated in Fig. 8. In Fig. 8a the panel velocity distribution is obtained from taking the mean value over one forcing period. In Fig. 8b the modal amplitudes are obtained from performing a spatial fast Fourier transform on the panel velocity. Both figures are normalized by the strongest observed value $x = - 0.41$. Evidently that the numerical panel responses agree well with the theoretical prediction. The panel vibration is dominated by in a narrowband with the 12-th axial mode as the peak (Fig. 8a). Consequently 12 vibration peaks are evident along the panel (Fig. 8b) where the strongest vibration occurs at the second peak close the leading edge of the panel. From a closer look in the same figure we can see that the present time-domain calculation succeeds to calculate all the peaks but the linear frequency-domain theory fails to predict the first peak at $x = - 0.48$, which is in fact very weak. This observation reveals that the strong ability of the present numerical methodology in capturing the nonlinearity of the fluid-panel interaction no matter how weak they are. The panel structural responses of cases with strong (${\text{TL}} = 20.8$) and with weak transmission loss $\left( {{\text{TL}} = 3.0} \right)$ are compared in Fig. 9. They occur with $L_{p} /H = 3.2$ and $L_{p} /H = 4.3$ respectively. Again structural damping is not included in the calculations. There is a distinct difference observed. In high TL case the dominant vibration mainly occurs in a narrowband of vibration modes (the 6-th to the 8-th modes) in the present. Same observation prevails in the case with $L_{p} /H = 5$. However, in low TL case, the panel vibration is dominated by a single peak (the 10-th mode). These observations suggest that as the modal content of the vibrating panel gets richer, the associated distension created by the fluid-panel interaction becomes richer and more prominent. That will increase the mismatch of the phases between the vibrating panel and the incident acoustic wave and lead to a more severe change in the impedance above the panel. Consequently more acoustical energy can be reflected so the TL becomes high. On the other hand, as there is only a single mode prevailing the in the panel vibration, the associated change in the impedance will be much limited. Only a very limited amount of reflection is possible so the TL becomes very small.

Fig. 8

Panel structural response of case $(L_{p} /H = 5)$. a Panel modal vibrating velocity amplitude. Circle theoretical result; cross numerical result. b Panel vibrating velocity amplitude along the panel. Line theoretical result; dashed line numerical result

Fig. 9

Structural responses with high and low TL. Left column panel modal velocity amplitude; right column modal velocity along the panel

4.2 Aeroacoustic-Structural Response

To demonstrate the ability of the proposed methodology to capture full aeroacoustic-structure interaction of the panel, we select the panel with $L_{p} /H = 3.2$ and $C = 0$ and impose an uniform mean flow with velocity $\hat{u}_{0}$ in the same direction of the incident acoustic wave in the duct. The Mach numbers attempted are $M = 0.1$, 0.5 and 0.8. The transmission loss calculated is illustrated in Fig. 10. In general, the mean flow acts to suppress the transmission loss of the flexible panel. The reduction of transmission loss gives a nonlinear trend with the mean flow velocity.

Fig. 10

Variation of TL with mean flow Mach number for undamped panel $(L_{p} /H = 3.2)$

Figure 11 shows the modal distribution of the panel vibration at all values of $M$ attempted. In the absence of the mean flow (i.e. M = 0), the panel vibration lies within a narrowband of axial mode number (Fig. 11a). When M is increased slightly to 0.1, broadening of the bandwidth is observed and the modal amplitudes reduce. Such change in the panel vibration, however, results in a significant reduction of 9 db in the transmission loss. When M is increased further to 0.5, the modal distribution changes from a unimodal one to a bimodal one with the stronger vibration prevailing at lower mode number. The separation and the amplitude difference between the two arms of bimodal distribution increases at a higher M = 0.8. In order to get a clearer picture of the changes mentioned, it would be informative to observe the panel flexural wave behaviours closely. Figure 12 shows the snapshots of panel displacements. It is interesting to observe that at this Mach number the two modal peaks observed in Fig. 11 in fact correspond to two flexural waves. The longer wavelength one (at the second mode) is propagating along the incident wave direction. On the contrary the shorter wavelength one (at the 12-th mode) is propagating opposite to the incident wave direction. Certainly these two kinds of flexural wave propagation will create two different kinds of fluid-panel interactions but their overall effect is counterproductive. This phenomenon has never been observed before, so a more detailed analysis is needed.

Fig. 11

Panel vibration with $L_{p} /H = 3.2$. a Modal velocity along the panel, circle, M = 0; diamond, M = 0.1; square, M = 0.5; cross, M = 0.8. b Modal peaks

Fig. 12

Snapshots of panel vibration with $L_{p} /H = 3.2$ and $M = 0.5$

5 Concluding Remarks

We have presented the development of a numerical methodology for the time-domain prediction of aeroacoustic-structural response of a flexible panel exposed to an incident acoustic wave in a flow duct. The methodology aims to correctly resolve the nonlinear coupling of the acoustics, fluid dynamics as well as structural dynamics simultaneously. Previous numerical attempts have relied on the approach in which the physical processes are individually solved and their solutions are communicated through three numerical interfaces for resolving the overall interaction. That way would lead to an increase in the errors in resolving the coupling due to frequent extrapolation of solutions from one dynamics solver to another. Such errors may be effectively reduced at the expense of prohibitively large demand in the computational resources. In the present approach, we solve the entire problems with solvers in two domains, namely the fluid domain and the flexible panel, with a single coupling procedure. In the fluid domain, we adopt a numerical solver based on the direct aeroacoustic simulation (DAS) approach which has been proven to be able to accurately solve the scale-disparate fluid dynamics and acoustics, as well as their interactions, simultaneously. We solve the structural dynamics of the flexible panel using a standard finite-difference scheme. Both staggered and iterative procedures are evaluated for coupling the aeroacoustic and structural solutions for resolving the fluid-panel interaction. We first calculate the acoustic-structural responses of a flexible panels with different length in the absence of flow and compared the numerical results with the predictions with existing theory. The numerical results are consistent with the theory. The maximum error in the calculation transmission loss is less than 1 db. This shows that the present numerical methodology is able to capture all the key acoustic and structural dynamic processes arising from the interaction. The comparison also shows that the iterative procedure gives much less error with a mild increase in the computational resources. We then include uniform mean flows of different Mach numbers into the problem. The numerical results show that the presence of mean flow changes the acoustic and panel structural responses entirely. The responses are completely different from those in no flow case. Consequently the transmission loss decreases rapidly with an increasing flow velocity. All the observations highlight the mean flow plays an important role in determining the nonlinear aeroacoustic-structural interaction.