Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Motivation

The quality of industrial machines suffers because of vibration due to their operation. To improve the quality of such products, it is important to find possibilities to suppress this unwanted side-effect. Adding massive material to the assembly is the classical way to achieve this. However, to reduce manufacturing costs and the impact on the environment (for instance, by saving energy), it is also desirable to construct machines that are as lightweight as possible. Therefore, an extensive effort in research of lightweight materials is underway. The Fraunhofer Institute of Advanced Manufacturing Technology and Materials (IFAM) in Dresden studies and manufactures structures constructed from hollow spheres. These structures can be used, e.g., in a sandwich configuration within the casings of machines, cf. Fig. 1.

Fig. 1
figure 1

Hollow sphere structures (©Fraunhofer IFAM-Dresden)

Full size image

To combine lightweight materials with vibration damping, research is now being focused on particle-filled hollow sphere structures, cf. Fig. 2. The inclusion of a ceramic powder inside the hollow spheres leads to a high damping [6]. Such a material possesses several properties that make its application very attractive. For instance, because of the metallic nature of these spheres, they are resistant to solvents and because of their small size, as an ensemble they can easily be adapted to a broad variety of shapes. To couple the spheres, different techniques can be employed, for instance, using glue, solder or embedding them into a matrix.

Fig. 2
figure 2

Schematic cross-section

Full size image

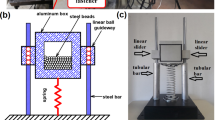
As a measure for the damping, the time between two bounces of a single sphere is used. The IFAM has an experimental test setup for this purpose that records the sound of the collisions with a fundament. Obtaining a numerical simulation to study the damping influence of the particles in this bouncing experiment is the goal of this work. This would allow for parameter studies, for example with respect to the optimal size or number of particles within the sphere. First simulations were conducted by Blase [1] for the two-dimensional case. She used a collision detection approach such that the system temporally evolved from collision to collision between the hull of the hollow sphere and a particle or between two particles. As the number of particles increases, this detection scheme breaks down due to the numerical effort. It has to be noted that within a single sphere, up to 2 ⋅ 105 particles have to be considered. Therefore, the high complexity of this approach requires a different method when expanding the simulation to the three-dimensional case. This alternative approach should thus be based on a time integration method.

2 Molecular Dynamics

For the simulation of the dynamic behavior of the filled spheres, the tracking of the translational and rotational movement of all enclosed particles is required. To achieve this, a variety of methods is available. One of them is molecular dynamics (MD), which typically considers the trajectories of molecules on the nanoscopic scale. MD simulations are able to track trillions of molecules [2]. Based on a program that is available at the University of Paderborn and was originally developed by Mader [7], an adaption to the present case is underway.

To compute the translational propagation of a particle i, the Newtonian equation of motion has to be considered

$$\displaystyle{\ddot{\mathbf{x}}_{i} = m_{i}^{-1}\mathbf{F}_{ i}\;,}$$

where \(\mathbf{x}_{i}\) is the position of the particle in space, and \(\mathbf{F}_{i}\) and m i denote the force acting on the particle and its mass, respectively. Rewriting this second order ordinary differential equation (ODE) as a system of first order ODE leads to

$$\displaystyle{\dot{\mathbf{v}}_{i} =\mathbf{ a}_{i} = m_{i}^{-1}\mathbf{F}_{ i}\;,\quad \dot{\mathbf{x}}_{i} =\mathbf{ v}_{i}\;.}$$

Here, \(\mathbf{v}_{i}\) is the velocity and \(\mathbf{a}_{i}\) the acceleration of the particle i. Using a Taylor expansion, these equations can be numerically solved over time using an explicit Leapfrog scheme [4]

$$\displaystyle\begin{array}{rcl} \mathbf{v}_{i}^{n+\frac{1} {2} } =\mathbf{ v}_{i}^{n-\frac{1} {2} } + \mathit{dt}\ m_{i}^{-1}\mathbf{F}_{i}^{n},& &{}\end{array}$$
(1)
$$\displaystyle\begin{array}{rcl} \mathbf{x}_{i}^{n+1} =\mathbf{ x}_{ i}^{n} + \mathit{dt}\ \mathbf{v}_{ i}^{n+\frac{1} {2} }\;.& &{}\end{array}$$
(2)

Note that the solutions for the velocities and positions of the particles are obtained alternatingly at each half time-step, giving the Leapfrog scheme its name.

Analogously to the translational movement, for the rotational movement of particle i, the angular velocity and the orientation θ i in space are needed. The angular velocity ω i is defined in terms of the angular momentum \(\mathbf{j}_{i}\) and the moment of inertia tensor I i

$$\displaystyle\begin{array}{rcl} \omega _{i} =\dot{ \theta }_{i} = \mathbf{I}_{i}^{-1}\mathbf{j}_{ i}\;.& &{}\end{array}$$
(3)

The torque τ i is the rate of change of the angular momentum

$$\displaystyle\begin{array}{rcl} \mbox{ $\tau $}_{i} = \frac{d\mathbf{j}_{i}} {\mathit{dt}} \;.& &{}\end{array}$$
(4)

Subsequently, Taylor expansions of Eqs. (3) and (4) can be integrated to obtain the desired physical properties. For the orientation \(\mathbf{q}_{i}\) in space, Fincham’s explicit rotational quaternion algorithm [3] was used that reduces the complexity of this calculation by saving one vector product evaluation. For the main part of the algorithm, Fincham proposed a quaternion representation matrix \(Q(\mathbf{q}_{i})\) and a modified angular velocity \(\mathbf{w}_{i}\) to obtain the spatial orientation. The change of the orientation over time is

$$\displaystyle{\frac{d\mathbf{q}_{i}} {\mathit{dt}} = Q(\mathbf{q}_{i})\mathbf{w}_{i}\;.}$$

On that basis, \(\mathbf{q}_{i}\) can be obtained with a Taylor expansion. The main equations of the rotational leapfrog scheme are

$$\displaystyle\begin{array}{rcl} \mathbf{j}_{i}^{n+\frac{1} {2} }& =& \mathbf{j}_{i}^{n-\frac{1} {2} } + \mbox{ $\tau $}_{i}^{n} {}\\ \mathbf{q}_{i}^{n+1}& =& \mathbf{q}_{ i}^{n} + \frac{\mathit{dt}} {2} Q(\mathbf{q}_{i}^{n+\frac{1} {2} })\mathbf{w}_{i}^{n+\frac{1} {2} }\;. {}\\ \end{array}$$

Combined with Eqs. (1) and (2), this then gives a full representation of the translational and rotational movement of a particle over time.

The forces and torques acting on the particles in are based on a pair-potential U which describes the force that one particle exerts on another particle as a function of their mutual distance. The force is given by the derivative of the potential with respect to their distance r ij

$$\displaystyle{\mathbf{F}_{\mathit{ij}} = -\frac{\mathit{dU}} {d\mathbf{r}_{\mathit{ij}}}\;.}$$

A popular interaction potential used in MD is the Lennard-Jones 12-6 potential

$$\displaystyle\begin{array}{rcl} U(r_{\mathit{ij}}) = 4\varepsilon \left (\left ( \frac{\sigma } {r_{\mathit{ij}}}\right )^{12} -\left ( \frac{\sigma } {r_{\mathit{ij}}}\right )^{6}\right )\;,& &{}\end{array}$$
(5)

where σ denotes the size parameter of the considered particle and \(\varepsilon\) is the depth of the potential well (cf. Fig. 3).

Fig. 3
figure 3

Lennard-Jones potential

Full size image

During simulation, the inter-particle potential (5) is only evaluated up to a certain cut-off distance r c around each particle, because particles that are far apart from each other interact only weakly. Additionally, cutting off the potential saves computational effort. Due to the steep slope of the potential, particles that are very close to each other will exert a large repulsive force, while particles further apart will attract each other. This behavior models real-world atomistic forces (repulsion by electronic overlap and attraction by dispersion) reasonably well.

3 Adapting Molecular Dynamics to Particle Dynamics

While MD methods are well suited for simulating the behavior of molecules on the nanoscopic scale, several adjustments have to be made for the present application where mesoscopic particles are considered. For instance, the periodic boundary conditions, that are usually assumed in MD, have to be changed to reflective boundary conditions for the interactions of the particles with the hollow sphere. In this work, two approaches were followed.

The first approach uses the conservation law of momentum to derive the velocities of the particles \({ \hat{\boldsymbol{v}}}_{p}\) and the hollow sphere \({ \hat{\boldsymbol{v}}}_{s}\) after their eventual collision

$$\displaystyle\begin{array}{rcl} m_{p}\vert \mathbf{v}_{p}\vert + m_{s}\vert \mathbf{v}_{s}\vert =\hat{ m}_{p}\vert { \hat{\boldsymbol{v}}}_{p}\vert +\hat{ m}_{s}\vert { \hat{\boldsymbol{v}}}_{s}\vert \;.& &{}\end{array}$$
(6)

For each time step, the masses and velocities of particles that are reflected by the hull are accumulated in a substitute particle with corresponding total mass m m and velocity \(\mathbf{v}_{m}\). Combining the definition of the coefficient of restitution (COR)

$$\displaystyle{\varepsilon = -\frac{\vert { \hat{\boldsymbol{v}}}_{p}\vert -\vert { \hat{\boldsymbol{v}}}_{s}\vert } {\vert \mathbf{v}_{p}\vert -\vert \mathbf{v}_{s}\vert }\;,}$$

with Eq. (6), the solution for the velocities of the reflected particles and the hull after central inelastic collisions are obtained by

$$\displaystyle\begin{array}{rcl} { \hat{\boldsymbol{v}}}_{s}& =\mathbf{ v}_{s} + \frac{m_{m}} {m_{s}+m_{m}}(1+\varepsilon )(\mathbf{v}_{m} -\mathbf{ v}_{s}),&{} \\ { \hat{\boldsymbol{v}}}_{p}& =\mathbf{ v}_{p} + \frac{m_{s}} {m_{s}+m_{p}}(1+\varepsilon )(\mathbf{v}_{s} -\mathbf{ v}_{p})\;. & \\ \end{array}$$
(7)

To account for the shape of the sphere, the resulting velocities of the particles are subjected to a reflection with the tangential plane at the point of impact. If \(\mathbf{n}\) is the normal vector of that tangential plane and \({ \hat{\boldsymbol{v}}}_{p}\) the velocity of the particle after the reflection, the new velocity vector \({ \hat{\boldsymbol{v}}}_{\mathit{pr}}\) is obtained by rotating \({ \hat{\boldsymbol{v}}}_{p}\) around \(\mathbf{n}\) by 180∘. Therefore, the resulting velocity of the skewed collision is

$$\displaystyle{{ \hat{\boldsymbol{v}}}_{\mathit{pr}} = { \hat{\boldsymbol{v}}}_{p} - 2\frac{{ \hat{\boldsymbol{v}}}_{p} \cdot \mathbf{ n}} {\|\mathbf{n}\|^{2}} \mathbf{n}\;,}$$

with \({ \hat{\boldsymbol{v}}}_{p}\) according to Eq. (7). If the COR is known, this gives an exact computation of the reflection. However, this discrete mechanical approach disrupts the otherwise continuous, potential-based nature of MD.

The second approach thus uses an interaction potential between the particles and for the spheric hull. As particles approach the hull of the sphere, the forces arising from the potential are evaluated. To prevent particles from exiting the sphere, an exponential barrier potential was used

$$\displaystyle\begin{array}{rcl} U_{\mathit{exp}}(r) =\delta \cdot (\exp (r) - r),& &{}\end{array}$$
(8)

where δ controls the force of the interaction and r is the distance between the particle and the hull of the sphere (cf. Fig. 4). For the collisions between particles, the LJ potential was used. To avoid attracting forces, the cut-off radius was selected as

$$\displaystyle{r_{c} = 2^{\frac{1} {6} }\sigma.}$$

In this way, the potential is 0 when particles have a distance greater than r c where it would normally be attracting. Also, the force reaches 0 at r c while staying continuously differentiable. This homogenizes the overall approach to use only continuous potentials for all interactions.

Fig. 4
figure 4

Exponential barrier potential

Full size image

The particles that are filled into the hollow sphere are manufactured using a complex process during which they assume different shapes and sizes. Common shapes include cylinders and spheres as well as particles with rugged edges and hooks. In MD, the same variation has to be considered, when simulating different molecule species. There, molecules are assembled from several spheres in a molecule-fixed coordinate system. This approach can be used for the particles considered here as well. Different shapes can be built from elementary spherical shaped parts and the number of each particle type can be specified as input for the algorithm (cf. Fig. 5).

Fig. 5
figure 5

Particle consisting of eight spheres

Full size image

For the initial configuration, instead of the regular lattice often used in MD, the particles were aligned in a spherical shape using spherical coordinates such that they do not overlap. The particle types were then randomly distributed throughout the initial configuration. In the present simulation, the particles were dropped first in the spherical hull and were given time to settle at the bottom. After this preparation, the particle-filled sphere was dropped towards the fundament. Thus, for the damping behavior, the initial setup was irrelevant. Figure 6 shows the initial configuration of 2 ⋅ 104 particles using the visualization tool MegaMol of the VISUS group at the University of Stuttgart [5].

Fig. 6
figure 6

Initial configuration with 2 ⋅ 104 particles

Full size image

4 Results

To study the damping behavior of the particle-filled spheres, the experimental setup of the IFAM was modeled in the computer. A sphere was dropped from a certain height h 0. To measure the damping, the time interval Δ t between the first two bounces was sampled. The comparison with the bouncing time interval of an empty sphere gives a good indication of the damping due to the particles. According to Jehring et al. [6], the resulting COR of the system can then be obtained using the equations of the vertical throw. It evaluates as

$$\displaystyle{\varepsilon _{r} = \sqrt{ \frac{g} {8h_{0}}\varDelta t^{2}}\;,}$$

where g is the gravitational acceleration. It was aimed at a comparison of this experiment with the present numerical simulations. A single hollow sphere with a diameter of 3 mm and a mass of 12. 518 mg was considered that was dropped onto a fundament from a height of 1. 5 mm. The spherical particles in the hollow sphere had a uniform diameter of 31 μm and a mass of 41 ng. For the reflection of the sphere on the surface, a barrier potential similar to Eq. (8) was used. The sphere was treated as a particle approaching the fundament with the imposed barrier potential for the interaction and rebound. The cut-off radius was set to 35 μm. The numerical results were obtained on the OCuLUS computer at the Paderborn Center for Parallel Computing (PC2). Table 1 lists the preliminary results that were obtained with a time step of 1 μs. Figure 7 shows the results for a variety of different time steps. For too large time steps, such as 5 μs, the simulation leads to false results due to inadequate numerical integration of the equations of motion. However, the choice of the time step size has no significant influence on the damping behavior as soon as it is small enough to discretize the particle motions and a reasonably large number of particles is used in the experiment.

Fig. 7
figure 7

Simulation results for different time step lengths

Full size image
Table 1 Time interval Δ t between the first and second bounce on the fundament
Full size table

As can be seen, the number of particles has a large effect on the damping. It is expected from the physical experiments that as the number of particles increases, reducing Δ t further at first, the damping properties of the filled hollow sphere will eventually start to deteriorate and approach the behavior of a solid sphere. Quantifying the number of particles when this happens is of great interest.

5 Future Work

As can be seen from the computation times in Fig. 8, the complexity of the standard MD algorithm is O(N 2), where N is the number of particles. Therefore, when larger particle numbers have to be considered, adaptations must be made to achieve reasonable computing times. One approach is the linked cell algorithm [4]. This algorithm retains the basic structure of the MD algorithm, but makes a crucial adaptation in the force computation algorithm. By dividing the simulation volume into equally sized cells when computing the forces that act on a certain particle, only particles in the same cell and in neighboring cells have to be considered. This reduces the complexity to O(N) [4]. However, the linked cell algorithm works best when the particles are evenly distributed throughout the simulation volume. In the present case, the particles tend to accumulate over time at the bottom of the hollow sphere, which results in a few cells that are crowded and many cells that do not contain any particles. To cope with this aggregation, the cells need to adapt to that situation to retain the efficiency of the algorithm. This will be the subject of future work.

Fig. 8
figure 8

Computation times for 400,000 steps and dt = 1 μs

Full size image

Increasing the particle number will allow to directly compare results from numerical simulation to physical experiments. To simulate the material on a larger scale, a significant number of filled spheres must be considered. The simulation therefore has to be extended in this respect. The nature of coupling between the different parts needs to be evaluated carefully as different types of assembly can be manufactured, e.g. by gluing or soldering. Deformations of the spheres occurring in the material may have to be considered as well. Natural parallelization by assigning a single sphere to each process should yield reasonable computing times for the numerical simulation of this complex material when combined with the linked cell algorithm.

6 Conclusion

Progress on the simulation of particle-filled spheres by adaption of molecular dynamics was presented. Preliminary results show the effect of an increasing number of particles on the damping of a filled hollow sphere. The dramatic effect of the particles seen in the physical experiment can also be seen in the numerical simulation. The complexity of the algorithm has to be improved, e.g., by an adapted linked cell algorithm, to allow for larger particle numbers. The modeling of friction between particles also plays an important role and there are several approaches that have to be evaluated.