High-Order Sliding Mode Control of DFIG-Based Wind Turbines

Abstract

Actually, variable speed wind turbines are continuously increasing their market share, since it is possible to track the changes in wind speed by adapting shaft speed, and thus maintaining optimal power generation. The more variable speed wind turbines are investigated, the more it becomes obvious that their behavior is significantly affected by the used control strategy. Typically, they use aerodynamic controls in combination with power electronics to regulate torque, speed, and power. The aerodynamic control systems, usually variable-pitch blades or trailing-edge devices, are expensive and complex, especially for larger turbines. This situation provides a motivation to consider alternative control approaches. This chapter deals, therefore, with high-order sliding mode control of doubly-fed induction generator-based wind turbines. This kind of control strategy presents attractive features such as chattering-free behavior (no extra mechanical stress), finite reaching time, and robustness with respect to external disturbances (grid faults) and unmodeled dynamics (generator and turbine). High-sliding mode control appropriateness will be highlighted in terms of sensorless control and enhanced fault-ride through capabilities. Simulations using the NREL FAST code will be shown for validation purposes.

1 Introduction

Actually, variable speed wind turbines are continuously increasing their market share, since it is possible to track the changes in wind speed by adapting shaft speed, and thus maintaining optimal power generation. The more variable speed wind turbines are investigated, the more it becomes obvious that their behavior is significantly affected by the used control strategy. Typically, they use aerodynamic controls in combination with power electronics to regulate torque, speed, and power. The aerodynamic control systems, usually variable-pitch blades or trailing-edge devices, are expensive and complex, especially for larger turbines [1]. This situation provides a motivation to consider alternative control approaches [2].

The main control objective of variable speed wind turbines is power extraction maximization. To reach this goal the turbine tip speed ratio should be maintained at its optimum value despite wind variations. Nevertheless, control is not always aimed at capturing as much energy as possible. In fact, in above-rated wind speed, the captured power needs to be limited. Although there are both mechanical and electrical constraints, the more severe ones are commonly on the generator and the converter. Hence, regulation of the power produced by the generator is usually intended, and this is the main objective of this chapter for a DFIG (Doubly-Fed Induction Generator)-based WT (Wind Turbine) using a second order sliding mode controller [3]. In particular, three control aspects will be presented: (1) A high-gain observer to estimate the aerodynamic torque [4]; (2) A high-order sliding mode speed observer [5]; (3) Fault-ride trough performance using high-order sliding mode control [6].

Simulations using the NREL FAST code will be shown for validation purposes.

2 The Wind Turbine Modeling

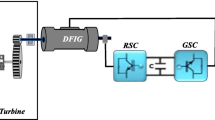
The global scheme for a grid-connected wind turbine is given in Fig. 2.1.

Fig. 2.1

Wind turbine global scheme

2.1 Turbine Model

The turbine modeling is inspired from [7]. In this case, the aerodynamic power P _a captured by the wind turbine is given by

$$ P_{a} = \frac{1}{2}\pi \rho R^{2} C_{p} \left( \lambda \right)v^{3} $$

(2.1)

where the tip speed ratio is given by

$$ \lambda = \frac{{R\omega_{\text{mr}} }}{v} $$

(2.2)

and where ω _mr is the wind turbine rotor speed, ρ is the air density, R is the rotor radius, C _p is the power coefficient, and v is the wind speed.

The C _p − λ characteristics, for different values of the pitch angle β, are illustrated in Fig. 2.2. This figure indicates that there is one specific λ at which the turbine is most efficient. Normally, a variable speed wind turbine follows the C _pmax to capture the maximum power up to the rated speed by varying the rotor speed to keep the system at λ _opt. Then it operates at the rated power with power regulation during high wind periods by active control of the blade pitch angle or passive regulation based on aerodynamic stall.

Fig. 2.2

Wind turbine power coefficient

The rotor power (aerodynamic power) is also defined by

$$ P_{a} =\upomega_{\text{mr}} T_{a} $$

(2.3)

where T _a is the aerodynamic torque.

As is in [7], the following simplified model is adopted for the turbine (drive train) for control purposes.

$$ J_{t} {\dot{\omega }}_{\text{mr}} = T_{a} - K_{t}\upomega_{\text{mr}} - T_{g} $$

(2.4)

Where J _t is the turbine total inertia, K _t is the turbine total external damping, and T _g is the generator electromagnetic torque.

2.2 Generator Model

The WT adopted generator is the DFIG (Fig. 2.3). DFIG-based WT will offer several advantages including variable speed operation (±33 % around the synchronous speed), and four-quadrant active and reactive power capabilities. Such system also results in lower converter costs (typically 25 % of total system power) and lower power losses compared to a system based on a fully fed synchronous generator with full-rated converter. Moreover, the generator is robust and requires little maintenance [8].

Fig. 2.3

Schematic diagram of a DFIG-based wind turbine

The control system is usually defined in the synchronous d − q frame fixed to either the stator voltage or the stator flux. For the proposed control strategy, the generator dynamic model written in a synchronously rotating frame d − q is given by Eq. (2.5).

$$ \left\{ {\begin{array}{*{20}l} {V_{\text{sd}} = R_{s} I_{\text{sd}} + \frac{{d\upphi_{\text{sd}} }}{dt} -\upomega_{s}\upphi_{\text{sq}} } \hfill \\ {V_{\text{sq}} = R_{s} I_{\text{sq}} + \frac{{d\upphi_{\text{sq}} }}{dt} +\upomega_{s}\upphi_{\text{sd}} } \hfill \\ {V_{\text{rd}} = R_{r} I_{\text{rd}} + \frac{{d\upphi_{\text{rd}} }}{dt} -\upomega_{r}\upphi_{\text{rq}} } \hfill \\ {V_{\text{rq}} = R_{r} I_{\text{rq}} + \frac{{d\upphi_{\text{rq}} }}{dt} +\upomega_{r}\upphi_{\text{rd}} } \hfill \\ {\upphi_{\text{sd}} = L_{s} I_{\text{sd}} + MI_{\text{rd}} } \hfill \\ {\upphi_{\text{sq}} = L_{s} I_{\text{sq}} + MI_{\text{rq}} } \hfill \\ {\upphi_{\text{rd}} = L_{r} I_{\text{rd}} + MI_{\text{sd}} } \hfill \\ {\upphi_{\text{rq}} = L_{r} I_{\text{rq}} + MI_{\text{sq}} } \hfill \\ {T_{\text{em}} = pM\left( {I_{\text{rd}} I_{\text{sq}} - I_{\text{rq}} I_{\text{sd}} } \right)} \hfill \\ \end{array} } \right. $$

(2.5)

where V is the voltage, I is the current, ϕ is the flux, ω _s is the synchronous, ω _r is the angular speed, R is the resistance, L is the inductance, M is the mutual inductance, T _em is the electromagnetic torque, and p is the pole pair number.

For simplification purposes, the q-axis is aligned with the stator voltage and the stator resistance is neglected. These will lead to Eq. (2.6).

$$ \left\{ {\begin{array}{*{20}l} {\frac{{dI_{\text{rd}} }}{dt} = \frac{1}{{\sigma L_{r} }}\left( {V_{\text{rd}} - R_{r} I_{\text{rd}} + s\omega_{s} \sigma L_{r} I_{\text{rq}} - \frac{M}{{L_{s} }}\frac{{d\phi_{\text{sd}} }}{dt}} \right)} \hfill \\ {\frac{{dI_{\text{rq}} }}{dt} = \frac{1}{{\sigma L_{r} }}\left( {V_{\text{rq}} - R_{r} I_{\text{rq}} - s\omega_{s} \sigma L_{r} I_{\text{rd}} - s\omega_{s} \frac{M}{{L_{s} }}\phi_{\text{sd}} } \right)} \hfill \\ {T_{\text{em}} = - p\frac{M}{{L_{s} }}\phi_{\text{sd}} I_{\text{rq}} } \hfill \\ \end{array} } \right. $$

(2.6)

where σ is the leakage coefficient (σ = 1 − M ²/L _s L _r ).

3 Control of the DFIG-Based Wind Turbine

3.1 Problem Formulation

Wind turbines are designed to produce electrical energy as cheaply as possible. Therefore, they are generally designed so that they yield maximum output at wind speeds around 15 m/sec. In case of stronger winds, it is necessary to waste part of the excess energy of the wind in order to avoid damaging the wind turbine. All wind turbines are therefore designed with some sort of power control. This standard control law keeps the turbine operating at the peak of its C _p curve.

$$ T_{\text{ref}} = k\upomega^{2} ,\;{\text{with}}\;k = \frac{1}{2}\pi \rho R^{5} \frac{{C_{\hbox{pmax} } }}{{\lambda_{\text{opt}}^{3} }} $$

(2.7)

There is a significant problem with this standard control. Indeed, wind speed fluctuations force the turbine to operate off the peak of its C _p curve much of the time. Tight tracking C _pmax would lead to high mechanical stress and transfer aerodynamic fluctuations into the power system. This, however, will result in less energy capture.

To effectively extract wind power while at the same time maintaining safe operation, the wind turbine should be driven according to the following three fundamental operating regions associated with wind speed, maximum allowable rotor speed, and rated power. The three distinct regions are shown by Fig. 2.4, where v _rmax is the wind speed at which the maximum allowable rotor speed is reached, while v _cut-off is the furling wind speed at which the turbine needs to be shut down for protection. In practice, there are three possible regions of turbine operation, namely, the high-, constant- and low-speed regions. High speed operation (III) is frequently bounded by the power limit of the machine while speed constraints apply in the constant-speed region. Conversely, regulation in the low-speed region (I) is usually not restricted by speed constraints. However, the system has nonlinear non-minimum phase dynamics in this region. This adverse behavior is an obstacle to perform the regulation task [9].

Fig. 2.4

Wind turbine control regions

A common practice in addressing DFIG control problem is to use a linearization approach [10–12]. However, due to the stochastic operating conditions and the inevitable uncertainties inherent in DFIG-based wind turbines, much of these control methods come at the price of poor system performance and low reliability. Hence, the need for nonlinear and robust control to take into account these control problems. Although many modern techniques can be used for this purpose [13], sliding mode control has proved to be especially appropriate for nonlinear systems, presenting robust features with respect to system parameter uncertainties and external disturbances. For wind turbine control, sliding mode should provide a suitable compromise between conversion efficiency and torque oscillation smoothing [7, 14, 15].

Sliding mode control copes with system uncertainty keeping a properly chosen constraint by means of high-frequency control switching. Featuring robustness and high accuracy, the standard (first-order) sliding mode usage is, however, restricted due to the chattering effect caused by the control switching, and the equality of the constraint relative degree to 1. High-order sliding mode approach suggests treating the chattering effect using a time derivative of control as a new control, thus integrating the switching [16].

3.2 High-Order Sliding Modes Control Design

As the chattering phenomenon is the major drawback of practical implementation of sliding mode control, the most efficient ways to cope with this problem is higher order sliding mode. This technique generalizes the basic sliding mode idea by acting on the higher order time derivatives of the sliding manifold, instead of influencing the first time derivative as it is the case in the standard (first order) sliding mode. This operational feature allows mitigating the chattering effect, keeping the main properties of the original approach [16].

The DFIG stator-side reactive power is given by

$$ Q_{s} = \frac{3}{2}\left( {V_{\text{sq}} I_{\text{sd}} - V_{\text{sd}} I_{\text{sq}} } \right) $$

(2.8)

For a decoupled control, a d − q reference frame attached to the stator flux was used. Therefore, setting the stator flux vector aligned with the d-axis, the reactive power can be expressed as

$$ Q_{s} = \frac{3}{2}\frac{{V_{s} }}{{L_{s} }}\left( {\upphi_{s} - MI_{\text{rd}} } \right) $$

(2.9)

Setting the reactive power to zero will, therefore, lead to the rotor reference current.

$$ I_{{{\text{rd}}\_{\text{ref}}}} = \frac{{V_{s} }}{{\upomega_{s} M}} $$

(2.10)

The DFIG-based WT control objective is to optimize the wind energy capture by tracking the optimal torque T _ref (Eq. 2.7). This control objective can be formulated by the following tracking errors.

$$ \left\{ \begin{aligned} e_{{I_{\text{rd}} }} = & I_{\text{rd}} - I_{{{\text{rd\_ref}}}} \\ e_{{T_{\text{em}} }} = & T_{\text{em}} - T_{\text{ref}} \\ \end{aligned} \right. $$

(2.11)

Then we will have

$$ \left\{ \begin{aligned} \dot{e}_{{I_{\text{rd}} }} = & \frac{1}{{\sigma L_{r} }}\left( {V_{\text{rd}} - R_{r} I_{\text{rd}} + s\omega_{s} L_{r} \sigma I_{\text{rq}} - \frac{M}{{L_{s} }}\frac{{d\phi_{\text{sd}} }}{dt}} \right) - \dot{I}_{{{\text{rd\_ref}}}} \\ \dot{e}_{{T_{\text{em}} }} = & - p\frac{M}{{\sigma L_{s} L_{r} }}\phi_{s} \left( {V_{\text{rq}} - R_{r} I_{\text{rq}} - s\omega_{s} L_{r} \sigma I_{\text{rd}} - s\omega_{s} \frac{M}{{L_{s} }}\phi_{\text{sd}} } \right) - \dot{T}_{\text{ref}} \\ \end{aligned} \right. $$

(2.12)

If we define the functions G ₁ and G ₂ as follows

$$ \left\{ {\begin{array}{*{20}l} {G_{1} = \frac{1}{{\sigma L_{r} }}\left( {s\omega_{s} \sigma L_{r} I_{\text{rq}} - \frac{M}{{L_{s} }}\frac{{d\phi_{\text{sd}} }}{dt} - R_{r} I_{\text{rd}} } \right) - \dot{I}_{{{\text{rd\_ref}}}} } \hfill \\ {G_{2} = - p\frac{M}{{\sigma L_{s} L_{r} }}\phi_{s} \left( { - R_{r} I_{\text{rq}} - s\omega_{s} \sigma L_{r} I_{\text{rd}} - s\omega_{s} \frac{M}{{L_{s} }}\phi_{\text{sd}} } \right) - \dot{T}_{\text{ref}} } \hfill \\ \end{array} } \right. $$

(2.13)

Thus, we have

$$ \left\{ {\begin{array}{*{20}l} {\ddot{\it{e}}_{{I_{rd} }} = \frac{1}{{\sigma L_{r} }}\dot{V}_{rd} + \dot{G}_{1} } \hfill \\ {\ddot{\it{e}}_{{\Gamma _{em} }} = - p\frac{M}{{\sigma L_{s} L_{r} }}\phi_{s} \dot{V}_{rq} + \dot{G}_{2} } \hfill \\ \end{array} } \right. $$

(2.14)

To overcome standard sliding mode control chattering, a natural modification is to replace the discontinuous function in the vicinity of the discontinuity by a smooth approximation. Nevertheless, such a smooth approximation is not easy to carry-out. This is why common approaches use current references. Therefore, a high-order sliding mode seems to be a good alternative.

The main problem with high-order sliding mode algorithm implementations is the increased required information. Indeed, the implementation of an nth-order controller requires the knowledge of $\dot{S},\,\ddot{\it{S}},\,\dddot S, \ldots ,S^{{\left( {n{-} 1} \right)}}$. The exception is the supertwisting algorithm, which only needs information about the sliding surface S [16]. Therefore, the proposed control approach has been designed using this algorithm.

Now, lets us consider the following second-order sliding mode controller based on the supertwisting algorithm [16]. In the considered case, the control could be approached by two independent High-Order Sliding Mode (HOSM) controllers. Indeed, the control matrix is approximated by a diagonal one. Hence, V _rd controls I _rd (reactive power) and V _rq controls the torque (MPPT strategy).

$$ \left\{ {\begin{array}{*{20}l} {V_{\text{rd}} = y_{1} - B_{1} \left| {e_{{I_{\text{rd}} }} } \right|^{\frac{1}{2}} \text{sgn} \left( {e_{{I_{\text{rd}} }} } \right),\;\dot{y}_{1} = - B_{2} \text{sgn} \left( {e_{{I_{\text{rd}} }} } \right)} \hfill \\ {V_{\text{rq}} = y_{2} + B_{3} \left| {e_{{T_{\text{em}} }} } \right|^{\frac{1}{2}} \text{sgn} \left( {e_{{T_{\text{em}} }} } \right),\;\dot{y}_{2} = + B_{4} \text{sgn} \left( {e_{{T_{\text{em}} }} } \right)} \hfill \\ \end{array} } \right. $$

(2.15)

where the constants B ₁, B ₂, B ₃, and B ₄ are defined as

$$ \left\{ {\begin{array}{*{20}l} {B_{1}^{2} > \frac{{2\sigma^{2} L_{r}^{2} \left( {\frac{{B_{2} }}{{\sigma L_{r} }} +\Phi _{1} } \right)}}{{\left( {\frac{{B_{2} }}{{\sigma L_{r} }} -\Phi _{1} } \right)}},\;B_{2} > \sigma L_{r}\Phi _{1} ,\;\left| {\dot{G}_{1} } \right| <\Phi _{1} } \hfill \\ {B_{3}^{2} > 2\left( {\frac{{\sigma L_{s} L_{r} }}{pM}} \right)^{2} \frac{{\left( {p\frac{M}{{\sigma L_{s} L_{r} }}B_{4} + \varPhi_{2} } \right)}}{{\left( {p\frac{M}{{\sigma L_{s} L_{r} }}B_{4} - \varPhi_{2} } \right)}},\;B_{4} > \frac{{\sigma L_{s} L_{r} }}{pM}\Phi _{2} } \hfill \\ {\left| {\dot{G}_{2} } \right| <\Phi _{2} } \hfill \\ \end{array} } \right. $$

(2.16)

In practice the parameters are never assigned according to inequalities. Usually, the real system is not exactly known, the model itself is not really adequate, and the parameters estimations are much larger than the actual values. The larger the controller parameters are the more sensitive will be the controller to any switching measurement noises. The right way is to adjust the controller parameters during computer simulations.

The above-described high-order sliding mode control strategy for a DFIG-based WT is illustrated by the block diagram in Fig. 2.5 [17].

Fig. 2.5

The high-order sliding mode control structure

3.3 High-Gain Observer

A high-gain observer can be used to estimate the aerodynamic torque. A key feature of a high-gain observer is that it will reduce the chattering induced by a sliding mode observer [18].

From Eq. (2.4), we have

$$ \dot{\omega } = \frac{{T_{a} }}{J} - \frac{{K_{t} \omega }}{J} - \frac{{T_{\text{em}} }}{J} $$

(2.17)

The following notations are introduced.

$$ \left\{ {\begin{array}{*{20}l} {x_{1} = \omega } \hfill \\ {x_{2} = \frac{{T_{a} }}{J}} \hfill \\ \end{array} } \right. $$

(2.18)

Thus, we have

$$ x = \left\{ {\begin{array}{*{20}l} {\dot{x}_{1} = x_{2} - \frac{K}{J}x_{1} - \frac{{T_{\text{em}} }}{J}} \hfill \\ {\dot{x}_{2} = f(t)} \hfill \\ \end{array} } \right. $$

(2.19)

or in matrix form

$$ \left\{ {\begin{array}{*{20}l} {\dot{x} = Ax + \varphi (x,u) + \varepsilon (t)} \hfill \\ {y = Cx} \hfill \\ \end{array} } \right. $$

where

$$ \left\{ {\begin{array}{*{20}l} {A = \left[ {\begin{array}{*{20}c} 0 & 1 \\ 0 & 0 \\ \end{array} } \right]} \hfill \\ {C = \left[ {\begin{array}{*{20}c} 1 & 0 \\ \end{array} } \right]} \hfill \\ {\varphi (x,u) = \left[ {\begin{array}{*{20}c} {\frac{{ - Kx_{1} - u}}{J}} \\ 0 \\ \end{array} } \right]} \hfill \\ {\varepsilon (t) = \left[ {\begin{array}{*{20}c} 0 \\ {f(t)} \\ \end{array} } \right]} \hfill \\ \end{array} } \right.. $$

A candidate observer could be [18]

$$ \dot{\hat{x}} = A\hat{x} + \varphi (\hat{x},u) - \theta\Delta _{\theta }^{ - 1} S^{ - 1} C^{T} C(\hat{x} - x) $$

(2.20)

where $\Delta _{\theta } = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & {\frac{1}{\theta }} \\ \end{array} } \right],\;S = \left[ {\begin{array}{*{20}c} 1 & { - 1} \\ { - 1} & 2 \\ \end{array} } \right]$

Let S be the unique solution of the algebraic Lyapunov equation

$$ S + A^{T} S + SA - C^{T} C = 0 $$

(2.21)

Let us define $\bar{x} =\Delta _{\theta } (\hat{x} - x)$ then

$$ \,\;\dot{\bar{x}} = \theta (A - S^{ - 1} C^{T} C)\bar{x} + \Delta_{\theta } \left( {\varphi (\hat{x}) - \varphi (x)} \right) - \Delta_{\theta } \varepsilon (t) $$

(2.22)

Consider the quadratic function

$$ V = \bar{x}^{T} S\bar{x} $$

(2.23)

then

$$ \left\{ {\begin{array}{*{20}l} {\dot{V} = 2\bar{x}^{T} S\dot{\bar{x}}} \hfill \\ {\dot{V} = - \theta V - \bar{x}^{T} C^{T} C\bar{x} + 2\bar{x}^{T} S\Delta _{\theta } \left( {\varphi (\hat{x}) - \varphi (x)} \right)} \hfill \\ {\quad \quad - 2\bar{x}^{T} S\Delta _{\theta } \bar{\varepsilon }(t)} \hfill \\ \end{array} } \right. $$

Therefore,

$$ \dot{V} \le - \theta V + 2\left\| {\bar{x}} \right\|\lambda_{\hbox{max} } (S)\left( {\begin{array}{*{20}l} {\left\| {\Delta _{\theta } \left( {\varphi (\hat{x}) - \varphi (x)} \right)} \right\|} \hfill \\ { + \left\| {\Delta _{\theta } \bar{\varepsilon }(t)} \right\|} \hfill \\ \end{array} } \right) $$

(2.24)

We can assume that (triangular structure and the Lipschitz assumption on φ)

$$ \left\{ {\begin{array}{*{20}l} {\left\| {\Delta _{\theta } \left( {\varphi (\hat{x}) - \varphi (x)} \right)} \right\| \le \xi \left\| {\bar{x}} \right\|} \hfill \\ {\left\| {f(t)} \right\| \le \delta } \hfill \\ \end{array} } \right.\,{\text{with}}\,\xi = \frac{K}{J} $$

It comes that

$$ \dot{V} \le - \theta V + 2\left\| {\bar{x}} \right\|^{2} \lambda_{\hbox{max} } (S)\xi + 2\left\| {\bar{x}} \right\|\lambda_{\hbox{max} } (S)\frac{\delta }{\theta } $$

then,

$$ \dot{V} \le - \theta V + c_{1} V + c_{2} \frac{\delta }{\theta }\sqrt V $$

with

$$ \left\{ {\begin{array}{*{20}l} {c_{1} = 2\frac{{\lambda_{\hbox{max} } (S)}}{{\lambda_{\hbox{min} } (S)}}\xi } \hfill \\ {c_{2} = 2\frac{{\lambda_{\hbox{max} } (S)}}{{\sqrt {\lambda_{\hbox{min} } (S)} }}} \hfill \\ \end{array} } \right. $$

Now taking

$$ \left\{ {\begin{array}{*{20}l} {\theta_{0} = \hbox{max} \left\{ {1,c_{1} } \right\}} \hfill \\ {\lambda = \sqrt {\frac{{\lambda_{\hbox{max} } (S)}}{{\lambda_{\hbox{min} } (S)}}} } \hfill \\ {\mu_{\theta } = \frac{{\theta - c_{1} }}{2}} \hfill \\ {M_{\theta } = 2\frac{{\lambda_{\hbox{max} } (S)}}{{\lambda_{\hbox{min} } (S)\left( {\theta - c_{1} } \right)}}} \hfill \\ \end{array} } \right. $$

and θ > θ ₀, we obtain

$$ \left\| {e(t)} \right\| \le \theta \lambda \exp ( - \mu_{\theta } t)\left\| {e(0)} \right\| + M_{\theta } \delta $$

(2.25)

With $\hat{T}_{a} = J\hat{x}_{2}$, it comes that

$$ \tilde{T}_{a} = \hat{T}_{a} - T_{a} \le J\left[ {\theta \lambda \exp ( - \mu_{\theta } t)\left\| {e(0)} \right\| + M_{\theta } \delta } \right] $$

(2.26)

A practical estimate of the aerodynamic torque is then obtained as M _θ decreases when θ increases. The asymptotic estimation error can be made as small as desired by choosing high enough values of θ. However, very large values of θ are to be avoided in practice since the estimator may become noise sensitive.

Now, the control objective can be formulated by the following tracking errors

$$ e_{T} = T_{\text{opt}} - T_{a} $$

(2.27)

where T _a is observed. Then we will have

$$ \dot{e}_{T} = 2k_{\text{opt}} \omega \left( {T_{a} - K_{t} \omega - T_{g} } \right) - \dot{T}_{a} $$

(2.28)

If we define the following functions

$$ \left\{ {\begin{array}{*{20}l} {F = 2k_{\text{opt}} \omega } \hfill \\ {G = 2k_{\text{opt}} \omega \left( {T_{a} - K_{t} \omega } \right) - \dot{T}_{a} } \hfill \\ \end{array} } \right. $$

(2.29)

then

$$ \ddot{\it{e}}_{T} = - F\dot{T}_{g} + \dot{G} $$

(2.30)

Let us consider the following observer based on the supertwisting algorithm [16, 19].

$$ \left\{ {\begin{array}{*{20}l} {T_{g} = y + B_{1} \left| {e_{T} } \right|^{\frac{1}{2}} \text{sgn} \left( {e_{T} } \right)} \hfill \\ {\dot{y} = + B_{2} \text{sgn} \left( {e_{T} } \right)} \hfill \\ \end{array} } \right. $$

(2.31)

The gains B ₁ and B ₂ are chosen as

$$ \left\{ {\begin{array}{*{20}l} {B_{1} > \frac{{\Phi _{2} }}{{\varGamma_{m} }}} \hfill \\ {B_{2}^{2} \ge \frac{{4\Phi _{2} \varGamma_{M} \left( {A_{1} +\Phi _{1} } \right)}}{{\Gamma _{m}^{2} \left( {A_{1} -\Phi _{1} } \right)}}} \hfill \\ {\left| {\dot{G}} \right| <\Phi _{2} } \hfill \\ {0 <\Gamma _{m} \le F <\Gamma _{M} } \hfill \\ \end{array} } \right. $$

(2.32)

Thus, we will guaranty the convergence of e _T to 0 in a finite time t _c . The aerodynamic torque estimation is then deduced.

$$ T_{a} = T_{\text{opt}} ,\;t > t_{c} . $$

(2.33)

The above-proposed high-gain observer principal is illustrated by the block diagram in Fig. 2.6.

Fig. 2.6

High gain observer principle

3.4 High-Order Sliding Mode Speed Observer

Figure 2.7 illustrates the main reference frames on which is based the proposed speed observer development.

Fig. 2.7

Stator S _α _ S _β , rotor R _α _ R _β , and d − q reference frames

In this case, θ _s can be easily determined using stator voltage measurements and a PLL.

If the stator flux is assumed to be aligned with the d-axis,

$$ \left\{ {\begin{array}{*{20}l} {\phi_{\text{sd}} = \phi_{s} } \hfill \\ {\phi_{\text{sq}} = 0} \hfill \\ \end{array} } \right. $$

(2.34)

then, the d − q rotor current can be estimated as

$$ \left\{ {\begin{array}{*{20}l} {\hat{I}_{\text{rd}} = \frac{{\phi_{s} }}{M} - \frac{{L_{s} }}{M}I_{\text{sd}} } \hfill \\ {\hat{I}_{\text{rq}} = - \frac{{L_{s} }}{M}I_{\text{sq}} } \hfill \\ \end{array} } \right. $$

Let us now define θ _r such as

$$ \hat{I}_{\text{rq}} = \sqrt \frac{2}{3} \left( {\begin{array}{*{20}l} { - I_{\text{ra}} \sin \theta_{r} + \frac{1}{2}I_{\text{rb}} \sin \theta_{r} } \hfill \\ { + \frac{\sqrt 3 }{2}I_{\text{rb}} \cos \theta_{r} + \frac{1}{2}I_{\text{rc}} \sin \theta_{r} } \hfill \\ { - \frac{\sqrt 3 }{2}I_{\text{rc}} \cos \theta_{r} } \hfill \\ \end{array} } \right) $$

(2.35)

Using $x = \tan \left( {\frac{{\theta_{r} }}{2}} \right)$, I _rq can be rewritten as

$$ \hat{I}_{\text{rq}} = \sqrt \frac{2}{3} \left( {\begin{array}{*{20}l} { - I_{\text{ra}} \frac{2x}{{1 + x^{2} }} + \frac{1}{2}I_{\text{rb}} \frac{2x}{{1 + x^{2} }}} \hfill \\ { + \frac{\sqrt 3 }{2}I_{\text{rb}} \frac{{1 - x^{2} }}{{1 + x^{2} }} + \frac{1}{2}I_{\text{rc}} \frac{2x}{{1 + x^{2} }}} \hfill \\ { - \frac{\sqrt 3 }{2}I_{\text{rc}} \frac{{1 - x^{2} }}{{1 + x^{2} }}} \hfill \\ \end{array} } \right) $$

(2.36)

After some algebraic manipulations, it comes that

$$ \hat{I}_{\text{rq}} = \frac{1}{{1 + x^{2} }}\sqrt \frac{2}{3} \left[ {\begin{array}{*{20}l} {x^{2} \left( {\frac{\sqrt 3 }{2}I_{\text{rc}} - \frac{\sqrt 3 }{2}I_{\text{rb}} } \right)} \hfill \\ {\quad \quad \quad + x\,\left( { - 2I_{\text{ra}} + I_{\text{rb}} + I_{\text{rc}} } \right)} \hfill \\ {\quad \quad \quad + \left( { - \frac{\sqrt 3 }{2}I_{\text{rc}} + \frac{\sqrt 3 }{2}I_{\text{rb}} } \right)} \hfill \\ \end{array} } \right] $$

(2.37)

This equation can further be rewritten in a compact form

$$ \hat{I}_{\text{rq}} = \frac{{x^{2} a + xb + c}}{{1 + x^{2} }} $$

(2.38)

$$ at^{2} + bt + c = 0\quad {\text{with}}\;\left\{ {\begin{array}{*{20}l} {a = \sqrt \frac{3}{2} \hat{I}_{\text{rq}} + \frac{\sqrt 3 }{2}\left( {I_{\text{rb}} - I_{\text{rc}} } \right)} \hfill \\ {b = 2I_{\text{ra}} - I_{\text{rc}} - I_{\text{rc}} } \hfill \\ {c = \sqrt \frac{3}{2} \hat{I}_{\text{rq}} - \frac{\sqrt 3 }{2}\left( {I_{\text{rb}} - I_{\text{rc}} } \right)} \hfill \\ \end{array} } \right. $$

The solutions of this equation are the following.

$$ \left\{ {\begin{array}{*{20}l} {x_{1} = \frac{{ - b + \sqrt {b^{2} - 4ac} }}{2a}} \hfill \\ {x_{2} = \frac{{ - b - \sqrt {b^{2} - 4ac} }}{2a}} \hfill \\ \end{array} } \right. $$

(2.39)

Now we will estimate the derivative of the following value $z = 2\arctan x_{1}$ using a second-order sliding mode. The same result is obtained with $\arctan x_{2}$.

As for the above-discussed problem, the proposed speed observer is designed using the supertwisting algorithm [19].

Let us therefore consider the following observer

$$ \left\{ {\begin{array}{*{20}l} {\dot{y} = - B_{2} \text{sgn} (e)} \hfill \\ {\dot{W} = y - B_{1} \left| e \right|^{\frac{1}{2}} \text{sgn} (e)} \hfill \\ \end{array} } \right. $$

(2.40)

where the constants B ₁ and B ₂ are defined as

$$ \left\{ {\begin{array}{*{20}l} {B_{2} > \phi } \hfill \\ {B_{1}^{2} > \frac{{4\left( {B_{2} + \phi } \right)^{2} }}{{2\left( {B_{2} - \phi } \right)}}} \hfill \\ \end{array} } \right. $$

(2.41)

Lets us consider the following tracking error.

$$ \left\{ {\begin{array}{*{20}l} {e = W - z} \hfill \\ {\dot{e} = y - B_{1} \left| e \right|^{\frac{1}{2}} \text{sgn} (e) - \dot{z}} \hfill \\ {\ddot{\it{e}} = - B_{2} \text{sgn} (e) - B_{1} \frac{{\dot{e}}}{{2\left| e \right|^{\frac{1}{2}} }} - \ddot{\it{z}}} \hfill \\ \end{array} } \right. $$

(2.42)

Assume now, for simplicity, that the initial values are $e = 0$ and $\dot{e} = \dot{e}_{0} > 0$ at t = 0. Let e _M be the intersection of the curve $\ddot{\it{e}} = - \left( {B_{2} - \phi } \right)$ with $\dot{e} = 0$, $\left| {\ddot{\it{z}}} \right| < \phi$. We have then

$$ 2e_{M} \left( {B_{2} - \phi } \right) = \dot{e}_{0}^{2} $$

(2.43)

$$ e > 0,\;\dot{e} < - \left( {B_{2} + \phi } \right)\frac{{2e_{M}^{1/2} }}{{B_{1} }} \Rightarrow \ddot{\it{e}} > 0 $$

Thus, the majorant curve with $e > 0$ may be taken as

$$ \left\{ {\begin{array}{*{20}l} {\dot{e}_{0}^{2} = 2\left( {B_{2} - \phi } \right)\left( {e_{M} - e} \right)\quad {\text{with}}\;\dot{e} > 0} \hfill \\ {e = e_{M} \quad {\text{with}}\; 0\ge \dot{e} > - \left( {B_{2} + \phi } \right)\frac{{2e^{\frac{1}{2}} }}{{B_{1} }}} \hfill \\ {\dot{e} = \dot{e}_{M} = - \left( {B_{2} + \phi } \right)\frac{{2e_{M}^{\frac{1}{2}} }}{{B_{1} }}\quad {\text{with}}\;\dot{e} < - \left( {B_{2} + \phi } \right)\frac{{2e^{\frac{1}{2}} }}{{B_{1} }}} \hfill \\ \end{array} } \right. $$

(2.44)

Let the trajectory next intersection with $e = 0$ axis be e ₁. Then, obviously

$$ \left| {\dot{e}_{1} /\dot{e}_{0} } \right| \le q\quad {\text{ with}}\;q = \left| {\dot{e}_{M} /\dot{e}_{0} } \right| = \sqrt {\frac{{\left( {\frac{2}{{B_{1} }}} \right)^{2} \left( {B_{2} + \phi } \right)^{2} }}{{2\left( {B_{2} - \phi } \right)}}} $$

(2.45)

Extending the trajectory into the half plane $e < 0$ and carrying-out a similar reasoning show that successive crossings of the $e = 0$ axis satisfy the inequality

$$ \left| {\frac{{\dot{e}_{i + 1} }}{{\dot{e}_{i} }}} \right| \le q $$

The q < 1 condition is sufficient for the algorithm convergence. Indeed, the real trajectory consists of an infinite number of segments. The total variance is given by

$$ Var\left( {\dot{e}} \right) = \sum {\left| {\dot{e}_{i} } \right|} \le \left| {\dot{e}_{0} } \right|\left( {1 + q + q^{2} + \cdots } \right) = \frac{{\left| {\dot{e}_{0} } \right|}}{1 - q} $$

(2.46)

Therefore, the algorithm obviously converges.

The convergence time is to be estimated now. Consider an auxiliary variable

$$ \eta = y - \dot{z} $$

(2.47)

$\eta = \dot{e}$ when $e = 0$. Thus, η tends to zero. Its derivative

$$ \ddot{\it{e}} = - B_{2} \text{sgn} (e) - G $$

(2.48)

satisfies the inequalities

$$ 0 < B_{2} - \phi \le - \dot{\eta }\text{sgn} (e_{{I_{rd} }} ) \le B_{2} + \phi $$

(2.49)

The real trajectory consists of an infinite number of segments between $\eta_{i} = \dot{e}_{i}$ and $\eta_{i + 1} = \dot{e}_{i + 1}$ associated to the time t _i and t _i+1, respectively. Consider $t_{c}$, the total convergence time.

$$ \left\{ {\begin{array}{*{20}l} {t_{c} = \sum {\left( {t_{i + 1} - t_{i} } \right) \le \sum {\frac{{\left| {\eta_{i} } \right|}}{{B_{2} - \phi }}} } } \hfill \\ {t_{c} \le \frac{1}{{B_{2} - \phi }}\sum {\left| {\dot{e}_{i} } \right|} } \hfill \\ {t_{c} \le \frac{{\left| {\dot{e}_{0} } \right|}}{{\left( {B_{2} - \phi } \right)\left( {1 - q} \right)}}} \hfill \\ \end{array} } \right. $$

(2.50)

This means that the observer objective is achieved. It exist t _c such as $\omega_{r} = \dot{W}$.

The above-presented sensorless HOSM control strategy using a HOSM speed observer is illustrated by the block diagram in Fig. 2.8.

Fig. 2.8

The high-order sliding mode sensorless control s structure

4 Simulation Using the FAST Code

The proposed HOSM control strategy, the high-gain, and the HOSM speed observers have been tested for validation using the NREL FAST code [20]. The FAST (Fatigue, Aerodynamics, Structures, and Turbulence) code is a comprehensive aeroelastic simulator capable of predicting both the extreme and fatigue loads of two- and three-bladed horizontal-axis wind turbines. This simulator has been chosen for validation because it is proven that the structural model of FAST is of higher fidelity than other codes [21]. An interface has been developed between FAST and Matlab-Simulink^® enabling users to implement advanced turbine controls in Simulink convenient block diagram form (Fig. 2.9). Hence, electrical model (DFIG, grid, control system, etc.) designed in the Simulink environment is simulated while making use of the complete nonlinear aerodynamic wind turbine motion equations available in FAST (Fig. 2.10). This introduces tremendous flexibility in wind turbine controls implementation during simulation.

Fig. 2.9

FAST wind turbine block

Fig. 2.10

Simulink model

4.1 Test Conditions

Numerical validations, using FAST with Matlab-Simulink^® have been carried-out on the NREL WP 1.5-MW wind turbine. The wind turbine and the DFIG ratings are given in the Appendix.

4.2 HOSM Control Performances

Validation tests were performed using turbulent FAST wind data with 7 and 14 m/sec minimum and maximum wind speeds, respectively (Fig. 2.11). As clearly shown in Figs. 2.12 and 2.13, very good tracking performances are achieved in terms of DFIG rotor current and WT torque with respect to wind fluctuations. The HOMS control strategy does not induce increased mechanical stress as there are no strong torque variations. Indeed and as expected, the aerodynamic torque remains smooth (Fig. 2.13).

Fig. 2.11

Wind speed profile

Fig. 2.12

Current I _rd tracking performance: Reference (blue) and real (green)

Fig. 2.13

Torque tracking performance: Reference (blue) and real (green)

4.3 HOSM Control Performances with High-Gain Observer

The observer validation is clearly illustrated by Fig. 2.14.

Fig. 2.14

Aerodynamic torque: T _opt (blue), T _a real (red), T _a observed (green)

Indeed, the aerodynamic torque tracks efficiently the optimal torque. As shown in Figs. 2.15 and 2.16, very good tracking performances are achieved in terms of DFIG rotor current and WT torque with respect to wind fluctuations. The control strategy does not induce increased mechanical stress as again there are no strong torque variations.

Fig. 2.15

Torque tracking performance: Reference (blue) and real (green)

Fig. 2.16

Current I _rd tracking performance: Reference (blue) and real (green)

4.4 Sensorless HOSM Control Performances

The performances of the proposed HOSM speed observer are illustrated by Fig. 2.17. The achieved results show quiet good tracking chattering free performances.

Fig. 2.17

Rotor speed: Observer (blue) and real (green)

Figures 2.18 and 2.19 illustrate the HOSM sensorless control performances in terms of DFIG rotor current and wind turbine torque. In this case, quiet good tracking performances are achieved according to the wind fluctuations. As mentioned above, the sensorless control strategy does not induce mechanical stress as there is no chattering in the wind turbine torque (Fig. 2.19).

Fig. 2.18

Current I _rd tracking performance: Reference (green) and real (blue)

Fig. 2.19

Torque tracking performance: Reference (green) and real (blue)

4.5 HOSM Control FRT Performances

This subsection deals with the fault ride-through capability assessment of a DFIG-based WT using a HOSM control. Indeed, it has been recently suggested that sliding mode control is a solution of choice to the fault ride-through problem [22, 23].

LVRT capability is considered to be the biggest challenge in wind turbines design and manufacturing technology. LVRT requires wind turbines to remain connected to the grid in the presence of grid voltage sags. The HOSM control performances are, therefore, assessed against this grid fault. In this context, when unbalanced sags occur (Fig. 2.20), very high current, torque, and power oscillations appear at double the electrical frequency, forcing a disconnection.

Fig. 2.20

Grid voltage

The LVRT performances are illustrated by Fig. 2.21 where an almost constant torque is achieved. Good tracking performances are also achieved in terms of DFIG rotor current (Fig. 2.22). Fault-tolerance performances are also confirmed by the quadratic error shown by Fig. 2.23.

Fig. 2.21

Torque tracking performance during unbalanced voltage sags: Reference (blue) and real (green)

Fig. 2.22

Current I _rd tracking performance during unbalanced voltage sags: Reference (blue) and real (green)

Fig. 2.23

Quadratic error between the reference torque and the SOSM control-based one (voltage sags)

5 Conclusions

This chapter dealt with high-order sliding mode control of doubly-fed induction generator-based wind turbines. Simulations using the NREL FAST code clearly show the HOSM control approach effectiveness and attractiveness in terms of robustness (FRT capability enhancement) and of sensorless control. Moreover, it has been confirmed that there is no mechanical extra stress induced on the wind turbine drive train as there are no strong torque variations.

6 Future Work

Future works should be oriented toward the evaluation of high-order sliding modes control for the following key investigations:

• Power control according to grid active and reactive power references.

• Wind turbine grid synchronization.

Appendix

Characteristics of the simulated wind turbine

Number of blades	3
Rotor diameter	70 m
Hub height	84.3 m
Rated power	1.5 MW
Turbine total Inertia	4.4532 × 105 kg m2

Parameters of the simulated DFIG

R s  = 0.005 Ω, L s  = 0.407 mH, R r  = 0.0089 Ω, L r  = 0.299 mH, M = 0.016 mH, p = 2

Control parameters

B 1 = 10, B 2 = 20000, B 3 = 7, B 4 = 500

Parameters of the emulated wind turbine

R = 1.5 m, J t  = 0.1 kg m2, C pmax = 0.4760, λ = 7

Parameters of the DC motor

6.5 kW, 3850 rpm, 310 V, 24.8 A

R s  = 78 Ω, R r  = 0.78 Ω, L r  = 3.6 H, J = 0.02 kg.m2

Parameters of the tested DFIG

R s  = 0.325 Ω, L s  = 4.75 mH, R r  = 0.13 Ω, L r  = 1.03 mH,

M = 57.3 mH, p = 2