Keywords

FormalPara Nomenclature

See Table 14.1.

1 Introduction

Wind turbines are complex systems with large flexible structures that work under very turbulent and unpredictable environmental conditions and for a variable electrical grid. When wind turbines are combined into large wind farms, additional turbine interaction problems, grid integration issues, and cooperative control matters add more complexity to the engineering design and control.

The efficiency and reliability of a wind farm strongly depend on the applied control strategies. Large nonlinear characteristics and high model uncertainty due to the interaction of the aerodynamics, mechanical, and electrical subsystems, both at the turbine level and the wind farm level are central difficulties in the design process. Stability problems, maximization of wind energy conversion issues, load reduction strategies, mechanical fatigue minimization problems, reliability matters, availability aspects, and costs per kWh reduction strategies demand advanced cooperative control systems to regulate variables such as pitch, torque, power, rotor speed, yaw orientation, temperatures, currents, voltages, and power factors of every wind turbine [1, 2].

Every new design and control idea in the wind energy field has to be tested and validated in a realistic scenario before moving forward to a final certification and commercial implementation. Frequently, this experimentation and validation is extremely expensive or even not possible. For all these reasons, this chapter presents a new low-cost and flexible test-bench wind farm for advanced research and education in optimum wind turbine/wind farm design and cooperative control.

2 System Description

Figure 14.1 shows a general view of the wind farm test-bench. It includes four variable-speed pitch-controlled wind turbines (1), a supervisory control and data acquisition (SCADA) system with a central control unit (2), a smart grid with batteries for energy storage, variable electrical loads, solar panels and switches for different grid topologies (3), and a group of fans to create different wind profiles and disturbances (4).

Fig. 14.1
figure 1

Wind farm general view: (1) wind turbines; (2) SCADA and central control system; (3) smart micro grid with batteries, electrical loads, switches and solar panels; (4) fan system

Full size image

2.1 Wind Turbine Description

Figure 14.2 shows a general view of each wind turbine unit. It is a variable-speed pitch-controlled wind turbine composed of a multi-blade aerodynamic rotor (1) able to support a set of 2, 3, 4, 5 or 6 blades.

Fig. 14.2
figure 2

Wind turbine general view: (1) 6-blade rotor; (2) generator; (3) micro-controller; (4) yaw motor; (5) pitch motor; (6) rotor speed encoder; (7) pitch angle sensor; (8) yaw angle sensor; (9) current sensor and current/torque actuator; (10) voltage sensor; (11) grid connection

Full size image

The drive-train has a mechanical gearbox with a brushless induction electrical generator (2) and a connection (11) to the grid system through the current/torque actuator (10). A set of micro-controllers (3) collect all the sensor information (6, 7, 8, 9, 10) and drives the pitch (5) and yaw (4) motors. The sensors collect in real-time data of rotor speed (6), pitch angle (7), yaw angle (8), and current (9) and voltage (10) at the output of the generator. In addition, with the above information, the system identifies in real-time the mechanical torque T r applied to the shaft—see Eq. (14.43)—and the power P—see Eq. (14.1)—generated by the wind turbine.

The mechanical structure of the turbine, including the foundation, tower, blades and gearboxes for the pitch and yaw systems are built of LEGO blocks and wheels, giving highly modular characteristics to the prototypes. The real-time control system runs on LEGO microprocessors (3) and an external computer with Matlab—(2) in Fig. 14.1.

2.1.1 Aerodynamics: Rotor Blades

Figure 14.3 presents the four wind turbines of the wind farm, with three different rotor options (3, 4 and 6 rotor-blade) and a particular site configuration, while generating power into the electrical grid, and with the hierarchical control system: five NXT LEGO microprocessors for the distributed individual wind turbine control and the central computer under Matlab for the SCADA and central control system.

Fig. 14.3
figure 3

Wind farm control for optimum energy production with 3, 4 and 6 rotor-blade wind turbines

Full size image

Each wind turbine uses a horizontal axis rotor that (1) can be configured to use two, three, four, five or six blades each, and (2) can be easily lengthened by adding an additional piece at the blades’ root. The blades themselves have a drag model airfoil design, meaning the drag coefficient C D of the blade is significantly larger than the lift coefficient C L . In addition to a drag model airfoil, the blades each have additional texturing near the end of the blade to contribute to the effectiveness of the drag system. Figure 14.4 shows a 3-blade and a 6-blade rotor options.

Fig. 14.4
figure 4

Aerodynamics: 3-blade and 6-blade rotor options

Full size image

2.1.2 Mechanics: Main Structures, Power Train, Tower, Nacelle, Gearboxes

The structure of the wind turbine is built around the pitch and yaw gearboxes. In order to change the angle of attack of the wind on the blades a pitch-controlled full sized wind turbine changes the pitch angle of the blades relative to the center of the rotor. This is infeasible on a small scale, so in order to implement control of the angle of attack in a comparable manner the actuators move the entire nacelle pitch angle relative to the horizontal axis. The effect on the rotor speed is very strong, as it is in a commercial wind turbine, so high precision is necessary, making a direct drive method (motor directly connected to the pitch shaft) ineffective. Thus a gearbox is implemented which gives the controller very high precision control of the pitch angle of the nacelle with minimal backlash (see Fig. 14.5). Then, the motor is connected to a series of gears which step up in size, decreasing the rate of rotation at each step. The largest of these moves a worm gear, giving a huge increase in the precision while simultaneously reducing backlash, with a total gearbox ratio of r tg  = 1/140. The worm moves two other gears, also stepping up in size, the larger of which is directly connected to the nacelle. In this way, the resulting pitch angle is the nacelle pitch angle relative to the horizontal axis perpendicular to the wind direction. It is represented as β in Fig. 14.12.

Fig. 14.5
figure 5

Pitch system: motor, gearbox, mechanical configuration and tower

Full size image

For the nacelle angle relative to the vertical axis, the yaw angle, we developed a second gearbox to move the entire tower relative to the base (see Fig. 14.6). This gearbox is much less complex; however, it does reduce error from the motor and increase precision. The base itself, aside from housing the motor and gearbox for the yaw control, is built to be relatively heavy to anchor the system better. It also allows for the NXT microcontroller to be attached. In this way, the resulting yaw angle is the tower angle relative to the vertical axis that passes through the center of the tower. It is represented as α in Fig. 14.12.

Fig. 14.6
figure 6

Yaw system: motor, gearbox, mechanical configuration, tower and foundation

Full size image

2.1.3 Electrical Components: Generator, Grid Connection

The wind turbines use a DC motor made by LEGO as a simple generator (the E-motor)—see Fig. 14.2, element (2) and Fig. 14.7a. It has a single rotor and a small gearbox with a 9.5:1 gearing ratio. It can either induce a voltage or be induced to move by an applied voltage. The linear characteristics of the E-motor/generator are calculated based on [8], so that:

$$P_{\text{mec}} = T_{r} \,\varOmega_{r} \;;\quad P_{\text{elec}} = u_{\text{gen}} \,i_{\text{gen}} \;;\quad P_{\text{elec}} = P_{\text{mec}} \,\eta_{g}$$
(14.1)
$$T_{g} = K_{T} \, i_{\text{gen}} ,\;{\text{where}}\;K_{T} = 0.0 60 9\;{\text{Nm}}/{\text{A}}$$
(14.2)
$$P_{\text{losses}} = P_{cu} + P_{\text{rotation}} { ;}\;\;P_{\text{cu}} = i_{\text{gen}}^{2} R_{a} ,\;\;R_{a} = 21.95\;{\text{ohm}};\;\;P_{\text{rotation}} = 0.1508\;{\text{W}}$$
(14.3)

being P mec the mechanical power at the generator shaft (in watts), T r the mechanical torque at the shaft (in Nm), Ω r the rotor speed (in rad/s), P elec the electrical power produced by the generator (in watts), u gen the voltage at the output of the generator (in volts), i gen the generator current (in A), η g the generator efficiency, T g the electrical torque (in Nm), and P losses the generator losses (in watts) due to the Joule effect P cu and friction P rotation.

Fig. 14.7
figure 7

a DC generator with gearbox (E-motor), b Actuator (NXT-motor), c Angle sensor (Glide-Wheel-AS), d CurrentMeter for NXT, e VoltMeter for NXT

Full size image

The generator is connected to the grid system through an actuator able to change the current i gen—see Fig. 14.2, element (9)- and therefore the electrical generator torque T g , which is opposite to the mechanical torque T r in Fig. 14.12, Table 14.1 and Eqs. (14.24), (14.27), (14.43) and (14.44).

Table 14.1 Parameters for wind turbine model (see Fig. 14.12 and [2])
Full size table

2.1.4 Sensors: Rotor Speed, Pitch and Yaw Angles, Voltage, Currents, Torque, Power, Wind

There are various electronics on each wind turbine, falling into two categories: actuators and sensors. There are three kinds of sensors on the wind turbine. On the nacelle there is a glide wheel angle sensor—see Fig. 14.2, number (6), Fig. 14.7c and Ref. [6], which is configured to record the rotor velocity. This sensor has a one degree resolution and very low resistance as it has almost exactly the same surface area as the generator, so it does not strongly affect the mechanics or aerodynamics of the system. For each angle (pitch and yaw), at the end of the actuator drive-train (end of the gearbox—see Figs. 14.5 and 14.6), there is an encoder. These encoders are the same as the glide wheel on the rotor (see Fig. 14.7c and [6]). They are configured to record the absolute angle of the nacelle and tower for the pitch and yaw angles, respectively—see Fig. 14.2, numbers (7) and (8).

For measuring the electrical properties of the wind turbine there is a current sensor (CurrentMeter for NXT) and a voltage sensor (VoltMeter for NXT) on each wind turbine—see Figs. 14.7d and e respectively, and Fig. 14.2, numbers (9) and (10). The current sensor has a resolution of 1 mA and can measure currents up to 12.5 A. The voltage sensor has a resolution of 1 mv and can measure voltages up to 26 v. These sensors are very reliable and the inherent offset errors are easily accounted for in software. Although they are not made by LEGO, they are built specifically to work with LEGO NXT Intelligent Brick firmware and are shaped to work the LEGO blocks [6]. Each sensor is directly connected to the NXT microcontroller.

2.1.5 Actuators: Pitch and Yaw Motors, Torque

The pitch and yaw actuators—see Fig. 14.2, numbers (5) and (4) respectively- are NXT motors (see Fig. 14.7b and [5]). They are DC motors and deliver a high torque thanks to its internal speed reduction gear train (gearing ratio = 1:48). Because of that, they turn slowly and efficiency is somewhat reduced. Although each one includes an internal rotation encoder to measure the position of the shaft with one degree resolution, we use glide wheel angle sensors at the end position of the actuator drive-train in order to have a direct measurement of the actual angles (see also Sect. 14.2.1.4).

The NXT motors consume a current of 60 mA in a no-load situation and up to 2 A in a stalled situation, with a maximum stalled torque of 50 N cm for a few seconds. The NXT motors are protected by a thermistor (Raychem RXE065 or Bourns MF-R065). That means that the high 2 A current and associated stalled torque can be sustained only for a few seconds. They have a non-standard phone plug type to connect to the NXT microprocessor. At the regular 9 v input the motors run at 170 revolutions per minute (rpm). For other inputs the motors follow the linear characteristics:

$$\varOmega_{\text{motor}} = (170/9) \,u$$
(14.4)
$$\varOmega_{\text{motor}} = - ( 1 7 0 / 5 0 ) { }\,T_{\text{motor}} + 170$$
(14.5)
$$i_{\text{motor}} = \left\{ {\begin{array}{*{20}l} { ( 00 . 9 4 / 3 0 ) { }\,T_{\text{motor}} + 0.06} \hfill & {({\text{for}}\,\,0 \le T_{\text{motor}} \le 30\,{\text{N.cm}})} \hfill \\ { ( 1 / 2 0 ) { }\,T_{\text{motor}} - 1/2} \hfill & {({\text{for}}\,\,T_{\text{motor}} > 30\,{\text{N.cm}})} \hfill \\ \end{array} } \right.$$
(14.6)

with Ω motor the motor speed in rpm, u the voltage applied to the motor in volts, T motor the motor torque in N. cm and i motor the motor current in A [8].

2.1.6 WT Microprocessors: Real-Time Control for Rotor Speed, Pitch, Yaw, Torque, Power

The individual wind turbine control system is based on the intelligent NXT 2.0 LEGO® brick, which has a 32-bit microprocessor, a large matrix display, 4 input and 3 output ports, and Bluetooth and USB communication links. The system is interchangeable with the new EV3 Intelligent LEGO® Brick [5] or the Arduino microcontroller [9].

Each wind turbine has one NXT microcontroller attached to the foundation (see Fig. 14.2). It is connected to the pitch and yaw motors (output ports) and the rotor speed, pitch angle, voltage, and current sensors (input ports). An additional NXT microcontroller is connected to the four yaw angle sensors (input ports) of the four wind turbines of the wind farm.

In this way, the wind farm control system presents a hierarchical structure, with a central computer that runs under Matlab for the Supervisory Control and Data Acquisition (SCADA) system, and the five LEGO microprocessors for the distributed wind turbine control units.

2.2 Wind Farm Description

The wind farm (see Fig. 14.1) is composed of (1) four variable-speed pitch-controlled wind turbines (2) a supervisory control and data acquisition (SCADA) system with a central control unit (3) a smart grid with batteries for energy storage, variable electrical loads, solar panels, and switches for different grid topologies, and (4) a group of fans to create different wind profiles and disturbances.

2.3 Supervisory Control and Data Acquisition (SCADA) System

The Supervisory Control and Data Acquisition (SCADA) system is the central computer-controlled system that monitors the wind farm (the four wind turbines and micro grid) and coordinates the distributed controllers of each wind turbine. It is based on Matlab [7] and runs on a personal computer. Figure 14.8 shows one of the main windows of the SCADA system, with real-time data collected by the sensors of the four wind turbines: voltages, currents, rotor speeds, powers, torques, pitch angles and yaw angles.

Fig. 14.8
figure 8

Supervisory control and data acquisition (SCADA) system

Full size image

2.4 Smart Micro Grid

An electrical smart micro grid with variable load is connected to the generators of the four wind turbines at the output of the farm. The micro grid is composed of a set of batteries for energy storage, variable electrical loads, solar panels as additional renewable generators and switches to create different grid topologies (see Fig. 14.9).

Fig. 14.9
figure 9

Smart micro grid: (1) wind turbines; (2) grid connection; (3) switches and electrical loads; (4) batteries; (5) solar panels; (6) SCADA and central control system

Full size image

2.5 Wind Source Equipment

A group of three fans creates the wind profile, with variable speed, direction and frequency of variation (see Fig. 14.1). The two largest fans are used to generate the main wind flow and the smallest one to create wind disturbances and turbulences in speed and direction.

3 Modeling of Wind Turbines

3.1 Power Curve of a Wind Turbine

A qualitative power curve of a variable-speed wind turbine is shown in Fig. 14.10. This graph presents the actual power P supplied by the wind turbine to the grid versus the undisturbed upstream wind speed v 1. Two main areas (below and above rated power P r ) and four regions (Regions 1 through 4) divide the graph.

Fig. 14.10
figure 10

Power curve of a variable-speed wind turbine (see [2])

Full size image

Below rated power (v 1 < V r ) the wind turbine produces only a fraction of its rated power, and therefore, an optimization strategy to capture the maximum amount of energy at every wind speed needs to be performed. Above rated power (V r  < v 1) the wind speed has more power than the rated power, and a limitation control strategy to generate only the rated power is required. The four regions of the power curve present the following characteristics:

  • Region 1. The objective in this region is to obtain the maximum efficiency. This is usually done by means of controlling the rotor speed Ω r by changing the electrical torque T g , to compensate the wind speed variations and keep the turbine at the maximum aerodynamic power coefficient C pmax (MPPT: Maximum Power Point Tracking). The power P supplied by the wind turbine to the grid follows the expression:

    $$P = P_{g} \,\eta_{c} = \frac{1}{2}{\kern 1pt} {\kern 1pt} \rho {\kern 1pt} {\kern 1pt} A_{r} {\kern 1pt} {\kern 1pt} C_{p} \,v_{1}^{3} \,\,\eta_{g} \,\eta_{c} = T_{r} \,\,\varOmega_{r} \,\,\eta_{g} \,\eta_{c} = P_{a} \,\,\eta_{g} \,\eta_{c}$$
    (14.7)

    where P g is the power supplied by the electrical generator, η c the efficiency from the output of the generator to the grid connection, ρ is the air density, A r  = π r 2 b the rotor effective surface, r b the rotor radius, C p the aerodynamic power coefficient (see also Sect. 14.3.3), v 1 the undisturbed upstream wind speed, η g the electrical generator efficiency, T r the mechanical torque at the shaft due to the wind, Ω r the rotor speed, P a the power at the shaft given by the aerodynamics, and λ is the tip speed ratio,

    $$\lambda = \varOmega_{r} r_{b} /v_{1}$$
    (14.8)

  • Region 2. It is the transition between a torque control with fixed pitch mode (Region 1) to a fixed torque with a variable pitch mode (Region 3).

  • Region 3. The objective in this region is to limit and control the incoming power at rated power, regulate the rotor speed and minimize the mechanical loads. This is done by means of controlling the rotor speed Ω r by changing the pitch angles β (Pitch control).

  • Region 4. An extended mode in very high winds can be obtained by means of varying the pitch closed-loop performance. Through a rotor speed Ω r limitation, the extreme loads can be reduced.

3.2 Power Generation According to the Number of Blades

It is well known that in the ideal scenario of an infinite number of blades and no losses the upper limit for the aerodynamic rotor power coefficient is the Betz limit: C pmax = 0.593. For a real situation, considering a finite number of blades N, typical frictional losses, and rotating wakes in the out-coming airflow, the aerodynamic power coefficient C p is always smaller than the Betz limit. Figure 14.11a presents some typical C p curves versus the tip speed ratio λ and for different pitch angles β. A numerical approximation of the aerodynamic power coefficient C p is given by the following equations (see [2], Chap. 12),

$$\begin{aligned} & C_{P} \left( {\lambda ,\beta } \right) = c_{1} \left( {\frac{{c_{2} }}{{\lambda_{i} }} - c_{3} \beta - c_{4} } \right){\kern 1pt} {\kern 1pt} {\kern 1pt} \exp ({{ - c_{5} } \mathord{\left/ {\vphantom {{ - c_{5} } {\lambda_{i} }}} \right. \kern-0pt} {\lambda_{i} }}) \\ & \lambda_{i} = \left( {\frac{1}{{\lambda + c_{6} \beta }} - \frac{{c_{7} }}{{\beta^{3} + 1}}} \right)^{ - 1} {\kern 1pt} \\ \end{aligned}$$
(14.9)
$$\text{where:}\,\,\,c_{1} = 0.39{\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} \,\,c_{2} = 116{\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} \,c_{3} = 0.4{\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} \,c_{4} = 5{\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} \,\,c_{5} = 16.5{\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} \,c_{6} = 0.089{\kern 1pt} {\kern 1pt} ;\,\,{\kern 1pt} c_{7} = 0.035{\kern 1pt}$$
Fig. 14.11
figure 11

a Typical aerodynamic power coefficient C p as a function of λ and β. b Maximum power coefficient C pmax for different number of blades N at a given β [2]

Full size image

The maximum value of these curves (maximum power coefficient C pmax) depends on the number of blades N. An experimental expression that presents the effect of the number of blades N in the maximum rotor power coefficient C pmax for a classical wind turbine with 25 < C L /C D  < ∞ is shown in (14.10),

$$C_{p\hbox{max} } = 0.593\,\lambda_{\text{opt}} \,\left[ {\lambda_{\text{opt}} + \frac{{1.32 + \left( {\frac{{\lambda_{\text{opt}} - 8}}{20}} \right)^{2} }}{{N^{2/3} }}} \right]^{ - 1} - \frac{{0.57\lambda_{\text{opt}}^{2} }}{{\frac{{C_{L} }}{{C_{D} }}\left( {1 + \frac{1}{2N}} \right)}}$$
(14.10)

where N is the number of blades, C L is the rotor lift coefficient and C D is the rotor drag coefficient (see also [2], Chap. 12). Figure 14.11b shows some calculations of C pmax using this expression with C L /C D  = 76 and for N = 3, 4 and 5

3.3 Dynamics of Rotor Speed Versus Torque, Pitch Angle and Wind Velocity Variation

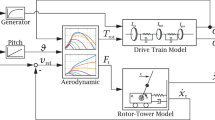
Figure 14.12 shows a variable-speed pitch-controlled wind turbine with a mechanical (gearbox) drive-train. A shaft connects a large inertia rotor at one end (blades) with a gearbox, which is coupled to a generator at the other end. The wind applies an aerodynamic torque T r to the rotor, which is connected to the low-speed shaft of the gearbox. At the other end of the drive-train, the generator, with a power converter, applies an antagonistic electrical torque T g on the high-speed shaft of the gearbox. The rotor presents a moment of inertia I r . The shaft has a torsional stiffness coefficient K s and a viscous damping coefficient B s . The generator shows a moment of inertia I g . The rotor angle is θ r , the rotor speed is Ω r  = dθ r /dt, and the generator angle is θ g . Also, ψ is the yaw angle error (nacelle-wind angle) and β is the pitch angle (blades).

Fig. 14.12
figure 12

A variable-speed pitch-controlled wind turbine (see [2])

Full size image

The excitation current, I x , is introduced in the rotor, and the active and reactive power, respectively P and Q, are supplied to the grid. f, U and ϕ are the frequency, voltage, and power factor at the grid connection point respectively.

The Euler−Lagrange method (energy-based approach) is applied to obtain general mechanical state space model of wind turbine. The main parameters of the wind turbine model are described in Table 14.1 (see [2] for more details).

The wind turbine dynamic equations of motion that describe the behavior of the system, under the influence of external forces (wind), and as a function of time, are developed as a set of mechanical differential equations. The equations of motion in Lagrangian mechanics are the Lagrange equations of the second kind, also known as the Euler−Lagrange equations. Note that E k is used for kinetic energy and E p for potential energy. D n is the dissipation function to include non-conservative forces, Q i the conservative generalized forces and q i for the generalized coordinates. Defining L as the Lagrangian function L = E k  – E p , the Euler−Lagrange equation is as follows:

$$\frac{\text{d}}{{{\text{d}}t}}\left( {\frac{\partial L}{{\partial \dot{q}_{i} }}} \right) - \frac{\partial L}{{\partial q_{i} }} + \frac{{\partial D_{n} }}{{\partial \dot{q}_{i} }} = Q_{i}$$
(14.11)

The generalized coordinates q i are (see also Fig. 14.12):

$$\varvec{q} = [q_{i} ] = \left[ {\begin{array}{*{20}l} {y_{t} } \hfill & \gamma \hfill & {\theta_{r} } \hfill & {\theta_{g} } \hfill & {\theta_{l} } \hfill \\ \end{array} } \right]^{T}$$
(14.12)

where y t is the axial displacement of the nacelle, γ is the angular displacement of the blades out of the plane of rotation, θ r is the rotor angular position, θ g is the generator angular position and θ l the gearbox low-speed shaft position.

The Energy and dissipation function equations, E k , E p , D n are:

$$E_{k} = \frac{{m_{1} }}{2}\dot{y}_{t}^{2} + \frac{{m_{2} }}{2}(r_{b} \dot{\gamma } + \dot{y}_{t} )^{2} + \frac{{I_{r} }}{2}\dot{\theta }_{r}^{2} + \frac{{I_{g} }}{2}\dot{\theta }_{g}^{2} + \frac{{I_{w} }}{2}\dot{\theta }_{l}^{2}$$
(14.13)
$$E_{p} = \frac{{K_{t} }}{2}y_{t}^{2} + \frac{N}{2}K_{b} (r_{b} \gamma )^{2} + \frac{{K_{l} }}{2}(\theta_{r} - \theta_{l} )^{2} + \frac{{K_{h} }}{2}(R_{t} \theta_{l} - \theta_{g} )^{2}$$
(14.14)
$$D_{n} = \frac{{B_{t} }}{2}\dot{y}_{t}^{2} + \frac{N}{2}B_{b} (r_{b} \dot{\gamma })^{2} + \frac{{B_{l} }}{2}(\dot{\theta }_{r} - \dot{\theta }_{l} )^{2} + \frac{{B_{h} }}{2}(R_{t} \dot{\theta }_{l} - \dot{\theta }_{g} )^{2}$$
(14.15)

Based on Eqs. (14.11) through (14.15), the state space description for the wind turbine is (see [2], Chap. 12, for details):

$$\dot{\varvec{x}} = \varvec{Ax} + \varvec{Bu};\;\varvec{y} = \varvec{Cx}$$
(14.16)
$$\varvec{A} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ { - \frac{{K_{t} }}{{m_{1} }}} & {\frac{{NK_{b} r_{b} }}{{m_{1} }}} & 0 & 0 & 0 & { - \frac{{B_{t} }}{{m_{1} }}} & {\frac{{NB_{b} r_{b} }}{{m_{1} }}} & 0 & 0 & 0 \\ {\frac{{K_{t} }}{{m_{1} r_{b} }}} & { - \frac{{(m_{1} + m_{2} )NK_{b} }}{{m_{1} m_{2} }}} & 0 & 0 & 0 & {\frac{{B_{t} }}{{m_{1} r_{b} }}} & { - \frac{{(m_{1} + m_{2} )NB_{b} }}{{m_{1} m_{2} }}} & 0 & 0 & 0 \\ 0 & 0 & { - \frac{{K_{l} }}{{I_{r} }}} & 0 & {\frac{{K_{l} }}{{I_{r} }}} & 0 & 0 & { - \frac{{B_{l} }}{{I_{r} }}} & 0 & {\frac{{B_{l} }}{{I_{r} }}} \\ 0 & 0 & 0 & { - \frac{{K_{h} }}{{I_{g} }}} & {\frac{{K_{h} R_{t} }}{{I_{g} }}} & 0 & 0 & 0 & { - \frac{{B_{h} }}{{I_{g} }}} & {\frac{{B_{h} R_{t} }}{{I_{g} }}} \\ 0 & 0 & {\frac{{K_{l} }}{{I_{w} }}} & {\frac{{K_{h} R_{t} }}{{I_{w} }}} & { - \frac{{K_{l} + K_{h} R_{t}^{2} }}{{I_{w} }}} & 0 & 0 & {\frac{{B_{l} }}{{I_{w} }}} & {\frac{{B_{h} R_{t} }}{{I_{w} }}} & { - \frac{{B_{l} + B_{h} R_{t}^{2} }}{{I_{w} }}} \\ \end{array} } \right]$$
(14.17)
$$\varvec{B} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ {\frac{1}{{m_{1} }}\left( {1 - \frac{{r_{p} }}{{r_{b} }}} \right)} & 0 & 0 \\ {\frac{1}{{m_{1} r_{b} }}\left( {\frac{{\left( {m_{1} + m_{2} } \right)r_{p} }}{{m_{2} r_{b} }} - 1} \right)} & 0 & 0 \\ 0 & {\frac{1}{{I_{r} }}} & 0 \\ 0 & 0 & { - \frac{1}{{I_{g} }}} \\ 0 & 0 & 0 \\ \end{array} } \right]$$
(14.18)
$$\varvec{C} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{array} } \right]$$
(14.19)

where:

$${\text{State}}\;{\text{variables}}:\varvec{x} = [\begin{array}{*{20}c} {y_{t} } & \gamma & {\theta_{r} } & {\theta_{g} } & {\theta_{l} } & {\dot{y}_{t} } & {\dot{\gamma }} & {\dot{\theta }_{r} } & {\dot{\theta }_{g} } & {\dot{\theta }_{l} } \\ \end{array} ]^{T}$$
(14.20)
$${\text{Inputs}}:\varvec{u} = [\begin{array}{*{20}c} {F_{T} } & {T_{r} } & {T_{g} } \\ \end{array} ]^{T}$$
(14.21)
$${\text{Outputs}}:\varvec{y} = [\begin{array}{*{20}c} {\dot{y}_{t} } & {\dot{\gamma }} & {\dot{\theta }_{r} } & {\dot{\theta }_{g} } & {\dot{\theta }_{l} } \\ \end{array} ]^{T}$$
(14.22)

According to the rotor aerodynamics and the characteristics of C p and C T (see [2] ), the inputs of Eqs. (14.16) and (14.21), F T and T r , depend on v 1 , β and Ω r in a nonlinear way. If the aerodynamic part of these equations is linearized around a working point (v 10, β 0, Ω r0), and the bias components are ignored, the inputs F T and T r can be described by a transfer matrix whose elements are just gains, so that,

$$\left[ {\begin{array}{*{20}c} {F_{T} \left( s \right)} \\ {T_{r} \left( s \right)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {K_{F\varOmega } } & {K_{FV} } & {K_{F\beta } } \\ {K_{T\varOmega } } & {K_{TV} } & {K_{T\beta } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varOmega_{r} \left( s \right)} \\ {v_{1} \left( s \right)} \\ {\beta \left( s \right)} \\ \end{array} } \right]$$
(14.23)

where the gains are calculated by using the C T and C p curves. Now, the transfer matrix description G(s) of the wind turbine is calculated by using the transformation \(\varvec{G}(s) = \varvec{C}\left( {s\varvec{I} - \varvec{A}} \right)^{ - 1} \varvec{B}\) for \(\varvec{y}(s) = \varvec{G}(s)\varvec{u}(s)\).

$$\left[ {\begin{array}{*{20}c} {\dot{y}_{t} \left( s \right)} \\ {\dot{\gamma }\left( s \right)} \\ {\varOmega_{r} \left( s \right)} \\ {\varOmega_{g} \left( s \right)} \\ {\varOmega_{l} \left( s \right)} \\ \end{array} } \right] = \varvec{P}(s)\left[ {\begin{array}{*{20}c} {\beta_{d} \left( s \right)} \\ {T_{gd} \left( s \right)} \\ \end{array} } \right] + \varvec{D}(s)v_{1} \left( s \right){\kern 1pt}$$
(14.24)

where the plant matrix and the disturbance matrix are,

$$\varvec{P}(s) = \left[ {\begin{array}{*{20}c} {\mu_{11} \left( s \right)\frac{{\mu_{32} \left( s \right){\kern 1pt} {\kern 1pt} \left( {K_{F\varOmega } K_{T\beta } - K_{F\beta } K_{T\varOmega } } \right) + K_{F\beta } }}{{1 - \mu_{32} \left( s \right)K_{T\varOmega } }}A_{\beta } (s)} & {\mu_{11} \left( s \right)\frac{{\mu_{33} \left( s \right)K_{F\varOmega } }}{{1 - \mu_{32} \left( s \right)K_{T\varOmega } }}A_{T} (s)} \\ {\mu_{21} \left( s \right)\frac{{\mu_{32} \left( s \right){\kern 1pt} {\kern 1pt} \left( {K_{F\varOmega } K_{T\beta } - K_{F\beta } K_{T\varOmega } } \right) + K_{F\beta } }}{{1 - \mu_{32} \left( s \right)K_{T\varOmega } }}A_{\beta } (s)} & {\mu_{21} \left( s \right)\frac{{\mu_{33} \left( s \right)K_{F\varOmega } }}{{1 - \mu_{32} \left( s \right)K_{T\varOmega } }}A_{T} (s)} \\ {\mu_{32} \left( s \right)\frac{{K_{T\beta } }}{{1 - \mu_{32} \left( s \right)K_{T\varOmega } }}A_{\beta } (s)} & {\mu_{33} \left( s \right)\frac{1}{{1 - \mu_{32} \left( s \right)K_{T\varOmega } }}A_{T} (s)} \\ {\mu_{42} \left( s \right)\frac{{K_{T\beta } }}{{1 - \mu_{32} \left( s \right)K_{T\varOmega } }}A_{\beta } (s)} & {\frac{{\mu_{42} \left( s \right)\mu_{33} \left( s \right)K_{T\varOmega } + \mu_{43} \left( s \right) - \mu_{43} \left( s \right)\mu_{32} \left( s \right)K_{T\varOmega } }}{{1 - \mu_{32} \left( s \right)K_{T\varOmega } }}A_{T} (s)} \\ {\mu_{52} \left( s \right)\frac{{K_{T\beta } }}{{1 - \mu_{32} \left( s \right)K_{T\varOmega } }}A_{\beta } (s)} & {\frac{{\mu_{52} \left( s \right)\mu_{33} \left( s \right)K_{T\varOmega } + \mu_{53} \left( s \right) - \mu_{53} \left( s \right)\mu_{32} \left( s \right)K_{T\varOmega } }}{{1 - \mu_{32} \left( s \right)K_{T\varOmega } }}A_{T} (s)} \\ \end{array} } \right]{\kern 1pt} {\kern 1pt}$$
(14.25)
$$\varvec{D}(s) = \left[ {\begin{array}{*{20}c} {\mu_{11} \left( s \right)\frac{{\mu_{32} \left( s \right){\kern 1pt} {\kern 1pt} \left( {K_{F\varOmega } K_{TV} - K_{FV} K_{T\varOmega } } \right) + K_{FV} }}{{1 - \mu_{32} \left( s \right)K_{T\varOmega } }}} \\ {\mu_{21} \left( s \right)\frac{{\mu_{32} \left( s \right){\kern 1pt} {\kern 1pt} \left( {K_{F\varOmega } K_{TV} - K_{FV} K_{T\varOmega } } \right) + K_{FV} }}{{1 - \mu_{32} \left( s \right)K_{T\varOmega } }}} \\ {\mu_{32} \left( s \right)\frac{{K_{TV} }}{{1 - \mu_{32} \left( s \right)K_{T\varOmega } }}} \\ {\mu_{42} \left( s \right)\frac{{K_{TV} }}{{1 - \mu_{32} \left( s \right)K_{T\varOmega } }}} \\ {\mu_{52} \left( s \right)\frac{{K_{TV} }}{{1 - \mu_{32} \left( s \right)K_{T\varOmega } }}} \\ \end{array} } \right]{\kern 1pt}$$
(14.26)

The rotational speed Ω r of the wind turbine rotor is continuously modified (a) by the controllers and actuators, which changes the blade pitch angles β d and the electrical torque T gd; (b) by the wind speed v 1; and (c) through the dynamics of the rotor speed Ω r itself (see Fig. 14.13).

Fig. 14.13
figure 13

Block diagram for rotor speed control system [2]

Full size image

The transfer functions of the rotor speed Ω r (s) versus the demanded blade pitch angle β d (s), the demanded electrical torque T gd(s), and the wind speed v 1(s), are (see Fig. 14.13 and Ref. [2], Chap. 12, for details),

$$\varOmega_{r} (s) = F_{1} (s)v_{1} (s) + F_{2} (s)\beta_{d} (s) + F_{3} (s)T_{gd} (s){\kern 1pt} {\kern 1pt} {\kern 1pt}$$
(14.27)

where,

$$F_{1} (s) = {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{K_{TV} \,n_{\mu 32} (s)}}{{d_{tf} (s)}} = D_{1} (s)$$
(14.28)
$$F_{2} (s) = {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{K_{T\beta } \,n_{\mu 32} (s)A_{\beta } (s)}}{{d_{tf} (s)}} = P(s)$$
(14.29)
$$F_{3} (s) = {\kern 1pt} \frac{{n_{\mu 33} (s)A_{T} (s)}}{{d_{tf} (s)}} = H(s)$$
(14.30)

and,

$$n_{\mu 32} (s) = I_{g} {\kern 1pt} I_{w} {\kern 1pt} s^{4} + (B_{h} {\kern 1pt} I_{w} + I_{g} {\kern 1pt} B_{l} + I_{g} {\kern 1pt} B_{h} {\kern 1pt} R_{t}^{2} ){\kern 1pt} s^{3} {\kern 1pt} + (B_{h} {\kern 1pt} B_{l} + I_{g} {\kern 1pt} K_{l} + I_{g} {\kern 1pt} K_{h} {\kern 1pt} R_{t}^{2} + K_{h} {\kern 1pt} I_{w} ){\kern 1pt} s^{2} +_{h} {\kern 1pt} B_{l} + B_{h} {\kern 1pt} K_{l} ){\kern 1pt} s + K_{h} {\kern 1pt} K_{l}$$
(14.31)
$$n_{\mu 33} (s) = - B_{h} {\kern 1pt} R_{t} {\kern 1pt} B_{l} {\kern 1pt} s^{2} - R_{t} {\kern 1pt} (K_{h} {\kern 1pt} B_{l} + B_{h} {\kern 1pt} K_{l} ){\kern 1pt} s - K_{h} {\kern 1pt} R_{t} {\kern 1pt} K_{l}$$
(14.32)
$$\begin{aligned} d_{tf} (s) & = d_{\mu 32} (s) - n_{\mu 32} (s)K_{T\varOmega } \\ & = {\kern 1pt} I_{r} {\kern 1pt} I_{w} {\kern 1pt} I_{g} {\kern 1pt} s^{5} + [(I_{r} {\kern 1pt} I_{g} {\kern 1pt} B_{l} + B_{h} {\kern 1pt} I_{r} {\kern 1pt} I_{w} + I_{r} {\kern 1pt} I_{g} {\kern 1pt} B_{h} {\kern 1pt} R_{T}^{2} + B_{l} {\kern 1pt} I_{w} {\kern 1pt} I_{g} ) - (I_{g} {\kern 1pt} I_{w} )K_{T\varOmega } ]{\kern 1pt} s^{4} \ldots \\ {\kern 1pt} & + [(K_{l} {\kern 1pt} I_{w} {\kern 1pt} I_{g} + B_{h} {\kern 1pt} I_{r} {\kern 1pt} B_{l} + B_{l} {\kern 1pt} I_{g} {\kern 1pt} B_{h} {\kern 1pt} r_{t}^{2} + K_{h} {\kern 1pt} I_{r} {\kern 1pt} I_{w} + I_{r} {\kern 1pt} I_{g} {\kern 1pt} K_{l} + B_{l} {\kern 1pt} B_{h} {\kern 1pt} I_{w} + I_{r} {\kern 1pt} I_{g} K_{h} {\kern 1pt} R_{t}^{2} ){\kern 1pt} \\ & - (B_{h} {\kern 1pt} I_{w} + I_{g} {\kern 1pt} B_{l} + I_{g} {\kern 1pt} B_{h} {\kern 1pt} R_{t}^{2} )K_{T\varOmega } {\kern 1pt} ]s^{3} \ldots \\ & + [(B_{l} {\kern 1pt} K_{h} {\kern 1pt} I_{w} + K_{l} {\kern 1pt} I_{g} {\kern 1pt} B_{h} {\kern 1pt} R_{t}^{2} + K_{h} {\kern 1pt} I_{r} {\kern 1pt} B_{l} + B_{h} {\kern 1pt} I_{r} {\kern 1pt} K_{l} + K_{l} {\kern 1pt} B_{h} {\kern 1pt} I_{w} + I_{g} {\kern 1pt} B_{l} {\kern 1pt} K_{h} {\kern 1pt} R_{t}^{2} ) \\ & - (B_{h} {\kern 1pt} B_{l} + I_{g} {\kern 1pt} K_{l} + I_{g} {\kern 1pt} K_{h} {\kern 1pt} R_{t}^{2} + K_{h} {\kern 1pt} I_{w} ){\kern 1pt} K_{T\varOmega } ]s^{2} \ldots \\ & + [(I_{g} {\kern 1pt} K_{l} {\kern 1pt} K_{h} {\kern 1pt} R_{t}^{2} + K_{h} {\kern 1pt} I_{r} {\kern 1pt} K_{l} + K_{l} {\kern 1pt} K_{h} {\kern 1pt} I_{w} ) - (K_{h} {\kern 1pt} B_{l} + B_{h} {\kern 1pt} K_{l} )K_{T\varOmega } ]s \\ & - {\kern 1pt} (K_{h} {\kern 1pt} B_{l} + B_{h} {\kern 1pt} K_{l} )K_{T\varOmega } \\ \end{aligned}$$
(14.33)

4 System Identification

Figure 14.14 shows the control system block diagram of the wind turbine. G p (s), G t (s), c 1 and c 2 are part of the control algorithm, which works in the metric system. G p (s) is the rotor speed pitch controller, G t (s) the torque controller, and c 1 and c 2 the coefficients needed to operate with the NXT motor and the Glide-Wheel sensor (see Sect. 14.2), which work in degrees and rpm respectively: c 1 = 180/π deg/rad and c 2 = π/30 rad/s/rpm.

Fig. 14.14
figure 14

WT control system block diagram

Full size image

The blocks F 1(s), F 2(s) and F 3(s) in Fig. 14.14 correspond to the Eqs. (14.28)–(14.30) developed in Sect. 14.3.3, all in the metric system. They represent respectively the transfer functions from the wind speed, pitch angle and electrical torque to the rotor speed. The following sections identify experimentally the parameters of the dominant dynamics of these transfer functions.

4.1 Rotor-Speed Versus Pitch-Angle Transfer Function F 2(S)

The dominant dynamics of the rotor-speed versus pitch-angle transfer function Ω rs(s)/β(s) = P 1(s), and the transfer function of the pitch-angle versus actuator-input β(s)/β di (s) = A β (s)r tg are identified experimentally by applying step inputs to the pitch motor of the wind turbines under different wind speeds. Figure 14.14 shows the input/output signals.

For the estimation of the first transfer function the wind speed is set as a periodic function v 1 = v 1m + v 1a sin(2πf t + θ) m/s, with v 1a  = 0.125 m/s, f = 0.2 Hz, and θ = 58°, and under three scenarios of average wind speed: v 1m = 3.68, 4.22, and 4.75 m/s. During the experiments the generator torque T gd and the yaw angle α = 0 are maintained constant. Then the pitch angle at the nacelle β is changed from 0 to 5° and the rotor speed Ω rs is measured. For the second transfer function a second experiment studies the wind turbine with no wind (v 1 = 0) and constant torque T gd, when the actuator input β di is changed from 0 to 700° and the actual pitch angle at the nacelle β is measured.

Using the signals obtained in these experiments and applying classical system identification techniques, the structure, parameters, and uncertainty of both transfer functions are found as shown in Eqs. (14.34) and (14.35).

$$\frac{{\varOmega_{\text{rs}} (s)}}{\beta (s)} = P_{1} (s) = \frac{{k_{1} }}{{\left( {\frac{s}{{\omega_{n1} }}} \right)^{2} + \frac{{2\,\zeta_{1} \,s}}{{\omega_{n1} }} + 1}}$$
(14.34)
$$\frac{\beta (s)}{{\beta_{{{\text{d}}i}} (s)}} = r_{\text{tg}} \,A_{\beta } (s)\, = \,r_{\text{tg}} \,\,\frac{1\,\,}{{\left[ {\left( {\frac{s}{{\omega_{n2} }}} \right)^{2} + \frac{{2\,\zeta_{2} \,s}}{{\omega_{n2} }} + 1} \right]^{2} }}\,{\text{represents}}\;{\text{the}}\;{\text{dynamics}}\;{\text{of}}\;{\text{the}}\;{\text{actuator}}$$
(14.35)

The estimated parameters for Eqs. (14.34) and (14.35) for different wind speeds, and with Ω rs in rpm and β and β di in degrees, are:

  • For v 1m = 3.68 m/s

    $$k_{1} = - 4 . 1 0 6 7,\,\,\omega_{n1} = 0 . 6 7 5\,\,{\text{rad}}/{\text{s}} ,\,\,\zeta_{1} = 0 . 4 8 1 5$$

  • For v 1m = 4.22 m/s

    $$k_{1} = - 5 . 4 7 5 6,\,\,\omega_{n1} = 0 . 6 7 5\,\,{\text{rad}}/{\text{s}} ,\,\,\zeta_{1} = 0 . 4 8 1 5$$

  • For v 1m = 4.75 m/s

    $$k_{1} = - 5 . 4 7 5 6,\,\,\omega_{n1} = 0 . 6 7 5\,\,{\text{rad}}/{\text{s}} ,\,\,\zeta_{1} = 0 . 4 8 1 5$$

  • For all v 1

    $$\omega_{n2} = 5\;\;{\text{rad}}/{\text{s}} ,\,\,\zeta_{2} = 0.83,\,\,r_{tg} = 1/140$$

Now, the complete plant F 2 (s) in Fig. 14.14 and expressions (14.27) and (14.29) is:

$$F_{2} (s) = P(s) = \frac{{\varOmega_{r} (s)}}{{\beta_{d} (s)}} = \,\,c_{2} \,P_{1} (s)\,\,r_{tg} \,A_{\beta } (s)\,c_{1} = c_{2} \frac{{K_{T\beta } \,n_{\mu 32} (s)}}{{d_{tf} (s)}}\,\,r_{tg} \,A_{\beta } (s)\,\,c_{1} \,\,;\,\,\frac{{[{\text{rad/sec}}]}}{{[{\text{rad}}]}}$$
(14.36)

Figures 14.15a–c present the first set of experiments for v 1m = 3.68, 4.22, and 4.75 m/s respectively, and with constant T gd. They show (a) the experimental rotor speed Ω rs in rpm, measured with the rotor speed Glide-Wheel sensor when the nacelle pitch angle β changes as a step input from 0 to 5°; and (b) the estimated rotor speed using Eq. (14.34) for the same pitch angle β.

Fig. 14.15
figure 15

System identification: (a–c) rotor-speed versus pitch-angle P 1(s) = Ω rs (s)/β(s); and (d) pitch-angle versus the actuator input A β (s)r tg = β(s)/β di (s). Sensor signals (solid lines) and estimated signals using Eqs. (14.34) and (14.35) (dashed lines). Sampling rate is 2.5 Hz

Full size image

Figure 14.15d presents the second set of experiments, with v 1 = 0 and a constant T gd, showing (a) the experimental pitch angle β measured with the nacelle Glide-Wheel sensor when a 0 to 700° step is applied to the actuator input β di and (b) the estimated nacelle pitch angle using Eq. (14.35) for the same actuator input β di .

4.2 Rotor-Speed Versus Electrical-Torque Transfer Function F3(S)

The dominant dynamics of the rotor-speed versus electrical-torque transfer function Ω rs(s)/T g (s) is identified experimentally by applying step inputs to the electrical torque of the wind turbines under different wind speeds and a constant pitch angle (see Figs. 14.14 and 14.24). The experimental rotor speed Ω rs is measured with the rotor speed Glide-Wheel sensor (in rpm), and the applied electrical torque T g is measured using the current sensor (Sect. 14.2.1.4), and is given in Nm. Using the signals obtained in these experiments and applying classical system identification techniques, the structure, parameters and uncertainty of the transfer function is found as shown in Eq. (14.37a). Figure 14.24a shows the applied input T g in mN.m and Fig. 14.24b the experimental rotor speed Ω rs and the estimated rotor speed with the model in Eq. (14.37), both in rpm.

$$\frac{{\varOmega_{\text{rs}} (s)}}{{T_{g} (s)}} = Q(s)\,\left( {\frac{1}{{c_{2} }}} \right) = \frac{{k_{\text{wt}} }}{{\left( {\frac{s}{{\omega_{\text{nwt}} }}} \right)^{2} + \frac{{2\,\zeta_{\text{wt}} \,s}}{{\omega_{\text{nwt}} }} + 1}}\left( {\frac{1}{{c_{2} }}} \right)$$
(14.37a)

where: \(k_{\text{wt}} = - 7165,\,\,\omega_{\text{nwt}} = 10.1256\,\,{\text{rad}}/{\text{s}} ,\,\,\zeta_{\text{wt}} = 0 . 7\), and where Ω rs is in rpm and T g in Nm.

The complete plant F 3 (s) in Fig. 14.14 and expressions (14.27) and (14.30) are (metric system):

$$F_{3} (s) = H(s) = = \frac{{\varOmega_{r} (s)}}{{T_{gd} (s)}} = \,\,A_{T} (s)\,Q(s)\, = A_{T} (s)\,\frac{{n_{\mu 33} (s)}}{{d_{tf} (s)}}\,\,\,;\,\,\frac{{[{\text{rad/s}}]}}{{[{\text{Nm}}]}}\,$$
(14.37b)

4.3 Rotor Speed Versus Wind Speed Transfer Function F1(S)

The gain of the rotor-speed versus wind-speed transfer function Ω rs(s)/v 1(s) is identified experimentally by changing the wind speed to different values—see Fig. 14.15a–c for v 1m = 3.68, 4.22 and 4.75 m/s, t < 30 s−, v 1 = v 1m + v 1a sin(2πf t + θ), as shown in Eq. (14.38).

$$\frac{{\varOmega_{\text{rs}} (s)}}{{v_{1} (s)}} = \frac{{k_{\text{wv}} }}{{\tau_{1} s + 1}}$$
(14.38a)

where: \(k_{wv} = 1 6 0 . 8 7 ;\;\tau_{ 1} = 1.35\;{\text{s}}\), v 1a  = 0.125 m/s, f = 0.2 Hz, θ = 58°, Ω rs in rpm and v 1 in m/s.

The plant F 1(s) in Fig. 14.14 and expressions (14.27) and (14.28) are (metric system):

$$F_{1} (s) = D_{1} (s) = \frac{{\varOmega_{r} (s)}}{{v_{1} (s)}} = \frac{{k_{\text{wv}} }}{{\tau_{1} s + 1}}c_{2} ;\;\frac{{[{\text{rad/s}}]}}{{[{\text{m/s}}]}}$$
(14.38b)

5 Control System Design

5.1 Rotor Speed Control System

The Quantitative feedback theory (QFT)—see [2–4]—has demonstrated to be an excellent controller design methodology to deal with the compromises between several, often conflicting, performance specifications, model uncertainty, and practical implementation. Its transparent design process allows the designer to consider all these compromises simultaneously, and to find the controller that satisfies the set of requested performance specifications for every plant within the model uncertainty while using the minimum amount of feedback. In this section, we present the QFT design of the controller to regulate the rotor speed of the wind turbines with the pitch angle actuators.

5.1.1 Control Objectives and Configuration

The main objective of the pitch control system (see Fig. 14.10 in Region 3) is: (a) to regulate the rotor speed at the rated (nominal) value Ω r  = Ω r-ref; (b) to reject the wind disturbances (effect of v 1 variation); and (c) to avoid over-speed situations (with significant ΔΩ r ) that can be dangerous for the turbine.

Based on Figs. 14.13 and 14.14 and Eqs. (14.27)–(14.38), Fig. 14.16 shows a simplified block diagram for the rotor speed/pitch control system.

Fig. 14.16
figure 16

Simplified block diagram for rotor speed control system [2]

Full size image

5.1.2 Modeling

The dynamics between the rotor-speed Ω rs(t), given by the pitch angle sensor at the nacelle, and the controller signal β di (t) at the actuator input was calculated in Eqs. (14.34) and (14.35), and is summarized here for convenience—see Eq. (14.39).

$$\frac{{\varOmega_{rs} (s)\,\,[{\text{rpm}}]}}{{\beta_{di} (s)\,\,[{ \deg }]}} = P_{1} (s)\,\,r_{tg} \,A_{\beta } (s) = \frac{{k_{1} }}{{\left( {\frac{s}{{\omega_{n1} }}} \right)^{2} + \frac{{2\,\zeta_{1} \,s}}{{\omega_{n1} }} + 1}}\;r_{tg} \;\frac{1}{{\left[ {\left( {\frac{s}{{\omega_{n2} }}} \right)^{2} + \frac{{2\,\zeta_{3} \,s}}{{\omega_{n2} }} + 1} \right]^{2} }}\,$$
(14.39)

with:

$$\begin{aligned} & k_{1} \in \left[ { - 5.4756,\, - 4.6733} \right] \pm 10\% ,\,\,\omega_{n1} \in \left[ { 0 . 6 7 5\pm 10\% } \right]\,\,{{\text{rad/sec}}},\,\,\zeta_{1} \in \left[ { 0 . 4 8 1 5\pm 10\% } \right] \\ & \omega_{n2} = 5\;{\text{rad}}/{\text{s}} ,\,\,\zeta_{2} = 0.83,\,\,r_{tg} = 1/140 \\ \end{aligned}$$

where the rotor-speed Ω r (s) is in rpm (the rotor sensor gives the information in rpm) and the demanded pitch angle β di in degrees (the NXT motor needs degrees).

The QFT templates of this model—Eq. (14.39)—, including the parametric uncertainty, are calculated with the QFT Control Toolbox [2, 3] and are shown in Fig. 14.17.

Fig. 14.17
figure 17

QFT templates for Ω rs(s)/β di (s) and ω = [0.001 0.005 0.01 0.05 0.1 0.3 0.5 0.7 1 1.1 1.3 1.5 2 3 5 7 10] rad/s

Full size image

5.1.3 Control Specifications

The performance specifications required for the rotor speed controllers include robust stability and robust disturbance rejection. They are defined in Eqs. (14.40) and (14.41).

  • Specification 1 (Robust Stability).

    $$\left| {\frac{{\varOmega_{r} (j\omega )}}{{\varOmega_{r\_ref} (j\omega )}}} \right| = \,\left| {\,\,\frac{{P\left( {j\omega } \right)\,G\left( {j\omega } \right)}}{{1 + P\left( {j\omega } \right)\,G\left( {j\omega } \right)}}\,\,} \right|\,\, \le \,\,\mu = 1.3\,\,,\,\,\forall \omega$$
    (14.40)

This stability specification, μ = 1. 3 in magnitude Eq. (14.40), is introduced in the QFT Control Toolbox [2, 3]. It implies a gain margin of 4.95 dB and a phase margin of 45.23°.

  • Specification 2 (Robust Output Disturbance Rejection).

    $$\left| {\frac{{\varOmega_{r} (j\omega )}}{d(j\omega )}} \right| = \,\left| {\,\,\frac{1}{{1 + P\left( {j\omega } \right)\,G\left( {j\omega } \right)}}} \right| \le \left| {\frac{6j\omega }{6\,j\omega + 1}} \right|,\;{\text{for}}\,\,\,\omega = \left[ {\begin{array}{*{20}l} { 0 . 0 0 1} \hfill & { 0 . 0 0 5} \hfill & { 0 . 0 1} \hfill & { 0 . 0 5} \hfill & { 0 . 1} \hfill \\ \end{array} } \right]{\text{ rad/s}}$$
    (14.41)

The QFT bounds are calculated with the QFT Control Toolbox [2, 3] and are shown in Fig. 14.18, with the worst case scenario (intersection of bounds) for the stability and output disturbance rejection specifications and for Ω rs(s)/β di (s)—Eq. (14.39)—at all the frequencies of interest.

Fig. 14.18
figure 18

QFT bounds and controller loop-shaping for L 0 (s) = P 0 (s)G p (s)c 2 c 1 = [Ω rs (s)/β di (s)]0 G p (s)c 2 c 1

Full size image

5.1.4 Controller Design

A robust controller G p (s) for the system Ω rs(s)/β di (s)—Eq. (14.39) and the above performance specifications—Eqs. (14.40) and (14.41)—is calculated by using the loop-shaping window of the QFT Control Toolbox [2, 3], as shown in Fig. 14.18. The controller G p (s) has a Proportional-Integral (PI) structure with a first order filter, as shown in Eq. (14.42). It meets all the performance specifications, which are the QFT bounds requirements at every frequency of interest, as is seen in Fig. 14.18.

$$G_{p} (s)\,c_{2} \,c_{1} = \frac{{\beta_{di} (s)}}{e(s)} = \frac{{ - 4.5\,\,\left( {\frac{s}{2} + 1} \right)}}{{s\,\,\left( {\frac{s}{4} + 1} \right)}}\quad \left( {{\text{analog}}\;^{{\prime \prime }} s^{{\prime \prime }} \;{\text{expression}}} \right)$$
(14.42a)
$$G_{p} (z)\,c_{2} \,c_{1} = \frac{{\beta_{di} (z)}}{e(z)} = \frac{{ - 7.8722\,z^{ - 1} + 1.1389\,z^{ - 2} }}{{1 - 1.0025\,z^{ - 1} + 0.0025\,z^{ - 2} }}\quad \left( {{\text{digital}}\;^{{\prime \prime }} z^{{\prime \prime }} \;{\text{expression}}} \right)$$
(14.42b)

The controller algorithm is:

  • Rotor speed data received from the sensor (Glide-Wheel AS): Ω rs(n) in rpm.

  • Error calculation: e(n) = Ω rs_ref(n)–Ω rs(n), with Ω rs_ref(n) and Ω rs(n) in rpm.

  • Control law, based on Eqs. (14.42a) and (14.42b):

$$\beta_{{{\text{d}}i}} (n) = 1.0025\,\,\beta_{{{\text{d}}i}} (n - 1) - 0.0025\,\,\beta_{{{\text{d}}i}} (n - 2) - 7.8722\,e(n-1) + 1.1389\,\,e(n - 2)$$
(14.42c)

being β di (n) the demanded pitch angle at the input of the NxT motor in degrees, e(n) = Ω rs_ref(n)–Ω rs (n) the control error in rpm, and T sampling = 1.5 s the sampling time (see also Fig. 14.14). An anti-wind-up function is also implemented in the algorithm to help the controller when the actuator is saturated at the upper or lower limits.

Equation (14.42a) shows the controller in continuous-time G p (s)c 2 c 1. Equation (14.42b) shows the controller in discrete-time G p (z)c 2 c 1 after a discretization with a zero-order hold approach and for a sampling time T sampling = 1.5 s. And Eq. (14.42c) shows the control algorithm in terms of the actuator inputs β di (n − k) (in degrees) and the control errors e(n − k) (in rpm), implemented in the microcontroller with a sampling time of 1.5 s.

5.2 Power/Torque Control System

Power maximization is typically achieved by optimizing in real-time the power coefficient C p for each tip speed ratio λ = Ω r r b /v 1—see Fig. 14.11a. As wind speed v 1 changes, the rotor speed Ω r is automatically modified in order to keep the machine at maximum C p . This is usually performed by controlling the electrical torque T g and pitch angle β.

The electrical torque T g is manipulated in Regions 1 and 2 (below rated, Fig. 14.10) in order to get a maximum aerodynamic efficiency C p . This strategy aims to keep optimal the relation between wind speed v 1 and rotor speed Ω r as long as possible—see λ opt in Fig. 14.11a. To do so, the rotor speed Ω r is modified by changing the electrical torque T g , opposite to the wind torque T r , to follow the wind speed changes, and then keep λ = λ opt.

From Eq. (14.7), the aerodynamic torque T r on the rotor is,

$$T_{r} (t) = \,\,{{0.5\,\,\rho \,\,A\,\,C_{p} (t)\,\,v_{1} (t)^{3} \,} \mathord{\left/ {\vphantom {{0.5\,\,\rho \,\,A\,\,C_{p} (t)\,\,v_{1} (t)^{3} \,} {\,\varOmega_{r} (t)}}} \right. \kern-0pt} {\,\varOmega_{r} (t)}}$$
(14.43)

Now, neglecting mechanical losses in the shaft, the resulting demanded electrical torque T gd that maximizes the power capture at every wind speed is:

$$T_{gd} (t) = \,\,K_{a} \,\,\varOmega_{r} (t )^{2}$$
(14.44)

with,

$$K_{a} = {{0.5\,\rho \,A\,\,r_{b}^{3} \,C_{p\hbox{max} } } \mathord{\left/ {\vphantom {{0.5\,\rho \,A\,\,r_{b}^{3} \,C_{p\hbox{max} } } {\lambda_{opt}^{3} }}} \right. \kern-0pt} {\lambda_{opt}^{3} }}$$
(14.45)

and where C pmax is the maximum power coefficient, obtained at λ opt—see Fig. 14.11a.

Equation (14.44) shows a very simple and useful expression to set up the torque in Regions 1 and 2 (below rated, Fig. 14.10). The expression is based on the rotor speed sensor Ω r and the C p /λ curves provided by the blade manufacturer (Fig. 14.11). These curves usually give only a first approach for steady state and laminar flow conditions. For a more complete approach, some improvement can be done by slightly changing Eqs. (14.44) and (14.45), taking into account drive-train losses and some additional dynamic conditions. Due to the erosion and dirtiness of the blades and the variation of the air density at different weather conditions, the aerodynamic power coefficient C p also becomes time variant. Then, for a more advanced approach, a reduction of the constant K a , or the application of adaptive techniques to estimate it, will be appropriate to optimize the energy capture (Maximum Power Point Tracking, MPPT).

6 Research and Education Experiments

6.1 Effect of Number of Blades, Aerodynamic and Generator Efficiency

As we saw in Sect. 14.2.1.3, the generator torque T g , and as a result the generator power P g and efficiency η g , varies with the rotor speed Ω r according to Eqs. (14.1)–(14.3)—see also Fig. 14.20a. At the same time, the number of blades of the rotor affects the rotor speed and then the aerodynamic power coefficient C p , as it was described in Sect. 14.3.2 and Eqs. (14.7) (14.8) and (14.10).

The rotor radius of each wind turbine is r b  = 0.13 m, and the rotor effective surface A r  = π r 2 b  = 0.0531 m2. Knowing the normal air density ρ = 1.225 kg/m3, and putting a wind turbine under the effect of an average wind speed of v 1 = 4.24 m/s, a constant pitch angle β = 0, a constant yaw angle α = 0 and a constant demanded electrical torque T gd, the results of the experiments for a rotor with 2,3,4, and 6 blades are shown in Table 14.2 and Fig. 14.19.

Table 14.2 Effect of number of blades on power generation and aerodynamic efficiency
Full size table
Fig. 14.19
figure 19

Effect of the number of blades on the rotor speed Ω r and on the generator power P g

Full size image

The last row shows the experimental results found for the aerodynamic power coefficient C p for a rotor with 2, 3, 4 and 6 blades—see also Fig. 14.20b.

Fig. 14.20
figure 20

a Efficiency η g of the electrical generator: all the experimental cases presented in Sects. 14.4.1, 14.6.1, 14.6.2 and 14.6.3. The maximum generator efficiency is 0.6131 at 945 rpm. b Aerodynamic power coefficient versus tip speed ratio as a function of number of blades for N = 2, 3, 4, 6

Full size image

The results are consistent with the typical aerodynamic power coefficient in classical drag-machines. Additionally, the profile of the C p /N curve found is similar to the experimental expression (14.10).

The generator efficiency—Fig. 14.20a is modeled as a second order polynomial, as shown in Eq.(14.46), where the rotor speed Ω r is in rpm and the generator efficiency η g in per unit.

$$\eta_{g} = - 6.8654 \times 10^{ - 7} \left( {\varOmega_{r} - 945} \right)^{2} + 0.6131$$
(14.46)

6.2 Rotor Speed Control with Pitch System

This section applies the control algorithm designed in Sect. 14.5.1—Eq. (14.42)- to regulate the rotor speed Ω r (t) of the wind turbine with the pitch angle actuator β d (t) in Region 3 (above rated, Fig. 14.10). The main objective of the pitch control system is to regulate the rotor speed at the rated (nominal) value Ω r  = Ω r-ref, rejecting the wind disturbances v 1, and avoiding over-speed situations that can be dangerous for the turbine.

Figures 14.14 and 14.16 show the control system configuration and Figs. 14.21, 14.22, 14.23 the results of this experiment. The wind speed is set as a periodic function v 1 = v 1m + v 1a sin(2πf t + θ) m/s, with v 1a  = 0.125 m/s, f = 0.2 Hz, θ = 58°, and v 1m = 3.66 m/s at 0 ≤ t < 25 s and t > 31 s, and v 1m = 4.3 m/s at 25 ≤ t ≤ 31 s—see Fig. 14.21a. The rotor speed control system is set at a set point rotor speed Ω r  = Ω r-ref = 320 rpm.

Fig. 14.21
figure 21

Rotor speed control experiment: a wind speed v 1; b actuator input β di /140 and nacelle pitch angle sensor β

Full size image
Fig. 14.22
figure 22

Rotor speed control experiment: a reference rotor speed Ω r-ref and measured rotor speed Ω r ; b mechanical power at rotor shaft P a and electrical power at the generator output P g

Full size image
Fig. 14.23
figure 23

Rotor speed control experiment: a wind speed v 1 and blade tip speed Ω r r b ; b tip-speed ratio λ; c aerodynamic power coefficient C p ; d C p versus λ

Full size image

Using the control algorithm calculated in Eq. (14.42), the wind turbine changes the controller output (the demanded pitch angle or motor input β di ) as shown in Fig. 14.21b, and then the nacelle pitch angle β, also shown in Fig. 14.21b, to keep the rotor speed Ω r at the nominal value Ω r-ref = 320 rpm, as shown in Fig. 14.22a.

The experimental mechanical power at the rotor shaft P a given by the wind speed v 1, and the electrical power at the generator output P g are both shown in Fig. 14.22b. Finally Fig. 14.23 shows experimental results for (a) the wind speed v 1 and blade tip speed Ω r r b ; (b) the tip-speed ratio λ; (c) the aerodynamic power coefficient C p ; and (d) the C p versus λ plot.

6.3 Maximum Power Point Tracking for Individual Wind Turbine

For Maximum Power Point Tracking (MPPT), Fig. 14.24 shows an experiment of a 6-blade wind turbine working with a constant pitch angle β = 0, a constant yaw angle α = 0, and under a wind speed profile v 1 = v 1m + v 1a sin(2πf t + θ), with v 1m = 4.75 m/s, v 1a  = 0.125 m/s and f = 0.2 Hz, θ = 58°. At time t = 20 s the antagonistic electrical torque T gd (generator torque command) varies from 5.45 to 4.5 mNm—see Fig. 14.24a. As a result the rotor speed Ω r speeds up from 560 rpm (58.64 rad/s) to 625 rpm (65.45 rad/s)—see Fig. 14.24c. This implies a change in the tip speed (the rotor radius is r b  = 0.13 m) from 7.62 to 8.51 m/s—see Fig. 14.24b. As the average wind speed is v 1m = 4.75 m/s, the average tip speed ratio changes accordingly from λ = 1.60 to λ = 1.79—see Fig. 14.24d and therefore the aerodynamic power coefficient from C p  = 0.179 to C p  = 0.156—see Fig. 14.25.

Fig. 14.24
figure 24

Effect of electrical torque T g on rotor speed Ω r : a Experimental electrical torque T g —in mNm; b Blade tip speed Ω rs  –in rpm; c Experimental and estimated rotor speed—in m/s; d Tip speed ratio λ

Full size image
Fig. 14.25
figure 25

Experimental estimation of the C p /λ characteristic of the 6-blade rotor wind turbine, β = 0

Full size image

These experimental results confirm the fact that the variation of the electrical torque T gd in Regions 1 and 2 (below rated, Fig. 14.10) can be used to optimize the energy production of each wind turbine. Then, as seen in Sect. 14.5.2, a MPPT strategy can be used to maximize the energy production—see Eqs. (14.44) to (14.45).

6.4 Estimation of the C p /λ Characteristic of the 6-Blade Rotor Wind Turbine

This section estimates the C p /λ characteristic of a 6-blade wind turbine. For a constant wind speed v 1m  = 3.65 m/s, pitch angle β = 0° and yaw angle α = 0°, the demanded electrical torque T gd of the generator is changed from a minimum to a maximum value (R load = 133 to 0 ohm). As a result the rotor speed Ω r and the generated power P g of the wind turbine change. Knowing the generator efficiency η g at different rotor speeds—Eq. (14.46) and Fig. 14.20a, and using Eq. (14.7) with the turbine’s parameters (r b  = 0.13 m, A r  = π r 2 b  = 0.0531 m2, ρ = 1.225 kg/m3), the C p /λ characteristic of the wind turbine is calculated according to Eq. (14.47), as shown in Fig. 14.25.

$$C_{p} = \frac{{\left( {P_{g} /\eta_{g} } \right)}}{{0.5\,\rho {\kern 1pt} {\kern 1pt} A_{r} {\kern 1pt} v_{1m}^{3} }};\quad \lambda = \frac{{\varOmega_{r} \,r_{b} }}{{v_{1m} }}$$
(14.47)

The maximum aerodynamic power coefficient is C pmax = 0.227 at an optimum tip-speed ratio λ opt = 1.224. A second order polynomial approach of the experimental data is shown in Eq. (14.48).

$$C_{p} = - 0.259\,\,\lambda^{2} + 0.640\,\,\lambda - 0.168$$
(14.48)

6.5 Power Curve for the 6-Blade Rotor Wind Turbine

After the estimation of the aerodynamic power coefficient at different tip-speed ratios for a 6-blade rotor wind turbine (C p /λ characteristic, Sect. 14.6.4) and the estimation of the generator efficiency at different rotor speeds—see Eq. (14.46) and Fig. 14.20a, this section presents the experimental power curves for the 6-blade rotor wind turbine.

The study applies the optimum MPPT control strategy presented in Eqs. (14.44) and (14.45), considering the generator losses—Eq. (14.46)- and with K a  = 8.8453 × 10−6. All the experiments maintain the pitch angle in Region 1 at β = 0°. Figure 14.26a shows the power curve (P g vs. v 1) for Regions 1, 2, and 3 (see also Fig. 14.10) of three scenarios: using a 100, 90 and 80 % of the maximum power coefficient C pmax. Figure 14.26b shows the rotor speed Ω r of the wind turbine at the operating wind speeds v 1 for the three cases.

Fig. 14.26
figure 26

Experimental characterization of a 6-blade rotor wind turbine for 100, 90 and 80 % C pmax : a Power curves; b Rotor speed versus wind speed

Full size image

The rated (nominal) power for the 6-blade wind turbine is P g_rated = 150 mWatts. For the 100 % C pmax case the rated power is achieved at a wind speed v 1_rated = 4.2 m/s with a rated rotor speed Ω r_rated = 324 rpm, the cut-in (wind turbine connection) is at v 1 = 2 m/s and Ω r  = 180 rpm, the cut-off (wind turbine disconnection) is at v 1 = 5.0 m/s and Ω r  = 324 rpm, Region 1 is between 2 m/s ≤ v 1 < 3.6 m/s, Region 2 between 3.6 m/s ≤ v 1 < 4.2 m/s, and Region 3 between 4.2 m/s ≤ v 1 < 5.0 m/s.

For the 90 % case, the rated power is achieved at a wind speed v 1_rated = 4.2 m/s with a rated rotor speed Ω r_rated = 333 rpm, the cut-in is at v 1 = 2 m/s and Ω r  = 180 rpm, the cut-off is at v 1 = 5.0 m/s and Ω r  = 333 rpm, Region 1 is between 2 m/s ≤ v 1 < 3.7 m/s, Region 2 between 3.7 m/s ≤ v 1 < 4.2 m/s, and Region 3 between 4.2 m/s ≤ v 1 < 5.0 m/s.

For the 80 % case, the rated power is achieved at a wind speed v 1_rated = 4.2 m/s with a rated rotor speed Ω r_rated = 344 rpm, the cut-in is at v 1 = 2 m/s and Ω r  = 180 rpm, the cut-off is at v 1 = 5.0 m/s and Ω r  = 344 rpm, Region 1 is between 2 m/s ≤ v 1 < 3.8 m/s, Region 2 between 3.8 m/s ≤ v 1 < 4.2 m/s, and Region 3 between 4.2 m/s ≤ v 1 < 5.0 m/s.

6.6 Wind Farm Topology Configurations and Effect on Power Efficiency

Topology configuration is critical to the efficiency and effective power generation of a wind farm system. The aerodynamic effects of each wind turbine on the wind profile around them are profound. In commercial wind farms, wind turbines are most often placed far enough apart that their effects are negligible (typically about 9 rotor diameters apart in the predominant wind direction and 5 rotor diameters apart in the perpendicular direction).

However, with an appropriate advanced controller it may be possible to place individual wind turbines closer together and compensate for the effects on the wind profile to maximize energy production in a fixed area. In order to accomplish this, these effects must first be observed and modeled. This section shows the convenience of the test bench for this analysis.

Figure 14.27 and Tables 14.3, 14.4, 14.5 shows the configuration of the wind farm for six different experiments. Each wind turbine has a 6-blade rotor, has no active controllers, a constant pitch angle β = 0, a constant yaw angle α = 0, and a constant demanded torque T gd. The geometric position of each wind turbine in the wind farm is shown in Fig. 14.27 and Table 14.3. The rotor velocity and electrical power generation is measured for each configuration. Tables 14.4 and 14.5 show the experimental results.

Fig. 14.27
figure 27

Wind farm topology configurations for different global power efficiency, with T1 , T2 , T3 , T4

Full size image
Table 14.3 Wind farm configuration: positions (cm)
Full size table
Table 14.4 Wind farm configuration: rotor speed (rpm)
Full size table
Table 14.5 Wind farm configuration: generated power (mW)
Full size table

The aerodynamic effects on the wind profile in some cases are strong enough to completely disrupt the airflow to some turbines (see zeroes in Table 14.5). The most efficient configuration is the second topology in which one turbine is placed at the front of the configuration, therefore receiving the strongest uninterrupted airflow. Interestingly, this is the most efficient, despite the fourth turbine being completely motionless.

7 Conclusions

This chapter presented a new low-cost, flexible test-bench wind farm for advanced research and education in optimum wind turbine and wind farm design, modeling, estimation, and multi-loop cooperative control. It is shown in detail the mechanical, electrical, electronic, and control system design of the wind turbines. The chapter also finds the dynamic models, estimates the parameters and model uncertainty, and designs some classical controllers. Moreover, the study presents a variety of experiments that (a) quantifies the effect of the number of blades in the aerodynamic efficiency, (b) estimates the generator efficiency, (c) validates the proposed rotor-speed pitch control system, (d) proves the concept of maximum power point tracking for individual wind turbines, (e) estimates the aerodynamic C p /λ characteristics, (f) calculates the power curve, and (g) studies the effect of wind farm topology configurations on the individual and global power efficiency. The experimental results proved that the performance dynamics of the lab test-bench corresponds very well with full-scale wind turbines. This fact makes the system appropriate for advanced research and education in wind energy systems.

8 Future Work

The wind turbine design, dynamics modeling, estimation and system identification, turbine control system, wind farm hierarchical control, and experimentation are going to be implemented as laboratory classes for undergraduate and graduate engineering courses on renewable energy and automatic control at the University. The excellent experimental results achieved with the test-bench wind farm, with a performance dynamics that corresponds well with full-scale wind turbines, will allow the students to conduct realistic hands-on experiments and understand wind energy concepts in depth. Also, the high modularity and flexibility of the wind turbines and the wind farm will facilitate to develop, implement, and validate experimentally new research ideas of all kind.