Keywords

1 Introduction

Nowadays, a significant growth of interest in Granular Computing (GrC) is regarded as a promising vehicle supporting the design, analysis and processing of information granules [1]. With regard of all processing faculties, information granules are collections of entities (elements), usually originating at the numeric level, which are arranged together due to their similarity, functional adjacency and in distinguishability or alike [1]. Given the similarity function to quantify the closeness between the samples, these data are clustered into certain granules, categories or classes [2]. The process of forming information granules is referred as information granulation.

GrC has begun to play important roles in bioinformatics, pattern recognition, security, high-performance computing and others in terms of efficiency, effectiveness, robustness as well as a structural representation of uncertainty [2]. Therefore, the need for sophisticated Intelligent Data Analysis (IDA) tools becomes highly justifiable when dealing with this type of information.

The above statement supported with the amount of data generated by social media, transactions, public and corporate entities, whose amount is scaled faster than computer resources allow (Big Data scenario). Add to that challenge, the volume of data is generated by Internet of Thing (IoT) such like smartphones, tablets, PCs or smart glasses; it becomes clear that traditional solutions of data storage and processing could hardly be applied to ingest, validate and analyze these volumes of data [3].

Accordingly, the developed method discussed here exhibits sound performance as far as computing time and an overall computation complexity are concerned. Fuzzy C-Means (FCM) clustering algorithm, introduced by Dunn in 1973 [4] and generalized by Bezdek in 1981, becomes one of the commonly used techniques of GrC when it comes to the formation of information granules [5, 6]. There has been a great deal of improvements and extensions of this clustering technique. One can refer here to the genetically-guided clustering algorithm called Genetic Algorithm-FCM (GA-FCM) and proposed by Hall et al. [4]. It has been shown that the GA-FCM algorithm can successfully alleviate the difficulties of choosing a suitable initialization of the FCM method. On the other hand, Ramli et al. proposed a real-time fuzzy regression model incorporating a convex hull method, specifically a Beneath-Beyond algorithm [7]. They have deployed a convex hull approach useful in the realization of data analysis in a dynamic data environment.

Associated with these two highlighted models (fuzzy regression and fuzzy clustering), the main objective of this study is to propose an enhancement of the fuzzy regression analysis for the purpose of analysis of information granules. From the IDA perspective, this research intends to augment the model that Bezdek given originally proposed by including the Ramli et al.’s approach. It will be shown that such a hybrid combination is capable of supporting real-time granular based fuzzy regression analysis.

In general, the proposed approach helps perform real time fuzzy regression analysis realized in presence of information granules. The proposed approach comprises four main phases. First, the use of GA-FCM clustering algorithm granulates the entire data set into a limited number of chunks-information granules. The second phase consists of constructing sub-convex hull polygons for the already formed information granules. Therefore, the number of constructed convex hulls should be similar to the number of identified information granules. Next, main convex hull is constructed by considering all sub convex hulls. Moreover, the main convex hull will utilize the outside vertices which were selected from the constructed sub-convex hulls. Finally, in the last phase, the selected vertices of the main constructed convex hull, which covers all sub-convex hull (or identified in-formation granules), are used to build a fuzzy regressions model. To illustrate the efficiency and effectiveness of the proposed method, a numeric example is presented.

This chapter is structured as follows. Section 2 serves as a concise and focused review of the fundamental principles of real-time data analysis, GrC as well as GA-FCM. Furthermore, this section also highlighted a review on convex hull approach; affine, supporting hyperplane as well as Beneath-Beyond algorithm. Additionally, some essentials of fuzzy linear regression augmented by the convex hull approach have been discussed. Section 3 discusses a processing flow of the proposed approach yielding real time granular based fuzzy regression models. Section 4 is devoted to a numerical experiment. Finally, Sect. 5 presents some concluding remarks.

2 Some Related Studies

Through this section, several fundamental issues to be used throughout the study are investigated.

2.1 Recall of Real-Time Data Analysis Processing

Essentially, real-time data analysis refers to studies where data revisions (updates, successive data accumulation) or data release timing is important to a significant degree. The most important properties of real-time data analysis are dynamic analysis and reporting, based on data entered into a system in a short interval before the actual time of the usage of the results [8].

An important notion in real-time systems is event, that is, any occurrence that results in a change in the sequential flow of program execution. Related to this situation, the time between the presentation of a set of inputs and the appearance of all the associated outputs (results) is called the response time [9, 10]. In addition, the shortest response time is an important design requirement.

2.2 Brief Review on Granular Information

Granular Computing (GrC) is a general computing paradigm that effectively deals with designing and processing information granules. The underlying formalism relies on a way in which information granules are represented; here it may consider set theory, fuzzy sets, rough sets, to name a few of the available alternatives [1]. In addition, GrC focuses on a paradigm of representing and processing information in a multiple level architecture. Furthermore, GrC can be viewed as a structured combination of algorithmic and non-algorithmic aspects of information processing [5].

Generally, GrC is a twofold process and includes granulation and computation, where the former transforms the problem domain to the one with granules, whereas the latter processes these granules to solve the problem [11]. Granulation of information is an intuitively appealing concept and appears almost everywhere under different names, such as chucking, clustering, partitioning, division or decomposition [12]. Moreover, the process of granulation and the nature of information granules imply certain formalism that seems to be the most suited to capture the problem at hand. Therefore, to deal with the high computational cost which might be caused by a huge size of information granule patterns, it was noted that FCM algorithm which is one of commonly selected approaches to data clustering implementation procedure.

In general, the problem of clustering is that of finding a partition that captures the similarity among data objects by grouping them accordingly in the partition (or cluster). Data objects within a group or cluster should be similar; data objects coming from different groups should be dissimilar. In this context, FCM arises as a way of formation of information granules represented by fuzzy sets [5]. Clustering approach as well as the FCM clustering algorithm have been discussed in this section.

Clustering is a process of grouping a data set in a way that the similarity between data within same cluster is maximized while the similarity of data between different clusters is minimized [13]. It classifies a set of observations into two or more mutually exclusive unknown groups based on combinations of many variables. Its aim is to construct groups in such a way that the profiles of objects in the same groups are relatively homogeneous whereas the profiles of objects in different groups are relatively heterogeneous [13].

FCM is a method of clustering which allows any data to belong to two or more clusters with some degrees of membership. Initially, consider a data set composed of n vectors \( X = \{ x_{1} ,x_{2} , \ldots ,x_{n} \} \) to be clustered into c clusters or groups. Each of \( x_{k} \in \Re^{K} ,k = 1,2, \ldots ,n \) is a feature vector consisting of K real-valued measurements describing the features of the objects. A fuzzy c-partition of the given data set is the fuzzy partition matric \( U = [\mu_{ik} ],i = 1,2, \ldots ,c \) and \( k = 1,2, \ldots ,n \) such that

$$ \begin{array}{*{20}l} {0 \le \mu_{ik} \le 1,} \hfill & {for} \; {1 \le i \le c,1 \le k \le n} \hfill \\ {0 \le \sum\limits_{k = 1}^{n} \mu_{ik} \le n,} \hfill & {for} \; {1 \le i \le c} \hfill \\ {\sum\limits_{i = 1}^{c} \mu_{ik} = 1,} \hfill & {for} \; {1 \le k \le n} \hfill \\ \end{array} $$
(1)

where \( \mu_{ik} \) is the membership of feature vector \( x_{k} \) to cluster \( c_{i} \). Furthermore, fuzzy cluster of the objects can be represented by a membership matrix called fuzzy partition. The set of all \( c \times n \) non-degenerate constrained fuzzy partition matrices denoted by \( M_{fcn} \) which is defined as

$$ \begin{array}{*{20}l} {M_{fcn} = \left\{ {U \in \Re^{c \times n} \left| {\sum\limits_{i = 1}^{c} = 1,0 < \sum\limits_{k = 1}^{n} U_{ik} < n,U_{ik} \in [0,1]} \right.;1 \le i \le c;1 \le k \le n} \right\}.} \hfill \\ \end{array} $$
(2)

Moreover, the FCM algorithm minimizes the following objective function

$$ J_{m} \left( {U,V} \right) = \sum\limits_{i = 1}^{c} \sum\limits_{k = 1}^{n} \left( {\mu_{ik} } \right)^{m} D_{ik}^{2} \left( {\varvec{v}_{i} ,\varvec{x}_{k} } \right) $$
(3)

where \( U \in M_{fcn} \) is a fuzzy partition matrix, \( V = (\varvec{v}_{1} ,\varvec{v}_{2} , \ldots ,\varvec{v}_{c} ) \) is a collection of cluster centers (prototypes). \( \varvec{v}_{i} \in \Re^{K} \forall i \) and \( D_{ik} (\varvec{v}_{i} ,\varvec{x}_{k} ) \) is a distance between \( \varvec{x}_{k} \) and the ith prototype while m is a fuzzification coefficient, \( m > 1 \).

The FCM optimizes (3) by iteratively updating the prototypes and the partition matrix. More specifically, some values of c, m and \( \varepsilon \) (termination condition—a small positive constant) have been chosen, then generate a random fuzzy partition matrix \( U^{0} \) and set an iteration index to zero, \( t = 0 \). An iterative process is organized as follows. Given the membership value \( \mu_{ik}^{(t)} \), the cluster centers \( \varvec{v}_{i}^{(t)} (i = 1, \ldots ,c) \) are calculated by

$$ \varvec{v}_{i}^{(t)} = \frac{{\sum\nolimits_{k = 1}^{n} \left( {\mu_{ik}^{(t)} } \right)^{m} \varvec{x}_{k} }}{{\sum\nolimits_{k = 1}^{n} \left( {\mu_{ik}^{(t)} } \right)^{m} }} $$
(4)

Given the new cluster centers \( \varvec{v}_{i}^{(t)} \) the membership values of the partition matrix \( \mu_{ik}^{(t)} \) are updated as

$$ \mu_{ik}^{t + 1} = \left[ {\sum\limits_{j = 1}^{c} \left( {\frac{{\left\| {\varvec{x}_{k} - \varvec{v}_{i}^{(t)} } \right\|}}{{\left\| {\varvec{x}_{k} - \varvec{v}_{j}^{(t)} } \right\|}}} \right)^{{\frac{2}{m - 1}}} } \right]^{ - 1} $$
(5)

This process terminates when \( |U^{(t + 1)} - U^{(t)} | \le \varepsilon \), or some predefined number of iterations has been reached [14]. In the following sub section, an enhancement of the FCM algorithm called GA-FCM is investigated.

2.3 Genetically-Guided Clustering Algorithm

There are several studies employed genetic algorithm based clustering technique in order to solve various types of problems [15–18]. More specifically, GA technique to determine the prototypes of the clusters located in the Euclidean space \( \Re^{K} \) has been exploited. At each generation, a new set of prototypes is created through the process of selecting individuals according to their level of fitness. In the sequel they are affected by running genetic operators [16, 18]. This process leads to the evolution of population of individuals that become more suitable given the corresponding values of the fitness function.

There are a number of research studies that have been completed which utilizing the advantages of GA-enhanced FCM. Genetically guided clustering algorithm proposed by Hall et al. was focused here. Based on [4], in any generation, element \( i \) of the population is \( V_{i} \), a \( c \times s \) matrix of cluster centers (prototypes). The initial population of size \( P \) is constructed by a random assignment of real numbers to each of the \( s \) features of the \( c \) centers of the clusters. The initial values are constrained to be in the range (determined from the data set) of the feature to which they are assigned.

In addition, as \( V \)’s will be used within the GA, it is necessary to reformulate the objective function for FCM for optimization purposes. Expression (3) can be expressed in terms of distances from the prototypes (as done in the FCM method). Specifically, for \( m > 1 \) as long as \( D_{jk} (\varvec{v}_{j} ,\varvec{x}_{k} ) > 0\,\forall \, j,k \), it have

$$ \mu_{ik} = {1 \mathord{\left/ {\vphantom {1 {\sum\limits_{j = 1}^{c} \left( {\frac{{D_{ik} (\varvec{v}_{i} ,\varvec{x}_{k} )}}{{D_{jk} (\varvec{v}_{j} ,\varvec{x}_{k} )}}} \right)^{{\frac{2}{m - 1}}} }}} \right. \kern-0pt} {\sum\nolimits_{j = 1}^{c} \left( {\frac{{D_{ik} (\varvec{v}_{i} ,\varvec{x}_{k} )}}{{D_{jk} (\varvec{v}_{j} ,\varvec{x}_{k} )}}} \right)^{{\frac{2}{m - 1}}} }}\quad for\quad 1 \le i \le c;1 \le k \le n. $$
(6)

Now, Eq. (6) was substituted into Eq. (2). This gives rise to the FCM functional reformulated as follows

$$ R_{m} (V) = \sum\limits_{k = 1}^{n} \left( {\sum\limits_{i = 1}^{c} D_{ik}^{1/(1 - m)} } \right)^{1 - m} . $$
(7)

which is concentrated on optimizing \( R_{m} \) with a genetically-guided algorithm (GGA) technique [4]. Additionally, Hathaway and Bezdek (1995) highlighted that have shown that local \( (V) \) minimizers of \( R_{m} \) and also \( (U) \) at expression (3) will produces local minimizers of \( J_{m} \) and, on the other hands, the \( V \) part of local minimizers of \( J_{m} \) acquiesce local minimizers of \( R_{m} \) [4].

Furthermore, there are a number of genetic operators, which relate to the GA-based clustering algorithm including Selection which consist of selecting parents for reproduction, performing Crossover with the parents and applying Mutation to the bits of the children [4]. Binary gray code representations where any two adjacent numbers are one bit different has been selected on this genetically-guided algorithm (GGA) approach and this encoding able to yields faster convergence and improve performance over a straightforward binary encoding [4].

The complete process of the GGA [4] is outlined as follows.

  1. GGA1:

    Choose \( m \), c, and \( D_{ik} \).

  2. GGA2:

    Randomly initialize P sets of c cluster centers. Confine the initial values within the space defined by the data to be clustered.

  3. GGA3:

    Calculate \( R_{m} \) by using (7) for each population member and apply modified objective function \( R_{m}^{\prime} (V) = R_{m} (V) + b \times R_{m} (V) \) where \( b \in [0,c] \) is the number of empty clusters.

  4. GGA4:

    Convert population members to binary equivalents (using the Gray code).

  5. GGA5:

    For i = 1 to number of generations, Do

    1. (i)

      Used k-fold tournament selection (default k = 1) to select P/2 parent pairs for reproduction.

    2. (ii)

      Complete a two-point crossover and bitwise mutation for each feature of the parent pairs.

    3. (iii)

      Calculate R m by using (7) for each population member and apply modified objective function \( R_{m}^{\prime} (V) = R_{m} (V) + b \times R_{m} (V) \) where b ∈ [0, c] is the number of empty clusters.

    4. (iv)

      Create a new generation of size P, which is selected from the two best members of the previous generation and the best children that are generated by using crossover and mutation.

  6. GGA6:

    Provide the cluster centers to the terminal population with the smallest \( R_{m}^{\prime} \) value and report \( R_{m}^{\prime} \).

2.4 A Brief Review of a Convex Hull Approach

The convex hull is the fundamental construct of mathematics and computational geometry. It is useful as a building block for a plethora of applications including collision detection in video games, visual pattern matching, mapping and path determination [19]. In what follows, a detailed description of this approach was presented.

2.4.1 Affine, Convex Hull Definition and Supporting Hyperplane

The affine hull of set S in Euclidean space \( \Re^{K} \) is the smallest affine set contained in S, or equivalently the intersection of all the affine sets containing S. Here, an affine set is defined as the translation of a vector subspace. The affine hull \( aff(S) \) of S is the set of all the affine combinations of elements of S, namely

$$ {aff(S) = \left\{ {\sum\limits_{j = 1}^{K} \alpha_{j} x_{j} \left| {x_{j} \in S,\alpha_{j} = \Re ,} \right.\alpha_{j} \ge 0,\sum\limits_{j = 1}^{K} \alpha_{j} = 1} \right\}.} $$
(8)

The convex hull of set S of points \( hull(S) \) is defined to be a minimal convex set containing S. A point \( P \in S \) is an extreme point of S if \( \notin hull(S - P) \). In general, if S is finite, then \( hull(S) \) is a convex polygon, and the extreme points of S are the corners of this polygon. The edges of this polygon are referred to as the edges of the \( hull(S) \).

A supporting hyperplane is a another geometric concept. A hyperplane divides a space into two half-spaces. A hyperplane is said to support a set S in Euclidean space \( \Re^{K} \) if it meets the following conditions:

  • S is entirely contained in one of the two closed half-spaces of the hyperplane, and

  • S has at least one point on the hyperplane.

In addition, if the dimension of the supporting line is higher than three, the related relationship can be written down as

$$ S = \left( {x \in \Re^{K} \left| {\sum\limits_{j = 1}^{K} \alpha_{j} x_{j} = b} \right.} \right) $$
(9)

where \( \varvec{\alpha}= [\alpha_{1} , \ldots ,\alpha_{K} ] \) denotes a unit vector, \( {\mathbf{x}} = [x_{1} , \ldots ,x_{K} ] \) is an arbitrary point and b assumes any arbitrary real value.

$$ S^{ + } = \left( {x \in \Re^{K} \left| {\sum\limits_{j = 1}^{K} \alpha_{j} x_{j} \ge b} \right.} \right) $$
(10)
$$ S^{ - } = \left( {x \in \Re^{K} \left| {\sum\limits_{j = 1}^{K} \alpha_{j} x_{j} \le b} \right.} \right) $$
(11)

In case when the following conditions are satisfied

$$ S\bigcap P \ne \phi \quad {\text{and}}\quad P \subset S^{ + } \quad {\text{or}}\quad P \subset S^{ - } , $$
(12)

it say that the supporting hyperplane S supports set P.

Using this definition, the reformulation of a convex hull called \( conv(P) \), can be expressed as follows:

$$ conv(P) = \bigcap\limits_{{S^{ + } :uppersupportinghyperplane}} S^{ + } $$
(13)
$$ conv(P) = \bigcap\limits_{{S^{ - } :lowersupportinghyperplane}} S^{ - } $$
(14)

2.4.2 Beneath-Beyond Algorithm

This algorithm incrementally builds up the convex hull by keeping track of the current convex hull, P i using an incidence graph. The Beneath-Beyond algorithm consists of the following steps [20]:

  1. Step 1:

    Select and sort points along one direction, say \( x_{1} \). Let \( s = P_{0} ,P_{1} , \ldots ,P_{n - 1} \) be input points after sorting. Process the points in an increasing order.

  2. Step 2:

    Take the first n points, which define a facet as the initial hull.

  3. Step 3:

    Let P i be the point to be added to the hull at the ith stage. Let \( P_{i} = conv(P_{0} ,P_{1} , \ldots ,P_{i - 1} ) \) be the convex hull polytope built so far. This step includes two kinds of hull updates:

    1. (a)

      A pyramidal update is done when \( P_{i} \notin aff(P_{0} ,P_{1} , \ldots ,P_{i - 1} ) \)—when \( P_{i} \) is not on the hyperplane defined by the current hull. A pyramidal update consists of adding a new node representing \( P_{i} \) to the incidence graph and connecting this node to all existing hull vertices by new edges.

    2. (b)

      A non-pyramidal update is done when the above condition is not met, i.e. \( P_{i} \) is in the affine subspace defined by the current convex hull. In this case, faces that are visible from \( P_{i} \) are removed and new facets are created.

2.5 A Convex Hull-Based Regression

In regression, deviations between observed and estimated values are assumed to be due to the random errors. Regression analysis is one of commonly encountered approaches in describing relationships among the analyzed data. The regression models explain dependencies between independent and dependent variables. The variables, which are used to explain the other variable(s) are called explanatory ones [21, 22].

Although conventional regression has been applied to various applications, problems may arise when they were encountered vague relationships between input and output variables in which cases there assumptions made for regression models are not valid any longer. This situation becomes a major reason behind a lack of relevance of regression models [23].

Recall that a standard numeric linear regression model comes in the following form:

$$ Y = A_{0} + A_{1} x_{1} + \cdots + A_{K} x_{K} . $$
(15)

As an interesting and useful extension, Tanaka et al. introduced an enhancement of the regression model by accommodating fuzzy sets thus giving rise to the term of fuzzy regression or possibilistic regression [24]. The models of this category reflect the fuzzy set based nature of relationships between the dependent and independent variables. The upper and lower regression boundaries in the fuzzy regression are used to quantify the fuzzy distribution of the output values.

As an alternative to the fuzzy specification, an inexact relationship among those dependent and independent variables can be represented via fuzzy linear regression expressed in the following form:

$$ \tilde{Y} = \tilde{A}_{0} x_{0} + \tilde{A}_{1} x_{1} + \cdots + \tilde{A}_{K} x_{K} = {\tilde{\mathbf{A}}}\varvec{x}^{t} $$
(16)

where \( {\mathbf{x}} = [x_{0} ,x_{1} , \ldots ,x_{K} ] \) is a vector of independent variables with \( x_{0} = 1;\,{\tilde{\mathbf{A}}} = [\tilde{A}_{0} ,\tilde{A}_{1} , \ldots ,\tilde{A}_{K} ] \) is a vector of fuzzy coefficients represented in the form of symmetric triangular fuzzy numbers and denoted by \( \tilde{A}_{j} = (\alpha_{j} ,c_{j} ) \) with membership function described as follows:

$$ u_{{\tilde{A}}} (a_{j} ) = \left\{ {\begin{array}{*{20}l} {1 - \frac{{|\alpha_{j} - a_{j} |}}{{c_{j} }},} \hfill & {c_{j} \ne 0,\alpha_{j} - c_{j} \le a_{j} \le \alpha_{j} + c_{j} ,} \hfill \\ {1,} \hfill & {c_{j} = 0,\alpha_{j} = a_{j} ,} \hfill \\ {0,} \hfill & {otherwise,} \hfill \\ \end{array} } \right. $$
(17)

where \( \alpha_{j} \) and \( c_{j} \) are the central value and the spread of the triangular fuzzy number, respectively.

From the computational perspective, the estimation of the membership functions of the fuzzy parameters of the regression is associated with a certain problem of Linear Programming (LP) [21].

Given the notation used above, Eq. (16) can be rewritten as follows

$$ \tilde{Y}_{i} = (\alpha_{0} ,c_{0} ) + (\alpha_{1} ,c_{1} )x_{1} + (\alpha_{2} ,c_{2} )x_{2} + \cdots + (\alpha_{K} ,c_{K} )x_{K} . $$
(18)

where \( \alpha_{j} \) and \( c_{j} (j = 1,2, \ldots ,K) \) are the center and the spread of the predicted interval of \( \tilde{A}_{j} \), respectively.

The weakness of the implementation of the multidimensional fuzzy linear regression can be alleviated by incorporating the convex hull approach [7, 25].

In the introduced modification, the construction of vertices of the convex hull becomes realized in real-time by using related points (convex points) of the graph. Furthermore, Ramli et al. stated that the real-time implementation of the method has to deal with a large number of samples (data). Therefore, each particular analyzed sample stands for a convex point and is possibly selected as a convex hull vertex. Some edges connecting the vertices need to be re-constructed as well [26].

Let us recall that the main purpose of fuzzy linear regression is to form the upper and lower bounds of the linear regression model. Both the upper line \( Y^{U} \) and lower line \( Y^{L} \) of the fuzzy linear regression are expressed in the form:

$$ {Y^{U} = \left\{ {A_{0} + A_{1} x_{1} + \cdots + A_{K} x_{K} } \right\}^{U} :\left\{ {\varvec{Ax}_{i}^{t} } \right\}^{U} = \varvec{\alpha x}_{i}^{t} + \varvec{c}\left| {\varvec{x}_{i}^{t} } \right|} $$
(19)
$$ {Y^{L} = \{ A_{0} + A_{1} x_{1} + \cdots + A_{K} x_{K} \}^{L} :\{ \varvec{Ax}_{i}^{t} \}^{L} = \varvec{\alpha x}_{i}^{t} - \varvec{c}|\varvec{x}_{i}^{t} |} $$
(20)

By using Eqs. (19) and (20), the problem was converted to a general fuzzy regression that is similar to the one shown below:

  1. 1.

    Evaluation (objective) function

$$ \mathop {\hbox{min} }\limits_{{\varvec{\alpha},{\mathbf{c}}}} \sum\limits_{i = 1}^{n} \sum\limits_{j = 2}^{K} c_{j} |P_{ij} |. $$
(21)
  1. 2.

    Constraints

$$ P_{i1} \in Y_{i} \Leftrightarrow \left\{ {\begin{array}{*{20}l} {P_{i1} \le \alpha_{0} + c_{0} + \sum\limits_{j = 2}^{K} \alpha_{j} P_{ij} + \sum\limits_{j = 2}^{K} c_{j} |P_{ij} |} \\ {P_{i1} \ge \alpha_{0} - c_{0} + \sum\limits_{j = 2}^{K} \alpha_{j} P_{ij} - \sum\limits_{j = 2}^{K} c_{j} |P_{ij} |} \\ {\quad (i = 1, \ldots ,n).} \\ \end{array} } \right. $$
(22)

The above expression can be further rewritten as follows:

$$ \begin{aligned} Y^{U} & = \{ Y_{i}^{U} \left| {i = 1, \ldots ,n} \right.\} \\ Y^{L} & = \{ Y_{i}^{L} \left| {i = 1, \ldots ,n} \right.\} \\ \end{aligned} $$
(23)

Here also arrive at the following simple relations for \( P_{i1} \)

$$ P_{i1} \le Y_{i}^{U} ,\quad P_{i1} \ge Y_{i}^{L} \quad (i = 1, \ldots ,n) $$
(24)

It is well known that any discrete topology is a topology which is formed by a collection of subsets of a topological space \( \chi \) and the discrete metric \( \rho \) on \( \chi \) is defined as

$$ \rho (x,y)\begin{array}{*{20}l} 1 \hfill & {if\;x \ne y} \hfill \\ 0 \hfill & {if\;x = y} \hfill \\ \end{array} $$
(25)

for any \( x,y \in X \). In this case, \( (X,\rho ) \) is called a discrete metric space or a space of isolated points. According to the definition of discrete topology, expression (24) is rewritten as follows:

$$ \begin{aligned} S(Y^{U} ) & = \sum\limits_{j = 1}^{K} \{ Y_{j} P_{ij} \}^{U} \ge 0 \\ S(Y^{L} ) & = \sum\limits_{j = 1}^{K} \{ Y_{j} P_{ij} \}^{L} \le 0 \\ \end{aligned} $$
(26)

where assume that \( P_{i1} = 1 \).

This formula corresponds with the definition of the support hyperplane. Under the consideration of the range of

$$ S\bigcap P \ne \phi \quad {\text{and}}\quad P \subset S^{ + } \quad {\text{or}}\quad P \subset S^{ - } , $$
(27)

the following relationship is valid:

$$ \bigcap S(Y^{U} ) = \bigcap S(Y^{L} ). $$
(28)

This is explained by the fact that regression formula \( Y^{U} \) and \( Y^{L} \) are formed by vertices of a convex hull. Therefore, it is apparent that the constructed convex hull polygon or more specifically, its vertices clearly define the discussed constraints of fuzzy mathematical programming, becomes more reliable as well as significant for the subsequent processes.

Recall that the convex hull of a set S of points while \( hull(S) \) is defined to be a minimum convex set containing S. A point \( P \in S \) is an extreme point of S if \( P \notin hull(S - P) \). Hence P denotes the set of points (input samples) and P C is the set of vertices of the convex hull where \( P_{C} \in P \). Therefore, the convex hull has to satisfy the following relationship:

$$ conv(P) = conv(P_{C} ) $$
(29)

Introduce here the following set

$$ P_{C} = \{ x_{Cl} \in \Re^{K} \left| {l = 1, \ldots ,m} \right.\} \subseteq P $$
(30)

where m is the number of vertices of the convex hull. Plugging this relationship into (22), at the following constraints was arrived.

$$ P_{i1} \in Y_{i} \Leftrightarrow \left\{ {\begin{array}{*{20}l} {P_{i1} \le \alpha_{0} + c_{0} + \sum\limits_{j = 2}^{K} \alpha_{j} P_{ij} + \sum\limits_{j = 2}^{K} c_{j} |P_{ij} |} \\ {P_{i1} \ge \alpha_{0} - c_{0} + \sum\limits_{j = 2}^{K} \alpha_{j} P_{ij} - \sum\limits_{j = 2}^{K} c_{j} |P_{ij} |} \\ {\quad (i = 1, \ldots ,m).} \\ \end{array} } \right. $$
(31)

In virtue of Eq. (31), the constraints of the LP of the fuzzy linear regression can be written in the following manner:

$$ y_{i} \in Y_{i} \Leftrightarrow \left\{ {\begin{array}{*{20}l} {y_{i} \le \alpha \varvec{x}_{i}^{t} + \varvec{c}|\varvec{x}_{i}^{t} |} \\ {y_{i} \ge \alpha \varvec{x}_{i}^{t} - \varvec{c}|\varvec{x}_{i}^{t} |} \\ {\quad (i = 1, \ldots ,m).} \\ \end{array} } \right . $$
(32)

Moreover, in order to form a suitable regression model based on the constructed convex hull, the connected vertex points are used as the constraints in the LP formulation of the fuzzy linear regression. Considering this process, the use of the limited number of selected vertices contributes to the minimized computing complexity associated with the model [1].

3 A Real-Time Granular Based Fuzzy Regression Models with a Convex Hull Implementation

In general, there are four major components of this proposed approach includes genetically-guided clustering, sub-convex hull construction process, main convex hull construction process and fuzzy regression solution. The description of related components is shown in Table 1.

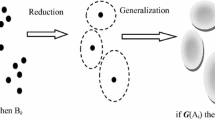
Table 1 A description of the main components of the proposed approach
Full size table

Furthermore, Fig. 1 shows the synopsis of the entire processes where there are examples of four clustered sample of data (clustered feature vectors). In addition, this clustered feature vectors were representing information granules. Sub-convex hull were built for each of clustered feature vectors and based on Fig. 1, constructed of sub-convex hulls are clearly defined. Consequently, highlighted also a main convex hull which was constructed depending on initially build of sub-convex hulls. Therefore, this solution will covers entire clustered samples of data or in other words, this proposed approach might consider for producing optimum regression results.

Fig. 1
figure 1

An illustration of constructed sub-clusters and a main cluster

Full size image

In order to make clearly understand of the proposed approach, the flow of the overall processing is presented, see Fig. 2. Some selected samples of granular data were load into the system. Then, GA-FCM is used for assigning relevance number of granules. Additionally, GA-FCM has been selected in this process because the ability to clearly define as well as separate the raw samples into associated granule. Even though GA-FCM could be required some additional processing time comparing with conventional FCM, the accurate result of produced classes are achievable.

Fig. 2
figure 2

A general flow of processing

Full size image

The following process involving convex hull construction where Beneath-Beyond algorithm has been selected here. During this process, the outer points of each constructed granule is completely identified. The selected outer points were connected each other for producing particular edges. The combination of connected edges will produce a convex hull polygon. In this situation, the produced convex hull categorized as sub-convex hull. Furthermore, these sub-processes will be iterated until desired point of data are classified under appropriate information granules.

The next sub-process is focusing on construction of main convex hull. This task will concentrate on finding the outer points which representing vertices of constructed sub-convex hulls by taking account of whole constructed sub-convex hull as once.

In the end, the final step consists of finding an optimal fuzzy regression model with utilization of main convex hull points or vertices. At this point, an optimal fuzzy regression models will be produced and process will be also terminated if the final group of data samples is fully arrived into the proposed approach and completely processed.

As a summarization of this part, some iterations of the overall procedure considering that more data become available in the future being completed. Say, new samples are provided within a certain time interval, e.g., they could be arrived every 10 s. Related to the comments made above, it becomes apparent that the quality of granular based fuzzy regression model can be improved by the hybrid combination of GA-FCM algorithm with convex hull-based fuzzy regression approach. The quality refers to the computing time as well as the overall computational complexity.

All in all, it do not have to consider the complete feature vectors for building regression models; just utilize the selected vertices, which are used for the construction of the convex hull. As mentioned earlier, these selected vertices come from a sub-convex hull, which represents appropriate information granules..

Therefore, this situation will lead to the decrease of the computation load. On the other hand, related to the computational complexity factor for the subsequent iteration, it will only consider the newly added samples of data together with the selected vertices of the previous convex hull (main constructed convex hull polygon). For that reason, this computing scenario will reduce the computational complexity because of the lower number of the feature vectors used in the subsequent processing of regression models.

4 A Numerical Example and Performance Analysis

A simple numerical example presented here, quantifies the efficiency of the proposed approach in the implementation of real-time granular based fuzzy regression.

As a guidance of this simulation example, Fig. 3 shows an illustration of a real-time reconstruction of a fuzzy classification analysis that involves a dynamic record/database. For instance, each of the iterations may have had the same amount of newly arrived data. As mentioned earlier, the amount of data increased as time progressed. Note that the initial group of samples was taken as the input for the first iteration process. It can see here the increase in the volume of data with the real-time arrival of new data.

Fig. 3
figure 3

An illustration of an increasing record/database along with time consumption

Full size image

Before going further into this precious section, affirmed here that, computer specification which has been used to perform the whole processes. The specifications of machine are; a personal notebook PC with Intel(R) Pentium CORE(TM) Duo 2 CPU (2.00 GHz) processors combined with 2 GB DDR2 type of RAM. Moreover, Windows Vista Business Edition (32 bit) was an operating system installed into this machine.

Based on Fig. 3, assume that an initial group of samples consists of 100 data of the well-known Iris data set [27]. Considering a distribution of these data, constructed sub-convex hull polygons, which become the boundary of each identified cluster (or information granule) were successfully completed, see Fig. 4.

Fig. 4
figure 4

Obtained clusters and constructed sub convex hulls for initial samples of data

Full size image

Referring to the figure highlighted (Fig. 4), there are 3 constructed sub-convex hulls called cl1, cl2 and cl3. Table 2 covers the details of all clusters.

Table 2 Details of the obtained cluster along with the number of selected vertices for initial group of data samples
Full size table

Next, a main convex hull which covers those sub-convex hulls has been constructed and among 22 of total selected clustered feature vectors (or loci points) as stated in Table 2, only 11 points were selected as convex hull vertices, see Fig. 5. In addition, these selected vertices are located as the outside points of the constructed clusters. By solving the associated LP problem that considered these selected vertices as a part of the constraint portion standing in the problem, we obtained the optimal regression coefficients, see below. In addition, h = 0.05 has been selected to express goodness of fit or compatibility of data and the regression model

$$ y = (2.071,0.163) + (0.612,0.096)C1 + (0.639,0.075)C2 - (0.412,0.000)C3 $$

where

C1:

input variable for Sepal Length,

C2:

input variable for Sepal Width, and

C3:

input variable for Petal Length,

with

  • Constant value = 2.071, spread = 0.163,

  • Coefficient of Sepal Length = 0.612, spread = 0.096,

  • Coefficient of Sepal Width = 0.639, spread = 0.075, and

  • Coefficient of Petal Length = 0.412, spread = 0.000.

Fig. 5
figure 5

Constructed of main convex hulls for initial samples of data

Full size image

To deal with a real-time scenario, a group of samples taken from the same data set, which consists of 50 patterns has been added into previously selected patterns. In this case, assume that an iteration process has been completed. Table 3 shows the details of each sub-convex hull for initial group together with newly added data samples and Fig. 6 illustrate this related outcome.

Table 3 Detailed description of the clusters and the number of selected vertices for initial group together with newly added data samples
Full size table
Fig. 6
figure 6

Obtained clusters and constructed sub convex hulls for initial together with the newly added samples of data

Full size image

The total number of selected vertices for this newly data volume is 26 and out of them, the main constructed convex hull only used 10 vertices, refer to Table 3. Finally, the obtained fuzzy regression model comes in the form;

$$ y = (1.855,0.173) + (0.651,0.102)C1 + (0.709,0.095)C2 - (0.556,0.000)C3 $$

where

C1:

input variable for Sepal Length,

C2:

input variable for Sepal Width, and

C3:

input variable for Petal Length,

with

  • Constant value = 1.855, spread = 0.173,

  • Coefficient of Sepal Length = 0.651, spread = 0.102,

  • Coefficient of Sepal Width = 0.7099, spread = 0.095, and

  • Coefficient of Petal Length = 0.556, spread = 0.000,

  • while Fig. 7 shows the clustered feature vectors.

    Fig. 7
    figure 7

    Construction of main convex hulls for initial configuration together with newly added samples of data

    Full size image

As early stated in the initial part of this research, one of main contribution towards this research is related with processing time factor. Consequently, the details of recoded time-length can be found in Table 4. In addition, this table also shows some related time instance which purposely for producing appropriate fuzzy regression models for identified information granules base on several conventional approaches. In this situation, the same samples of data were used while FCM as well as GA-FCM (both purposely for obtaining information granules class) together with conventional regression approach have been implemented accordingly.

Table 4 Granules-based fuzzy regression performance: details
Full size table

It can see here, time-length recorded for initial samples of data (first cycle) is only 00.28 s and for the second following cycle is only needs 00.09 s additional time-length which becomes 00.37 s in total. Comparing with both combination of FCM with conventional fuzzy regression as well as GA-FCM with conventional fuzzy regression, notice that, the proposed approach looks more significant especially in term of time consumption. In addition, both of these combinations approach are likely not too much different particularly related to the time expenditure point of view and it can be realized here, that although some number of data samples are added together with initial group of data samples, the overall time consumption as well as computational complexity can be extremely decreased.

As previously discussed in the early portion of this section, the proposed approach can shorten overall time length due to the reused of produced sub as well as main convex hull polygon. Shown here also, deployment of FCM and GA-FCM with conventional regression approach, as tabled results, both of these combination have to consider all analyzed data for the first cycle and reconsider them again plus with newly arrived data for the second cycle, see Table 4. This situation requires additional time-length and computational complexity might be increased.

On the other hand, focusing to the accuracy factor of the produced regression models employing the proposed approach, noticed that those constructed models are likely similar comparing with the models which was generated through utilization of both FCM as well as GA-FCM classification approach combined with conventional regression approach. Additionally, the differences range of desire constant, coefficient and spread values are between 0.006. Therefore, it can be concluded that, the precision level of obtained fuzzy regression models with the use of the proposed approach is greatly accepted.

In summary, it can be highlighted here that, the proposed of granular-based fuzzy regression reaches the best performance for real-time data processing.

5 Conclusion and Future Works

In this chapter, an enhancement of the IDA tool of fuzzy regression completed in the presence of information granules have been proposed. Generally, the proposed approach first constructs a limited number of information granules and afterwards the resulting granules are processed by running the convex hull-based regression [6]. In this way, it have realized a new idea of real-time granular based fuzzy regression models being viewed as a modeling alternative to deal with real-world regression problems.

It is shown that information granules are formed as a result of running the genetic version of the FCM called GA-FCM algorithm [3]. Basically, there are two parts of related process, which utilize the convex hull approach or specifically Beneath-Beyond algorithm; constructing sub-convex hull for each identified clusters (or information granules) and building a main convex hull polygon which covers all constructed sub-convex hulls. In other word, the main convex hull is completed depending upon the outer plots of the constructed clusters (or information granules). Additionally, the sequential flow of processing was carried out to deal with dynamically increasing size of the data.

Based on the experimental developments, one could note that, this approach becomes a suitable design alternative especially when solving real-time fuzzy regression problems with information granules. It works efficiently for real-time data analysis given the reduced processing time as well as the associated computational complexity.

This proposed approach can be applied to real-time fuzzy regression problems in large-scale systems present in real-world scenario especially involving granular computing situation. In addition, each of the implemented phases, especially GA-FCM process and both sub and main convex hull construction processes have their own features in facing with dynamically changes of samples volume within a certain time interval. As a result, this enhancement (or hybrid combination) provides an efficient platform for regression purposes. Although in this paper it dealt with small data sets (and this was done for illustrative purposes), it is worth noting that method scales up quite easily.

In further studies, it plan to expand the proposed approach by incorporating some other technologies of soft computing and swarm intelligence techniques such particle swarm optimization (PSO) or ant colony optimization (ACO).