Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Introduction

Evaluating the performances of thermoelectric devices is usually a hard task to achieve, since it involves the solution of the coupled field equations of the thermoelectric effects on three-dimensional domains (thermoelectric chips). No analytical solution normally can be found even with simplified geometries and, for this reason, numerical strategies must be implemented. Numerical methods generally employed are based on the discretization of the domains, in order to convert the continuous operator problem (differential equations) to a discrete problem (iterative solution of linear systems) that leads to the evaluation of the values of temperature and electric potential on the nodes linking the adjacent subdomains. In this work, the finite element method was used to solve the coupled thermal-electrical equations of the thermoelectric effect; other numerical procedures available are the finite difference method and the finite volume method [1].

The thermoelectric effect is governed by the equations of heat flow and continuity of electric charge [1, 2]:

$$ \rho C\frac{\partial T}{\partial t}+\nabla \cdot q=Q $$
(12.1)
$$ \nabla \cdot J=\frac{\partial {\rho}_c}{\partial t} $$
(12.2)

where T is the temperature [K], ρ is the density [kg/m3], C is the specific heat [J kg−1 K−1], q is the heat flux vector [W/m2], Q is the heat generation rate per unit volume [W/m3], J is the electric current density vector [A/m2], and ρ c is the space charge density [A/m3]. In Eqs. (12.1) and (12.2), q and j are given by the thermoelectric constitutive equations:

$$ q= PJ-k\nabla T $$
(12.3)
$$ J=\sigma \left(E-\alpha \nabla T\right)=\sigma \left(-\nabla V-\alpha \nabla T\right) $$
(12.4)

where P is the Peltier coefficient [V], k the thermal conductivity [W m−1 K−1], σ the electrical conductivity [S/m], E the electric field intensity vector [V/m], V the electrical potential [V], and α is the Seebeck coefficient [V/K]. Furthermore, the internal heat source, including the Joule heating contribution, is defined by:

$$ Q=J\cdot E $$
(12.5)

For steady-state analyses Eqs. (12.1) and (12.2) become:

$$ \nabla \cdot \left(-k\nabla T+P\left(-\sigma \nabla V-\sigma \alpha \nabla T\right)\right)=\left(-\sigma \nabla V-\sigma \alpha \nabla T\right)\cdot \left(-\nabla V\right) $$
(12.6)
$$ \nabla \cdot \left(-\sigma \nabla V-\sigma \alpha \nabla T\right)=0 $$
(12.7)

The aim is to calculate the distribution of temperature T and electric potential V on the thermoelectric material (domain). Joule heating in Eq. (12.7) makes the problem nonlinear [3]; furthermore, the temperature dependency of material properties k, σ, α must be taken into account.

The thermoelectric effect, described by Eqs. (12.1) and (12.2), is a coupled problem and in general, in the applications such as evaluation of thermoelectric generators (TEG) with different operating conditions, Eqs. (12.1) and (12.2) need to be considered together with further equations governing other involved physics. Therefore, a multiphysics approach can be considered as a suitable strategy for modelling thermoelectric devices and the finite element method can be easily used to implement multiphysics simulation.

FE Analysis

The finite element version of Eqs. (12.6) and (12.7) was implemented through the Physics Builder Interface of COMSOL Multiphysics [4] in the weak form of the problem [5, 6]:

$$ \underset{\varOmega }{{\displaystyle \int }}\left(\nabla \cdot q\right){w}_T\partial \varOmega =\underset{\varOmega }{{\displaystyle \int }}Q{w}_T\partial \varOmega $$
(12.8)
$$ \underset{\varOmega }{{\displaystyle \int }}\left(\nabla \cdot J\right){w}_V\partial \varOmega =0, $$
(12.9)

where w T and w V are H1 (Ω) Sobolev weight functions.

Equations (12.8) and (12.9) are solved on the discretized domain (mesh) [2] where:

$$ T=N\cdot {T}_{\mathrm{e}} $$
(12.10)
$$ V=N\cdot {V}_{\mathrm{e}} $$
(12.11)

where T e and V e are the values of T and V on the nodes of the mesh, and N the shape functions that approximate the shape of the distribution of temperature and electric potential within the finite elements. In this work, the FEM procedure is used to perform analyses on (a) single TE chips (height h = 6–15 mm) and on (b) an embedded in air 16-leg TEG (legs height h = 10 mm), calculating the temperature and electric potential distributions using Eqs. (12.10) and (12.11) in the chips, in the connecting Cu elements, and in the fluid (the domains). The thermoelectric materials are assumed to be isotropic, considering k, σ and α as scalar quantities instead of 3 × 3 matrices [k], [σ], [α] [2]; the temperature dependency of these properties is taken into account. In the finite element approximation of Eqs. (12.10) and (12.11), quadratic Lagrange elements are used. The resulting mesh was almost coarse with a maximum size of the elements varying from 0.6 mm up to 2.0 mm; finer meshes did not lead to a significantly higher accuracy in the results.

In order to consider thermal and electrical resistances, boundary features have been implemented. This is useful to avoid the introduction of thin geometric domains, which would force the mesh to be, locally, extremely fine. For the thermal contact resistance, heat flux across the resistive boundary is defined by [4]:

$$ -{n}_{\mathrm{d}}\cdot \left(-{k}_{\mathrm{d}}\nabla {T}_{\mathrm{d}}\right)=-{k}_{\mathrm{s}}\frac{T_{\mathrm{u}}-{T}_{\mathrm{d}}}{d_{\mathrm{s}}} $$
(12.12)
$$ -{n}_{\mathrm{u}}\cdot \left(-{k}_{\mathrm{u}}\nabla {T}_{\mathrm{u}}\right)=-{k}_{\mathrm{s}}\frac{T_{\mathrm{d}}-{T}_{\mathrm{u}}}{d_{\mathrm{s}}} $$
(12.13)

where T is the temperature, u and d subscripts stand for upside and downside of the contact surface [4], and k s and d s, thermal conductivity and thickness of an equivalent thin domain, are defined through the thermal contact resistivity R t = d s/k s [m2 K/W]. In the same way, for the electrical contact resistance, the current density across the boundary is defined by [4]:

$$ n\cdot {J}_{\mathrm{d}}=\frac{1}{\rho_{\mathrm{s}}}\left({V}_{\mathrm{u}}-{V}_{\mathrm{s}}\right) $$
(12.14)
$$ n\cdot {J}_{\mathrm{u}}=\frac{1}{\rho_{\mathrm{s}}}\left({V}_{\mathrm{s}}-{V}_{\mathrm{u}}\right) $$
(12.15)

where V is the electric potential and ρ s is the electrical resistivity of the contact surface.

Results of the FE Analysis on Silicide-Based TEG

Finite element analyses were performed on a single chip and a 16-chip thermoelectric generator. In the first case, the analysis was carried out to verify the conformity of numerical results with open-circuit voltage and output power data measurements, reported in Iida, Sakamoto et al. [7]. In the second case, the goal is to find out the efficiency of a thermoelectric module, embedded in dry air, with different values of the cross-section ratio of the p-type HMS legs and the n-type Bi-doped Mg2Si legs. This latter analysis led to the identification of an optimal geometrical configuration, which can improve the results obtained through a simplified analytical method based on the mean values for k, σ and α [8].

Steady-State Analysis of a Single Undoped Mg2Si Chip

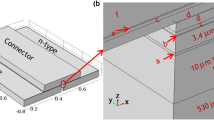
FEM simulation was performed on a parallelepiped-shaped sample with cross-section area 2 mm × 2 mm and height varying from 6.0 to 15.0 mm, for ΔT = 500 K (cold side T c = 373 K, hot side T h = 873 K). The results of the numerical analysis were compared to those obtained by Iida, Sakamoto et al. in [7]. In Fig. 12.1a, b the values of measured thermal and electrical conductivities and Seebeck coefficient are plotted [7].

Fig. 12.1
figure 1

(a) Temperature dependence of the thermal conductivity of the undoped Mg2Si sample over the temperature range from 300 to 860 K (Iida, Sakamoto et al. [7]). (b) Temperature dependence of the electrical conductivity and the Seebeck coefficient of the undoped Mg2Si sample (Iida, Sakamoto et al. [7])

Full size image

Thermal contact resistivity values were taken into account on both the cold and the hot side; reference values were considered 0.3195 × 10−4 m2 K/W at the cold side and 0.8241 × 10−4 m2 K/W at the hot side, being at both sides d s = 0.10 mm, corresponding to a feasible value of roughness of the contact layer [9]. Steady-state FE analysis was developed on a geometrical model with the same cross-section area and with different height values from 6.0 to 15 mm for the thermoelectric domain; on the bottom and the top two 1.0 mm thick Cu layer were considered. Boundary conditions were defined at the lower and upper faces, forcing temperature values to be 373 and 873 K respectively. The temperature distribution on the Mg2Si and Cu domains is reported in Fig. 12.2.

Fig. 12.2
figure 2

Temperature distribution on the Mg2Si chip with the bottom and top Cu layers, height of the TE chip h = 7.5 mm plotted as a function of z-coordinate: discontinuities occur where thermal contact resistivity conditions are defined

Full size image

Open-circuit voltage and output power were also calculated; Fig. 12.3 shows the leg height dependency of open-circuit voltage to be compared with experimental measurements reported in Iida et al. [7]. Numerical analysis yields an open-circuit voltage value V oc=102.6 mV with h = 7.5 mm, whereas measured value for the same height is V oc = 101.1 mV. Numerically evaluated maximum output power density for h = 7.5 mm is 1.58 W/cm2 whereas the measured value is 1.42 W/cm2. The higher difference between measured and calculated values of power density may be related to the fact that no electrical contact resistance has been defined. The electrical contact resistance would affect output power with no effect on the open-circuit voltage. The output power density calculated with FEM procedure is plotted on Fig. 12.4 as function of the electric current.

Fig. 12.3
figure 3

Numerically evaluated open-circuit voltage for different values of the height of the 2 × 2mm2 Mg2Si chip; the numerically evaluated open-circuit voltage with h = 7.5 mm is V oc,num = 102.6 mV whereas the measured value [7] is 101.1 mV

Full size image
Fig. 12.4
figure 4

Numerically evaluated power density [W/cm2] as function of current intensity [mA]. The maximum value of power density is 1.58 W/cm2 for load resistance 42 mΩ

Full size image

Steady-State Analysis of a 16-Chips Thermoelectric Generator (TEG)

A finite element analysis has been carried out on a 16-element thermoelectric module with HMS p-type legs and Bi-doped Mg2Si n-type legs with different values of cross-sectional ratios A p/A n and with ΔT = 500 K. The thermoelectric legs were considered to be embedded in a medium with the temperature dependent thermal properties of the dry air. For the n-type legs (1 % Bi-doped Mg2Si) the values of the thermal and electrical resistivities and Seebeck coefficient were taken as reported in Fiameni et al. in [10]; p-type legs where characterized with the properties of higher manganese silicide reported in Famengo et al. in [11]. The n-type legs were considered with a fixed 4.0 × 4.0 mm2 cross section, whereas for the p-type leg was considered A p = 4.0 × Lyp mm2 with Lyp varying from 4.0 to 8.0 mm (1.0 ≤ A p/A n ≤ 2.0); for all legs, the height was taken h = 10 mm.

In Fig. 12.5, the distributions of the temperature (yz-plane) and the electric potential (zx-plane) on the thermoelectric, the connecting Cu element and the fluid domains are shown for cross-sectional ratio A p/A n = 1.25. At first, no thermal/electrical contact resistances have been defined for the interfaces; the cross-sectional ratio dependence of conversion efficiency has been investigated.

Fig. 12.5
figure 5

Distribution of temperature T [K] (yz plane) and electric potential V [V] (zx plane) on the thermoelectric, connection and fluid domains for cross-sectional ratio A p/A n = 1.25

Full size image

With 1.0 ≤ A p/A n ≤ 2.0, the internal resistance of the thermoelectric legs varies from 0.1821 to 0.2561 Ω. The FE analysis shows that for a load resistance R load equal to the mean value R int,m ≈ 0.21 Ω, the optimum value of the cross-sectional ratio for the conversion efficiency is (A p/A n)opt,eff ≈ 1.30. The maximum value for conversion efficiency with no electrical contact resistance was found to be η t,max =5.33 %. The optimum value for A p/A n can be compared with the result obtained with mean values for the thermoelectric properties [8]:

$$ {\varPsi}^{*}=\sqrt{\lambda_{\mathrm{n}}{\rho}_{\mathrm{p}}/{\lambda}_{\mathrm{p}}{\rho}_{\mathrm{n}}} $$
(12.16)

Taking the mean values for thermal conductivity and the electrical resistivity for the n,p-legs:

λ n,mean = 3.36 Wm−1 K−1; ρ n,mean = 2.172 × 10−5 Ωm; λ p,mean = 2.91Wm−1 K−1; ρ p,mean = 2.940 × 10−5 Ωm; Eq. (12.16) yields Ψ* = 1.25.

Defining internal boundary conditions, introducing electrical contact resistance on the interface between thermoelectric legs and the metallic connections on the cool side, using as reference value ρ int=12 × 10−4 Ω cm2, the optimum value of (A p/A n), for R load = R int,m = 0.21 Ω shifts to (A p/A n)opt,eff * ≈ 1.15, as shown in Fig. 12.6, whereas (A p/A n)opt,eff * = 1.30 for R load = R int,m = 0.18 Ω. The maximum value of conversion efficiency itself decreases: for R load = R int,m=0.21 Ω, the maximum value was found to be η*t,max ≈ 3.9 %.

Fig. 12.6
figure 6

Conversion efficiency as function of cross-sectional ratio A p/A n (1.0 ≤ A p/A n ≤ 2.0), R load = R int.m = 0.21 Ω, (a) without and (b) with electrical contact resistance taken into account

Full size image

Conclusions

Numerical investigations on the performances of uni-leg and multi-leg silicide-based thermoelectric generators have been carried out using the finite element method. The numerical solution of the thermoelectric coupled field equations has been based on experimental measured properties in all analyses, and on measured data for open-circuit voltage and output power in the case of the uni-leg TEG. The task to match measured data led to the implementation of boundary features to reproduce the effect of thermal and electrical contact resistances; the temperature dependence of the thermoelectric properties was taken into account. The numerical analyses have been performed on a single undoped Mg2Si leg [7] and on a 16-element thermoelectric module, with Bi-doped Mg2Si n-type legs and HMS p-type legs. In the first case, numerical results fit the available experimental data for the evaluation of the open-circuit voltage with the definition of thermal contact resistance conditions on the interfaces between the metallic and the thermoelectric elements. On the other hand, a closer agreement was expected in the case of the output power; this can reasonably be related to the fact that no electrical contact resistance was taken into account. In the second case, the numerical evaluation of the conversion efficiency, with different ratios of cross-sectional areas for the n, p-type legs, was performed without and with electrical contact resistance defined at the cool side. On the first analysis, the best geometrical configuration was found to be (A p/A n)opt,eff ≈ 1.30, whereas the calculation with mean (temperature independent) thermoelectric properties yielded (A p/A n)*opt,eff ≈ 1.25. The calculated maximum value for the efficiency with no electrical resistance taken into account dramatically decreases from 5.33 to 3.91 %; in the second analysis, the optimum configuration is found to be A p/A n)opt,eff * ≈ 1.15.