Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Failures of engineered systems (e.g., vehicle, aircraft, and material) lead to significant maintenance/quality-care costs and human fatalities. Examples of such system failures have been found in many engineering fields: DC-10-10 aircraft engine loss (1979), the explosion of the Challenger space shuttle (1986), Ford Explorer rollover (1998–2000), the interstate 35W bridge failure in Minneapolis, MN (2007), etc. Today, US industry spends $200 billion each year on reliability and maintenance. Many system failures can be traced back to various difficulties in evaluating and designing complex systems under highly uncertain manufacturing and operational conditions and our limited understanding of physics of failures. Thus, reliability analysis under uncertainty, which assesses the probability that a system performance (e.g., fatigue, corrosion, fracture) meets its marginal value while taking into account various uncertainty sources (e.g., material properties, loads, geometries), has been recognized as of significant importance in product design and development (Haldar and Mahadevan 2000).

Reliability analysis involving a single performance function is referred to as component reliability analysis. In engineering practice, it is also very likely to encounter reliability analysis problems involving multiple performance functions and these performance functions often describe different physical phenomena (associated with system performances) that are coupled together via the common random variables shared by the functions. We refer to this type of reliability analysis as system reliability analysis. System reliability analysis aims at analyzing the probability of system success while considering multiple system performances (e.g., fatigue, corrosion, and fracture). For example, the design of a truss structure requires both the displacement at a critical node and the stress of a critical truss element satisfy the reliability requirements. Here we have two performance functions in reliability analysis, i.e., the nodal displacement and the elemental stress. This example has two failure criteria, namely, displacement and stress. Another example is the design of a lower control A-arm in a vehicle. In this example, even if we only consider a single failure criterion (i.e., stress), we still need to deal with multiple performance functions which are the stresses at multiple hotspots of the control arm.

The task may become more challenging if we have different system configurations (e.g., series, parallel, and mixed). In order to ensure high reliability of complex engineered systems against deterioration or natural and man-made hazards, it is essential to have an efficient and accurate method for estimating the probability of system failure regardless of different system configurations (series, parallel, and mixed systems). Although tremendous advances have been made in component reliability analysis and design optimization, the research in system reliability analysis has been stagnant due to the complicated nature of the multiple system failure modes and their interactions, as well as the costly computational expense of system reliability evaluation (Youn and Wang 2009; Wang et al. 2011). Since system reliability prediction is of great importance in civil, aerospace, mechanical, and electrical engineering fields, its technical development will have an immediate and major impact on engineered system designs. This chapter is devoted to providing an in-depth discussion of the recently developed numerical methods for system reliability analyses of series, parallel, and mixed systems with an aim to give insights into the merits and limitations of these methods.

2 Overview of Reliability Analysis Under Uncertainty

The formal definition of reliability is the probability that an engineered system will perform its required function under prescribed conditions (for a specified period of time). We intentionally use a bracket in this definition to indicate the existence of two different types of reliabilities: time-independent reliability and time-dependent reliability. The former type is often used in designing an engineered system to provide a high built-in reliability at the very beginning of operation (i.e., it generally does not consider the health degradation during the life cycle); the later type is often employed in supporting an engineered system to ensure a high operational reliability (i.e., the health degradation during the life cycle is taken into account to estimate the reliability). The discussion in this chapter only focuses on the time-independent reliability which can be defined as the probability that the actual performance of an engineered system meets the required or specified design performance under various uncertainty sources (e.g., material properties, loads, geometric tolerances). This section discusses the types of uncertainty and provides an overview of component and system reliability analyses under uncertainty.

2.1 Types of Uncertainty

Uncertainty present in engineering applications can be formally classified into two categories: aleatory uncertainty and epistemic uncertainty (Swiler and Giunta 2007). Aleatory uncertainty characterizes the inherent uncertainty in a random input of the performance function under study. Aleatory uncertainty is objective and irreducible and is used when sufficient data on the random input are available. Aleatory uncertainties can be characterized by using appropriate probability distributions. Epistemic uncertainty, on the other hand, characterizes the lack of knowledge on the appropriate value to use for an input that has a fixed value. Epistemic uncertainty is subjective and can be reduced by gathering more data for the input. Epistemic uncertainty reflects the degree of “belief” and can be represented by fuzzy sets (Möller and Beer 2004), possibility theory (Youn et al. 2007), or imprecise probability (Ferson et al. 2003).

This chapter assumes that sufficient random input data are available and, thereafter, only considers aleatory uncertainty. In engineering practice, the aleatory uncertainty of a random input X can be characterized with three sequentially executed steps (Xi et al. 2010):

  • Step 1: Obtain optimal distribution parameters for candidate probability distributions using the maximum likelihood method. It can be formulated as

    $$ \mathrm{maximize}\kern1em L\left( X\Big|\boldsymbol{\updelta} \right)={\displaystyle \sum_{l=1}^K{ \log}_{10}\kern0.5em \left[ f\left({x}_l\Big|\boldsymbol{\updelta} \right)\right]} $$
    (1)

    where δ is the unknown distribution parameter vector; x l is the lth random data point (or realization) of X; L(·) is the likelihood function; K is the number of random data points (or realizations); and f is the probability density function (PDF) of X for the given δ.

  • Step 2: Perform the Chi-Square goodness-of-fit tests on the candidate distribution types with the optimum distribution parameters obtained in Step 1. It is noted that, depending on the specific engineering application, the Kolmogorov–Smirnov (K–S) test or the Anderson–Darling (AD) test may be more appropriate than the Chi-Square goodness-of-fit test.

  • Step 3: Select the distribution type with the maximum p-value as the optimal distribution type for X.

2.2 Overview of Component Reliability Analysis

The (time-independent) component reliability can be defined as the probability that the actual performance of an engineered system meets the required or specified design performance under various uncertainty sources (e.g., material properties, loads, geometric tolerances). This definition is often used in reliability-based design of civil structural systems, mechanical systems, and aerospace systems. In order to formulate the component reliability in a mathematical framework, random variables are often used to model uncertainty sources in engineered systems. The time-independent reliability can then be formulated as

$$ R(\mathbf{X})= P(G(\mathbf{X})<0)=1- P(G(\mathbf{X})\ge 0) $$
(2)

where the random vector X = (X 1, X 2, … , X N )T models uncertainty sources such as material properties, loads, geometric tolerances; G(X) is a system performance function and the system success event E sys = {G(X) < 0}. The uncertainty of the vector X further propagates and leads to the uncertainty in the system performance function G. In reliability analysis, equating the system performance function G to zero, i.e., G = 0, gives us the so-called limit-state function which separates the safe region G(X) < 0 from the failure region G(X) > 0. Depending on the specific problems, a wide variety of system performance functions can be defined to formulate component reliabilities. The most well-known example is the safety margin between the strength and load of an engineered system.

The concept of component reliability analysis in a two-dimensional case is illustrated in Fig. 1. The dashed lines represent the contours of the joint PDF of the two random variables X 1 (operational factors) and X 2 (manufacturing tolerance). The basic idea of component reliability analysis is to compute the probability that X is located in the safety region {G < 0}. Mathematically, this probability can be expressed as a multidimensional integration of the performance function over the safety region

Fig. 1
figure 1

Concept of time-independent reliability analysis

Full size image
$$ R(\mathbf{X})= P(G(\mathbf{X})<0)={\displaystyle \int \cdots {\displaystyle {\int}_{\Omega^{\mathrm{S}}}{f}_{\mathbf{X}}(\mathbf{x}) d\mathbf{x}}} $$
(3)

where X = (X 1, X 2, … , X N )T models uncertainty sources such as material properties, loads, geometric tolerances; f X (x) denotes the joint PDF of this random vector; the safety domain ΩS is defined by the limit-state function as ΩS = {X: G(X) < 0}.

Neither analytical multidimensional integration nor direct numerical integration is computationally affordable for large-scale engineering problems where the numbers of random variables are relatively large. The search for efficient computational procedures to estimate the component reliability has resulted in a variety of numerical and simulation methods. In general, these methods can be categorized into four groups: (1) expansion methods; (2) most probable point (MPP)-based methods; (3) sampling methods; and (4) stochastic response surface methods (SRSMs). In what follows we intend to give an overview of these methods.

Expansion methods obtain the second-moment statistics of the performance function based on the first- or second-order Taylor series expansion of this function at the mean values of the input random variables (Haldar and Mahadevan 2000). Reliability can be computed by assuming that the performance function follows a normal distribution. It can be seen, therefore, that expansion methods involve two approximations, i.e., the first-order (linear) or second-order (quadratic) approximation of the performance function at the mean values and the normal approximation to the PDF of the performance function. The approximations lead to the fact that these methods are only applicable for engineering problems with relatively small input uncertainties and weak output nonlinearities.

Among many reliability analysis methods, the first- or second-order reliability method, FORM (Hasofer and Lind 1974) or SORM (Breitung 1984; Tvedt 1984), is most commonly used. The FORM/SORM uses the first- or second-order Taylor expansion to approximate a limit-state function at the most probable failure point (MPP) where the limit-state function separates failure and safety regions of a product (or process) response. Some major challenges of the FORM/SORM include (1) it is very expensive to build the probability density function (PDF) of the response and (2) structural design can be expensive when employing a large number of the responses.

The sampling methods include the direct or smart Monte Carlo simulation (MCS) (Rubinstein 1981; Fu and Moses 1988; Au and Beck 1999; Hurtado 2007; Naess et al. 2009). Assuming that we know the statistical information (PDFs) of the input random variables, the direct MCS generally involves the following three steps:

  • Step 1: The MCS starts by randomly generating a large number of samples based on the PDFs of the random inputs.

  • Step 2: In this step, the performance function is evaluated at each of the random samples. Simulations or experiments need to be conducted for this purpose. Upon the completion of this step, we obtain a large number of random values or realizations of the performance function.

  • Step 3: We extract from these random realizations the probabilistic characteristics of the performance function, including statistical moments, reliability, and PDF.

Although the direct MCS (Rubinstein 1981) produces accurate results for reliability analysis and allows for relative ease in the implementation, it demands a prohibitively large number of simulation runs. Thus, it is often used for the purpose of a benchmarking in reliability analysis. To alleviate the computational burden of the direct MCS, researchers have developed various smart MCS methods, such as the (adaptive) importance sampling methods (Fu and Moses 1988; Au and Beck 1999; Hurtado 2007) and the enhanced MCS method with an optimized extrapolation (Naess et al. 2009). Despite the improved efficiency than the direct MCS, these methods are still computationally expensive.

The SRSM is an emerging technique for reliability analysis under uncertainty. As opposed to the deterministic response surface method whose input variables are deterministic, the SRSM employs random variables as its inputs. The aim of the SRSM is to alleviate the computational burden required for accurate uncertainty quantification (i.e., quantifying the uncertainty in the performance function) and reliability analysis. This is achieved by constructing an explicit multidimensional response surface approximation based on function values given at a set of sample points. Generally speaking, uncertainty quantification and reliability analysis propagation of input uncertainty through a model using the SRSM consists of the following steps: (1) determining an approximate functional form for the performance function (possible based on the statistical information of the input random variables); (2) evaluating the parameters of the functional approximation based on function values at a set of sample points; (3) conducting MCS or numerical integration based on the functional approximation to obtain the probabilistic characteristics (statistical moments, reliability, and PDF) of the performance function. The current state-of-the art SRSMs for uncertainty quantification include the dimension reduction (DR) methods (Rahman and Xu 2004; Xu and Rahman 2004; Youn et al. 2008, Youn and Xi 2009), stochastic spectral methods (Ghanem and Spanos 1991; Wiener 1938; Xiu and Karniadakis 2002; Foo et al. 2008; Foo and Karniadakis 2010), and stochastic collocation methods (Smolyak 1963; Grestner and Griebel 2003; Klimke 2006; Ganapathysubramanian and Zabaras 2007; Xiong et al. 2010; Hu and Youn 2011).

2.3 Overview of System Reliability Analysis

System reliability analysis aims at analyzing the probability of system success while considering multiple system performances (e.g., fatigue, corrosion, and fracture). Figure 2 illustrates the concept of system reliability analysis with a simple series system involving two performance functions (i.e., fatigue safety G 1 and wear safety G 1) and two random variables (i.e., operational factors X 1 and manufacturing tolerance X 2). We have two limit state functions G 1 = 0 and G 2 = 0 which divides the input random space into four subspaces {G 1 < 0 and G 2 < 0}, {G 1 < 0 and G 2 > 0}, {G 1 > 0 and G 2 < 0}, {G 1 > 0 and G 2 > 0}. Component reliability analysis aims at quantifying the probability that a random sample x falls into the component safety region (i.e., {G 1 < 0} or {G 2 < 0}) while system reliability analysis (assuming a series system) aims at quantifying the probability that a random sample x falls into the system safety region (i.e., {G 1 < 0 and G 2 < 0}). Clearly, the component reliability (for {G 1 < 0} or {G 2 < 0}) is larger than the system reliability since the component safety region has a larger area than the system safety region by the area of an intersection region {G 1 < 0 and G 2 > 0} or {G 1 > 0 and G 2 < 0}.

Fig. 2
figure 2

Concept of system reliability analysis (two performance functions)

Full size image

The aforementioned discussion leads to a mathematical definition of system reliability as a multidimensional integration of a joint probability density function over a system safety region, expressed as

$$ {R}_{\mathrm{sys}}={\displaystyle \int \cdots {\displaystyle {\int}_{\Omega^{\mathrm{S}}}{f}_{\mathbf{X}}\left(\mathbf{x}\right) d\mathbf{x}}} $$
(4)

where X = (X 1, X 2, … , X N )T models uncertainty sources such as material properties, loads, geometric tolerances; f X (x) denotes the joint PDF of this random vector; ΩS denotes the system safety domain. We can see that this formula bears a striking resemblance to that of component reliability analysis. The only difference between these two formulae lies in the definition of the safety domain. For component reliability analysis, the safety domain can be defined in terms of a single limit-state function as ΩS = {x: G(x) < 0}. For system reliability analysis involving nc performance functions, the safety domains can be expressed as

$$ \begin{aligned}[b] {\Omega}^{\mathrm{S}}&=\left\{ x:{\displaystyle {\cap}_{i=1}^{nc}{G}_i(x)<0}\right\}\ \mathrm{series}\ \mathrm{system}\nonumber\\ {\Omega}^{\mathrm{S}}&=\left\{ x:{\displaystyle {\cup}_{i=1}^{nc}{G}_i(x)<0}\right\}\ \mathrm{parallel}\ \mathrm{system}\nonumber\\ {\Omega}^{\mathrm{S}}&=\left\{ x:{\displaystyle {\cup}_{k=1}^{np}{\displaystyle {\cap}_{i\in {P}_k}{G}_i(x)<0}}\right\}\ \mathrm{mixed}\ \mathrm{system} \end{aligned} $$
(5)

where P k is the index set in the kth path set and np is the number of mutually exclusive path sets.

It can be observed that a series system requires all the performance functions satisfy the reliability requirements, resulting in the system safety events being an intersection of component safety events, expressed as

$$ {E}_{\mathrm{series}}={\displaystyle {\cap}_{i=1}^{nc}{G}_i\left(\mathbf{x}\right)<0} $$
(6)

In this case, the system survives if and only if all of its constraints satisfy the reliability requirements.

In contrast to a series system, a parallel system has multiple path sets with each being its component safety event, expressed as

$$ {E}_{\mathrm{parallel}}={\displaystyle {\cup}_{i=1}^{nc}{G}_i\left(\mathbf{x}\right)<0} $$
(7)

In this case, the component survives if any of its constraints satisfy the reliability requirement. A comparison between a series system and a parallel system is graphically shown in Fig. 3, where we observe that the safety domain of a parallel system contains two more regions {G 1 > 0 and G 2 < 0} and {G 1 < 0 and G 2 > 0}, resulting in a higher system reliability value.

Fig. 3
figure 3

Comparison between a series system and a parallel system (two performance functions)

Full size image

The logic becomes more complicated for a mixed system. We often need to describe the system success event of a mixed system in terms of the mutually exclusive path sets of which each path set Path k is a series system with multiple component safety events specified in Path k . Thus, we have the following expression

$$ {E}_{\mathrm{mixed}}={\displaystyle {\cup}_{k=1}^{np}{\displaystyle {\cap}_{i\in {\mathrm{Path}}_k}{G}_i\left(\mathbf{x}\right)<0}} $$
(8)

In probability theory, two events are said to be mutually exclusive if they cannot occur at the same time or, in other words, the occurrence of any one of them automatically implies the nonoccurrence of the other. Here, system path sets are said to be mutually exclusive if any two of them are mutually exclusive.

By employing the system safety event E sys, we can derive another important formula for system reliability analysis as

$$ {R}_{\mathrm{sys}}= \Pr \left({E}_{\mathrm{sys}}\right) $$
(9)

where E sys represents E series, E parallel, and E mixed, for a series system, a parallel system, and a mixed system, respectively.

We note that, in practice, it is extremely difficult to perform the multidimensional numerical integration for system reliability analysis in Eq. (4) due to the high nonlinearity and complexity of the system safety domain. In contrast to the tremendous advances in component reliability analysis as discussed in Sect. 2.2, the research in system reliability analysis has been stagnant, mainly due to the complicated nature of the multiple system failure modes and their interactions, as well as the costly computational expense of system reliability evaluation (Wang et al. 2011).

Due to the aforementioned difficulties, most system reliability analysis methods provide the bounds of system reliability. Ditlevsen proposed the most widely used second-order system reliability bound method (Ditlevsen 1979), which gives much tighter bounds compared with the first-order bounds for both series and parallel systems. Other equivalent forms of Ditlevsen’s bounds were given by Thoft-Christensen and Murotsu (1986), Karamchandani (1987), Xiao and Mahadevan (1998), Ramachandran (2004). Song and Der Kiureghian formulated system reliability to a Linear Programming (LP) problem, referred to as the LP bound method (Song and Der Kiureghian 2003) and latterly the matrix-based system reliability method (Nguyen et al. 2010). The LP bound method is able to calculate the optimal bounds for system reliability based on available reliability information. However, it is extremely sensitive to accuracy of the available reliability information, which is the probabilities for the first-, second-, or higher-order joint safety events. To assure high accuracy of the LP bound method for system reliability prediction, the probabilities must be given very accurately.

Besides the system reliability bound methods, one of the most popular approaches is the multimodal Adaptive Importance Sampling (AIS) method, which is found satisfactory for the system reliability analysis of large structures (Mahadevan and Raghothamachar 2000). The integration of surrogate model techniques with Monte Carlo Simulation (MCS) can be an alternative approach to system reliability prediction as well (Zhou et al. 2000). This approach, which can construct the surrogate models for multiple limit-state functions to represent a joint failure region, is quite practical but accuracy of the approach depends on fidelity of the surrogate models. It is normally expensive to build accurate surrogate models.

Most recently, Youn and Wang (2009) introduced a new concept of the complementary intersection event and proposed the Complementary Intersection Method (CIM) for series system reliability analysis. The CIM provides not only a unique formula for system reliability but also an effective numerical method to evaluate the system reliability with high efficiency and accuracy. The CIM decomposes the probabilities of high-order joint failure events into probabilities of complementary intersection events. For large-scale systems, a CI matrix was proposed to store the probabilities of component safety and complementary intersection events. Then, series system reliability can be efficiently evaluated by advanced reliability methods, such as dimension reduction method and stochastic collocation method. Later, the GCIM framework was proposed to generalize the original CIM so that it can be used for system reliability analysis regardless of system structures (series, parallel, and mixed systems) (Wang et al. 2011). In the subsequent sections, we will review in details the most widely used system reliability bound methods (Ditlevsen 1979) as well as the recently developed point estimation method (Youn and Wang 2009; Wang et al. 2011).

3 System Reliability Analysis for Serial System

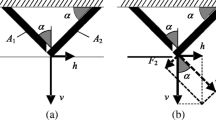
A series system succeeds only if all of its components succeed and, in other words, the system fails if any of its components fails. Let us start with a simple series system, namely, a steel portal frame structure shown in Fig. 4 (Ditlevsen 1979). The structure is subjected to a vertical load V at the center of the top beam and a horizontal load F at the hinge joint between the top and bottom-left beams. These two loads are assumed to be Gaussian random variables. According to the yield hinge mechanism theory, the frame structure has three distinct failure modes: beam failure, sway failure, and combined failure, as shown in Fig. 4.

Fig. 4
figure 4

Loading condition and three failure modes of the portal frame structure (Ditlevsen 1979). (a) Loading condition, (b) beam failure, (c) sway failure, and (d) combined failure

Full size image

If we assume an identical yield moment M y for all three beams, we then have the following performance functions for the three failure modes

$$ \begin{array}{l}\begin{array}{cc} \mathrm{Beam}: & {G}_1= Vl-4{M}_{\mathrm{y}} \end{array}\\ \begin{array}{cc} \mathrm{Sway}: & {G}_2= Fh-4{M}_{\mathrm{y}} \end{array}\\ \begin{array}{cc} \mathrm{Combined}: & {G}_3= Vl+ Fh-6{M}_{\mathrm{y}} \end{array}\end{array} $$
(10)

The limit-state functions for the three failure modes are graphically shown in Fig. 5. The failure domain for each failure mode, or the component failure domain, can be expressed as {(F, V)| G i  > 0}, for i = 1, 2, 3, as shown in Fig. 5. Since the occurrence of any of the three failure modes causes system failure, the system failure domain is a union of the component failure domains and has a larger area than any of the component failure domain (see Fig. 5). If we define the failure event of the ith failure mode as Ē i , the probability of system failure for the portal frame structure can be expressed as

Fig. 5
figure 5

Limit-state functions and system failure domain of the portal frame structure

Full size image
$$ {p}_{fs}= P\left({\overline{E}}_1\cup {\overline{E}}_2\cup {\overline{E}}_3\right) $$
(11)

where p fs represents the probability of system failure. The above equation can be further derived in terms of the probabilities of component and joint failure events, expressed as

$$ \begin{aligned}[b]{p}_{fs}&= P\left({\overline{E}}_1\right)+ P\left({\overline{E}}_2\right)+ P\left({\overline{E}}_3\right)\nonumber\\ &\quad-\,P\left({\overline{E}}_1\cap {\overline{E}}_2\right)- P\left({\overline{E}}_2\cap {\overline{E}}_3\right)- P\left({\overline{E}}_1\cap {\overline{E}}_3\right)\nonumber\\ &\quad+\,P\left({\overline{E}}_1\cap {\overline{E}}_2\cap {\overline{E}}_3\right)\end{aligned} $$
(12)

where Ē i  ∩ Ē j is the second-order joint failure event composed of the component failure events Ē i and Ē j , for 1 ≤ i < j ≤ 3, and Ē 1 ∩ Ē 2 ∩ Ē 3 is the third-order joint failure event composed of the component failure events Ē 1, Ē 2, and Ē 3.

As the number of component events increases, we may have fourth- and higher-order joint events. Considering a series system with m components, the probability of system failure can be expressed as

$$ {p}_{fs}= P\!\left(\underset{i=1}{\overset{m}{\cup }}{\overline{E}}_i\right)\,{=}\,{\displaystyle \sum_{j=1}^n{\left(-1\right)}^{j+1}{P}_j}\kern1em \mathrm{with}\kern1em {P}_j\,{=}\,{\displaystyle \sum_{1\le {i}_1<\cdots <{i}_j\le n} P\!\left(\underset{k\in \left\{{i}_1,\dots, {i}_j\right\}}{\cap }{\overline{E}}_k\!\right)} $$
(13)

where p fs represents the probability of system failure and Ē i denotes the failure event of the ith component. It can be observed that, to exactly analyze system reliability with m series connected components, we generally need to compute the probabilities of joint events up to the mth order. Unlike the computation of the probability of a component failure or safety event discussed earlier, the computation of a joint failure or safety event is very difficult and even practically impossible unless we employ the very expensive MCS or direct numerical integration. The research efforts to alleviate the computational burden have resulted in a set of system reliability bound methods, such as the first- and second-order bound methods, and the point estimation method or the complementary intersection method (CIM) (Youn and Wang 2009).

3.1 First- and Second-Order Bound Methods

The simplest system reliability bounds are the so-called first-order bounds. Based on the well-known Boolean bounds in Eq. (14), the first-order bounds of probability of system failure are given in Eq. (15).

$$ \underset{i}{ \max}\left( P\left({\overline{E}}_i\right)\right)\le P\left(\underset{i=1}{\overset{m}{\cup }}{\overline{E}}_i\right)\le {\displaystyle \sum_{i=1}^m P\left({\overline{E}}_i\right)}$$
(14)
$$ \max \left[ P\left({\overline{E}}_i\right)\right]\le {p}_{fs}\le \min \left[{\displaystyle \sum_{i=1}^m P\left({\overline{E}}_i\right)},1\right] $$
(15)

The lower bound in Eq. (15) is obtained by assuming the component events are perfectly independent and the upper bound is derived by assuming the component events are mutually exclusive. Despite the simplicity (only component reliability analysis required), the first-order bound method provides very wide bounds of system reliability that are not practically useful. Thus, the second-order bound method was proposed by Ditlevsen (1979) in Eq. (16) to give much narrower bounds of probability of system failure.

$$ \begin{aligned}[b] &P\left({\overline{E}}_1\right)+{\displaystyle \sum_{i=2}^m \max \left\{\left[ P\left({\overline{E}}_i\right)-{\displaystyle \sum_{j=1}^{i-1} P\left({\overline{E}}_i{\overline{E}}_j\right)}\right],0\right\}}\le {p}_{fs}\nonumber\\ &\quad\le \min \left\{\left[{\displaystyle \sum_{i=1}^m P\left({\overline{E}}_i\right)}-{\displaystyle \sum_{i=2}^m\underset{j< i}{ \max } P\left({\overline{E}}_i{\overline{E}}_j\right)}\right],1\right\}\end{aligned} $$
(16)

where E 1 is the event having the largest probability of failure.

3.1.1 Case Study 1

Consider a statically determinate truss structure (Ditlevsen 1979; Song and Der Kiureghian 2003) in Fig. 6. In this structure, the failure of any truss member leads to the failure of the truss. Thus, the truss structure can be treated as a series system with the seven truss members as its components. For this illustration, we assume the following probabilities of the component and joint failure events (with P i  = P(Ē i ), and P ij  = P(Ē i  ∩ Ē j )): P 1 = 1.88E−4, P 2 = 1.88E−4, P 3 = 1.88E−4, P 4 = 1.88E−4, P 5 = 1.88E−4, P 6 = 1.88E−4, and P 7 = 1.88E−4, P 12 = 5.73E−5, P 13 = 4.35E−5, P 14 = 5.42E−5, P 15 = 4.59E−5, P 16 = 5.13E−5, P 17 = 4.85E−5, P 23 = 6.08E−5, P 24 = 7.79E−5, P 25 = 6.47E−5, P 26 = 7.42E−5, P 27 = 6.87E−5, P 34 = 5.75E−5, P 35 = 4.86E−5, P 36 = 5.43E−5, P 37 = 5.14E−5, P 45 = 6.10E−5, P 46 = 6.88E−5, P 47 = 6.48E−5, P 56 = 5.76E−5, P 57 = 5.44E−5, and P 67 = 6.11E−5. Compute the first- and second-order bounds for the probability of failure of the truss.

Fig. 6
figure 6

Statically determinate truss structure system (Ditlevsen 1979; Song and Der Kiureghian 2003)

Full size image

Solution

Let us first compute the first-order bounds with Eq. (15) as:

$$ \max \left[ P\left({\overline{E}}_i\right)\right]\le {p}_{fs}\le \min \left[{\displaystyle \sum_{i=1}^m P\left({\overline{E}}_i\right)},1\right] $$

The lower and upper bounds can be computed as

$$ \begin{array}{l} \max \left[ P\left({\overline{E}}_i\right)\right]=1.88\mathrm{E}-4\\ \min \left[{\displaystyle \sum_{i=1}^m P\left({\overline{E}}_i\right)},1\right]= \min \left[1.32\mathrm{E}-3,1\right]=1.32\mathrm{E}-3\end{array} $$

Thus, the first-order bounds are [1.88E−4, 1.32E−3]. Then we compute the second-order bounds with Eq. (16). The lower and upper bounds are computed as 4.02E−4 and 9.12E−4, respectively. Thus, the second-order bounds are [4.02E−4, 9.12E−4]. We can clearly see that, compared to the first-order bound method, the second-order bound method gives much narrower bounds of probability of system failure (and thus system reliability).

3.2 Point Estimation Method

In reliability-based design, it is more desirable to have a unique point estimate of system reliability than an interval estimate. In what follows, we introduce a recently developed point estimate method (Wang et al. 2011), namely, the generalized complementary intersection method (GCIM).

Since the probabilities of all events are nonnegative, the following inequalities must be satisfied as

$$ \underset{i}{ \max}\left( P\left({\overline{E}}_i\right)\right)\le \sqrt{{\displaystyle \sum_{i=1}^m{\left[ P\left({\overline{E}}_i\right)\right]}^2}}\le {\displaystyle \sum_{i=1}^m P\left({\overline{E}}_i\right)} $$
(17)

Based on Eqs. (16) and (17), the probability of system failure (p fs ) of a series system failure can be simplified to a unique explicit formula as

$$ {p}_{fs}\cong P\left({\overline{E}}_1\right)+{\displaystyle \sum_{i=2}^m\left\langle P\left({\overline{E}}_i\right)-\sqrt{{\displaystyle \sum_{j=1}^{i-1}{\left[ P\left({\overline{E}}_i{\overline{E}}_j\right)\right]}^2}}\right\rangle } $$
(18)

It can be proved that this approximate probability lies in the second-order bounds in Eq. (16). Based on Eq. (18), serial system reliability can be assessed as (1 − the probability of system failure) and formulated as

$$ \begin{aligned}[b]{R}_{\mathrm{sys}}&= P\left({E}_1{E}_2\cdots {E}_{m-1}{E}_m\right)\cong P\left({E}_1\right)-{\displaystyle \sum_{i=2}^m\left\langle P\left({\overline{E}}_i\right)-\sqrt{{\displaystyle \sum_{j=1}^{i-1}{\left[ P\left({\overline{E}}_i{\overline{E}}_j\right)\right]}^2}}\right\rangle}\kern1.25em \nonumber\\ &\quad\mathrm{where}\kern1.25em \left\langle A\right\rangle \equiv \left\{\begin{array}{c} A,\kern1.25em \mathrm{if}\kern0.75em A>0 \\ 0,\kern1.25em \mathrm{if}\kern0.75em A\le 0 \end{array}\right.\nonumber\\[-1pc]\end{aligned} $$
(19)

Note that the terms inside the bracket, 〈·〉, should be ignored if it is less than zero and R sys should be set to zero if the approximated one given by Eq. (19) is less than zero. It is noted that Eq. (19) provides an explicit and unique formula for system reliability assessment based on the second-order reliability bounds shown in Eq. (16) and an inequality Eq. (17).

3.2.1 Case Study 2

Consider an internal combustion engine for series system reliability analysis (Liang et al. 2007). Five random variables are considered in this example: the cylinder bore b, compression ratio c r, exhaust valve diameter d E, intake valve diameter d I, and the revolutions per minute (rpm) at peak power, ω. From a thermodynamic viewpoint, nine component safety events are defined as follows:

$$ \begin{array}{l}{E}_1=\left\{1.2{N}_c b-400\le 0\right\}\kern1em \left( \min.\mathrm{bore}\ \mathrm{wall}\ \mathrm{thickness}\right)\\ {E}_2=\left\{{\left[8 V/\left(200\pi {N}_c\right)\right]}^{0.5}- b\le 0\right\}\kern1em \left( \max.\mathrm{engine}\ \mathrm{height}\right)\\ {E}_3=\left\{{d}_{\mathrm{I}}+{d}_{\mathrm{E}}-0.82 b\le 0\right\}\kern1em \left(\mathrm{valve}\ \mathrm{geometry}\ \mathrm{and}\ \mathrm{structure}\right)\\ {E}_4=\left\{0.83{d}_{\mathrm{I}}-{d}_{\mathrm{E}}\le 0\right\}\kern1em \left( \min.\mathrm{value}\ \mathrm{diameter}\ \mathrm{ratio}\right)\\ {E}_5=\left\{{d}_{\mathrm{E}}-0.89{d}_{\mathrm{I}}\le 0\right\}\kern1em \left( \max.\mathrm{value}\ \mathrm{diameter}\ \mathrm{ratio}\right)\\ {E}_6=\left\{9.428\times {10}^{-5}\left[4 V/\left(\pi {N}_c\right)\right]\left(\omega /{d_{\mathrm{I}}}^2\right)-0.6{C}_s\le 0\right\}\kern1em \left( \max.\mathrm{Mech}/\mathrm{Index}\right)\\ {E}_7=\left\{0.045 b+{c}_{\mathrm{r}}-13.2\le 0\right\}\kern1em \left(\mathrm{knock}\hbox{-} \mathrm{limit}\ \mathrm{compression}\ \mathrm{ratio}\right)\\ {E}_8=\left\{\omega -6.5\le 0\right\}\kern1em \left( \max.\mathrm{torque}\ \mathrm{converter}\ \mathrm{rpm}\right)\\ {E}_9=\left\{230.5 Q{\eta}_{tw}-3.6\times {10}^6\le 0\right\}\kern1em \left( \max.\mathrm{fuel}\ \mathrm{economy}\right)\end{array} $$

where

$$ \begin{array}{l}{\eta}_{tw}=0.85951\left(1-{c}_{\mathrm{r}}^{-0.33}\right)-{S}_v,\kern1em V=1.859\times {10}^6\kern0.5em {\mathrm{mm}}^3\\ Q=43{,}958\kern0.5em \mathrm{kJ}/\mathrm{kg},{C}_s=0.44,\kern1em \mathrm{and}\kern1em {N}_c=4\end{array} $$

All the random variables are assumed to follow normal distribution with statistical information presented in Table 1. Perform system reliability analyses at the eight reliability-based optimum design points as listed in Table 2 using the first-order bounds (FOB), second-order bounds (SOB), and GCIM methods (Wang et al. 2011).

Table 1 Statistical information of input random variables for internal combustion engine
Full size table
Table 2 Eight different design points for system reliability analysis
Full size table

Solution

Equations (15), (16), and (19) are used to compute the first-order system reliability bounds in the FOB, the second-order system reliability bounds in the SOB, and the point system reliability estimate in the GCIM, respectively. The probabilities of component and second-order joint failure events are computed with the direct MCS. The results of system reliability analysis at the eight design points are summarized in Table 3 and also graphically shown in Fig. 7 (Wang et al. 2011). From the results, it is found that the first-order bound method gives too wide bounds to be of practical use. On the contrary, the second-order bound method gives tighter bounds. It is expected based on the results that the GCIM can predict system reliabilities accurately at various reliability levels and the estimation errors tend to be lower at high system reliability levels (e.g., greater than 0.95), which are often encountered in engineering practices, than those at low system reliability levels.

Table 3 Results of system reliability analysis with MCS, FOB using MCS, SOB using MCS, and GCIM using MCS (M = 1,000,000)
Full size table
Fig. 7
figure 7

Results of system reliability analysis at eight different reliability levels (Wang et al. 2011)

Full size image

This case study considers the first- and second-order joint failure events. The GCIM produces numerical error because of the ignorance of the probabilities of the third- or higher-order joint failure events. The effects of the third- or higher-order joint failure events tend to increase as the system reliability decreases, simply because the probabilities of joint failure events are usually bigger at low reliability level than at high reliability level. This is also true for the reliability bound methods. As can be observed from Table 3 and Fig. 7, the lower the system reliability, the larger the GCIM estimation error and the wider the bounds produced by the FOB and SOB. Thus for series systems, the GCIM produces smaller numerical error at a high system reliability level than that at a lower level. This is valid only for series systems. When only probabilities of the first- and the second-order joint events are used for system reliability analysis, the GCIM will provide comparable results with the average of SOBs. However, compared with SOBs, the GCIM provides system reliability analysis formula with probabilities of any-order joint events.

3.3 Computation of Joint Events

In Case Study 2, we use the direct MCS to compute the probabilities of joint events (Ē i  ∩ Ē j  = {G 1 > 0 and G 2 > 0}. In practice, however, the direct MCS requires an intolerably large number of function evaluations. On the other hand, the component reliability analysis methods (e.g., FORM/SORM, DR methods, stochastic spectral methods, and stochastic collocation methods) discussed earlier cannot be directly used to compute these probabilities since there are neither explicit nor implicit performance functions associated with the joint events. Therefore, the primary challenge in system reliability analysis lies in efficient and accurate determination of the probabilities of joint safety events. In what follows, we review a newly developed method to efficiently evaluate the probabilities of the second- or higher-order joint safety events. This method is embedded in the aforementioned GCIM as a solver for the probabilities of joint events (Youn and Wang 2009; Wang et al. 2011).

The second-order CI event can be denoted as E ij  ≡ {X|G i  ⋅ G j  ≤ 0}. The CI event can be further expressed as E ij  = Ē i  E j  ∪ E i Ē j where the component failure events are defined as Ē i  = {X|G i  > 0}, Ē j  = {X|G j  > 0}. The CI event E ij is thus composed of two events: E i  Ē j  = {X|G i  ≤ 0 ∩ G j  > 0} and Ē i  E j  = {X|G i  > 0 ∩ G j  ≤ 0}. Since the events, Ē i  E j and E i  Ē j , are disjoint, the probability of the CI event E ij can be expressed as (Youn and Wang 2009)

$$ \begin{aligned}[b] P\left({E}_{i j}\right)&\equiv P\left( X\right|{G}_i\cdot {G}_j\le 0\Big)\nonumber\\ &= P\left( X\Big|{G}_i>0\cap {G}_j\le 0\right)+ P\left( X\right|{G}_i\le 0\cap {G}_j>0\Big)\nonumber\\ &= P\left({\overline{E}}_i{E}_j\right)+ P\left({E}_i{\overline{E}}_j\right)\end{aligned} $$
(20)

Based on the probability theory, the probability of the second-order joint safety event E i  ∩ E j can be expressed as

$$ \begin{aligned}[b] P\left({E}_i{E}_j\right)&= P\left({E}_i\right)- P\left({E}_i{\overline{E}}_j\right)\nonumber\\ &= P\left({E}_j\right)- P\left({\overline{E}}_i{E}_j\right)\end{aligned} $$
(21)

From Eqs. (20) and (21), the probabilities of the second-order joint safety and failure events can be decomposed as

$$ P\left({E}_i{E}_j\right)=\frac{1}{2}\left[ P\left({E}_i\right)+ P\left({E}_j\right)- P\left({E}_{i j}\right)\right] $$
(22)
$$ P\left({\overline{E}}_i{\overline{E}}_j\right)=1-\frac{1}{2}\left[ P\left({E}_i\right)+ P\left({E}_j\right)+ P\left({E}_{i j}\right)\right] $$
(23)

It is noted that each CI event has its own limit state function, which enables the use of any component reliability analysis method. The decomposition of joint failure events into component safety and CI events is graphically shown in Fig. 8. We observe that a joint failure event without any limit-state function is decomposed into two component safety events and one CI events, all of which have their own limit-state function and thus allows for the use of any component reliability analysis method.

Fig. 8
figure 8

Decomposition of a joint failure event into component safety and CI events

Full size image

We have discussed the definition of the second-order CI event. In general, this definition can be generalized to any higher-order event. Let an Kth-order CI event denote E 12…K  ≡ {X|G 1 ⋅ G 2 ⋅ … G K  ≤ 0}, where the component safety (or first-order CI) event is defined as E i  = {X|G i  ≤ 0, i = 1, 2, … , K}. The defined Kth-order CI event is actually composed of K distinct intersections of component events E i and their complements Ē j in total where i, j = 1, …, K and i ≠ j. For example, for the second-order CI event E ij , it is composed of two distinct intersection events, E 1 Ē 2 and Ē 1 E 2. These two events are the intersections of E 1 (or E 2) and the complementary event of E 2 (or E 1).

Based on the definition of the CI event, the probability of an Nth-order joint safety event can be decomposed into the probabilities of the component safety events and the CI events as (Youn and Wang 2009)

$$ \begin{array}{lll} &P\left({\displaystyle \underset{i=1}{\overset{N}{\cap }}{E}_i}\right)\\ &=\frac{1}{2^{N-1}}\left[\begin{array}{@{}l@{}}{\displaystyle \sum_{i=1}^N P\left({E}_i\right)}-{\displaystyle \sum_{\begin{array}{l} i=1;\\ j=2;\\ i< j\end{array}}^N P\left({E}_{i j}\right)}+{\displaystyle \sum_{\begin{array}{l} i=1;\\ j=2;\\ k=3\\ i< j< k\end{array}}^N P\left({E}_{i j k}\right)}+\cdots +\\ {\left(-1\right)}^{m-1}{\displaystyle \sum_{\begin{array}{@{}l@{}} i=1;\\ j=2;\\ \kern1em \vdots \\ l= m\\ i< j<\cdots < l\end{array}}^N P\left({E}_{\underset{m}{\underbrace{ i j\cdots l}}}\right)}+\cdots +{\left(-1\right)}^{N-1} P\left({E}_{12\cdots N}\right)\end{array}\right]\end{array} $$
(24)

It is again noted that each CI event has its own limit state function, which enables the use of any component reliability analysis methods. In general, higher-order CI events are expected to be highly nonlinear. As a good trade-off between computational efficiency and accuracy, the use of the first- and second-order CI events in Eq. (24) is suggested for system reliability analysis of most engineered systems. However, we still note that more terms in Eq. (24) can be obtained within the same computational budget as advanced component reliability analysis methods are developed in future.

3.3.1 Case Study 3

Consider the steel portal frame structure shown in Fig. 4. In the three performance functions for the three failure modes in Eq. (10), the vertical load G and the horizontal load F are assumed to be Gaussian random variables with means both means being 35,000 N and standard deviations being 7,000 N. The other variables in the performance functions are assumed to be deterministic and take the following values: l = h = 5 m, and M y  = 60,000 Nm.

  1. 1.

    Compute the probabilities of component safety events and second-order CI events with the direct MCS.

  2. 2.

    Based on the results from (1), compute the probabilities of second-order safety events.

  3. 3.

    Determine the first- and second-order bounds.

Solution

(1) If we conduct a direct MCS with M random samples x 1, x 2, … , x M , the probabilities of component safety events can be computed as

$$ \begin{aligned} P\left({E}_i\right)&= E\left( I\left({G}_i\left(\mathbf{x}\right)<0\right)\right)\\ &\approx \frac{1}{M}{\displaystyle \sum_{k=1}^M I\left({G}_i\left({\mathbf{x}}_j\right)<0\right)},\kern1em \mathrm{for}\kern1em i=1,2,3\end{aligned} $$

The probabilities of second-order CI events can be computed as

$$ \begin{aligned} P\left({E}_{i j}\right)&= E\left( I\left({G}_i\left(\mathbf{x}\right){G}_j\left(\mathbf{x}\right)<0\right)\right)\\ &\approx \frac{1}{M}{\displaystyle \sum_{k=1}^M I\left({G}_i\left({\mathbf{x}}_k\right){G}_j\left({\mathbf{x}}_k\right)<0\right)},\kern1em \mathrm{for}\kern1em \left( i, j\right)=\left(1,2\right),\left(1,3\right),\left(2,3\right)\end{aligned} $$

We can conveniently write these probabilities in a CI matrix. For this example with three components in total, the CI matrix can be defined as

$$ \mathrm{CI}=\left[\begin{array}{c@{\ \ }c@{\ \ }c} P\left({E}_1\right) & P\left({E}_{12}\right) & P\left({E}_{13}\right) \\ - & P\left({E}_2\right) & P\left({E}_{23}\right) \\ - & - & P\left({E}_3\right) \end{array}\right] $$

In the upper triangular CI matrix, the diagonal elements correspond to the component reliabilities (or probabilities of the first-order CI events) and the element on ith row and jth column corresponds to the probability of the second-order CI event E ij if j < i. The CI matrix computed with a direct MCS with 1,000,000 random samples reads

$$ \mathrm{CI}=\left[\begin{array}{c@{\ \ }c@{\ \ }c} 0.9686 & 0.0610 & 0.3891 \\ - & 0.9682 & 0.3891 \\ - & - & 0.5811 \end{array}\right] $$

It is noted that all the probabilities in the CI matrix (the probabilities of component events and second-order CI events) can be computed using any component reliability analysis method (e.g., FORM/SORM, DR, PCE) instead of the direct MCS.

(2) Based on the CI matrix obtained from (1) and according to Eq. (23), we can obtain the probabilities of second-order failure events as P(Ē 1 Ē 2) = 0.0011,P(Ē 1 Ē 3) = 0.0306, and P(Ē 2 Ē 3) = 0.0308. For example, the probability of the second-order failure event P(Ē 2 Ē 3) can be computed as

$$ \begin{aligned} P\left({\overline{E}}_2{\overline{E}}_3\right)&=1-\frac{1}{2}\left[ P\left({E}_2\right)+ P\left({E}_3\right)+ P\left({E}_{23}\right)\right]\\ &=1-\frac{1}{2}\left[0.9682+0.5811+0.3891\right]\\ &=0.0308\end{aligned} $$

(3) The first-order bounds can be computed with Eq. (15) as:

$$ 1- \min \left[{\displaystyle \sum_{i=1}^m P\left({\overline{E}}_i\right)},1\right]\le {R}_{sys}\le 1- \max \left[ P\left({\overline{E}}_i\right)\right] $$

The lower and upper bounds can be computed as

$$ \begin{aligned}1- \min \left[{\displaystyle \sum_{i=1}^m P\left({\overline{E}}_i\right)},1\right]&=1- \min \left[0.4812,1\right]=0.5188\\ 1- \max \left[ P\left({\overline{E}}_i\right)\right]&=1-0.4189=0.5811\end{aligned} $$

Thus, the first-order bounds read [0.5188, 0.5811]. Note that the above bounds are the first-order bounds of system reliability. The corresponding bounds of system probability failure can be easily obtained by exchanging the lower and upper bounds and subtracting both from 1. Then we compute the second-order bounds with Eq. (16) as [0.5793, 0.5801]. We can again clearly see that, compared to the first-order bound method, the second-order bound method gives much narrower bounds of system reliability.

4 System Reliability Analysis for Parallel System

Unlike a series system whose success requires the success of all its components, a parallel system succeeds as long as one of its components succeeds. In other words, a parallel system fails only if all its components fail, and the probability of system failure is the probability of the intersection of all component failure events, expressed as

$$ {p}_{fs}= P\left(\underset{i=1}{\overset{m}{\cap }}{\overline{E}}_i\right) $$
(25)

Consider a 10-bar parallel system in Fig. 9 (Wang et al. 2011), where 10 brittle bars are connected in parallel to sustain a vertical load applied at one end. Ten bars are all brittle with different fracture strain limits ε fi , 1 ≤ i ≤ 10, which are sorted in an ascending order. If the exerted strain ε is between the (i – 1)th and ith fracture strain limits, i.e., n i–1) ≤ ε < ε fi , bar components with fracture strains below ε fi will fail, and the allowable load is then the sum of the strength of components with fracture strains equal to or above ε fi . Therefore, the strain level corresponding to the overall maximum allowable load is among the 10 fracture strain limits.

Fig. 9
figure 9

Ten brittle bar parallel system: (a) system structure model; (b) brittle material behavior in a parallel system (Wang et al. 2011)

Full size image

Ten success scenarios where the tem-bar system can withstand the vertical load are listed as (Wang et al. 2011):

  • First success scenario (ε = ε f1): No fracture occurs, and the system strength R T , as the sum of strength of all the 10 brittle bars, is larger than the load F. The performance function can be expressed as

    $$ {G}_1= F-{\displaystyle \sum_{j=1}^{10}{R}_j\left({\varepsilon}_{f1}\right)}= F-{\displaystyle \sum_{j=1}^{10}\left({E}_j{A}_j\right)}\cdot {\varepsilon}_{f1} $$
    (26)

    where R j represents the allowable load that can be sustained by the jth brittle bar, A j the cross section area of the jth brittle bar, and E j the Young’s modulus of the jth brittle bar.

  • Second success scenario (ε = ε f2): The first brittle bar fails due to the fracture and no longer contributes to the overall system strength. The system strength R T , as the sum of strength of the other nine brittle bars, is larger than the load F. The performance function can be expressed as

    $$ {G}_1= F-{\displaystyle \sum_{j=2}^{10}{R}_j\left({\varepsilon}_{f2}\right)}= F-{\displaystyle \sum_{j=1}^{10}\left({E}_j{A}_j\right)}\cdot {\varepsilon}_{f2} $$
    (27)

  • Tenth success scenario (ε = ε f10): The first nine brittle bars fail due to the fracture and no longer contribute to the overall system strength. The system strength R T , as the sum of strength of the remaining one bar, is larger than the load F. The performance function can be expressed as

    $$ {G}_1= F-{R}_{10}\left({\varepsilon}_{f10}\right)= F-\left({E}_{10}{A}_{10}\right)\cdot {\varepsilon}_{f10} $$
    (28)

    The brittle bar system fails to sustain the load F only if we have the nonoccurrence of all the 10 success scenario or, in other words, the system strength at any of the 10 fracture strains is smaller than the load F. Therefore, this is a parallel system with 10 components, corresponding to the 10 fracture strains.

4.1 First- and Second-Order Bound Methods

A parallel system reliability formula can be obtained based on the formula of series system reliability by using the De Morgan’s law (Wang et al. 2011). According to the De Morgan’s law, the probability of parallel system failure can be expressed as

$$ P\left(\underset{i=1}{\overset{m}{\cap }}{\overline{E}}_i\right)=1- P\left(\overline{\underset{i=1}{\overset{m}{\cap }}{\overline{E}}_i}\right)=1- P\left(\underset{i=1}{\overset{m}{\cup }}{E}_i\right) $$
(29)

where Ē i is the ith component failure event. Equation (29) relates the probability of parallel system failure with the probability of series system safety (reliability). If we treat E i as the ith component failure event in a series system, the right side of Eq. (29) is then the series system reliability.

Based on this relationship and the first-order bounds for a series system in Eq. (15), the first-order bounds for a parallel system can be derived as

$$ \max \left\{\left[1-{\displaystyle \sum_{i=1}^m P\left({E}_i\right)}\right],0\right\}\le {p}_{fs}\le \min \left[ P\left({\overline{E}}_i\right)\right] $$
(30)

The lower bound is obtained by assuming the component events are mutually exclusive and the upper bound is derived by assuming the component events are perfectly independent.

Similarly, based on the second-order bounds for a series system in Eq. (16), the second-order bounds for a parallel system can be derived as

$$ \begin{aligned}[b] &\max \left\{\left[{\displaystyle \sum_{i=1}^m P\left({\overline{E}}_i\right)}-{\displaystyle \sum_{i=2}^m\underset{j< i}{ \min } P\left({\overline{E}}_i\cup {\overline{E}}_j\right)}\right],0\right\}\le {p}_{fs}\nonumber\\ &\quad\le P\left({\overline{E}}_1\right)-{\displaystyle \sum_{i=2}^m \max \left\{\left[\begin{array}{l}2- i- P\left({\overline{E}}_i\right)\\ +{\displaystyle \sum_{j=1}^{i-1} P\left({\overline{E}}_i\cup {\overline{E}}_j\right)}\end{array}\right],0\right\}}\end{aligned} $$
(31)

where E 1 is the event having the largest probability of failure.

4.2 Point Estimation Method

Based on the aforementioned relationship between a series system and a parallel system, the probability of parallel system failure can be obtained from Eq. (19) by treating the safe events in the series system as the failure events in the parallel system as (Wang et al. 2011)

$$ {p}_{fs}\cong P\left({\overline{E}}_1\right)-{\displaystyle \sum_{i=2}^m\left\langle P\left({E}_i\right)-\sqrt{{\displaystyle \sum_{j=1}^{i-1}{\left[ P\left({E}_i{E}_j\right)\right]}^2}}\right\rangle },\kern1em \left\langle A\right\rangle \equiv \left\{\begin{array}{c} A,\kern1.25em \mathrm{if}\kern0.75em A>0 \\ 0,\kern1.25em \mathrm{if}\kern0.75em A\le 0 \end{array}\right. $$
(32)

Finally, parallel system reliability can be obtained from Eq. (32) by one minus the probability of system failure as

$$ {R}_{sys}\cong P\left({E}_1\right)+{\displaystyle \sum_{i=2}^m\left\langle P\left({E}_i\right)-\sqrt{{\displaystyle \sum_{j=1}^{i-1}{\left[ P\left({E}_i{E}_j\right)\right]}^2}}\right\rangle },\kern1em \left\langle A\right\rangle \equiv \left\{\begin{array}{c} A,\kern1.25em \mathrm{if}\kern0.75em A>0 \\ 0,\kern1.25em \mathrm{if}\kern0.75em A\le 0 \end{array}\right. $$
(33)

5 System Reliability Analysis for Mixed Systems

A mixed system may have various system structures as mixtures of series and parallel systems. The success and failure logics of such systems are more complicated than those of series and parallel systems. Consider a cantilever beam-bar system (Song and Der Kiureghian 2003; Wang et al. 2011) which is an ideally elastic–plastic cantilever beam supported by an ideally rigid–brittle bar, with a load applied at the midpoint of the beam, as shown in Fig. 10. There are three failure modes and five independent failure events Ē 1–Ē 5. These three failure modes are formed by different combinations of failure events as:

Fig. 10
figure 10

A cantilever beam-bar system (Song and Der Kiureghian 2003)

Full size image

  • First failure mode: The fracture of the brittle bar (event Ē 1) occurs, and subsequently the formation of a hinge at the fixed point of the beam (event Ē 2).

  • Second failure mode: The formation of a hinge at the fixed point of the beam (event Ē 3) followed by the formation of another hinge at the midpoint of the beam (event Ē 4).

  • Third failure mode: The formation of a hinge at the fixed point of the beam (event Ē 3) followed by the fracture of the brittle bar (event Ē 5).

The five safety events can be expressed as:

$$ \begin{array}{l}{E}_1=\left\{ X, T\Big|5 X/16- T\le 0\right\}\\ {E}_2=\left\{ X, L, M\Big| LX- M\le 0\right\}\\ {E}_3=\left\{ X, L, M\Big|3 LX/8- M\le 0\right\}\\ {E}_4=\left\{ X, L, M\Big| LX/3- M\le 0\right\}\\ {E}_5=\left\{ X, L, M, T\Big| LX- M-2 LT\le 0\right\}\end{array} $$
(34)

Considering these three failure modes, the system success event can be obtained as (Wang et al. 2011):

$$ {E}_S=\left({E}_1\cup {E}_2\right)\cap \left\{{E}_3\cup \left({E}_4\cap {E}_5\right)\right\} $$
(35)

It is not possible to derive any bounds or point estimates of system reliability based on the system success event in Eq. (35) which contains a mixture of intersection and union logics.

One way to tackle this difficulty is to decompose the mixed system success event into mutually exclusive success events or path sets (see an example in Fig. 11), of which each is a series system. As a result, system reliability of this mixed system can be expressed as a sum of the probabilities of these mutually exclusive series events. This method is embedded in the GCIM (Wang et al. 2011).

Fig. 11
figure 11

Decomposition of a mixed system success event into mutually exclusive series system success events

Full size image

Considering a mixed system with N components, the following procedure can be proceeded to derive the mutually exclusive path sets and conduct system reliability analysis in search for a point system reliability estimate (Wang et al. 2011).

Step I: Constructing a System Structure Matrix

An SS matrix, a 3-by-M, can be used to characterize any system structural configuration (components and their connections) in a matrix form. The SS matrix contains the information about the constituting components and their connection. The first row of the matrix contains component numbers, while the second and third rows correspond to the starting and end nodes of the components. Generally, the total number of columns of a SS matrix, M, is equal to the total number of system components, N. In the case of complicated system structures, one component may repeatedly appear in between different sets of nodes and, consequently, M could be larger than N, for example a 2-out-of-3 system.

Let us consider the mixed system example shown in Fig. 11. The SS matrix for the system can be constructed as a 3 × 4 matrix, as shown in Fig. 12. The first column of the system structure matrix [1, 1, 2]T indicates that the first component connects nodes 1 and 2.

Fig. 12
figure 12

Conversion of the system block diagram to SS matrix (Wang et al. 2011)

Full size image

Step II: Finding Mutually Exclusive System Path Sets

Based on the SS matrix, the Binary Decision Diagram (BDD) technique (Lee 1959) can be employed to find the mutually exclusive system path sets, of which each path set is a series system. As discussed in Chap. 2, two events are said to be mutually exclusive if they cannot occur at the same time or, in other words, the occurrence of any one of them automatically implies the nonoccurrence of the other. Here, system path sets are said to be mutually exclusive if any two of them are mutually exclusive. We note that, without the SS matrix, it is not easy for the BDD technique to automate the process to identify the mutually exclusive path sets. The mixed system shown in Fig. 12 can be decomposed into the two mutually exclusive path sets using the BDD, which is shown in Fig. 13. Although the path sets \( {E}_1{\overline{E}}_2{E}_3{E}_4 \) and E 1 E 3 E 4 represent the same path that go through from the left terminal 1 to the right terminal 0 in Fig. 13, the former belongs to the mutually exclusive path sets while the latter does not. This is due to the fact that the path sets E 1 E 3 E 4 and E 1 E 2 are not mutually exclusive. We also note, however, that we could still construct another group of mutually exclusively path sets, {E 1 E 3 E 4, \( {E}_1{E}_2{\overline{E}}_3 \)}, which contains the path set E 1 E 3 E 4 as a member. This is due to the fact that a mixed system may have multiple BDDs with different configurations depending on the ordering of nodes in BDDs and these BDDs result in several groups of mutually exclusive path sets, among which the one with the smallest number of path sets is desirable. Another point deserving of notice is that the mixed system considered here consists of only two mutually exclusive path sets. In cases of more than two mutually exclusive path sets, any two path sets are mutually exclusive. This suggests that the system path sets can equivalently be said to be pairwise mutually exclusive.

Fig. 13
figure 13

BDD diagram and the mutually exclusive path sets (Wang et al. 2011)

Full size image

Step III: Evaluating All Mutually Exclusive Path Sets and System Reliability

Due to the property of the mutual exclusiveness, the mixed system reliability is the sum of the probabilities of all paths as

$$ {R}_{\mathrm{sys}}= P\left({\displaystyle \underset{i=1}{\overset{np}{\cup }}{\mathrm{Path}}_i}\right)={\displaystyle \sum_{i=1}^{np} P\left({\mathrm{Path}}_i\right)} $$
(36)

where Path i is the ith mutually exclusive path set obtained by the BDD and np is the total number of mutually exclusive path sets. For the mixed system shown in Fig. 12, the system reliability can be calculated as

$$ \begin{aligned}[b]{R}_{\mathrm{sys}}&= P\left({\displaystyle \underset{i=1}{\overset{2}{\cup }}{\mathrm{Path}}_i}\right)={\displaystyle \sum_{i=1}^2 P\left({\mathrm{Path}}_i\right)}\nonumber\\ &= P\left({E}_1{E}_2\right)+ P\left({E}_1{\overline{E}}_2{E}_3{E}_4\right)\end{aligned} $$
(37)

where the probability of each individual path set can be calculated using the point estimate formula for the series system reliability given by Eq. (19).

Case Study 4

Consider the cantilever beam-bar system (Song and Der Kiureghian 2003; Wang et al. 2011)) shown in Fig. 10. In the performance functions for the five component safety events, random variables and their random properties are summarized in Table 4. Compute the system reliability with the GCIM method at 10 different reliability levels that correspond to 10 different loading conditions (X), 100, 90, 85, 80, 70, 60, 50, 40, 20, and 10.

Table 4 Statistical information of input random variables for the cantilever beam-bar system
Full size table

Solution

The reliability block diagram along with the SS matrix is shown in Fig. 14 (Wang et al. 2011). Based on this SS matrix, the BDD diagram can be constructed as shown in Fig. 15. The BDD indicates the following mutually exclusive system path sets as (Wang et al. 2011)

Fig. 14
figure 14

System block diagram and SS matrix for the cantilever beam-bar example (Wang et al. 2011)

Full size image
Fig. 15
figure 15

BDD diagram for the cantilever beam-bar example (Wang et al. 2011)

Full size image
$$ \mathrm{Path}\ \mathrm{sets}=\left\{{E}_1{E}_3,\kern0.5em {\overline{E}}_1{E}_2{E}_3,\kern0.5em {E}_1{\overline{E}}_3{E}_4{E}_5,\kern0.5em {\overline{E}}_1{E}_2{\overline{E}}_3{E}_4{E}_5\right\} $$

The system reliability can be calculated as

$$ \begin{aligned}{R}_{sys}&={\displaystyle \sum_{i=1}^4 P\left({\mathrm{Path}}_i\right)}\\ &= P\left({E}_1{E}_3\right)+ P\left({\overline{E}}_1{E}_2{E}_3\right)+ P\left({E}_1{\overline{E}}_3{E}_4{E}_5\right)+ P\left({\overline{E}}_1{E}_2{\overline{E}}_3{E}_4{E}_5\right)\end{aligned} $$

We can then use Eq. (33) to compute the reliability of each path set to derive a point system reliability estimate of this mixed system.

The system reliability analysis is carried out with 10 different loading conditions (10 different u x values for the X) as presented in Table 5 (Wang et al. 2011). The probabilities of component and second-order joint failure events are computed with the direct MCS. The MCS is used for a benchmark solution and the results are also summarized in Table 5. We expect based on the results that the GCIM can give accurate system reliability estimates for mixed systems at various reliability levels.

Table 5 Results of different system reliability analysis methods: GCIM and MCS (ns = 1,000,000)
Full size table

6 Conclusion

The chapter reviews advanced numerical methods for system reliability analysis under uncertainty, with an emphasis on the system reliability bound methods and the GCIM (point estimation method). The system reliability bound methods provide system reliability estimates in the form of two-sided bounds for a series or parallel system, while the GCIM offers system reliability estimates in the form of single points for any system structure (series, parallel, and mixed systems). The GCIM generalizes the original CIM so that it can be used for system reliability analysis regardless of system structures. Four case studies are employed to demonstrate the effectiveness of the system reliability bound methods and the GCIM in assessing system reliability. As observed from the case studies, the GCIM offers a generalized framework for system reliability analysis and thus shows a great potential to enhance our capability and understanding of system reliability analysis.