Keywords

1 Introduction

This paper is closely related to the studies that deal with the motions of robotic systems with variable configuration in resistive media. The control variables in such systems are either the forces acting between the components of the system or the rate at which the generalized coordinates that characterize the relative positions of these components change. When the configuration of the system changes, the velocities of its components, in the general case, change too, which causes a change in the external resistance forces.

One of the classes of systems outlined above are multilink systems moving along a horizontal plane, subject to dry friction. In papers [1–3] control problems for two-link and three-link systems that form an open chain of consecutively connected bodies are solved. It was proved that these multilink systems can be driven to any prescribed position in a plane by alternating slow (quasi-static) and fast motions.

There were also studied the quasi-static motions of multilink systems in the plane in the presence of dry friction forces, i.e., the motions where accelerations and velocities can be neglected. The control forces in a quasi-static motion coincide in order of magnitude with the forces of friction. It was proved [4] that multilink systems with at least four links can move quasi-statically along a straight line, whereas two-link systems are quasi-statically uncontrollable and their motion is fully preset by the initial position [5]. A three-link system of star-like type, as well as a three-link system with consecutive connection of the links can be moved to any position in the plane [6]. However, these motions are rather complex because of the kinematic constraints between vertices of the system.

In this paper, a three-body locomotion system on which no kinematic constraints are imposed is considered. The forces of interaction between the bodies are taken as the control forces. Dry friction forces act between the contact points and the plane. The system under consideration can be a model of a mobile robot that can move along a plane. Since the system has three contact points, it is statically determinate.

2 Equation of a Quasi-static Motion

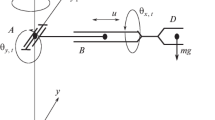
Let us consider the system consisting of three point masses M i , i = 1, 2, 3, on a horizontal plane (Fig. 1). Between each pair of masses M i , control forces act. The system is a model of a mobile robot that can move along a plane, and we study possible quasi-static motions of the system.

Fig. 1
figure 1

Three-body mechanism

Full size image

Dry friction force F i exerted upon point M i of mass m i is given by equations

$$ {\mathbf{F}}_{i} = - k_{i} m_{i} g\frac{{{\mathbf{v}}_{i} }}{{|{\mathbf{v}}_{i} |}},\;{\mathbf{v}}_{i} \ne 0,\quad |{\mathbf{F}}_{i} | \le k_{i} m_{i} g,\;{\mathbf{v}}_{i} = 0, $$
(1)

where v i is the velocity of point M i , k i is the friction coefficient, and g is the gravity acceleration. For any pair of indices \( i\; \ne \;j \) , we have the interaction control force f ij acting from point M i upon point M j and directed along M i M j

$$ {\mathbf{f}}_{ij} = - {\mathbf{f}}_{ji} ,\quad {\mathbf{f}}_{ij} \times ({\mathbf{r}}_{i} - {\mathbf{r}}_{j} ) = 0,\quad i,j = 1,2,3,\quad i \ne j $$
(2)

where r i is the radius-vector of M i . We consider only such control forces f ij that lead to quasi-static motion of each point M i . In such motions, the equilibrium equations hold

$$ {\mathbf{F}}_{i} + {\mathbf{f}}_{ji} - {\mathbf{f}}_{ik} = 0,\quad i \ne j \ne k,\quad i,j,k = 1,2,3. $$
(3)

From Eqs. (2), (3), it follows

$$ \sum\limits_{i = 1}^{3} {{\mathbf{F}}_{i} = 0,} \quad \sum\limits_{i = 1}^{3} {{\mathbf{r}}_{i} \times {\mathbf{F}}_{i} = 0.} $$
(4)

It is shown that if forces F i satisfy Eq. (4), then forces f ij exist such that Eq. (3) hold. Suppose the parameters of the system satisfy the following triangle inequality

$$ k_{1} m_{1} + k_{2} m_{2} \ge k_{3} m_{3} $$
(5)

and two other analogous inequalities that differ from (5) by the permutation of indices. It can be shown that (5) is a necessary condition for the possibility to move mass M 3.

3 Quasi-Static Motions with One Moving Point

Let us find all quasi-static motions such as two masses of the system (for example, M 1 and M 2) do not move, whereas the third mass (M 3) moves. Let D be the intersection of the circles with centers at points M 1 and M 2 and radii \( ak_{2} m_{2} /(k_{3} m_{3} ),\;ak_{1} m_{1} /(k_{3} m_{3} ) \) respectively, where a is the distance between the fixed points. The radii of the circles are the distance a between the fixed points multiplied by the ratio of the maximal friction forces at the fixed points to the maximal friction force at the moving point. Set D is not empty, according to inequality (5).

Proposition 1

Quasi-static motion of mass M 3, with points M 1 and M 2 fixed, is possible iff the straight line containing point M 3 and parallel to its velocity intersects set D.

Corollary

Under conditions (5) the system consisting of three masses M 1, M 2, and M 3 is quasi-statically controllable, i.e., can be quasi-statically brought to any preset position.

4 Optimal Quasi-static Motions

Let us consider optimal control problem for the moving mass. Let two points A and B be fixed on the plane. It is required to move quasi-statically mass M 3 from point A to point B with minimal work against friction, i.e., to construct the trajectory of quasi-static motion for mass M 3 with the minimum length. If the straight line AB intersects set D, then the trajectory with the minimum length is the segment AB.

Proposition 2

If the intersection of the set D with the straight line AB is empty, then the trajectory with the minimum length for mass M 3 quasi-statically moving from point A to point B ,is polygonal chain ACB.The line segments AC and BC belong to the supporting straight lines of set D ; here, point A and set D are located on different sides of straight line BC , and point B and set D are located on different sides of straight line AC (Fig. 2 ).

Fig. 2
figure 2

Optimal trajectory

Full size image

The algorithm for the displacement of the three—body system from any initial position to any given terminal one is presented. At any moment, only one mass M i is moving, and each mass moves only during one time interval. There exist six ways of displacement, corresponding to six possible permutations of mass numbers. If permutation (i, j, k) is chosen, then points M i , M j , M k move one after another, while two other masses are at rest. During each time interval the moving mass follows along the shortest trajectory which is either a straight line or a polygonal chain of two line segments, according to Proposition 2. Comparing these six ways of displacement, the algorithm corresponding to the minimum work can be chosen.

5 Conclusions

Quasi-static motions of a three-body system on a horizontal plane in the presence of dry friction is analyzed. Interaction forces between each pair of bodies are considered as controls. The case in which one body is moving whereas two others are at rest is considered. It is shown that, if the triangle inequality for the masses and friction coefficients holds, then the moving body can be relocated from any initial position to any terminal one. Optimal trajectory (minimizing the work against friction along the trajectory) is found and is proved to be a polygonal chain of one or two line segments. Quasi-static controllability of the system is established. The algorithm for relocating of the system to the given state is presented. The results obtained can be used for the development of control for mobile robotic systems.