A Dynamic Customer-Centric Pricing Approach for the Product Line Pricing Problem

Abstract

In this paper, we address a service provider’s product line pricing problem for substitutable products. We consider a market that is composed of different customer segments of various sizes. The customers belonging to a segment have the same segment-specific preference rankings. The seller is able to adopt a dynamic pricing strategy and offer different prices for the products to different customer segments. We introduce a mixed-integer linear programming formulation for this problem which is solved by means of IBM ILOG CPLEX. We conduct several computational experiments and present some preliminary results.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction and Problem Description

In the literature, the problem of determining optimal prices for a product line has been discussed from multiple points of view and a number of optimization models and procedures have been proposed. Among those, the most prominent models derive from [1–3]. In general, the standard product line pricing problem can be described as follows: A monopolistic seller offers his products $i\in \{1,...,I\}$ at prices $p_i$ for each product $i$ that are selected from a pre-defined set of price points $p_{ia}\ (a=1,\dots ,A_i)$, i.e. $p_i\in \{p_{i1},\dots , p_{iA_i}\}$ in order to maximize his revenue. We consider an extended version of this standard problem by addressing a service provider’s product line pricing problem for substitutable products in services. The products are sold during a common selling season at the end of which the corresponding services are delivered. During the selling season the seller is allowed to update the prices for the products at points in time $t\in \{0,\dots ,T\}$. The costs of supplying a single unit of a service are not constant but depend on the total amount of service units sold. For this purpose, we introduce piecewise linear cost functions with $l\in \{0,\dots ,L_i\}$ intervals affiliated with the total amount of service units sold. An easy example might be a service provider who has a certain internal capacity at free disposal and is able to buy additional units at a spot market. Finally, we assume that the market is composed of different customer segments with different segment specific preference rankings. The seller can exploit these differences by offering not only time dependent but also segment specific prices for the products. An example might be an online service provider who has identified different customer segments based on their booking history and wants to offer them different prices.

Table 1 Products and price points

Table 2 Preference lists (PL)

In Sect. 2 we present the demand model. The mathematical modelling is introduced in Sect. 3. After the presentation of some computational experiments in Sect. 4 the paper ends with a conclusion in Sect. 5.

2 Demand Model

Customer behavior is modeled by using a general non-parametric approach (see, e.g., [5]). We consider a market that is composed of different customer segments $s\in \{1,\ldots ,S\}$ of various sizes. The customers belonging to a segment have the same preference ranking (or preference list) $\sigma _s(B)$ with $B=\{I\times P_i:\ i\in \{1,\ldots ,I\}\}\cup \{(0,p_0)\}=\{(i,p_i):i\in \{0,\ldots ,I\},\ p_i\in \{p_{i1},\dots , p_{iA_i}\}\}$ for all product–price point–combinations (PPPC) including the no-purchase option, “product” $i=0$ that is always offered at $p_{01}=$ €0. $\sigma _s(B): B\rightarrow 1,\dots ,|B|$ is a bijective mapping with the following property: If customer segment $s$ prefers combination $b_1\in B$ to combination $b_2\in B$ then $\sigma _s(b_1)>\sigma _s(b_2)$ holds. Based on the decision of the service provider which PPPCs $B'\subseteq B$ to offer, the customers of segment $s$ will choose the combination $b^*=(i^*,p_i^*)\in B'$ with the highest valued $\sigma _s(b^*)$. Preference rankings are assumed not to change during the selling season. In Tables 1 and 2, a short example is given.

There are $I=2$ products with $A_1=A_2=2$ price points and $S=2$ customer segments with different preference lists $\sigma _1(B)$ and $\sigma _2(B)$. Assume that the service provider sets the prices $p_{12}=$ €5 for $i=1$ and $p_{22}=$ €6 for $i=2$, i.e. $B'=\{(0,$ €0), (1, €5), (2, €6)}. All available PPPCs $B'$–including the no-purchase option–are printed in bold face in Tables 1 and 2. In this example, all customers belonging to segment $s=1$ decide to purchase $i=1$ for $p_{12}=$ €5 because $\sigma _1(1,$ €5)$>\sigma _1(0,$ €0)$>\sigma _1(2,$ €6). All segment $2$ customers accordingly choose the no-purchase option ($0,$ €0). We call the set $B'$ a price list. Following this definition, the seller alternatively could have offered one of the following three price lists: {(0, €0), (1, €2), (2, €4)}, {(0, €0), (1, €2), (2, €6)}, and {(0, €0), (1, €5), (2, €4)}. The service provider has the option to define up to $K$ price lists with $K\le S$. For each customer segment he has to decide which of the price lists $k\in \{1,\dots ,K\}$ he wants to assign to it. The seller is able to adopt a dynamic pricing strategy with a number of price list updates $h\in \{0,\dots ,H\}$ at points in time $t$ with $H<T-1$. At each price list update the seller has the possibility to reassign price lists to the customer segments. Relating to the example given above, assume that $H=1$ price list update takes place and $K=2$ different price lists can be chosen. That means that the service provider can assign different price lists to the two customer segments at the beginning of the selling season ($h=0$ at $t=0$). At some point in time during the selling season, the seller is allowed to update these price list assignments.

3 Mathematical Modelling

We introduce a mixed-integer linear programming formulation for this problem. The notation is given below.

Input Parameters:

$p_{hkia}$::

   $a^{th}$ price point of product $i$ $(=p_{ia})$ in price list $k$ at price list update $h$

$\sigma _{sia}$::

   preference value of segment $s$ for product $i$ at price point $p_{ia}$

$\Delta _{st}$::

   expected total demand of segment $s$ customers which arrive in $[0,\dots , t]$

$Q_{il}$::

   end point of interval $l$ of the piecewise linear cost function of service $i$

$m_{il}$::

   gradient of interval $l$ of the piecewise linear cost function of service $i$

$\Delta f_{il}$::

   jump of the piecewise linear cost function of service $i$ at the left endpoint of interval $l$

$M$::

   sufficiently large number

Decision Variables:

$z_{skh} \in \{0,1\}=1$,:

   if price list $k$ is assigned to segment $s$ at price list update $h$

$\mu _{ht} \in \{0,1\}=1$,:

   if price list update $h$ takes place in $t$ (with $\mu _{00}=1$ and $\mu _{H+1,T}=1$)

$x_{shkia} \in \{0,1\}=1$,:

   if customer segment $s$ chooses product $i$ at price point $p_{ia}$ in price list $k$ after price list update $h$

$\pi _{hkia} \in \{0,1\}=1$,:

   if product $i$ is offered at price point $p_{ia}$ in price list $k$ after price list update $h$

$\delta _{il} \in \{0,1\}=1$,:

   if the total amount of services $i$ sold extends into interval $l$ $d_{il}\ge 0$       total amount of services $i$ sold in interval $l$

$\theta _{shkia}\ge 0\,$ :

   expected demand of segment $s$ customers which buy product $i$ at price point $p_{ia}$ in price list $k$ and which arrive between price list update $h$ and price list update $h+1$

 

The objective function aims to maximize total profits:

$$\begin{aligned} \mathrm Max \ F(\mathbf {z},\varvec{\mu },\mathbf {x},\varvec{\pi },\varvec{\delta },\mathbf {d})&= \sum _{s=1}^{S}\sum _{h=0}^{H}\sum _{k=1}^{K}\sum _{i=1}^{I}\sum _{a=1}^{A_i}(\sum _{t=0}^{T}\mu _{h+1,t}\Delta _{ st}-\sum _{t=0}^{T}\mu _{ ht}\Delta _{ st})x_{ shkia}p_{ hkia} \nonumber \\&-\sum _{i=1}^{I}\sum _{l=1}^{L_i}(\Delta f_{il}\delta _{il}+d_{il}m_{il})\;. \end{aligned}$$

(1)

The revenue is calculated in the first term by multiplying the expected demand of customer segments between two price list updates with the respective price points of the assigned price lists. In the second term, the costs are captured by determining the respective points of the services’ cost functions.

To linearize the objective function, we follow the approach by [4] and introduce a continuous auxiliary variable $\theta _{shkia}$ such that

$$ \theta _{shkia}= {\left\{ \begin{array}{ll} \sum \limits _{t=0}^{T}\mu _{h+1,t}\Delta _{ st}-\sum \limits _{t=0}^{T}\mu _{ ht}\Delta _{ st}\text {, if} \ x_{ shkia}=1 \\ 0, \quad \text {otherwise}\\ \end{array}\right. }.$$

The constraints enforcing this linearization are omitted. The remaining constraints can be divided into three groups.

The first couple of constraints, constraints (2) and (3), determine the points in time for the price updates:

$$\begin{aligned}&{}\sum _{t=0}^{T}\mu _{ht}=1 \ \ \ \ \ \ \ \text {for all} \ h=1,\dots ,H \end{aligned}$$

(2)

$$\begin{aligned}&{}\sum _{t=0}^{T}\mu _{h+1,t}t\ge \sum _{t=0}^{T}\mu _{ht}(t+1) \ \ \ \ \ \ \ \text {for all} \ h=0,\dots ,H-1\;. \end{aligned}$$

(3)

The auxiliary variables $\mu _{ht}$ are used to determine the points in time when price list updates take place. Constraints (2) ensure that every price list update is made at exactly one point in time. Note, if less than $H$ price list updates were optimal, the model would determine points in time for the price list updates but the price lists would not change. A chronological ascending order of the price list updates is assured by constraints (3), i.e. price list update $h+1$ takes place after price list update $h$.

The second group of constraints, constraints (4–8), are the essential constraints for the product line pricing problem with price points and different price lists.

$$\begin{aligned}&{}\sum _{k=1}^{K}z_{shk}=1 \ \ \ \ \ \ \ \text {for all} \ s=1,\dots ,S, \ h=0,\dots ,H \end{aligned}$$

(4)

$$\begin{aligned}&{}\sum _{i=0}^{I}\sum _{a=1}^{A_i}x_{shkia}=z_{shk} \ \ \ \ \ \ \ \text {for all} \ s=1,\dots ,S, \ h=0,\dots ,H,\ k=1,\dots ,K \end{aligned}$$

(5)

$$\begin{aligned}&{}\sum _{a=1}^{A_i}\pi _{hkia}=1 \ \ \ \ \ \ \ \text {for all} \ h=0,\dots ,H,\ k=1,\dots ,K,\ i=0,\dots ,I \end{aligned}$$

(6)

$$\begin{aligned}&{}x_{shkia}\le \pi _{hkia} \ \ \ \ \ \ \ \text {for all} \ s=1,\dots ,S,\ h=0,\dots ,H,\ k=1,\dots ,K, \nonumber \\&{} \ i=0,\dots ,I,\ a=1,\dots ,A_i \end{aligned}$$

(7)

$$\begin{aligned}&{}\sum _{j=0}^{I}\sum _{p=1}^{A_i}\sigma _{sjp}x_{shkjp}\ge \sigma _{sia}\pi _{hkia}-(1-z_{shk})M \ \ \ \ \ \ \ \text {for all} \ s=1,\dots ,S, \nonumber \\&{} h=0,\dots ,H,\ k=1,\dots ,K,\ i=0,\dots ,I,\ a=1,\dots ,A_i\;. \end{aligned}$$

(8)

The following five sets of constraints hold for all price list updates. One price list is assigned to every customer segment (see constraints (4)). Constraints (5) ensure that each customer segment chooses one PPPC of the price list it is assigned to. Constraints (6) enforce that for every product exactly one price point is chosen in every price list, i.e. all customers get a complete price list for all products. It is ensured by constraints (7) that customers can only choose from PPPCs that are offered. Constraints (8) represent the well-known incentive compatibility constraints: Every customer segment chooses the available PPPC that ranks highest in its preference list. Besides, it is ensured that only the PPPCs of the respective price lists are considered.

The last group of constraints, constraints (9–11), determine the costs of the services that are sold.

$$\begin{aligned}&{} \sum _{s=1}^{S}\sum _{h=0}^{H}\sum _{k=1}^{K}\sum _{a=1}^{A_i}\theta _{shkia}=\sum _{l=1}^{L_i}d_{il} \ \ \ \ \ \ \ \text {for all} \ i=1,\dots ,I \end{aligned}$$

(9)

$$\begin{aligned}&{} d_{il}\le \Delta Q_{il}\delta _{il} \ \ \ \ \ \ \ \text {for all} \ i=1,\dots ,I,\ l=1,\dots ,L_i \end{aligned}$$

(10)

$$\begin{aligned}&{} d_{i,l-1}\ge \Delta Q_{i,l-1}\delta _{il} \ \ \ \ \ \ \ \text {for all} \ i=1,\dots ,I,\ l=2,\dots ,L_i\;. \end{aligned}$$

(11)

Constraints (9) ensure that costs are captured for all services that are sold. In every interval of the linear cost function the total amount of service units sold is restricted by the interval length $\Delta Q_{il}=Q_{il}-Q_{i,l-1}$ with $\Delta Q_{iL_i}=\infty$ for all $i\in \{1,\dots ,I\}$. Furthermore, if the total amount of services extends into an adiacent interval $l+1$ of the cost function, the total amount of service units sold in the previous interval $l$ is enforced to $\Delta Q_{il}$. That holds for every service (see constraints (10) and (11)).

4 Computational Experiments

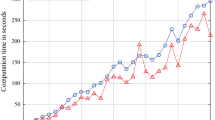
We implemented the mixed-integer linear program in IBM ILOG OPL and solve small instances by means of IBM ILOG CPLEX 12.5 to optimality. All of the tests were performed on a server architecture with an Intel(R) Core(TM) i7 CPU at 2.80 GHz, 8 GB RAM, and Windows 7 Enterprise. In the computational experiments we focus on the effects of some essential contributions to the product line pricing literature on the demand side: We allow the seller to adopt a dynamic pricing strategy and offer different prices for the products to different customer segments. That means, the seller is able to offer $K$ price lists to the customer segments and make $H$ price list updates. We fix the number of customer segments to $5$, consider $5$ products with $5$ price points, a selling season with a length of $12$ and piecewise linear cost functions with two intervals. We vary the number of price lists $K$ from $1$ to $3$ and the number of price updates $H$ from $0$ to $4$. The computation times are given in Table 3. Referring to the total profits, the model with $K=1$ and $H=0$ serves as a benchmark. Table 4 shows the improvements of the total profits in percentage terms.

Table 3 Computation times in seconds

Table 4 Improvements of total profits

For our computational experiments, we chose an instance where the flexibility for the seller gained by the incorporation of more price lists and price list updates helps to allocate the demand in a way to avoid the high costs of the spot market. Hence, total profits increase significantly as the number of price lists as well as price list updates is raised. Furthermore, the computing times are increasing significantly as well. As the instances are getting bigger in practice, the service provider has to decide how much (computing) time he wants to invest in order to make his pricing decisions. Furthermore, he must determine how many price lists and price list updates are applicable from a marketing and from a technical point of view.

5 Conclusion

In this paper, we address a service provider’s product line pricing problem. Our approach differs from the standard product line pricing problem introduced in the literature in multiple ways. The main contributions on the demand side are the modelling of customer behavior by using preference lists, the incorporation of dynamic pricing and the possibility for the seller to set different prices for the products for different customer segments. On the supply side, the costs of supplying a single unit of a service are not constant but depend on the total amount of service units sold. For this purpose, we introduce piecewise linear cost functions affiliated with each service total amount of units sold.