Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

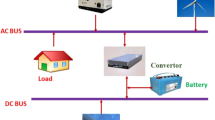
Most research on stand-alone hybrid energy systems is focused on design and simulation rather than optimization of system control [2]. In this work, we discuss the latter problem in terms of finding a welfare-maximal power distribution of a hybrid energy system supplying a small community. We consider a decentralized system, where every household has its own solar panel, battery, and an optional diesel generator as backup device. The households are connected via a mini-grid to facilitate energy trading. The considered system is extended by an additional smart component that is able to defer the operation times of so-called smart devices on the consumer side to times with electricity excess.

2 Model Derivation

In this section, we derive the objective function together with the most important constraints of our model. We consider a set \(\fancyscript{N}=\{1,\dots ,N\}\) of households connected through a grid. The set of households equipped with a diesel generator is denoted by \(\fancyscript{N}_D \subseteq \fancyscript{N}\). Our planning horizon is subdivided into a set \(\fancyscript{I}\) of time intervals of length one hour. Further, we assume all households to have similar consumption and production possibilities and that the number of households is high enough such that no household has any market power.

2.1 Consumer Problem

We distinguish between profile loads and so called deferrable loads. For profile loads, the variables \(x^{\text {pro}}_{n,i} \in \fancyscript{X}_{n,i}^{\text {pro}}\) denote the aggregated demands of a household \(n\) in time interval \(i\) for all \(n \in \fancyscript{N}\) and \(i \in \fancyscript{I}\). The bounded sets \(\fancyscript{X}_{n,i}^{\text {pro}}\subset \mathbb {R}_{\ge 0}\) are the possible consumption quantities, which depend on historical load profiles but are assumed to be given herein. The demand functions \(d_{n,i}(\pi ): [0,\overline{\pi }]\rightarrow \fancyscript{X}_{n,i}^{\text {pro}}\) give the quantities of maximal utility for every price \(\pi \in [0,\bar{\pi }]\) and are supposed to be strictly decreasing, bounded and continuous. The inverse demand, i.e., the marginal willingness to pay, is denoted by \(p_{n,i}(x_{n,i}^{\text {pro}}):\fancyscript{X}_{n,i}^{\text {pro}}\rightarrow [0,\overline{\pi }]\). Then, the gross benefit \(B_{n,i}\) of consumer \(n\) at time interval \(i\) is given by

$$\begin{aligned} B^{\text {pro}}_{n,i}(x_{n,i}^{\text {pro}}) = \int \limits _{0}^{x_{n,i}^{\text {pro}}}p_{n,i}(z)\,dz. \end{aligned}$$
(1)

In our model, we incorporate piecewise linear approximations of the demand functions by means of the so-called incremental method [4] and are thus able to give a closed-form expression of the gross benefit. Suppose that all consumers get the same price, then let \((\bar{x}_{n,i,h},\;\bar{\pi }_h)\), with \(h\in \fancyscript{H}\), denote the consumption bundles at the breakpoints of the approximation of the demand function \(d_{n,i}\). Then, for each \(n \in \fancyscript{N}\) and \(i \in \fancyscript{I}\) the demand together with the marginal willingness to pay is modeled by

$$\begin{aligned} x_{n,i}^{\text {pro}}&= \bar{x}_{n,i,1} + \sum _{h=1}^{|\fancyscript{H}|-1}(\bar{x}_{n,i,h+1}-\bar{x}_{n,i,h})\,\delta _{i,h},\end{aligned}$$
(2a)
$$\begin{aligned} \pi _{i}&= \bar{\pi }_{1}+\sum _{h=1}^{|\fancyscript{H}|-1}(\bar{\pi }_{h+1}-\bar{\pi }_{h})\,\delta _{i,h}, \end{aligned}$$
(2b)
$$\begin{aligned} 1&\ge \delta _{i,1} \ge z_{i,1} \ge \cdots \ge z_{i,|\fancyscript{H}|-2} \ge \delta _{i,|\fancyscript{H}|-1} \ge 0, \end{aligned}$$
(2c)
$$\begin{aligned} z_{i,h}&\in \{0,1\}, \quad \text{ for } h=1, \ldots , |\fancyscript{H}|-2. \end{aligned}$$
(2d)

Thus, we obtain a unique representation of each \(x_{n,i}^{\text {pro}}\in \fancyscript{X}_{n,i}^{\text {pro}}\) in terms of the additional variables \(\delta _{i} = (\delta _{i,1}, \ldots , \delta _{i,|\fancyscript{H}|})\). A similar derivation of the gross benefit, according to a piecewise linear demand function, has been given in [5]. In our case, the gross benefit, illustrated in Fig. 1, of consumer \(n\) at time interval \(i\) is given by

$$\begin{aligned} B^{\text {pro}}_{n,i}(\delta _{i})=\,&(\bar{x}_{n,i,h+1}-\bar{x}_{n,i,h})\,(\delta _{i,h}-1)\, \bar{\pi }_{h}\nonumber \\&+\frac{1}{2}(\bar{x}_{n,i,h+1}-\bar{x}_{n,i,h})\, (\bar{\pi }_{h+1}-\bar{\pi }_{h})\,(\delta _{i,h}^2-1) + \bar{x}_{n,i,|\fancyscript{H}|}\,\bar{\pi }_{|\fancyscript{H}|}. \end{aligned}$$
(3)
Fig. 1
figure 1

Gross benefit of consumer \(n\) at time interval \(i\) for a consumption of \(x^*_{n,i}\) and price \(\pi _i^*\)

Full size image

In contrast to profile loads, deferrable loads are not time dependent but rather have a specified run time and energy demand \(X^{\text {def}}_{n,|\fancyscript{I}|}\in [\underline{X}^{\text {def}}_{n},\overline{X}^{\text {def}}_{n}]\). The smart component must decide at which point in time, within a predefined time window \([\underline{i}_n,\overline{i}_n]\subseteq \fancyscript{I}\), such a consumer is turned on. By \(x^{\text {def}}_{n,i}\) we denote the amount of power used for the smart devices of household \(n\) in time interval \(i\) for all \(n \in \fancyscript{N}\) and \(i \in \fancyscript{I}\). The set of possible consumption quantities is described in terms of binary variables \(s^{\text {on}}_{n,i}\) and \(s_{n}\). The variables \(s_n\) indicate whether the energy demand of household \(n\) is met within the planning horizon, while \(s^{\text {on}}_{n,i}=1\), if and only if voltage is fed to the deferrable loads of household \(n\) during time interval \(i\), i.e.,

$$\begin{aligned} \underline{x}^{\text {def}}_{n}\, s^{\text {on}}_{n,i}&\le \;\, x^{\text {def}}_{n,i}\;\, \le \overline{x}^{\text {def}}_{n}\, s^{\text {on}}_{n,i},&\forall n\in \fancyscript{N}\,\forall i\in \fancyscript{I}, \end{aligned}$$
(4a)
$$\begin{aligned} X^{\text {def}}_{n,i}&= X^{\text {def}}_{n,i-1} + x^{\text {def}}_{n,i},&\forall n\in \fancyscript{N}\,\forall i\in \fancyscript{I}, \end{aligned}$$
(4b)
$$\begin{aligned} \underline{X}^{\text {def}}_{n}\, s_n&\le X^{\text {def}}_{n,|\fancyscript{I}|} \le \overline{X}^{\text {def}}_{n}\, s_{n},&\forall n\in \fancyscript{N},\end{aligned}$$
(4c)
$$\begin{aligned} s^{\text {on}}_{n,i},\, s_n&\in \{0,1\},&\forall n\in \fancyscript{N}\,\forall i\in \fancyscript{I}. \end{aligned}$$
(4d)

The gross benefit \(B^{\text {def}}_n(X^{\text {def}}_{n,|\fancyscript{I}|})\) obtained from the satisfaction of demands from deferrable loads of each household \(n \in \fancyscript{N}\) is linear in the amount of energy consumed for these loads over the whole planning horizon if \(X^{\text {def}}_{n,|\fancyscript{I}|}\in [\underline{X}^{\text {def}}_{n},\overline{X}^{\text {def}}_{n}]\) and zero otherwise.

2.2 Producer Problem

The variables \(y^{\text {sol}}_{n,i} \in \fancyscript{X}^{\text {sol}}_n \subseteq \mathbb {R}_{\ge 0}\) denote the quantity of power produced by the solar panel of household \(n\) in time interval \(i\) for all \(n\in \fancyscript{N}\) and \(i\in \fancyscript{I}\). The corresponding cost functions \(C^{\text {sol}}_n(y^{\text {sol}}_{n,i})\) are supposed to be affine.

Next, we introduce a variable \(l_{n,i} \in [0,l^{\max }_n]\) for the battery charge level of household \(n\) in time interval \(i\) for all \(n \in \fancyscript{N}\) and \(i \in \fancyscript{I}\). The capacity of the battery in household \(n\) is denoted by \(l^{\max }_n\). Additionally, we assume fixed initial battery charge levels \(\overline{l}_{n,0}\) and lower bounds \(l^{\min }_n\) for the battery charge levels at the end of the planning horizon to be given. The variable \(l^+_{n,i} \in [0, l^{+}_{n,\max }]\) denotes the power used to charge the battery and \(l^-_{n,i} \in [0,l^{-}_{n,\max }]\) denotes the power withdrawn from the battery of household \(n\) during time interval \(i\). Discharging a battery is considered as a production facility with affine cost functions \(C^{\text {bat}}_n(l^-_{n,i})\). To properly model battery charge levels we add the following constraints:

$$\begin{aligned} l_{n,i}&= l_{n,i-1} + l^+_{n,i} - l^-_{n,i},&\qquad \quad \forall n\in \fancyscript{N}\,\forall i\in \fancyscript{I}, \end{aligned}$$
(5a)
$$\begin{aligned} l^+_{n,i}&\le l^{+}_{n,\max }\, b_{n,i},&\qquad \qquad \qquad \forall n\in \fancyscript{N}\,\forall i\in \fancyscript{I}, \end{aligned}$$
(5b)
$$\begin{aligned} l^-_{n,i}&\le l^{-}_{n,\max }\, (1-b_{n,i}),&\qquad \quad \forall n\in \fancyscript{N}\,\forall i\in \fancyscript{I}, \end{aligned}$$
(5c)
$$\begin{aligned} b_{n,i}&\in \{0,1\},&\qquad \qquad \qquad \; \forall n\in \fancyscript{N}\,\forall i\in \fancyscript{I}. \end{aligned}$$
(5d)

Finally, for the diesel generators, we assume linear variable costs with non-sunk fixed costs \( C^{\text {gen}}_n(s^{\text {gen}}_{n,i},y^{\text {gen}}_{n,i})= c^{\text {gen}}_{n,v}\,y^{\text {gen}}_{n,i} + c^{\text {gen}}_{n,f}\, s^{\text {gen}}_{n,i}\) as in [1]. Here, the binary variables \(s^{\text {gen}}_{n,i} \in \{0,1\}\) are used to decide whether the diesel generator of household \(n \in \fancyscript{N}_D\) is used for production during time interval \(i\). The amount of generated power is denoted by \(y^{\text {gen}}_{n,i} \in \fancyscript{X}^{\text {gen}}_n \subseteq \mathbb {R}_{\ge 0}\). The non-sunk fixed costs and the variable costs of the generators are denoted by \( c^{\text {gen}}_{n,f}, c^{\text {gen}}_{n,v} > 0\), respectively.

In general, the supply correspondence, i.e., the set of profit maximizing production quantities, without battery discharge, for household \(n \in {\fancyscript{N}}_D\) and given price \(\pi _{i}^{*}\) at time interval \(i \in {\fancyscript{I}}\) is given by

$$\begin{aligned} \begin{array}{rl} \text {arg max} &{} \quad \pi _{i}^{*}\, (y^{\text {sol}}_{n,i} + y^{\text {gen}}_{n,i}) - C^{\text {sol}}_n(y^{\text {sol}}_{n,i}) - C^{\text {gen}}_n(s^{\text {gen}}_{n,i},y^{\text {gen}}_{n,i}) \\ \text {s.t.}\quad &{} \qquad \quad y^{\text {sol}}_{n,i} \in {\fancyscript{X}}^{\text {sol}}_n, \\ \quad &{} \qquad \left( \begin{matrix}y^{\text {gen}}_{n,i}\\ s^{\text {gen}}_{n,i}\end{matrix}\right) \in {\fancyscript{X}}^{\text {gen}}_n. \end{array} \end{aligned}$$
(6)

Since any demand \(d(\pi ^{*}) \in (0, y^{\text {gen}}_{\max })\) would potentially lead to infeasibility of the overall model, using a supply function is not appropriate for cost structures with non-sunk fixed costs as illustrated in Fig. 2. In order to allow the whole set of profitable outputs instead, we incorporate the profit maximization problem underlying (6) into our model.

Fig. 2
figure 2

Diesel generator costs: The corresponding production function is drawn with thick lines. Note, that for the price \(\pi ^*\) the producer is indifferent between producing either \(y_{\max }\) or nothing at all. The area, where production is profitable, is depicted in gray

Full size image

2.3 Welfare-Maximal Power Distribution

The objective of our model is to maximize the global welfare of the whole community. That is the summed gross benefits of the loads minus the production costs:

$$\begin{aligned} \max&\sum _{n \in \fancyscript{N}}\sum _{i \in \fancyscript{I}} B^{\text {pro}}_{n,i}(\delta _{i}) + \sum _{n \in \fancyscript{N}} B^{\text {def}}_n(X^{\text {def}}_{n,|\fancyscript{H}|}) - \sum _{n \in \fancyscript{N}_D}\sum _{i \in \fancyscript{I}} C^{\text {gen}}_n(s^{\text {gen}}_{n,i},y^{\text {gen}}_{n,i}) \nonumber \\&-\sum _{n \in \fancyscript{N}}\sum _{i \in \fancyscript{I}} \left( C^{\text {sol}}_n(y^{\text {sol}}_{n,i}) + C^{\text {bat}}_n(l^-_{n,i})\right) , \end{aligned}$$
(7)

subject to the constraints from above. Due to the gross benefit of the profile loads, the objective function is (convex) quadratic. Additionally, we have to add a clearing condition:

$$\begin{aligned} \sum _{n\in \fancyscript{N}} \left( x^{\text {pro}}_{n,i} + x^{\text {def}}_{n,i} + l^+_{n,i}\right) = \sum _{n\in \fancyscript{N}} \left( y^{\text {sol}}_{n,i} + l^-_{n,i} \right) + \sum _{n \in \fancyscript{N}_D} y^{\text {gen}}_{n,i}, \qquad \forall i\in \fancyscript{I}. \end{aligned}$$
(8)

3 Results and Conclusions

We performed computational experiments on several test instances with 3–200 households, i.e., \(|\fancyscript{N}| \in \{3,5,15, 50, 100, 200\}\) and \(|\fancyscript{I}| \in \{24,48,72,96\}\), where every fifth household is equipped with a diesel generator. We are thankful to the Siemens AG, for providing us with load and production profiles, see also [3]. All computations have been carried out with a time limit of 6 h on a computer with a 6-Core AMD Opteron 2435 processor with 2.6 GHz and 64 GB RAM. As MIQP-solver we used Cplex 12.5.0.0, which has been instructed to terminate, as soon as the relative optimality gap falls below 5 %. From the results we observed that only some of the largest instances, with 200 households and 96 time intervals, hit the time limit, whereas smaller instances, with up to 15 households, can reliably be solved within a few minutes.

Figure 3 illustrates the results for the single household, which is equipped with a diesel generator, from the solution of an instance with \(|\fancyscript{N}|=3\) and \(|\fancyscript{I}|=48\). To meet all demands, the power generated by the solar panels is not sufficient. Thus, the diesel generator runs once a day.

Fig. 3
figure 3

Power distribution of the household with diesel generator

Full size image

The power distributions of the two other households are basically similar, i.e., the deferrable loads are operated by the diesel generator or the excess power from the solar panel. The prioritization of the loads depends on the given demand and gross benefit functions. Besides, these functions ensure that every household receives as much energy as it is willing to pay.

Until now, our model does not account for compensation payments for households producing for other ones. For instance, the Shapley Value [6] defines fair and unique compensation payments for every participant. Consequently, future research could focus on an incorporation of the Shapley Value into our model. Beyond, polyhedral studies could help to close the gaps earlier and speed up computation.