Building Non Singular Morse-Smale Flows on 3-Dimensional Lens Spaces

Abstract

Fat handles are flow manifolds diffeomorphic to tori; therefore, each attractive (repulsive) fat handle can be identified along its boundary with a solid torus with one repulsive (attractive) orbit in its core in such a way that a NMS flow on a lens space L(p, q) is obtained.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Morse-Smale flows are the structurally stable flows on 2-dimensional manifolds, forming a dense open subset of C^∞ -vector fields. For the three dimensional case, Morse-Smale flows are not dense but they define an open set in the set of C¹-vector fields; in most cases they can be studied from Non-Singular Morse-Smale flows.

Non Singular Morse Smale flows (NMS for short) have been widely studied. D. Asimov [1] showed that every manifold with Euler characteristic zero admits this type of flows unless its dimension is three. J.W. Morgan [7] proved that a 3-dimensional manifold prime to S ² × S ¹ admits such flows if and only if it is a graph manifold.

This kind of flows are characterized by their non-wandering set consisting of a finite number of closed hyperbolic orbits and the transversal intersections of their stable and unstable manifolds.

It is not easy to find a complete characterization of flows defined on three-dimensional manifolds. Some achievements in this direction has been made by M. Wada [8], who obtains the topological characterization of the links of periodic orbits in S ³. This characterization for NMS flows in the space $S^{2} \times S^{1}$ have been obtained by A. Cordero et al. in [6].

Despite these important results, different NMS flows can be characterized by the same link. Therefore, to obtain the complete description of a flow it is necessary to reproduce its phase space. To obtain the phase portrait is very hard for 3-manifolds, especially when the number of periodic orbits increases. In a previous paper [2], we obtain some NMS flows on lens spaces, with only one saddle orbit.

We prove in [5] that flows with unknotted and unlinked saddle orbits, denoted as $\mathcal{F}_{A}\left (S^{3}\right )$, can be obtained from the identification of fat handles along their boundaries.

From these results, in this paper we obtain flows on lens spaces by identifying fat handles (Proposition 4): one attractive (repulsive) fat handle is identified with one solid torus with one repulsive (attractive) orbit in its core in such a way that a flow on a lens space L(p, q) is obtained.

Now, we recall some definitions and results on which our work is based.

A non singular Morse-Smale flow (or NMS for short) is a flow without fixed points, consisting of a finite number of hyperbolic periodic orbits where the intersections of stable and unstable manifolds of the saddle orbits are transversal.

D. Asimov [1] and J.W. Morgan [7] established a correspondence between NMS flows and round handle decompositions of the corresponding manifold. These flows are defined on flow manifolds. A flow manifold is a pair $(M,\partial _{-}M)$ where a nonsingular vector field on M exists, pointing inwards on $\partial _{-}M$ and outwards on $\partial _{+}M$ and satisfying $\partial M = \partial _{-}M \cup \partial _{+}M$, $\partial _{-}M \cap \partial _{+}M = \varnothing$.

Proposition 1 (Morgan)

Given a flow manifold (X, $\partial _{-}$ X) with a NMS flow, then (X, $\partial _{-}$ X) has a round handle decomposition whose core circles are the closed orbits of the flow.

For the case of dimension 3, the round handles are diffeomorphic to tori and correspond to 0-handles when there is a repulsive periodic orbit in the core, to 2-handles if there is an attractive periodic orbit in the core and to 1-handles if the orbit is a saddle; 0, 1 and 2 are the indices of the periodic orbits. A set of indexed periodic orbits is called an indexed link.

Fig. 1

Round 1-handle

The round handle decomposition for a compact, orientable 3-manifold M was modified by Morgan:

$$\displaystyle{ \varnothing = M_{0} \subset M_{1} \subset \cdots \subset M_{i} \subset M_{i+1} \subset \cdots \subset M_{N} = M }$$

(1)

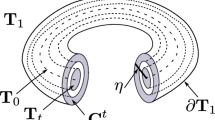
where each manifold M _i , called fat round handle, is obtained from M _i−1 by attaching a round 1-handle by means of one or two attaching circles (see Fig. 1).

The round handle decomposition of a NMS flow gives the sequence of 1-handle attachments. Each attachment on a fat round handle yields to a new fat round handle. In the following section we show in detail these fat handles and we see the different types of fat handles obtained when the number of saddle orbits increases.

2 Fat Handles

The 3-sphere S ³ is obtained joining two solid tori, by identifying transversal circles of one torus with longitudinal circles of the other.

Therefore, a polar NMS flow on S ³ can be obtained by identifying properly one repulsive and one attractive tori along their boundaries.

In [5] we obtain NMS flows on S ³ with unknotted and unlinked saddle orbits, denoted by $\mathcal{F}_{A}(S^{3})$, by identifying one repulsive and one attractive tori along their boundaries. These tori, with a flow going inwards or outwards, correspond to the fat round handles.

Given a flow $\varphi \in \mathcal{F}_{A}(S^{3})$, a repulsive fat handle is obtained by removing one attractive orbit and an attractive fat handle is obtained by removing one repulsive orbit. The basic fat round handles are the fat handles with one saddle orbit (see Figs. 2 and 3) and we denote them by describing the periodic orbits that contain. If the fat handle has an attractive or repulsive orbit in its core we refer to it as thick torus; if it has no orbit in its core, we refer to it as solid torus.

In the following, let h denote the Hopf link, let d denote a trivial separated knot corresponding to an attractive or repulsive orbit, let u denote a trivial separated knot corresponding to a saddle orbit and let ⋅ denote the separated sum of links.

Fig. 2

Basic fat handles of class [I]. (a) Repulsive fat round handle: (h.d.u); (b) Attractive fat round handle: (h.d.u); (c) Repulsive fat round handle: (d.d.u); (d) Attractive fat round handle: (d.d.u)

Fig. 3

Basic fat handles of class [II] and [III]

We classify the fat handles obtained from $\mathcal{F}_{A}(S^{3})$ flows in the following way:

• A repulsive (attractive) fat handle belongs to class $\left [I\right ]$ if it corresponds to a thick torus with a repulsive (attractive) orbit filling the essential hole of the torus and the invariant manifolds of the saddles orbits go outwards (inwards) the torus by means of inessential circles.

• A repulsive (attractive) fat handle belongs to class $\left [\mathit{II}\right ]$ if it corresponds to a solid torus, the invariant manifolds of the saddles orbits go outwards (inwards) the torus by means of essential circles and there is not any attractive or repulsive orbit in the canonical region of the identification.

• A repulsive (attractive) fat handle belongs to class $\left [\mathit{III}\right ]$ if it corresponds to a solid torus, the invariant manifolds of the saddles orbits go outwards (inwards) the torus by means of essential and inessential circles and there is one attractive or repulsive orbit, filling a non essential hole in the torus, in the canonical region of the identification.

From the identification of one attractive and one repulsive basic fat handles we obtain the $\mathcal{F}_{A}(S^{3})$ flows with two saddle orbits; by removing one repulsive (attractive) orbit in these flows we obtain iterated fat handles with two saddles. Following this process we obtain fat handles with n saddle orbits (see [5]) and we prove that they can be classified in one of these three classes defined above.

Proposition 2

For $\mathcal{F}_{A}\left (S^{3}\right )-$ flows, a fat handle with n saddle orbits belongs to class $\left [I\right ],$ $\left [\mathit{II}\right ]$ or $\left [\mathit{III}\right ].$

When there are not heteroclinic trajectories connecting saddles, a fat handle with n saddle orbits is obtained by the iterated connected sum of tori [3]. Two examples are showed in Fig. 4.

Fig. 4

Fat handles of class $\left [I\right ]$ and [III]

Let us remark that the identification along their boundaries of two fat handles without any orbit in their cores yields to a transversal intersection of two invariant manifolds of saddle orbits (see [4]).

Along the proof of these results, in [4], all the flows $\varphi$ with n unlinked saddles are obtained. Therefore,

Theorem 1

A flow $\varphi \in \mathcal{F}_{A}\left (S^{3}\right )$ with n saddle orbits can be obtained by identifying fat handles along their boundaries.

This result enables to build any flow on the 3-sphere with unlinked and unknotted saddle orbits. We reproduce the complete phase space of these NMS flows on the 3-sphere when two fat handles are identified along their boundaries in such a way that S ³ is obtained; that is, by identifying longitudinal circles of one of the tori with the transversal circles of the other torus. Let us remark that the fat handles must be properly identified in order to reach a flow on S ³. For example, a fat handle of class [I] can not be identified with fat handle of class [II] because a bitorus is obtained (see Fig. 5) and the boundaries of round handles embedded in S ³ must be tori.

Fig. 5

Identification of one fat handle of class $\left [I\right ]$ and one of class $\left [\mathit{II}\right ]$

This method also permits to obtain NMS flows on different 3-manifolds if the circles of the tori are identified in another way. Following the same process used on S ³ we build NMS flows on other lens spaces. Let us notice that, for the 3-sphere all the orbits are local and we can obtain a flow by identifying the fat handles along their boundaries. But for any L(p, q) lens space there can be local and global orbits and a very complicated picture may appear. So, we only can assure a NMS flow if we identify one of the previous fat handles with one torus with one attractive (or repulsive) orbit in its core.

3 Building Flows in Lens Spaces

The lens space $L\left (p,q\right )$ is the 3-manifold of Heegaard genus 1 whose Heegaard diagram consists of a $\left (p,q\right )-$ torus knot on the surface of a solid torus; namely, $L\left (p,q\right )$ is the result of joining two solid tori τ ₁ and τ ₂ via a homeomorphism $h: \partial \tau _{1} \rightarrow \partial \tau _{2}$ where h takes a meridian m on $\partial \tau _{1}$ to a $\left (p,q\right )$-torus knot on $\partial \tau _{2}$. The 3-manifold resulting directly from this identification is difficult to visualize except, perhaps, $L\left (1,0\right )$ that corresponds to the 3-sphere and $L\left (0,1\right )$, equivalent to $S^{2} \times S^{1}.$ As we have seen before S ³ is obtained by identifying latitudes on $\partial \tau _{1}$ with meridians on $\partial \tau _{2}$ and vice versa. Similarly, $S^{2} \times S^{1}$ is obtained by identifying longitudinal circles on $\partial \tau _{1}$ with longitudinal circles on $\partial \tau _{2}$ and transversal circles with transversal circles. We can see these spaces in Figs. 6 and 7. In both cases, one attractive and one repulsive orbit are in the core of each solid torus, and they are linked. So, the easier flow in both spaces is a polar flow corresponding to the Hopf link.

Fig. 6

S ³

Fig. 7

$S^{2} \times S^{1}$

Proposition 3

A polar flow always can be obtained on a lens space.

Proof

The polar flow is obtained by the identification along their boundaries of one torus with an attractive orbit (a 2-handle) in its core and another torus with a repulsive orbit in its core (a 0-handle). This identification is made via a homeomorphism $h: \partial \tau _{1} \rightarrow \partial \tau _{2}$ where h takes a meridian m on $\partial \tau _{1}$ to a $\left (p,q\right )$-torus knot on ∂ τ ₂. We have the simplest round handle decomposition and its corresponding NMS flow on a lens space $L\left (p,q\right )$ is obtained. This flow is called polar flow and the set of its periodic orbits is the Hopf link. □ 

The fat handles showed in Sect. 2 are flow manifolds diffeomorphic to tori; therefore, each of these attractive (repulsive) fat handles can be identified with one solid torus with one repulsive (attractive) orbit in its core in such a way that a flow on a lens space L(p, q) is obtained.

For example, we show in Fig. 8a the flow on S ³ obtained by identifying longitudinal circles of the repulsive basic fat handle h ⋅ d ⋅ u with transversal circles of one attractive solid torus and we show in Fig. 8b the flow on S ² × S ¹ obtained by identifying longitudinal circles of the repulsive basic fat handle h ⋅ d ⋅ u with longitudinal circles of one attractive solid torus.

Let us observe that the link of periodic orbits is the same for both flows, h ⋅ h ⋅ u, but the topology of the orbits is different. All the periodic orbits embedded in S ³ are local whereas in $S^{2} \times S^{1}$, some of them can be global. Recall that a local orbit is an orbit that can be isolated in a three-dimensional disk D ³ and an global orbit can not be isolated in a D ³.

Fig. 8

NMS flows on different lens spaces. (a) NMS flow defined on S ³; (b) NMS flow defined on $S^{2} \times S^{1}$

Similarly, from the flows on S ³ we can obtain NMS flows on different lens spaces depending on the way the tori are identified.

Proposition 4

Given a flow on one attractive (repulsive) fat handle τ ₁ , a NMS flow on a lens space L(p,q) can be obtained by identifying meridians on $\partial \tau _{1}$ with (p,q)-torus knots on the boundary of a repulsive (attractive) solid torus τ ₂ .

Proof

As we said before, L(p, q) can be formed by the identification of two solid tori τ ₁ and τ ₂, via a homeomorphism $h: \partial \tau _{1} \rightarrow \partial \tau _{2}$ where h takes a meridian m on $\partial \tau _{1}$ to a $\left (p,q\right )$-torus knot on $\partial \tau _{2}$.

We proved in [5] that the fat handles with n unknotted and unlinked saddles orbits are tori. So, we can consider τ ₁ as one repulsive (attractive) fat handle with n saddle orbits and τ ₂ as one solid torus with one attractive (repulsive) orbit in its core, i.e., τ ₂ is a 2-handle (0-handle).

These two tori are identified by means the homeomorphism previously defined from $\partial \tau _{1}$ onto $\partial \tau _{2}$.

As τ ₂ has only one attractive (repulsive) orbit in its core, the whole flow going inwards through $\partial \tau _{2}$ is collected by this orbit. The result is a NMS flow on the 3-dimensional lens space $L\left (p,q\right )$. □