Minimal Gain Time Marching Schemes for the Construction of Accurate Steady-States

Abstract

Accurate reference solutions are very important in stability analysis, where they must act as a reliable base-state. They are also quite useful for unsteady numerical simulations, where they play key roles as initial conditions and in the implementation of boundary conditions, such as buffer zones. Quite often they are approximate solutions for a simplified version of the particular problem at hand, such as boundary-layer solutions. However, these approximate solutions are usually not available, their development is problem dependent and they may not be accurate enough. Hence, there is a need for methodologies that are capable of generating steady-states for arbitrary unsteady differential models. One attempt in this direction is the selective frequency damping technique, despite being developed for problems with a well defined self-excitation frequency. Another attempt to do so is the physical-time damping technique, but temporal dissipation is proportional to the time step. Since numerical instability can keep this time step too small in many nonlinear problems, this technique may not be able to introduce enough dissipation for the damping of all perturbations in very unstable flows. The present work overcomes this problem by noting that optimal damping is not introduced through maximum temporal dissipation, but minimal gain. The implicit Euler scheme employed in the physical-time damping technique achieves both in the limit of infinite CFL numbers, which usually cannot be imposed due to nonlinear effects. This time marching scheme was modified in order for its minimal gain to occur at smaller CFL numbers. Several test cases confirm the efficacy of this new approach.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Reference solutions are not only useful but often required for numerical simulation studies in many different areas. Stability analysis is one such example, where the reference solution should be a representative profile of the flow under consideration. It is usually called base flow in this context. In order to verify the stability of a given flow field, one must perturb its base flow and measure the growth or decay of the perturbations introduced. In a rigorous sense, this base flow should be a solution of the unperturbed governing equations, although early studies employed approximate profiles that fit well available experimental data [1]. However, such a procedure might lead to incorrect predictions, since numerical residues in the base flow become forcing terms in the perturbation governing equations. This difficulty is transformed into an asset by the Method of Manufactured Solutions for code verification [2, 3], where the force term created is reintroduced into the governing equations. Hence, an approximate solution of the original governing equations becomes an exact solution of the modified governing equations. Both approaches have been blended recently, where a linear stability analysis of a time-averaged solution is performed through direct numerical simulations of the modified governing equations [4]. On the other hand, this approach makes the numerical residue an integral part of the model, which undermines its ability to reproduce the correct flow physics. A preferred alternative in this field is the development of similarity solutions of a simplified model to be used as base flows [5]. However, this may not be enough to improve accuracy in the analysis of complex flow fields. Linear stability analyzes of transverse jets using approximate [6] and similar [7] profiles as base flows show opposite trends for the range of unstable frequencies with respect to the jet to cross flow velocity ratio. This is compelling evidence that an inaccurate base flow can and will lead to qualitatively incorrect predictions [8]. As the numerical tools available for eigenvalue calculations improved over the years, the computer time required by a linear stability analysis of complex base flows became smaller to the point such studies are commonplace nowadays [9]. Hence, the need for new methods capable of generating accurate base flows is greater than ever.

Initial and boundary conditions are yet another example where accurate reference solutions are important. Both approximate and similar solutions introduce unwanted oscillations when used as initial conditions in the unsteady numerical simulation of absolutely unstable mixing-layers [10]. Although the amplitude of these oscillations is much smaller in the latter case, their frequency content is much richer as well. This problem manifests itself in the calculation of the temporal growth rates, which can have relative errors as high as 18 % due to the use of approximate initial conditions even though high order schemes are employed [11]. It is important to emphasize another problem caused by inaccurate initial conditions. Their use in the simulation of flows around two-dimensional bodies lead to the presence of large perturbations at early times [12, 13]. Hence, large simulation times are required for these numerical waves to be convected out of the simulated domain before accurate flow statistics can be extracted. Accurate reference solutions are also very useful for a type of boundary condition known as absorbing layers [14] or sponge zones [15], since they can improve its effectiveness. This is specially relevant in aeroacoustics [16] and receptivity [17] studies, where both problems become quite worse since the perturbations of interest are much smaller in magnitude than the vorticity waves that feed them. In the simulation of acoustic fields over airfoils [18, 19], these problems were minimized with the use of steady-states as reference solutions for both initial condition and sponge zones. A similar procedure was adopted to minimize numerical errors in receptivity studies of compressible mixing-layers [20]. Hence, a new method that is able to generate steady-states from the governing equations of interest would yield the most accurate reference solutions available.

A few methods exist today for the construction of accurate steady-states. The most traditional one is the class of Newton iteration methods, usually adapted to use continuation techniques as well [21]. However, they are very sensitive to initial conditions, require heavy computational resources for large systems and have severe convergence difficulties for globally unstable problems. Selective frequency damping (SFD) was developed to overcome these difficulties [22]. It works by introducing a source term in the governing equations that forces the time marching scheme to converge towards a reference solution, which is a filtered version of the unsteady solution being marched in time. Since this source term disappears at steady-state, the reference solution becomes the steady-state in this limit. Furthermore, it is quite simple to implement and requires the adjustment of only two additional parameters. However, this method has been applied to flows that only have a single dominant self-excited frequency that needs to be filtered. Applications where a broad range of frequencies must be damped, such as convectively unstable flows with intrinsic sources of noise, have yet to be investigated with this method. Recently, Physical-Time Damping (PTD) was developed to generate steady-states for both convectively and absolutely unstable flows [23]. This method uses a dual-time-stepping technique to switch the time-marching scheme of the unsteady code being used to an implicit Euler scheme. Since time marching schemes used by most codes are explicit, doing so avoids the need to implement the more complex algorithms associated with implicit time marching schemes. If the dissipative properties of the implicit Euler scheme are able to damp perturbations, a steady-state is reached without jeopardizing spatial resolution accuracy. Furthermore, it is quite easy to implement, requiring only a simple source term to switch time marching schemes and an outer loop for the dual-time-stepping. It works well for convectively unstable flows, but its temporal dissipation might not be strong enough for absolutely unstable flows with large temporal growth rates. This is caused by nonlinear effects, which limit the maximum time steps and, hence, the dissipative properties of the implicit Euler scheme. The present paper describes an attempt to improve this method.

2 Minimal Gain Schemes

In order to improve the damping capabilities of a time marching scheme, one must first quantify this property. This is traditionally done in numerical analysis through an evaluation of its gain. If one considers the differential system of equations

$$\begin{aligned} \frac{\partial {\mathbf {q}}}{\partial t} = \mathbf {f}(\mathbf {q}) \, , \end{aligned}$$

(1)

where $t$ is time, $\mathbf {q}$ is the unknown variable vector and $\mathbf {f}$ is the steady-state residue. A possible generalization of the implicit Euler scheme (IES) is

$$\begin{aligned} \theta _1 \, \frac{{\mathbf q}^{n+1} - {\mathbf q}^{n}}{\varDelta t} + (1 - \theta _1)\,\frac{{\mathbf q}^{n+1} - {\mathbf q}^{n-1}}{2 \varDelta t} \, = \, \theta _2 \, {\mathbf f}({\mathbf q}^{n+1}) + (1 - \theta _2) \, {\mathbf f}({\mathbf q}^{n}) \, , \end{aligned}$$

(2)

where the IES is recovered when $\theta _1 = \theta _2 = 1$. The truncation error of Eq. (2) requires $\theta _1 \ne 2\,\theta _2$ to maintain its dissipative properties. Assuming $\mathbf {f}(\mathbf {q}) = \lambda \, \mathbf {q}$, a traditional linear stability analysis of this new numerical scheme yields the gain $G$ as a funtion of $\beta = \lambda \, \varDelta t$, where $\varDelta t$ is the time step and $\lambda$ is the overall growth or decay rate of the solution. Linearization can be avoided if the modified equation is employed to estimate $\mathbf {f}(\mathbf {q})$ [24], leading to the nonlinear stability result

$$\begin{aligned} G&= e^{{ - \beta }} \left( {e^{\beta } } \left( {\beta (\theta _{2} - 1)} \left( {\beta \left( {6\beta \theta _{2}^{2} - 3(\beta + 2)\theta _{2} + \beta } \right) + 6} \right) - 3\theta _{1}\right. \right. \\ \nonumber&\quad \left. { \times \left. {\left( {\beta ^{2} \left( {\theta _{2} - 1} \right) \left( {\beta \theta _{2} - 1} \right) + 2} \right) } \right) + 3\theta _{1} - 3} \right) /\left( {\beta ^{3} \theta _{2} (1 - 3} \right. \\ \nonumber&\quad \left. {\left. { \times (\theta _{1} - 2\theta _{2} + 1)\theta _{2} } \right) + 3\beta ^{2} \left( {\theta _{1} - 2\theta _{2} } \right) \theta _{2} + 6\beta \theta _{2} - 3\left( {\theta _{1} + 1} \right) } \right) , \\ \nonumber \end{aligned}$$

(3)

whose behavior is shown in Fig. 1 for $\theta _1=1$ and $\theta _2=1$. Equation (3) yields a similar behavior and will not be discussed here. It is important to note that $\lambda <0$ implies the governing equation is stable and a steady-state can always be achieved without modifications to the marching scheme. Hence, we focus on the behavior of the new scheme when $\lambda >0$. This figure indicates that it is possible to achieve improved damping properties at small time steps by decreasing $\theta _1$ or increasing $\theta _2$. Hence, the new scheme is less sensitive to the maximum time step restriction caused by the loss of numerical stability due to nonlinear effects.

Fig. 1

Absolute value of the nonlinear gain function in Eq. (3) for $\theta _1=1$ (left) and $\theta _2=1$ (right)

3 Results

3.1 Lorenz Equations

Two test cases are utilized to evaluate the performance of Physical-Time Damping when the implicit Euler scheme is replaced by Eq. (2). The first one is given by the Lorenz equations. Figure 2 (left) shows the unsteady behavior of a solution of this problem for a set of control parameters that do not allow the fourth-order explicit Runge-Kutta scheme to reach steady-state. However, it does so with Physical-Time Damping, even if it is turned on after the exponential temporal growth leads the solution to nonlinear saturation. Figure 2 (right) shows the measured overall damping rate $\lambda$ as a function of $\varDelta t$. It confirms the theoretical finding that improved damping rates are achieved by decreasing $\theta _1$ or increasing $\theta _2$ at small $\varDelta t$. This result is important because it confirms that a linear stability analysis can be utilized to construct minimal gain time marching schemes.

Fig. 2

Lorenz solution unsteady behavior with physical-time damping turned on and off (left) as well as the overall temporal decay rate of Eq. (2) when applied to the Lorenz equations (right). Solid circles are the smallest time steps that are able to generate a solution at the specified tolerance

3.2 Spatially Periodic Planar Mixing-Layer

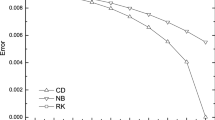
In order to provide a more difficult challenge to the new method, the absolutely unstable planar mixing-layer is simulated with the new minimal gain scheme given in Eq. (2). Details of this code are provided elsewhere [23]. Figure 3 shows a performance comparison between the implicit Euler scheme $(\theta _1 = \theta _2 = 1)$ and a modified scheme with $\theta _1 = 1$ and $\theta _2 = 1.5$. The left plot in this figure shows that the number of pseudo-time iterations versus physical-time step only asymptotes to one for the modified scheme. The reason why is clear in the right plot of this figure, which shows that only the modified scheme is able to reduce the residue of the streamwise velocity component until it reaches steady-state.

Fig. 3

Number of pseudo-time iterations (left) and streamwise velocity component increment (right) per physical-time step for $\theta _1=\theta _2=1.0$ as well as $\theta _1=1.0$ and $\theta _2=1.5$

4 Conclusions

A new method was developed to improve the performance of PTD. It is based on constructing time marching schemes that achieve minimal gain at the smallest time step possible. Future work will compare it with SFD using different test cases.