Entropy-Diminishing CVFE Scheme for Solving Anisotropic Degenerate Diffusion Equations

Abstract

We consider a Control Volume Finite Elements (CVFE) scheme for solving possibly degenerated parabolic equations. This scheme does not require the introduction of the so-called Kirchhoff transform in its definition. The discrete solution obtained via the scheme remains in the physical range whatever the anisotropy of the problem, while the natural entropy of the problem decreases with time. Moreover, the discrete solution converges towards the unique weak solution of the continuous problem. Numerical results are provided and discussed.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 The Continuous Problem and Objectives

Let $\varOmega$ be a polygonal open bounded and connected subset of ${\mathbb {R}}^2$, and let ${t_\mathrm{f}} >0$ be a finite time horizon. We aim to approximate the solution of the (possibly) degenerate parabolic equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t u - \nabla \cdot \left( \eta (u) \varLambda \nabla p(u) \right) = 0 &{} \text {in }Q_{t_\mathrm{f}} := \varOmega \times (0,{t_\mathrm{f}}), \\ \eta (u) \varLambda \nabla p(u) \cdot \mathbf{n} = 0 &{} \text {on } \partial \varOmega \times (0,{t_\mathrm{f}}), \\ u_{|_{t=0}} = u_0 &{} \text {in }\varOmega . \end{array}\right. } \end{aligned}$$

(1)

In (1), $\varLambda :\varOmega \rightarrow {\fancyscript{M}}_2({{\mathbb {R}}})$ should be a measurable function, and we assume that there exists $0 < \underline{\lambda } \le \overline{\lambda }$ such that

$$ \varLambda (\mathbf{x}) = \varLambda (\mathbf{x})^T, \qquad \underline{\lambda } | \mathbf{v} |^2 \le \varLambda (\mathbf{x}) \mathbf{v} \cdot \mathbf{v} \le \overline{\lambda } | \mathbf{v} |^2 \quad \text {for all} \, \mathbf{v} \in {\mathbb {R}}^2 \, \text {and a.a.} \mathbf{x} \in \varOmega . $$

The function $\eta$ is assumed to be continuous, to be such that $\eta (s) > 0$ if $s \in (0,1)$ and $\eta (s) = 0$ otherwise. The function $p$ belongs to $C^1((0,1);{\mathbb {R}}) \cap L^1(0,1)$, is supposed to be increasing, and to be such that $\lim _{s \rightarrow \{0,1\}}\eta (s)p(s) = 0$. Note that $p$ is not necessarily bounded in the vicinity of $0$ and $1$. We also assume that $\sqrt{\eta } p'$ belongs to $L^1(0,1)$, so that the Kirchhoff transforms

$$\phi :u \mapsto \int _0^u \eta (s) p'(s) \mathrm{d} s \quad \text { and } \quad \xi :u \mapsto \int _0^u \sqrt{\eta (s)} p'(s) \mathrm{d} s$$

are continuous and increasing on $[0,1]$. The initial data $u_0$ is assumed to belong to $L^\infty (\varOmega )$, and to be such that $0 \le u_0(\mathbf{x}) \le 1$ for a.a. $\mathbf{x} \in \varOmega$.

Using the Kirchhoff transform $\phi$, the problem (1) can be rewritten as

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t u - \nabla \cdot \left( \varLambda \nabla \phi (u) \right) = 0 &{} \text {in }Q_{t_\mathrm{f}}, \\ \varLambda \nabla \phi (u) \cdot \mathbf{n} = 0 &{} \text {on } \partial \varOmega \times (0,{t_\mathrm{f}}), \\ u_{|_{t=0}} = u_0 &{} \text {in }\varOmega . \end{array}\right. } \end{aligned}$$

(2)

Following [1, 10], there exists a unique weak solution to the problem (2). Moreover, the monotonicity of the problem ensures that

$$\begin{aligned} 0 \le u(\mathbf{x},t) \le 1 \quad \text {for a.a. } (\mathbf{x},t) \in Q_{t_\mathrm{f}}. \end{aligned}$$

(3)

Considering formally $p(u) - p(1/2)$ as a test function in (2) yields, for all $t \in [0, {t_\mathrm{f}}]$,

$$\begin{aligned} \int _\varOmega H(u(\mathbf{x},t)) \mathrm{d} \mathbf{x} + \int \int _{Q_t} \varLambda \nabla \xi (u) \cdot \nabla \xi (u) \mathrm{d} \mathbf{x} \mathrm{d} \tau = \int _\varOmega H(u_0(\mathbf{x})) \mathrm{d} \mathbf{x} < \infty , \end{aligned}$$

(4)

where $H(u) = \int _{1/2}^u (p(s) - p(1/2)) \mathrm{d} s$ is a nonnegative convex entropy to the problem (1), which is supposed to physically meaningful. As a consequence of (4), the function $\xi (u)$ belongs to $L^2((0,T);H^1(\varOmega ))$.

Since in many configurations like for example porous media flows, the physical meaning of the Kirchhoff transform $\phi$ is unclear (see e.g. [3, 11]), we aim to discretize the problem in its form (1) rather than in its form (2). Moreover, we aim to derive a method such that the $L^\infty$-estimate (3) remains true at the discrete level despite the anisotropy of the problem, such that the discrete counterpart of the entropy $\int _\varOmega H(u(\mathbf{x},t)) \mathrm{d}\mathbf{x}$ decreases with time as prescribed by (4) in the continuous setting, and such that the discrete solution converges towards the unique weak solution as the discretization steps tend to $0$. Let us stress that the decay of the entropy $\int _\varOmega H(u(\mathbf{x},t)) \mathrm{d}\mathbf{x}$ plays an important role in the long-time behavior of the continuous and discrete solutions [5, 6].

2 The Implicit Nonlinear CVFE Scheme

Let ${\fancyscript{T}}$ be a conforming triangulation of $\varOmega$ with size $h_{\fancyscript{T}} = \max _{T \in {\fancyscript{T}}} h_T$, where $h_T$ is the diameter of $T$, and regularity $\theta _{\fancyscript{T}} = \max _{T \in {\fancyscript{T}}}\frac{h_T}{\rho _T}$ where $\rho _T$ is the diameter of the incircle of the triangle $T$. We denote by ${\fancyscript{V}}$ the set of the vertices and by ${\fancyscript{E}}$ the set of the edges of ${\fancyscript{T}}$. For all $K\in {\fancyscript{V}}$ (located at $\mathbf{x}_K$), we denote by ${\fancyscript{T}}_K$ the set of the triangles of ${\fancyscript{T}}$ admitting $K$ as a vertex, by ${\fancyscript{V}}_K$ the subset of ${\fancyscript{V}}$ made of the vertices connected to $K$ via an edge, and by ${\fancyscript{E}}_K$ the set of the edges having $\mathbf{x}_K$ as an endpoint. The edge joining two vertices $K$ and $L$ is denoted by $\sigma _{KL}$. For all $K \in {\fancyscript{V}}$, the star-shaped open subset $\omega _K$ of $\varOmega$ is delimited by the centers of gravity $\mathbf{x}_T$ of the triangles $T \in {\fancyscript{T}}_K$ and $\mathbf{x}_{\sigma }$ of the edges $\sigma \in {\fancyscript{E}}_K$, yielding the dual barycentric mesh ${\fancyscript{M}}$. We denote by

$$ V_{\fancyscript{T}} = \{ f \in C(\varOmega ) \; | \; f_{|_{T}} \in {{\mathbb {P}}}_1(T), \; \forall T \in {\fancyscript{T}} \} $$

the usual ${\mathbb {P}}_1$-finite element space, and by $\left( e_K\right) _{K\in {\fancyscript{V}}}$ the canonical basis of $V_{\fancyscript{T}}$. We also introduce the set

$$ X_{\fancyscript{M}} = \{ f \in L^\infty (\varOmega ) \; | \; f_{|_{\omega _K}} \in {{\mathbb {P}}}_0(K), \; \forall K \in {\fancyscript{V}} \} $$

of the piecewise constant functions on the dual cells. For the ease of notations, we restrict our study to the case of uniform time discretizations with step ${\varDelta t} = {t_\mathrm{f}}/N$. Setting $t_n = n{\varDelta t}$ for $0 \le n \le N$, we introduce the discrete functional sets

$$\begin{aligned} V_{{\fancyscript{T}}, {\varDelta t}}\,=\,&\{ f \in L^\infty (Q_{t_\mathrm{f}})\; | \; f(\cdot , t) = f(\cdot , n{\varDelta t}) \in V_{\fancyscript{T}}, \; \forall t \in (t_{n-1}, t_n], \; 1 \le n \le N\},\\ X_{{\fancyscript{M}}, {\varDelta t}}\,=\,&\{ f \in L^\infty (Q_{t_\mathrm{f}}) \; | \; f(\cdot , t) = f(\cdot , n{\varDelta t}) \in X_{\fancyscript{M}}, \; \forall t \in (t_{n-1}, t_n], \; 1 \le n \le N\}. \end{aligned}$$

Hence, given $\left( \nu _K^{n}\right) _{K\in {\fancyscript{V}}, 1 \le 0 \le N}$, there exist two reconstructions $\nu _{{\fancyscript{T}}, {\varDelta t}} \in \nu _{{\fancyscript{T}},{\varDelta t}}$ and $\nu _{{\fancyscript{M}}, {\varDelta t}} \in X_{{\fancyscript{M}},{\varDelta t}}$ such that

$$ \nu _{{\fancyscript{T}},{\varDelta t}} (\mathbf{x}_K, t_n) = \nu _{{\fancyscript{M}},{\varDelta t}} (\mathbf{x}_K, t_n) = \nu _K^n, \text {for all}\, K \in {\fancyscript{V}} {\text {and}} \, n \in \{1, \dots , N\}. $$

For $K \in {\fancyscript{V}}$, we set $m_K = \int _{\omega _K} \mathrm{d} \mathbf{x} = \int _\varOmega e_K(\mathbf{x}) \mathrm{d}\mathbf{x}$. The initial data $u_0$ is discretized by $u^0_{\fancyscript{M}} \in X_{\fancyscript{M}}$, where

$$\begin{aligned} u_K^0 = \frac{1}{m_K} \int _{\omega _K} u_0(\mathbf{x}) \mathrm{d}\mathbf{x}, \qquad \forall K \in {\fancyscript{V}}. \end{aligned}$$

(5)

We introduce now the so-called implicit nonlinear CVFE scheme [2], which is closely related to ${\mathbb {P}}_1$-finite elements with mass lumping. Let $n \ge 1$, then for $\left( u_K^{n-1}\right) _{K\in {\fancyscript{V}}}$ in $[0,1]^{\#{\fancyscript{V}}}$, we look for $\left( u_{K}^n\right) _{K\in {\fancyscript{V}}}$ such that

$$\begin{aligned} \frac{u_K^n - u_K^{n-1}}{{\varDelta t}}m_K + \sum _{L \in {\fancyscript{V}}_K} a_{KL} \eta _{KL}^{n}\left( p(u_K^n) - p(u_L^n)\right) = 0, \qquad \forall K \in {\fancyscript{V}}. \end{aligned}$$

(6)

In (6), we have set $a_{KL} = -\int _\varOmega \varLambda \nabla e_K\cdot \nabla e_L \mathrm{d}\mathbf{x} = a_{LK}$ and

$$ \eta _{KL}^n = {\left\{ \begin{array}{ll} \max _{s \in I_{KL}^n} \eta (s)&{} \text { if }a_{KL} > 0, \\ \min _{s \in I_{KL}^n} \eta (s)&{} \text { if }a_{KL} \le 0, \end{array}\right. } \qquad \text { with } I_{KL}^n = \left[ \min (u_K^n, u_L^n), \max (u_K^n, u_L^n)\right] . $$

Setting $F_{KL}^n = a_{KL} \eta _{KL}^{n}\left( p(u_K^n) - p(u_L^n)\right)$, it is easy to check that for all $n \ge 1$,

$$ {\left\{ \begin{array}{ll} F_{KL}^n + F_{LK}^n = 0, &{} \forall \sigma _{KL} \in {\fancyscript{E}}, \\ \frac{u_K^n - u_K^{n-1}}{{\varDelta t}}m_K + \sum _{L \in {\fancyscript{V}}_K} F_{KL}^n = 0, &{} \forall K \in {\fancyscript{V}}, \end{array}\right. } $$

leading naturally to the following statement.

Proposition 1

The scheme (6) is locally conservative on the dual mesh ${\fancyscript{M}}$.

As usually in CVFE schemes, the accumulation term is obtained thanks to mass-lumping. The originality here comes from the treatment of the diffusion term. The flux $F_{KL}^n$ is obtained as the flux across the interface $x=0$ corresponding to the simili Riemann problem

$$ {\left\{ \begin{array}{ll} \partial _t v + \partial _x \left( \eta (v) q_{KL}^n\right) = 0, &{}\text { in } {\mathbb {R}} \times {\mathbb {R}}_+^*,\\ v_{|_{t=0}} = u_K^n \mathbf{1}_{x<0} + u_L^n \mathbf{1}_{x>0} &{} \text { in } {\mathbb {R,}} \\ q_{KL}^n = a_{KL} (p(u_K^n) - p(u_L^n)). \end{array}\right. } $$

3 Discrete Estimates and Convergence of the Scheme

All the numerical analysis results stated in this section are thoroughly justified in the forthcoming paper [4]. First, let us give some a priori estimates.

Proposition 2

For all $n \ge 1$, one has

$$\begin{aligned}&{\sum _{K \in {\fancyscript{V}}} H(u_K^n) m_K + {\varDelta t} \sum _{\sigma _{KL} \in {\fancyscript{E}}} a_{KL} \left( \xi (u_K^n) - \xi (u_L^n)\right) ^2} \nonumber \\&\le \sum _{K \in {\fancyscript{V}}} H(u_K^n) m_K + {\varDelta t} \sum _{\sigma _{KL} \in {\fancyscript{E}}} a_{KL}\eta _{KL}^n \left( p(u_K^n) - p(u_L^n)\right) ^2 \le \sum _{K \in {\fancyscript{V}}} H(u_K^{n-1}) m_K. \end{aligned}$$

(7)

Sketch of the proof. In order to prove the second inequality of (7), multiply the scheme (6) by ${\varDelta t} \left( p(u_K^n) - p(1/2)\right)$ and to sum over $K \in {\fancyscript{V}}$. The inequality

$$(u_K^n - u_K^{n-1})\left( p(u_K^n)-p(1/2)\right) \ge H(u_K^n) - H(u_K^{n-1})$$

stems from the definition and the convexity of $H$.

The first inequality of (7) is a consequence of the definitions of $\xi$ and $\eta _{KL}^n$, which ensure that

$$a_{KL}\eta _{KL}^n \left( p(u_K^n) - p(u_L^n)\right) ^2 \ge a_{KL} \left( \xi (u_K^n) - \xi (u_L^n)\right) ^2,$$

for all $\sigma _{KL} \in {\fancyscript{E}}$ and all $n \ge 1.$

Denoting by $\xi _{{\fancyscript{T}}}^n$ the function of $V_{{\fancyscript{T}}}$ with nodal values $\left( \xi (u_K^n)\right) _{K\in {\fancyscript{V}}}$, and by $u_{\fancyscript{M}}^n$ the function of $X_{\fancyscript{M}}$ with nodal values $\left( u_K^n\right) _{K\in {\fancyscript{T}}}$, then Proposition 2 implies that

$$ \int _\varOmega H(u_{\fancyscript{M}}^n) \mathrm{d}\mathbf{x} + \int _{t_{n-1}}^{t_n}\int _\varOmega \varLambda \nabla \xi _{\fancyscript{T}}^n \cdot \nabla \xi _{\fancyscript{T}}^n \mathrm{d}\mathbf{x}\mathrm{d} t \le \int _\varOmega H(u_{\fancyscript{M}}^{n-1}) \mathrm{d}\mathbf{x}, $$

ensuring that the entropy is dissipated at each time step.

The discrete diffusion operator appearing in the scheme (6) can be split into two parts:

• a monotone part

  $$\left( u_K^n\right) _K \mapsto \left( \sum _{L \in {\fancyscript{V}}_K} \left( a_{KL}\right) ^+ \eta _{KL}^n \left( p(u_K^n) - p(u_L^n)\right) \right) _K$$

  whose contribution preserves the maximum principle. This contribution consists also in a diffusion operator, but it is not a consistent discretization of the continuous operator $u \mapsto -\nabla \cdot \left( \varLambda \eta (u) \nabla p(u) \right)$;

• a correcting part

  $$\left( u_K^n\right) _K \mapsto \left( - \sum _{L \in {\fancyscript{V}}_K} \left( a_{KL}\right) ^- \eta _{KL}^n \left( p(u_K^n) - p(u_L^n)\right) \right) _K$$

  that ensures the consistency of the scheme. Due to the definition of $\eta _{KL}^n$, this contribution is continuous and vanishes where $\eta (u_K^n) = 0$, i.e.,

  $$ \sum _{L \in {\fancyscript{V}}_K} \left( a_{KL}\right) ^- \eta _{KL}^n \left( p(u_K^n) - p(u_L^n)\right) = 0 \quad \text {if } u_K^n \in \{0,1\}. $$

Therefore, the scheme preserves the natural $L^\infty$ bounds $0$ and $1$. This is the purpose of Proposition 3 (the proof is given in [4]), that moreover ensures that all the terms in (6) are finite.

Proposition 3

For all $n \ge 1$ and for all $K \in {\fancyscript{V}}$, $0 \le u_K^n \le 1$. Moreover, if there exist $K_\star$ (resp. $K^\star$) in ${\fancyscript{V}}$ such that $u_{K_\star }^0 >0$ (resp. $u_{K^\star }^0 <1$), and if $\lim _{s \rightarrow 0}p(s) = -\infty$ (resp. $\lim _{s \rightarrow 1}p(s) = +\infty$), then for all $K\in {\fancyscript{V}}$ and all $n \ge 1$, one has

$$\begin{aligned} u_K^n \ge c(u_{K_\star }^0, {\fancyscript{T}}, {\varDelta t}, n, \varLambda ) >0 \qquad \text {(resp.}\; u_K^n\le 1-c(u_{K^\star }^0, {\fancyscript{T}}, {\varDelta t}, n, \varLambda )<1). \end{aligned}$$

(8)

All these a priori estimates allow us to prove the existence of a discrete solution $\left( u_K^n\right) _{K\in {\fancyscript{V}}, n\ge 0}$ to the scheme (5)–(6).

Proposition 4

For all $n\in \{1 ,\dots , N\}$, there exists a solution $\left( u_K^n\right) _{K\in {\fancyscript{V}}}$ to the scheme (5)–(6).

The proof of Proposition 4 is inspired from the existence proof given in [7] and relies on a topological degree argument. Nevertheless, in the case where $p$ is unbounded, the application $\left( u_K^n\right) _{K \in {\fancyscript{V}}} \mapsto \sum _{L \in {\fancyscript{V}}_K} a_{KL} \eta _{KL}^{n} \left( p(u_K^n) - p(u_L^n)\right)$ is not continuous on $[0,1]^{\#{\fancyscript{V}}}$. Therefore, the enhanced $L^\infty$-estimates (8) are mandatory to restrict the study on a smaller domain $[\epsilon , 1-\epsilon ]^{\#{\fancyscript{V}}}$ on which the discrete operator is uniformly continuous.

In what follows, we denote by $u_{{\fancyscript{M}}, {\varDelta t}}$ the unique element of $X_{{\fancyscript{M}}, {\varDelta t}}$ such that

$$\begin{aligned} u_{{\fancyscript{M}}, {\varDelta t}}(\mathbf{x}_K, t_n) = u_K^n, \qquad \forall K \in {\fancyscript{V}}, \; \forall n \in \{1, \dots , N\}. \end{aligned}$$

(9)

The convergence of the discrete solution $u_{{\fancyscript{M}}, {\varDelta t}}$ as the space and time discretization steps tend to $0$ towards the unique weak solution $u$ of the continuous problem is the purpose of the following theorem, whose proof is contained in [4].

Theorem 1

Let $\left( {\fancyscript{T}}_m\right) _{m\ge 1}$ be a sequence of conforming triangulations of $\varOmega$ such that $h_{{\fancyscript{T}}_m} \rightarrow 0$ as $m \rightarrow \infty$, and such that $\theta _{{\fancyscript{T}}_m} \le \theta ^\star < \infty$, and let $\left( {\varDelta t}_m \right) _{m\ge 1}$ be a sequence of time steps such that ${\varDelta t}_m \rightarrow 0$ as $m \rightarrow \infty$, then, for all $q \in [1,\infty )$, the discrete solution $u_{{\fancyscript{M}}_m, {\varDelta t}_m}$ converges in $L^q(Q_{t_\mathrm{f}})$ towards the unique weak solution $u$ of the problem (2) as $m\rightarrow \infty$.

The proof of Theorem 1 follows (with some additional technical difficulties) the path proposed in §4.3 of [8], that consists in first proving some compactness on the family of discrete solutions $\left( u_{{\fancyscript{M}}_m, {\varDelta t}_m}\right) _{m\ge 1}$, and then to identify any limit value (up to a subsequence) $u = \lim _{m\rightarrow \infty } u_{{\fancyscript{M}}_m, {\varDelta t}_m}$ as the unique weak solution to the problem (2). The uniqueness of the limit ensures the convergence of the whole sequence.

Remark 1

The choice of homogeneous Neumann boundary condition is not mandatory. A similar convergence result can be obtained in the case where an inhomogeneous Dirichlet condition $u_D$ is imposed on a part of the boundary as long as $u_D$ and $p(u_D)$ are sufficiently regular. In this case, the entropy of the system if not necessarily decreasing (but it remains bounded) because of a contribution coming from the boundary.

4 Numerical Illustration

This section illustrates the numerical behavior of the scheme (6). In order to compare the numerical solution with an analytical solution, we apply our discretization strategy on a test case that does not fully fits with our assumptions. Indeed, Dirichlet boundary conditions are prescribed. But as mentioned in Remark 1, the convergence of the scheme can be proved also in this case. The meshes used for the discretization of the domain $\varOmega = (0,1)^2$ are issued from a 2D benchmark on anisotropic diffusion problem [9]. These triangle meshes show no symmetry which could artificially increase the convergence rate, and all angles of triangles are acute. This allows to compare situations where all coefficients $a_{KL}$ defined previously are positive, with situations where some of them are negative by introducing anisotropic permeability tensors. This family of meshes is built through the same pattern, which is reproduced at different scales.

In the following numerical experiments, we consider a diagonal permeability tensor $\varLambda = \mathrm{diag}(l_x, l_y)$. A first constant time step, denoted by ${\varDelta t}_1$, is associated to the coarsest mesh and then between two successive meshes, the time step is divided by four since the mesh size is divided by two, so that the error due to the implicit Euler-time discretization remains negligible compared to that issued from the space discretization. The nonlinear systems obtained at each time step are solved by a Newton-Raphson algorithm.

The test case deals with a degenerate parabolic equation with a Dirichlet boundary condition. The functions involved in (1) are defined by $\eta _{n\ell }(u)=2\min (u,1-u)$ and $p_{n\ell }(u)=u$. Since the continuous solution and the discrete one computed with the nonlinear scheme (6) remain bounded between $0$ and $0.5$ (cf. Tables 1 and 2), this amounts to consider the porous medium equation

$$ \partial _t u - \nabla \cdot \left( \varLambda \nabla u^2 \right) = 0, $$

and we compare the results with the scheme obtained by taking the following functions $p_\ell (u)=u^2$ and $\eta _\ell (u) = 1$ where the subscript $\ell$ has been added for this formulation called the quasilinear one. The numerical convergence of both schemes has been studied through the following analytical solution,

$$ \tilde{u}((x,y),t) = \mathrm max ( 2l_x t - x , 0), $$

for $(x,y) \in \varOmega$, $t \in (0,{t_\mathrm{f}})$, and where the final time ${t_\mathrm{f}}$ has been fixed to $0.25$ s and the first time step is given by ${\varDelta t}_1=0.01024$ s. The values of $\tilde{u}$ on $\partial \varOmega \times (0,t_\mathrm{f})$ are prescribed as Dirichlet boundary condition. Two permeability tensors have been tested : the isotropic one $l_x = l_y = 1$ (cf. Table 1) and an anisotropic one $l_x = 1$, $l_y = 10^2$ (cf. Table 2). For all tests we have computed the errors in the classical discrete $L^1(Q_{t_\mathrm{f}})$ and $L^{\infty }(Q_{t_\mathrm{f}})$ norms. Each table provides the mesh size $h$, the discrete errors and the associated convergence rate, and finally the minimum and maximum values of the discrete solutions.

Table 1 $l_x = l_y =1$: the isotropic case

Table 2 $l_x =1$, $l_y =10^2$: the anisotropic case. The subscript $n\ell$ stands for nonlinear scheme (6) while the subscript $\ell$ stands for the quasilinear scheme

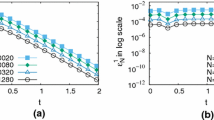
We observe that, as expected, the convergence rates of the linear implementation are better. Nevertheless, in the anisotropic case, the magnitude of the undershoots (illustrated by Fig. 1) is such that the absolute value of the observed error is lower in the nonlinear implementation than in the quasilinear one for the coarsest meshes, which are currently used in industrial applications.

Fig. 1

2nd mesh. Discrete unknown $u$ and its iso-values, for each scheme (right: quasilinear diffusion scheme, left: nonlinear scheme), with an anisotropic tensor at the end of the simulation