Keywords

9.1 Introduction

Water is distributed within the earth, on its surface, and also in the atmosphere in liquid, solid, and gaseous forms, respectively. Of the total available water on the earth, 97 % is saline stored in the oceans and the remaining 3 % is only in the form of fresh water. Out of this 3 % of fresh water, groundwater constitutes only 30.1 %. The remaining is in the form of icecap and glaciers (68.7 %), liquid surface water (0.3 %), and in atmosphere and living being (0.9 %). Of the liquid surface fresh water, 87 % is stored in lakes, 11 % in swamps, and only 2 % flows into the rivers (source: Wikipedia-a free encyclopedia). Accordingly, groundwater constitutes the second largest reserve of fresh water available on the earth. The main source of groundwater is precipitation. Precipitated water falls on the ground surface and enters below it. This entering process is known as infiltration. Infiltrated water moves downward and gets stored in pores of subsurface geological formations or in geological structures such as fractures, faults, joints, etc. in the case of hard rocks. This leads to the evolution of groundwater regime below the earth’s surface. Geological formations capable of storing groundwater and allowing its movement from one place to another place under ordinary field conditions are known as aquifers. Sands, sandstone, weathered mantle, highly fractured rock, etc. are examples of aquifers. On the other hand, there are some geological formations such as massive basalt and granite units which can neither store the groundwater nor allow the movement of groundwater. Such geological formations are known as aquifuge. There is another category of geological formation such as clay which can store good amount of groundwater but does not allow the movement of groundwater because of lack of interconnectivity of its pores. Such formations are known as aquiclude. Vertical distribution of groundwater is characterized into two zones: unsaturated and saturated. In the unsaturated zone the entire pores contain both water and air, whereas in the saturated zone the entire pore space is filled with water. If the saturated zone is bounded by two impermeable formations from top and bottom, it is called a confined aquifer.

In confined aquifer water is stored at more than atmospheric pressure. That is why water level in the well penetrating a confined aquifer is at a higher elevation than the elevation of the upper boundary of the confined aquifer. Elevation of the water level in the well penetrating confined aquifer is called piezometric head and is measured from a reference stratum. If the upper boundary of the saturated zone is the water table (or phreatic surface), it is called unconfined aquifer. On the water table, the pressure is equal to the atmospheric pressure. An unconfined aquifer (or part of it) that rests on a semi-pervious layer is a leaky unconfined aquifer. Similarly, a confined aquifer (or part of it) that has at least one semi-pervious layer containing stratum is called a leaky confined aquifer. A schematic diagram of the aquifer’s type and zones of vertical distribution of groundwater are shown in Fig. 9.1.

Fig. 9.1
figure 1

Aquifer types and vertical distribution of groundwater zones

Full size image

The advantage of unconfined aquifers over confined aquifers to serve as a subsurface reservoir is that the storage of groundwater in large quantity is possible only in unconfined aquifer. This is because the storativity of the unconfined aquifer is linked to the porosity and not to the elastic properties of water and the solid matrix, as in the case of the confined aquifer [1]. Also, the vast surface area of the unconfined aquifer above the water table is available to receive the surface applied recharge, whereas in the case of confined aquifer, only a small open area exposed to the ground surface or leaky portion of the aquifer boundary is available to receive the recharge as shown in Fig. 9.1. Sources of surface water are not available everywhere. Therefore, their use to meet the demand of water supply for irrigation, industrial, and domestic purposes is restricted to those areas where water can be transported through canals from these sources. Also surface water bodies such as rivers, lakes are more vulnerable to contamination. On the other hand, groundwater resources are distributed globally and are less vulnerable to contamination compared to surface water bodies. Therefore, groundwater plays a major role in augmenting water supply to meet the ever-increasing demand, especially in developing counties such as India, where agriculture sector provides job opportunity to a large rural population and is the main source of income to them. Increasing dependence of water supply on groundwater resources is resulting in increasing use of aquifers as a source of fresh water supply and subsurface reservoir for storing excess surface water.

Natural replenishment of aquifers occurs very slowly. Therefore, withdrawal of groundwater at a rate greater than the natural replenishment rate causes declining of groundwater level, which may lead to decrease in water supply, contamination of fresh water by polluted water from nearby sources, seawater intrusion into the aquifer of coastal areas, etc. To increase the natural replenishment, artificial recharging of the aquifer is becoming increasingly important in groundwater management. In many cases, excess recharging also leads to the growth of water table near the ground surface and causes several types of environmental problems, such as water logging, soil salinity, etc. In such a situation, proper management of groundwater resources is needed to overcome the shortage of water supply on one hand and to prevent the environmental problems on the other hand. In order to address the management problem, one must be able to predict the response of the aquifer system to any proposed operational policy of groundwater resources development such as artificial recharging and pumping. Such problems are referred to as forecasting problems. Its solution will provide the new state of the groundwater system. Once the new state is known, one can check whether the related recharging and/or pumping scheme is feasible to meet the preset objectives of the sustainable development and management of groundwater resources. Such problems can be tackled by applying mathematical modeling techniques. Mathematical models help in making judicious selection of an appropriate development scheme such as designing of recharging and pumping schemes out of many proposed development schemes by comparing responses of different proposed recharge/pumping schemes in order to select the best scheme without resorting to the expensive field works. This chapter deals with mathematical modeling of groundwater flow in unconfined aquifer and related problems. Mathematical modeling needs simplification of complex geohydrological environ and processes based on assumptions to make it amenable to the mathematical treatment without compromising the physical characteristics of the problem. One such simplification is the hydraulic approach.

9.2 Hydraulic Approach

In general, flow through a porous medium is 3-D . However, as the geometry of most aquifers is such that they are thin relative to their horizontal dimension on regional scale, a simpler approach called hydraulic approach is introduced for modeling purpose. According to this approach, it is assumed that the flow in the aquifer is essentially horizontal everywhere neglecting its vertical component [1–2]. The approximation of horizontal flow in unconfined aquifer is the basis of Dupuit assumption which will be discussed later. However, this assumption fails in regions where the flow has a large vertical component, for example, in the vicinity of partially penetrating wells, or at boundaries with open water bodies such as lakes, rivers, etc.

9.3 Mathematical Modeling

Modeling of groundwater flow begins with a conceptual understanding of the physical problem. The next step is translating the physical problem into a mathematical framework in the form of a set of mathematical equations governing groundwater flow, boundary, and initial conditions (in the case of unsteady state flow). Its solutions are used to describe the dynamic behavior of water table in the flow system under consideration in response to the hydraulic stresses such as recharging, pumping, leakages, stream aquifer interaction etc. Mathematical model may be deterministic, statistical, or some combination of the two. Deterministic models retain a good measure of physical insight while permitting a number of problems of the same class to be tackled with the same model. Our discussion is confined to the development of governing groundwater flow equations, methods of solutions, and related deterministic models used for predicting water table fluctuation induced by recharging and/or pumping, which are the essential components of groundwater resources development. Formulations of groundwater flow equations are based on the conservation principles dealing with mass and momentum. These principles require that the net quantity of mass (or momentum) entering or leaving a specified volume of aquifer during a given time interval be equal to the change in the amount of mass (or moment) stored in the volume. Groundwater flow equations for specific aquifer systems are formulated by combining the equation of motion in the form of Darcy’s law, which follows principle of conservation of momentum with the mass balance equation, also known as mass conservation equations or continuity equations, which follows the principle of conservation of mass.

9.3.1 Darcy’s Law

Consider flow of water under confined condition through a sand filled cylinder of cross sectional area A and length L as shown in Fig. 9.2. Cylinder is representing a propos media through which water is flowing from one end to another end under gravitational flow because of elevation difference between piezometric heads at both ends. According to Darcy’s law, the rate of flow (volume of water per unit time), Q, is proportional to the crosssectional area A of the porous media, proportional to the piezometric heads difference between two points \(( {{\phi }_{1}}\ -\ \phi {}_{2} ),\) and inversely proportional to the length of the porous media, L as shown in Fig. 9.3. Mathematically, it can be expressed as:

Fig. 9.2
figure 2

Flow of water through an inclined porous media

Full size image
Fig. 9.3
figure 3

Diagrammatic representation of the Dupuit assumption

Full size image
$$ Q=KA\frac{{{\phi }_{1}}-{{\phi }_{2}}}{L}, $$
(9.1)

in which K is the coefficient of proportionality, called hydraulic conductivity. K depends on the properties of fluid as well as solid matrix and is expressed by \(K\text{=}k\rho g/\mu \) in which k is the solid medium permeability, \(\rho \) is the density of fluid (taken 1 in case of water), \(g\) is the gravitational acceleration, and \(\mu \) is the dynamic viscosity. The piezometric head is expressed as \(\phi =z+p/\gamma ,\) in which z is the elevation head, p is atmospheric pressure, and \(\gamma \) is specific weight of water [1]. Equation 9.1 can also be rewritten as:

$$ q\ =\frac{Q}{A}=\ K\frac{{{\phi }_{1}}\ -{{\phi }_{2}}}{L}, $$
(9.2)

where q is the specific discharge defined as the volume of water flowing through unit crosssectional area of the cylinder. Writing \(( {{\phi }_{1}}-\phi {}_{2} )/L\) in differential form by defining \(( {{\phi }_{1}}-{{\phi }_{2}} )\to \text{d}\phi \ \text{and}\ L\to \text{d}L\) and introducing a minus sign to indicate that flow is in the direction of decreasing \(\phi ,\) Eqs. 9.1 and 9.2 can be expressed as:

$$ Q=\ -KA\frac{d\phi }{dL} $$
(9.3)

and

$$ q=\ -K\frac{d\phi }{dL}. $$
(9.4)

In case of unconfined aquifer, Eqs. 9.3 and 9.4 can be written as:

$$ Q=\ -KA\frac{dh}{dL} $$
(9.5)
$$ q\ =\ -K\frac{dh}{dL}, $$
(9.6)

where dh is difference of water table heights between two points separated by distance dl. Eqs. 9.5 and 9.6 are known as the equation of motion. It is evident from Eq. 9.6 that for dh/dl = 1, K = q. Groundwater flow equation for an unconfined aquifer is derived by combining the equation of motion modified by the Dupuit assumption with the mass balance equation.

9.3.2 Dupuit Assumption

Consider a vertical cross section of unconfined groundwater flow as shown in Fig. 9.4. Dupuit assumption is based on the field observation that the slope of the water table, \(\theta ,\) is generally very small on regional scale. It implies that the flow is almost horizontal and dL≈dx (Fig. 9.3). Replacing dL by dx, Eq. 9.6 becomes:

Fig. 9.4
figure 4

Groundwater flow in a control box of an unconfined aquifer

Full size image
$$ q=\ -{{K}_{x}}\frac{dh}{dx}. $$
(9.7)

If groundwater flow takes place through a saturated vertical column of thickness h, then Eq. 9.7 can be rewritten as:

$$ Q_{x}^{'}=\ -{{K}_{x}}h\frac{dh}{dx}. $$
(9.8)

9.3.3 Mass Balance Equation

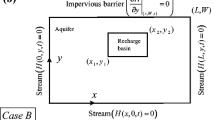
To derive the mass balance equation, consider groundwater flow through a control box in an unconfined aquifer (Fig. 9.4). The box is bounded by vertical surfaces at \((x-\delta x/2,y)\ \text{and}\ (x+\delta x/2,y)\). parallel to the y-axis and at \((x,y-\delta y/2)\ \text{and}\,(x,\ y+\delta y/2)\) parallel to the x-axis. The box has a horizontal impervious base and the water table forms its upper boundary. The control box receives vertical recharges with N(x, y, t) rate. The rate of recharge is the volume of water added to the water table in unit time through unit cross-sectional area and has the unit of velocity. In principle N(x, y, t) is the sum of all recharge rates from distributed sources (recharge basins, ponds, streams, etc.) and withdrawal rates from distributed sinks (wells, leakage sides, etc.).Here, N(x, y, t) is considered as recharge rate only from a single source to simplify the derivation of the mass balance equation.

Because of the excess mass inflow during time, \(\delta t,\) the water table rises from the initial height h(t) to a new height \(h(t\text{+}\delta t)\). The mass balance equation based on the Dupuit assumption can now be written as:

$$ \begin{array}{*{35}{l}} \delta t\{\delta y\left[ Q_{x}^{'}\left( x-\frac{\delta x}{2},y \right)-Q_{x}^{'}\left( x+\frac{\delta x}{2},y \right) \right]\\ +\delta x\left[ Q_{y}^{'}\left( x,y-\frac{\delta y}{2} \right)-Q_{y}^{'}\left( x,y+\frac{\delta y}{2} \right) \right]\\ +\delta x\delta yN(x,y,t)\}={{S}_{y}}\delta x\delta y[h(t+\delta t)-h(t)]\\\end{array}. $$
(9.9)

where \(Q_{x}^{'}\,\text{and}\,Q_{y}^{'}\) are discharges per unit width in the x and y directions, respectively; \(h(t)\,\text{and}\,h(t\text{+}\delta t)\) are the water table heights at times \(t\,\text{and}\,(t\text{+}\delta t),\) respectively, \(\rho \) is the density of water which is normally taken as one and Sy is the specific yield which is defined as the volume of water added to (or released from) the aquifer per unit horizontal area of aquifer and per unit rise (or decline) of water table. Sy is dimensionless aquifer parameter. By expanding \(Q_{x}^{'},Q_{y}^{'}\ \text{and}\ h(t+\delta t)\ \) about x, y, and t, respectively, by Taylor series and dropping all terms containing second and higher order derivatives gives:

$$ Q\left( x+\frac{\delta x}{2} \right)={{Q}_{x}}\ +\frac{\partial {{Q}_{x}}}{\partial x}\frac{\delta x}{2} $$
(9.10)
$$ Q\left( x\ -\ \frac{\delta x}{2} \right)={{Q}_{x}}-\frac{\partial {{Q}_{x}}}{\partial x}\frac{\delta x}{2} $$
(9.11)
$$ Q_{y}^{'}\left( x,y+\frac{\delta y}{2} \right)={{Q}_{y}}+\frac{\partial {{Q}_{y}}}{\partial y}\frac{\delta y}{2} $$
(9.12)
$$ Q_{y}^{'}\left( x,y-\ \frac{\delta y}{2} \right)={{Q}_{y}}-\frac{\partial {{Q}_{y}}}{\partial y}\frac{\delta y}{2} $$
(9.13)
$$ h(t+\delta t)=h(t)+\frac{\partial h}{\partial t}\frac{\delta h}{2}. $$
(9.14)

Substituting these values in Eq. 9.9, and thereafter dividing both sides of Eq. 9.9 by \(\delta x,\delta y,\delta t\ \) and letting \(\delta x,\delta y\ \text{and}\ \delta t\ \to 0\), we obtain the following mass balance equation for an inhomogeneous and anisotropic unconfined aquifer:

$$ -\frac{\partial }{\partial x}( Q_{x}^{'} )\ -\frac{\partial }{\partial y}( Q_{y}^{'} )+N(x,y,t)\ =\ {{S}_{y}}\frac{\partial h}{\partial t}. $$
(9.15)

Inserting the expressions for Qx’ and Qy’ from Eq. 9.8 into Eq. 9.15 yields:

$$ \frac{\partial }{\partial x}\left( {{K}_{x}}h\frac{\partial h}{\partial x} \right)+\frac{\partial }{\partial y}\left( {{K}_{y}}h\frac{\partial h}{\partial y} \right)+\ N(x,y,t)=\ {{S}_{y}}\frac{\partial h}{\partial t}. $$
(9.16)

For an inhomogeneous isotropic aquifer K = K(x, y), Eq. 9.16 becomes:

$$ \frac{\partial }{\partial x}\left( {{K}_{{}}}h\frac{\partial h}{\partial x} \right)+\frac{\partial }{\partial y}\left( {{K}_{{}}}h\frac{\partial h}{\partial y} \right)\ +N(x,y,t)={{S}_{y}}\frac{\partial h}{\partial t}. $$
(9.17)

9.3.4 Groundwater Flow Equation for a Leaky Unconfined Aquifer

In this case, an unconfined aquifer is separated from an underlying confined aquifer by a partly semi-pervious layer as shown in Fig. 9.2. The mass balance equation for a control box in inhomogeneous anisotropic unconfined aquifer, taking into account a leakage of rate q L between the aquifers is given by:

$$ \begin{array}{*{35}{l}} \delta t\{\delta y\left[ Q_{x}^{'}\left( x-\frac{\delta x}{2},y \right)-Q_{x}^{'}\left( (x+\frac{\delta x}{2},y) \right) \right]\\ +\delta x\left[ Q_{y}^{'}\left( x,y-\frac{\delta y}{2} \right)-Q_{y}^{'}\left( x,y+\frac{\delta y}{2} \right) \right]\\ +\partial x\partial yN(x,y,t)+\partial x\partial y{{q}_{L}}\}\ \ =\ {{S}_{y}}\delta x\delta y[h(t\ +\ \delta t)\ -\ h(t)]\\\end{array}, $$
(9.18)

where h is water table height in an unconfined aquifer, \(\phi \) is piezometric head in underlying confined aquifer. q L for \(h<\phi \) is expressed as:

$$ {{q}_{L}}=\frac{\phi -h}{\sigma }, $$
(9.19)

in which \(\sigma \text{=}{B}'\text{/}{K}',{B}'\) being the thickness and K’ the hydraulic conductivity of the semi-pervious layer. For \(h>\phi ,\,{{q}_{L}}\) becomes negative because groundwater outflows from the unconfined aquifer. For \(h<\phi ,\) groundwater flows into the unconfined aquifer and hence q L becomes positive. After simplification, Eq. 9.18 becomes:

$$ \frac{\partial }{\partial x}\left( {{K}_{x}}h\frac{\partial h}{\partial x} \right)+\frac{\partial }{\partial y}\left( {{K}_{y}}h\frac{\partial h}{\partial y} \right)+N(x,y,t)+\frac{\phi \ -\ h}{\sigma }=\ {{S}_{y}}\frac{\partial h}{\partial t}. $$
(9.20)

Equation 9.20 is the desired governing equation for groundwater flow in a leaking unconfined aquifer. The equation for an inhomogeneous isotropic aquifer (K = K(x, y)) and a homogeneous isotropic aquifer (K = constant) can be obtained from Eq. 9.20 as in the previous cases.

9.3.5 Linearization of Groundwater Flow Equation

Generally, Eqs. 9.16, 9.17, and 9.20 are used for development of groundwater flow models. These are nonlinear second order partial differential equations and their exact solutions are difficult to obtain. The nonlinearity is because of the presence of h as coefficient in the partial derivatives on the left hand side. Therefore, linearization of these equations is essential to obtain analytical solutions. We consider Eq. 9.17 to describe the linearization procedures an example. For homogenous isotropic aquifers (K = constant), Eq. 9.17 can be written in the following two forms:

$$ K\left[ \frac{\partial }{\partial x}\left( h\frac{\partial h}{\partial x} \right)+\frac{\partial }{\partial y}\left( h\frac{\partial h}{\partial y} \right) \right]+N(x,y,t)=\ {{S}_{y}}\frac{\partial h}{\partial t} $$
(9.21)
$$ \frac{{{\partial }^{2}}{{h}^{2}}}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}{{h}^{2}}}{\partial {{y}^{2}}}+\frac{2N(x,y,t)}{K}\ \ =\frac{{{S}_{y}}}{Kh}\frac{\partial {{h}^{2}}}{\partial t}. $$
(9.22)

Two procedures of linearization are commonly used. According to the first procedure, i.e., the Baumann procedure of linearization, if the variation in h is much less than the initial height of the water table h 0, then the coefficient h appearing on the left hand side of Eq. 9.21 can be replaced by h 0. Then Eq. 9.18 can be rewritten as:

$$ T\left( \frac{{{\partial }^{2}}h}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}h}{\partial {{y}^{2}}} \right)+\ N(x,y,t)=\ {{S}_{y}}\frac{\partial h}{\partial t}, $$
(9.23)

where T = Kh 0. Now Eq. 9.23 is linear in h. In the second procedure, i.e., the Hantush’s procedure of linearization, h appearing in the denominator on the right hand side of Eq. 9.22 is replaced by the weighted mean of the depth of saturation \(\bar{h};\) a constant of linearization which is approximated by 0.5[h 0 + h(t e)]; t e is the period at the end of which \(\bar{h}\) is to be approximated. Then Eq. 9.23 becomes:

$$ \frac{{{\partial }^{2}}{{h}^{2}}}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}{{h}^{2}}}{\partial {{y}^{2}}}\ +\frac{2N(x,y,t)}{K}=\frac{{{S}_{y}}}{K\bar{h}}\frac{\partial {{h}^{2}}}{\partial t}. $$
(9.24)

Now Eq. 9.24 becomes linear in h 2. Substitution of a new variable H, defined as \(H\text{=}{{h}^{2}}-h_{0}^{2},\) Eq. 9.24 can be rewritten as:

$$ \frac{{{\partial }^{2}}{{H}^{2}}}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}{{H}^{2}}}{\partial {{y}^{2}}}+\frac{2N(x,y,t)}{K}=\ \frac{{{S}_{y}}}{K\bar{h}}\frac{\partial H}{\partial t}. $$
(9.25)

Equation 9.25 is being extensively used for development of groundwater flow models. Here, it should be mentioned that in case of using Eq. 9.25 for development of mathematical models, the initial and boundary conditions should be also described in the form of H to preserve linearity of the problem.

Now, to make use of Eq. 9.24 (or 9.25) for the development of groundwater flow models, one needs to compute the value of \(\bar{h}\). Marino [3] suggested the method of successive approximation for computation of \(\bar{h}\) value. In this method, the weighted mean of the depth of saturation is taken as a first approximation equal to the initial depth of saturation, h 0. The first approximated height of the water table is then calculated by using a solution of Eq. 9.25. In the second trial, the weighted mean of the depth of saturation is approximated by the average of the initial depth of saturation h 0 and the first approximation of the height of the water table. This procedure is repeated until the value of the calculated height of the water table converges. The last estimated value of \(\bar{h}\) for which the calculated water table height converges at a given time and position is the desired value of \(\bar{h}\) for that particular time and position. Thus, for each time and position one has to compute \(\bar{h}\) and the conversed value of water table height for this value of \(\bar{h}\) is the desired water table height at the given position and time. By comparing results of analytical solutions based on the Hantush linearization procedure with the experimental results obtained from Hele-shaw model, Marino[3] found that for N ≤ 0.2 K and h−h 0 ≤ 0.5h 0, the maximum deviation between both the results was 6 %. Even for h−h 0 ≥ 20 h 0, the maximum deviation was 12.2 %. It shows that the results of analytical model agree reasonably well with the experimental results. Rao and Sarma [4] have reported that both the linearization methods yield results which have satisfactory agreement with those of the experiments (within ± 5 %) for the rise of the water table up to 40 % of its initial height. Beyond this limit the Hantush linearization scheme gave a more satisfactory agreement. Thus, Hantush method was found to have wider applicability. However, Hantush method involves computation of weighted mean of the depth of saturation through successive iteration and hence requires more computation time than the Baumann procedure of linearization. However, time is not at all an issue in this era of fast computers. Equations 9.23–9.25 are popularly known as linearized Boussinesq equations.

9.3.6 Groundwater Flow Equations for Sloping Aquifer

The groundwater flow equation in a sloping 2-D unconfined aquifer is described by: [5–6]

$$ \frac{{{\partial }^{2}}s}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}s}{\partial {{y}^{2}}}-\,2a\frac{\partial s}{\partial t}+\frac{2N(t)}{K}=\frac{1}{\Re }\frac{\partial s}{\partial t}, $$
(9.26)

where s = h 2, h = variable water table height, a = q/2D, q = slope of the base, D =  the mean depth of saturation, and \(\Re =KD/Sy.\)

9.3.7 Groundwater Flow Equations in Cylindrical Coordinates

This type of equation is used to describe groundwater flow induced by recharging/pumping through circular shape recharge basin/well and is given by: [7–8]

$$ S\frac{\partial h}{\partial t}=-\frac{1}{r}\frac{\partial }{\partial r}(rQ)+N(r,t), $$
(9.27)

where r is the radial distance measured from the center of recharge basin, and q is defined by Darcy law as:

$$ Q=-Kh\left( \frac{\partial h}{\partial r} \right). $$
(9.28)

Equations 9.23–9.25 describe 2-D groundwater flow. Equation for 1-D flow, for example in the x direction, can be obtained by simply substituting zero for the derivative of y. Groundwater flow equations for a steady-state condition can be obtained by substituting zero for time derivatives.

Groundwater flow equations presented here are in the form of partial differential equations having infinite numbers of solutions. To obtain a unique solution for a particular problem, some more information about the problem under consideration is needed, such as the values of aquifer parameters, geometry of the flow domain, leakage rate, recharge rate, pumping rate, initial conditions, boundary conditions, etc. depending on the physical condition of the problem under consideration. Aquifer parameters can be deduced from field as well as experimental methods [1, 9]. A brief description about the initial and boundary conditions commonly used in groundwater flow problems are discussed below.

9.3.8 Initial Conditions

Initial conditions describe the distribution of h at all points of the flow domain at the beginning of the investigation, i.e., at t = 0. This is expressed as:

$$ h=\ {{h}_{0}}(x,y,0), $$
(9.29)

where h 0 is a known value of h for all points of the flow domain at t = 0. Now, to make use of initial condition for the solution of Eq. 9.25, Eq. 9.29 can be written as:

$$ H(x,y,0)=0, $$
(9.30)

in which \(H={{h}^{2}}\ -h_{0}^{2}.\)

9.3.9 Boundary Conditions

These conditions describe the nature of interaction of the aquifer along its boundaries with its surrounding environs such as reservoir, rivers, groundwater divide, etc. Three types of boundary conditions are generally encountered in groundwater flow problems.

Dirichlet boundary condition: In this case, h is prescribed for all points of the boundary for the entire period of investigation. This is expressed as:

$$ h\text{=}{{h}_{0}}(x,y,t), $$
(9.31)

where \({{h}_{0}}\,(x,y,t)\) are known values of h at all points on the boundary.

Neumann boundary condition: This type of boundary condition prescribes the flux across the boundary of the flow system and can be expressed as:

$$ q={{\psi }_{1}}\,(x,y,t), $$
(9.32)

where \({{\psi }_{1}}\,(x,y,t)\) are the known values of flux at boundaries. A special case of this boundary condition is the no-flow boundary condition in which flux is zero. This condition occurs at impermeable surfaces or at the groundwater divide, a surface across which no flow takes place.

Cauchy boundary condition: This boundary condition is encountered at the semi-pervious boundary layer between the aquifer and an open water body such as river. Because of the resistance to the flow offered by the semi-pervious boundary that lies between the aquifer and the river, the water level in the river differs from that in the aquifer on the other side of the semi-pervious boundary. In this case, the flux is defined by:

$$ q=\ {{K}^{'}}\frac{h\ -\ {{h}_{0}}}{b}, $$
(9.33)

where \(h\) is the head at x = 0, h 0 is the water level in the river, b and K’ are the thickness and hydraulic conductivity, respectively, of the semi-pervious boundary layer.

9.3.10 Estimation of Rate of Recharge and Pumping

Recharging and pumping are the essential components of groundwater development schemes. The purpose of groundwater recharging is to store groundwater in order to reduce, stop, or even reverse the declining trend of water table. On the other hand, pumping is used for water supply. Thus, recharging and pumping have significant effects on the dynamics of water table. Therefore, accurate estimation of recharge and pumping rates are very crucial for prediction of water table fluctuation. Many mathematical models have been developed to predict water table fluctuations in response to recharge from basins of different geometrical shapes [3, 10–15]. Most of the models are based on the assumption of constant rate of recharge applied continuously. However, rate of recharge largely depends on the infiltration rate which is influenced by several factors. The infiltration rate decreases initially mainly due to dispersion and swelling of soil particles at the bottom of the basin. After some time, it increases owing to displacement of the entrapped air from pores. After attaining a maximum value, it again decreases owing to clogging of the soil pores [1, 16–17].

Clogging is caused by silt and clay deposition over and immediately below the base of basin. The rate of recharge follows almost a similar pattern of variation of infiltration rate with comparatively less intensity and with some time lag due to the time taken by the infiltrated water to reach the water table. When the rate of recharge decreases to a minimum prescribed level, the recharge operation is discontinued for some time and after drying, cleaning, and if necessary, scrapping of the silted bottom of the basin, recharge rate is brought back almost to its initial value and the basin is again put back to use for the next phase of recharge operation. Zomorodi [18] has demonstrated with the help of field examples that the solutions based on the assumption of constant rate of recharge are unable to predict the rise and subsequent decline of the water table which is due to decrease in the rate of recharge. He suggested that the recharge rate should be treated as a variable in time in order to simulate actual field conditions. Several schemes have been proposed to approximate time varying recharge rate in order to develop predictive groundwater flow models. Rai and Singh [19] have used two linear elements to approximate exponentially decaying recharge rates applied from a strip basin to a semi-infinite aquifer. Some workers [20–22] used exponential function to approximate one cycle of time varying recharge applied from a single basin. Yue-zan and others [23] have used a scheme in which the duration of time varying recharge is divided into several time zones according to the actual variation in the recharge rate. In each time zone, the variation range of recharge rate should be considered so small that it can be represented by the constant average value of recharge rate of that particular zone. Yue-zan and colleagues referred this recharge rate approximation as stepped variable scheme.

Manglik and others [24] have proposed a new scheme for approximation of time varying recharge rate. In this scheme, time varying recharge rate is approximated by a series of line elements of different lengths and slopes. The number, lengths, and slopes of the line elements depend on the nature of variation of recharge rate. Advantage of this approximation scheme is that any complex nature of recharge rate variation can be approximated with more accuracy. This scheme was extended for the recharge operation from multiple basins [25] and combination of recharging and pumping from a number of basins and wells [26]. In a real field condition, artificial recharging and pumping operations are carried out intermittently from more than one site according to necessity. In groundwater flow equations, for example in Eq. 9.25, N(x, y, t) is the sum of all recharge and withdrawal rates from distributed sources (recharge basins, ponds, streams, etc.) and from distributed sinks (wells, leakage sides, etc.). According to the scheme considered in [26], N(x, y, t) is represented by:

$$N(x,y,t) = \left\{ \begin{array}{l} \sum\limits_{i = 1}^n {{N_i}(t)\;{\rm{for}}\;{x_{i1}} \le x \le {x_{i2}},{y_{i1}} \le y \le {y_{i2}}} \\ \\ {\text{0elsewhere }} \end{array} \right.,$$
(9.34)

where n is the total number of basins and/or well, \({{N}_{i}}(t)\) is the time-varying recharge (or pumping) rate for the ith basin (or well, respectively) and \({{x}_{i1}},{{x}_{i2}},{{y}_{i1}},{{y}_{i2}}\) are the coordinates of ith basin (or well). \({{N}_{i}}(t)\) is positive for recharge to the aquifer and negative for pumping and leakage out of the aquifer.

For demonstration purpose, Fig. 9.5 illustrates approximation of two cycles of time varying recharge and pumping rates by using this scheme. In this example, two cycles of recharge operations each of 20 days duration with 20 days gap are considered. In each cycle the rate of recharge decreases from 0.8 to 0.7 m/d during the first 2 days and again reaches maximum value of 0.9 m/d during the next 2-day period. Thereafter, it continuously decreases to 0.2 m/d during the next 14 days period. After that recharge operation is discontinued. As a result, the rate of recharge decreases to zero in the next 2 days (Fig. 9.5a). The second cycle of recharge starts after a gap of 20 days. In the second cycle also variation of the rate of recharge is considered in the same way. This kind of time varying recharge rate is approximated by using 11 linear elements of different lengths and slopes. In this example two cycles of pumping each of 10 days duration with a gap of 20 days is considered at a rate of 80 m3/d. The first cycle of pumping begins after 10th day from the beginning of the first cycle of recharge and continues till the 20th day, i.e., the last day of the first cycle of recharging. After a gap of 20 days, the second cycle of pumping starts on the 40th day and continues till the 50th day (Fig. 9.5b). This time varying pumping rate is approximated by nine linear elements [27–30] used the same scheme to approximate time-dependent recharge, pumping and/or leakage to develop analytical models to predict water table fluctuation. Results of analytical models are verified by comparing with the numerical results obtained by using MODFLOW.

Fig. 9.5
figure 5

Approximation of two cycles of time varying recharge and pumping. [27]

Full size image

9.4 Analytical Methods of Solution

The purpose of solving a groundwater flow equation is to obtain the values of water table height, h(x, y, t). Generally two types of methods, namely analytical methods and numerical methods are used for this purpose. Most of the field problems are of complex nature because of the inhomogeneous anisotropic nature of flow systems and irregular shape of their boundaries. Such problems are not easily amenable to analytical methods and can be solved by using numerical methods. Development of numerical methods is based on two schemes: finite difference and finite elements. Accordingly, these methods are called finite difference and finite elements. These methods are described in detail in many published works [1, 31–36]. Based on these numerical methods, many computer programs such as SUTRA, MODFLOW, PORFLOW, etc. are being developed and widely used to solve actual field problems of groundwater flow.

Although the application of analytical solutions is restricted to the relatively homogeneous isotropic flow system having boundaries of simple geometrical shapes, their application is fast and simple compared with that of the numerical methods. Analytical solutions are also useful for other purposes such as sensitivity analysis of the effects of various controlling parameters such as aquifers properties, initial and boundary conditions, intensity and duration of recharge rate, shape, size, and location of the recharge basin, etc. on water table fluctuation. Such information is very essential for making judicious selection of an appropriate development scheme out of many proposed schemes to achieve the preset objectives of groundwater resources management. Besides these applications, analytical solutions are also used for checking validity and calibration of numerical models under development by comparing results obtained from both the approaches. Analytical methods commonly used for the solution of groundwater problems include the Laplace transforms, integral balance methods, method of separation of variables, approximate analytic methods, Fourier transforms, etc. Details about these methods and their applications in the solution of groundwater flow problems or in heat conduction problems can be found in many books [1, 37–42]. A review of analytical solutions has been presented in [43]. Some commonly used analytical methods are discussed in the following subsections.

9.4.1 Laplace Transform

The technique of the Laplace transformation is widely used for solving diffusion type differential equation that contains a first order differential in time. By using the Laplace transform the partial derivative with respect to time variable is removed from the second order partial differential equation (in this case groundwater flow). As a result, the original second order partial differential equation is reduced in second order ordinary differential equation. When the ordinary differential equation is solved and this solution is inverted by using inversion of the associated the Laplace transform; the desired solution of the unknown variable such as water table height is obtained. The Laplace transform of a function h(t) is defined as:

$$ L[h(t)]\equiv h(p)=\int_{0}^{\infty }{{{e}^{-pt}}h(t')dt'}, $$
(9.35)

and its inversion is:

$$ h(t)\equiv \frac{1}{2\pi i}\int\limits_{y -i\infty }^{y +i\infty }{{{e}^{pt}}h(p)}dp, $$
(9.36)

where y is a constant so large that all the singularities lie to the left of the line (y − i∞, y + i∞) on the complex p-plane. Generally, the Laplace transform of a function and its inverse are given in several books [38, 44–45]. Application of the Laplace transform in the solution of groundwater flow problems can be found in [19, 46–49].

9.4.2 The Integral Balance Method

This method is applicable to both linear and nonlinear 1-D transient boundary value problem for certain boundary conditions. The results are approximate. But several solutions obtained by applying this method when compared with the exact solutions have confirmed that the accuracy is generally acceptable. The following steps are followed in the application of this method:

  • (i) The differential equation describing 1-D groundwater flow is integrated over the length of the aquifer in order to remove the derivative with respect to space coordinate.

  • (ii) A suitable profile is chosen for the distribution of water table height. A polynomial profile is generally preferred for this purpose. Experience has shown that there is no significant improvement in the accuracy of the solution by choosing a polynomial greater than the fourth degree. Coefficients in the polynomial are determined by applying boundary conditions.

  • (iii) When the expression of the polynomial profile is introduced into the integrated groundwater flow equation and the indicated operations are performed, a first order ordinary equation is obtained for the average height of the water table with time as the independent variable. The solution of this differential equation subject to the initial condition gives an expression of the initial condition for average height of the water table.

  • (iv) Now the first order differential equation for the average water table height is solved subject to the initial condition for the average height to get the desired solution of the water table height.

Singh and Rai [50–51] have used this method in the solution of ditch-drainage problems in the presence of time varying recharge rate.

9.4.3 Approximate Analytic Methods

Approximate analytic methods are attempted in solving groundwater flow governing equation in its nonlinear form. One example of such a method is presented by Basak [52] in solving a ditch-drainage problem based on the assumption that the first derivative of the water table height with respect to time is independent of the space coordinate, i.e., dh/dt ≠ f(x) and is a function of time only. This approximation is valid when the successive water table profiles are almost parallel. This condition is satisfied almost in the entire region except near the drains. The accuracy of approximate solution is verified by comparing the results with the results of known exact solutions. Basak’s solution is found to be in close agreement with an exact solution of the same problem. Singh and Rai, [50, 53] used this method to obtain a model to describe water table fluctuation induced by exponentially decaying recharge rates.

9.4.4 Method of Separation of Variables

In this method groundwater flow equation is separated into ordinary differential equations for each independent variable. The resulting ordinary differential equations are solved and the complete solution is constructed by the linear superposition of all separated solutions. Examples of application of this method can be found in [54] for 1-D sloping aquifer, in [6] for 2-D sloping aquifer, and in [55] for radial flow.

9.4.5 Finite Fourier Transforms

These transforms are useful in solving boundary value problems in which at least two of the boundaries are parallel and separated by a finite distance.

9.4.5.1 1-D Finite Fourier Sine Transform

This transform is used when value of a variable is specified at the boundaries. For 1-D case, the finite Fourier sine transform S(m, t) with respect to x of a function H(x, t), 0 < x < A is defined as:

$$ {{F}_{s}}[H(x,t)]=S(m,t)=\int\limits_{0}^{A}{H( x,t )}\sin \left( \frac{m\pi x}{A} \right)dx, $$
(9.37)

its inversion is given by:

$$ H(x,t)=\frac{2}{A}\sum\limits_{m=1}^{\infty }{S(m,t)}\sin \left( \frac{m\pi x}{A} \right), $$
(9.38)

in which m is integer representing the number of Fourier coefficients and A is the length of the aquifer. Application of this transform in the solution of groundwater flow problem can be found in [21, 56, 57].

9.4.5.2 2-D Finite Fourier Sine Transform

Finite Fourier sine transform, S(m, n, t) with respect to x and y of a function H(x, y, t), 0 < x < A and 0 < y < B is given by:

$$ {{F}_{s}}[H(x,y,t)]=S(m,n,t)=\int\limits_{0}^{B}{\int\limits_{0}^{A}{H(x,y,t)}}\sin \frac{m\pi x}{A}\sin \frac{n\pi y}{B}dxdy, $$
(9.39)

in which m and n are integers representing number of Fourier coefficients and A and B are length and width of the aquifer in the x and y directions, respectively. Its inversion formula is given by:

$$ H(x,y,t)=\frac{4}{AB}\sum\limits_{m=0}^{\infty }{\sum\limits_{n=0}^{\infty }{S(m,n,t)}}\sin \left( \frac{m\pi x}{A} \right)\sin \left( \frac{n\pi y}{B} \right)\text{.} $$
(9.40)

Example of application of this transform in the solution of groundwater flow equation can be found in [27, 58]. Recently, [29] have used this transform to develop a model to describe water table fluctuation in anisotropic aquifer.

9.4.5.3 1-D Finite Fourier Cosine Transform

This transform is used to solve 1-D flow equation where flux is defined at the boundaries. The finite Fourier cosine transform in the interval \(0<x<A\) is defined as:

$$ C(m,t)=\int\limits_{0}^{A}{H(x,t)}\cos \left( \frac{m\pi x}{A} \right)dx, $$
(9.41)

and its inverse is given by:

$$ H(x,t)=\frac{1}{A}C(0,t)+\frac{2}{A}\sum\limits_{m=1}^{\infty }{C(m,t)}\cos \left( \frac{m\pi x}{A} \right). $$
(9.42)

Examples of application of this transform can be found in [21, 59].

9.4.5.4 2-D Finite Fourier Cosine Transform

This transform is used for the solution of those problems in which the boundary conditions are characterized by flux across the two parallel boundaries. For 2-D problem, the finite Fourier cosine transform C(m, n, t) with respect to x and y of a function H(x, y, t) in the intervals \(0<x<A\,\text{and}\,0<y<B\) is defined as:

$$ C(m,n,t)=\int\limits_{0}^{A}{\int\limits_{0}^{B}{H(x,y,t)}}\cos \left( \frac{m\pi x}{A} \right)\cos \left( \frac{n\pi y}{B} \right)dydx, $$
(9.43)

and its inverse is given by:

$$ \begin{array}{*{35}{l}} H(x,y,t)=\frac{1}{AB}C(0,0,t)+\frac{2}{AB}\sum\limits_{m=1}^{\infty }{C(m,0,t)}\cos \left( \frac{m\pi x}{B} \right)\\ +\frac{2}{AB}\sum\limits_{m=1}^{\infty }{C(0,n,t)}\cos \left( \frac{n\pi y}{A} \right)+\frac{4}{AB}\sum\limits_{m=1}^{\infty }{\sum\limits_{n=1}^{\infty }{C(m,n,t)}}\cos \left( \frac{m\pi x}{B} \right)\cos \left( \frac{n\pi y}{A} \right).\\\end{array} $$
(9.44)

Example of application of this transform is in [20, 28].

9.4.5.5 1-D Extended Finite Fourier Cosine Transform

This transform is used when the flow problem is characterized with mixed boundary conditions, i.e., at one boundary flux is defined and at its parallel boundary head is defined. This transform in the interval \(0<x<A\) is defined as:

$$ {{C}_{e}}[m,t]=\int\limits_{0}^{A}{H(x,t)}\cos \frac{(2m+1)\pi x}{2A}dx, $$
(9.45)

and its inverse is given by:

$$ H(x,t)=\frac{2}{A}\sum\limits_{m=0}^{\infty }{{{C}_{e}}(m,t)}\cos \left( \frac{(2m+1)\pi x}{2A} \right)\text{.} $$
(9.46)

Application of this transform in the solution of 1-D groundwater flow can be found in [55].

9.4.5.6 2-D Extended Finite Fourier Cosine Transform

For 2-D flow problem, the transform C(m, n, t) with respect to x and y in the interval 0 < x < A and 0 < y < B of a function H(x, y, t) is defined as:

$$ {{C}_{e}}(m,n,t)=\int\limits_{0}^{B}{\int\limits_{0}^{A}{H(x,y,t)}}\cos \frac{(2m+1)\pi \text{ }x}{2A}\cos \frac{(2n+1)\pi y}{2B}dxdy, $$
(9.47)

its inversion formula is given by:

$$ H(x,y,t)=\frac{4}{AB}\sum\limits_{m=0}^{\infty }{\sum\limits_{n=0}^{\infty }{{{C}_{e}}(m,n,t)}}\cos \left( \frac{(2m+1)\pi x}{2A} \right)\cos \left( \frac{(2n+1)\pi y}{2B} \right). $$
(9.48)

This transform has been used in [25] to develop a groundwater flow model.

9.5 Summary

Recharging and pumping are the essential components of water resources development. Therefore, prediction of water table fluctuations in response to proposed schemes of recharging and pumping are essential to make judicious selection of an appropriate development scheme out of many to achieve the preset objectives of sustainable management. This is accomplished by carrying out sensitivity analysis of the effects of changes in the controlling parameters on the dynamic behavior of the water table. Controlling parameters include shape, size, and location of recharge basins and wells, intensity of recharge and pumping rates, duration and number of cycles of recharge and pumping operations, etc. Solution of the prediction problem lies in the solution of the governing flow equations subject to the initial and boundary conditions associated with the physical problems under consideration. In this chapter groundwater flow equations have been presented to describe 2-D groundwater flows in inhomogeneous anisotropic unconfined aquifer (Eq. 9.16), inhomogeneous, isotropic unconfined aquifer (Eq. 9.17), in leaky unconfined aquifer (Eq. 9.20) in sloping homogeneous isotropic sloping aquifer (Eq. 9.26) in response to intermittently applied time varying recharge and/or pumping from multiple basins of rectangular shapes and wells, respectively, along with the initial and boundary conditions and methods of their solutions. Groundwater flow equations to describe 1-D flow can be obtained by substituting zero for the derivative of one space coordinate.

Governing flow equation in cylindrical coordinate system (Eq. 9.27) is also presented to describe groundwater flow induced by time varying recharge from circular basin. Groundwater flow equations for steady state can be obtained by substituting zero for the time derivative. The above mentioned governing flow equations are used for the development of analytical/numerical models to predict water table fluctuations in the flow system under consideration. Examples of the analytical models have been cited from the papers published in reputed journals which can be easily accessible to the interested readers. Though the application of analytical models are restricted to the flow system having boundaries of simple geometrical shapes, their application is fast and simple compared to numerical methods. Analytical models are also used to check the validity of numerical models under development, because of the assured accuracy of the results of analytical models.