Keywords

The Theory of Didactical Situations (named TDS in this volume) began to develop in the 1960s in France, initiated by Guy Brousseau who has led its development since that time. A first synthesis was published in 1997 in English (Brousseau 1997) but the theory has since developed considerably in its conceptual notions as much as its research methodologies, as attested to for instance by the special issue of the journal Educational Studies in Mathematics (Laborde et al. 2005) or the proceedings of the 2009 Summer School devoted to didactical engineering (Margolinas et al. 2011). Important aspects of these developments were motivated by the increasing investment of TDS in the study of ordinary classrooms, and many researchers worldwide have made contributions. This chapter introduces some main elements of TDS structured by principles, questions, methodologies, and key constructs as presented in Chap. 1 of this book, and invites the reader to make sense of these elements through the analysis of the two first episodes of the video of Carlo and Giovanni, introduced in Chap. 2.

1 Theory of Didactical Situations: An Overview

TDS is a “home-grown” theory (Sriraman and English 2010); those who have contributed to its development share with the initiator the conviction that the field of mathematics education needs to develop its own theorizations and not just borrow and adapt theories developed in connected fields such as psychology, sociology, or anthropology. In the limited space allocated to this introduction, we focus on three characteristics that create the specific lens through which TDS considers the teaching and learning of mathematics: the systemic nature of teaching and learning; the epistemology of mathematical knowledge; and the vision of learning as a combination of adaptation and acculturation. These characteristics determine the questions that TDS raises and tries to answer, as well as the methodologies it privileges.

1.1 Principles

Since its beginnings, TDS has adopted a systemic perspective, conceiving the didactics of mathematics as the study of the conditions for the dissemination and appropriation of mathematical knowledge through educational institutions. This systemic perspective is reflected in the organization of the theory around the idea of situation. A situation is itself a system, “the set of circumstances in which the student finds herself, the relationships that unify her with her milieu, the set of ‘givens’ that characterize an action or an evolution” (Brousseau 1997, p. 214). TDS is interested in didactical situations, that is, those designed and utilized with teaching and learning aims. Brousseau distinguishes two possible perspectives on didactical situations: a vision of these as the student’s environment organized and piloted by the teacher; and a broader vision including the teacher and the educational system itself.

A first important characteristic of TDS is the attention it pays to mathematics and its epistemology. In the theory, this sensibility is expressed in different ways, notably through the reference to Bachelard’s epistemology and the didactic conversion of his notion of epistemological obstacle, and also through the notion of fundamental situation. Referring to Bachelard’s studies in physics which led to a list of obstacles of epistemological nature, Brousseau (1997, p. 83) extends its application to the field of didactics of mathematics, defining epistemological obstacles as forms of knowledge that have been relevant and successful in particular contexts, including often school contexts, but that at some moment become false or simply inadequate, and whose traces can be found in the historical development of the domain itself (see also Schneider 2013).

A fundamental situation for a given concept is a mathematical situation or, better, a family of mathematical situations for which the concept constitutes a priori an optimal solution. This epistemological analysis, connecting mathematical knowledge and situations, constitutes what Brousseau calls today a theory of mathematical situations, a first level of modeling and analysis in TDS, the second one being that of didactical situations. The well-known situation of puzzle enlargement (Brousseau 1986, 2008) can for instance be seen as a fundamental situation for linearity.

A second important distinction in TDS is linked to the following epistemological characteristic: mathematical knowledge is something that allows us to act on our environment, but the pragmatic power of mathematics is highly dependent on the specific language it creates, and on its forms of validation. This characteristic reflects in TDS through the distinction between three particular types of situations: situations of action, situations of formulation, and situations of validation. The first chapter in Brousseau (1997) illustrates this distinction taking as an example a succession of situations developed around the famous problem “Race to 20”, conceived as a fundamental situation for Euclidian division.

The third important characteristic refers to students’ cognitive dimension, particularly to the combination of the two processes adaptation and acculturation. Regarding adaptation, Brousseau’s discourse shows an evident proximity with Piagetian epistemology:

the student learns by adapting herself to a milieu which generates contradictions, difficulties and disequilibria, rather as human society does. This knowledge, the result of the students’ adaptation, manifests itself by new responses which provide evidence for learning. (Brousseau 1997, p. 30)

But this adaptation is not sufficient; acculturation is necessary to link students’ constructions with forms of knowledge that are socially shared, culturally embedded, and institutionally legitimated, being called “savoirs” in French. Such a change in the status of knowledge requires the teacher’s didactic intervention and can be achieved in many different ways (Brousseau 1997).

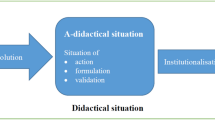
TDS key constructs take these two types of processes into account: independent adaptation through the notions of a-didactical situation and milieu, acculturation through the notions of didactical situation and didactical contract, and the relationships between these processes through the dual notions of devolution and institutionalization (see Sect. 4.1.4).

1.2 Questions

The questions that TDS tries to answer are diverse but coherent with these principles. They regard:

  • the functioning of didactical systems, leading to the identification of regularities, and their elaboration into didactical phenomena;

  • the determination of fundamental situations associated with specific mathematical concepts, and their possible actualizations into didactical situations, taking into account the conditions and constraints of particular educational contexts;

  • the dependence between situations and the progression of knowledge in particular domains, paying the necessary attention to both adaptation and acculturation processes.

Even if TDS has the ultimate goal of improving students’ mathematics learning, the learner is not at the center of the theory. TDS gives priority to the understanding of how the conditions and constraints of didactical systems enable or hinder learning, and how the functioning of such systems can be improved.

1.3 Methodologies

The systemic perspective and TDS ambition of developing didactics as a genuine fundamental and applied field of research have also shaped the methodological development of the theory. Among the diversity of methodologies used in TDS, the systemic view led to being especially valued those methodologies giving access to the complexity of didactic systems, what resulted in an original concept: that of didactical engineering (Artigue 1989, 2013). It is a methodology which is structured around a phase of preliminary analysis combining epistemological, cognitive, and didactical perspectives, and aiming at the understanding of the conditions and constraints to which the didactical system considered is submitted, a phase of design and a priori analysis of situations reflecting its optimization ambition; and, after the implementation, a phase of a posteriori analysis and validation. As pointed out by Artigue (2008), the TDS theoretical basis explains:

the importance given in it to the a priori analysis, and the rejection of usual validation processes based on the comparison between the pre and post characteristics of experimental and control groups, at the benefit of an internal comparison between the a priori analysis and the a posteriori analysis of classroom realizations. (Artigue 2008, p. 11)

The TDS constructs mentioned above are essential tools for researchers to design situations and carry out a priori and a posteriori analyses. In the design of learning situations, for instance, particular attention is paid to the constituents of the milieu organized for the learner, and to the optimization of the possibilities it offers, both in terms of action and feedback, to foster the emergence of the targeted strategies and knowledge. Attention is also paid to the way the devolution process is organized. An important part of the analyses is devoted to the situation itself: what mathematical sense can emerge from the interactions between the student and the milieu; is the situation sufficiently accessible and efficient to enable the student to have access, by adaptation, to an appropriate meaning of the target concept? This analysis often relies on an epistemological analysis of the concept at stake.

Since the 1990s, the increasing use of TDS for the study of ordinary classrooms has led to the development of new methodologies based on participative and naturalistic observations, but there is no doubt that didactical engineering, which has itself evolved as a methodology (Margolinas et al. 2011), remains the privileged methodology in TDS when a research project includes a design dimension.

1.4 Key Constructs

We focus in this part on the key constructs necessary for making sense of the video analysis developed in section “Illustrating the theory through analysis of the video of Carlo, Giovanni, and the exponential function”, but do not enter into the recent developments of TDS. Complementary insights will be introduced in other chapters of the book.

1.4.1 A-Didactical Situation and Milieu

The notions of a-didactical situation and milieu are attached to the vision of learning as an adaptation process and to the ambition of optimizing such a process. This means elucidating and creating the conditions for making the target mathematical knowledge emerge from students’ interaction with a milieu, as the optimal solution to a mathematical problem. As explained by Brousseau (1997, p. 30), in a-didactical situations the students accept to take the mathematical responsibility of solving a given problem, and the teacher refrains from interfering and suggesting the target mathematical knowledge for making such adaptation processes possible. As Brousseau (1997) stresses:

The student knows very well that the problem was chosen to help her acquire a new piece of knowledge, but she must also know that this knowledge is entirely justified by the internal logic of the situation and that she can construct it without appealing to didactical reasoning. (p. 30)

Hence comes the name of a-didactical situation, the prefix “a” indicating that the situation has been temporally freed from its didactical intentionality. Initially, the development of TDS was tightly linked to the development of a-didactical situations, as evidenced by the impressive work that has been carried out in the experimental center COREM in Bordeaux since 1972.

The milieu is the system with which the students interact in the a-didactical situation and an essential role of the teacher or the researcher is to organize this milieu. It includes material and symbolic resources, possibly calculators, computer devices, or all types of machinery. It conditions the didactical variables of the situation, that is to say those which affect the cost and economy of solving strategies. Learning being conceived as an adaptation process, the milieu must be a source of contradictions, imbalances, what is captured through the idea of antagonist milieu. The milieu must allow students to experience the limitations of their initial strategies, but its possibilities of action and feedback should also make possible an evolution towards winning strategies, which attest the construction of new knowledge.

Of course, these constraints impose desirable conditions on the problems themselves whose solving is the motive of such a-didactic interaction student–milieu as expressed in Brousseau (2008, p. 249):

  • The mathematical knowledge aimed at should be the only good method of solving the problem.

  • The assignment (i.e. the given task) should not refer to any of the knowledge that one wishes to have appear. It determines the decisions permitted, the initial state, and the gain or loss represented by the final states.

  • Students can start to work with inadequate “basic knowledge”.

  • They can tell for themselves whether their attempt succeeded or failed.

  • Without determining the solution, these verifications are suggestive (they favour some hypotheses, bring in some appropriate information, neither too open nor too closed).

  • Students can make a rapid series of “trial and error” attempts, but anticipation should be favoured.

  • Amongst the empirically acceptable solutions only one takes care of all objections.

  • The solution can be found and tested by some of the students in a reasonable amount of time in an ordinary class, and swiftly shared and verified by the others.

  • The situation can be re-used, and will then provide some questions that relaunch the whole process.

Naturally, these conditions describe an ideal and are rarely fulfilled by real scenarios. They constitute a theoretical reference for researchers, helping them to anticipate the a-didactical potential of a given scenario and its limitation, and to better understand the contingency of classroom realizations.

1.4.2 Didactical Situation and Contract

Quite soon researchers relying on TDS acknowledged that a theory of mathematical and a-didactical situations is not sufficient for approaching mathematics teaching and learning. The processes of devolution and institutionalization were introduced for connecting the acculturation and adaptation dimensions of the educational enterprise. Both are under the responsibility of the teacher. Through devolution, the teacher makes her students accept the mathematical responsibility of solving the problem without trying to decode her didactical intention, and maintains it, creating thus the conditions for learning through adaptation. Through institutionalization, the teacher helps students to connect the contextualized knowledge they have constructed in the a-didactical situation to the target cultural and institutional knowledge and she organizes its decontextualization and transformation into “savoirs”.Footnote 1 She thus restores the intentionality of the didactic interaction, which was not prominent in the a-didactical situation, and makes acculturation possible.

Devolution is not easy and is in some sense paradoxical. In a didactical situation, the teacher being the voice of the institution has a precise learning aim in mind but, as pointed out by Brousseau (1997, p. 41), “everything that she (the teacher) undertakes in order to make the student produce the behaviours that she expects tends to deprive this student of the necessary conditions for the understanding and the learning of the target notion.” If the teacher tells the student what to do, the student cannot learn. In TDS, this paradox of devolution is linked to another essential construct, that of didactical contract, which emerged from research work developed by Brousseau with students presenting elective failure in mathematics (Brousseau and Warfield 1999; Brousseau 1980). The concept of didactic contract expresses the fact that teacher–students interactions are subject to rules regarding the mathematical knowledge at stake. These constitute a set of reciprocal obligations and mutual expectations, and are the result of an often implicit negotiation. The rules of the didactical contract remain themselves mostly implicit, in contrast to an ordinary contract, and often only become visible when the contract is broken for one reason or another. The process of devolution is conceived as the negotiation by the teacher of a didactical contract that temporarily allows the transfer of responsibility regarding the knowledge aimed at from the teacher to the student.

This explains why often, in the literature, didactical situations are presented as made of an a-didactical situation and a didactical contract. The didactical contract is source of diverse phenomena and paradoxes. Very early, some of these have been identified: the “Topaze” and the “Jourdain” effects, the metacognitive shift, the improper use of analogy, or the obsolescence of teaching situations. The Topaze effect will be discussed in Chap. 12.

We now invite the reader to gain a deeper insight into the previously introduced concepts through the analysis of the video and its Episodes 1 and 2 with the two students Carlo and Giovanni. However, it must be said that this presentation of TDS is very basic. TDS is much more complex, and it is interesting to notice that many recent developments result from its use for understanding the functioning of ordinary classrooms: scale of didacticity in the didactical contract (Brousseau 1995), refined in different levels of granularity (Hersant and Perrin-Glorian 2005), vertical structuration of the milieu differentiating the students’ milieu and the teacher’s milieu (Margolinas 1998, 2002). Other developments such as the theory of joint action between students and teachers combine in an original way affordances both of TDS and ATD (Sensevy 2011; Sensevy et al. 2005).

2 Illustrating the Theory Through Analysis of the Video of Carlo, Giovanni, and the Exponential Function

The classroom situation we analyze here with TDS was not conceived within this framework. As mentioned above, analyzing data from classrooms that were not designed within the TDS framework is now a current form of use of the theory.

For analyzing the data, we introduce three situations, associated with the three tasks and the work with the three dynamic geometry files. In this section, we consider only Task 1 and Task 2, in which students are asked to work autonomously and in which the intervention of the teacher is minimal. An a-didactical analysis seems thus appropriate. For carrying it out, we try to characterize the milieu of the situations, anticipate what the interactions with this milieu are likely to produce, compare this analysis with what we know about the mathematical aims of the teacher when proposing these tasks to the students, and question the potential of this situation for making the mathematical knowledge aimed at by the teacher emerge through autonomous adaptation. This a priori analysis is then contrasted with the a posteriori analysis of the video data.

2.1 Initial Analysis

In the initial analysis, the use of TDS raised difficulties for at least three reasons. First, the information initially provided was limited to the dynamic geometry files and the tasks, which was insufficient for developing the systemic analysis typical for TDS. The files are essential components of the milieu, but for anticipating the interaction they may produce, we needed information about the mathematical and instrumental knowledge that the students are able to engage in this interaction. Any a priori analysis makes hypotheses at this level considering a generic student and her supposed experience; this involves a lot of knowledge about the whole educational system and the particular institution at stake. Of course, these hypotheses are not necessarily fulfilled by the actual individual student, influencing the real dynamics of the situation and its cognitive outcomes, as well as the teacher–students interaction. The varying knowledge of individual students is a normal source of discrepancies with the a priori analysis, which are systematically looked for and questioned in the a posteriori analysis. In this video analysis, filling the gaps of the provided information was all the more difficult for us as the video concerned another educational culture with a different approach to exponential functions (in France, exponential functions are introduced in grade 12 as solutions of differential equations).

The second reason is the form of Task 1, which does not constitute a problem-situation in the sense of Brousseau (1997, p. 214) but is an exploration task:

  • Open with Cabri II the file “y = (2.7)^x”.

  • In this file you will see: the point x on the x-axis and the point y = 2.7^x, on the y-axis.

  • Move the point x on the x-axis and check what happens to the point y = 2.7^x on the y-axis; that is, observe how (2.7)^x varies as x is changing.

  • In order to make these observations, modify also the measure unit on the y-axis of your worksheet. After some trials, use animation. Move the point x towards the left until arriving nearly to the end of the field of variation of the negative x’s, and then animate with a spring the point x so that it moves from the left towards the right.

  • Share all the observations that you think interesting on the coordinate movement of the two points, and describe briefly (but clearly) your argument on the sheet that has been given to you. (Task 1; see Sect. 2.1.3, Fig. 2.1)

In this task, the expectations remain rather fuzzy. What criteria can students have for knowing that they have completed the task? Autonomous work of the students supposes that an appropriate didactical contract has already been negotiated regarding such tasks, in particular helping students appreciate when they can consider that they have solved the task. However, no information on this point was provided in the initial data.

The third reason is the difficulty of categorizing the situation according to the TDS categories: we first categorized it as a situation of action as the interaction with the milieu obeys a dialectics of action. Nevertheless, in this task, formulation has an explicit and important place, and the conjectures produced and made explicit in one task become elements of the milieu for the following ones. Thus the situation is more than a situation of action.

Despite these difficulties, partially overcome thanks to the complementary information obtained from the teacher, the use of TDS for the analysis of the video of Carlo and Giovanni was productive, as we show in the following subsections.

2.1.1 Initial a Priori Analysis

We present the a priori analysis made with the initial information given before showing how it was refined taking into account the teacher’s answers to the questionnaire. Then we contrast it with the a posteriori analysis. Due to the role played by technology, we combine the affordances of TDS with those of the instrumental approach (Guin et al. 2004; Artigue 2002). In this context, the instrumental approach is useful for not underestimating the instrumental knowledge needed for a productive interaction with the milieu and for anticipating how mathematical knowledge and instrumental knowledge, instrumented and paper and pencil techniques, can be combined in the exploration process. One could think that instrumental needs are limited, as files in the Dynamic Geometry Software (DGS) are provided and used as black boxes. However, research shows that, even in that case, actions undertaken and interpretations of the feedback are highly dependent on the students’ state of instrumental genesis (Restrepo 2008).

Considering the exploration tasks proposed to the students, we tried to understand what could result from the autonomous interaction of the students with the two DGS files for Task 1 and Task 2. The first file (Fig. 4.1) displays a curve representing the exponential function of base 2.7. This curve has been obtained as the locus of a point P whose coordinates (x, y) are displayed. On the right upper side of the screen, an equality is added: 2.7^x = numerical value, this numerical value being the current value of 2.7^x, thus the second coordinate of P.

Fig. 4.1
figure 1

The dynamic geometry file for Task 1

Full size image

Students are asked to explore how y varies when x increases, then when x decreases and takes negative values. They are also asked to prepare an animation and it is suggested that they can change the units. There is no doubt that the situation offers a rich potential for a-didactical interaction with the milieu, and that several conjectures can a priori emerge:

C1::

When x increases, y increases, too, and it increases more and more quickly.

C2::

When x approaches 0, y approaches 1 (and potentially the inference for x = 0, y = 1, even if this cannot be exactly observed).

C3::

When x approaches 1, y approaches 2.7, the number given in the task and visible on the screen (and potentially the inference for x = 1, y = 2.7 even if, once again, this cannot be exactly observed).

C4::

When x takes negative values which become smaller and smaller, y approaches more and more 0 and from some moment takes the value 0 (note that the final part of this conjecture is not mathematically true but it corresponds to the material evidence provided by exploration with the DGS file).

A good level of instrumental knowledge (Lagrange 2005; Artigue 2002) allows students to infer the above-mentioned conjectures, which go beyond what is observable on the computer screen. It could also lead students to work on the conjecture C4, which may lead them to question the value 0 taken for negative x, and to change the semiotic register (Duval 1995), moving to the symbolic algebraic register for testing the conjectures and even producing proofs. But such a change requires both a change in semiotic register and a change in attitude: the move from a situation of action to a situation of validation. We hypothesize that this is not likely to appear unless the didactical contract has established and valued such attitudes. Conversely, limited instrumental knowledge concerning discretization processes and their graphical and numerical effects at the interface can lead students to lose time, for instance if they try to obtain the exact values 0 and 1 for x. They can also lose time preparing the required animation which, in our opinion, does not add much to the a-didactical potential of the situation. The fact that the teacher asks for this animation and suggests to change the units, without giving any technical hint, leads us to hypothesize that the students have a good familiarity with the DGS. Nevertheless, if this familiarity has been built in geometry, students may not have developed the instrumental knowledge regarding discretization phenomena which is required when working with functions. We could go on with this a priori analysis, but considering space limitations move to the situation with Task 2.

In this episode (Fig. 4.2), the exploration process uses a second file. In this file, a horizontal half-line with a mobile point A on it has been added; there are thus two mobile points: A and P. The segment joining A to the origin of the half-line (on the y axis) is drawn and an expression “a = numerical value”, in which “a” can be interpreted as the measure of the length of the segment or the abscissa of A, is displayed. The curve on which P moves represents the exponential function of base a and the expression “y = a^numerical value” is also displayed, the numerical value being the current value of the abscissa of P. It is possible to get the exact value 1 for a, and thus to see the horizontal line which makes the transition between increasing and decreasing exponentials.

Fig. 4.2
figure 2

DGS screen configuration for Task 2 (From Fig. 2.2)

Full size image

Task 2 is fuzzily described: students are simply asked to understand the base a of the exponential function. Nevertheless, the interaction with the milieu can be productive and through the move of point A and its effects on the curve, several new conjectures can emerge:

C5::

If a > 1 the exponential function is increasing and the more a increases, the more it becomes vertical (the more it increases quickly).

C6::

If a < 1 the exponential function is decreasing and the more a decreases, the more it decreases quickly.

C7::

For a = 1 the exponential function is constant (the curve is a horizontal line).

C8::

If x is close to 1, y is close to a (and potentially the inference if x = 1 then y = a).

C9::

  • If a > 1 (respectively a < 1): When x takes negative values smaller and smaller (respectively positive values bigger and bigger), y approaches more and more 0 and, from some moment, it takes the value 0 (the final part of these conjectures is not mathematically true but it corresponds to the material evidence provided by exploration).

  • And for a in a small interval around the value 1, the moment when y approaches (or “takes” as shown in the file) the value 0 increases and even is not visible on the screen for values of a very close to 1.

According to their degree of instrumentation, the students can move the window or reduce the zoom display in DGS in order to make visible the part of the curve where the x-axis seems to join the curve and thus conjecture that the function has the same shape in any case, except for a = 1. Otherwise, the limited screen window may lead students to conjecture that the function is of different type for values of a in a small interval around 1, not just for a = 1.

Of course different formulations of these conjectures are possible. Students can speak of functions or curves, or mix the two notions, and use a more or less mathematical language. Their formulations are a source of information on their comprehension of the notion of function but also on the didactical contract regarding mathematical discourse at this stage of the learning process. These formulations may also be influenced by the use of the instrument. As we did in the first situation, we can investigate what is needed for going beyond conjectures based on graphical evidence. We do not detail this analysis for the second situation, but it shows once again that the emergence of proofs is rather improbable.

2.2 Need for Extension of Data and Extended Analysis

For complementing the initial a priori analysis, we especially needed some more information about the didactical contract, the students’ mathematical and instrumental background, and the teacher’s expectations. The teacher’s answers to the questionnaire designed after the initial a priori analysis (Sect. 2.2.2) provided the necessary information.

The didactical contract: The teacher’s answers confirm that this kind of exploration task is usual in his classrooms. We can thus suppose the existence of an established didactic contract for exploration tasks in a computer environment, making clear what can be the end of an exploration phase, the kind of writing expected, and the role of the teacher. These answers also show that, beyond its mathematical components, the didactical contract includes some general rules concerning students’ interactions: active interaction and collaborative supporting attitude, mutual listening; and concerning teacher–students interactions: the teacher enters in a working group if called by the students, if he realizes that they are stuck, or for provoking deeper reflection on interesting ideas.

The students’ mathematical background: This session represents the students’ first encounter with (continuous) exponential functions but they have previously met discrete exponential dynamics and associated these to the invariance of the ratio of two consecutive terms. Students could thus mobilize this discrete vision of exponentials and associated algebraic techniques in the exploration. This could help them question graphical evidence, for instance the fact that the exponential function actually reaches the value 0, or conjecture properties not directly accessible at the interface such as a^1 = a.

The students’ instrumental background: The teacher’s answers confirm the students’ familiarity with DGS – they have used it from the beginning of the year. We also learn that they have approached functions numerically, graphically, and symbolically using spreadsheets, Graphic Calculus and TI-Interactive, thus we can suppose that they have already faced discretization phenomena and questions linked to window framing. What is missing is information about the familiarity that students have in working with DGS for studying functions, which requires different instrumental competences from those used for using DGS in geometry. The familiarity gained with other technologies is not necessarily enough for ensuring a possible transfer to DGS. This can have an effect on the conjectures made, as explained in the initial a priori analysis.

The teacher’s expectations: The teacher’s expectations regarding this situation which precedes the formal introduction of the derivative are high, up to an approach of the differential characteristic property of the exponential function. He writes:

The activity intends to clarify the principal features of increasing behaviours and of exponential functions. In particular, it intends to explain the reason why at the increasing of x an exponential of base greater than 1 will increase, definitively, more than any other polynomial function of x, whatever grade of the polynomial. In the project, exponential functions and sequences are used to cope with problem situations coming from exponential models. (Answer to question 17, see Sect. 2.2.2)

How the proposed exploration can lead students to the conviction that exponential functions with base greater than 1 dominate any kind of polynomial function is not evident. The a-didactic milieu seems too weak for leading to such a conviction without the teacher’s mediation, and even weaker for finding reasons for this phenomenon as expressed above by the teacher.

In the initial a priori analysis, we pointed out the possibility of different levels of language. It is interesting to note that the teacher is sensitive to this question of language, and considers that he has an important role to play in the evolution of the linguistic expressions. He supports this position by a discourse involving the notion of semiotic game, which is extensively discussed in Chap. 3. He also adds that he anticipates such a role for him only from Episode 3. We thus suppose that the didactic contract makes clear for students that they can express the results of the exploration in their own terms. Nevertheless, due to the familiarity already gained in the work with polynomial functions, we expect the use of mathematical terms for expressing and comparing function variations.

In the teacher’s answers no allusion is made to proof. We pointed out that the production of proofs for exponential variations did not seem accessible to the students without substantial teacher mediation. Considering the expectations he expresses and the role he anticipates for himself, we consider that his goal is not the production of proof. Rather, he wants the students to make sense of the variations of exponential functions and the role played by the exponential basis through exploration, and access some form of understanding supported by graphical evidence. This seems coherent with the vision he presents of the use of technology: “In my opinion technological tools have to be used to empower the possibility to experience the mathematical environment and mathematical objects” (answer to question 3, Sect. 2.2.2).

2.2.1 A Posteriori Analysis

We synthesize now the results of the a posteriori analysis. We pay particular attention to the similarities and discrepancies detected in the comparison with the a priori analysis, and use this comparison for understanding the functioning of the specific didactic system at stake. We start the a posteriori analysis by comparing the students’ conjectures with our anticipations.

Students’ conjectures: Most of the anticipated conjectures appear, but also some more. In fact, six conjectures are proposed by the students during the first situation and five during the second, which confirms the a-didactical potential of these situations. Discrepancies between a priori and a posteriori analysis are mainly due to Carlo’s work in the semiotic register of algebraic expressions to which, in the a priori analysis, we only gave a role of control and validation. Indeed, we linked the production of conjectures to the interaction with the DGS component of the milieu. The first conjecture articulated regards the value of the function for x = 0 (C2 in the a priori analysis). It emerges very early (line 3 of the transcript), is directly expressed by Carlo in terms of equality, and proved algebraically. Thus it does not result from the interpretation of the graphical representation. The students then test the effect of a change in the unit of the y-axis and Giovanni notes that the form of the graph does not change (Giovanni, lines 16, 18) while Carlo seems sensitive to the change in the perception of the rate of growth. The second conjecture is articulated by Carlo immediately after line 19 and expresses the fact that if 2.7 is replaced by 1, the graph becomes a straight line (C7). This conjecture was anticipated but only for Task 2. The first DGS file, indeed, does not allow the students to change the value of the basis of the exponential. The conjecture thus necessarily results here from the connection made by Carlo between the perceptive change in the rate of growth and the algebraic fact that 1^x = 1 for every x. The third produced conjecture is C4: when x goes towards negative values, y gets closer to 0 (Giovanni, line 40), and from some value on, x is always 0 (Giovanni, line 42). The students try to determine the value where the function reaches the value 0 (from line 111); however, for this conjecture we do not notice any attempt of control or validation in the algebraic register. The fourth conjecture states that the ratio f(2)/f(1) equals 2.7 (Carlo, line 90). Once again, it emerges from algebraic work and expresses the connection that students make between this situation and the work developed on discrete exponential models. Connecting 2.7 to particular values of the function, this conjecture plays the role given to C3 in the a priori analysis, but does it in a way that suggests a deeper connection with the nature of exponential growth. The attempts made by the students for checking this conjecture in the DGS environment are not successful, due to uncontrolled discretization phenomena. The fifth conjecture is the first concerning the variations of the function and refines C4 (Giovanni, line 109): for negative x, the function decreases towards 0. It apparently results from the manipulation of the software. For finding the exact value for which 2.7^x becomes 0, Giovanni moves the mobile point from the right to the left, which gives a perception of decrease. The sixth conjecture, a variant of C1, connects variation and limits: f(x) tends towards infinity when x tends towards infinity. Carlo justifies this assertion by invoking the nature of exponential dynamics (line 122) while Giovanni checks it with DGS (line 123).

While dealing with Task 2, the two students quickly understand that by increasing the value of a they obtain exponential curves increasing more and more quickly (C5). Giovanni expresses this conjecture in ordinary language: “If you change this… that is it becomes more tightened or it increases more or less” (Giovanni, line 152), and Carlo (line 153) goes on using a language more mathematical and involving the idea of increasing rate of change. Later on, when Carlo begins to write the report, another expression emerges: “For the same space, the differences are ever greater” (Carlo, line 192) which shows once again the influence of previous work on discrete dynamics. The second conjecture is C7 (case a = 1) which was already articulated in the exploration of Task 1. It is expressed by Carlo as a confirmation (line 173) but Giovanni does not seem so sure. The end of the episode is not easy to analyze from the transcript but it seems that at least three other conjectures are produced, expressing the decreasing nature of the exponential curve for a < 1 (C6), and the fact that the curve never reaches the x-axis (line 186). Carlo tries to mobilize the algebraic register for justifying this conjecture but using 1 instead of a as the base of the exponential: “If I raise 1 to any number I have not zero” (Carlo, line 199). Later on, another conjecture emerges expressing that when the base a tends towards 0, the curve gets closer to the x-axis but does not touch it (lines 211–215).

Note that, for a = 2.7, exploring what happens when x decreases, the students conclude that y reaches 0, whereas in the second exploration they insist on the fact that for a < 1, when x increases, y decreases towards 0 but never takes this value. Apparently, they do not make any connection between the two situations. Subtle differences in the information provided at the interface for the two DGS files (in the first file, the y value is displayed and becomes 0 once x is about –5 for instance), in the way the questions are phrased and thus the exploration is carried out (leading to them paying more attention to the coordinates of P in the first situation, and more attention to the global behaviour in the second), may have contributed to this.

The sharing of roles between students: From the beginning, Giovanni takes the mouse and works with the computer while Carlo works mainly with paper and pencil and seems in charge of writing the report. In the first minutes, it seems that he wants to pilot the DGS exploration from this external position, but quickly Giovanni establishes his autonomy. Even if the students collaborate, this sharing of roles creates an evident dissymmetry in their interactions with the milieu, with notable impact as shown above. In fact, we could say that they do not interact with the same milieu; only Giovanni interacts with the milieu of the a priori analysis. This seems the main source of discrepancy between the a priori and a posteriori analysis. We did not anticipate this sharing of roles, and nor did the teacher, although it appears frequently in group-work with technology. When questioned about it, the teacher considers that there is some dysfunction, the interaction between students respecting neither his ethical values nor his vision of cognitive development.

Instrumental issues: Instrumental issues impact the students’ relationship with the milieu. Most of the instrumental difficulties met by the students had been anticipated in the a priori analysis, but not all of them, for instance those attached to the distinction between what is fixed or what is not fixed in the first DGS drawing. We supposed that, due to their familiarity with DGS, the students would not have difficulties with this distinction. This was the case for Giovanni, who seemed to understand quickly that the curve was drawn through the use of a formula involving a value 2.7 (lines 30–32) that could be changed into another value. This was not the case for Carlo, who met serious problems, confusing 2.7 with the unit of the y-axis, and thinking thus that by changing the unit he could change the base of the exponential. Note that the difficulties met by the students and anticipated in the a priori analysis were not expected by the teacher. We take this as a symptom of the general underestimation of the complexity of instrumental geneses, and of their mathematical and technical needs. The strong semiotic sensitivity of the teacher did not fully compensate for that.

The role of the teacher: The role of the teacher perfectly corresponds to the anticipation of the a priori analysis. During these two episodes, he only intervenes for solving a few technical problems, and the two students work in full autonomy.

3 Conclusion

The video of Carlo and Giovanni comes from a classroom session that has not been designed within the frame of TDS. Nevertheless, these episodes present characteristics which make an analysis through the lens of TDS and the instrumental approach fully pertinent. Students interact with a milieu offering a rich potential of actions and retroactions, and the experience of the students, both mathematical and instrumental, allows them to benefit from this potential, in the autonomous mode which characterizes a-didactical situations. Moreover, the didactical contract makes clear the respective expectations of teacher and students, even if the written exploration tasks do not seem precisely defined.

We developed thus our analysis using the usual techniques of TDS, that is to say, preparing an a priori analysis focusing on the determination of the cognitive potential of an a-didactic interaction with the milieu, for a generic and epistemic student, that is, a student accepting the a-didactical game and able to invest in it the mathematical and instrumental knowledge supposed by the teacher. We then compared the results of the a priori analysis with the a posteriori analysis of the video. In doing so, we showed that the tools we had used in the a priori analysis allowed us to make realistic anticipations regarding the cognitive a-didactic potential of the two situations, and also to anticipate limitations and difficulties underestimated by the teacher himself. Thanks to this technique, the students’ behavior becomes more understandable, and we can separate in the contingency of the actual realization what results from the logic of the situation from what results from other conditions. In particular, we can observe the discrepancies created by the fact that, in the a priori analysis one considers an epistemic and generic student, while in the reality of classrooms teachers work with individuals with different background and motivation, who enter more or less into the game proposed by the teacher and most often do it with different knowledge from that supposed. In this case study, the two students accept the a-didactical game and the devolution process is successful. They behave as epistemic actors of the situation: they try to answer the questions posed by the teacher, using their mathematical knowledge for piloting and making sense of the exploration; they do not try to guess the answers expected by the teacher from some didactical hints (this phenomenon is the object of Chap. 12 on the Topaze effect). This being said, they interact differently with the milieu, in fact not exactly with the same milieu. Comparing the a priori and the a posteriori analysis, we point out new elements not envisaged in the a priori analysis, and identify their effects, both on the cognitive trajectory of each student and on the global trajectory of the group.

We do not pretend that this TDS analysis tells everything that is didactically pertinent about this part of the video. Nevertheless, through its specific lens, it substantially contributes to our understanding of the video.

In this conclusion, we also would like to come back to the issue of “significant unit” for didactical analysis. The vision of what is a significant unit always depends on the adopted theoretical framework. We were able to productively put TDS at the service of the analysis of the episode, but we want to stress again that what this video makes accessible is very limited with regard to the systemic perspective of TDS. What we access is a very small part of the teaching of exponential functions in this classroom and of what makes the teacher able to fulfill the aims he details in his answers to the questionnaire. We have access, for one particular group of students, to a moment of “first meeting” (according to the ATD terminology) with exponential functions. They intervene through technological black-boxes that the students have to explore. Some statements emerge from this exploration whose mathematical status is not clear at this stage. How do these statements situate with respect to the statements produced by other groups? How will the teacher exploit them? How will they be related both in their content and form to the institutional knowledge aimed at? And what use will be made of that knowledge, once institutionalized? What level of technical operationality will be aimed at in the different semiotic registers? We just see a tiny part of a mathematical and didactical organization, something interesting and insightful but very insufficient for someone who would like to understand what can be the teaching and learning of exponential functions in such a context.