Multi-valued Logic for a Point-Free Foundation of Geometry

Abstract

The paper starts from the observation that in the inclusion-based approach to point-free geometry there are serious difficulties in defining points. These difficulties disappear once we reformulate this approach in the framework of continuous multivalued logic. So, a theory of ‘graded inclusion’ is proposed as a counterpart of the usual ‘crisp inclusion’ of mereology. Again, a second theory is considered in which the graded predicates ‘to be close’ and ‘to be small’ are assumed as primitive. In both cases a suitable notion of abstractive sequence and of equivalence between abstractive sequences enables us to define the points. In the resulting set of points a distance is defined in a natural way and this enables a metrical approach to point-free geometry and therefore to go beyond mereotopology.The general idea is that it is possible to search for mathematical formalizations of the naive theory of the space an ordinary man needs to have in its everyday life. To do this we have to direct our attention not only to regions and the related relation of inclusion as it is usual in point-free geometry, but also to those (vague) properties which are geometrical in nature.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Łukasiewicz’s many-valued logic (see Hájek 1998), Chang and Keisler’s continuous logic (1966) and Pavelka’s fuzzy logic (1979) define very interesting chapters of formal logic. Recently, under the name ‘continuous logic’, these researches were reconsidered to extend the powerful tools of model theory to classes of structures which are not definable in classical first order logic. This since these structures assume as primitive a real-valued function. Examples are the metric spaces, the normed spaces, the probabilities (see for example Yaacov and Usvyatsov 2010).

The basic ideas of point-free geometry were firstly formulated by A. N. Whitehead in An Inquiry Concerning the Principles of Natural Knowledge (Whitehead, 1919) and in The concept of Nature (Whitehead, 1920), where he proposed as primitive notions events and extension relation between events (in geometrical terms, regions and inclusion relation). Later, in Process and Reality (Whitehead, 1929), Whitehead proposed a different treatment, inspired by De Laguna (1922), in which the topological notion of ‘connection’ between two regions was assumed as primitive and the inclusion was defined (see Gerla 1994). Successively, in a series of papers, metric-based approaches to point-free geometry were proposed in which, apart the inclusion relation, distances and diameters are also considered (see Di Concilio and Gerla 2006; Gerla 1990; Gerla and Miranda 2004). The resulting notion of point-free pseudo-metric space is a promising base for a metric foundation of geometry in accordance with the ideas of L.M. Blumenthal (1970). Indeed, it is possible to associate every point-free pseudo-metric space with a metric space via a natural definition of point and distance.

In this exploratory paper we suggest the possibility of applying the ideas of continuous logic to point-free geometry. This is done by assuming as primitives predicates, geometrical in nature, as ‘to be included’, ‘to be small’, ‘to be close’. Indeed, since these predicates apply at different grades, we have to interpret them as fuzzy relations and therefore we have to refer to a first order multi-valued logic. Perhaps we can look the resulting formalisms as a way to modelize the passage from the original, naive, predicate based description of the geometrical space, qualitative in nature, to the modern real-number based approach to geometry, quantitative in nature.

More precisely, in Sect. 5.2 we propose the notion of inclusion space corresponding to some of the geometrical properties of the inclusion analyzed in Whitehead (1919, 1920). In Sect. 5.3 we give the notion of connection space corresponding to the analysis given in Whitehead (1929). Taking in account of the difficulties of the inclusion-based proposal in defining the notion of point, in Sects. 5.4 and 5.5 we reformulate it in the framework of multi-valued logic. This means that the inclusion is intended as a graded notion. We show that this enables us to overcome the observed difficulties. Finally, in Sect. 5.6 we reformulate the metric-based theory of point-free geometry into a theory in a multi-valued logic involving the graded predicates ‘to be close’ and ‘to be small’.

2 Inclusion Spaces

We isolate the main properties considered by Whitehead (1919) and we transform them into a system of axioms. Indeed, we consider the following first order theory in a language L_≤ containing only the binary predicate ≤ . As usual, we write x < y to denote the formula $(x \leq y) \wedge (\neg (x = y))$.

Definition 1.

An inclusion space is a structure satisfying the following axioms:

• I1 $\forall x\,(x \leq x)$ (reflexivity)

• I2 $\forall x\forall y\forall z\,((x \leq z \wedge z \leq y) \Rightarrow x \leq y)$ (transitivity)

• I3 $\forall x\forall y\,(x \leq y \wedge y \leq x \Rightarrow x = y)$ (anti-symmetry)

• I4 $\forall z\exists x\,(x < z)$ (there is no minimal region)

• I5 $\forall x\forall y\,(x < y \Rightarrow \exists z\,(x < z < y))$ (density)

• I6 $\forall x\forall y\,(\forall x^{\prime}(x^{\prime} < x \Rightarrow x^{\prime} < y) \Rightarrow x \leq y)$ (below approximation)

• I7 $\forall x\forall y\,\exists z(x \leq z \wedge y \leq z)$ (upward-directed).

We call regions the elements of an inclusion space and inclusion relation the relation ≤ . Then an inclusion space is an ordered set (S, ≤ ) such that ≤ has not a minimum, it is dense and upward-directed. Moreover, in this set it is possible to approximate every region from below. To find a model for this theory, we refer to the notion of bounded closed regular subset of the Euclidean space $\mathbb{R}^{n}$. This is a natural candidate to represent the idea of region which is usually accepted in literature.

Definition 2.

Given a topological space we call closed regular a subset which is a fixed point of the operator creg defined by setting

$$\displaystyle{\mathit{creg}(X) = \mathit{cl}(\mathit{int}(X))}$$

where we denote by cl and int the closure and the interior operators, respectively.

We denote by $RC(\mathbb{R}^{n})$ the class of all the closed regular subsets of $\mathbb{R}^{n}$. $RC(\mathbb{R}^{n})$ is a very interesting example of complete atomic-free Boolean algebra. We are interested to the class $\mathcal{R}$ of the nonempty bounded elements of $RC(\mathbb{R}^{n})$. It is easy to prove the following theorem.

Theorem 1.

The structure $(\mathcal{R},\subseteq )$ is an inclusion space.

We call canonical inclusion space the structure $(\mathcal{R},\subseteq )$. Whitehead (1919) defines the points by the following basic notion.

Definition 3.

Given an inclusion space (S, ≤ ), we call abstractive sequence any sequence $(r_{n})_{n\in \mathbb{N}}$ of regions such that

• (i) $(r_{n})_{n\in \mathbb{N}}$ is order-reversing with respect to the inclusion

• (ii) There is no region which is contained in all the regions in $(r_{n})_{n\in \mathbb{N}}$.

We denote by AS the class of abstractive sequences.

Whitehead’s idea is that an abstractive sequence $(r_{n})_{n\in \mathbb{N}}$ represents an ‘abstract object’ which is obtained as a ‘limit’ of $(r_{n})_{n\in \mathbb{N}}$. On the other hand, it is possible that two different abstractive sequences define the same abstract object. Then, we introduce the following equivalence relation.

Definition 4.

The covering relation ≤ _c is the relation in AS defined by setting, for every $(r_{n})_{n\in \mathbb{N}}$ and $(s_{n})_{n\in \mathbb{N}}$,

$$\displaystyle{(r_{n})_{n\in \mathbb{N}} \leq _{c}(s_{n})_{n\in \mathbb{N}} \Leftrightarrow \forall n\exists m\ r_{n} \leq s_{n}.}$$

The relation $\equiv$ is defined by setting

$$\displaystyle{(r_{n})_{n\in \mathbb{N}} \equiv (s_{n})_{n\in \mathbb{N}} \Leftrightarrow (r_{n})_{n\in \mathbb{N}} \leq _{c}(s_{n})_{n\in \mathbb{N}}\text{ and }(s_{n})_{n\in \mathbb{N}} \leq _{c}(r_{n})_{n\in \mathbb{N}}.}$$

It is possible to prove that ≤ _c is a pre-order and therefore that $\equiv$ is an equivalence. Then we can consider the quotient $AS/ \equiv$ and an order relation in $AS/ \equiv$ by setting

$$\displaystyle{[(r_{n})_{n\in \mathbb{N}}] \leq _{c}[(s_{n})_{n\in \mathbb{N}}] \Leftrightarrow (r_{n})_{n\in \mathbb{N}} \leq _{c}(s_{n})_{n\in \mathbb{N}}.}$$

The following definition remembers Euclid’s definition of point.

Definition 5.

We call geometrical element any element of the quotient $\mathit{AS}/ \equiv$, i.e. any class of equivalence $[(r_{n})_{n\in \mathbb{N}}]$ modulo $\equiv$. A point is a geometrical element which has no part, i.e. which is minimal in $(\mathit{AS}/ \equiv,\leq _{c})$.

Unfortunately, in spite of the evident elegance of this definition of point, it is possible to prove the following theorem (see Gerla and Miranda 2004, 2008).

Theorem 2.

In a canonical inclusion space the definition of point is empty, i.e. there is no minimal element in $(\mathit{AS}/ \equiv,\leq _{c})$ .

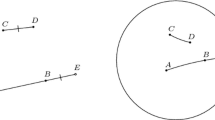
Instead of an precise exposition of the proof of this theorem, we prefer to illustrate the idea which is on its basis by the following example. Consider in the Euclidean plane the abstractive sequence G defined by the sequence (B_n) of closed balls with center in the origin (0,0) and radius $r_{n} = 1/n$. From an intuitive point of view such an abstractive sequence represents a point. Unfortunately, we can consider the sequences G₁ and G₂ defined by the closed balls with radius r_n and centre in $(-1/n,0)$ and (1∕n, 0), respectively (see Fig. 5.1). It is immediate that [G] > G₁, [G] > G₂ and that [G], [G₁] and [G₂] are three different geometrical elements. This means that [G] is not minimal and therefore that [G] is not a point.

Fig. 5.1

Three different “points” in the origin

Such an argument holds true if we start from any abstractive sequence. Perhaps Whitehead’s passage from the inclusion-based approach to the connection-based approach was done to avoid such a counterintuitive behaviour. This theorem shows that the proposal of Whitehead of assuming as a primitive only the mereological notion of inclusion is unsatisfactory.

3 Connection Structures

Some years later the publication of Whitehead (1919, 1920), Whitehead (1929), proposed a different idea based on the primitive notion of connection relation. By isolating the main properties of the connection relation considered by Whitehead, we obtain the following theory. The considered language L_C has only a binary relation symbol C.

Definition 6.

Denote by x ≤ y the formula $\forall z(\mathit{zCx} \Rightarrow \mathit{zCy})$. Then we call connection space theory the following list of axioms.

• C1 $\quad \forall x\forall y\,(\mathit{xCy} \Rightarrow \mathit{\mathit{yCx}})$ (symmetry)

• C2 $\quad \forall z\exists x\exists y\,((x \leq z) \wedge (y \leq z) \wedge (\neg \mathit{xCy}))$

• C3 $\quad \forall x\forall y\exists z\,(\mathit{zCx} \wedge \mathit{zCy})$

• C4 $\quad \forall x(\mathit{xCx})$

• C5 $\quad \forall x\forall y\,((x \leq y \wedge y \leq x) \Rightarrow x = y).$

The intended interpretation is that the connection is either a surface contact or an overlap. It is easy to prove that in any connection space the relation ≤ is an order relation. We denote by xOy the formula $\exists z(z \leq x \wedge z \leq y)$ and we call overlapping relation the corresponding relation. Again we use the class $\mathcal{R}$ to find a model of this theory. We denote again by C the interpretation of the relation symbol C in $\mathcal{R}$.

Theorem 3.

Define in $\mathcal{R}\subseteq RC(\mathbb{R}^{n})$ the relation C by setting

$$\displaystyle{\mathit{XCY } \Leftrightarrow X \cap Y \neq \varnothing.}$$

Then $(\mathcal{R},C)$ is a connection space in $\mathbb{R}^{n}$ , whose associated order coincides with the set-theoretical inclusion.

We call canonical connection space a connection space defined in such a way. The observation of a canonical connection space makes evident way the connection relation is different from the overlapping relation. Indeed, while XCY means that there is a point belonging in both the regions, XOY means that there is a region contained in both the regions. To obtain an adequate definition of point, we need the notion of nontangential inclusion.

Definition 7.

Given a connection space (S, C), we say that two regions have a tangential connection when

• (i) They are connected,

• (ii) They do not overlap.

We say that x is non-tangentially included in y and we write $x \prec y$ provided that

• (j) x is included in y,

• (jj) There is no region having a tangential connection with both x and y.

The following is a simple characterization of the non-tangential inclusion.

Proposition 1.

The non-tangential inclusion is the relation defined by the formula

$$\displaystyle{ \forall z(zCx \Rightarrow zOy). }$$

(5.1)

It is possible to prove that in a canonical connection space

$$\displaystyle{X \prec Y \Leftrightarrow X \subseteq \mathit{int}(Y ).}$$

Definition 8.

An abstractive sequence in a connection space is a sequence $(r_{n})_{n\in \mathbb{N}}$ of regions such that

• (j) $(r_{n})_{n\in \mathbb{N}}$ is order-reversing with respect to the non-tangential inclusion,

• (jj) There is no region which is contained in all the regions of $(r_{n})_{n\in \mathbb{N}}$.

The notions of covering, equivalence, geometrical element, point are defined as in Sect. 5.2. Differently from the case of the inclusion spaces, in the canonical connection space $(\mathcal{R},C)$ Whitehead’s definition of point works well. Indeed the following theorem holds (see Coppola et al. 2010).

Theorem 4.

Consider the canonical space $(\mathcal{R},C)$ and denote by B _n (p) the closed ball centered in p and with radius 1∕n. Then the map associating every point p in $\mathbb{R}^{n}$ with the geometrical element $[(B_{n}(p))_{n\in \mathbb{N}}]$ is a one-to-one map from $\mathbb{R}^{n}$ to the set of points in $(\mathcal{R},C)$ .

This theorem shows that connection space theory gives to point-free geometry a more suitable framework than the one of inclusion space theory. A further reason in furnished by the following theorem.

Theorem 5.

While in a canonical connection space $(\mathcal{R},C)$ we can define the inclusion relation, in a canonical inclusion space $(\mathcal{R},\subseteq )$ it is not possible to define the connection relation.

The proof of this theorem is based on the fact that if a relation is definable in a structure, then it is invariant with respect to all the automorphisms of this structure. So, it is sufficient to exhibit an one-to-one map preserving the inclusion and not preserving the connection (for a complete proof see Gerla and Miranda 2004).

4 Multi-valued Logic for an Inclusion-Based Point-Free Geometry

As we have seen, there are some troubles in the inclusion-based point-free geometry. Indeed in rather natural models Whitehead’s definition of point is empty, moreover the topological notion of connection cannot be defined. In spite of that, we claim that an inclusion-based approach it is possible provided that we consider the inclusion as a graded notion and therefore provided that we shift from classical logic to multi-valued logic. Namely, we refer to the first order logic associated with a continuous triangular norm $\otimes: [0,1] \times [0,1] \rightarrow [0,1]$ (see for example Hájek 1998) and therefore to a first order language with:

• Two logical connectives $\wedge$ and ⇒ , interpreted by ⊗ and the related residuum → ,

• Two logical constant $\underline{0}$ and $\underline{1}$ to denote 0 and 1

• The quantifiers $\forall$ and $\exists$ interpreted by the operators inf and sup.

In addition, we consider a connective Ct we interpret by the function ct: [0, 1] → [0, 1] such that ct(x) = 1 if x = 1 and ct(x) = 0 otherwise. This means that the intended meaning of a formula as Ct(α) is ‘α is completely true’. To fix the ideas, we assume that ⊗ is the usual product and therefore that the implication is interpreted by the operation → such that x → y = 1 if x ≤ y and $x \rightarrow y = y/x$ otherwise. Given a set D, an n-ary fuzzy relation in D is a map r: Dⁿ → [0, 1]. We call crisp a fuzzy relation assuming only the values 0 and 1 and we identify a classical relation $R \subseteq D^{n}$ with the crisp relation c_R: Dⁿ → [0, 1] defined by setting c_R(d₁, …, d_n) = 1 if (d₁, …, d_n) ∈ R and c_R(d₁, …, d_n) = 0 otherwise. In other words, we identify R with its characteristic function c_R.

A multi-valued interpretation (D, I) is defined by a nonempty domain D and by a function I associating every constant c with an element I(c) ∈ D, every n-ary operation symbol with an n-ary operation in D and every n-ary relation symbol $\underline{r}$ with an n-ary fuzzy relation $r = I(\underline{r})$, i.e. a map r: Dⁿ → [0, 1]. Given a multi-valued interpretation (D, I), the interpretation I(t): Dⁿ → D of a term t is defined as in classical logic. The valuation of the sentences is defined in a truth-functional way as follows.

Definition 9.

Given a multi-valued interpretation (D, I), a formula α whose variables are among x₁, …, x_n and d₁, …, d_n in D, we define the value Val(α, d₁, …, d_n) by recursion on the complexity of α, by the equations:

• (i) $\quad \mathit{Val}(\underline{r}(t_{1},\ldots,t_{p}),d_{1},\ldots,d_{n}) = I(\underline{r})(I(t_{1})(d_{1},\ldots,d_{n}),\ldots,I(t_{p})(d_{1},\ldots,d_{n}))$

• (ii) $\quad \mathit{Val}(\alpha _{1}\underline{ \diamond}\alpha _{2},d_{1},\ldots,d_{n}) = \mathit{Val}(\alpha _{1},d_{1},\ldots,d_{n}) \diamond V al(\alpha _{q},d_{1},\ldots,d_{n})$

• (iii) $\quad \mathit{Val}(\underline{\bullet }\alpha,d_{1},\ldots,d_{n}) =\bullet (V al(\alpha,d_{1},\ldots,d_{n}))$

• (iv) $\quad \mathit{Val}(\forall x_{h}\beta,d_{1},\ldots,d_{n}) =\inf (\{\mathit{Val}(\beta,d_{1},\ldots,d_{h-1},d,d_{h+1},\ldots,d_{n}): d \in D\})$

• (v) $\quad \mathit{Val}(\exists x_{h}\beta,d_{1},\ldots,d_{n}) =\sup (\{\mathit{Val}(\beta,d_{1},\ldots,d_{h-1},d,d_{h+1},\ldots,d_{n}): d \in D\})$

where we denote by $\underline{\diamond}$ (by $\underline{\bullet }$) a binary (an unary) connective and by $\diamond$ (by •) the corresponding interpretation.

We say that d₁, …, d_nsatisfy α if Val(α, d₁, …, d_n) = 1. If α is a closed formula, then the value Val(α, d₁, …, d_n) does not depend on the elements d₁, . . , d_n and we write Val(α) instead of Val(α, d₁, …, d_n). In the case there are free variables in α, we write Val(α) to denote $\mathit{Val}(\forall x_{1}\ldots \forall x_{n}(\alpha ))$ where $\forall x_{1}\ldots \forall x_{n}(\alpha )$ is the universal closure of α.

Definition 10.

Given a theory T, we say that (D, I) is a multi-valued model of T if Val(α) = 1 for every α ∈ T.

The so defined multi-valued logic is rather expressive. For example, if $\underline{r}$ is an n-ary relation symbol then the formula

$$\displaystyle{\forall x_{1}\ldots \forall x_{n}(\mathit{Ct}(\underline{r}(x_{1},\ldots,x_{n})) \leftrightarrow \underline{ r}(x_{1},\ldots,x_{n}))}$$

is satisfied if and only if $\underline{r}$ is interpreted by a crisp relation. Indeed it is sufficient to observe that this formula is satisfied if and only if ct(r(d₁, …, d_n)) = r(d₁, …, d_n) for every d₁, …, d_n in D. In other words, ‘to be crisp’ is a first order property. This entails that all the classical notions which are definable in classical first order logic are definable in our multi-valued logic, too. In particular, the notion of order relation is definable.

Definition 11.

Let (D, I) be a multi-valued interpretation and α be a formula whose free variables are among x₁, …, x_n. Then the extension of α in (D, I) is the fuzzy relation r_α: Dⁿ → [0, 1] defined by setting r_α(d₁, …, d_n) = Val(α, d₁, …, d_n) for every d₁, …, d_n in D. In such a case we say that r_αis defined by α. We call crisp extension of α the extension r_Ct(α) of Ct(α). In such a case we say that r_Ct(α) is the crisp relation defined by α.

Then the crisp relation defined by α is the (characteristic function of the) relation

$$\displaystyle{\{(d_{1},\ldots,d_{n}) \in D^{n}:\alpha \text{ is satisfied by }d_{ 1},\ldots,d_{n}\}.}$$

Coming back to point-free geometry, we consider the first order language with a binary relation symbol Incl and we write x ≤ y to denote the formula Ct(Incl(x, y)). An interpretation of such a language is defined by a pair (S, incl) where S is a nonempty set and incl: S × S → [0, 1] a fuzzy binary relation. The interpretation of ≤ is the (characteristic function of the) relation ≤ defined by setting

$$\displaystyle{ x \leq y \Leftrightarrow \mathit{incl}(x,y) = 1. }$$

(5.2)

We call the crisp inclusion associated with incl this relation.

If Sim(x, y) denotes the formula $\mathit{Incl}(x,y) \wedge \mathit{Incl}(y,x)$, then the interpretation of Sim(x, y) is the fuzzy relation sim: S × S → [0, 1] defined by setting

$$\displaystyle{ \mathit{sim}(x,y) = \mathit{incl}(x,y) \otimes \mathit{incl}(y,x). }$$

(5.3)

We call the graded identity associated with incl this fuzzy relation.

Definition 12.

A graded preorder structure, in brief graded preorder, is a multi-valued model (S, incl) of the following theory:

• A1 $\quad \forall x(\mathit{Incl}(x,x))$

• A2 $\quad \forall x\forall y\forall z((\mathit{Incl}(x,z) \wedge \mathit{Incl}(z,y)) \rightarrow \mathit{Incl}(x,y)).$

Then a fuzzy relation incl is a graded preorder if and only if, for every x, y, z ∈ S,

• a1 incl(x, x) = 1                         (reflexivity)

• a2 incl(x, y) ⊗incl(y, z) ≤ incl(x, z)  (transitivity).

If the symmetry axiom is also satisfied then the fuzzy relation is called fuzzy equivalence or similarity. Then a similarity is a fuzzy relation sim: S × S → [0, 1] such that

• b1 sim(x, x) = 1                         (reflexivity)

• b2 sim(x, y) ⊗sim(y, z) ≤ sim(x, z)   (transitivity)

• b3 sim(x, y) = sim(x, y)                (symmetry).

This notion is a graded extension of the one of equivalence. It is easy to prove that the fuzzy relation sim defined by (5.3) is a similarity. A fuzzy equality is a similarity satisfying the following ‘separation axiom’

• b4 $\quad \mathit{sim}(x,y) = 1 \Leftrightarrow x = y.$

To simulate Whitehead’s definition of point, we define a notion of ‘point-likeness’ suggested by Euclid’s definition of point as minimal element, i.e. an element x such that x′ ≤ x entails x′ = x.

Definition 13.

We call point-likeness property the property expressed by the formula,

$$\displaystyle{Pl(x) \equiv \forall x^{\prime}(x^{\prime} \leq x \rightarrow \mathit{Sim}(x,x^{\prime})).}$$

The extension of Pl is the fuzzy subset of regions pl defined by

$$\displaystyle{pl(x) =\inf \{ \mathit{incl}(x,x^{\prime}): x^{\prime} \leq x\}.}$$

This means that all the regions are points at a suitable degree. The formula Pl(x) enables us to express the next two axioms. The first axiom claims that if we apply the graded inclusion to regions which are (approximately) points, then such a relation is (approximately) symmetric.

• A3 $\quad \mathit{Pl}(x) \wedge \mathit{Pl}(y) \rightarrow (\mathit{Incl}(x,y) \rightarrow \mathit{Incl}(y,x))$.

This axiom is satisfied if and only if, for every x and y,

• a3 $\quad \mathit{pl}(x) \otimes \mathit{pl}(y) \leq (\mathit{incl}(x,y) \rightarrow \mathit{incl}(y,x)).$

The further axiom claims that every region x contains a point:

• A4 $\quad \forall x\exists x^{\prime}((x^{\prime} \leq x) \wedge \mathit{Pl}(x^{\prime}))$.

Such an axiom is satisfied if and only if for every x,

• a4 $\quad \sup _{x^{\prime}\leq x}\mathit{pl}(x^{\prime}) = 1$

i.e. if and only if for every x

$$\displaystyle{\exists \epsilon >\ 0\text{ there is }x^{\prime} \leq x\text{ such that }pl(x^{\prime}) \geq 1 -\epsilon.}$$

Definition 14.

We call graded inclusion space every model of A1–A4.

The following notion enables us to emphasize the metrical nature of the graded inclusion spaces.

Definition 15.

A hemimetric space is a structure (S, d) such that S is a nonempty set and d: S × S → [0, ∞] is a mapping such that, for all x, y, z ∈ S,

• d1 d(x, x) = 0

• d2 d(x, y) ≤ d(x, z) + d(z, y).

Then, a metric space is a hemimetric space which is symmetric, i.e. such that d(x, y) = d(y, x) for every x, y ∈ S, and such that d(x, y) = 0 only if x = y. Every hemimetric space is associated with a pre-order in the following way.

Proposition 2.

Let (S,d) be a hemimetric space, then the relation ≤ defined by setting:

$$\displaystyle{x \leq y \Leftrightarrow d(x,y) = 0}$$

is a pre-order such that d is order-preserving with respect to the first variable and order-reversing with respect to the second variable.

In the case d is a metric, ≤ coincides with the identity relation. Given x ∈ S, we call diameter of x the number

$$\displaystyle{\delta (x) =\sup \{ d(x_{1},x_{2}): x_{1} \leq x,x_{2} \leq x\}.}$$

Observe that this definition entails that

$$\displaystyle{ \delta (x) \geq d(y,x)\text{ for every }y \leq x. }$$

(5.4)

In the case d is a metric, all the diameters are equal to 0.

The following proposition shows that the notion of hemimetric distance is ‘dual’ of the one of graded preorder. As usual, we put $10^{-\infty } = 0$ and $\mathit{Log}(0) = -\infty$.

Proposition 3.

Given a hemimetric space (S,d), the fuzzy relation incl defined by setting

$$\displaystyle{\mathit{incl}(x,y) = 10^{-d(x,y)}}$$

is a graded preorder such that $pl(x) = 10^{-\delta (x)}$ . Conversely, let incl: S × S → [0,1] be a graded preorder and let d be defined by setting

$$\displaystyle{d(x,y) = -\mathit{Log}(\mathit{incl}(x,y)).}$$

Then d is a hemimetric such that $\delta (x) = -\mathit{Log}(\mathit{pl}(x))$ .

In the case d is a pseudo-metric the associated fuzzy relation incl is a similarity, obviously. We consider the following class of hemimetrics.

Definition 16.

A hemimetric space of regions is a hemimetric space (S, d) such that for every x and y,

• d3 $\quad \vert d(x,y) - d(y,x)\vert \leq \delta (x) +\delta (y)$

• d4 $\quad \forall \epsilon >\ 0\exists x^{\prime} \leq x,\delta (x^{\prime}) \leq \epsilon$.

The following theorem shows a duality between the class of hemimetric spaces of regions and the one of the graded inclusion spaces (see also Di Concilio and Gerla 2006).

Theorem 6.

For every hemimetric space of regions (S,d), the fuzzy relation incl defined by setting

$$\displaystyle{\mathit{incl}(x,y) = 10^{-d(x,y)}}$$

defines a graded inclusion space of regions. Conversely, let (S,incl) be a graded inclusion space of regions and let d: S × S → [0,+∞] be defined by setting

$$\displaystyle{d(x,y) = -\mathit{Log}(\mathit{incl}(x,y)).}$$

Then (S,d) is a hemimetric space of regions.

5 Canonical Graded Inclusion Spaces, Connection and Points

The most famous hemimetric is the excess measure used to define the Hausdorff distance.

Definition 17.

Given a metric space (M, d) the excess measure is the map $e: \mathcal{P}(M) \times \mathcal{P}(M) \rightarrow [0,\infty ]$ defined, for every pair X and Y of subsets of M, by setting

$$\displaystyle{e(X,Y ) =\sup _{p\in X}\inf _{q\in Y }d(p,q).}$$

The following proposition is proved in Di Concilio and Gerla (2006).

Proposition 4.

Let $\mathcal{R}$ be the class nonempty, bounded, closed regular subsets of (M,d). Then the excess measure defines in $\mathcal{R}$ a hemimetric space of regions. Consequently, by setting

$$\displaystyle{\mathit{incl}(X,Y ) = 10^{-e(X,Y )} = \mathit{inf }_{ p\in X}\mathit{sup}_{q\in Y }10^{-d(p,q)}}$$

we obtain a graded inclusion space. The induced order is the usual set theoretical inclusion and the point-likeness property is defined by

$$\displaystyle{\mathit{pl}(X) = 10^{-\vert X\vert },}$$

where |x| is the usual diameter in a metric space.

We call canonical graded inclusion space the inclusion space obtained by such a proposition. Observe that if we consider a fuzzy equality eq: M × M → [0, 1], then by setting $d(x,y) = -\mathit{Log}(eq(x,y))$ we obtain a metric. Indeed, it is evident that d(x, y) = 0 if and only if eq(x, y) = 1 if and only if x = y. By applying Proposition 4, we obtain that

$$\displaystyle{\mathit{incl}(X,Y ) = \mathit{inf }_{p\in X}\mathit{sup}_{q\in Y }eq(p,q).}$$

Assume that in the language there is a name Eq to denote eq. Then, in accordance with the usual interpretation of the quantifiers in multi-valued logic, we can interpret the value incl(X, Y ) as the interpretation of the formula $\forall p \in X\exists q \in Y (Eq(p,q))$, i.e. of the claim ‘every point in X is (approximately) equal with a point in Y ’.

We will show that, differently from Whitehead’s inclusion spaces, in a graded inclusion space we can define the connection relation as the crisp extension of the formula expressing the overlapping relation in an inclusion space.

Theorem 7.

Consider in a canonical graded inclusion space $(\mathcal{R},\mathit{incl})$ the formula $O(x,y) \equiv \exists z(\mathit{Incl}(z,x) \wedge \mathit{Incl}(z,y))$ . Then the connection relation C in the canonical connection space $(\mathcal{R},C)$ is defined by the formula Ct(O(x,y)).

In other words, we can define the connection between two regions by saying that the two regions completely overlaps (at degree 1).

The second question is to show that in a graded inclusion space it is possible to give a nonempty notion of point.

Definition 18.

Given a graded inclusion space, we call abstraction process any sequence $< p_{n} >\ _{n\in \mathbb{N}}$ of regions which are order-reversing with respect to the order associated with the graded inclusion. We extend the point-likeness property to the abstraction processes by setting

$$\displaystyle{pl(< p_{n} >\ _{n\in \mathbb{N}}) = \mathit{lim}_{n\rightarrow \infty }pl(p_{n}) = \mathit{sup}_{n}pl(p_{n}).}$$

We say that $< p_{n} >\ _{n\in \mathbb{N}}$represents a point if $pl(< p_{n} >\ _{n\in \mathbb{N}}) = 1$ and we denote by Pr the class of abstraction processes representing a point.

Observe that A4 enables us to prove that every region of a graded inclusion space ‘contains’ an abstraction process representing a point and therefore that $Pr\neq \varnothing$. Indeed, in accordance with a4, for every region x there is x′ ≤ x such that $pl(x^{\prime}) \geq 1 - 1/n$. Then we can consider the sequence $< p_{n} >\ _{n\in \mathbb{N}}$ defined by setting p₁ = x and p_n equal to a region such that p_n ≤ p_n−1 and $pl(p_{n}) \geq 1 - 1/n$. Obviously, $pl(< p_{n} >\ _{n\in \mathbb{N}}) = 1$.

The following theorem shows that in the class of abstraction processes representing points it is possible to define a pseudo-metric d. We give the proof in order to emphasize the role of A3 and therefore of d3 in proving the symmetry of d.

Theorem 8.

Let (S,incl) be a graded inclusion space and d′ be the associated hemimetric. Then the map d: Pr × Pr → [0,∞] obtained by setting

$$\displaystyle{d(< p_{n} >\ _{n\in \mathbb{N}},< q_{n} >\ _{n\in \mathbb{N}}) = lim_{n\rightarrow \infty }d^{\prime}(p_{n},q_{n}),}$$

defines a pseudo-metric space (Pr,d).

Proof.

To prove the convergence of the sequence $< d^{\prime}(p_{n},q_{n}) >\ _{n\in \mathbb{N}}$, let n and k be natural numbers and assume that n ≥ k. Then, since d′(p_n, p_k) = 0 and, by (5.4), d′(q_k, q_n) ≤ δ(q_k) we have that,

$$\displaystyle{d^{\prime}(p_{n},q_{n}) \leq d^{\prime}(p_{n},p_{k}) + d^{\prime}(p_{k},q_{k}) + d^{\prime}(q_{k},q_{n}) \leq d^{\prime}(p_{k},q_{k}) +\delta (q_{k})}$$

and therefore,

$$\displaystyle{d^{\prime}(p_{n},q_{n}) - d^{\prime}(p_{k},q_{k}) \leq \delta (q_{k}).}$$

Likewise, since d′(q_n, q_k) = 0 and d′(p_k, p_n) ≤ δ(p_k),

$$\displaystyle{d^{\prime}(p_{k},q_{k}) \leq d^{\prime}(p_{k},p_{n}) + d^{\prime}(p_{n},q_{n}) + d^{\prime}(q_{n},q_{k}) \leq d^{\prime}(p_{n},q_{n}) +\delta (p_{k})}$$

and therefore

$$\displaystyle{d^{\prime}(p_{k},q_{k}) - d^{\prime}(p_{n},q_{n}) \leq \delta (p_{k}).}$$

This entails

$$\displaystyle{\vert d^{\prime}(p_{n},q_{n}) - d^{\prime}(p_{k},q_{k})\vert \leq \max \{\delta (q_{k}),\delta (p_{k})\}.}$$

Obviously, in the case n ≤ k

$$\displaystyle{\vert d^{\prime}(p_{n},q_{n}) - d^{\prime}(p_{k},q_{k})\vert \leq \max \{\delta (q_{n}),\delta (p_{n})\}.}$$

Thus

$$\displaystyle{\vert d^{\prime}(p_{n},q_{n}) - d^{\prime}(p_{k},q_{k})\vert \leq \max \{\delta (q_{n}),\delta (p_{n}),\delta (q_{k}),\delta (p_{k})\}.}$$

The convergence of the diameters entails that $< d^{\prime}(p_{n},q_{n}) >\ _{n\in \mathbb{N}}$ is a Cauchy sequence.

It is evident that $d(< p_{n} >\ _{n\in \mathbb{N}},< p_{n} >\ _{n\in \mathbb{N}}) = 0$ and that d satisfies the triangular inequality.

To prove the symmetry, observe that, by d3, $\vert d^{\prime}(p_{n},q_{n}) - d^{\prime}(q_{n},p_{n})\vert \leq \delta (p_{n}) +\delta (q_{n})$ and therefore, since $\mathit{lim}_{n\rightarrow \infty }\delta (p_{n}) +\delta (q_{n}) = 0$, $\mathit{lim}_{n\rightarrow \infty }\vert d^{\prime}(p_{n},q_{n}) - d^{\prime}(q_{n},p_{n})\vert = 0$. Since the sequences $< d^{\prime}(p_{n},q_{n}) >\ _{n\in \mathbb{N}}$ and $< d^{\prime}(q_{n},p_{n}) >\ _{n\in \mathbb{N}}$ are both convergent, $\mathit{lim}_{n\rightarrow \infty }d^{\prime}(p_{n},q_{n}) = \mathit{lim}_{n\rightarrow \infty }d^{\prime}(q_{n},p_{n})$. Thus

$$\displaystyle\begin{array}{rcl} d(< p_{n} >\ n \in \mathbb{N},< q_{n} >\ n \in \mathbb{N})& =& \mathit{lim}_{n\rightarrow \infty }d^{\prime}(p_{n},q_{n}) = \mathit{lim}_{n\rightarrow \infty }d^{\prime}(q_{n},p_{n}) {}\\ & =& d(< q_{n} >\ _{n\in \mathbb{N}},< p_{n} >\ _{n\in \mathbb{N}}). {}\\ \end{array}$$

 □ 

Such a proposition enables us to associate any graded inclusion space with a metric space. Indeed, recall that the quotient of a pseudo-metric space (X, d) is the metric space $(\underline{X},\underline{d})$ defined by assuming that

• $\underline{X}$ is the quotient of X modulo the relation $\equiv$ defined by setting x ≡ x′ if and only if d(x, x′) = 0,

• $\underline{d}([x],[y]) = d(x,y)$ for every [x], [y] ∈ X′.

Definition 19.

We call metric space associated with a graded inclusion space (S, incl) the quotient $(\underline{\mathit{Pr}},\underline{d})$ of the pseudo-metric space (Pr, d). We call point any element in $\underline{\mathit{Pr}}$.

Then, the metric space $(\underline{\mathit{Pr}},\underline{d})$ associated with a graded inclusion space (S, incl) is obtained

• By starting from the class Pr of abstraction processes,

• By setting $\underline{\mathit{Pr}}$ equal to the quotient of Pr modulo the equivalence relation $\equiv$ defined by

  $$\displaystyle{< p_{n} >\ _{n\in \mathbb{N}} \equiv < q_{n} >\ _{n\in \mathbb{N}} \Leftrightarrow \mathit{lim}_{n\rightarrow \infty }\mathit{incl}(p_{n},q_{n}) = 1,}$$

• By defining $\underline{d}:\underline{ \mathit{Pr}} \times \underline{\mathit{Pr}} \rightarrow [0,\infty ]$ by the equation

  $$\displaystyle{\underline{d}(P,Q) = \mathit{lim}_{n\rightarrow \infty }-\mathit{Log}(\mathit{incl}(p_{n},q_{n}))}$$

  where $P = [< p_{n} >\ _{n\in \mathbb{N}}]$ and $Q = [< q_{n} >\ _{n\in \mathbb{N}}]$ are elements in $\underline{\mathit{Pr}}$.

6 To Be Closed and To Be Small

In a series of papers a metric approach to point-free geometry is proposed in which, in addition to the inclusion relation, the notions of diameter of a region and distance between two regions are assumed as primitives (see Gerla 1990).

Definition 20.

A point-free pseudo-metric space, in short a ppm-space, is a structure (S, ≤ , Δ, δ), where (S, ≤ ) is an ordered set, Δ: S × S → [0, ∞) is order-reversing, δ: S → [0, ∞] is order-preserving and, for every x, y, z ∈ S:

• D1 Δ(x, x) = 0

• D2 Δ(x, y) = Δ(y, x)

• D3 $\quad \varDelta (x,y) \leq \varDelta (x,z) +\varDelta (z,y) +\delta (z)$.

The elements in S are called regions, the order ≤ inclusion relation, Δ(x, y) distance between x and y, δ(x) the diameter of x. Inequality D3 is a weak form of the triangular inequality taking in account the diameters of the regions. The notion of ppm-space extends the one of pseudo-metric space (and therefore of metric space). Indeed, if all the diameters are equal to zero, then D3 coincides with the triangular inequality and the ppm-space is a pseudo-metric space. More precisely, we can identify the pseudo-metric spaces with the ppm-spaces in which ≤ is the identity and all the diameters are equal to zero. We identify the metric spaces with the ppm-spaces satisfying these conditions and such that Δ is finite and Δ(x, y) = 0 entails x = y.

Notice that we can also assume as primitive a function Δ satisfying D1 and D2 and define a diameter by setting $\delta (z) =\sup \{\varDelta (x,y) -\varDelta (x,z) -\varDelta (z,y): x,y \in S\}$. Indeed, to prove that the resulting structure (S, ≤ , Δ, δ) is a pmm-space, we observe that by setting $x = y = z$ we obtain that δ(z) is greater or equal to 0. It is evident that δ is order-preserving and that D3 holds true by definition. It is also possible to assume as primitive only the diameter function (see Gerla and Paolillo 2010; Pultr 1988).

The following proposition gives prototypic examples of ppm-space (see Gerla 1990).

Proposition 5.

Let (M,d) be a pseudo-metric space and let C be a nonempty class of bounded and nonempty subsets of M. Define Δ and δ by setting

$$\displaystyle{\varDelta (X,Y ) =\inf \{ d(x,y): x \in X,y \in Y \}}$$

$$\displaystyle{\delta (X) =\sup \{ d(x,y): x,y \in X\},}$$

respectively. Then (C,⊆,Δ,δ) is a ppm-space.

In particular, we call canonical ppm-space the space $(\mathcal{R},\subseteq,\varDelta,\delta )$. By referring to the just defined class of ppm-spaces, the meaning of the proposed axioms becomes evident. For example, the meaning of D3 is given by Fig. 5.2:

Fig. 5.2

Approximate triangular inequality

Indeed, it is evident that in this case Δ(X, Y ) > Δ(X, Z) +Δ(Z, Y ) and therefore that the usual triangular inequality cannot be assumed. Instead, it is matter of routine to prove that $\varDelta (X,Y ) \leq \varDelta (X,Z) +\varDelta (Z,Y ) +\delta (Z)$. The notion of point is defined as in Sect. 5.5. Indeed, we call abstraction process any sequence $< p_{n} >\ _{n\in \mathbb{N}}$ of regions which are order-reversing and we call distance between two abstraction processes $< p_{n} >\ _{n\in \mathbb{N}}$ and $< q_{n} >\ _{n\in \mathbb{N}}$ the number:

$$\displaystyle{d(< p_{n} >\ _{n\in \mathbb{N}},< q_{n} >\ _{n\in \mathbb{N}}) = lim_{n\rightarrow \infty }\varDelta (p_{n},q_{n})}$$

and diameter of an abstraction process $< p_{n} >\ _{n\in \mathbb{N}}$ the number

$$\displaystyle{\delta (< p_{n} >\ _{n\in \mathbb{N}}) = lim_{n\rightarrow \infty }\delta (p_{n}).}$$

Definition 21.

We say that $< p_{n} >\ _{n\in \mathbb{N}}$represents a point if its diameter is zero and we denote by Pr the class of abstraction processes representing a point.

It is matter of routine to prove that (Pr, d) is a pseudo-metric space.

Definition 22.

A point is an element of the metric space $(\underline{\mathit{Pr}},\underline{d})$ associated with (Pr, d).

The logical counterpart of the ppm-space is defined as follows. We refer to a first order language L_CS with the predicate symbols ≤ , Cl and Sm. The intended meaning of Cl(x, y) is ‘x and y are close’, the intended meaning of Sm(x) is ‘x is small’. We denote by (S, ≤ , cl, sm) an interpretation of L_CS.

Definition 23.

A CS-space is an interpretation (S, ≤ , cl, sm) of L_CS such that ≤ is a crisp order relation and such that the following axioms are satisfied:

• CS1 $\forall x\,\mathit{Cl}(x,x)$

• CS2 $\forall x\forall y\,(\mathit{Cl}(x,y) \Rightarrow \mathit{Cl}(y,x))$

• CS3 $\forall x\forall y\forall z\,(\mathit{Cl}(x,z) \wedge \mathit{Cl}(y,z) \wedge \mathit{Sm}(z) \Rightarrow \mathit{Cl}(x,y))$

• CS4 $\forall y\forall x\forall x^{\prime}\,(x \leq x^{\prime} \Rightarrow (\mathit{Cl}(x,y) \Rightarrow \mathit{Cl}(x^{\prime},y)))$

• CS5 $\forall x\forall x^{\prime}\,(x \leq x^{\prime} \Rightarrow (\mathit{Sm}(x^{\prime}) \Rightarrow \mathit{Sm}(x))).$

Observe that, as observed in Sect. 5.4, the logical connective Ct enables us to express the condition ‘ ≤ is a crisp relation’ by a first order formula in the multi-valued logic. Notice also that in Gerla (2008) the structures satisfying CS1, CS2, CS3 are called approximate similarity structures and that they are proposed for a solution of Poincaré paradox.

The proof of the following proposition is obvious.

Proposition 6.

An interpretation (S,≤,cl,sm) of L _CS is a CS-space if and only if ≤ is an order relation, cl is order-preserving, sm is order-reversing and

• (i) cl(x,x) = 1,

• (ii) cl(x,y) = cl(y,x),

• (iii) cl(x,z) ⊗ (y,z) ⊗ (z) ≤cl(x,y).

The following theorem shows that there is a duality between the notions of ppm-space and the one of CS-space.

Theorem 9.

Let (S,≤,Δ,δ) be a ppm-space and define cl and sm by setting

$$\displaystyle{cl(x,y) = 10^{-\varDelta (x,y)}\,\,\,\,;\,\,\,\,\mathit{sm}(x) = 10^{-\delta (x)}.}$$

Then (S,≤,cl,sm) is a CS-space. Conversely, let (S,≤,cl,sm) be an approximate CS-space and set

$$\displaystyle{\varDelta (x,y) = -\mathit{Log}(\mathit{cl}(x,y))\,\,\,\,\,;\,\,\,\,\,\delta (x) = -\mathit{Log}(\mathit{sm}(x)).}$$

Then (S,≤,Δ,δ) is a ppm-space.

In particular, by starting from the canonical ppm-space $(\mathcal{R},\subseteq,\varDelta,\delta )$, we define the canonical CS-space$(\mathcal{R},\subseteq,\mathit{cl},\mathit{sm})$ by setting $cl(X,Y ) = 10^{-\varDelta (X,Y )}$ and $\mathit{sm}(X) = 10^{-\delta (X)}$.

Theorem 10.

In the canonical CS space we can define the connection relation by the formula Ct(Cl(x,y)).

Proof.

It is sufficient to observe that cl(X, Y ) = 1 if and only if Δ(X, Y ) = 0 if and only if X ∩ Y ≠ ∅.