Kaldorian Assumptions and Endogenous Fluctuations in the Dynamic Fixed-Price IS-LM Model

Abstract

With the aim of better understanding the conditions which determine endogenous fluctuations at business cycle frequencies, recent literature has revived interest in the Schinasi’s variant of the dynamic, intermediate-run, IS-LM model (Schinasi 1981, 1982). Results, however, remain confined to Kaldorian-type economies, namely to those economies which present a greater-than-unity marginal propensity to spend out of income. This paper contributes to the debate by showing that, in the case of a negative interest rate sensitivity of savings, stable endogenous cycles can actually emerge as equilibrium solutions of the model also in the case of non Kaldorian-type economies. To this end, we combine the instruments of the global analysis, specifically the homoclinic bifurcation Theorem of Kopell and Howard (1975), with numerical methods.

Introduction

Fixed-price, dynamic IS-LM models of Schinasi’s type (1981, 1982) have recently re-gained centrality in the literature regarding deterministic fluctuations at business cycle frequencies. A strand of contributions is using the imposition of time-delayed feedbacks in the tax collection function to obtain or suppress endogenous fluctuations (cf inter al., Cai 2005; de Cesare and Sportelli 2005; Fanti and Mandredi 2007; Neantu, Opris and Chilarescu 2007). Other scholars (cf, inter al., Gandolfo 1997; Makovinyiova 2011; Neri and Venturi 2007, Sasakura 1994; Zimka 1999) remain more in line with the original structure of the model, and look for the existence of oscillating solutions in specific regions of the parameters space mainly by the use of the Hopf bifurcation Theorem. In general terms, it is important to point out that the interest for the model is largely undermined by the severe functional restrictions needed to generate the required oscillating behavior of the variables. In particular, a Kaldorian $S$-shaped investment function, in turn implying the possibility of an upward sloping IS curve, is appealed by this literature to show that the model can originate endogenous fluctuations.

This paper contributes to the debate by showing that, provided that the interest elasticity of savings is negative, stable endogenous cycles can emerge as equilibrium solutions of the model also in the case of non Kaldorian-type economies. To prove this, we combine the instruments of the global analysis, specifically the homoclinic bifurcation Theorem of Kopell and Howard, 1975,¹ with numerical methods, to show that a trajectory, starting in the vicinity of a saddle steady state (where the economy is of non Kaldorian-type) can approach from outside a limit cycle enclosing a non saddle steady state (where the economy is of Kaldorian-type).

The paper develops as follows. The second section introduces the model and studies the long-run equilibrium. The third section establishes some stability properties of the long-run equilibrium from the perspective of the local analysis. In particular, we provide here confirmation that stable limit cycles can only emerge if the economy is of a Kaldorian type. The fourth section shows that the more powerful instruments of the global analysis allow us to prove the possibility of stable limit cycles also for a non-Kaldorian economy. The fifth section discusses an example. A brief conclusive section reassesses the main findings of the paper. All necessary proofs are provided in a specific Appendix.

The Model

Schinasi, in a series of different papers, revises "classical" Kaldor’s (1940) business cycle model by replacing the capital stock with the interest rate and taking into account financial markets and a Government budget constraint in which both money and bond financing are alternative means of financing budget gaps. A non linearity in the income variable is assumed in the investment function. The shape of the investment function, crucial for the derivation of feasible oscillating solutions, is originally postulated by Kaldor (1940) as a way to model a non-linear reaction of investors to changes in market conditions such as excess demand and excess supply. More formally, Kaldor’s view assumes that

$$\begin{aligned} I_{Y}>0;\qquad \qquad I_{YY}\left\{ \begin{array}{c} >0,\ \ \text {for}\,\,Y<Y^{*} \\ <0,\ \ \text {for}\,\,Y>Y^{*} \end{array} \right\} \end{aligned}$$

where $I$ is investment and $Y$ income. $I_{Y}$ and $I_{YY}$ represents first and second-order partial derivatives of the investment function with regard to income, respectively. Finally, $Y^{*}$ is the "normal" level of output.² What is crucial for us is that:

Remark 1

Since the investment function is not constrained to be linear, the IS curve needs not be linear too.

In a formal perspective, let $S(R,Y^{D})$ represent savings as a function of the interest rate and disposable income, with $Y^{D}=Y-T\left( Y\right)$ where $T\left( Y\right)$ is the tax collection function. Given the non-linearity in the investment function, as output increases above expected levels, firms will increase investment but less than they would have in a linear model, since they expect Government to be "active" in stabilizing economic activity. Therefore, it could be the case that the crucial quantity $I_{Y}-\left[ S^{\prime }(1-T^{\prime })-T^{\prime }\right]$ be negative. Notice that, as it will become clearer below, the quantity above presented connected with the slope of the IS curve in a ($R,Y$) space, with regard to which presents an opposite sign (cf. Schinasi 1981, for a detailed discussion).

After this preparatory discussion, we are ready to present the system of differential equations originated by Schinasi’s variant of the IS-LM model. Referring to Sasakura (1994) for a detailed derivation, in the case of an instantaneous adjustment in the money market, the following planar system of first order differential equations is implied

where $\dot{R}=dR/dt$ and $\dot{Y}=dY/dt$. It is assumed that all functions are continuously differentiable at a suitable order. $L\left( \cdot \right)$ is the liquidity preference function, relating the demand for money to $R$, the (real) interest rate, and $Y$, the income level. It follows that $L_{Y}(R,Y)$ and $L_{R}(R,Y)$ are partial derivatives of the liquidity preference function with respect to income and the interest rate, respectively. $I(R,Y)$ is the investment function which is assumed to depend on income and on the interest rate. Finally $G>0$ is the (constant) government expenditure and $\alpha$ is a scale parameter. Notice that system $\mathcal {M}$ is a crucially extended variant of standard Schinasi’s model (1981) and (1982) where the $S\left( \cdot \right)$ function takes into account the interest rate as a further argument (cf., inter al., Cai 2005; and Makovinyiova 2011, for similarly augmented models).

For the sake of a simple representation, we shall assume that the tax raising function is linear in $Y$, so that we have $T\left( Y\right) =\tau Y$. Thus $Y^{D}=Y-T\left( Y\right) =\ \left( 1-\tau \right) Y$ is disposable income. The signs of the derivatives are crucial for the scopes of the paper. Consider first the liquidity preference and the tax raising functions, for which the literature assumes

$$\begin{aligned} L_{Y}\left( \cdot \right) >0;L_{R}\left( \cdot \right) <0 \end{aligned}$$

Less clear is the case of the investment and savings functions; whereas there is no theoretical and empirical disagreement on the following

$$\begin{aligned} I_{R}\left( \cdot \right) <0;I_{Y}\left( \cdot \right) >0;S_{Y}\left( \cdot \right) >0 \end{aligned}$$

the sign of $S_{R}\left( \cdot \right)$ remains ambiguous (cf. inter al. Abrar 1989). Basic economic courses show that the interest elasticity of saving can be decomposed into a (positive) “substitution” effect and an “income” effect, which works in opposite directions. Which effect prevails depends on the specific model and/or parameter configurations. We shall assume, in the rest of the paper, that it is possible for the savings interest rate sensitivity $S_{R}\left( \cdot \right)$ to be negative.

Steady State

We obtain now some information on the long-run properties of system $\mathcal {M}$. Let $\left( R^{*},Y^{*}\right)$ be values of $\left( R,Y\right)$ such that $\dot{R}=\dot{Y}=0$. To simplify notation, and considering $Y^{D}=\left( 1-\tau \right) Y$, we define the following

$$\begin{aligned} H(R,Y)=I(R,Y)-S(R,Y) \end{aligned}$$

Simple algebra shows that, at the steady-state, we have

$$\begin{aligned} Y^{*} =\frac{G}{\tau } \end{aligned}$$

(2.1)

$$\begin{aligned} H(R^{*},Y^{*}) =0 \end{aligned}$$

(2.2)

We now study conditions for existence and uniqueness of the steady state. Let $\phi \rightarrow \mathbb {R}$ be defined as:

$$\begin{aligned} \phi (R)=H(R,Y^{*}) \end{aligned}$$

(2.3)

with $\phi$ conveniently smooth in all its arguments. Let also $\phi ^{\prime }(R)$ and $\phi ^{{\prime \prime }}(R)$ be the first and second-order derivative of $\phi (R)$ with respect to $R$. If $\phi ^{\prime }(R)$ is negative (positive) in the domain $D=\{(R):R>0\}$, the function $\phi (R)$ monotonically decreases (increases) with the interest rate and we can only have one intersection with the $R$-axis (one steady state). Conversely, if it changes sign, for specific values of the interest rate, it can have multiple intersections with the $R$-axis (multiple steady states). To simplify the analysis, without loosing generality, consider the following regularity condition

Assumption 1 $\phi ^{\prime \prime }(R)$ does not change sign in the domain $D=\{(R):R>0\}$.

Assumption 1 implies that, if $\phi ^{\prime }(R)$ changes sign in $D,\ \phi (R)$ is unimodal, and the maximum number of possible intersections with the $R$-axis is limited to two. Let now $\omega \in \Omega$ represent the set of all parameters. Let also $\bar{\Omega }\equiv \left\{ \omega \in \Omega :=R^{*}\in D\right\}$. Then

Lemma 1

Recall Assumption $1$. Let $\hat{\Omega }\equiv \{\omega \in \bar{\Omega }:=\phi ^{\prime }(R)$ is positive or negative$\}$ and, complementarily, $\check{\Omega }\equiv \{\omega \in \bar{\Omega }:=\phi ^{\prime }(R)$ changes sign at $R=\hat{R}\}= \bar{\Omega }-\hat{\Omega }$. Then, if $\omega \in \hat{\Omega }$, the steady state is always unique. Consider now $\omega \in \check{\Omega }$ and assume $\phi ^{\prime \prime }(R)>0$. Then, if

• $\phi (\hat{R})<0$ there are two steady states, one with a low interest rate $\left( R_{-}^{*},Y^{*}\right)$ and one with a high interest rate $\left( R_{+}^{*},Y^{*}\right) ;$

• $\phi (\hat{R})=0$ there is one steady state;

• $\phi (\hat{R})>0$ there are no steady states.

The statements are inverted if $\phi ^{\prime \prime }(R)<0$.

Proof

Let $\omega \in \hat{\Omega }$. Since, by assumption, the first derivative does not vanish in $D$, the function $\phi (R)$ is always monotonically decreasing/increasing in $D$ and only one steady state is possible. Let now $\omega \in \check{\Omega }$. Then $\phi (R)$ is unimodal. Assume first $\phi ^{\prime \prime }(R)>0$. Assume, furthermore, there is a (generic) parameter with the properties in Proposition. Then, the three intersection possibilities with the $\phi (R)=0$ axis must apply. Inverse statements apply in the case of $\phi ^{\prime \prime }(R)<0$.

Some numerical applications will be provided in Section “Some Numerical Simulations”, for specific functional forms.³

Local Stability Analysis

Consider trajectories in which $R$ and $Y$ remain bounded in a small neighborhood of the steady state. In Appendix A, we show that the linearization matrix associated with system $\mathcal {M}$ evaluated at the steady state, is

$$\begin{aligned} {\mathbf {J}}_{\mathcal {M}}^{*}{\small \,=\,}\left[ \begin{array}{cc} -\alpha \frac{L_{Y}^{*}}{L_{R}^{*}}H_{R}^{*} &{}\quad -\alpha \frac{L_{Y}^{*}}{L_{R}^{*}}H_{Y}^{*}+\left( \alpha \tfrac{L_{Y}^{*}}{L_{R}^{*}}-\frac{1}{L_{R}^{*}}\right) \tau \\ \alpha H_{R}^{*} &{} \alpha (H_{Y}^{*}-\tau ) \end{array} \right] \end{aligned}$$

(2.4)

where, for the sake of a simple notation, the arguments of the partial derivatives have been dropped. Consider the characteristic polynomial associated with $\mathbf J _{\mathcal {M}}^{\mathbf {*}}$

$$\begin{aligned} \text {Det}\left( \lambda \mathbf {I-J}_{\mathcal {M}}^{\mathbf {*}}\right) =\lambda ^{2}-\text {Tr}({\mathbf {J}}_{\mathcal {M}}^{\mathbf {*}})\lambda + \text {Det}({\mathbf {J}}_{\mathcal {M}}^{\mathbf {*}}) \end{aligned}$$

(2.5)

where I is the identity matrix. Tr$({\mathbf {J}}_{\mathcal {M}}^{\mathbf {*}}){\small }$ and Det$({\mathbf {J}}_{\mathcal {M}}^{\mathbf {*}})$ are Trace and Determinant of ${\mathbf {J}}_{\mathcal {M}}^{\mathbf {*}}$, respectively. In Appendix A, they are shown to be

$$\begin{aligned} \text {Det}({\mathbf {J}}_{\mathcal {M}}^{\mathbf {*}})&=\alpha \frac{\tau }{L_{R}^{*}}H_{R}^{*} \\ \text {Tr}({\mathbf {J}}_{\mathcal {M}}^{\mathbf {*}})&=\alpha \left( H_{Y}^{*}-\frac{L_{Y}^{*}}{L_{R}^{*}}H_{R}^{*}-\tau \right) \end{aligned}$$

To study the stability properties in a planar system from the local analysis perspective, it is crucial to establish the signs of Det$({\mathbf {J}}_{\mathcal {M}}^{\mathbf {*}})$ and Tr$({\mathbf {J}}_{\mathcal {M}}^{\mathbf {*}})$. Simple algebra shows that necessary conditions for the birth of attracting orbits, from the perspective of the local analysis, are the following

$$\begin{aligned} H_{R}^{*} < 0 \end{aligned}$$

(2.6)

$$\begin{aligned} H_{Y}^{*}-\frac{L_{Y}^{*}}{L_{R}^{*}}H_{R}^{*}-\tau > 0 \end{aligned}$$

(2.7)

which guarantee that the steady state is an unstable node or focus. More precisely

Proposition 1

Recall Lemma $1$. Let $\omega \in \hat{\Omega }$ and first assume $H_{R}^{*}<0$. Then, the ($unique$) steady state is an unstable node or focus if (2.7) is satisfied. Conversely, if $H_{R}^{*}>0$, the steady state is a saddle.

Let now $\omega \in \check{\Omega }$ and assume first $\phi ^{\prime \prime }(R)>0$. As shown in Lemma $1$, we can either have a dual steady state, one steady state or no steady states at all. In the former case, at $\left( R_{-}^{*},Y^{*}\right)$,$\ H_{R}^{*}<0$, so that the low interest rate equilibrium is an unstable node or focus if (2.7) is satisfied. The other steady state $\left( R_{+}^{*},Y^{*}\right)$ has $H_{R}^{*}>0$ and is therefore a saddle. The low interest rate steady state and the high interest rate steady state interchange their stability properties if $\phi ^{\prime \prime }(R)<0$.

Proof

To exclude a saddle we need Det$({\mathbf {J}}_{\mathcal {M}}^{\mathbf {*}})>0$, which happens if (2.6) applies. Furthermore if (2.7) is satisfied, Tr $({\mathbf {J}}_{\mathcal {M}}^{\mathbf {*}})>0$ and the steady state is an unstable node or focus.

Recall that

Remark 2

Conditions in (2.6), imply an upwards sloping IS curve. As above discussed, this property can be justified in a Kaldorian perspective, namely with the assumption of an S-shaped investment function.

We find it useful, for a clear presentation of the main results of the paper, to give the following

Definition 1 Let an economy (not) satisfying conditions in (2.6) be called a (non) Kaldorian-type economy.

Thus

Corollary 1

Recall Lemma $1$. Then, from the perspective of the local analysis, only a Kaldorian-type economy can give rise to stable deterministic cycles.

Proof

From the local analysis point of view, only in the neighborhood of the non-saddle steady state we can have oscillating solutions. Therefore the case $H_{R}^{*}>0$ must be discarded. We are only left therefore with the $H_{R}^{*}<0$ possibility. In this case, since $L_{R}^{*}<0$, Tr $({\mathbf {J}}_{\mathcal {M}}^{\mathbf {*}})=H_{Y}^{*}-\frac{L_{Y}^{*}}{L_{R}^{*}}H_{R}^{*}-\tau$ is positive only if $H_{Y}^{*}-\tau >0$. As above discussed this implies a positively sloping IS curve which, in turn, can be justified with an $S$-shaped Investment function.

Remarkably, it is interesting to point out here that a negative interest elasticity of savings is also crucial for the emergence of endogenous cycles in discrete-time overlapping generations models (cf. inter al. Azariadis and Guesnerie 1986; and Grandmond 1985).

Global Analysis

In contrast with the conclusion of Section. “Steady State”, the global bifurcation analysis will allow us to prove that, when system $\mathcal {M}$ admits a dual steady state, a non Kaldorian-type economy can undergo endogenous fluctuations. What we actually do is to show that there exist trajectories originating in the neighborhood of the saddle steady state (the one at which the economy is of a non-Kaldorian type) which are bound to converge to a limit cycle around the non-saddle steady state (the one at which the economy is of a Kaldorian type). To obtain this result, we make use of the homoclinic bifurcation Theorem of Kopell-Howard, 1975, which allows to locate the regions in the parameter space implying the existence of a closed orbit or of a saddle connection. The application of the Theorem is not trivial and requires several steps to be accomplished (cf Appendix C).

In any case, before proceeding, we need first to assume some specific functional forms. Therefore, with regard to the original system $\mathcal {M}$:

• 1. the liquidity preference function $L(R,Y)$ is assumed linear in its two arguments (cf. Cai, 2005, for a similar approach). Therefore, $L(R,Y)=-\beta R+\gamma Y$ where $(\gamma ,\beta )>0$ measure the sensitivity of $L\left( \cdot \right)$ to the interest rate and income, respectively;

• 2. a convenient explicit form for the $H\left( \cdot \right) =I\left( \cdot \right) -S\left( \cdot \right)$ function is harder to propose. In Makovinyiova (2011) the investment and savings functions are assumed to have the following form

  $$\begin{aligned} I&=\varepsilon _{1}\sqrt{Y^{3}}-\varepsilon _{2}R \\ S&=\varepsilon _{3}\left( Y^{D}\right) ^{2}+\varepsilon _{4}R+\varepsilon _{5} \end{aligned}$$

  to match the characteristics of the Slovakian economy, where ($\varepsilon _{1},\varepsilon _{2},\varepsilon _{3},\varepsilon _{4},\varepsilon _{5})\in \mathbb {R}^{++}$ and $R$ (the real interest rate) is expressed in percentage terms. However, to account for a dual steady state,⁴ we need the $H\left( \cdot \right)$ function to be non-linear in $R$. Therefore, we propose the following generalization of the $H\left( \cdot \right)$ function

  $$\begin{aligned} H\left( R,Y\right) =\varepsilon _{1}\sqrt{Y^{3}}-\varepsilon _{2}R-\varepsilon _{3}\left( Y^{D}\right) ^{2}-\varepsilon _{4}R-\varepsilon _{5}-\delta \tfrac{Y}{R} \end{aligned}$$

  (2.8)

  with $\delta >0$. Notice that we can interpret the factor $Y/R$ as a proxy for wealth. This makes it easier to introduce a negative savings sensitivity to the interest rate. It is useful to point out that parameters lie in the $\check{\Omega }$ set and that Assumption 1 is satisfied; consequently, recalling Lemma 1, system $\mathcal {S}$ can give rise to two steady states.

With Eq. (2.8), and recalling $Y^{D}=(1-\tau )Y$, system $\mathcal {M}$ becomes

As shown in Appendix B, the linearization matrix associated with system $\mathcal {S}$ is

$$\begin{aligned} {\mathbf {J}}_{\mathcal {S}}^{\mathbf {*}}{\small =}\left[ \begin{array}{cc} \frac{\gamma \alpha }{\beta }H_{R}^{*} &{} \frac{\gamma \alpha }{\beta } H_{Y}^{*}-\frac{\gamma \alpha -1}{\beta }\tau \\ \alpha H_{R}^{*} &{} \alpha (H_{Y}^{*}-\tau ) \end{array} \right] \end{aligned}$$

where

$$\begin{aligned} H_{R}^{*}&= -(\varepsilon _{2}+\varepsilon _{4})+\delta \frac{Y^{*}}{R^{*}{}^{2}}\end{aligned}$$

(2.9)

$$\begin{aligned} H_{Y}^{*}&= \frac{3}{2}\varepsilon _{1}\sqrt{\frac{G}{\tau }}-2\varepsilon _{3}(1-\tau )^{2}\frac{G}{\tau }-\frac{\delta }{R^{*}} \end{aligned}$$

(2.10)

Simple algebra leads to the following

$$\begin{aligned} \text {Det}({\mathbf {J}}_{\mathcal {S}}^{\mathbf {*}})&= -\tfrac{\alpha \tau H_{R}^{*}}{\beta } \\ \text {Tr}({\mathbf {J}}_{\mathcal {S}}^{\mathbf {*}})&= \alpha \left( H_{Y}^{*}+\tfrac{\gamma }{\beta }H_{R}^{*}-\tau \right) \end{aligned}$$

A first requirement of the Kopell Howard Theorem is that there exist regions in the parameter space at which the linearization matrix ${\mathbf {J}}_{\mathcal {S}}^{\mathbf {*}}$ has a double-zero eigenvalue. In the two-dimensional case, this happens if Det$({\mathbf {J}}_{\mathcal {S}}^{\mathbf {*}})$ and Tr$({\mathbf {J}}_{\mathcal {S}}^{\mathbf {*}})$ vanish simultaneously. Taking $\delta$ and $\tau$ as bifurcation parameters, we can state the following

Lemma 2

Let $\left( \bar{R}^{*},\bar{Y}^{*}\right)$ be the levels of the interest rate at the bifurcation point. Let furthermore $\bar{\delta }$ and $\bar{\tau }$ be the values of $\delta$ and $\tau$ which solve Det$({\mathbf {J}}_{\mathcal {S}}^{\mathbf {*}})=0$ and Tr$({\mathbf {J}}_{\mathcal {S}}^{\mathbf {*}})=0$, respectively. Then, if $\delta =\bar{\delta }$ and $\tau =\bar{\tau }$, ${\mathbf {J}}_{\mathcal {S}}^{\mathbf {*}}$ has a zero eigenvalue of multiplicity $2$. Considering (2.9) and (2.10), simple algebra shows

$$\begin{aligned} \bar{\delta }=\frac{(\varepsilon _{2}+\varepsilon _{4})\bar{R}^{*2}}{G}\bar{\tau }\ \end{aligned}$$

and

$$\begin{aligned} \frac{3}{2}\varepsilon _{1}\sqrt{\frac{G}{\bar{\tau }}}-2\varepsilon _{3}(1-\bar{\tau })^{2}\frac{G}{\bar{\tau }}-\frac{\bar{\delta }}{\bar{R}^{*}}-\bar{\tau }=0. \end{aligned}$$

where

$$\begin{aligned} \bar{R}^{*}=\frac{\varepsilon _{1}\sqrt{(\tfrac{G}{\tau })^{3}}-\varepsilon _{3}(1-\tau )^{2}(\tfrac{G}{\tau })^{2}-\varepsilon _{5}}{2\bar{\delta }} \end{aligned}$$

Proof

To have a linearization matrix with a zero eigenvalue with multiplicity 2 at the bifurcation, we need to make sure that the determinant and the trace vanish simultaneously. Since Det$({\mathbf {J}}_{\mathcal {S}}^{\mathbf {*}})$ and Tr$({\mathbf {J}}_{\mathcal {S}}^{\mathbf {*}})$ vanish, respectively, when $\delta =\bar{\delta }$ and $\tau =\bar{\tau }$ the statement in Lemma 2 is implied.

We are now ready to prove the main proposition.

Proposition 2

Recall Lemma $2$. Assume $H(R,Y)$ be approximated by the expression in (2.8). Then, for $\delta$ and $\tau$ close to the bifurcation values $(\bar{\delta },\ \bar{\tau })$, there exist trajectories originating in a close neighborhood of the saddle steady state which either spiral towards the non-saddle steady state or converge to a limit cycle around it. By Proposition $1$, the saddle steady state is $\left( R_{-}^{*},Y^{*}\right)$ whereas the non-saddle steady state is $\left( R_{+}^{*},Y^{*}\right)$.

Proof

To prove the Proposition, we show in Appendix C that system $\mathcal {S}$ satisfies, for specific parameter values, the Kopell-Howard’s homoclinic bifurcation Theorem. Since in our case $\phi ^{\prime \prime }(R)=-2\delta \frac{Y^{*}}{R^{*3}}<0$, by Proposition 1, $\left( R_{-}^{*},Y^{*}\right)$ is a saddle while $\left( R_{+}^{*},Y^{*}\right)$ is non-saddle. In the case of a saddle connection, spiralling towards the non-saddle steady state requires Tr$({\mathbf {J}}_{\mathcal {S}}^{\mathbf {*}})|_{(R_{+}^{*},Y^{*})}<0$. Convergence of trajectories starting in the neighborhood of the saddle steady state to a limit cycle requires the orbit to be attractive. We will show in the next section, by means of numerical simulations, that this ordinarily happens for system $\mathcal {S}$.

Proposition 2 immediately implies the following

Corollary 2

Recall Definition 1. Then, a non Kaldorian-type economy can give rise to stable deterministic fluctuations.

Proof

Since there exist trajectories originating in the neighborhood of the saddle steady state (where conditions in 2.6 and 2.7 do not apply) which approach a limit cycle, then non-Kaldorian type economies can exhibit deterministic fluctuations (also cf Definition 1).

Interestingly, a negative interest elasticity of savings is also crucial for the emergence of endogenous cycles in discrete-time overlapping generations models (cf. inter al. Azariadis and Guesnerie 1986; and Grandmond 1985). We conjecture that the result is also likely to arise in models with alternative specifications of the non linearity in the interest rate in both the investment and savings functions.

Although the existence of a limit cycle approached by trajectories originating in the neighborhood of the saddle steady state is our main result, it must not be underestimated the possibility of a saddle connection between the two steady states which, in the case of a low decay factor, is not inconsistent with the observation of a fluctuating behavior of real economies.

In Section “Some Numerical Simulations” we provide an extensive simulation study based on system $\mathcal {S}$.

Some Numerical Simulations

Let now $\check{\Omega }_{\mathbf{M }}\equiv (\alpha ,\beta ,\gamma ,G,\varepsilon _{1},\varepsilon _{2},\varepsilon _{3},\varepsilon _{4},\varepsilon _{5})$ be set as in Table 2.1.⁵

Table 2.1 Baseline parameter

At the bifurcation, there is a unique steady state such that $\left( \bar{R}^{*},\bar{Y}^{*}\right) \approx \left( {1.36,4.39}\right)$.⁶ The parameter values are essentially taken from Makovinyiova with some crucial differences. First of all, to obtain a reasonable amplitude of the cycle, in the case of an economy starting close to the saddle steady state (in the case of a large distance between the two steady state values of the interest rate), we found it necessary to lower the parameter $\alpha$ to 0.1. Furthermore, $\gamma$, the elasticity of the demand for money with respect to $Y$, is set to 0.1 instead of 0.2. Finally $\varepsilon _{3}$ is set to $0.00132$ instead of $0.001$. These further changes are necessary to allow for a positive Tr$({\mathbf {J}}_{\mathcal {S}}^{\mathbf {*}})|_{{\small (R}_{+}^{*}{\small ,Y}^{*}{\small )}}$, and therefore for the most interesting case of an attracting orbit to be obtained.

The implied critical values of the bifurcation parameters in the baseline simulation are respectively $\left( \bar{\delta },\bar{\tau }\right) \approx (0.03787, 0.17732)$. Notice that the critical value of the tax rate is very close to the value of the tax rate reported in Makovinyiova for the Slovakian economy in 2007.

Consider now the following example. Set $\check{\Omega }_{\mathbf {M}}$ as in Table 2.1. Assume furthermore $\delta =0.03<\bar{\delta }$ and $\tau =0.1801>\bar{\tau }$. Then, a dual steady state emerges. We have $(R_{-}^{*},Y^{*})\approx \left( 0.9613,4.331\right)$ and $(R_{+}^{*},Y^{*})\approx \left( 1.9309,4.331\right)$. We also obtain Det$({\mathbf {J}}_{\mathcal {S}}^{\mathbf {*}})|_{(R_{-}^{*},Y^{*})}>0$, Det$({\mathbf {J}}_{\mathcal {S}}^{\mathbf {*}}|)_{(R_{+}^{*},Y^{*})}<0$, Tr$({\mathbf {J}}_{\mathcal {S}}^{\mathbf {*}})|_{(R_{-}^{*},Y^{*})}<0$ and $Tr({\mathbf {J}}_{\mathcal {S}}^{\mathbf {*}})|_{(R_{+}^{*},Y^{*})}>0$. Therefore, the low interest rate steady state is a saddle and the high interest rate steady state is a source.

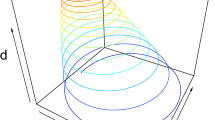
The following Fig. 2.1 shows, for the above reported parameter values, the convergence to a limit cycle of a non Kaldorian-type economy starting at $(1.2$,$4.33)$. It is interesting to observe that for these parameter values, the high interest rate steady state is virtually a center, since the trajectory approaches the orbit from outside at a very slow speed.

Fig. 2.1

A non-Kaldorian type economy (slowly) converging to a cycle

Fig. 2.2

Solution trajectories for varying parameters

We have also conducted a sensitivity analysis by changing some crucial parameters. As it appears clear in Fig. 2.2, what we find is that raising (decreasing) $\beta$ and $\gamma$ with respect to their baseline values stabilizes (destabilizes) the non saddle steady state. Moreover, we find that small variations of $G$, measuring the "size" of public expenditure, cause the double steady state to disappear. In Fig. 2.2, therefore, we report trajectories obtained for very small variations of $G$ with respect to its baseline value.

Conclusions

This paper innovates the literature regarding dynamic IS-LM models of Schinasi’s type (1981) and (1982). First of all, we find that, if the interest rate sensitivity of savings is negative, the model admits a dual steady state, characterized by the same long-run level of income but by different interest rates. One of these steady states is a saddle and the other is a non-saddle equilibrium. From the local analysis perspective, our results remain in line with the “Kaldorian tradition”, namely endogenous fluctuation can only arise if the IS curve is upward sloping.

However, the global analysis provides a different perspective. By means of the homoclinic bifurcation Theorem of Kopell and Howard (1975) we are able to prove that (for specific functional forms and parameter configurations) there exist trajectories originating in the neighborhood of the non-Kaldorian steady state which spiral towards the other steady state, or to a limit cycle around it. This implies that an economy not satisfying the Kaldorian assumptions can start, at some point in time, to exhibit oscillating behavior.

We conclude the paper by proposing the results of an extensive sensitivity analysis.

Appendices

Appendix A

Linearization matrix associated with system $\mathcal {M}$.

As shown in the text, Schinasi’s model (1981) and (1982) gives rise to the following system of first-order differential equations

Let J $_{\mathcal {M}}^{*}$ be the Jacobian of the right hand side of system $\mathcal {M}$ evaluated at the steady state. The single elements of J $_{\mathcal {M}}^{*}$ are

$$\begin{aligned} j_{11}^{*} =&{\small \partial \dot{R}/\partial R|}_{ss}=-\alpha \frac{L_{Y}^{*}}{L_{R}^{*}}H_{R}^{*} \\ j_{12}^{*} =&{\small \partial \dot{R}/\partial Y|}_{ss}=-\alpha \frac{L_{Y}^{*}}{L_{R}^{*}}H_{Y}^{*}+\tfrac{\alpha L_{Y}^{*}-1}{L_{R}^{*}}\tau \\ j_{21}^{*} =&{\small \partial \dot{Y}/\partial R|}_{ss}=\alpha H_{R}^{*} \\ j_{22}^{*} =&{\small \partial \dot{Y}/\partial Y|}_{ss}=\alpha (H_{Y}^{*}-\tau ) \end{aligned}$$

where, for the sake of a simple representation, the arguments of the functions have been dropped. Therefore, we have

$$\begin{aligned} {\mathbf {J}}_{\mathcal {M}}^{*}{\small =}\left[ \begin{array}{cc} -\alpha \frac{L_{Y}^{*}}{L_{R}^{*}}H_{R}^{*} &{} -\alpha \frac{L_{Y}^{*}}{L_{R}^{*}}H_{Y}^{*}+\tfrac{\alpha L_{Y}^{*}-1}{L_{R}^{*}}\tau \\ \alpha H_{R}^{*} &{} \alpha (H_{Y}^{*}-\tau ) \end{array} \right] \end{aligned}$$

(A.1)

The eigenvalues of (A.1) are the solutions of the characteristic equation

$$\begin{aligned} \det \left( \lambda \mathbf {I-J}_{\mathcal {M}}^{*}\right) =\lambda ^{2}-\text {Tr}({\mathbf {J}}_{\mathcal {M}}^{*})\lambda +\text {Det}({\mathbf {J}}_{\mathcal {M}}^{*}) \end{aligned}$$

where I is the identity matrix. Tr$({\mathbf {J}}_{\mathcal {M}}^{*})$ and Det$({\mathbf {J}}_{\mathcal {M}}^{*})$ are Trace and Determinant of ${\mathbf {J}}_{\mathcal {M}}^{*}$, respectively. We obtain

$$\begin{aligned} \text {Tr(}{\mathbf {J}}_{\mathcal {M}}^{*}\text {)}=\alpha \left( H_{Y}^{*}-\tau -\frac{L_{Y}^{*}}{L_{R}^{*}}H_{R}^{*}\right) \end{aligned}$$

$$\begin{aligned} \text {Det(}{\mathbf {J}}_{\mathcal {M}}^{*}\text {)}=\alpha \tau \frac{H_{R}^{*}}{L_{R}^{*}} \end{aligned}$$

Appendix B

Linearization matrix associated with system $\mathcal {S}$.

Consider now system $\mathcal {S}$ in the text

$$\begin{aligned} \dot{Y}&= \alpha \left[ \varepsilon _{1}\sqrt{Y^{3}}-\varepsilon _{2}R-\varepsilon _{3}(1-\tau )^{2}Y^{2}-\varepsilon _{4}R-\varepsilon _{5}- \tfrac{\delta Y}{R}+G-\tau Y\right] \end{aligned}$$

Let J $_{\mathcal {S}}^{*}$ be the Jacobian of the right hand side of system $\mathcal {S}$ evaluated at the steady state. The single elements of $\mathbf J _{\mathcal {S}}^{*}$ are the following

$$\begin{aligned} j_{11}^{*} =&{\small \partial \dot{R}/\partial R|}_{ss}=-\tfrac{\gamma \alpha }{\beta }\left( -\varepsilon _{2}-\varepsilon _{4}+\tfrac{\delta }{R^{*}{}^{2}}\right) \\ j_{12}^{*} =&{\small \partial \dot{R}/\partial Y|}_{ss}=-\tfrac{\gamma \alpha }{\beta }\left( \frac{3}{2}\varepsilon _{1}\sqrt{\tfrac{G}{\tau }}-2\varepsilon _{3}(1-\tau )^{2}\tfrac{G}{\tau }\right) -\tfrac{\gamma \alpha -1}{\beta }\tau \\ j_{21}^{*} =&{\small \partial \dot{Y}/\partial R|}_{ss}=\alpha \left[ -\varepsilon _{2}-\varepsilon _{4}+\tfrac{\delta }{R^{*}{}^{2}}\right] \\ j_{22}^{*} =&{\small \partial \dot{Y}/\partial Y|}_{ss}=\alpha \left( \frac{3}{2}\varepsilon _{1}\sqrt{\tfrac{G}{\tau }}-2\varepsilon _{3}(1-\tau )^{2}\frac{G}{\tau }-\tau \right) \end{aligned}$$

where, for the sake of a simple representation, the arguments of the functions have been dropped. Therefore, we have

$$\begin{aligned} {\mathbf {J}}_{\mathcal {S}}^{\mathbf {*}}{\small =}\left[ \begin{array}{cc} \frac{\gamma \alpha }{\beta }H_{R}^{*} &{} \frac{\gamma \alpha }{\beta } H_{Y}^{*}-\frac{\gamma \alpha -1}{\beta }\tau \\ \alpha H_{R}^{*} &{} \alpha (H_{Y}^{*}-\tau ) \end{array} \right] \end{aligned}$$

(B.1)

where $H_{R}^{*}=-\varepsilon _{2}-\varepsilon _{4}+\tfrac{\delta Y^{*}}{R^{*}{}^{2}}$ and $H_{Y}^{*}=\frac{3}{2}\varepsilon _{1} \sqrt{\frac{G}{\tau }}-2\varepsilon _{3}(1-\tau )^{2}\frac{G}{\tau }-\tau$. Therefore,

$$\begin{aligned} \text {Tr(}{\mathbf {J}}_{\mathcal {S}}^{\mathbf {*}}\text {)}=\alpha (H_{Y}^{*}-\tau )+\tfrac{\gamma \alpha }{\beta }H_{R}^{*} \end{aligned}$$

$$\begin{aligned} \text {Det(}{\mathbf {J}}_{\mathcal {S}}^{\mathbf {*}}\text {)}=-\tfrac{\alpha \tau H_{R}^{*}}{\beta } \end{aligned}$$

Appendix C

For the sake of a simple discussion, we shall refer to the original version of the two-parameter homoclinic bifurcation Theorem in Kopell and Howard (1975) (Theorem 7.1, p. 334).

Let $(\delta ,\tau )$ be our control parameters. Posit $\mu =\delta -\bar{\delta }$ and $\nu =\tau -\bar{\tau }$ where $\bar{\delta }$ and $\bar{\tau }$ be the critical values of our bifurcation parameters. Let also $\bar{R}^{*}$ and $\bar{Y}^{*}$ be the particular steady state values of the interest rate and income implied by $\mu =\nu =0$.

Preliminarily, we translate our system of differential equation to the origin and provide a second-order Taylor expansion.

Let $\tilde{R}=R-\bar{R}^{*}$ and $\tilde{Y}=Y-\bar{Y}^{*}$. We have, from system $\mathcal {S}$

$$\begin{aligned} \overset{\cdot }{\tilde{R}}&= \tfrac{\gamma \alpha }{\beta }\tilde{H}\left( (\bar{Y}^{*}+\tilde{Y}),(\bar{R}^{*}+\tilde{R}),(\bar{\delta }+v),(\bar{\tau }+\mu )\right) \nonumber \\&\quad +\tfrac{\gamma \alpha -1}{\beta }\left[ G-(\bar{\tau } +\mu )(\bar{Y}^{*}+\tilde{Y})\right] \\ \overset{\cdot }{\tilde{Y}}&= \alpha \tilde{H}\left( (\bar{Y}^{*}+ \tilde{Y}),(\bar{R}^{*}+\tilde{R}),(\bar{\delta }+v),(\bar{\tau }+\mu )\right) +\alpha [ G-(\bar{\tau }+\mu )(\bar{Y}^{*}+\tilde{Y}))] \end{aligned}$$

(C.1)

where

$$\begin{aligned} \tilde{H}&=\varepsilon _{1}\sqrt{(\bar{Y}^{*}+\tilde{Y})^{3}}-\varepsilon _{2}(\bar{R}^{*}+\tilde{R})-\varepsilon _{3}(1-\bar{\tau }-\mu )^{2}\left( \bar{Y}^{*}+\tilde{Y}\right) ^{2} \\&\quad -\varepsilon _{4}(\bar{R}^{*}+\tilde{R})-\varepsilon _{5}-\tfrac{\left( \bar{\delta }+v\right) \left( \bar{Y}^{*}+\tilde{Y}\right) }{(\bar{R}^{*}+\tilde{R})} \end{aligned}$$

System C.1 corresponds to the generic two-parameter family of ordinary differential equations $\dot{X}=F_{\mu ,v}\left( X\right)$ in Kopell-Howard’s original Theorem. We present now, in sequence, the computation necessary to apply the homoclinic bifurcation Theorem 7.1 in Kopell and Howard to system C.1.

• 1. Computation of $dF_{\mu ,\nu }\left( \mathbf {0}\right)$. We obtain

  $$\begin{aligned} dF_{\mu ,\nu }\left( \mathbf {0}\right) =\left[ \begin{array}{cc} \frac{2\alpha \gamma }{\beta }\varepsilon _{3}(1-\bar{\tau }-\mu )\bar{Y}^{*}{}^{2}-\frac{\alpha \gamma -1}{\beta }\bar{Y}^{*} &{} -\frac{\alpha \gamma }{\beta }\frac{\bar{Y}^{*}}{\bar{R}^{*}} \\ 2\alpha \varepsilon _{3}(1-\bar{\tau }-\mu )\bar{Y}^{*}{}^{2}-\alpha \bar{Y}^{*} &{} -\frac{\alpha \bar{Y}^{*}}{\bar{R}^{*}} \end{array} \right] \end{aligned}$$

  (C.2)

  Simple algebra gives

  $$\begin{aligned} Tr\ dF_{\mu ,v}(0)&= \tfrac{2\alpha \gamma }{\beta }\varepsilon _{3}(1-\bar{\tau }-\mu )\bar{Y}^{*2}-\tfrac{\alpha \gamma -1}{\beta }\bar{Y}^{*}-\tfrac{\alpha \bar{Y}^{*}}{\bar{R}^{*}} \\ \det dF_{\mu ,v}(0)&= -\tfrac{\alpha \bar{Y}^{*2}}{\beta \bar{R}^{*}} \end{aligned}$$

  At $(\mu ,v)=(0,0)$ (C.2) becomes

  $$\begin{aligned} dF_{0,0}(0)=\left[ \begin{array}{cc} \frac{2\gamma \alpha }{\beta }\varepsilon _{3}(1-\bar{\tau })\bar{Y}^{*}{}^{2}-\frac{\gamma \alpha -1}{\beta }\bar{Y}^{*} &{} -\frac{\gamma \alpha }{\beta }\frac{\bar{Y}^{*}}{\bar{R}^{*}} \\ 2\alpha \varepsilon _{3}(1-\bar{\tau })\bar{Y}^{*}{}^{2}-\alpha \bar{Y}^{*} &{} -\frac{\alpha \bar{Y}^{*}}{\bar{R}^{*}} \end{array} \right] \end{aligned}$$

Since $dF_{0,0}(0)$ has a double zero eigenvalue, the first requirement of the Theorem is satisfied.

• 2. Computation of the mapping $\left( \mu ,v\right) \rightarrow \left( \det dF_{\mu ,v}(0),\ \text {Tr\ }dF_{\mu ,v}(0)\right)$.

  We have

  $$\begin{aligned} \left[ \begin{array}{cc} \frac{\partial }{\partial \mu }\det dF_{\mu v}(0) &{} \frac{\partial }{\partial v}\det dF_{\mu v}(0) \\ \frac{\partial }{\partial \mu }\text {Tr}dF_{\mu v}(0) &{} \frac{\partial }{\partial v}\text {Tr}dF_{\mu v}(0) \end{array} \right] \end{aligned}$$

  which reduces to

  $$\begin{aligned} \left[ \begin{array}{cc} 0 &{} 0 \\ -2\frac{\alpha \gamma }{\beta }\varepsilon _{3}\bar{Y}^{*2} &{} 0 \end{array} \right] \ne 0 \end{aligned}$$

  Therefore the second requirement of the Theorem is satisfied.

  $$\begin{aligned} \tilde{H}&=\varepsilon _{1}\sqrt{(\bar{Y}^{*}+\tilde{Y})^{3}}-\varepsilon _{2}(\bar{R}^{*}+\tilde{R})-\varepsilon _{3}(1-\bar{\tau }-\mu )^{2}\left( \bar{Y}^{*}+\tilde{Y}\right) ^{2} \\&\quad -\varepsilon _{4}(\bar{R}^{*}+\tilde{R})-\varepsilon _{5}-\tfrac{\left( \bar{\delta }+v\right) \left( \bar{Y}^{*}+\tilde{Y}\right) }{\bar{R}^{*}+\tilde{R}} \end{aligned}$$

• 3. Computation of the $Q(e,e)$ matrix.

Let $\mathbf {P}_{i}$, $i=1,2$ be the matrices of the second order derivatives of system C.1 evaluated at $\left( \mu ,v\right) =\left( 0,0\right)$. We have

$$\begin{aligned} \mathbf {P}_{1}=\tfrac{\alpha \gamma }{\beta }\left[ \begin{array}{cc} -\frac{2\bar{\delta }\bar{Y}^{*}}{\bar{R}^{*3}} &{} \frac{\bar{\delta }}{\bar{R}^{*2}} \\ \frac{\bar{\delta }}{\bar{R}^{*2}} &{} \varepsilon _{1}\frac{3}{4}\frac{1}{\sqrt{\bar{Y}^{*}}}-2\varepsilon _{3}(1-\bar{\tau })^{2} \end{array} \right] \end{aligned}$$

$$\begin{aligned} \mathbf {P}_{2}=\alpha \left[ \begin{array}{cc} -\frac{2\bar{\delta }\bar{Y}^{*}}{\bar{R}^{*3}} &{} \frac{\bar{\delta }}{\bar{R}^{*2}} \\ \frac{\bar{\delta }}{\bar{R}^{*2}} &{} \frac{3\varepsilon _{1}}{4}\frac{1}{\sqrt{\bar{Y}^{*}}}-2\varepsilon _{3}(1-\bar{\tau })^{2} \end{array} \right] \end{aligned}$$

Let us now compute the right eigenvector $\mathbf {e} =(e_{1},e_{2})^{T}$ of ${\mathbf {J}}_{\mathcal {S}}^{*}$. A possible candidate is

$$\begin{aligned} \mathbf {e}= \left[ \begin{array}{c} e_{1} \\ e_{2} \end{array} \right] =\left[ \begin{array}{c} -\frac{\frac{\alpha \gamma }{\beta }\left( \frac{3}{2}\varepsilon _{1}\sqrt{\bar{Y}^{*}}-2\varepsilon _{3}(1-\tau )^{2}\bar{Y}^{*}-\frac{\delta }{\bar{R}^{*}}\right) -\frac{\alpha \gamma -1}{\beta }\bar{\tau }}{\frac{\gamma \alpha }{\beta }\left( -(\varepsilon _{2}+\varepsilon _{4})+\delta \frac{\bar{Y}^{*}}{\bar{R}^{*}{}^{2}}\right) } \\ 1 \end{array} \right] \end{aligned}$$

Therefore

$$\begin{aligned} Q(e,e)=\frac{1}{2}\left( \begin{array}{c} e^{T}\mathbf {P}_{1}e \\ e^{T}\mathbf {P}_{2}e \end{array} \right) =\frac{\alpha }{2}\left( \begin{array}{c} -\left( \frac{j_{12}^{*}}{j_{11}^{*}}\right) ^{2}\frac{\gamma }{\beta }\frac{2\bar{\delta }\bar{Y}^{*}}{\bar{R}^{*3}}+\frac{\gamma }{\beta }\left( \frac{3\varepsilon _{1}}{4}\frac{1}{\sqrt{\bar{Y}^{*}}}-2\varepsilon _{3}(1-\bar{\tau })^{2}\right) \\ -\left( \frac{j_{12}^{*}}{j_{11}^{*}}\right) ^{2}\frac{2\bar{\delta }\bar{Y}^{*}}{\bar{R}^{*3}}+\frac{3\varepsilon _{1}}{4}\frac{1}{\sqrt{\bar{Y}^{*}}}-2\varepsilon _{3}(1-\bar{\tau })^{2} \end{array} \right) \end{aligned}$$

Finally

$$\begin{aligned} \left[ dF_{0,0}(0),Q(e,e)\right] =\left[ \begin{array}{cc} &{}\frac{2\alpha \gamma }{\beta }\varepsilon _{3}(1-\bar{\tau })\bar{Y}^{*2}-\frac{\alpha \gamma -1}{\beta }\bar{Y}^{*} -\left( \frac{j_{12}^{*}}{j_{11}^{*}}\right) ^{2}\frac{\gamma }{\beta }\frac{2\bar{\delta }\bar{Y}^{*}}{\bar{R}^{*3}}\\ &{}+\frac{\gamma }{\beta }\left( \frac{3\varepsilon _{1}}{4}\frac{1}{\sqrt{\bar{Y}^{*}}}-2\varepsilon _{3}(1-\bar{\tau })^{2}\right) \\ &{}2\alpha \varepsilon _{3}(1-\bar{\tau })\bar{Y}^{*2}-\alpha \bar{Y}^{*} -\left( \frac{j_{12}^{*}}{j_{11}^{*}}\right) ^{2}\frac{2\bar{\delta }\bar{Y}^{*}}{\bar{R}^{*3}}\\ &{}+\varepsilon _{1}\frac{3}{4}\frac{1}{\sqrt{\bar{Y}^{*}}}-2\varepsilon _{3}(1-\bar{\tau })^{2} \end{array} \right] \end{aligned}$$

(C.3)

where $j_{11}^{*}=\frac{\gamma \alpha }{\beta }\left( -(\varepsilon _{2}+\varepsilon _{4})+\delta \frac{\bar{Y}^{*}}{\bar{R}^{*}{}^{2}}\right)$ and $j_{12}^{*}=\frac{\gamma \alpha }{\beta }\left( \frac{3}{2}\varepsilon _{1}\sqrt{\bar{Y}^{*}}-2\varepsilon _{3}(1-\tau )^{2}\bar{Y}^{*}\right.$ $\left. -\frac{\delta }{\bar{R}^{*}}\right) -\frac{\alpha \gamma -1}{\beta }\tau$. Since (C.3) has rank 2, the third requirement of the Theorem is satisfied.