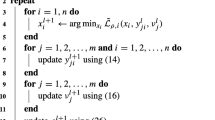Keywords

1 Introduction

In the research project Automated Extension of Fixed Point PDE Solvers for Optimal Design with Bounded Retardation we focus on design optimization problems of the form

$$\displaystyle{ \min _{(u,y)\in U\times Y }f(u,y)\quad \text{ s. t. }\quad c(u,y) = 0 }$$
(DOP)

where \(f: U \times Y \rightarrow \mathbb{R}\) denotes an objective function and c: U × Y → H with \(\dim H =\dim Y = n\) represents some state equation. This scenario has been approached by many computational scientist with inexact variants of large-scale SQP methods. For a partial survey we recommend [1–3, 12, 21].

As a key assumption we require that for any control u ∈ U there is a non-singular solution y(u) ∈ Y of the state equation c(u, y) = 0. Moreover, we assume that the state constraint can be equivalently written as a fixed-point equation with some contractive function G: U × Y → Y, i.e.

$$\displaystyle{ \;\left \|G_{y}(u,y)\right \| \leq \rho _{0} < 1\quad \text{ for all }(u,y) \in U \times Y, }$$

such that the fixed-point iteration \(y_{k+1} = G(u,y_{k})\) provides a solution y(u) = lim k → ∞ y k of the original state equation for any fixed control u ∈ U and initial state y 0 ∈ Y. We also assume in the statement and for the execution of numerical algorithms that the functions are at least once continuously differentiable to guarantee well posedness of the problem and twice continuously differentiable for the convergence theory.

Thus, by standard results from nonlinear optimization [16] we see in the finite dimensional case (n < ∞) that for any local minimum (u ∗, y ∗) of (DOP) in the interior of U × Y there exists a Lagrange multiplier \(\bar{y}_{{\ast}}\in \mathbb{R}^{n}\) such that the first order necessary optimality conditions

$$\displaystyle{0 = L_{u}(u_{{\ast}},y_{{\ast}},\bar{y}_{{\ast}}),\;y_{{\ast}} = G(u_{{\ast}},y_{{\ast}}),\text{ and }0 = L_{y}(u_{{\ast}},y_{{\ast}},\bar{y}_{{\ast}})}$$

hold, where \(L: U \times Y \times \mathbb{R}^{n} \rightarrow \mathbb{R}\) denotes the Lagrangian function

$$\displaystyle{L(u,y,\bar{y}) = f(u,y) +\bar{ y}^{\top }\!\left (G(u,y) - y\right ).}$$

Assuming that second order sufficient optimality conditions are satisfied we find that the projected Hessian of the Lagrangian

$$\displaystyle\begin{array}{rcl} H_{{\ast}}:= \left [\begin{array}{*{10}c} I,&Z^{\top } \end{array} \right ]\left [\begin{array}{*{10}c} L_{\mathit{uu}} & L_{\mathit{uy}} \\ L_{\mathit{yu}} & L_{\mathit{yy}} \end{array} \right ]\left [\begin{array}{*{10}c} I\\ Z \end{array} \right ]\quad \text{with}\quad Z:= (I - G_{y})^{-1}\,G_{ u}& &{}\end{array}$$
(1.1)

evaluated at a strict local minimum \((u_{{\ast}},y_{{\ast}},\bar{y}_{{\ast}})\) is positive definite and the same holds true in an neighborhood of the minimizer.

In the first part of our project we pursued a so-called (Jacobi) One-shot strategy [4, 8, 9, 11]

$$\displaystyle{ \begin{array}{ll} u_{+} & = u -\alpha _{\mathit{step}}B_{\mathit{Jac}}^{-1}L_{u}(u,y,\bar{y})\! \\ y_{+} & = G(u,y) \\ \bar{y}_{+} & =\bar{ y} + L_{y}(u,y,\bar{y})\, \end{array} }$$
(1.2)

or in short

$$\displaystyle{ \ldots \rightarrow (\;\mbox{DESIGN, STATE, ADJOINT}) \rightarrow \ldots }$$

to find first order optimal points. Here \(\alpha _{\mathit{step}} \in \mathbb{R}\) denotes some step-multiplier and B is a suitable symmetric positive definite preconditioner, which may depend on the variables \((u,y,\bar{y})\), the given functions f, G and their derivatives. As a special choice we investigate the augmented Lagrangian preconditioner

$$\displaystyle{ B_{\mathit{Jac}} = L_{\mathit{uu}} +\alpha \, G_{u}G_{u}^{\top }\! +\beta \, L_{\mathit{ uy}}L_{\mathit{yu}}\, }$$

and BFGS approximations of it with some suitable coefficients \(\alpha,\beta \in \mathbb{R}\).

Beside the original (Jacobi) one-step One-shot method [8], several other stepping schemes can be found. Therefore, we also propose the Multistep-Seidel-version

$$\displaystyle{ \ldots \rightarrow (\text{DESIGN}) \rightarrow (\text{STATE})^{s} \rightarrow (\text{ADJOINT})^{s} \rightarrow \ldots, }$$

where after one design update several repeated state updates are followed by the same number of repeated adjoint updates, or in detail,

$$\displaystyle\begin{array}{rcl} \begin{array}{llll} u_{+} & = u -\alpha B_{\mathit{Seid}}^{-1}L_{u}(u,y,\bar{y})&&\text{single design update}, \\ y_{+} & = G^{s}(u_{+},y) &&\text{s state updates}, \\ \bar{y}_{+} & =\bar{ G}^{s}(u_{+},y_{+},\bar{y}) &&\text{s adjoint updates}\,.\end{array} & &{}\end{array}$$
(1.3)

where

$$\displaystyle\begin{array}{rcl} G^{k+1}(u,y)&:=& G\left (u,G^{k}(u,y)\right )\;\text{ and } {}\\ \bar{G}^{k+1}(u,y,\bar{y})&:=& \bar{G}\left (u,y,\bar{G}^{k}\left (u,y,\bar{y}\right )\right ) {}\\ \end{array}$$

for \(k = 1,\ldots,s - 1\) with \(\bar{G}(u,y,\bar{y}):= L_{y}(u,y,\bar{y}) +\bar{ y}\).

In contrast to before, the preconditioner B Seid  ≈ H ∗ may also depend on the number of state/adjoint updates s. We present the basic ideas (cf. [5]) needed to prove that the Multistep One-shot method is locally convergent for a sufficient choice of α, B Seid and the step number s which is mainly depending on the contraction rate ρ 0 of G and problem specific derivative information.

In the sequel, we will give a short summary of our project for the last research period of the DFG SPP-1253 project. The structure is as follows:

In Sects. 2–4 we present some of our results for the Jacobi method containing the findings for the exact quantification of the retardation factor, an application in marine science and the extension of the approach to function space. For the Multistep One-shot method we will state sufficient conditions for the convergence of the method in terms of problem dependent quantities and present some numerical examples for an application in aerodynamic shape optimization, which is done in Sects. 5 and 6, respectively. Furthermore, we will consider in Sect. 7 the case where the constraint mapping c represents a PDE only allowing for unsteady solutions.

2 Exact Quantification of Retardation

In One-shot methods, retardation refers to the increase of steps needed for a comparable reduction in the residuals when going from simulation to optimization in the coupled iteration. Bounded retardation, i.e., a limited increase of these steps, has been achieved by many groups in the priority program. However, a general theoretical statement to quantify the factor of retardation for the Jacobi method has not been achieved yet. In the second period, we obtained theoretical results for separable problems [9], where \(L_{\mathit{yu}} = L_{\mathit{uy}} = 0\). We investigated:

  1. 1.

    A Newton scenario for separable problems,

  2. 2.

    Jacobi and multigrid scenarios for a standard elliptic problem.

In the Newton scenario for the separable case, we have G y  = 0 and thus \(G_{u} = \mathit{dy}/\mathit{du}\). We expect the observed results to remain valid also in the case when G represents an inner iteration. We tested the example of several multigrid cycles that resolve the state equation with higher accuracy before a change of the design variables. In this case, the retardation factor was found to be γ∕3, where \(\gamma =\| \Gamma \|\) is the weighted Euclidean norm of \(G_{u}^{\top }L_{\mathit{yy}}G_{u}\) w.r.t. to the projected Hessian H.

In the Jacobi and multigrid scenarios, we consider an elliptic boundary value problem with a tracking type objective function and Tikhonov regularization on the L 2 norm of the control with the weighting parameter μ. This standard test problem was solved by the rather slow Jacobi method and the rather fast multigrid method. Here, we find that the preconditioner should be a multiple of the identity and its optimal scaling can be found by solving a system of three cubic polynomials, which can be reduced to a single polynomial in the convergence factor ρ 0.

In Fig. 1, the retardation factors as a function of the reciprocal 1∕μ for three different grid sizes N are shown. As one can see, the retardation factor for the Jacobi scenario is very small until 1∕μ is about 102, then grows quite rapidly until it becomes a linear function of 1∕μ, and finally for very large 1∕μ it becomes constant. The same behavior is also observed for the V-cycle multigrid case with Jacobi smoother. In all cases, we observed a much better retardation factor than the theoretical upper bound without optimized step multiplier (yellow line).

Fig. 1
figure 1

Retardation factor for Jacobi and multigrid methods

Full size image

3 Application in Marine Science

Parameter optimization is an important task in all models that simulate parts of the climate system, as for example ocean or atmosphere models. In these models, many processes are not well-understood or cannot be resolved. These processes are parametrized using simplified model functions with parameters that have to be optimized for calibration according to measurements or other models’ data. The parameters appear as factors of the state variables, thus leading to nonseparability in the state equations. Often, calibration is performed for a steady stationary or periodic solution, the latter representing a stable annual cycle. Computation of a steady state is usually the result of a spin-up, i.e., a time integration until no significant changes are observed. For ocean models, the spin-up needs thousands of years of model time, which reflects the long time scales of the global ocean circulation. In three space dimensions, the pure simulation of the ocean circulation is a challenging computational task which requires considerable time. As a consequence, the One-shot method is a promising approach for parameter optimization in ocean models. However, the additional computational effort of simultaneous update of the state and parameter corrections must not be ignored and we propose simplifications of the strategy. We considered two examples.

3.1 Calibration of a Box Model of the North Atlantic Circulation

At first, we calibrated a conceptual box model of the North-Atlantic thermohaline circulation by Rahmstorf [20]. It has eight nonlinear ODEs and a global warming parameter that varies in a given range and is not to be optimized. For each value of this parameter f 1, the amount of water overturning m(u, y(f 1)) is obtained as an aggregated quantity from the state variables and the parameters. The model is numerically integrated into a steady state where c(u, y(f 1)) = 0 by an explicit Euler scheme. Since it is computationally cheap and has been calibrated using other methods (see [18]), we used it to investigate the applicability of the One-shot method and to compare results and performance in a real world problem. Data m d from a more complex model (see [18]) are used as desired state in a tracking type functional with regularization term incorporating a prior guess u guess for the six parameters to be optimized:

$$\displaystyle\begin{array}{rcl} \min _{u,y}f(u,y)&:=& \frac{1} {2}\|m(u,y(f_{1})) - m_{d}\|_{2}^{2} + \frac{\epsilon } {2}\|u - u_{\mathit{guess}}\|_{2}^{2}, {}\\ \mathrm{ s.t.} \quad 0& =& c(u,y(f_{1,i})),\quad i = 1,\ldots,l.{}\\\end{array}$$

The parameters are subject to box constraints, which were not treated explicitly in the One-shot method. Without regularization, typically several local minima occur.

We compared the One-shot results both with full computation of the preconditioner B Jac and using its BFGS approximation on the one hand with results obtained by direct optimization using a full spin-up in every function evaluation on the other hand. For the direct optimization we applied our own BFGS implementation as well as the L-BFGS and L-BFGS-B codes from [19].

As summarized in [14], the One-shot method was successful, even though no contractivity, but only quasi-contractivity (see [7]) is given. Simplifications of the algorithm as fixing the parameter ρ representing the contraction factor to 0.9 and limiting the exact computation of B Jac to every 1,000th iteration was adequate. The latter reduced computational time to about half of the time needed in optimization runs with computation of B Jac in each iteration. The final states obtained by the two One-shot variants are close to the data and to the ones obtained by the direct methods, also with small regularization parameter ε. The parameters computed by One-shot were to some extent similar to those of the direct optimization with L-BFGS-B. They stayed in acceptable ranges without any explicit constraint treatment, but differ among the chosen methods when ε < 1, which is due to the ill-posedness of the problem.

As can be seen in Fig. 2, the One-shot strategy showed good performance: The number of iterations was about 10–40 times larger than those for a spin-up. Direct optimization strategies needed at least 30 optimization steps, each requiring several complete spin-ups. Using full computation of B Jac performs well for most regularization parameters ε, whereas the One-shot-BFGS strategy does not show good performance. This behavior also varies with respect to the global warming parameter, likely because the model itself has difficulties finding the steady state for high values of this parameter.

Fig. 2
figure 2

Typical optimization run for parameter optimization of the box model: comparison of total necessary Euler steps by direct BFGS optimization and One-shot method with full computation of the preconditioner

Full size image

3.2 Calibration of a 3-D Marine Ecosystem Model

Marine ecosystem models describe the physical and bio-geochemical processes that determine the oceanic part of the global carbon cycle. They are non-linearly coupled transport or advection-diffusion-reaction equations, with ocean circulation data as forcing. In three dimensions, the computation of a steady annual cycle of such models takes several days on a parallel machine.

We performed parameter optimization for a characteristic model (see [17]) consisting of two spatially distributed state variables (tracers), namely phosphate and dissolved organic phosphorus. The parameter optimization problem is of tracking type including a regularization term with an initial parameter guess:

$$\displaystyle\begin{array}{rcl} \min _{u,y}f(u,y)&:=& \frac{1} {2}\|y - y_{\mathit{data}}\|^{2} + \frac{\epsilon } {2}\|u - u_{\mathit{guess}}\|^{2}\text{ s.t. }0 = c(u,y) {}\\ \end{array}$$

At first synthetic data created by the model were used as desired state, tests with real data taken from the World Ocean Atlas are work in progress. Direct optimization runs that are still possible in coarse resolutions suggest that for this configuration several local minima exist. Nevertheless, the One-shot optimization method without regularization found the correct parameters u ∗ for synthetic data. Figure 3 shows an example with regularization parameter ε = 0. 01, but where the initial guess u guess did not equal the value u ∗ used to create the synthetic desired state. The convergence of the parameters differs. The cost function is significantly reduced, as can be seen in Fig. 4. Comparing performance, the One-shot method leads to results comparable with a direct optimization after about 15,000 steps (equal model years). A usual spin-up takes about 5,000 years, but it has to be noticed that a One-shot iteration requires additional effort due to adjoint and parameter updates. In this example, the One-shot iteration step requires about 23 times the computational time needed for one step of the spin-up. The costs can be reduced to a factor of only eight, if the update of B Jac is performed only every fifth iteration step.

Fig. 3
figure 3

Some parameters during optimization, u guess ≠ u ∗, ε = 0. 01. Straight lines represent optimal values u ∗

Full size image

Table 1 summarizes the use of Automatic Differentiation (AD) in the realization of the One-shot method.

Fig. 4
figure 4

Typical tracer distribution at the ocean surface (left) and cost function f during One-shot optimization (u guess ≠ u ∗, ε = 0. 01)

Full size image
Table 1 Computation of derivatives using different approaches
Full size table

4 One-Shot in Function Spaces

For the treatment of the One-shot method in function spaces we again consider problem (DOP) for general Hilbert spaces U and Y. Here, c(u, y) = 0 with \(c: U \times Y \rightarrow Y ^{{\ast}}\) denotes the governing equations in form of a PDE. In order to define the Lagrange function with respect to the fixed point operator G(u, y) in a Hilbert space setting correctly we need to consider the transition from the PDE to the fixed-point formulation. According to [13], this is given in terms of a linear, bounded and bijective operator \(F(y): Y \rightarrow Y ^{{\ast}}\) so that

$$\displaystyle\begin{array}{rcl} c(u,y) = F(y)[y - G(u,y)].& & {}\\ \end{array}$$

For the sake of simplicity, we assume F(y) to be independent of u. The Lagrangian is now defined incorporating the fixed-point formulation as follows

$$\displaystyle\begin{array}{rcl} L(u,y,\bar{y})& =& f(u,y) -\langle \bar{ y},c(u,y)\rangle _{Y,Y ^{{\ast}}} \\ & =& f(u,y) -\langle F(y)^{{\ast}}\bar{y},y - G(u,y)\rangle _{ Y ^{{\ast}},Y }.{}\end{array}$$
(4.1)

Computing the KKT system based on (4.1) yields a fixed-point formulation of the optimality system and a simultaneous update of state, adjoint and design equation

$$\displaystyle\begin{array}{rcl} y_{+}& =& G(u,y){}\end{array}$$
(4.2)
$$\displaystyle\begin{array}{rcl} \bar{y}_{+}& =& \Phi (u,y,\bar{y}){}\end{array}$$
(4.3)
$$\displaystyle\begin{array}{rcl} u_{+}& =& u - B^{-1}L_{ u}(u,y,\bar{y}).{}\end{array}$$
(4.4)

with an appropriate preconditioner B. Here, the operator \(\Phi (u,y,\bar{y})\) in (4.3) is the fixed-point operator of the adjoint equation and defined by (see [13])

$$\displaystyle\begin{array}{rcl} \langle F(y)^{{\ast}}\Phi (u,y,\bar{y}),w\rangle _{ Y ^{{\ast}},Y }&:=& f_{y}(u,y)w -\langle \bar{ y},F_{y}(y)w[y - G(u,y)]\rangle _{Y,Y ^{{\ast}}} {}\\ & & \quad +\langle F(y)^{{\ast}}\bar{y},G_{ y}(u,y)w\rangle _{Y ^{{\ast}},Y } {}\\ \end{array}$$

for all w ∈ Y. Note that it holds

$$\displaystyle{ L_{y}(u,y,\bar{y})w =\langle F(y)^{{\ast}}\Phi (u,y,\bar{y}),w\rangle _{ Y ^{{\ast}},Y } -\langle F(y)^{{\ast}}\bar{y},w\rangle _{ Y ^{{\ast}},Y }. }$$

In [13] a convergence proof is given for the general case and specified for model problems including the solid fuel ignition model and the viscous Burgers equations. In the following, we only note the leading steps of the general convergence proof. Therefore, consider the augmented Lagrangian defined as

$$\displaystyle{ L^{a}(u,y,\bar{y}) = L(u,y,\bar{y}) + \frac{\alpha } {2}\|G(u,y) - y\|_{Y }^{2} + \frac{\beta } {2}\|\Phi (u,y,\bar{y}) -\bar{ y}\|_{Y }^{2} }$$
(4.5)

with the penalty parameters α, β > 0. The convergence proof follows the idea of the finite dimensional setting to show that the augmented Lagrangian acts as a penalty function, i.e. that every local minimum of the original optimization problem (DOP) is also a local minimum of L a. Further, we show that the One-shot method yields descent on L a and therefore reaches the minimum correctly. The next theorem (cf. [13]) is the main result in this procedure and ensures the equivalence of the stationary points as well as the descent condition.

Theorem 4.1.

If there exist constants α > 0 and β > 0 such that the following conditions are fulfilled

$$\displaystyle\begin{array}{rcl} & \alpha (1 -\rho _{0}) -\frac{\alpha ^{2}} {2\tilde{\gamma }}\|G_{u}\|^{2} >\| F(y)\| + \frac{\beta } { 2}\|\Phi _{y}\|, & {}\\ & \beta (1 -\rho _{0}) >\| F(y)\| + \frac{\beta } {2}\|\Phi _{y}\|,\quad \text{and}\quad \gamma > \frac{\tilde{\gamma }} {2},& {}\\ \end{array}$$

for a positive preconditioner B with \((\mathit{Bh},h)_{U} \geq \gamma \| h\|_{U}^{2}\) , \(\|\Phi _{\bar{y}}\| \leq \rho _{0} < 1\) and a constant \(\tilde{\gamma }> 0\) , then a point is a stationary point of L a if and only if it is a solution of the KKT-system to (DOP).Additionally, the increment vector of the One-shot method is a descent direction for L a.

These general conditions are difficult to verify. Nevertheless, for specific model problem they can be simplified and tested [13]. Numerical investigations of the method, with a preconditioner chosen as a scaled identity operator, show a mesh-independent behavior for several model problems:

Example (see [13]).

Consider the minimization of the tracking type functional

$$\displaystyle{ \min f(y,u):= \frac{1} {2}\int _{\Omega }\vert y - z_{d}\vert ^{2}\,\mathit{dx} + \frac{\epsilon } {2}\int _{\Omega }\vert u\vert ^{2}\,\mathit{dx} }$$

subject to \((y,u) \in H_{0}^{1}(\Omega ) \times L^{2}(\Omega )\) fulfilling the Viscous Burgers equation

$$\displaystyle{ \begin{array}{l} -\nu \Delta y + (y\,\mbox{$ \cdot$ }\,\nabla )y = u\;\;\text{ in }\Omega,\quad \text{and}\quad y = 0\;\;\text{ on }\Gamma. \end{array} }$$

The corresponding first order optimality system

$$\displaystyle\begin{array}{rcl} -\nu \Delta y + (y\,\mbox{$ \cdot$ }\,\nabla )y - u& =& 0,y\vert _{\Gamma } = 0 {}\\ -\nu \Delta \bar{y} - (y\,\mbox{$ \cdot$ }\,\nabla )\bar{y} -\mathop{ div}\nolimits (y)\bar{y} + (\nabla y)^{T}\bar{y} - y + z_{ d}& =& 0,\bar{y}\vert _{\Gamma } = 0 {}\\ \epsilon u +\bar{ y}& =& 0\text{ a.e. in }\Omega. {}\\ \end{array}$$

was solved by the One-shot iteration:

$$\displaystyle\begin{array}{rcl} y_{+}& =& G(y,u) = (-\nu \Delta + y\,\mbox{$ \cdot$ }\,\nabla )^{-1}(u) {}\\ \bar{y}_{+}& =& (-\nu \Delta - y\,\mbox{$ \cdot$ }\,\nabla -\mathop{ div}\nolimits (y))^{-1}(y - z_{ d} - (\nabla y)^{T}\bar{y}) {}\\ u_{+}& =& u -\frac{1} {\gamma } (\epsilon u +\bar{ y}) {}\\ \end{array}$$

The resulting number of iterations for the 2D case are given in Table 2.

It is important to note that in this example the focus does not lie on the efficiency of the method, it rather demonstrates the mesh-independency. Therefore, the total number of iterations necessary for the optimization does not increase significantly. The formulation and analysis of the method in function spaces as well as the numerical mesh-independent behavior motivates an extension of the method in terms of an additional adaptive step (cf. [13]).

Table 2 2D Burgers equation with ε = 0. 01, ν = 0. 1 and \(z_{d} \equiv 1\)
Full size table

5 Adaptive Sequencing of Primal, Adjoint and Control Updates

As a part of our research we also considered various stepping schemes, one of them being the Multistep One-shot (1.4). Assuming for the analysis that the design variables were transformed in such a way that the projected Hessian is the identity, i.e., we set \(u = T\tilde{u}\) and \(\tilde{u} = T^{-1}u\) if \(T^{-\top \!}T^{-1}:= H_{{\ast}} = H(1)\), we were able (see [5]) to bound all complex eigenvalues of the Jacobian

$$\displaystyle{J_{{\ast}} = \frac{\partial (u_{+},y_{+},\bar{y}_{+})} {\partial (u,y,\bar{y})} }$$

for the coupled iteration in terms of the problem dependent quantities

$$\displaystyle{ d\; \equiv \;\| L_{\mathit{yy}}\|\,\|\tilde{Z}\|^{2},\;\;e\; \equiv \;\left \|L_{ y\tilde{u}} + L_{\mathit{yy}}\tilde{Z}\right \|\,\|\tilde{Z}\|,\;\;\text{and}\;\;\gamma \; \equiv \;\| I -\alpha _{\mathit{step}}\tilde{B}_{\mathit{Seid}}^{-1}\|. }$$

Here \(\tilde{Z} = Z\,T\) and \(\tilde{B}_{\mathit{Seid}} = T^{\top }\!B_{\mathit{Seid}}T\) represent the transformed quantities.

Proposition 5.1.

Under the stated assumptions all eigenvalues \(\lambda \in \mathbb{C}\) of J ∗ for the Multistep One-shot iteration with the preconditioner matrix B Seid satisfy

$$\displaystyle\begin{array}{rcl} \vert \lambda \vert \leq \eta \quad \text{ or }\quad \vert \lambda \vert \leq \gamma +\nu \,\left [d\,\mu ^{2}(\eta,\vert \lambda \vert ) + 2\,e\,\mu (\eta,\vert \lambda \vert )\right ].& &{}\end{array}$$
(5.1)

where \(\eta =\rho _{ 0}^{s}\) , \(\nu =\alpha _{\mathit{step}}\|\tilde{B}_{\mathit{Seid}}^{-1}\|\) and \(\mu (\eta,\vert \lambda \vert ) =\;\eta (\vert \lambda \vert + 1)/(\vert \lambda \vert -\eta )\) .

Note that \(L_{\mathit{yy}} = \partial L_{y}/\partial y\) is the partial derivative of the adjoint equation w.r.t. y and \(L_{\mathit{yy}}Z + L_{\mathit{yu}} = \mathit{dL}_{y}/\mathit{du}\) is the total derivative of the adjoint equation w.r.t. u. thus, e and d can be understood as a measure for the sensitivity of the adjoint equation with respect to state and design, respectively. Moreover, we have:

Proposition 5.2.

If γ < 1, then by adjusting s and thus \(\eta =\rho _{ 0}^{s}\) , any rate ρ ∈ (γ,1) can be attained as upper bound of the spectrum of J ∗ . The following relation between s, η and ρ for given e, d, γ and ν is sufficient:

$$\displaystyle\begin{array}{rcl} \rho _{0}^{s} =\eta \leq \eta _{ {\ast}}(\rho ) = \frac{\rho (\rho -\gamma )} {(\rho -\gamma ) +\nu (1+\rho )\left (\sqrt{d(\rho -\gamma )/\nu + e^{2}} + e\right )}& &{}\end{array}$$
(5.2)

In other words, we found a sufficient condition on the number s of primal and adjoint iterations that ensures the local convergence of the approach in terms of the above mentioned quantities.

Corollary 5.3.

The spectral radius ρ of J ∗ is less than 1 if the number of inner iterations \(s \in \mathbb{N}\) satisfies

$$\displaystyle{s >\underline{ s} =\log _{(1/\rho _{0})}\left [1 + 2\left (\sqrt{d\,(1-\gamma )/\nu + e^{2}} + e\right )\nu /(1-\gamma )\right ]}$$

This theoretical lower bound on the number s of primal and adjoint updates was used to implement an self-adapting algorithm ABOSO. Within the algorithm all required quantities, such as e, δ, γ, and ρ 0, are approximated by difference quotients and other already computed information instead of the exact calculation which is in general too expensive. Also, the measurements are averaged over the last iterations to have more reliable estimates.

Example.

The self-adapting algorithm was verified on various examples, e.g. on the non-linear problem Bratu problem (see [15])

$$\displaystyle\begin{array}{rcl} & & \min _{(u,y)}\;\;\frac{1} {2}\|\partial _{2}y(\,\mbox{$ \cdot$ }\,,1) -\phi _{1}\|_{\mathcal{L}^{2}(\Omega )}^{2} + \frac{\mu } {2}\|u\|_{\mathcal{H}^{1}(\Omega )}^{2},\quad (u,y) \in \mathcal{H}^{1}(\Omega ) \times \mathcal{H}_{ 0}^{1}(\Omega )\text{ s.t. } {}\\ & & -\Delta y =\lambda \exp (y)\text{ in }\Omega,\quad y(s,1) = u(s),\quad y(s,0) =\phi _{2}(s),\quad y(1,t) = y(0,t) {}\\ \end{array}$$

that describes the combustion of solids over the unit square \(\Omega = [0,1]^{2} \subset \mathbb{R}^{2}\) for given functions ϕ 1 and ϕ 2. The fixed-point function \(y_{+} = z = G(u,y)\) was computed on purpose in a Seidel type iteration by solving the implicit univariate equations

$$\displaystyle{z_{\mathit{ij}} -\frac{h^{2}} {4} \mathit{exp}(z_{\mathit{ij}}) = y_{\mathit{mean}} = \frac{1} {4}(y_{i,j-1} + y_{i,j+1} + y_{i-1,j} + y_{i+1,j})}$$

using the equidistant grid points \((i/m,j/m)\) with m = 12 so that y m, j  = y 0, j and copying the values u i into z i, m after each inner iteration. Naturally, there are faster solvers for this elliptic problem, but we deliberately wished to mimic slow fixed point solvers in more complicated application areas. The behavior of the algorithm is displayed in Fig. 5 for the parameters λ = 1 and \(\mu = 10^{-4}\). In particular, it can be seen by comparing the residual of the simulation without design changes on the left side and the residual of the optimization on the right that the retardation factor is approximately 2. 5, i.e. for achieving the same residual in the optimization only an small number of additional simulation steps by a factor of 2. 5 is required.

Fig. 5
figure 5

Residuals for the simulation (right)and optimization(left)

Full size image

6 Application in Aerodynamic Shape Optimization

We have applied the Multistep One-shot method for the shape optimization of a NACA0012 airfoil at transonic flow conditions using Euler equations. As the shape parameterization, the free-node parametrization is chosen, in which all the mesh points on the airfoil surface are taken as shape parameters. This type of parameterization enables that maximum degree of freedom can be given to the optimization algorithm. The shape sensitivities, which are required for the One-shot method, are computed using the consistent discrete adjoint approach based on Automatic Differentiation [6]. Although this approach is slower than the continuous and hand-discrete adjoint approaches, it has been chosen because of its robustness and its ability to compute exact derivative information without utilizing any approximations. The test case is chosen as the inviscid drag minimization scenario at constant lift. The Mach number and the angle of attack for this case are chosen as 0.85 and 2 respectively. The grid used for the study is the 325 × 65 C-type grid with 196 grid points on the airfoil surface. As it can be seen in the Fig. 6, the initial NACA0012 airfoil creates a strong inviscid shock on the suction side of the airfoil, which leads to a high amount of drag in the transonic flow regime (left figure). In the right figure, the pressure distribution for the optimized shape is illustrated. It can be observed that inviscid shock disappears in the optimized airfoil, which leads to a substantial drag reduction of 60 % while maintaining the lift.

Fig. 6
figure 6

Initial NACA0012 and optimized airfoils with pressure contours for the transonic case

Full size image

In order to assess the performance of Multistep One-shot method, we have made a comparison between a nested optimization approach using BFGS method with line searches and One-shot method with s = 10. The performance results of both methods compared to a single primal simulation are presented in Table 3. The nested approach takes totally 11 adjoint and 65 primal solver evaluations. Note that in the nested approach, the number of iterations taken by the primal and adjoint solvers for each run vary since five decade residue fall is set as the stopping criteria. The nested approach takes totally 192, 788 primal/dual steps and the optimization takes ca. 28 h on a 2.4 GHz Intel machine. The retardation factor of the nested approach is measured as 73. 8 in iteration counts and 107 in run-time. As it can be observed from the results, the One-shot method is significantly faster than the nested approach and has a factor of retardation 3. 9 in iteration counts and 36. 1 in run-time.

Table 3 Iteration count and run-time measurements for the primal simulation, nested optimization and One-shot optimization
Full size table

7 One-Shot Optimization with Unsteady PDE Constraints

For time-dependent PDEs, the state variable varies with time and thus is a function y: [0, T] → Y. The objective function to be minimized is typically given by some time averaged quantity. The general formulation of the optimization problem with unsteady PDEs reads

$$\displaystyle\begin{array}{rcl} \begin{array}{l} \min _{u,y}\, \frac{1} {T}\int _{0}^{T}\,f(u,y(t))\,\mathit{dt}\quad \text{s.t.}\quad \left \{\begin{array}{@{}l@{\quad }l@{}} \frac{\partial y(t)} {\partial t} + c(u,y(t)) = 0\quad &\forall t \in [0,T] \\ y(0) = y_{0}\,. \quad & \end{array} \right. \end{array} & &{}\end{array}$$
(7.1)

Unsteady PDEs are typically discretised by an implicit time marching scheme. The resulting implicit equations are solved iteratively by applying a fixed point solver at each physical time step until a steady-state solution at that time step is achieved:

$$\displaystyle{ \text{for }i = 1,\ldots,N: \quad y_{k+1}^{i} = G(u,y_{ k}^{i},y_{ {\ast}}^{i-1},y_{ {\ast}}^{i-2},\ldots )\mathop{\longrightarrow}\limits_{}^{k \rightarrow \infty }y_{ {\ast}}^{i} }$$
(7.2)

Here, \(y_{{\ast}}^{i}\) denotes the converged steady-state at the discrete time step \(t_{i} = i\Delta t\). N is the total number of time steps, given by \(T = N\Delta t\). The contractive fixed-point iterator G not only depends on the design variable but also on the converged state solutions at previous time steps.

In order to extend to One-shot, where one incorporates design updates already during the primal flow computation, the time marching scheme (7.2) is modified as

$$\displaystyle{ \text{for }k = 1,2,\ldots:\;\;\, y_{k+1}^{i} = G(u,y_{ k}^{i},y_{ k+1}^{i-1},y_{ k+1}^{i-2},\ldots )\quad \forall i \in \{ 1,\ldots,N\}\,. }$$
(7.3)

In contrast to (7.2), where fixed point iterations are performed at each time step for a state y i, in the One-shot framework (7.3) the complete trajectory of the unsteady solution is updated within one iteration. Interpreting the state as a discrete vector from the product space \(y \in Y ^{N}:= Y \times \ldots \times Y\) with state components y i, we can write (7.3) in terms of an update function

$$\displaystyle{ y_{k+1} = \mathcal{H}(u,y_{k}) }$$
(7.4)

where \(\mathcal{H}: U \times Y ^{N} \rightarrow Y ^{N}\) performs the update formulas (7.3) for all time steps. Using the contractivity of the fixed point iterator G it can be shown, that \(\mathcal{H}\) is contractive with respect to y ∈ Y N and, thus, y k converges to the unsteady solution of the PDE (cf. [10]).

Replacing the unsteady PDE constraint by the fixed point equation \(y = \mathcal{H}(u,y)\), the Lagrangian function corresponding to the unsteady optimization problem is defined as

$$\displaystyle{ L(u,y,\bar{y}):= I(u,y) +\bar{ y}^{T}\left (\mathcal{H}(u,y) - y\right )\,, }$$
(7.5)

where \(I(u,y) = \frac{1} {N}\sum _{i=1}^{N}f(u,y^{i})\) approximates the objective function. This formulation has the same structure as the definition of the Lagrangian in Sect. 1. Thus, the concept of One-shot optimization can be applied in the same way by replacing the fixed point iterator with the mapping \(\mathcal{H}\) and the objective function with the approximation I.

For a fixed design u ∈ U, iterating only in the state and the adjoint variable simultaneously in the so called piggy-back iteration is implemented for the problem of optimal active flow control around a 2D cylinder. Eight actuation slits are installed on the surface of the cylinder where sinusoidal blowing and suction is applied in order to reduce vorticity downstream the cylinder. Amplitude and phase shift of the actuation are used as design variables. The governing incompressible URANS (unsteady Reynolds-averaged Navier-Stokes) equations are solved by applying the new approach to a second order implicit finite volume code. To study the convergence behavior, the L 2-norm of the state and the adjoint residuals \(\|y -\mathcal{H}(u,y)\|_{2}\), \(\|L_{y}(u,y,\bar{y})\|_{2}\) are computed. From Fig. 7 it can be observed, that both variables converge with the same asymptotic convergence rate. In future, a preconditioned control update will be incorporated in the piggy-back iteration for the implementation of One-shot in unsteady framework.

Fig. 7
figure 7

Convergence history of primal and adjoint states for incompressible URANS in One-shot framework

Full size image

Conclusion

In the second phase of the project, the theoretical results and the applications from the first one have been extended in different ways. First of all, it was possible to quantify the retardation factor of some test problems and Newton, Jacobi and multigrid iterations. Moreover, the application of the One-shot method in its Jacobi variant was shown to be feasible and successful for parameter optimization in complex, spatially three-dimensional climate models using a fixed-point type iteration to compute steady seasonal cycles. These results show a high potential for application on various real-world problems in climate research, thus emphasizing the interdisciplinary benefit of the project.

Whereas these theoretical results and applications are based on the finite-dimensional setting of the method, we additionally extended the theory for the One-shot Jacobi variant on two prominent infinite-dimensional problems, namely the viscous Burger and the solid fuel ignition model. For both cases also numerical studies were performed.

Furthermore, we developed the Multistep One-shot method that uses an adaptive sequencing or adjustment of the number of primal, adjoint and control updates used during the algorithm. For this method, we provide a theory relating the number of necessary primal and adjoint steps per control update to the spectral radius of the Jacobian and thus the convergence speed of the coupled iteration. This modified method was applied successfully in shape optimization in Computational Fluid Dynamics. In this context, we also extended the method to non-linear (inner) iterations in non-stationary flow solvers.