Damage Detection Using Derringer’s Function based Weighted Model Updating Method

Abstract

Aim of this research paper is to present the application of Derringer’s function based weighted model updating method for damage detection in a cantilever beam structure installed near an electric motor. Individual desirability functions have been used to provide scale-free representations of ten sub-objectives of model updating based multi-objective optimization problem. First five vibration modes of beam structure are considered for model updating purpose and hence ten individual desirability functions (sub-objectives) are formulated. Maximization of an individual desirability function leads to minimization of error in corresponding finite element response to which the individual desirability function is attached. Since there are more chances of excitation of those vibration-modes which lie close to the operational frequency of the electric motor; more relative importance is given to such modes by increasing the relative importance index of their individual desirability function. Such kind of relative importance selection is not possible in widely used model updating methods such as response function method. Comparative study is performed for Derringer’s function based non-weighted and weighted model updating methods. Results show that weighted model updating method performs better than its non-weighted counterpart.

27.1 Introduction

Use of thin parts made up of low density materials in latest machines and structures is increasing day by day. Thin and light weight products have lot more tendencies to vibrate than their thick and heavy weight counterparts. Excessive vibrations may even cause pre-mature failure of products. Therefore prediction of accurate dynamic behavior is a major step in design of machines and structures. Dynamic behavior can be represented by natural frequencies, mode-shapes, damping ratios, frequency response functions etc. Further, to analyze the dynamic behavior of structures, either experimental route or theoretical approach [1, 2] can be followed. Theoretical route involves the formation of an analytical model of the system either using a classical method [3] or through Finite Element (FE) method [4]. Application of classical method is generally limited to simple systems only, while FE method is preferred for real life complex systems. However, FE method is not able to predict dynamic responses of structures with complete accuracy due to presence of certain errors in FE model. Thus there is a need to correct an FE model so that its vibration behavior matches with the actual dynamic response obtained experimentally. The procedure used to update the FE model is called Finite Element Model Updating (FEMU) [5–7].

FEMU methods can be broadly classified into direct and iterative methods. Direct (non-iterative) methods are essentially the one step methods such as those proposed by Baruch and Bar-Itzhack [8], Baruch [9], Berman [10], Berman and Nagy [11]. Updated FE models produced by such methods may not be symmetric and positive definite, hence such methods are not much useful in industry. Industrial applications generally rely upon the use of iterative methods such as those proposed by Collins et al. [12], Lin and Ewins [13], Atalla and Inman [14], Li [15], Lin and Zhu [16], Arora et al. [17, 18] and Silva [19].

This paper makes use of Derringer’s function based iterative FEMU method developed by Sehgal and Kumar [20]. In this method, FEMU is treated as multi-objective optimization problem; where number of objectives need to be defined in such a way as to reduce errors in responses predicted by FE model. In this paper, it is shown that by using Derringer’s function based FEMU one can attach relative importance indices with sub-objectives of different modes of vibration. This is particularly helpful when one particular mode of vibration is quite more important than rest of the modes of vibration. In this paper, fourth mode of vibration is considered to be more important than others and this aspect is very well formulated and handled in Derringer’s function based FEMU.

Basic theory of Derringer’s function based FEMU technique used in this research paper is discussed in Sect. 27.2. In order to apply Derringer’s function based FEMU technique, FE, Simulated Experimental (SE) results and Response Surface (RS) models are required as explained in Sect. 27.3. Section 27.4 presents the current research work related to damage detection using weighted model updating method. Section 27.5 discusses the conclusions drawn out of the present research work.

27.2 Theory

Derringer’ function based FEMU technique [20] is based upon the use of D-optimal design, Response Surface Method (RSM) and desirability function; basic theory of which is presented in Sects. 27.2.1, 27.2.2 and 27.2.3 respectively. Section 27.2.4 presents the details about Derringer’s function based weighted FEMU method.

27.2.1 D-Optimal Design

There are several design optimality criterion available in literature such as D-optimality, A-optimality, G-optimality. Among all, D-optimality is the most popular one [21]. It is a type of computer-generated designs, which are an outgrowth of the original work by Kiefer [22, 23] and Kiefer and Wolfowitz [24]. In general, modeling accuracy, namely, goodness-of-fit, can be measured by a variance-covariance matrix V given by (27.1).

$$ \mathbf{V}={\sigma}^2{\left({\mathbf{X}}^{\mathbf{\prime}}\mathbf{X}\right)}^{-1} $$

(27.1)

where σ is the standard deviation and X is the design matrix being a set of value combinations of coded parameters. Naturally, it is expected to minimize (X′X)^− 1 in order to obtain an accurate RS model. In statistics, minimizing (X′X)^− 1 is equivalent to maximizing the determinant of X′X. Therefore, the criteria for constructing the design matrix with a maximized |X′X| from a set of candidate samples can be defined as the D-optimality. The initial “D” stands for “determinant”. By using D-optimal designs, the generalized variance of a predefined model is minimized, which means the “optimality” of a specific D-optimal design is model dependent. Unlike standard designs, D-optimal designs are straight optimization and their matrices are generally not orthogonal with the effect estimates correlated.

27.2.2 Response Surface Method

RSM is a collection of mathematical and statistical techniques that are useful for modeling and analysis of problems in which a response of interest is influenced by several input variables and the objective is to optimize this response [25–27].

By conducting experiments and applying regression analysis, a model of the response to some independent input variables can be obtained. Based on the model of the response, a near optimal point can then be deduced. RSM is often applied in the characterization and optimization of processes. In RSM, it is possible to represent independent process parameters in quantitative form as written in (27.2).

$$ Y=f\left({X}_1,{X}_2,{X}_3,\dots {X}_m\right)\pm \varepsilon $$

(27.2)

where Y is the response, f is the response function, ε is the experimental error, and X ₁, X ₂, X ₃, … X _m are independent parameters. By plotting the expected response of Y, a surface, known as RS is obtained. The form of f is unknown and may be very complicated. Thus, RSM aims at approximating f by a suitable lower ordered polynomial in some region of the independent process variables. If the response can be well modeled by a linear function of the m independent variables, the function Y can be written as:

$$ Y={C}_0+{C}_1{X}_1+{C}_2{X}_2+\dots +{C}_m{X}_m\pm \varepsilon $$

(27.3)

However, if a curvature appears in the system, then a higher order polynomial such as the quadratic model as shown in (27.4) may be used.

$$ Y={C}_0+{\displaystyle {\sum}_{i-1}^m{C}_i{X}_i}+{\displaystyle {\sum}_{i-1}^m{D}_i{X}_i^2}\pm \varepsilon $$

(27.4)

Objective of using RSM is not only to investigate the response over entire factor space, but also to locate the region of interest where the response reaches its optimum or near optimal value. By studying carefully the RS model, the combination of factors, which gives the best response, can then be established.

27.2.3 Desirability Function

Derringer and Suich [28] describe a multiple response method called desirability. The method makes use of an objective function, D _o , called overall desirability function and transforms an estimated response into a scale free value (d _i ) called ith individual desirability function. The desirable ranges are from zero to one (least to most desirable, respectively). The factor settings with maximum D _o value are considered to be the optimal parameter conditions. The simultaneous objective function is a geometric mean of all transformed responses as sown in (27.5).

$$ {D}_o={\left({d}_1^{r_1}\times {d}_2^{r_2}\times {d}_3^{r_3}\times {d}_4^{r_4}\times \dots \times {d}_i^{r_i}\right)}^{\raisebox{1ex}{$1$}\left/ \raisebox{-1ex}{${\displaystyle \sum }{r}_i$}\right.}$$

(27.5)

where r_i represents the relative importance index of ith individual desirability function. If any of the responses falls outside the desirability range, the overall desirability function becomes zero. Desirability is an objective function that ranges from zero outside of the limits to one at the goal. The numerical optimization finds a point that maximizes the desirability function. For several responses, all goals get combined into one desirability function. For simultaneous optimization, each response must have a lower and upper limit assigned to each goal. The “Goal” field for responses must be one of five choices: “none”, “maximum”, “minimum”, “target”, or “in range”. Factors will always be included in the optimization at their design range by default, or as a maximum, minimum of target goal. The meanings of the goal parameters are:

• Maximum:

  • d _i  = 0 if response < lower limit

  • 0 ≤ d _i  ≤ 1 as response varies from lower to upper limit

  • d _i  = 1 if response > upper limit

• Minimum:

  • d _i  = 1 if response < lower limit

  • 1 ≤ d _i  ≤ 1 as response varies from lower to upper limit

  • d _i  = 0 if response > upper limit

• Target:

  • d _i  = 0 if response < lower limit

  • 0 ≤ d _i  ≤ 1 as response varies from lower limit to target

  • 1 ≥ d _i  ≥ 0 as response varies from target to upper limit

  • d _i  = 0 if response > upper limit

• Range:

  • d _i  = 0 if response < lower limit

  • d _i  = 1 as response varies from lower to upper limit

  • d _i  = 0 if response > upper limit

The d _i for “in range” are included in the product of the overall desirability function “D _o ”, but are not counted in determining “n”: $D={\left({\displaystyle \prod }{d}_i\right)}^{\raisebox{1ex}{$1$}\left/ \raisebox{-1ex}{$n$}\right.}$. If the goal is none, the response will not be used for the optimization.

Fig. 27.1

Algorithm for Derringer’s function based weighted FEMU method

27.2.4 Weighted Model Updating using Derringer’s Function based Updating Method

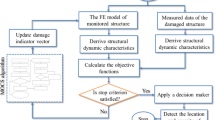
In this paper model updating method of Sehgal and Kumar [20] is used in a damage detection application where all modes of vibration are not equally important. Figure 27.1 shows the algorithm of Derringer’s function based weighted FEMU method. First step in the proposed model updating technique is to generate initial FE and SE results. If experimental set-up is available then SE results can be better replaced by actual experimental results. After that experimental design matrix is formed as per central composite design method. Experimental design matrix is then used to produce corresponding data set for response variables. This data set is then used for developing response surfaces for all response variables such as natural frequencies and Modal Assurance Criterion (MAC) values by regression analysis. Response surface models are then checked for their accuracy and significance by using ANalysis Of VAriance (ANOVA) method. If RS models are not good enough then these are to be modified and checked again for their adequacy. After achieving adequate RS models for all response variables, individual desirability functions are formulated using Derringer’s function approach. Individual desirability functions for natural frequencies and MAC values are of the type “Target” and “Maximum” respectively due to their different nature. All individual desirability functions are then combined to produce D _o as per (27.5); thereby transforming the complex multi-objective type FEMU problem to a rather simpler single-objective type. Maximum value of D _o is then searched out using an optimization algorithm. Corresponding to the maximum value of D _o , the values of all individual desirability functions are found out and are then checked for attaining or exceeding their desired values. If any individual desirability function does not attain its desired value then the relative importance index of that individual desirability function is increased. This leads to the formation of new overall desirability function, which is then again maximized. This process of increasing the relative importance indices is continued till all the individual desirability functions achieve their desired level. After that updating parameters are found corresponding to maximum value of overall desirability function and are then used for forming an updated FE model which is then simulated to produce updated structural dynamic results and error indices.

27.3 Development of RS Models

A cantilever beam structure as drawn in Fig. 27.2 is considered in present study. This beam structure is taken because of its resemblance with many real life products such as blade of rotor of a turbine, wing of an airplane, wing of a ceiling fan, an integrated chip of a mechatronic product etc. Cantilever beam is having the dimensions 910 × 49 × 7 mm³, density 6,728 kg/m³ and Young’ modulus of elasticity as 200 GPa. Initial FE model of undamaged beam is constructed using 30 beam elements each having two nodes.

The FE model developed in Matlab [29] is then used for producing initial FE natural frequencies and mode-shapes for first five modes of undamaged beam. After that, perturbation is introduced into the FE model of beam structure by reducing the value of modulus of elasticity of six finite elements as per the data provided in Table 27.1. Six damage locations have been selected in such a way so as to distribute these over entire length of beam. FE model of damaged beam is then processed in Matlab to produce SE natural frequencies and mode-shapes, which are later treated as target results. SE results have been used earlier also by many researchers as target results for model updating related research work [30–33]. In this paper, responses such as natural frequencies of first five modes (ω ₁ to ω ₅) and first five diagonal elements of MAC matrix (MAC ₁₁ to MAC ₅₅) are used during formulation of objective functions of FEMU problem.

Fig. 27.2

FE model of a damaged cantilever beam structure

Table 27.1 Physical parameters of undamaged and damaged beams

RS models are a basic requirement for Derringer’s function based FEMU. In order to develop RS models, firstly an experimental design matrix is generated by using D-optimal design in Design-Expert software [34]. Range of each input physical parameter (E ₁, E ₅, E ₉, E ₁₃, E ₁₇ and E ₂₄) is decided. Lower and upper limits for all the input parameters are taken as 20 and 60 % of their corresponding initial FE values respectively. Thus lower limit for each input parameter is taken as 40 GPa and the upper limit of the input parameter is taken as 120 GPa. Six coded parameters (A, B, C, D, E and F) are defined in such a way that each coded parameter varies linearly between −1 and +1 over complete range of its corresponding physical parameters (E ₁, E ₅, E ₉, E ₁₃, E ₁₇ and E ₂₄). Coordinate exchange method [35] is used for candidate selection, because it does not require a candidate list, which if unchecked grows exponentially as the size of the problem increases [36]. D-optimality criterion is used to develop the design matrix of actual physical variables. Design matrix is consisting of a total of 33 test runs and contains the information about various combinations of different levels of input physical parameters at which different SE runs need to be performed. Design matrix is then imported in Matlab and used as input to FE model. FE model is then used to produce response variables matrices as its output. The matrices of response variables are then supplemented to the experimental design matrix available in Design-Expert. Relationship between the set of input parameters (E ₁, E ₅, E ₉, E ₁₃, E ₁₇ and E ₂₄) and corresponding set of response variables (ω ₁, ω ₂, ω ₃, ω ₄, ω ₅, MAC ₁₁, MAC ₂₂, MAC ₃₃, MAC ₄₄ and MAC ₅₅) is assumed to be quadratic. A quadratic fit is assumed because it is giving better results than a linear or a cubic model. In order to check adequacy of the RS model, ANOVA is performed [37]. F-test method is used to carry out the hypothesis testing to check significance of different parameters. Regression analysis is used in developing the RS model for first natural frequency, as given by the polynomial equation in (27.6).

$$ \begin{array}{lll}{\widehat{\omega}}_1=&6.18+0.37A+0.25B+0.15C+0.08D+0.03E+0.04 AB+0.03 AC+0.02 AD+0.02 BC\\ &-0.17{A}^2-0.13{B}^2-0.05{C}^2-0.04{D}^2-0.03{E}^2+0.02{F}^2\end{array} $$

(27.6)

Similar analysis is also performed for next nine RS predicted response variables viz. $\widehat{\omega_2},\widehat{\omega_3},\widehat{\omega_4},\widehat{\omega_5},\break{\widehat{ MAC}}_{11},{\widehat{ MAC}}_{22},{\widehat{ MAC}}_{33},{\widehat{ MAC}}_{44},\mathrm{and}\kern0.24em {\widehat{ MAC}}_{55}$. After fitting RS models to actually observed results, the RS models for next nine responses (in coded terms) are given by the regression equations (27.7)–(27.15).

$$ \begin{aligned}\widehat{\omega_2}=&39.40+1.94A+0.20B+0.27C+1.17D+1.42E+0.30F+0.11 AB-0.09 AC+0.14 AE\\ &-0.05 BD +0.09 CD+0.09 CE+0.19 DE+0.05 EF-0.63{A}^2-0.12{B}^2-0.18{C}^2\\&-0.57{D}^2-0.68{E}^2\end{aligned} $$

(27.7)

$$ \begin{array}{lll}\widehat{\omega_3}&=112.08+4.15A+0.43B+3.24C+0.89D+1.28E+3.68F-0.41 AB+0.26 AD-0.23 AE\\ &+0.30 AF+0.36 CD+0.29 CF+0.41 EF-1.10{A}^2-1.39{C}^2-0.44{D}^2-0.59{E}^2-1.88{F}^2 \end{array} $$

(27.8)

$$ \begin{array}{lll}\widehat{\omega_4}=&214.34+6.12A+3.79B+2.56C+3.58D+4.15E+9.25F-0.87 AB+0.59 AC-0.55 AD\\ &+0.70 AE +0.73 BC-0.28 BD+0.46 BE-0.47 CD+0.95 DE+0.75 DF-0.94 EF-1.20{A}^2\\&-2.03{B}^2-1.08{C}^2 -1.58{D}^2-1.48{E}^2-\end{array}$$

(27.9)

$$ \begin{array}{l}\widehat{\omega_5}=358.61+8.18A+11.60B+1.95C+9.33D+8.85E+7.32F-0.57 AB-0.55 AC+1.42 AD\\ {}\kern2.34em -1.28 BC+2.10 BD+0.68 CD-1.83 DE-0.66 DF+0.64 EF-1.06{A}^2-4.22{B}^2-3.64{D}^2\\{}\kern2.34em-3.26{E}^2-2.12{F}^2\end{array} $$

$$ \widehat{ MA{C}_{11}}={10}^{-4}\times \left(\begin{array}{l}9998.94-2.57A-0.96B+0.49C+1.07D+0.50E\\ {}\begin{aligned}{}&-1.33 AB+1.70 AC+2.40 AD+1.58 AE+0.66 BD-0.79\\ &{}\quad CD-0.72 DE-2.37{A}^2-1.87{D}^2\end{aligned}\end{array}\right) $$

(27.11)

$$ \widehat{ MA{C}_{22}}={10}^{-4}\times \left(\begin{array}{l}9991.36-14.19A+1.29B-2.85C-4.65D+5.51E+6.69F\\ {}-5.83 AC-1.78 AD+16.12 AE+7.13 AF-2.24 CD+4.50 CE+3.45 CF\\ {}+3.20 DF-12.30{A}^2+3.95{C}^2-11.13{E}^2-5.60{F}^2\end{array}\right) $$

(27.12)

$$ \widehat{ MA{C}_{33}}={10}^{-4}\times \left(\begin{array}{l}9986.63-33.57A-11.77C+38.82F-15.94 AB-19.63 AC+8.83 AD\\ {}+55.40 AF+16.58 BF+32.80 CF+8.34 DE-10.18 DF+26.83 EF\\-34.20{A}^2-70.70{F}^2\end{array}\right) $$

(27.13)

$$ \widehat{ MA{C}_{44}}={10}^{-4}\times \left(\begin{array}{l}9925.18-69.34A-40.64B-30.36D+40.53E\\ {}+104.23F-56.69 AB+29.06 AE+88.89 AF\\ {}-21.35 BD+22.89 BE+52.74 BF+26.02 CF+35.00 DE+20.52 DF\\ {}-51.93{E}^2-122.71{F}^2\end{array}\right) $$

(27.14)

$$ \widehat{ MA{C}_{55}}={10}^{-4}\times \left(\begin{array}{l}9931.21-32.15A+45.96C-62.02D+69.05E+80.61F-84.45 AB-19.27 AC\\ {}+59.11 AE+53.46 AF-40.75 BC+30.14 BD+44.71 BE+58.88 BF+35.52 CD\\ {}+24.57 DF-46.67 EF-43.15{A}^2-57.74{C}^2-58.64{E}^2-76.35{F}^2\end{array}\right) $$

(27.15)

After having generated RS models for all response variables, next major step is the objective-function-formulation for Derringer’s function based FEMU problem and its use in damage detection.

27.4 Damage Detection using Weighted Model Updating

All modes of vibration may not be equally important. In this study it is assumed that that there is an electric motor (or any other exciter) situated near to the beam and operating at a rotational speed of 213 Hz. Because of presence of an external exciter the main excitation frequency is 213 Hz. Therefore that mode of vibration of beam has more chances of getting excited easily which lies closest to the main excitation frequency of 213 Hz rather than other modes of vibration. Hence fourth mode with a natural frequency of 213.02 Hz should be given more importance over other modes. Such method of assigning the relative importance is not possible with response function method [13], but can be easily implemented using Derringer’s function based model updating method. Considering fourth mode as the most important mode of vibration, the minimum acceptable desirability value for d ₄ and d ₉ are taken as 1 and 0.35 respectively. On the other hand the minimum acceptable desirability values for all other d _i ’s are taken as 0.35. To start with, relative importance indices are set to unity. Corresponding updating results related to individual desirability functions are drawn in Fig. 27.3.

Fig. 27.3

Desirability graph (taking relative importance index of both d ₄ and d ₉ as one)

Figure 27.3 shows that d ₄ and d ₉ have attained only 0.76355 and 0.263511 respectively. These results do not seem to be quite satisfying considering the importance of fourth mode. Therefore in order to obtain better updating results for fourth mode, the relative importance indices for d ₄ and d ₉ are to be increased. Figure 27.4 shows the results obtained by setting the relative importance indices of d ₄ and d ₉ to 2. It is seen that as the relative importance indices for d ₄ and d ₉ are increased, values attained by them during FEMU get increased, thereby depicting that better updating results related to fourth mode of vibration are obtained. But still the values of d _i ’s related to fourth mode of vibration are lesser than their desired values, so the relative importance indices of d ₄ and d ₉ are successively increased to 3, 4 and 5 in three stages. Results of these three stages are presented in Figs. 27.5, 27.6, and 27.7. Finally desired values of d ₄ and d ₉ are attained when relative importance indices of d ₄ and d ₉ are set to 5 as shown in Fig. 27.7.

Fig. 27.4

Desirability graph (taking relative importance index of both d ₄ and d ₉ as two)

Fig. 27.5

Desirability graph (taking relative importance index of both d ₄ and d ₉ as three)

Fig. 27.6

Desirability graph (taking relative importance index of both d ₄ and d ₉ as four)

Fig. 27.7

Desirability graph (taking relative importance index of both d ₄ and d ₉ as five)

Figures 27.8 and 27.9 show the improvement trend in the values of d ₄ and d ₉ respectively. It is seen that d ₄ gets stagnant at relative importance index 3 after achieving its highest possible value of unity. However d ₉ keeps on increasing almost linearly and steadily with increase in value of relative importance index. Table 27.2 presents the FEMU results when relative importance indices of d ₄ and d ₉ are set to 5. Updating results show that final average error in damage detection is only 3.06 %, which is far below its initial level of 161.11 %. Natural frequencies and MAC values are also predicted sufficiently accurately with an error of just 0.15 and 0.01 % respectively. Further it is observed that during weighted model updating (when relative importance indices are set to 5), d ₄ and d ₉ attain a value of 1 and 0.374376 respectively. While during non-weighted model updating (when all relative importance indices are set to 1) d ₄ and d ₉ attain a value of only 0.76355 and 0.263511 respectively. This shows that weighted model updating performs better than it non-weighted counterpart by 30.97 % considering the value of d ₄. Performance of weighted model updating method is again superior to its non-weighted counterpart by 42.07 % when value of d ₉ is considered.

Fig. 27.8

Improvement trend in the value of d ₄

Fig. 27.9

Improvement trend in the value of d ₉

27.5 Conclusion

In this paper, weighted model updating has been performed for damage detection of a beam. Fourth mode of vibration is considered more important than others in the numerical example considered in this paper. Effect of increasing the relative importance index of individual desirability functions related to fourth mode of vibration is studied. It is seen that as the relative importance index increases, corresponding individual desirability function value also increases thereby leading to better updating results for fourth mode of vibration. Moreover weighted model updating performs better than its non-weighted counterpart. In this paper importance of only one mode has been studied and presented but the method can be easily extended to more number of modes and individual desirability functions.

Table 27.2 Updating results (taking relative importance index of both d ₄ and d ₉ as five)