Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Introduction

To make sense of the world around us, it is common in natural sciences to encode physical phenomena as scalar functions. Sometimes this is done directly, as when pressure measurements are recorded during physical experiments. Other times such functions are derived from the data, e.g., when the geometry of a shape is encoded in its distance function. It is rarely feasible to understand such functions directly: the data sets have become too large. Data analysis and visualization techniques, therefore, focus on extracting salient features that elucidate interesting behavior in the data. In this context, topological techniques are particularly attractive because they provide robust descriptors and help quantify the significance of detected patterns.

Broadly speaking, topological data analysis can be viewed as a two-step process. First, we compute a topological descriptor that summarizes the given data set. Then we use this descriptor to extract the relevant information. In this work we focus on a way to describe the connectivity of isosurfaces of a scalar function. Familiar in two dimensions as contours on a topographic map, isosurfaces consist of all points in the domain of a function that have the same value. Isosurface extraction [10, 13, 15] is a versatile technique in visualization and data analysis. One reason is that isosurfaces often have an immediate physical interpretation. For example, isosurfaces for certain charge densities in molecular simulations indicate boundaries of atoms or molecules; in combustion simulations, an isotherm (isosurface of temperature) can represent the location of the flame.

By varying the function value and computing the corresponding isosurfaces, it is possible to explore the behavior of the data. In this process, it is useful to know the values where interesting changes occur. A contour tree [2] is a standard tool to describe such changes. It is a graph whose nodes represent extrema and saddles where the number of connected components of the isosurface changes. Applications of the contour trees include speeding up isosurface extraction by identifying and extracting each one of their connected components by region growing [22]; manipulating individual connected components of “flexible isosurfaces”: for example, hiding a connected component that encloses relevant portions of the isosurface [3]; and segmenting data for volume rendering [24]. Arge and Revsbaek [1] consider the problem of I/O-efficient contour tree simplification. Contour trees are a special case of Reeb graphs [18], which have been used, among many other applications, for shape matching [9], tracking burning regions in combustion simulations [23], and identifying pore structures in porous media [21].

In the above two-step view of topological data analysis, the first step is performed once—there is only one contour tree, Morse–Smale complex, persistence diagram, etc. associated with a scalar function—but the second step, such as the extraction of a specific isosurface, depends on additional parameters. Therefore, a user usually repeats it over and over again (often in an interactive setting) as she explores the structure hidden in the input.

As the size of the available data grows, it is natural for researchers to turn to larger, parallel computers to meet their analysis needs. Most of the work on parallelization of topological computation focuses on the first step of the above process, on using multiple processors to compute a particular topological descriptor. Cole-McLaughlin and Pascucci [16] study parallelization of merge tree computation. Gyulassy et al. [7] study parallel computation of Morse–Smale complexes. Shivashankar et al. [19, 20] consider the same problem in shared memory (and on GPUs). Without focusing on the details of those procedures, we note that their outcome is always the same: a single, monolithic topological descriptor.Footnote 1 Such a representation makes it difficult to take advantage of the multiple available processors during the analysis step.

We suggest taking a holistic view and develop techniques that focus not only on how long it takes to compute a descriptor, but also on how efficiently we can analyze it in parallel. In an earlier work [14], we introduced a local–global representation of a merge tree. Explained in detail in Sect. 3, it combines local information (the immediate responsibility of a given processor) with extra global information that specifies where the local data fits globally. In this chapter, we show that having such representations of two merge trees serves as a local–global representation of a contour tree. Specifically, it provides enough information to answer queries about level sets of a function on a simply connected domain.

Background

Scalar functions. The central object of our study is a continuous scalar function, \(f: \mathbb{X} \rightarrow \mathbb{R}\). We assume its domain \(\mathbb{X}\) is simply connected, meaning any loop inside it can be contracted to a point. For computational purposes, we restrict our view further. We assume that \(\mathbb{X}\) is a simplicial complex, and function f is defined on its vertices and is linearly interpolated on the interiors of its simplices.

Given a scalar function \(f: \mathbb{X} \rightarrow \mathbb{R}\), we say that two points \(x,y \in \mathbb{X}\) are related, x ∼ y, if they belong to the same component of the level set \({f}^{-1}(f(x)) = {f}^{-1}(f(y))\). A Reeb graph is a quotient space of \(\mathbb{X}\) with respect to this relation, \(\mathbb{X}/\sim \); in other words, we construct a Reeb graph by continuously contracting the level set components of f to points. Intuitively, a Reeb graph tracks connectivity of level sets of the function—how they merge and split—as we vary the level set threshold. When the domain of our function is simply connected, the Reeb graph is a tree, called a contour tree [2].

If instead of the level sets of a function, we examine its sublevel sets, i.e. the sets of the form \({f}^{-1}(-\infty,a]\), we get a merge tree. Specifically, we say that two points x and y are related, if they have the same function value, and they belong to the same component of the sublevel set \({f}^{-1}(-\infty,f(x)] = {f}^{-1}(-\infty,f(y)]\). The quotient space of \(\mathbb{X}\) with respect to this relation is called a merge tree of the function. Intuitively, it tracks the evolution of sublevel sets of f as we vary the defining threshold parameter a. (Symmetrically,Footnote 2 we can consider the merge tree of − f, which tracks the evolution of the superlevel sets of f.) Below we use \(\mathbb{X}_{a} = {f}^{-1}(-\infty,a]\) and \({\mathbb{X}}^{a} = {f}^{-1}[a,\infty )\) to denote the sublevel and superlevel sets of f, respectively.

The full merge tree of the function f consists of the following nodes. Its leaves represent the minima of the function; its root is the global maximum. Its internal nodes correspond to those saddles of the function where multiple sublevel set components merge. It is often convenient to implicitly add each of the remaining vertices to the branch of the merge tree that represents the component of the sublevel set where the vertex first appears. Such additional vertices always have degree two in the merge tree.

Carr et al. [2] give a linear-time algorithm that combines merge trees of functions f and − f into a contour tree of function f.

Parallel setup. We assume that we have a collection \(\mathcal{U} =\{ U_{i}\}\) of sets that cover the domain of our function, \(\mathbb{X} = \cup \ \mathcal{U}\). We assume that \(\vert \mathcal{U}\vert = p\), and we are given p processors, each responsible for a single set in \(\mathcal{U}\). Specifically, we use the same indexing for processors as for the cover sets and say that processor P i is responsible for the set U i . We note that this formulation fits especially well with the so-called in situ analysis, where an external code decides how the input data is split among the different processors. In this case, the initial set U i is the union of the in situ blocks assigned to processor P i ; we make no assumptions about the topology of U i . The processors communicate by message passing.

Local–Global Representation

Let \(T_{\mathbb{X}}\) denote the full merge tree of the function f. In an earlier work [14], we introduced a local–global representation of a merge tree. Its key idea is the following. In a distributed setting, where the domain of the function is split among many processors, in addition to the information about the connectivity of the sublevel sets restricted to the local portion of the domain, one may record how these sublevel sets fit into the domain globally. Such global information creates only minor overhead; it can be computed efficiently in parallel; and, most importantly, it minimizes the need for communication during analysis. In this section, we review this representation.

Local–global merge tree. A local–global representation of the full tree \(T_{\mathbb{X}}\) is defined with respect to a subset \(U \subseteq \mathbb{X}\); we denote it by \(T_{\mathbb{X}}(U)\). For each vertex x ∈ U, we record all the sublevel set components that contain it. We represent each component by the minimum of the function inside it. At first, x belongs to the component of m 0 in \(\mathbb{X}_{f(x)}\). As we increase the threshold of the function, this component grows until eventually, at s 1, it merges into the component of m 1, which, in turn, merges into the component of m 2 at s 2, and so on.

Fig. 1
figure 1

Local–global representation of a vertex x. On the left, the lines represent the contours of the relevant saddles. On the right, the local–global subtree induced by x

Full size image

We get a sequence of minima and saddles, \(m_{0},s_{1},m_{1},s_{2},m_{2},\ldots,m_{n}\), with

$$\displaystyle{m_{n} < m_{n-1} <\ldots < m_{0} \leq x \leq s_{1} <\ldots < s_{n}.}$$

Setting s 0 = x for convenience, in the sublevel sets \(\mathbb{X}_{a}\), for a ∈ [s i , s i+1), x belongs to the component with the lowest minimum m i ; see Fig. 1. It is important to note that the minima m i and the saddles s i do not necessarily belong to U—hence, the “global” part of the representation. A reader familiar with the theory of persistent homology [6] will notice that the pairs (m i , s i+1) belong to the 0–dimensional persistence diagram of function f.

Naturally, all the relevant information appears in the merge tree \(T_{\mathbb{X}}\), which, after all, records all the components of all the sublevel sets of the function. We can think of the local–global representation of a vertex as a subtree of \(T_{\mathbb{X}}\) (to be precise, a subdivision of this representation is a subtree of \(T_{\mathbb{X}}\)). Accordingly, we can represent the local–global representations of multiple vertices compactly as a subtree of \(T_{\mathbb{X}}\), thus avoiding duplication of the minima whose components contain many of the local vertices. By definition, the local–global representation of \(T_{\mathbb{X}}\) with respect to U is the tree formed as the union of (subdivided) representations of all the vertices in U.

Construction. It is easy to extract a local–global representation from the full merge tree \(T_{\mathbb{X}}\). To do so, we perform a post-order traversal that identifies the branches of the tree that contain the vertices in U as well as the branches (with deeper minima) that they merge into.

An important contribution of [14] is an algorithm that computes the local–global representation in parallel without assembling the entire tree \(T_{\mathbb{X}}\) first. In log p iterations, the processors can interleave merging and sparsification steps to compute \(T_{\mathbb{X}}(U_{i})\) with respect to their local subsets of the domain. Another significant argument in favor of this representation is its size. In all our experiments, the local–global tree \(T_{\mathbb{X}}(U)\) is only slightly larger than the merge tree T U of f  | U , the function restricted to U. In other words, most of the global merging data is the same for the vertices in the local domain and, thus, creates only minor overhead; see Table 1.

Table 1 Maximum local and local–global tree sizes on any processor. In all cases, we count only the critical nodes in the trees. The time is listed as the time to compute the local tree plus the extra time to compute the local–global tree using our parallel algorithm [14]. Data from http://volvis.org: prone16 is a CT scan of an abdomen; vertebra16 is a rotational angiography scan of a head with an aneurysm; backpack16 is a CT scan of a backpack
Full size table

Analysis routine. To understand why the local–global representation is useful, consider the following problem. Given a threshold t, we would like to find the volume of the component of the sublevel set \(\mathbb{X}_{t}\) that contains a given point x. This component may be distributed across many processors, all but one of which know nothing about x. However, very little communication is actually required. The processor P i responsible for x, i.e., x ∈ U i , identifies the minimum m in the component of \(\mathbb{X}_{t}\) that contains x. It does this by first marching up from x towards the root of the tree \(T_{\mathbb{X}}(U_{i})\) until it finds a saddle s with f(s) ≤ t, but f(s′) > t for its parent s′. P i then finds the lowest minimum m in the subtree of s. (We will re-use this operation multiple times in the following section, so from now on we call it \( COMPONENT(x,t,T_{\mathbb{X}}(U_{i}))\).)

Processor P i broadcasts m (and t) to the rest of the processors. Each processor P j finds all the vertices in U j that fall into the component of \(\mathbb{X}_{t}\) that contains m. To do so, it traverses up from m until it identifies the last saddle s before the traversal crosses the threshold t. (Naturally, if m is not in \(T_{\mathbb{X}}(U_{j})\), P j has nothing to do.) The processor then counts the number of the local vertices in the subtree rooted at s. The processors combine their counts via a standard reduction.

The entire process has only two communication steps: the initial broadcast and the final reduction; the rest of the work is performed by the processors independently.

Contour Tree

Carr et al. [2] give an algorithm to combine merge trees of f and − f into a contour tree of f. However, since we are not trying to compute the full contour tree anyway, we do not need to combine the trees. Instead, we use the algorithm of [14] on each processor P i to compute the local–global merge trees \(T_{\mathbb{X}}^{+}(U_{i})\) and \(T_{\mathbb{X}}^{-}(U_{i})\) of the functions f and − f with respect to the cover set U i .

Chiang and Lu [4] use an implicit representation of a contour tree as two merge trees. It is, however, unclear how to use their scheme in our (distributed) setting, since they label edges of the contour tree by the edges of the merge trees. To do so in a distributed setting, one would have to assemble the entire merge tree on a single processor, an expensive operation we carefully avoid. Below, instead, we use extrema as level set labels.

In this section, we describe three problems efficiently solved using contour trees; one can interpret them as operations on “flexible isosurfaces” [3]. We explain how to solve these problems in the distributed setting using the local–global representation. In all cases, our emphasis is on minimizing the communication between processors.

Levelset Component

Imagine a user interactively exploring a data set. She picks a point x and wants to see the component of the level set f −1(f(x)) that contains x. Imagine that the data set is so large that it does not fit in the memory of a single processor; therefore, it is distributed across multiple compute nodes.

Fig. 2
figure 2

The level set f −1(f(x)) consists of three components. Bold line highlights the intersection of the component that contains point x with the cover set U. Of the five components of the level set inside U only four belong to this intersection

Full size image

Each processor must find the intersection of its local domain with the level set component that contains the given point x. As Fig. 2 illustrates, this intersection need not be connected. We solve this problem in three steps:

  1. 1.

    First, we identify the component of the level set that contains point x. Suppose that x ∈ U i . The processor P i identifies the component of the sublevel set \(\mathbb{X}_{f(x)}\) and the component of the superlevel set \({\mathbb{X}}^{f(x)}\) that contain x. As before, it identifies the component by its minimum (or, symmetrically, maximum), which it finds by the traversals of the subtrees rooted at x, \( COMPONENT(x,f(x),T_{\mathbb{X}}^{+}(U_{i}))\) and \( COMPONENT(x,f(x),T_{\mathbb{X}}^{-}(U_{i}))\). We denote these extrema by min x and max x . Processor P i broadcasts this pair to the rest of the processors.

  2. 2.

    Each processor P j records all the local points in the subtree of \(T_{\mathbb{X}}^{+}(U_{j})\) at level f(x) that contains min x . We denote these points by \(\mathrm{Sub}_{x}(U_{j})\); they are exactly the vertices of the intersection of the set U j with the sublevel set component that contains x. Similarly, P j records all the points in the subtree of \(T_{\mathbb{X}}^{-}(U_{j})\) at level f(x) that contains max x as \(\mathrm{Sup}_{x}(U_{j})\). Naturally, if min x or max x do not belong to their respective trees, the sets \(\mathrm{Sub}_{x}(U_{j})\) or \(\mathrm{Sup}_{x}(U_{j})\) are empty.

  3. 3.

    A simple (brute-force) way to extract a level set is to filter all the maximal simplices of the domain detecting those that have both a vertex below the prescribed threshold f(x) and one above it. We modify this procedure and find all those maximal simplices in U j that contain a vertex in \(\mathrm{Sub}_{x}(U_{j})\) and a vertex in \(\mathrm{Sup}_{x}(U_{j})\). Every maximal simplex that has such a pair of vertices is not only intersected by the level set f −1(f(x)), but it intersects the component of this level set that contains x.

We note that the only required communication is the broadcast of the identification of the queried component, namely, the pair (min x , max x ). The rest of the procedure identifying the local contribution to a level set is carried out completely independently. Naturally, an extra fourth step is necessary to somehow collect the data, but its details depend on our specific goal. Computing total volume of the level set component requires a single reduction; compositing such a distributed level set for rendering is a well-studied topic in visualization [11, 12, 17].

Correctness. Why does the above procedure find on each processor P j the intersection of U j with the component of the level set f −1(f(x)) that contains x? The following theorem implies the answer.

Theorem 1.

If \(\mathbb{X}\) is simply connected, then a component of the sublevel set \(\mathbb{X}_{b}\) can intersect a component of the superlevel set \({\mathbb{X}}^{a}\) in at most one component of the interlevel set f −1 [a,b].

Proof.

Informally, the statement and the proof of the theorem are simple: if a component of \(\mathbb{X}_{b}\) intersected a component of \({\mathbb{X}}^{a}\) in two components of f −1[a, b], then we could take two paths from the first component to the second. The first path would lie entirely in \(\mathbb{X}_{b}\), while the second path would lie entirely in \({\mathbb{X}}^{a}\). Composed together these paths would form a non-contractible loop in \(\mathbb{X}\), contradicting the assumption that \(\mathbb{X}\) is simply connected.

To make this proof formal, we turn to the Mayer–Vietoris long exact sequence, a standard tool in algebraic topology. To proceed, we need the notion of homology, which we have not defined. Fortunately, we only need its very basic form. Using coefficients in a field, the 0–th homology group of a space Y, denoted by H 0(Y ), is a vector space spanned by the components of Y. Similarly, the first homology group, H 1(Y ), keeps track of 1–dimensional cycles. If \(\mathbb{X}\) is simply connected, its first homology group is 0, \(\mathsf{H}_{1}(\mathbb{X}) = 0\).

The necessary portion of the Mayer–Vietoris sequence has the following form:

$$\displaystyle{\ldots \rightarrow \mathsf{H}_{1}(\mathbb{X})\stackrel{{\partial }^{{\ast}}}{\rightarrow }\mathsf{H}_{ 0}({f}^{-1}[a,b])\stackrel{({i}^{{\ast}},{j}^{{\ast}})}{\longrightarrow }\mathsf{H}_{ 0}(\mathbb{X}_{b}) \oplus \mathsf{H}_{0}({\mathbb{X}}^{a}) \rightarrow \ldots }$$

The linear map ∂ ∗ is induced by the intersection of 1–dimensional cycles in \(\mathbb{X}\) with the interlevel set f −1[a, b]; the maps i ∗ and j ∗ are induced by the inclusions of the interlevel set into the respective sub- and super-level sets.

The Mayer–Vietoris sequence is exact, which, by definition, means that the image of the map ∂ ∗ is equal to the kernel of the map (i ∗, j ∗). Since \(\mathsf{H}_{1}(\mathbb{X}) = 0\), the image of ∂ ∗ is also 0. Therefore, the kernel of (i ∗, j ∗) is 0, meaning that the inclusion of components of f −1[a, b] into the components of \(\mathbb{X}_{b}\) and \({\mathbb{X}}^{a}\) is an injection. Were a component of \(\mathbb{X}_{b}\) to intersect a component of \({\mathbb{X}}^{a}\) in two components, the inclusion of these components back into \(\mathbb{X}_{b}\) and \({\mathbb{X}}^{a}\) would not be injective, i.e., we would get a contradiction. □ 

Let Lvl x denote the component of the level set f −1(f(x)) that contains x. We denote its intersection with U j by \(\mathrm{Lvl}_{x}(U_{j})\). The following corollary implies the correctness of our three-step algorithm. Recall that we assume that f is linearly interpolated on the interiors of the simplices.

Corollary 1.

A simplex σ ∈ U j has a vertex u in \(\mathrm{Sub}_{x}(U_{j})\) and a vertex v in \(\mathrm{Sup}_{x}(U_{j})\) if and only if the point y on the edge (u,v) with f(y) = f(x) belongs to \(\mathrm{Lvl}_{x}(U_{j})\) .

Proof.

Let \(a = b = f(x)\). Suppose u ∈ σ belongs to the component of x in \(\mathbb{X}_{b}\), and v ∈ σ belongs to the component of x in \({\mathbb{X}}^{a}\). Let y be the point on the edge (u, v) with f(y) = f(x) (such a point exists because the function is continuous; it is unique because the function is linearly interpolated). Point y also belongs to the components of x in \(\mathbb{X}_{b}\) and in \({\mathbb{X}}^{a}\). Since these two components can intersect in at most one component of f −1(f(x)), y belongs to the same component of the level set as x.

Conversely, if point y on the edge (u, v), with f(y) = f(x) and f(u) < f(v), belongs to \(\mathrm{Lvl}_{x}(U_{j})\), then y belongs to the boundaries of the components of \({\mathbb{X}}^{a}\) and \(\mathbb{X}_{b}\) that contain x. Since the function is linear on the edge (u, v), vertex u belongs to the component of \(\mathbb{X}_{b}\) that contains x and, therefore, to \(\mathrm{Sub}_{x}(U_{j})\). Similarly, vertex v belongs to the component of \({\mathbb{X}}^{a}\) that contains x and, therefore, to \(\mathrm{Sup}_{x}(U_{j})\). □ 

Remark 1.

We note that one cannot uniquely identify a branch of the contour tree of f by a minimum–maximum pair in the respective merge trees \(T_{\mathbb{X}}^{+}\) and \(T_{\mathbb{X}}^{-}\). However, what Theorem 1 and Corollary 1 imply is that, at a fixed level a, such a pair uniquely identifies a point on the contour tree.

Component labeling. A variation on the problem of finding a single component is the consistent assignment of labels to all components of a level set. For example, the user may want to decorate each component of a level set f −1(a) with a unique color.

To solve this problem, each processor P i extracts all the different components of the level set f −1(a) that intersect its local domain U i . It identifies each component as the intersection of components in the sub- and the super-level sets by finding the minimum in \(\mathbb{X}_{a}\) and the maximum in \({\mathbb{X}}^{a}\) that identify each component. As noted before (and as Fig. 2 illustrates), locally disconnected components may get the same identification.

There are multiple ways to assign consistent labels to the components. Perhaps the simplest approach—the one requiring no communication—is for each processor to simply hash its minimum–maximum pairs. The components get consistent values across all the processors (since the extrema pairs are global); with high probability, all the assigned values are unique.

Interlevel Set

Imagine that we are interested in a branch of the contour tree, or, more generally, a monotone path in the contour tree between two points x and y (we assume that such a path exists). Often such paths correspond to interesting features in the data [24].

Theorem 1 suggests that each point on this path is uniquely identified by a minimum–maximum pair as well as the function value. Assume f(x) < f(y). Processor P i responsible for point x, i.e., x ∈ U i , finds the local–global representation of x in the tree \(T_{\mathbb{X}}^{+}(U_{i})\). In other words, it finds all the minima m i x and saddles s i x that describe the components of the sublevel sets of the function that contain point x. Similarly, processor P j responsible for point y finds its local–global representation in the tree \(T_{\mathbb{X}}^{-}(U_{j})\), the maxima m i y and the saddles s i y. The two processors broadcast these sequences of critical points.

The two representations together uniquely identify each point on the path from x to y in the contour tree. Specifically, let z be a point on this path. Let a = f(z) and suppose that \(a \in [s_{i}^{x},s_{j}^{y}]\). The component of z in the level set f −1(a) is the unique intersection of the component of \(\mathbb{X}_{a}\) that contains the minimum m i x and of the component of \({\mathbb{X}}^{a}\) that contains the maximum m j y.

Having received the broadcasts from P i and P j , each processor identifies its local contribution to the path x–y. As before, all the processors compute independently, except for the initial broadcast and the final collective operation (for example, to compute the total volume of the feature).

Contour Tracking

Consider another problem. The user has extracted a level set f −1(s) for some threshold s. The software has identified its different components and highlighted them with distinct colors. Now the user would like to vary the threshold a little and extract a nearby level set f −1(t), with t > s. When visualizing it, we would like to preserve the colors of the different components as much as possible, to maintain consistency with the level set f −1(s).

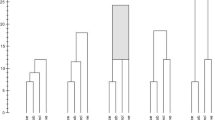
To solve this problem, we want to match the components of the two level sets. Specifically, we want to find which components of the lower and of the higher level sets map into the same components of the interlevel set f −1[s, t]. Put another way, we want to find the components of f −1(s) and f −1(t) connected in the contour tree restricted to the interlevel set f −1[s, t]; see Fig. 3.

Fig. 3
figure 3

An interlevel set of a contour tree (left). The graph of paired components (right)

Full size image

Each component x of the level set f −1(s) is identified by a minimum–maximum pair (min x , max x ). Similarly, each component y of the level set f −1(t) is identified by the pair (min y , max y ). Recall that Theorem 1 tells us that if a component of \(\mathbb{X}_{t}\) intersects a component of \({\mathbb{X}}^{s}\), then it does so in at most a single component of f −1[s, t]. Therefore, to check if the component x and the component y belong to the same component of f −1[s, t], it suffices to check if x belongs to the component of \(\mathbb{X}_{t}\) identified by min y and if y belongs to the component of \({\mathbb{X}}^{s}\) identified by max x . To be precise, we test the following equalities:

       \(\min _{y} = COMPONENT(x,t,T_{\mathbb{X}}^{+}(U_{{\ast}}))\);

       \(\max _{x} = COMPONENT(y,s,T_{\mathbb{X}}^{-}(U_{{\ast}}))\).

If both equalities are true, we know that the component of x in the superlevel set \({\mathbb{X}}^{s}\) intersects the component of y in the sublevel set \(\mathbb{X}_{t}\). Each processor can find all such intersections locally. The result is a bipartite graph on the components of the two level sets, which is constructed without any communication. As in Fig. 3, this graph may not be a matching, so an auxiliary rule is necessary to break the ties.

Experiments

To experiment with the local–global representation, we implemented the algorithm of Sect. 4.1. Given a local–global representation of merge trees \(T_{\mathbb{X}}^{-}\) and \(T_{\mathbb{X}}^{+}\), the processor that contains a given point x locates the minimum–maximum pair that identifies the connected component of x in its level set and broadcasts the pair to the rest of the processors. Each processor finds the intersections of the components of the sublevel and superlevel sets that contain point x with its local domain. If neither one of these intersections is empty, the processor iterates over every tetrahedron of the Freudenthal triangulation of its local domain U i . For each tetrahedron, we check whether it contains a point in the sublevel set component and another point in the superlevel set component. If it does, we find and record its intersection with the level set f −1(f(x)).

As a reference for the running times, we extract the same level sets and label their connected components using VisIt [5], a state-of-the-art visualization tool. VisIt uses the algorithm described by Harrison et al. [8] for the parallel connected component labeling. Although the two procedures are seemingly different—extracting a component of the level set that contains a given point versus labeling all the components of the level set—the comparison is not absurd. In VisIt, to extract a prescribed component, one must first label all the components and then filter out all but one of them. In other words, we measure a lower bound for the running time of this operation. At the same time, using local–global representation, labeling the components requires no communication, as Sect. 4.1 explains. Accordingly, specific component extraction is a more involved (and, therefore, interesting) procedure.

Figure 4 shows the times it takes to perform these procedures for the same data sets as Table 1. The clear trend is the steady decline of the running times, for the local–global representation, as we increase the number of processors.

Fig. 4
figure 4

Times to extract a level set component that contains a prescribed point using the local–global representation, and the times to label all the components of a level set in VisIt (Local–global representation times are taken as the average of ten runs each; VisIt times show the best of ten runs)

Full size image

Conclusion

We have presented the idea of local–global representations of contour trees and explained how it can be used for fast parallel analysis of the level sets of a function on a simply connected domain. These representations are small, only slightly larger than the merge trees of the local domain. Our earlier work [14] presents an efficient parallel algorithm to compute them.

Local–global representations scale down well as we increase the number of processors and, thus, really stand out when it comes to analysis. As our Sect. 4 explains, because they incorporate all the necessary global information, these compact representations let us perform variety of tasks with minimal communication.

The most logical directions for future work are extending our construction to the more general case of Reeb graphs and devising a seed point scheme, similar to the work of van Kreveld et al. [22], compatible with the local–global representation. For the latter, there is a natural map from the local to the local–global merge tree. By storing both trees and this map, we believe it is possible to improve the parallel algorithms for level set component extraction.