Contact Invariants in Floer Homology

Abstract

In a pair of seminal papers Peter Ozsváth and Zoltan Szabó defined a collection of homology groups associated to a 3-manifold they named Heegaard-Floer homologies. Soon after, they associated to a contact structure ξ on a 3-manifold, an element of its Heegaard-Floer homology, the contact invariant c(ξ). This invariant has been used to prove a plethora of results in contact topology of 3-manifolds. In this series of lectures we introduce and review some basic facts about Heegaard Floer Homology and its generalization to manifolds with boundary due to Andras Juhász, the Sutured Floer Homology. We use the open book decompositions in the case of closed manifolds, and partial open book decompositions in the case of contact manifolds with convex boundary to define contact invariants in both settings, and show some applications to fillability questions.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Heegaard Floer Homology—A Very Quick Introduction

In a pair of seminal papers [24, 25] Peter Ozsváth and Zoltan Szabó defined a collection of homology groups they named Heegaard-Floer homologies. To define these groups, they first associate to a 3-manifold M a Heegaard diagram, use it to define a chain complex, and then show that the associated homology groups do not depend on choices made.

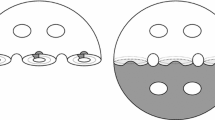
A Heegaard decomposition of a 3-manifold is a decomposition M=H ₁∪H ₂ into two handlebodies with Σ _g =∂H ₁=−∂H ₂=H ₁∩H ₂. We can define a genus g handlebody as a 3-manifold obtained by gluing g “handles” D ²×[0,1] to B ³ by attaching D ²×0 and D ²×1 along disjoint pairs of discs in S ² and smoothing. Every 3-manifold has a Heegaard decomposition. The easiest way to “visualize” one is to take a triangulation of M and take the neighborhood of the 1-skeleton as H ₁ and the complement as H ₂, It is clear that H ₁ is a handlebody—if we take a maximal tree T in the 1-skeleton and cut the neighborhood along the discs perpendicular to the edges not in T, we have a ball. The complement is a neighborhood of the dual 1-skeleton, so is a handlebody by the same argument.

Another way to obtain a Heegaard decomposition is to look at Morse functions on M. Assume that a Morse function f:M→[0,3] is self-indexing, i.e. that it has critical points of index i at critical values i=0,…,3. When there are g critical points of index 1 and 2, the mid-level surface Σ=f ⁻¹(3/2) has genus g. The descending discs $D_{p_{i}}$ of the index 2 critical points {p _i |i=1,…,g} and the ascending discs $D_{q_{i}}$ of the index 1 critical points {q _i |i=1,…,g} cut the handlebodies H ₁=f ⁻¹[3/2,3] and H ₂=f ⁻¹[0,3/2] into 3-balls (see Figure 1).

Fig. 1.

Self-indexing Morse function f:M→[0,3] with critical points of index 1 and their ascending discs in red, and critical points of index 2 and their descending discs in blue tracing the Heegaard diagram on $\varSigma = f^{-1}(\frac{3}{2})$

Collections of their boundary curves $\{\alpha_{i} | \alpha_{i} = \partial D_{p_{i}}\}$ (correspondingly $\{\beta_{i} |\beta_{i} = \partial D_{q_{i}}\}$) cut the Heegaard surface Σ _g into a 2g-times punctured sphere. The Heegaard diagram (Σ,{α _i },{β _i }) determines M—it can be obtained from Σ×[−1,1] by gluing compressing discs along α _i ×{−1} and along β _i ×{1}, thickening the discs and then finally gluing in two copies of B ³. It is a theorem of Reidemeister and Singer [28, 31] that any two Heegaard diagrams for the same 3-manifold can be related to each other by three moves: (1) stabilization, in which genus of Σ is increased by adding a one handle and a pair of dual curves α ₀,β ₀ is added to {α _i }, {β _i } (and destabilization), (2) isotopy of multicurves {α _i }, {β _i } and (3) handle slides, where {α ₁,α ₂,…} is replaced by {α ₁+α ₂,α ₂…}.

Heegaard Floer homology is a variant of Lagrangian Floer homology applied to the two Lagrangian submanifolds $\mathbb{T}_{\alpha}= \alpha_{1}\times\dots\times\alpha_{g}$ and $\mathbb{T}_{\beta}= \beta_{1}\times\dots\times\beta_{g}$ in the singular symplectic manifold Sym ^g(Σ _g ), the symmetric product of g copies of Σ _g . In [24, 25] Ozsváth and Szabó define several versions of this invariant. To describe the simplest of them, $\widehat{HF(M)}$ with $\mathbb {Z}/2$ coefficients, we define the chain group $\widehat{CF}(\varSigma,\alpha,\beta) = \text{Span}_{Z/2} \{\mathbf{x} | \mathbf{x} \in\mathbb{T}_{\alpha}\cap\mathbb{T}_{\beta}\}$ to be the free $\mathbb {Z}/2$-module generated by the points x=(x ₁,…,x _g ) in $\mathbb{T}_{\alpha}\cap\mathbb{T}_{\beta}$. Note that such a g-tuple x=(x ₁,…,x _g ) contains one point on each α _i and one point on each β _i curve.

Grading and the boundary maps are defined by considering pseudoholomorphic discs in Sym ^g(Σ _g ) with boundary on $\mathbb{T}_{\alpha}$ and $\mathbb{T}_{\beta}$. More precisely, we look at maps ϕ from the unit disc $D^{2}\subset \mathbb {C}$ to Sym ^g(Σ) that map −i↦x, i↦y, S ¹∩{Re z≥0} to $\mathbb{T}_{\alpha}$ and S ¹∩{Re z≤0} to $\mathbb{T}_{\beta}$. We denote the set of homotopy classes of such maps by π ₂(x,y). With a generic choice of almost complex structure on Sym ^g(Σ _g ), the space of pseudoholomorphic discs in the homotopy class of ϕ∈π ₂(x,y) is a smooth manifold $\mathcal{M}(\phi)$. These spaces carry a free $\mathbb {R}$ action by translation. To see this translation action we think of a biholomorphism between D ²∖{i,−i} and $[-1,1]\times \mathbb {R}$ taking ±i to ±∞ and translate in the $\mathbb {R}$ direction. The dimension of the space $\mathcal{M}(\phi)$ of holomorphic maps in the homotopy class of ϕ is calculated via the Maslov index μ(ϕ), which defines a relative grading on $\widehat{CF}(\varSigma,\alpha,\beta)$. When the dimension of $\mathcal{M}(\phi)$ is one, compactness arguments give finiteness of $\widehat{\mathcal{M}}_{\phi} = \mathcal{M}(\phi)/\mathbb {R}$, and we define the boundary operator on $\widehat{CF}(\varSigma,\alpha,\beta)$ by counting (mod 2) the number of points in the 0-dimensional space $\widehat{\mathcal{M}}_{\phi}$. If we fix a marked point z in the complement of the α and β curves, the function n _z (ϕ) on π ₂(x,y) is given by the intersection number of ϕ(D ²) with z×Sym ^g−1(Σ). If the image of ϕ misses z×Sym ^g−1(Σ) then n _z (ϕ)=0. The differential

$$\partial \mathbf{x} = \sum_{\mathbf{y}} \sum _{\substack{ \phi\in\pi_2( \mathbf{x}, \mathbf{y}) \\ \mu(\phi)=1, n_z(\phi)=0}} \#(\widehat{\mathcal{M}}_{\phi}) \mathbf{y} $$

has grading −1 and satisfies ∂∘∂=0.

To understand better what we are summing over, note that the map ϕ:D ²→Sym ^g(Σ) corresponds to a map $\widetilde{\phi}: \widetilde{D} \to\varSigma$ from a g-fold branched cover $\widetilde{D}$ of D ² to Σ (branching is over the preimage of the intersection of ϕ(D ²) with the diagonal in Sym ^g(Σ)). The two marked points i and −i on the boundary of D ² lift to 2g marked points on the boundary of $\widetilde{D}$, and under $\widetilde{\phi}$ these are mapped in alternating fashion to the coordinates x _i and y _i of x and y. The segments on the boundary of $\widetilde{D}$ between these 2g points are mapped in alternating fashion to segments on α and β curves connecting x _i and y _j . The image of the map $\widetilde{\phi}$ is a union of domains D _i in the complement of the α and β curves in Σ, and the Maslov index can be computed from this picture according to a combinatorial formula of Lipshitz [20]. Analysis of the moduli spaces corresponding to Maslov index 2 maps shows that the boundary map satisfies ∂ ²=0. The resulting homology is shown in [24] to be independent of the choice of a marked Heegaard diagram (Σ,α _i ,β _i ,z) for M, and therefore an invariant of the 3-manifold M.

Given a marked point z, each intersection point x=(x ₁,…,x _g ) in $\mathbb{T}_{\alpha}\cap \mathbb{T}_{\beta}$ defines a spin^c structure s(x) on the 3-manifold M determined by the Heegaard diagram. If there is a topological disc from x=(x ₁,…,x _g ) to y=(y ₁,…,y _g ) with boundary contained in the union of two tori $\mathbb{T}_{\alpha}$ and $\mathbb{T}_{\beta}$ the two spin^c structures s(x) and s(y) agree. Therefore $\widehat{CF}(\varSigma,\alpha,\beta,z)$ splits as the sum of $\widehat{CF} ((\varSigma,\alpha,\beta, z), \mathbf{s})$ and, as is clear from the definition, the boundary map preserves this splitting. Hence the complex, and the homology of the complex as well, split according to spin^c structures:

$$\widehat{HF}(M) = \sum_{\mathbf{s} \in \mathit{Spin}^c(M)} \widehat{HF}(M, \mathbf{s}) $$

Other versions of Heegaard Floer homology, HF ^∞ and HF ⁺, are defined by considering the free $\mathbb {Z}/2[U, U^{-1}]$ or $\mathbb {Z}/2[U]$ modules, respectively, generated by points in $\mathbb{T}_{\alpha}\cap \mathbb{T}_{\beta}$ and counting also the pseudoholomorphic curves that cross the marked point z in the differential, by recording n _z (ϕ):

$$\partial \mathbf{x} = \sum_{\mathbf{y}} \sum _{\substack{ \phi\in\pi_2( \mathbf{x}, \mathbf{y}) \\ \mu(\phi)=1}} \#(\widehat{\mathcal{M}}_{\phi}) U^{n_z(\phi)}\mathbf{y} $$

Defining orientations on the moduli spaces $\widehat{\mathcal{M}}_{\phi}$ makes it possible to count the number of points in the 0-dimensional moduli spaces $\widehat{\mathcal{M}}_{\phi}/\mathbb {R}$ with sign in order to work over $\mathbb {Z}$.

It is highly nontrivial to count the number of points in the moduli spaces $\widehat{\mathcal{M}}_{\phi}$ for a general ϕ, as that count depends on the choice of almost complex structure on Sym ^g(Σ). However, if the image of $\widetilde{\phi}$ is a topological disc connecting two intersection points x=(x ₁,x ₂,x ₃…x _g ) and y=(y ₁,x ₂,x ₃…x _g ) that differ in just one coordinate, called a bigon domain (see Figure 2), or between two intersection points x=(x ₁,x ₂,x ₃…x _g ) and y=(y ₁,y ₂,x ₃…x _g ) that differ in exactly two coordinates, called a rectangular domain (and constant maps on other components of the cover), there is a unique holomorphic disc in that homotopy class.

Fig. 2.

A bigon and a rectangular domain

This makes it possible to have a combinatorial calculation of the chain complex and the homology. Sarkar and Wang [30] described a method to produce “nice Heegaard diagrams”, i.e. diagrams for which all but one distinguished domain are bigons and rectangles and when the base point z is placed in that distinguished domain, the count involved in calculating $\widehat{HF}(M)$ becomes combinatorial. There are other combinatorial approaches to calculating the Heegaard Floer homology and a variant associated to a knot K⊂M, the knot Floer homology $\widetilde{HFK}(M,K)$, notably the gird diagrams and convenient diagrams ([22, 27] and many other sources).

2 Open Book Decompositions, Contact Structures and Convex Surfaces

Let S be a surface with boundary and let Aut(S,∂S)={h∈Diff(S,∂S)|h| _∂S =id}. Moding S×[0,1] out by the equivalence relation (x,1)∼ _h (h(x),0) produces a manifold M(S,h) with a torus boundary component for each component of ∂S. Moding out the boundary by further identifying (x,t)∼ _h (x,t′) for all t,t′∈[0,1] and x∈∂S reduces each torus boundary component to a knot in a closed 3 manifold M _(S,h)=S×[0,1]/∼ _h (Figure 3). Denote by B _(S,h)⊂M _(S,h) the image of ∂S×[0,1] under the quotient projection. The complement of a small neighborhood of B _(S,h) in M _(S,h) is diffeomorphic to M(S,h) and fibers over S ¹=[0,1]/0∼1. The link B _(S,h) is called the binding of the open book and the image of each S×{t} under the quotient projection is a page. The projection π:Int(S)×[0,1]/∼ _h →[0,1]/_0∼1 induces a bundle structure on the complement of the binding with the preimage of a point in t∈S ¹=[0,1]/_0∼1 being the interior of the page S _t .

Fig. 3.

A neighborhood of the binding in an open book decomposition

An open book decomposition for a 3-manifold M with page S, binding B and monodromy h∈Aut(S,∂S) is a projection p:M∖B→S ¹ and a homeomorphism Φ:(M,B)→(M _(S,h),B _(S,h)) that commutes with projections p and π. We say in this case that (S,h) is a formal open book decomposition for (M,B,p).

It is a theorem of Alexander that every 3-manifold has an open book decomposition. Different open book decompositions of the same manifold are related by sequences of positive/negative stabilizations, where stabilization changes S by adding a 1-handle to S and changes h by composing it with a positive/negative Dehn twist about a curve γ dual to the handle. More precisely, we attach a handle H=[0,1]×[−ϵ,ϵ] to S along {0,1}×[−ϵ,ϵ] to obtain S′ and let h∪id be extension of h by identity on [0,1]×[−ϵ,ϵ]. Let γ be any simple closed curve in S′ that intersects the co-core 1/2×[−ϵ,ϵ] of the handle H once, and let R _γ ($R_{\gamma}^{-1}$) be the right (left) handed Dehn twist. If $h' = R_{\gamma}^{\pm1} \circ( h \cup \mathit{id})$ we say that (S′,h′) is a positive (negative) stabilization of (S,h). It is not hard to see that if (S′,h′) is a positive (negative) stabilization of (S,h), and (S,h) is a formal open book decomposition of (M,B,p), then (S′,h′) gives a formal open book decomposition of (M,B′,p′) where the binding B′ is obtained by a Murasugi sum along γ of the binding B with a positive (negative) Hopf link. For a nice description see [29].

Open book decompositions of 3-manifolds are intimately related to contact topology. A contact structure ξ on a 3-manifold M is a 2-plane filed which is the kernel of a nondegenerate 1-form α, the contact form. (Nondegeneracy means that α∧dα=d vol.) The contact structure ξ is said to be supported by the open book decomposition (M,B,p) if:

• 1. B is transverse to ξ,

• 2. there is a contact 1-form α for which dα induces a symplectic form on each fiber S _t =p ⁻¹(t) of p:M∖B→S ¹,

• 3. the orientation on B given by α is the same as the boundary orientation induced from S _t oriented by the symplectic structure induced by dα.

Thurston and Winkelnkemper [32] showed that any open book decomposition (S,h) of M supports a contact structure ξ by constructing a contact form ξ _(S,h) on M _(S,h) with these properties. Torisu [33] and Giroux [10] proved that the converse is true, namely that every contact manifold is supported by (has a compatible) open book decomposition. Giroux established the following correspondence:

Theorem 2.1

(Giroux)

Any contact structure (M,ξ) on a closed 3-manifold M is supported by an open book decomposition (S,h). Moreover, any two open book decompositions (S,h) and (S′,h′) which support the same contact structure (M,ξ) are equivalent under a sequence of positive stabilizations/destabilizations.

To give an indication of how a compatible open book decomposition can be found for a given a contact manifold (M,ξ), we need to first talk about convex decomposition methods in contact topology. In the early 90’s Emanuel Giroux introduced an important tool in contact topology—convex surfaces. A vector field $\overrightarrow{v}$ in a contact manifold (M,ξ) is called contact if its flow preserves ξ. A surface S⊂M is called convex if there exists a contact vector field $\overrightarrow{v}$ transverse to S. Note that a convex surface S can be transverse to many different contact vector fields. To a convex surface S and a contact vector field $\overrightarrow{v}$ transverse to S one can associate

$$\varGamma_S = \bigl\{ x\in S | \overrightarrow{v}(x)\in \xi(x)\bigr\} $$

its dividing set (see Figure 4). It is not hard to show that Γ _S is a smooth multicurve, and that the isotopy class of Γ _S is independent of $\overrightarrow{v}$.

Fig. 4.

Convex surface and its characteristic foliation and dividing set

If g( , ) is a Riemannian metric on M and we denote by $\overrightarrow{n}_{\xi}$ a normal vector field to ξ, the dividing set on a convex surface S⊂M determined by a contact vector field $\overrightarrow{v}(p)$ can be described as $\varGamma_{S} = \{p\in S \mid g(\overrightarrow{v}(p),\overrightarrow{n}_{\xi}(p))=0\}$. The dividing set Γ clearly divides the convex surface S into two regions R ₊(S) and R ₋(S) where $R_{+}= \{p\in S\mid g(\overrightarrow{v}(p), \overrightarrow{n}_{\xi}(p))\geq0\}$ and $R_{-}= \{p\in S \mid g(\overrightarrow{v}(p), \overrightarrow{n}_{\xi }(p))\leq0\}$. It is not hard to see that, if S is a closed convex surface in the contact manifold (M,ξ), the contact class of ξ evaluates on S as χ(ξ)[S]=χ(R ₊(S))−χ(R ₋(S)).

A knot is Legendrian if it is everywhere tangent to contact planes. Contact planes (cooriented by $\overrightarrow{n}_{\xi}$) induce, on a surface S oriented by $\overrightarrow{v}$, an oriented singular foliation $\mathcal{F}$ by Legendrian curves called the characteristic foliation. The regions R _± correspond to “source” and “sink” regions in this picture. Legendrian curves of the foliation intersect the dividing set transversally as in Figure 4. If a convex surface S has Legendrian boundary, then the dividing set intersects the boundary in an even number of points 2n, and n describes the number of twists that the contact plane makes relative to the framing for the Legendrian boundary curve coming from the convex surface.

We can decompose a contact manifold (M,ξ) by cutting it along properly embedded convex surfaces Σ. For a gentler introduction see [12]. When (M,ξ) is a contact manifold with boundary we assume that the boundary ∂M is convex, and that the convex cutting surface Σ has Legendrian boundary L=∂Σ⊂S. A standard neighborhood theorem says that if L intersects the dividing set Γ _Σ geometrically 2n times, there is a neighborhood N _ε (L) of L in M and local coordinates (x,y,z) on it so that N _ε (L)={(x,y,z)|x ²+y ²<ε,x≤0} in $\mathbb {R}^{2} \times(\mathbb {R}/\mathbb {Z})$ (see Figure 5).

Fig. 5.

Standard neighborhood of a Legendrian curve at the intersection of two perpendicular convex surfaces

Here L lies on the z axis, the set of points with x=0 corresponds to an annular neighborhood of L in Σ, the set of points with y=0 corresponds to a neighborhood of L in S, and the contact structure ξ is given as the kernel of α=sin(2πnz)dx+cos(2πnz)dy, n≠0. If we choose the contact vector fields for S and Σ to be $v_{S}=\frac{\partial}{\partial x}$ and $v_{\varSigma} = \frac{\partial}{\partial y}$ it is not hard to calculate that the dividing sets are $\varGamma_{S} = \{(0, y, \frac{k}{2n})| 0 \le k < 2n\}$ and $\varGamma_{\varSigma} = \{(x, 0, \frac{1 + 2k}{4n})| 0 \le k < 2n\}$.

After cutting M along Σ and rounding corners to obtain M′, transverse contact vector fields on the new boundary components of ∂M′=S′ can be chosen to be $v_{S}=a\frac{\partial}{\partial x} + b\frac{\partial}{\partial y}$ so that they rotate between $\frac{\partial}{\partial x}$ and $\frac{\partial}{\partial y}$. A simple calculation shows that the new dividing set on ∂M′ is obtained by the “turn to the right” method illustrated in Figure 6.

Fig. 6.

Smoothing of the dividing set after cutting along convex surface Σ and rounding corners

Giroux and Honda showed that isotoping a convex surface S through a contact manifold preserves the isotopy class of the dividing set except for at finitely many levels of the isotopy. Honda described how at these levels the product contact structure changes by adding a “bypass” to the product structure on S×I, i.e. engulfing a “half overtwisted disc” B bounded by a Legendrian arc α in S connecting three dividing curves (possibly not globally different), and an Legendrian arc β along which the contact planes coincide with the tangent planes of B. Thickening the bypass disc to B×[−ε,ε] attached along α×[−ε,ε], looking at the dividing set and rounding to obtain S′ we see that the change in the dividing set after adding a bypass is as pictured in Figure 7.

Fig. 7.

Adding a bypass

To describe briefly how to find an open book compatible with a given contact structure ξ on M we start with a triangulation of M that is fine enough so that each 3-simplex is contained in a standard contact chart for ξ. The 1-skeleton can then be perturbed to be Legendrian in such a way that the relative twisting of the contact planes along the boundaries of the discs in the 2-skeleton is such that these discs can be made convex with the given Legendrian boundary. By adding extra pieces to the 1-skeleton to divide the discs in the 2-skeleton in such a way that each contains exactly one arc in its dividing set we can achieve the following:

• (1) There is a handlebody decomposition of the 3-manifold into H ₁=ν(M ⁽¹⁾), the neighborhood of the 1-skeleton, and the complementary handlebody $H_{2}= \nu(\bar{M}^{(1)})$ which is the nighbourhood of the dual 1-skeleton.

• (2) The common boundary Σ is a convex surface.

• (3) The contact handlebodies H ₁ and H ₂ with convex boundary are disc decomposable, i.e. there is a family of compressing discs with Legendrian boundary such that the boundary of each disc intersects the dividing set in exactly two points.

Note that the convex discs in (3) are just small discs transverse to the 1-cells of the 1-skeleton in H ₁ and the 2-cells of the subdivided complex for H ₂. By cutting along the compressing discs until we obtain B ³, we can see that contact handlebodies H _i are contactomorphic to product contact manifolds R×I where R is homeomorphic to Σ ₊ (and Σ ₋), as we think of obtaining H _i by gluing contact 1-handles onto a standard ball with convex boundary S ² and dividing set S ¹. The simplest case, of a genus one surface with two parallel longitudinal dividing curves, is shown in Figure 8.

Fig. 8.

Cutting a genus one handlebody along a convex compressing disc

Note that when we consider Σ as the boundary of H ₂ the roles of Σ ₊ and Σ ₋ are reversed in comparison to what they are when we consider Σ as the boundary of H ₁ (due to the change of orientation on Σ). We identify H ₁ with R×[0,1/2] in such a way that Σ ₋ corresponds to R×{0} and Σ ₊ corresponds to R×{1/2}, and identify H ₂ with R×[1/2,1] in such a way that Σ ₋ corresponds to R×{1/2} and Σ ₊ to R×{1}. Then the identification of R×{0} and R×{1} coming form the way H ₁ and H ₂ are glued inside M defines the monodromy map h:R→R which realizes M as corresponding to the open book (R,h), and the open book inside M is compatible with ξ (see Figure 9).

Fig. 9.

Gluing disc decomposable contact structures on H ₁ and H ₂

We say that a contact structure ξ on a 3-manifold M is overtwisted if there is an embedded D ² in M such that the tangent plane T _P D ² and the contact plane ξ _P agree at all points P∈∂D ². If ξ is not overtwisted we say it is tight. There are familiar examples of tight contact structures. It is a theorem of Bennequin [4] that the standard contact structure on $\mathbb {R}^{3}$ is tight. Giroux showed that a product neighborhood of a convex surface is tight if and only if it has no contractible dividing curve, or is S ² with Γ=S ¹.

A theorem of Eliashberg [5] says that overtwisted contact structures are classified up to isotopy through contactomorphisms (contact isotopy) by the homotopy class of their plane fields, i.e. two overtwisted contact structures that are homotopic as plane fields are isotopic through a family of contact structures. This is not true in the case of tight contact structures, which are more closely related to the finer topology of the manifold. A central question in contact topology on 3-manifolds is to construct, recognize and classify tight contact structures on a given M ³.

There is a rich source of tight examples; the fillable contact structures. A contact manifold (M,ξ) is Stein fillable if there is a compact complex Stein manifold W with convex boundary such that M=∂W and contact planes are complex lines in TM. (M,ξ) is strongly symplectically fillable if M is the boundary of a symplectic manifold (W,ω) which looks like a Stein manifold near the boundary. Finally, (M,ξ) is weakly symplectically fillable if M is boundary of a symplectic manifold (W,ω) and ω| _ξ ≥0. It is a theorem of Gromov and Eliashberg that fillable contact structures are tight [7, 11].

To describe tightness in the framework of open book decompositions we use the notion of “right-veering” homeomorphisms [13]. We say that a homeomorphism h∈Aut(S,∂S) is right-veering if every properly embedded oriented arc α in S is mapped “to the right” of α as in Figure 10. For two properly embedded arcs α and β with the same initial point α(0)=β(0) which are isotoped rel boundary to intersect transversally in a minimal number of points, we say that β is to the right of α if the tangent vectors {β′(0),α′(0)} define the orientation of S.

Fig. 10.

The image arc h(α) is to the right of α

Theorem 2.2

(Honda-Kazez-Matić)

A contact 3-manifold (M,ξ) is tight if and only if all of its adapted open book decompositions have right-veering monodromy.

Right-veering diffeomorphisms of S form a monoid Veer(S,∂S) in Aut(S,∂S). Monodromies in the submonoid Dehn ⁺(S,∂S)⊂Veer(S,∂S) consisting of diffeomorphisms that are products of positive Dehn twists give rise to Stein fillable structures by the work of Eliashberg [6]. That every Stein fillable structure has a monodromy in Dehn ⁺(S,∂S) is a theorem by Loi-Piergallini and Akbulut-Ozbagci [1, 21]. John Baldwin [3] and Baker, Etnyre and Van-Horn Morris [2] have shown that there are open books for Stein fillable contact structures that are not in Dehn ⁺(S,∂S). They have also shown that the open book monodromies corresponding to Stein, strongly and weekly fillable contact structures form monoids. The natural inclusions Dehn ⁺(S,∂S)⊆̷Stein(S,∂S)⊆̷Strong(S,∂S)⊆̷Week(S,∂S)⊆̷Tight(S,∂S)⊆̷Veer(S,∂S) are all proper according to work of, in order, Baker-Etnyre-VanHorn Morris and independently Wand, Ghiggini, Eliashberg, Ghiggini and Honda-Kazez-Matić and Goodman. However, it is not clear that Tight(S,∂S) is a monoid, or how to describe the tightness in terms of one open book. It is easy to show that any open book can be stabilized to be right veering, hence there are right veering open books supporting overtwisted contact structures. Even if we know that an open book has right veering monodromy and that it is not the result of a stabilization, this does not guarantee tightness, as first shown by Lekili [19].

3 From Open Books to Contact Invariants

Ozsváth and Szabó [26] used the one-to-one correspondence between equivalence classes of open books for M under positive stabilization and isotopy classes of contact structures on M to define an invariant c(ξ) of contact structures that lives in the Heegaard Floer homology of −M. To do this they associated to an open book decomposition (M,B,p) compatible with ξ the fibered manifold M ₀(B) obtained by performing 0-framed surgery with respect to the page framing on the binding B. Heegaard Floer homology for a fibered 3-manifold is special—it is one dimensional in the spin^c structure corresponding to the fibration. Ozsváth and Szabó defined c(ξ) to be the image of the generator of this group under the map induced by the cobordism defined by the 0-handle attachment from $\widehat{HF}(-M_{0}(B))$ to $\widehat{HF}(-M)$. It has the property that c(ξ)=0 if ξ is overtwisted, and that c(ξ)≠0 when ξ is fillable.

To see a concrete generator of c(ξ) we will use the open book decomposition to construct a Heegaard diagram in which this generator sits in a distinguished way. An open book decomposition adapted to ξ gives rise to a Heegaard decomposition into two handlebodies $H_{1}=S \times[0,1/2] / _{\sim_{h}}$ and $H_{2}=S \times[1/2,1] / _{\sim_{h}}$.

A basis of arcs for the surface with boundary S is a collection of properly embedded arcs {a _i |i=1,…,r} that cuts the surface into a disc, S∖(⋃a _i )=D ². Given a basis of arcs we can construct the family of compressing discs $D_{a_{i}}=a_{i}\times[0,1/2]$ for H ₁ which cut H ₁ into a ball. We perturb the a _i slightly to obtain a basis of arcs b _i such that each b _i intersects a _i transversely at exactly one point (positively) and consider discs $D_{b_{i}}=b_{i}\times[1/2,1]$ which are a set of compressing discs that cut H ₂ down to a ball.

Taking the boundary curves of these discs $\alpha_{i}=\partial(D_{a_{i}})$ and $\beta_{i}=\partial(D_{b_{i}})$ and looking at them as curves in the separating surface Σ=S×{1/2}∪−S×{0}=S×{1/2}∪−S×{1} (here Σ is the common boundary of H ₁ and H ₂, and S×{1} is identified with S×{0} via the monodromy h), we obtain a Heegaard diagram (Σ,α _i ,β _i ,z) (see Figure 11). There is a distinguished generator x=(x ₁,…,x _i ,…) for $\widehat{CF}(\varSigma, \alpha_{i},\beta_{i}, z)$ that is contained in Σ=S×{1/2} where x _i =α _i ∩β _i . If we choose the marked point z to lie in Σ=S×{1/2} and outside the thin strips bounded by α _i and β _i curves, it is easy to see that x is a cycle, and in fact:

Fig. 11.

The Heegaard decomposition and the diagram determined by a basis of arcs for the page of an open book decomposition

Theorem 3.1

[14]

The generator x=(x ₁,x ₂,…,x _r ) is a cycle in $\widehat{CF}(\varSigma, \beta_{i}, \alpha_{1},z)$ and its homology class is the Ozsváth-Szabó contact class, $\mathbf{x}=c(\xi)\in \widehat{HF}(-M)$.

In particular, for a different open book decomposition compatible with the same contact structure ξ, we get the same class $c(\xi)\in \widehat{HF}(-M)$. Note that we needed to switch the role of α and β curves, hence the orientation of M in order for x to be a cycle.

From this description it is easy to see that for an overtwisted contact structure c(ξ)=0. Specifically, an overtwisted contact structure has a compatible open book decomposition and a basis of arcs such that the holonomy takes at least one of the arcs, we can name it α ₁, to the left of itself. Then in the corresponding Heegaard diagram, there is a bigon connecting y=(y ₁,x ₂,…,x _r ) to x=(x ₁,x ₂,…,x _r ), which gives ∂ y=x, hence x=0 in homology. When looking at the Figure 12, it might seem that α ₁ is in fact mapped to the right, but that is an artifact of reversal of orientation on −S×{0}.

Fig. 12.

The Heegaard diagram determined by a basis of arcs and the contact element x=(x ₁,x ₂)

Given that c(ξ)=0 for overtwisted contact structure, and that c(ξ)≠0 when ξ is fillable (by a theorem of Gromov and Eliashberg [7, 11]), it was a natural question to ask whether c(ξ)≠0 is a characterization of tightness. Ghiggini [8] showed that there are tight contact manifolds with c(ξ)=0. The examples he found contain Giroux torsion, i.e. a contact embedding of $T^{2} \times[0,1] =\mathbb{R}^{2}/\mathbb{Z}^{2} \times[0,1]$ with contact structure given by ξ _tor =ker(cos(2πz)dx−sin(2πz)dy).

The question then was reformulated to ask if c(ξ)=0 is equivalent to the requirement that ξ contains Giroux torsion. The answer was obtained with the use of a contact invariant defined for contact manifolds with boundary, the sutured contact invariant, which we will discuss in the next section. On one hand, the invariant is used in [9] to prove that any contact manifold containing Giroux torsion has c(ξ)=0. On the other hand, it is used in [16] to show that for a general surface with boundary S there are S ¹-invariant contact structures on S×S ¹ generalizing Giroux torsion that have the property that any contact manifold that contains them has c(ξ)=0, and is hence not fillable.

4 Sutured Manifolds and Partial Open Books

When a 3-manifold M has nonempty boundary, we will study contact structures on M for which the boundary ∂M is a convex surface with a prescribed dividing set Γ⊂∂M dividing ∂M into R ₊ and R ₋ regions. A pair (M,Γ) of a manifold and a dividing set Γ on the boundary (which divides every boundary component) is called a sutured manifold. Sutured manifolds were first defined by Gabai for use in the study of foliations. When χ(R ₊)=χ(R ₋) we call the sutured manifold (M,Γ) balanced (Figure 13).

Fig. 13.

A balanced sutured manifold

We say that the balanced sutured manifold (M,Γ) carries a compatible contact structure ξ with convex boundary if the suture Γ agrees with the dividing set Γ _ξ on the boundary. Recall that on a closed convex surface Σ in a contact manifold (M,ξ) the contact class evaluates as c(ξ)[Σ]=χ(R ₊(Σ))−χ(R ₋(Σ)). Since ∂M=Σ is zero in homology, c(ξ)[Σ]=0 and χ(R ₊(Σ))=χ(R ₋(Σ)). Hence a sutured manifold that supports a contact structure with convex boundary is balanced.

We want to define an analogue of a Heegaard diagram in the case of a manifold with boundary, and sutured manifolds provide the right framework. A sutured Heegaard diagram consists of a surface with boundary Σ of genus g and two families of attaching curves {α _i |i=1,…,k} and {β _i |i=1,…,l} with k,l≤g. When we attach 2-handles to Σ×[0,1] along those curves we will build a 3-manifold with boundary. It will have a suture $\varGamma= \partial\varSigma\times\{\frac{1}{2}\}$ which divides the boundary into two regions: R ₊ which is obtained by compressing Σ×{1} along α _i curves (cutting open along α and filling in by attaching pairs of discs), and R ₋ obtained by compressing Σ×{0} along β _i curves. On the 3-manifold with boundary we obtain this way there is clearly a Morse function picture, analogous to the closed case, that has the centers of the attached 2-handles as critical points (see Figure 14). Note that in the case of a closed manifold and a classical Heegaard diagram of genus g and α and β curves cutting it to a 2g times punctured sphere, adding 2-handles to the Heegaard surface along the α and β curves produces first a manifold with two S ² boundary components to which, in the end, we add two 3-handles. A way to build a closed manifold from the sutured manifold is to attach enough handles until we obtain a union of sutured spheres on the boundary, one for each of the boundary components of the Heegaard surface, and then add 3-balls. It is easy to see that in the sutured Heegaard diagram where k=l, i.e. when we attach the same number of compressing discs to Σ×{1} as to Σ×{0}, the sutured manifold we build is balanced.

Fig. 14.

A Morse function picture of a balanced sutured manifold

Andras Juhasz [17] defined Sutured Floer Homology for a balanced sutured manifold in analogy to the Heegaard Floer Homology $\widehat{HF}$. As is done in the case of a closed manifold, he associated to a balanced Heegaard diagram (Σ,α _i ,β _i ) a chain complex generated by the intersection points of the two tori $\mathbb{T}_{\alpha}= \alpha_{1}\times\dots\times\alpha_{k}$ and $\mathbb{T}_{\beta}= \beta_{1}\times\dots\times\beta_{k}$ in Sym ^k(Σ) and defined the boundary operator by counting holomorphic disc. The role played by the base-point z in the closed case is played by the boundary ∂Σ, namely we consider only domains that do not go out to the boundary. The homology of this complex is denoted by SFH(M,Γ) and Juhasz proved it does not depend on the choice of the sutured Heegaard diagram for (M,Γ).

We want to associate to a contact structure ξ with convex boundary supported by (M,Γ) an element in the Sutured Heegaard Floer homology SFH(−M,−Γ). The change of orientation is parallel to the fact that contact invariant in the closed case lives in $\widehat {HF} (-M)$. In order to define c(ξ)∈SFH(−M,−Γ), we first need to define an analogue of open book decompositions for manifolds with sutured boundary.

Definition 4.1

A partial open book (S,P,h) consists of the following data: a compact, oriented surface S with nonempty boundary, and a “partial” monodromy map h:P→S defined on a subset P⊂S such that ∂P∩∂S≠0 and h| _∂P∩∂S =id.

To obtain a sutured manifold associated to a partial open book decomposition (S,P,h) define an equivalence relation ∼ _h on S×[0,1] by setting (x,1)∼ _h (h(x),0) for x∈P, and (x,t)∼ _h (x,t′) for t,t′∈[0,1] x∈∂S (see Figure 15). It is not difficult to see that the glued-up space can be smoothed out to a manifold with boundary, where R ₊=(S∖P)×{1} and R ₋=(S∖h(P))×{0} and the dividing set is Γ=∂(S∖int P).

Fig. 15.

Gluing to obtain a partial open book

To motivate this definition let us think about the construction of the open book compatible with a contact structure ξ in the closed case that we described in Section 2. We will adapt this construction to the case of balanced sutured (M,Γ). We again take a cell decomposition of M by cells small enough so that the contact structure on them is standard, make the 1-skeleton Legendrian and 2-cells convex (keeping the boundary fixed), and this time consider a Legendrian 1-complex L that consists of the portion of the Legendrian 1-skeleton that is in the interior of the manifold together with enough of the Legendrian 1-simplices that come out and meet the boundary in points on the dividing set to meet every component of it in at least 2 points. If we take the cell decomposition to be fine enough, we can ensure that the neighborhood of L is a disc-decomposable contact handlebody H ₂ with convex boundary, and that its complement H ₁ is also a disc-decomposable handlebody [15].

The boundary of H ₂=ν(L) consists of a “tube region” P and some discs that are part of the boundary and intersect the dividing set Γ in one segment each (see Figure 16). The tube P is divided by its dividing set into two regions P _± and the boundary of the complement H ₁ consists of S ₊=R ₊∪P ₊ and S ₋=R ₋∪P ₋ (we are being a bit sloppy and identifying R _± with R _±∖∂(ν(L)). The choice of a fine enough decomposition ensures that the two contact handlebodies H ₁ and H ₂ are disc-decomposable and we can identify H ₁=S×[0,1/2] and H ₂=P×[1/2,1], where S=R ₊∪P ₊=R ₋∪P ₋ (see Figure 17). For simplicity of notation we ignore in this picture the fact that in the product handlebodies we mod out by (x,t)∼(x,t′) to get to the real disc decomposable handlebody picture. By looking at the gluing of H ₂ to H ₁ inside M we see that we can think of M as obtained first by gluing along P ₋ to obtain the glued up S×[0,1/2]∪ _P×{1/2} P×[1/2,1] as homeomorphic to S×[0,1], and of the final gluing along P ₊ as gluing by the partial monodromy (after we identify S×[0,1/2]∪ _P×{1/2} P×[1/2,1] with S×[0,1] in an obvious way).

Fig. 16.

Neighborhood of the Legendrian skeleton L near the boundary

Fig. 17.

The partial open book and the handlebody decomposition

We now want to associate a sutured Heegaard diagram to this decomposition. Define a basis of arcs in P to be a collection {a _i |i=1,…,k} of disjoint properly embedded arcs in P with boundary on ∂P∩∂S such that S∖⋃{a _i } _i=1,…,k deformation retracts onto R ₊=S−P. In our example in Figures 17 and 18, the basis consists of just one arc a ₁. Let b _i , i=1,…,k, be pushoffs of a _i in the direction of ∂S so that a _i and b _i intersect exactly once at a point x _i . It is not hard to see that if we set $\varSigma=(S\times\{0\})\cup(P\times\{{1\over2}\})$, $\alpha_{i}=\partial (a_{i}\times[0,{1\over2}])$ and $\beta_{i}= (b_{i}\times\{{1\over 2}\})\cup(h(b_{i})\times\{0\})$, then (Σ,β,α) is a Heegaard diagram for (−M,−Γ). See Figure 19.

Fig. 18.

The partial open book and the Heegaard diagram

Fig. 19.

The Heegaard diagram determined by a basis of arcs a ₁ and the contact element x=(x ₁)

We can again look at the special generator x=(x ₁,…,x _i ,…) for SFH(Σ,β,α) and, as in the case of the closed manifold, x=[(x ₁,…,x _k )] is a cycle. It is shown in [15] that it defines a contact invariant.

Theorem 4.2

The point x=[(x ₁,…,x _k )] is independent of choices up to ±1 and generates the sutured contact invariant c(ξ)∈SFH(−M,−Γ).

A concrete example we will look at here is a partial open book decomposition for a neighborhood of an overtwisted disc. The corresponding sutured manifold is (B ³,Γ) with the dividing set consisting of 3 parallel curves. It is enough to take just one segment connecting two nonadjacent components of the dividing set for the Legendrian 1-complex L, to get the complement to be a disc-decomposable handlebody. The segment comprising L is the core of the cylinder in Figure 20, while P _± are two halves of the cylinder, and the basis of arcs consists of a single arc a on P. In the left-hand diagram of Figure 20 arc a is shown on P×{1/2}⊂S×{1/2} (thus might more properly be denoted by a×{1/2}). Isotoping a (rel endpoints) through N(L) where we use the homeomorphism N(L)=P×[1/2,1] produces, by the definition of the monodromy h, the arc h(a)×{0}⊂S×{0}. Finally pushing h(a)×{0} (rel endpoints) through the fibration M−N(L) that identifies M−N(L)=S×[0,1/2] results in h(a)×{1/2}⊂S×{1/2}, and this is denoted simply by h(a). The right side of the figure shows a and h(a) in S=S×{1/2}.

Fig. 20.

A partial open book decomposition and a Heegaard diagram for a neighborhood of an overtwisted disc

5 Gluing Theorem for Sutured Manifolds

In [13] we work to understand the effect of cutting and gluing of contact manifolds along convex surfaces in sutured manifolds in the context of the contact invariant. We say that one balanced sutured manifold (M′,Γ′) is a sutured submanifold of another balanced sutured manifold (M,Γ) if M′ is a submanifold with boundary of M and M′⊂int(M). A contact structure ξ defined on M⊂int(M′) is compatible with the sutured manifold structures of M and M′ if the dividing set of ξ on the boundary of M−int(M′) is Γ∪−Γ′. In this section we will define a map on sutured Floer homology induced by the inclusion of (M′,Γ′) into (M,Γ) in the presence of a compatible contact structure in the complement. We will see how triviality of the contact invariant on a sutured submanifold implies the triviality of the contact invariant of the manifold itself. In the next section we will use the gluing theorem to calculate the contact invariant in some examples, and obtain some interesting obstructions to fillability. For simplicity, we can think of all constructions as done over $\mathbb {Z}/2\mathbb {Z}$, so we do not have to worry about the sign ambiguity.

If a connected component N of M∖int(M′) contains no components of ∂M we say that N is isolated. When M∖int(M′) has no isolated components we have the following:

Theorem 5.1

[13]

Let (M′,Γ′) be a sutured submanifold of (M,Γ), and let ξ be a compatible contact structure on M∖int(M′). Assume that M−int(M′) has no isolated components. Then ξ induces a natural map:

$$\varPhi_\xi: \mathit{SFH}\bigl(-M',-\varGamma' \bigr)\rightarrow \mathit{SFH}(-M,-\varGamma) $$

Moreover, if ξ′ is any contact structure on M′ compatible with Γ′ then

$$\varPhi_\xi\bigl(c\bigl(M',\varGamma', \xi'\bigr)\bigr)= c\bigl(M,\varGamma,\xi'\cup\xi\bigr) $$

where ξ′∪ξ is a contact structure on M that restricts to ξ on M∖int(M′) and to ξ′ on M′.

There is a more complicated statement in the case of existence of isolated components which involves considering multi-pointed Heegaard diagrams and tensoring with $\widehat{HF}(S^{1}\times S^{2})$, see [13].

Brief description of Φ _ξ

To define this map we have to carefully extend a sutured Heegaard diagram for (M′,Γ′) to a diagram for (M,Γ). For details of this construction look at [13]. Here is just a very quick idea. We use, in an essential way, the contact structure ξ on M∖int(M′) compatible with the sutures Γ and Γ′ to define the map. We start from a Heegaard surface for M′. If we are given ξ′ on M′ take (Σ′,β′,α′) to be defined by a partial open book compatible with ξ′. If we are not given a ξ′, let (Σ′,β′,α′) be a Heegaard diagram arising from a partial open book decomposition of some contact structure ζ which has dividing set Γ′ on ∂M′. We would like to join this Heegaard diagram to one generated by ξ on M∖int(M′). However, that is in general not precise enough, as it does not provide enough compressing discs for the union. To connect the two sides, we need to start with N, a contact product neigbourhood of ∂M′ in M∖int(M′), and let M″=M∖int(M′∪N). We carefully choose a Heegaard surface Σ _N which is compatible with the [0,1]-invariant contact structure ξ| _N , as well as a basis of arcs $\{a_{i}^{N}\}$ for it. We then extend Σ _N to a Heegaard surface Σ _M″ and denote a basis of arcs on the union extending $\{a_{i}^{N}\}$ in a way necessary to obtain sutured Heegaard diagram for (M∖int M′,Γ∪Γ′) by $\{\alpha_{i}''\}$. This needs to be done in a way compatible with ξ∪ζ, i.e. so that after $\{a_{i}''\}$ and their perturbations $\{b_{i}''\}$ are chosen, and we look at boundaries $\{ \alpha_{i}''\}$ and $\{\beta_{i}''\}$ of corresponding compressing discs, the special point $\mathbf{x}'' = (\dots,\mathbf{x}_{i}'',\dots)$, consisting of $x_{i} ''=a_{i}''\cap b_{i}''$, is the contact class of ξ∪ζ. After gluing we get a Heegaard diagram for (M,Γ) by taking α=α′∪α″ and β′=β′∪β″. We then define

$$\begin{aligned} \varPhi_\xi: \mathit{CF}\bigl(\varSigma',\beta', \alpha'\bigr) & \rightarrow \mathit{CF}\bigl(\varSigma ,\beta'\cup \beta'', \alpha'\cup\alpha'' \bigr), \\ \mathbf{y}& \mapsto\bigl(\mathbf{y}, \mathbf{x}''\bigr). \end{aligned} $$

 □

Above theorem has as an immediate consequence:

Theorem 5.2

[13]

Let i:(M′,Γ′,ξ′)→(M,Γ,ξ) be an inclusion such that ξ| _M′=ξ′. If $c(M,\varGamma,\xi) \not=0$, then $c(M',\varGamma', \xi')\not=0$.

Juhász [17] showed that we can recover the Heegaard Floer Homology of a closed manifold M by calculating the sutured Floer homology of the manifold with sutured boundary (M∖B ³,Γ) obtained by removing a solid ball B ³ from M and letting the suture Γ be S ¹⊂S ² on the boundary S ²=∂(M∖B ³). This isomorphism is one to one on generators when we consider the sutured Heegaard diagram on M∖B ³ and the corresponding Heegaard diagram on M obtained by closing the Heegaard surface by adding a disc along its boundary and making its center a marked point. This isomorphism takes in a natural way the sutured contact invariant of (M∖B ³,S ¹) to the contact invariant of the closed manifold. Since fillable structures have nonzero contact invariants we have:

Theorem 5.3

[13]

If c(M,Γ,ξ)=0, then (M,Γ,ξ) does not embed into any fillable contact structure.

It is clear from the construction, as we had remarked after defining the contact invariant generator in the closed case, that an arc that is taken to the left by the monodromy produces a holomorphic disc that kills the contact invariant. The partial open book we constructed in Figure 20 shows that c(ξ)=0 for the sutured manifold which is the neighborhood of the overtwisted disc (there is a disc from y to x making ∂y=x). From this, coupled with the embedding theorem, we see another proof that c(ξ)=0 for any overtwisted contact structure.

6 A TQFT Aspect of c(ξ) and Fillability Obstructions

In this section we study S ¹ invariant contact structures ξ on Σ×S ¹, such that Σ×{t} is convex surface with Legendrian boundary, and for all the components of ∂Σ there is twisting of ξ with respect to the framing determined by Σ. These contact structures are classified by their dividing sets Γ _ξ which are properly embedded multicurves (disjoint union of curves and arcs) that intersect every component of the boundary of Σ in an even number of points, and divide Σ and hence ∂Σ into positive and negative regions. We say that a properly embedded multicurve K⊂Σ is isolating if Σ∖K contains a component that does not intersect ∂Σ (see Figure 21). Examples of contact structures with c(M,Γ,ξ)=0 can now be obtained quite easily from:

Fig. 21.

An isolating dividing set on a punctured torus

Theorem 6.1

[13]

Let ξ _K be the S ¹ invariant contact structures on Σ×S ¹, such that Σ×{t} is convex with dividing set Γ _Σ =K. If K is isolating then c(Σ×S ¹,ξ _K )=0.

To prove this theorem we use some TQFT-like properties of contact invariants for S ¹ invariant contact structures on Σ×S ¹. Consider a “bordered” surface with boundary (Σ,F), i.e. a surface Σ with a finite subset F⊂∂Σ consisting of 2n points that divide the boundary γ=∂Σ into alternating positive and negative regions γ _±, with γ∖F=γ ₋⊔γ ₊. We say that a union K of closed curves and properly embedded arcs in Σ with ∂K=F is a dividing set on (Σ,F), or that K divides Σ, if Σ∖K is a disjoint union of positive and negative regions R _±, and ∂R _±=K∪γ _±. Denote by $\mathcal {D}(\varSigma,F)$ the family of all dividing sets for (Σ,F). We will use Sutured Floer Homology and sutured contact invariants to define a map that assigns a vector space V(Σ,F) to each (Σ,F) and an element in that vector space to each $K \in \mathcal {D}(\varSigma,F)$ with following TQFT-like properties:

• 1. If Σ is connected, then

  $$V(\varSigma,F)=\mathbb {F}^2 \otimes\dots\otimes \mathbb {F}^2, $$

  where $\mathbb {F}=\mathbb {Z}/2\mathbb {Z}$, the number of copies of $\mathbb {F}^{2}$ is r=n−χ(Σ), and $\mathbb {F}^{2}=\mathbb {F}\oplus \mathbb {F}$ is a graded $\mathbb {F}$-module whose first summand has grading 1 and the second summand has grading −1. If (Σ,F) is the disjoint union of (Σ ₁,F ₁) and (Σ ₂,F ₂), then

  $$V(\varSigma_1\sqcup \varSigma_2,F_1\sqcup F_2)\simeq V(\varSigma_1,F_1)\otimes V( \varSigma_2,F_2). $$

• 2. To each $K \in \mathcal {D}(\varSigma,F)$ it assigns c(K)∈V(Σ,F). If K has a homotopically trivial closed component, then c(K)=0.

• 3. Given (Σ,F), possibly disconnected, let δ,δ′⊂∂Σ be mutually disjoint submanifolds of ∂Σ, such that their endpoints do not lie in F, and let τ be a diffeomorphism $\tau:\delta\stackrel{\sim}{\rightarrow}\delta'$ which identifies $\delta\cap F\stackrel{\sim}{\rightarrow}\delta'\cap F$ and preserves the ± labeling and reverses the orientation on δ,δ′ inherited from ∂Σ. Denote by (Σ′,F′) the result of identifying γ and γ′ via τ. For every $K \in \mathcal {D}(\varSigma,F)$ denote by $\overline{K}$ the dividing set obtained from K by gluing K| _γ and K| _γ′. Then there exists a map

  $$\varPhi_{\tau}:V(\varSigma,F)\rightarrow V\bigl(\varSigma',F' \bigr), $$

  which satisfies

  $$c(K)\mapsto c(\overline{K}). $$

Figure 22 shows the case when Σ is a union of disjoint surfaces Σ″ and Σ‴, and hence Σ′ is obtained by gluing Σ″ and Σ‴.

Fig. 22.

Gluing (Σ″,K″) and (Σ‴,K‴)

To define this assignment for every (Σ,F,γ _±), we first perturb F by moving it slightly in the direction opposite to the one defined by the orientation on γ=∂Σ to obtain F ⁰, and shifting γ _± in the same way to obtain $\gamma_{\pm}^{0}$. We then consider the sutured 3-manifold (Σ×S ¹,Γ) where Γ=F ⁰×S ¹ and $R_{\pm}=\gamma_{\pm}^{0} \times S^{1}$. Denote by V(Σ,F) the sutured Floer homology of (−Σ×S ¹,−Γ). A dividing set $K \in \mathcal {D}(\varSigma,F)$ defines an S ¹-invariant contact structure ξ _K on (Σ×S ¹,Γ), and hence the corresponding contact invariant c(K)=c(ξ)∈V(Σ,F). We use F ⁰ instead of F since the two convex surfaces Σ×{t} and ∂(Σ×S ¹) are transverse, so the two dividing sets have to mark “interlocking points” along the Legendrian intersection curve, i.e. points in F ⁰=Γ∩∂Σ must lie between the endpoints F of K (see Figure 5).

To prove that $V(\varSigma,F)=\mathbb {F}^{2} \otimes\dots\otimes \mathbb {F}^{2}$ with appropriate number of factors, we first need to calculate SFH(D ²×S ¹,Γ ₂) for a solid torus with dividing set Γ ₂ made up of 4 longitudinal curves. It is shown in [13, Section 5, Example 3] that the result is $\mathit{SFH}( D^{2} \times S^{1}, \varGamma_{2})=\mathbb {F}^{2}=\mathbb {F}_{(1)}\oplus \mathbb {F}_{(-1)}$. There are exactly two S ¹ invariant contact structures compatible with these sutures, each determined by one of the two dividing sets on D ² consisting of two arcs, and each generating one of the $\mathbb {F}_{(\pm1)}$. We cut the surface Σ repeatedly by properly embedded arcs that connect + and − regions of ∂Σ until we get a disc. Every time we do a cut, each of the two new arcs in the boundary that correspond to the cut gets one marked point in F, thus each cut adds two points to the boundary, increasing n by one. A tensor product formula by Juhász [18, Proposition 8.10] that holds for splitting sutured manifolds along product annuli applies. The annulus here is product of a cutting arc with S ¹. The number of summands, r=n−χ(Σ) corresponds to the number of discs, each with 4 marked points on the boundary, that Σ is finally cut into, and the $\mathbb {F}^{2}$ factor corresponds to the contribution of each such disc to SFH.

If K has a homotopically trivial closed component, then ξ _K is overtwisted and hence c(K)=0 since we defined c(K)∈V(Σ,F) to be the value of the contact invariant for the S ¹-invariant contact structure ξ _K determined by K.

The Gluing Theorem 5.1 applied to Σ×S ¹⊂Σ′×S ¹ gives us the map Φ _τ . We think of Σ as a subset of Σ′ as in Figure 23, where Σ=Σ″⊔Σ‴ and Σ″ and Σ‴ are identified with slightly shrunk copies inside σ′.

Fig. 23.

The dividing set K ₀ on Σ′∖Σ is given in red

The contact structure on Σ′×S ¹∖Σ×S ¹ is the S ¹ invariant structure determined by the dividing set K _τ on Σ′∖Σ determined by F″,F‴ and the identification τ.

By studying what we have in the case of Σ=D ² and |F|=6 we see in [16] that for dividing sets K ₁,K ₂,K ₃ as in Figure 24 we have that the corresponding c(K ₁),c(K ₂),c(K ₃) are nonzero and distinct, and satisfy c(K ₁)=c(K ₂)+c(K ₃). Note that these three configurations are related by bypass addition. In fact, K ₂ is obtained by adding a bypass to the front of K ₁ along an arc connecting the three dividing curves, and K ₃ is obtained by adding a bypass from the back of K ₁ (digging a bypass).

Fig. 24.

Dividing sets on Σ=D ² for |F|=6

When we combine this with the gluing theorem, we obtain the same relationship for any three dividing sets {K _i , i=1,2,3} related by bypass addition on a general Σ. We will quickly argue that c(ξ _K )=0 for our example in Figure 21.

It is not hard to see that by adding and digging bypasses along the bypass arc δ given in blue in K ₁ in Figure 25, we obtain dividing curves as in K ₂ and K ₃. Cutting Σ along the green curve τ and looking at the dividing sets $K_{2}'$ and $K_{3}'$ resulting from K ₂ and K ₃ on the resulting annulus, we see that $c(K_{2}')=c(K_{3}')$. Juházs’ annulus theorem says gluing along τ induces an isomorphism, so that we get c(K ₂)=c(K ₃). This completes the proof that $c(\xi_{K_{1}})=0$ since c(K ₁)=c(K ₂)+c(K ₃)=0 as we are working over $\mathbb {F}=\mathbb {Z}/2\mathbb {Z}$.

Fig. 25.

Bypass adition in the proof of c(ξ _K )=0 for an isolating dividin set

More general isolating dividing sets on surfaces of higher genus can be dealt with by similar methods or reduced to this case, thus proving Theorem 6.1. For full explanation see [16]. The fact that the contact invariant vanishes for isolating dividing sets was proved over $\mathbb {Z}$ coefficients by Patrick Massot [23].

Theorem 6.1 together with Theorem 5.3 shows that (Σ×S ¹,ξ _K ) with contact structures corresponding to an isolating K form a vast family of universally tight contact structures that do not embed into fillable structures and are thus generalizing Giroux torsion. Similar results were obtained by looking at holomorphic curves and contact homology by Chris Wendl [34].