Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Nomenclature

\({\textit{r}}\)

Volume fraction (dimensionless)

\({\rho }\)

Density (Kg/m \(^{3}\))

\({\textit{U}}\)

Velocity (ft/s)

\({\textit{F}}\)

Drag force per unit volume (N m\(^{-3}\))

\(\sigma \)

Stress (kpsi)

\({\varvec{g}}\)

Gravity (m/s\(^{2}\))

\({\mu }\)

Viscosity (m\(^{2}\)/s)

\(\textit{y}\)

Liquid level (m)

C

Drag Coefficient (dimensionless)

Subscripts

\(\textit{f} \)

Fatigue Safety Factor

\(\textit{sl}\)

Superficial

\(\textit{sg}\)

Superficial gas velocity

\({\alpha }\)

Phase

\(\textit{y}\)

Yield Safety Factor

\(\textit{l}\)

Liquid

\(\textit{g}\)

Gas liquid velocity

1 Introduction

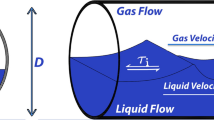
There are many obstacles regarding the simulation of multiphase flows. For instance, it is well-known that energy, mass, and momentum transfer rates are sensitive to the geometric distribution of the phases, known as the flow regimes. One of these regimes is the slug flow pattern, which is of paramount importance in numerous industrial processes such as the production of oil and gas, the geothermal production of steam, the boiling and condensation processes, the handling and transport of cryogenic fluids, and the emergency cooling of nuclear reactors.

The primary characteristic of slug flow is its inherent intermittence of the fluid phases involved. For example, for a gas-liquid flow, an Eulerian observer looking along the axis of a pipe will see the passage of a sequence of slugs of liquid containing dispersed bubbles alternating with sections of separated flow within long bubbles. The flow is unsteady, even when the flow rates of gas and liquid are kept constant at the pipe inlet. The existence of slug flow can create severe problems for the designer or operator. For instance, the high momentum of the liquid slugs can produce considerable forces as they change direction through elbows and tees. In addition, severe damage can also take place along large piping structures as the low frequencies of slug flow can be in resonance with them. However, a number of practical benefits can also result from operating in the slug flow pattern. For example, due to the high liquid velocities, it is possible to move larger amounts of liquids in smaller lines than would otherwise be possible in two-phase flow. Moreover, these high velocities cause very high convective heat and mass transfers, resulting in very efficient transport operations.

Owing to its importance in the chemical and petroleum engineering industries, several theoretical and experimental studies have been conducted to find out and control slug flow parameters (e.g., Taitel and Dukler 1976; Nydal et al. 1992; Emerson and Leonardo 2005; Gu and Gue 2008). However, on the computational side only a few attempts have been made to simulate slug flow, most of which are related to the study of rising Taylor bubbles (Baritto and Segura 2008). Other existing numerical simulations are based on the so-called slug capturing technique in which the slug flow regime is predicted as a mechanistic and automatic outcome of the growth of hydrodynamic instabilities (Issa and Woodburn 1998; Issa and Kempf 2003). These simulation models rely on the two-fluid model (Ishii 1975), which has also been implemented in several industrial codes such as PLAC (Black et al. 1990) and OLGA (Bendiksen et al. 1991). However, it has never been demonstrated conclusively that the model can capture in a natural way the development of slug flow from the growth of instabilities in stratified flow. On the other hand, Frank (2005) and Vallée et al. (2007) have used an Eulerian model to simulate the slug flow regime in horizontal channels, noting a dependence of the results on the inlet boundary conditions. In this work, we rely on the two-phase fluid model implemented by Frank (2005) to simulate slug flow in horizontal pipes with the commercial code Ansys CFX.

2 Governing Equations

The basis of a two-fluid model is the formulation of two sets of conservation equations for the balance of mass, momentum, and energy for each of the phases. As was pointed out by Frank (2005), slug flow may include gas entrainment in the liquid phase (bubbles) and so a realistic treatment of this type of flow requires the numerical solution of these sets of partial differential equations.

The present study is based on the transport equations for an isothermal flow. Hence the equations that are solved for the conservation of mass and momentum for the gas and liquid phases, written in Eulerian form, are:

$$\begin{aligned} \frac{\partial }{\partial t}(r_\alpha \rho _\alpha ) + \nabla \cdot (r_\alpha \rho _\alpha \varvec{U}_\alpha ) = 0, \end{aligned}$$
(1)
$$\begin{aligned} \frac{\partial }{\partial t}(r_\alpha \rho _\alpha \varvec{U}_\alpha )&+ \nabla \cdot (r_\alpha \rho _\alpha \varvec{U}_\alpha \varvec{U}_\alpha ) = -r_\alpha \nabla \rho _\alpha + r_\alpha \rho _\alpha \varvec{g} +\nonumber \\&\qquad \qquad \qquad \nabla \cdot (r_\alpha \mu _{\alpha \tau }(\nabla \varvec{U}_\alpha + (\nabla \varvec{U}_\alpha )^{\tau })) + \varvec{F}_\alpha , \end{aligned}$$
(2)

where the subscript \(\alpha \) refers to the gas (g) and liquid (l) phases such that \(r_{l}\) + \(r_{g}\) = 1. It is implicit in Eqs. (1) and (2) that there is no mass transfer between the liquid and gas phases. The term \(F_{\alpha }\) in Eq. (2) stands for the frictional forces per unit volume between each phase and the walls of the pipe. The turbulent viscosity is calculated with the Shear Stress Transport model, which represents an improvement over the traditional \( k-\omega \) approach since it has a better prediction of flow separation under adverse pressure gradients, and it has been used in other simulations of multiphase flow (Al Issa et al. 2007). The only interfacial force present is the drag force, which is calculated using a drag coefficient \(C_{D}\) = 0.44.

3 Boundary Conditions and Models

The boundary geometry considered here is a horizontal pipe of total length L = 8 m and circular cross-section of diameter D = 54 mm, split by a symmetry plane. The resulting mesh has 153,298 tetrahedral and prismatic elements, with four inflation layers in the circular wall. This mesh was the result of a sensitivity analysis. To do so we have used a single-phase transient model with a water inlet velocity of 1 m/s and 140 time steps. Successive runs were performed using a finer mesh each time, until the pressure drop variation was below 1 %.

A total number of 17 transient cases were chosen with different superficial velocities for the air and water, each of them corresponding to different flow regimes in the Mandhane flow diagram. The superficial velocities are used to calculate an inlet mixture velocity \(U_{m}\) for each case. The level of liquid at the inlet and the liquid volume fraction were initialized using the following function:

$$\begin{aligned} y_L = y_0 + A_Lsin\left( 2\pi \frac{U_m t}{p_L}\right) \!. \end{aligned}$$
(3)

where \({y}_{0}\) = 0, the amplitude \(A_{L}\) = 0.25 D, and \( p_{L}=0.25\,{ L}\). The wavelength and amplitude were as determined by Lex (2003). A time-independent form of this function that depends only on the geometry was used for initialization. The walls of the pipe were set to be hydraulically smooth with no-slip conditions for both phases. Outlet boundary conditions at the exit of the pipe were specified. In all cases, the velocity fields were initialized with inlet values in the whole domain area. For all time steps with 70 coefficient loops, a maximum error of 0.001 RMS is guaranteed for the numerical solutions of Eqs. (1) and (2). Such an error is sufficiently small to achieve a quantitative accurate understanding of the flow field and variables. For all runs, the time step size was set to 0.005 s, implying about 1,600 steps per run.

Fig. 1
figure 1

Volume fraction gradients of slug flow at 1.5 s, with \(U_{sl}\) = 5 ft/s and \(U_{sg}\) = 12 ft/s

Full size image
Fig. 2
figure 2

Pressure gradients of slug flow at 4 s, top \(U_{sl}\) = 5 ft/s and \(U_{sg}\)= 12 ft/s, bottom \(U_{sl}\) = \(U_{sg}\)= 3.28 ft/s

Full size image

4 Results for Slug and Annular Flow

The results for slug flow are shown in Figs. 1 and 2, where the volume fraction and pressure gradients are depicted. The free surface is represented as an iso-surface where \(r=0.5\). The volume fraction gradients show the expected shape for the chosen velocity in the Mandhane diagram. Slug flow appears after 1.5 s and lasts for all the evolution up to 7 s. When the superficial velocity \(U_{sg}\) is decreased, the gradients for slug flow are affected, producing pressure fluctuations due to the limitations imposed by the boundary conditions used. All velocity pairs (\(U_{sl}, U_{sg}\)) for slug behaviour come from experimental limits in the Mandhane diagram; the pairs out of these limits did not exhibit slug flow.

As expected, the pressure gradient increases just before the slug (Fig. 2). A similar result was also obtained by Frank (2005).

Figure 3 shows the results of a model simulation for annular flow. Since in this case a run with the SST model diverged, the turbulence viscosity was calculated using the \(k- \varepsilon \) model. The liquid volume fraction (\(r\)) gradient evolved fully into the annular pattern in the middle of the domain. Further tests were employed to predict the boundary between slug and annular flow by increasing the superficial gas velocity \(U_{sg}\).

Fig. 3
figure 3

Water fraction gradients for annular flow at 6 s, \(U_{sl}\) = 1 ft/s, \(U_{sg}\) = 300 ft/s

Full size image

5 Sensitivity of the Results to the Inlet Wave Function

In order to check the sensitivity of the model to the periodic inlet boundary condition, a case was run with half of the original amplitude chosen by Lex (2003). The superficial velocities were the same as in a previous case run (i.e., \(U_{m}\) = 2 ft/s), and only the amplitude was varied. The results show that there is a minimum amplitude necessary for the inlet function to generate the slug flow as in the previous cases. Figure 4 displays how, after 1.5 s, the reduced amplitude can prevent the formation of a complete slug as compared to the case where the normal amplitude is employed.

Fig. 4
figure 4

Top slug flow, reduced amplitude. Bottom Slug flow, normal amplitude. Both at 1.5 s and with \(U_{m}\) = 2 ft/s

Full size image

6 An Application Example

One useful application of the present simulations of slug flow is just to analyze the impact of the implicit pressure increases that are generated. Using a commercial code, it is possible to generate plots with a wall force as a function of time and this information can be used to calculate safety factors. To illustrate this, a simulation of an elbow subject to slug flow was run for two different cases. Assuming the wall stress to be a pure shear stress, in the framework of Gerber’s fatigue theories, AISI 4340 properties, and a thickness of 2 mm, it is possible to calculate static and dynamic safety factors, as shown in Table 1. Figure 5 shows the geometry employed for the pipe plus elbow model.

The columns in Table 1, starting from the second, list the superficial liquid and gas velocities in units of ft/s, the direction in a Cartesian coordinate frame in which the safety factors were calculated (note that the flow is towards the z-axis), the minimum and maximum stresses exerted on the pipe walls, the yield safety factor, and the fatigue safety factor, respectively. Although the assumptions used here are ill-advised for a complete structural analysis, these data clearly show how a slight increase in the superficial liquid velocity can affect the stresses and the safety factors regardless of the gas superficial velocities.

Table 1 Safety factors for an elbow subject to slug flow
Full size table
Fig. 5
figure 5

Top Pipe and elbow geometry. Bottom Elbow geometry and mesh

Full size image

7 Conclusion

In this chapter, we have shown preliminary results of slug flow simulations along a pipe, using a two-fluid model approach. The results of the simulations show that it is possible to obtain realistically slug flow patterns by using the commercial code Ansys CFX, with a periodic inlet function and the SST model for the calculation of the turbulent viscosity. For a sequence of runs with increasing superficial velocity, we have also possibly identified the boundary between slug and annular flow. Finally, the model was applied to determining structural safety factors in pipeline systems.