Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Introduction

Although standard measure may have been used in ancient civilizations to measure fields or for other practical considerations, it is fair to assume that the architectural masterpieces of antiquity were created by using the elements of pure geometry. It is our conjecture that the architects of antiquity used various geometrical tools of the trade: the Sacred Cut, based on √2 geometry; a geometrical construction based on the geometry of the half-square, discovered by Danish engineer Tons Brunés (Brunés 1967) and referred to by us as the Brunés star; the square-within-a-square (ad quadratum); circle grids; a system of proportions originating in ancient Rome; the law of repetition of ratios (Kappraff 1998).

There is scant evidence to support the use of this sacred geometer’s tool kit since there are few records of the architects’ plans for these ancient structures, but several scholarly investigations have been made of ancient Roman rains that support our point of view (Watts and Watts 1986: 132–139, 1987: 265–276). However, even in these instances there is a great deal of speculation. Therefore, Ben Nicholson ’s detailed study of a series of geometric pavement designs executed in terracotta that lie beneath the floorboards of the Laurentian Library in Florence and his investigation of their geometry is of great interest. The results of his work have given additional evidence of the use of the sacred geometer’s tool kit.

The Laurentian Library

In 1774, a portentous accident occurred in the Reading Room of the Laurentian Library , designed by Michelangelo (Nicholson 1997). The shelf of desk 74, overladen with books, gave way and broke. During the course of its repair, workmen found a red and white terracotta pavement hidden for nearly 200 years beneath the floorboards. The librarian had trapdoors, still operable today, built into the floor so future generations could view these unusual pavements. In 1928 another mishap resulted in the exposure of the entire pavement, which allowed photographs to be made of the 15 panels on the West side of the library before the wooden floor was replaced.

Overall the pavement consists of two side aisles and a figurative centre aisle. Each side aisle is composed of a series of 15 panels, each measuring about 8′6″ × 8′6″, and is of a different design. The 15 panels mirror each other’s form but differ by a very small degree and in subtle ways. When juxtaposed in a series, the 15 pairs of panels appear to tell a story about the essentials of geometry and numbers. Each panel settles upon a theme: the tetractys (Panel 5); Brunés ’s star, √2 and the Sacred Cut (Panels 7 and 11); Plato ’s lambda (Panel 14); the Golden Mean (Panel 13). When assembled together they form an encyclopedia of the essential principles handed down from ancient geometers.

Although they are hidden from view today, Nicholson believes that the panels were laid according to a plan for a furniture layout that would have exposed them, but that this plan was changed after the panels had been made. He suggests that the original intention was to infuse the spectator with the foundations of ancient geometry as he walked through the Reading Room of the Laurentian Library , the geometry being a perfect complement for the 3,000 classical texts chosen to reveal the body of ancient and modern learning.

Interpreting the Pavement

Ben Nicholson has worked with students over a 10-year period to reconstruct the system that the team of geometers and theologians, which may have included Michelangelo , used to create the original panels. He has recently collaborated with artist Blake Summers and architecture graduate student Saori Hisano to replicate all 15 panels at full scale. Working largely with straightedge and compass, Nicholson and his team have stumbled upon ancient tenets of geometry which have been infused with an ingenious Mannerist twist to promote ideas of irrationality and void, criss-crossed with the witty numerical conundrums so admired in the late Renaissance.

At first glance, the panels appear to be square. However, curious irregularities guide the dimensioning of each panel. Each panel is set into a rectangular frame that measures approximately 4 braccia (233 cm) by 4 1/4 braccia (248 cm), but the size of each panel is slightly different. Nicholson proposes that the geometric grids and numerology in the pavement respond to the essential theological and scholastic questions posed in the sixteenth century. For example, Plato ’s lambda orders panel 14, which is aligned in its general appearance with descriptions in the Timaeus setting the lambda within four interconnecting circles (Fig. 56.1).

Fig. 56.1
figure 1

Laurentian Library , Florence, panel based on Plato ’s lambda

Full size image

Nicholson ’s proposition that each pair of panels differs very slightly from East to West now becomes relevant to the discussion. For example, there is evidence to suggest that Panel 14 East is laid out on a grid of 81 parts, and that Panel 14 West is laid out on a grid of 80 parts. The ratio 80:81 is a measure of the comma’s difference between the Pythagorean and Just musical scales (Kappraff 1998). Can these matters have been intentional? In the remainder of this chapter, we shall present some details of two panel reconstructions.

The Medici Panel

Panel 2 is called the “Medici panel”. The painted reconstruction by Nicholson and Summers of the original terracotta design is shown in Fig. 56.2.

Fig. 56.2
figure 2

Reconstruction of the “Medici panel” based on the rosette

Full size image

It seems to be wholly symmetrical and it has the same appearance as the antique rosettes, of which there are many examples in Renaissance design. At the centre of the rosette lies the emblema of Cosimo I from the house of the Medici, advertising the threefold symmetry of the pattern. However, at second glance the panel exhibits the mannerist tell-tale irregularities that are common to all the Laurentian pavement designs: the panel is not square, but a rectangle with sides in the ratio of 12:13; curving white bands radiate from the centre, a graphic treatment never present in the antique form; ovals are inserted into the residual spaces between these bands.

The following steps show that Panel 2 is created by superimposing 96 circles on a 12:13 rectangle that is composed upon a 13 × 13 square:

  1. 1.

    Form a 12:13 rectangle by dividing one axis of a square into 26 parts and extend the left and right edges of the rectangle to form a 13:13 square as shown in Fig. 56.3a. The diagonals of the 12:13 rectangle and 13:13 square are shown (Fig. 56.3a).

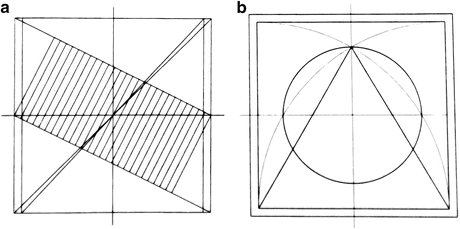
    figure 3

    Fig. 56.3

  2. 2.

    Draw a second 12:12 square within the 13:13 square and place the x- and y-axes at the centre of the squares.

  3. 3.

    Draw an equilateral triangle with side equal to the base of the 12:12 square. The distance from the apex of this triangle to the centre of the square determines the radius of a circle (Fig. 56.3b). This circle is called the pitch circle. The radius of the pitch circle differs from 1/4 the diameter of the 12:13 rectangle by less than 1 %. Either value can be used for this construction. However we use the first because of its elegance.Footnote 1

  4. 4.

    Place x- and y-axes at the centre of the rectangle and draw a rosette pattern with 24 circles by the following procedure:

    1. (a)

      Draw six circles whose radii are the same as the radius of the pitch circle. The first circle has its centre point at the intersection of the pitch circle and the upper y-axis; each of the other five circles’ centre points are intersection points between the pitch circle and the preceding circle (Fig. 56.4a). The centres of these circles define two sets of three axes through the centre of the rectangle corresponding to the threefold axes of the Cosimo symbol in the centre of the design. Notice that four of the circles intersect the vertices of the 12:12 square. It is also worth noting that the rosette produces a series of intersections between adjacent circles, known as the Vesica Pisces, a key figure of sacred geometry (Kappraff 1991: 54, 87). It was in this region that images of Christ were placed in many sacred designs.

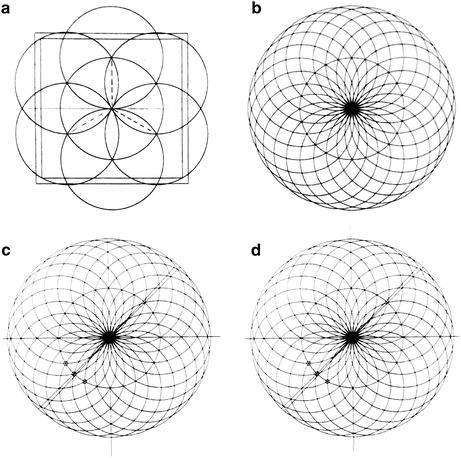
      figure 4

      Fig. 56.4

    2. (b)

      Draw six more circles using the same method as step 4a, beginning this time with the intersection point of the pitch circle and the right hand x-axis as the first centre point.

    3. (c)

      Repeat steps 4a and b by using intersection points between the pitch circle and diagonal lines of the 13:13 square as centre points to create 12 additional circles forming the 24-circle rosette pattern (Fig. 56.4b).

  5. 5.

    The rosette is composed of a grid of curvaceous diamonds formed by the intersection of the first 12 circles and the second 12 circles. Using as centres the midpoints of the arcs on the pitch circle connecting adjacent circles of the rosette pattern, draw 24 additional circles using the same method as in step 5 (Fig. 56.4c).

  6. 6.

    The small mismatch between the diagonals of the square and rectangle leaves space to construct a reference circle. Draw 24 circles, identical to the reference circle, with centres at the intersection points of the pitch circle and the latest 24 circles. Two of these 24 reference circles are shown on opposite sides from the original reference circle.

  7. 7.

    Draw 48 circles with the same radius as the pitch circle and the intersection points of the pitch circle and the 24 reference circles from the previous step as centres (Fig. 56.4d). These circles are to become the white bands of the Medici Panel. This step demonstrates how the panel makes “Mannerist space” out of the difference between the series of circles generated by the 12:13 and 13:13 diagonals.

  8. 8.

    In the final step ovals of eight different types are created, to fill the diamond shapes. The detail of this step is beyond the scope of this chapter.

Nicholson hypothesizes that this design represents an interplay between the circle, representing the cosmic realm, and the square and rectangle, representing the earthly domain. The ratio of 12:13 represents the solar and lunar cycles since the sun goes through the 12 signs of the zodiac in approximately the time that the Moon undergoes 13 revolutions about the Earth. The 96 circles that make up the pattern and the original pitch circle are grouped in the series: 1, 3 + 3, 6, 12, 24, 48. We recognize this series as the series that was used by Bode to determine the relative distances to the sun of the planets up to Saturn (all the planets known in the year 1550) (Kappraff 1998). Therefore, the designer of this pavement was able, either consciously or unconsciously, to compress a great deal of cosmic information into a geometrical setting. The panel on the other side of the library is identical except that it fits into an 11:12 rectangle. Nicholson conjectures that the numbers 12 and 11 refer to the number of Christ’s disciples with and without Judas.

The Mask Panel

Nicholson has named Panel 13 the “Mask” panel (Fig. 56.5). When looked at either directly or from the side it appears like the classical masks of the theatre with either a happy or sad face popular at the time. Michelangelo made a number of carvings of the “mask of night.” Saori Hisano and Hingan Wibisono were able to use a combination of the Golden Mean and the Brunés star to reconstruct this panel.

Fig. 56.5
figure 5

The “Mask” panel

Full size image

To construct a rectangle with Golden Mean proportions, begin with a square and add the semilength of a side to the length from a vertex to the midpoint of the opposite side (Fig. 56.6).

figure 6

Fig. 56.6

To construct a Brunés star, begin with a square divided into four half squares, and place a pair of diagonals into each half-square (Fig. 56.7a). The Brunés star provides a means for dividing a line segment into from 1 to 12 equal subdivisions. Figure 56.7b shows positions for subdividing a line segment into 1, 2, 3, …, 8 equal segments (7 is missing but can be approximated by another construction) (Kappraff 1998).

figure 7

Fig. 56.7

Rather than go into detailed explanations, we present in Fig. 56.8 one of the diagrams in which Nicholson has defined a central unit square and two symmetrically placed golden rectangles (proportions 1:ϕ).

figure 8

Fig. 56.8

The construction lines to create the golden rectangle are shown in the figure. The central square is trisected by the methods of Brunés into first a 3 × 3 grid, then each third is divided again by the Brunés star into a 4 × 4 grid. As a result the original square is divided into a 12 × 12 grid. Notice that the star and the golden rectangle share construction lines. Once again, the panel is just off from being a square, with the difference between the length and width being equal to 1/6, i.e., a width of 1/12 placed on either side of the short side.

In Fig. 56.9 four circles of radius 1/ ϕ are drawn about each vertex of the central square as centres. The width of the four oblong regions of intersection of these circles equals the diameters of the four black circles of the mask pattern. They are equal to 1/ ϕ 2 units. These oblong regions are somewhat reminiscent of the Vesica Pisces regions that formed the basis of panel 2. From this construction, Nicholson was able to deduce that the widths of the white annuli around the black circles and the narrow white annuli in the left and right sections of the pavement were related to the Golden Mean and summed to 1/12, the width derived from the Brunés star.

figure 9

Fig. 56.9

The reconstructed terracotta Mask panel was created by Nicholson , Hisano , and Wibisono (see Fig. 56.5). The geometer, who may have been Michelangelo himself, appears to have found ingenious ways of wedding two geometrically different worlds, the one of the Golden Mean and the other of the Brunés star.

Conclusion

The pavement panels of the Laurentian library have presented us with a set of geometrical puzzles and are remarkable because they represent, in a single building, an almost complete set of the predominant forms of ancient geometry. It is Nicholson ’s hope that his work will generate sufficient interest among the officials at the Laurentian Library to open these beautiful pavements to public view, as well as affording the possibility of making a conclusive set of measurements against which his thesis can be checked. Nicholson believes that the panels are an unambiguous expression of Mannerism, which has long been associated with a somewhat wilful and uncontrolled adjustment of Renaissance principles of perceived wholesomeness. He considers the pavement as constituting a ‘document’ of Mannerist number theory, albeit expressed in the difficult language of geometry, that spells out, in a wholly reasoned way, issues of paradox, void and a confrontation of the status quo for which Mannerist art is so famous. It is also possible that this pavement forms the treatise on proportion that Michelangelo had in mind to write and that was alluded to by Condivi in his biography of Michelangelo (1553).

The panels are certainly in accordance with the ancient tenets of sacred geometry, but new procedures are added to the construction of each panel inferring a considered development of the extant body of knowledge. Panel 2 does spring forth from a single point that leads to a circle representing the undifferentiated cosmos, but the geometer introduces a radius based upon a distillation of the numbers 12 and 13, which throws a controlled, but irrational, haze over the whole construction. Elsewhere, the appearance of a square shows up in several panels: their well-defined vertical and horizontal axes classically imply the immutable polarity of opposites—made more succinct by the crossing at its centre, representing the essential generative qualities of male and female, necessary for the sustenance of earth and nature. The crossing in Panel 14 follows this tradition, but one of the limbs is measured with a string of whole number integers and the second limb is formed by a √2 evolution of the first limb: thus the crossing is caught in the tension of two systems that pit rational against irrational—and the observer is left to gaze upon the whole and wonder why.