Abstract
The earliest material evidence of Indian mathematics is found among the ruins of the Harappa civilization, including an elaborate system of weights and measures related to binary and decimal series. The Harappa culture’s use of kiln-fired bricks provides a link between the “frozen” geometry unearthed by archaeologists and the earliest written geometry, a guide to constructing Vedic brick altars. The Sulbasutras and the Sathapatha Brahmana contain valuable information about the geometry of ancient India, including instructions for constructing sacrificial altars and locating sacred fires. The procedures described for constructing the altars used during Agnicayana involve methods for approximating the values for the square roots of 2 and 5. One theory of the origins of geometry in India suggests that it must have come into being when there was already an advanced form of brick technology with a long tradition behind it.
First published as: George Gherveghese Joseph, “The Geometry of Vedic Altars”, pp. 97–113 in Nexus: Architecture and Mathematics, ed. Kim Williams, Fucecchio (Florence): Edizioni dell’Erba, 1996.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
Introduction
The earliest material evidence of Indian mathematics is found among the ruins of the Harappa civilization, which dates back to the start of the third millennium before the Christian Era. Archaeological finds show an elaborate system of weights and measures. Plumb-bobs of uniform size and weight found throughout the vast area of this culture conform to two series (binary and decimal) and their combinations, in the ratio of 1, 2, 4, 8, 16, 32, 64 and 10, 20, 40, 160, 200, 300, 640, 1,600, 6,400, 8,000, and 12,800. Until recently, equivalent weights formed the basis of an elaborate system of barter in certain parts of India, with conversion rates almost identical to some of the above ratios.
Scales and instruments for measuring length have been found at major urban centres of this civilization, such as Mohenjo-Daro, Harappa and Lothal. The Mohenjo-Daro scale is a fragment of shell 66.2 mm long, with nine carefully sawn, equally spaced parallel lines, on average 6.7056 mm apart. The accuracy of the graduation is remarkably high, with a mean error of only 0.075 mm. One of the lines is marked by a hollow circle, and the sixth line from the circle is shown by a large circular dot. The distance between the two markers is 1.32 in. (33.5 mm) and is known as the ‘Indus inch’.Footnote 1
A notable feature of the Harappa culture was its extensive use of kiln-fired bricks for building and flood control. This bricks were exceptionally well baked and of high quality, and could still be used provided care is taken in removing them in the first place. They contain no straw or other binding material. While 15 different sizes of Harappan bricks have been identified, the standard ratio of the three dimensions—the length, breadth and thickness—is close to 4:2:1. Even today this is considered the optimal ratio for efficient bonding.
In the absence of any written evidence (the Harappa script has not yet been deciphered), these bricks may serve as the only “link” over a period of 1,500 years between the Harappa civilization and the beginning of the Vedic period of Indian history—a link, as it were, between the “frozen” geometry from archaeology and the first appearance of written geometry in the form of a surveyor’s guide to constructing Vedic brick altars.
Geometry of the Vedic Age
An examination of the earliest written record of geometry in India involves a study of the Sulbasutras,Footnote 2 conservatively dated around 800–500 bc, although knowledge from earlier times is incorporated as well.Footnote 3 The Sulbasutras contain instructions for the construction of sacrificial altars (vedi) and the location of sacred fires (agni), which, in order to be effective instruments of worship and sacrifice, had to conform to clearly laid-down requirements about their orientation, shapes and size. There were two main types of ritual: worship at home and communal worship. Square and circular altars were sufficient for household rituals, while more elaborate altars, of shapes which were combinations of these and other basic figures, were required for public worship.
The composers of the Sulbasutras made it clear that their work was not original but was to be found in earlier texts, notably the Samhitas and the Brahmanas, of which the most relevant extant text, the Sathapatha Brahmana, is at least 3,000 years old.Footnote 4 Despite its obscurities and archaic character, this text contains a valuable discussion of the technical aspects of altar construction.
An important section of the Sathapatha Brahmana deals with the construction of altars to carry out a 12-day Agnicayana (“piling up of Agni”) ceremony. The ceremony often took place in an area containing two sections (Fig. 10.1):
-
i.
The Mahavedi (Great Altar): Shaped as an isosceles trapezium, the two parallel sides of this structure were constructed so that the larger side measured 30 prakramas on the west and the smaller side 24 prakramas on the east, with the altitude of the trapezium being 36 prakramas.Footnote 5 Contained within the Mahavedi was a falcon-shaped brick altar (Vakrapraksa-syena) representing time.Footnote 6 Since many of the interesting results in Vedic geometry arose from the construction of this altar, it will be discussed in the next section.
-
ii.
To the west of the Mahavedi was a smaller rectangular area called Pracinavamsa in which, at specified positions, were three fire altars called Garhapatya (of circular shape symbolising the earth), Dakshinagni (of semicircular shape representing space) and Ahavaniya (a square indicating the sky). In the Sulbasutras, there is the suggestion that the areas of the three fire altars were equivalent and equalled 1 square purusha.Footnote 7
There were other structures contained in the Mahavedi and Pracinavamsa (H, H* and S in Fig. 10.1) of functional and ritual significance, but yielding little of mathematical interest.
The instructions for the design of the Mahavedi provide an insight into the practical nature of the texts of the period. The Apastamba Sulbasutra (V.2) contains the following instructions, a longer version of the original cryptic instruction:
To a cord of length 36 prakramas, add 18 prakramas. Make two marks on the cord, one at 12 prakramas and the other at 15 prakramas from the western end. Tie the ends [of the cord] to pegs on the ends of the East–west [prsthya] line of length 36 prakramas. Take the cord by the mark at 15 prakramas and stretch it to the south and mark the point with a peg. Do the same to the north. These are respectively the south west and the north west corners of the Mahavedi. Untie the ends of the cord from the East–west line and retie the end that was fastened previously to the peg on the east end to the west end and vice versa. Repeat the previous procedure but using the mark at 12 prakramas to obtain the south east and north east corners of the Mahavedi.
In Fig. 10.2, the length of the extended cord is 36 + 18 = 54 prakramas. From the other end, the 12th mark is half of the smaller parallel side while the 15th mark forms the base (AB) of a right-angled triangle (ABC), with its hypotenuse (BC) being the remainder of the cord (i.e., 36 + 3 = 39 prakramas) and the other side being the East–west line (AC) which measures 36 prakramas.
Apastamba gave other rational right-angled triangles that would satisfy the measurements required by the Mahavedi. These are the Pythagorean triples (3, 4, 5) multiplied by 4 or 5; (12, 5, 13) multiplied by 3; (15, 8, 17) and (12, 35, 37). All these triples may have been chosen initially to ensure that at least one side was of the same length as one side of the Mahavedi. In the same text appears a modification to the method of designing the Mahavedi that is suitable for any length of a given side.Footnote 8
Another problem that led to some interesting mathematics related to the precise distances and relative positions of the three fire altars, Garhapatya, Dakshinagni and Ahavaniya contained in the Pracinavamsa, shown in Fig. 10.1. The general requirement was: Dakshinagni should lie south of the line joining the other two fire altars and its distance from the Garhapatya should be one third the distance between the other two fire altars.
The Baudhyana Sulbasutra contains three different versions of how this could be achieved. To quote the relevant passages, as given in Datta (1932, pp. 203–205), with some modifications for sake of clarity:
-
(1)
With the third part of the length [i.e. the distance between Garhapatya (G) and Ahavaniya (A)], construct three squares closely following one another [from west towards the east]. Garhapatya is at the northwestern corner of the western square; Dakshinagni (D) is at its southeastern corner; and Ahavaniya at the northeastern corner of the eastern square (Baudhyana Sulbasutra 1.67).
-
(2)
Divide the distance between the Garhapatya and Ahavaniya into five or six [equal] parts; add [to it] a sixth or seventh part; Divide [a cord as long as] the whole increased length into three parts and mark the end of the two parts from the eastern end [of the cord]. Fasten the two ends of the cord [to two] pegs at either end of the distance between the Garhapatya and Ahavaniya, stretch it towards the south, having taken it to the mark and fix a peg at the point reached This is the position of the Dakshinagni (Baudhyana Sulbasutra 1.68).
-
(3)
Increase the measure [between the Garhapatya and Ahavaniya] by a fifth; divide [a cord of that length] into five parts and make a mark at the end of two parts from the western end [of the cord] after fastening the two ends to the east–west line. Stretch the cord towards the south having taken it to the mark and fix a peg at the point reached. This is the position of the Dakshinagni (Baudhyana Sulbasutra 1.69).
The figure constructed by Datta on the basis of these instructions, is shown in Fig. 10.3. He obtained various estimates of the relative distances between the fire altars.
Thus, if AG = x, it is easily shown that:
Moreover, if one assumes that the relative positions of all three fire altars are the same irrespective of the rule used, then the estimates for √5 and √2 are:
√5 = 2.333, 2.286, 2.169; √2 = 1.166, 1.143, 1.44
None of these estimates are accurate approximations, the best being only correct to the first place of decimals. These rules were essentially practical “rules of thumb” that an early surveyor might use, without mathematical considerations being predominant. However, this does not mean that considerations of accuracy did not occur in early Indian geometry. For example, to calculate the square root of 2, the following instructions are given both by Apastamba (1.6) and Katyayana (2.13) who came after Baudhyana: “Increase the measure by its third and this third by its own fourth less the thirty-fourth part of that fourth. This is the value of a special quantity in excess [which needs to be deducted]”.
If we take one unit as the dimension of the side of a square, the above formula gives the approximate length of its diagonal as:
The true value is 1.414213…
The Sulbasutras contain no clue as to the manner in which this accurate approximation was arrived at over 2,500 years ago. A number of theories or explanations have been proposed. Of these, a plausible one is that of Datta (1932), based on the “dissection and reassembly” principle, and discussed in Joseph (1992, pp. 234–36).
The Geometry of the Falcon-Shaped Altar
One of the most elaborate of the public altars (also found in the Mahavedi constructed for the Agnicayana ceremony) was shaped like a giant falcon just about to take flight (Fig. 10.4). It was believed that offering a sacrifice on such an altar would enable the soul of a supplicant to be conveyed directly to heaven by a falcon.
The first layer of a Vakrapaksa-syena altar: the wings are each made from 60 bricks of type a, and the body, head and tail from 50 type b, 6 type c, and 24 type d bricks. Each subsequent layer was laid out using different patterns of bricks with the total number of bricks equalling 200. Drawing: author
Most falcon-shaped altars were constructed with five layers of 200 bricks,Footnote 9 with each of these constructions reaching the height of the knee. For special occasions 10, 15, and, improbably, up to a maximum of 95 layers of bricks were used in their construction. The top layer of the basic altar was constrained to an area of 7.5 square purushas.Footnote 10 A purusha was defined as the height of a man with his arms stretched above him, say 2 m, which would give the altar an area measure of approximately 30 m2. For the second layer from the top, the prescription was that 1 square purusha should be added, so that the total area would be 8.5 square purushas.Footnote 11 Similarly, each successive layer area was increased by 1 square purusha, so that in the rather exceptional (or more likely hypothetical) case of the 94th successive increase of 1 square purusha, the area of the base of this huge construction would be 101.5 square purushas or about 400 m2!Footnote 12
Clearly, if in the construction of these altars the builders had to conform to certain basic shapes and prescribed areas or perimeters, two geometrical problems would soon arise:
-
(1)
the problem of finding a square equal in area to two or more given squares;
-
(2)
the problem of converting other shapes (for example, a circle or a trapezium or a rectangle) into a square of equal area or vice versa.
The constructions were probably achieved through a judicious combination of concrete geometry (the principle of dissection and reassembly),Footnote 13 and the application of ingenious algorithms, including the so-called Pythagorean theorem.
In the Katyayana Sulbasutra (named after one of the authors) appears the following proposition: “The cord [stretched along the length] of the diagonal of a rectangle makes an [area] which the vertical and horizontal sides make together” (2.11).
Using this version of the Pythagorean theorem, the Sulbasutras showed how to construct both a square equal to the sum of two given squares and a square equal to the difference of two given squares. Other constructions, including the transformation of a rectangle (square) to a square (rectangle) of equal area and of square (circle) to a circle (square) of approximately equal area, were part of the repertoire. In geometrical terms, the constructions “doubling the square” and “squaring the circle” lead naturally to the devising of algorithms for the square root of 2 and other numbers in the first case, and the discovery of the inexact nature of the relationship between circumference of the circle and the diagonal (diameter) of the square in the second case.Footnote 14
Apart from equivalences through area, the Vedic texts contain equivalences established between phenomena through numbers. The starting point is the centrality of the number 360 in the Vedic calendar and philosophy. Parallels are drawn between human anatomy and planetary motions. Thus, the Caraka Samhita, an early medical text, reckons the total number of asthis (or bones, teeth, nails, hard cartilages) in the human body to be 360, obtained from considering the 308 bones of the newborn babe (before they fuse into a smaller number of 206 in the adult), 32 teeth and 20 nails where each of these asthis are associated with each day of the year. The parallel between the nominal year (360 days) and man (purusha) is carried further in Sathapatha Brahmana where the basic falcon-shaped altar of 7.5 square purushas or 108,000 square angulas (1 purusha = 120 angulas) is linked to 10 nominal years or 108,000 muhurtas (1 muhurta = 48 min).Footnote 15 It is interesting in this context that a total of 10,800 ordinary (or lokamprina) bricks were used in the construction of the three fire altars found in the Pracinavamsa, the same as the number of muhurtas in a nominal year.Footnote 16
Kak (1993) has argued that the concept of equivalence is of central importance in interpreting Vedic astronomical knowledge, so that in the design of altars an astronomical code was present which required deciphering. For example, the circular Garhapatya fire altar, which symbolised earth or the womb, was constructed with 21 ordinary bricks and had an area of 1 square purusha.Footnote 17 If the basic falcon-shaped altar having an area of 7.5 square purusha corresponded to 360 days, then 1 square purusha would be equivalent to 48 days. The augmentation of the basic falcon-shaped altar by 1 square purusha at a time was to be seen as a correction to make the altar correspond closer to an actual year (366 days or 372 tithis or lunar days). A nakshatra year was taken as the number of nakshatras (27) multiplied by the number of months (12) which would give 324 days (or tithis). An additional 48 tithis as a correction was needed to get an actual year. However, this would mean an excess of 0.93761 tithi every year, since the number of tithis in a solar year is 371.06239. Thus, by constructing a falcon-shaped altar of 95 layers symbolising a 95-year cycle, with each augmentation being 1 square purusha (or 48 tithis), starting from 7.5 square purushas to 101.5 square purushas at the end of that cycle, the practice of a major adjustment every 95 years to the calendar by 90 tithis (or 3 lunar months) made sense. Such a correction implied that the length of the solar year is: 372 − (90/95) = 371.05263 tithis which corresponds to 365.24675 days. Comparing this value to the present-day estimate for the tropical year of 365.25636 days, we are struck by the accuracy of estimates which are at least 3,000 old.
Conclusion
There is a view that Indian mathematics originated in the service of religion. The proponents of this view have sought their main support in the complexity of motives behind the recording of the Sulbasutras. Since time immemorial, they argue, the needs of religion have determined not only the character of Indian social and political institutions, but also the development of her scientific, knowledge. Astronomy was developed to help determine the auspicious day and hour for performing sacrifices. The 49 verses of Jyotisutras (the Vedanga containing astronomical information) gave procedures for calculating the time and position of the Sun and Moon in various nakshatras (signs of the zodiac). A strong reason in Vedic India for the study of phonetics and. grammar was to ensure perfect accuracy in pronouncing every syllable in a prayer or sacrificial chant. So too, the construction of altars and the location of sacred fires, as we have seen, had to conform to clearly laid-down instructions about their shapes and areas if they were to be effective instruments of sacrifice.
However, there is a danger that the magico-religious beliefs surrounding the Vedic rituals may be overly emphasized when considering the origins of Indian mathematics. We have seen the crucial role played by the Agnicayana ceremony in generating geometrical concepts and techniques found in the Sulbasutras. The rituals associated with the construction of fire altars may be looked at from two standpoints. The first is from the standpoint of the beliefs connecting the shapes of altars with the specific desires to be fulfilled by their use in the sacrifices. The second is that of technology pure and simple: How exactly were the altars constructed to conform to specific shapes, specified size and by using a specific numbers and types of bricks?
It is clear that the geometry originating in the Sulbasutras had little to do with the first standpoint. Thus, for example, whether a falcon-shaped altar ensured for the sacrificer heaven or the annihilation of enemies was totally irrelevant to the problem of constructing it to conform to certain size and shape. As a matter of fact, these problems would be the same if somebody wanted a structure to be built in the garden for ornamental purposes. In other words, the geometry developed in the Sulbasutras was aimed at solving technological problems involved in constructing brick structures. It is this geometry that is being studied by historians of mathematics.Footnote 18
Once the Sulbsutras are seen as primarily manuals for technicians, the questions then arise of where and when the practical knowledge relating to bricks and brick technology were acquired. References to bricks are conspicuous by their absence from the most sacred and earliest of Vedic literature, the Rigveda Samhita. When they do make an appearance in a recension (Tattiriya Samhita) of a later Veda, the Yajurveda Samhita, bricks are viewed as marvellous and mysterious entities.Footnote 19 In the same text, there are exhortations that “tiles or potsherds” from the ruined Harappa cities should be gathered for ritual purposes. It is, therefore, likely that the priests were acquainted with the burnt bricks from the same sites and would in course of time invest them with magico-religious properties.
In one of the last recensions to Yajurveda appears the Sathapatha Brahmana, which, as mentioned earlier, contains a description of the Agnicayana. The magico-religious elements of this ritual are accompanied by a short discourse on the construction of brick altars of various shapes and sizes. While the discussion lacks the geometrical sophistication of the Sulbasutras, it is clear that the knowledge of brick technology which was abundantly evident in the Harappa culture was slowly percolating into the Vedic rituals, to become the most critical element of Vedic constructions.
Where, then are we to look for the origins of geometry in India? The common view is that the Sulbasutras are the source. However, one hypothesis is that if the geometry embodied in the Sulbasutra texts is to be viewed as the outcome of a long and sophisticated tradition of brick technology, this geometry must have come into being when there was in fact an advanced form of brick technology with a long tradition behind it. This, in other words, would mean that whatever may be the time of the actual codification of the Sulbasutras, their contents come down from a different period. That must have been a period of flourishing brick technology. Only one period answering to all this is known in ancient Indian history, and that is the period of the Harappa civilisation mentioned in the introduction. The presumption, in short, is that geometry which was eventually codified in the Sulbasutras could have come down from the Harappan period. If this presumption is correct, the first and earliest of the discontinuity in the chronology of Indian mathematics has been filled with the assistance of bricks.
Notes
- 1.
There are a number of interesting links between this unit of length (if indeed that is what it was) and others found elsewhere. A Sumerian shushi is exactly half an Indus inch, which supports other archaeological evidence of contacts between the two ancient civilizations. In northwest India, a traditional yard known as the gaz was in use from very early times. In the sixteenth century, the Mughal Emperor Akbar attempted unsuccessfully to have the gaz adopted as a standard measure in his kingdom. The gaz, which is 33 in. (or 5,840 mm) by our measurement, equals 25 Indus inches. Furthermore, the gaz is only a fraction (0.36 in.) longer than the megalithic yard, a measure that seems to have been prevalent in northwest Europe around the second millennium BC. This has led to the conjecture that a decimal scale of measurement, originating somewhere in Western Asia, spread widely as far as Britain, ancient Egypt and the Indus Valley (Mackie 1977).
- 2.
Three of the more mathematically important Sulbasutras were the ones recorded by Baudhyana, Apastamba and Katyayana. Little is known about these sulhakaras (i.e., authors of Sulbusutras) except that they were not just scribes but also priest-craftsmen performing a multitude of tasks including design, construction and maintenance of sacrificial altars (Thibaut 1875, Sen and Bag 1983).
- 3.
Chronologically, this period of Indian astronomy and mathematics should be taken to commence from when the Vedic hymns began to be composed, which some date as going back to 1500 bc. Certain issues regarding early Indian chronology have unfortunately become tug-of-war between those Westerners who see themselves as the guardians and promoters of impartial scholarship and invariably adopt conservative dating, and certain Indians who make excessive claims of antiquity for the early sources of Indian mathematics and astronomy. The tunnel vision of both groups make the task of incorporating recent discoveries in archaeology, necessitating drastic revisions the conservative dating of the Vedic period, more difficult. What this evidence would indicate is that earlier versions of both Sathapatha Brahmana and Sulbasutras should be placed about a 1,000 years earlier than the conservative dates attributed to these texts. For further details on recent evidence from archaeology, see Frawley (1991) and Kak (1987, 1993). A thorny question on the history of early Indian mathematics is how much importance should be given to oral evidence compared to written texts. Ignoring the oral evidence and regretting the paucity of written evidence has led to a fissure in the ranks of historians of Indian mathematics, generating more heat than light even in current discussions of the subject.
- 4.
The literature includes, four Vedic Samhitas (i.e., Rigveda, Yajurveda, Samayeda and Atharavdveda) in their various recensions, being the collection and presentation in a classified form of a large number of Vedic hymns; a set of elucidatory literature called Brahmanas of which the Sathapatha Brahmana is the most important for our purposes; a set of philosophical treatises called Upanishads; and six Vedangas, written for the purpose of instilling the correct methods of recitation of the Vedas and performing Vedic rituals, of which two, the Jyotisa and the Kalpa, are particularly important, since the first contains early knowledge of astronomy and the last contains the Sulbasutras.
- 5.
The measures used in the Sathapatha Brahmana were the same as in the Sulbasutras. The important units of measurement were:
1 pada = 15 angulas,
1 prakrama = 2 padas,
1 purusha = 4 prakramas = 120 angulas.
A prakarama is about 0.5 m.
- 6.
In Vedic mythology, time was represented by the metaphor of a bird. The year was divided into six seasons, with the head of the bird being the vasant, the body being both hemanta and sisira the wings being sarad and grishma and the tail being varsha.
- 7.
Seidenberg (1983, pp. 113–116) contains an interesting discussion of the ambiguities in the Vedic texts relating to equivalences of area as well as the philosophical underpinnings of such a requirement.
- 8.
Apastamba’s procedure may be interpreted as follows: Let the cord placed on the East-west line be x units in length. If the length of the cord is extended by half the original length (x + l/2x), and a mark is made at a distance of 5x/12 from one end, then remaining part of the cord is 13x/12. If we now tie the cord to the ends of the East-west line, and stretch it up to the mark, we get a right-angled triangle who sides are x, 5x/12 and 13x/l2. This relationship will hold for any integral value of x.
- 9.
Two different types of bricks were used in altar construction. There were ordinary bricks (lokamprina) and special (yajushmatt) bricks, each of which was consecrated and then marked for purposes of identification. The bricks varied by size and shape and were used in different combinations in constructing different layers of the altars. Thus for example, the first, third and fifth layers of a falcon-shaped altar with six-tipped wings was made of 38 squares, 58 rectangles (of two sizes) and 104 triangles (of two sizes); the second and fourth layers were constructed from 11 squares, 88 rectangles (of two sizes) and 101 triangles (of six sizes and five shapes). Different configurations of these basic figures were used in construction of falcon-shaped altars with five-tipped wings, with different rituals being performed on different altars. Staal (1978) provides a detailed description of the construction of these altars and their accompanying rituals, with one of the most recent ones involving a five-tipped falcon-shaped altasr being performed in Kerala, South India, in 1990.
- 10.
Apart from minor variations, the body of the top layer of the falcon-shaped altar was 4 square purushas. The wings and tail were 1 square purusha each plus the wing increased by 1/5 of a square purusha each and the tail by 1/10 of a square purusha so that the image would more closely approximate the shape of a falcon. Thus the total area of the top layer is: 4 + (2 × 1.2) + 1.1 = 7.5 square purushas or approximately 30 m2.
- 11.
In Katyayana Sulbasutra (5.4) appears the following instruction: “For the purpose of adding a square purusha [to the original falcon-shaped altar], construct a square equivalent to the original altar together with the wings and tail, add to it a square of one purusha. Divide the sum [i.e., the resulting square] into fifteen parts and combine two of these into a square. This will be the [new] unit of square purusha [for the construction of the enlarged figure]”.
- 12.
The instructions given in Sathapatha Brahmana (X.2.3.11–14) for constructing a falcon-shaped altar consisting of 95 layers of bricks may be interpreted as follows:
Area of the body = 56 + (12/7)(56)
Area of two wings = 2(14) + (3/7)(14) + (1/5)(1/7)(3)(14)
Area of tail = 14 + (3/7)(14) + (1/10)(1/7)(3)(14)
The total area is about 116 square purushas, which is an over-estimate of the actual 101.5 square purushas, arising in part from a rounding-off error resulting from taking 14 rather than (13 + 8/15). Baudhyana Sulbasutra contains an explanation of how the estimate of the total area was obtained. Expressed in modem notation:
Let the new unit after the mth augmentation be x.
Then
x 2 = 1 + (2m/15) where m runs from 1 to 94.
For m = 94,
x 2 = 13 + 8/15.
So we see that 14, the estimate used, is a rounding-up of this number. The use of the more accurate figure gives the calculated total area as 110 square purusha.
- 13.
The essence of this method involves two commonsense assumptions:
-
i.
Both the area of a plane figure and the volume of a solid remain the same under rigid translation to another place.
-
ii.
If a plane figure or solid is cut into several sections, the sum of the areas or volumes of the sections is equal to the area or volume of the original figure or solid. For example, the following sizes and shapes of bricks used to construct one of the layers of a falcon-shaped altar can be “dissected and reassembled” from a square:
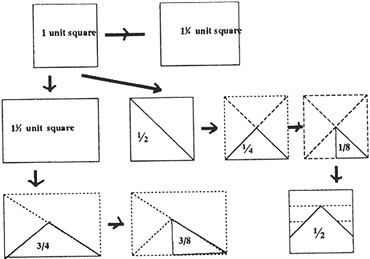
The reasoning behind this approach was very different from that behind Euclidean geometry, but the method was often just as effective, as shown in the Indian (and Chinese) “proofs” of the Pythagorean theorem. For further details, see Joseph (1992, 1994).
-
i.
- 14.
There are interesting similarities and differences between the geometry of Greece and that of Vedic India. Both were used in the construction of sacred altars for ritual purposes; both had to solve the fundamental practical problem of how to construct a square equal to the area of a given rectangle. However, an important difference which shaped the way geometry developed in the two cultures was the Greek concentration on volume, notably the problem of “doubling the cube”, while in India the principal questions involved the area of altars: the circular, the square, the trapezoid and combinations of these shapes. For a discussion of these constructions and the mathematics underlying them, see Joseph (1992, pp. 228–236; 1993, pp. 6–11; 1994, p. 184–189).
- 15.
Various rituals required the day-time and night-time to be divided into 2, 3, 4, 5 and 15 equal parts. In the 15-fold division, each part was a muhurta, which would be equivalent to 1/15 of (12 × 60), or 48 min.
- 16.
A number of other parallels based on the equivalence of numbers is found the Vedic literature of the period. For further examples, see Kak (1993).
- 17.
The choice of 21 is supposedly symbolic. It is the sum of 12 months, 5 seasons, 3 worlds and the sun; or the three sets of rishis (or planets); or the sum of five elements (earth, water, fire, air, space), five breaths (prana, apana, vyana, udana, samana), five organs of cognition (jnanednriyas), five organs of action (karmendriyas) and the inner ear (antakarana).
- 18.
There are indications in the texts that the authors of the Sulbasutras were aware of this distinction, for often one comes across expressions, “thus we are told”, “such are our instructions”, etc. The implication is that these instructions (say, on the sacrificial efficacy of different shaped altars or the astronomical codes to be adhered to) were not particularly relevant to the main purposes of the texts. These instructions were simply taken for granted, while the texts themselves paid exclusive attention to the technique of executing them. In fact, the texts are exemplars of how exact science may grow directly out of applications.
- 19.
Consider the following passage from the Taittiriya Samhita (iv.4.11): “May these bricks, O Agni, be milch cows for me, one, and a thousand, and a million, and ten million, and a hundred million, and a thousand million, and ten thousand million,.,,; may these bricks, O Agni, be for me milkers of desires named the glorious yonder in yon world”.
References
Datta, B. 1932. The Science of the Sulba. Calcutta: University Press.
Frawley, D. 1991. Gods, Sages and Kings. Salt Lake City: Passage Press.
Joseph, G. G. 1992. The Crest of the Peacock: Non-European Roots of Mathematics, 3rd printing. London: Penguin. (A third and greatly expanded third edition was published in 2011 by Princeton University Press)
———. 1993. What is a Square Root: A study of geometrical representation in different mathematical traditions. Pp. 3–14 in Proceedings of the 1993 Annual Meeting of CM.E.S.G., M. Quigley, ed. Calgary: University of Calgary.
———. 1994. Different Ways of Knowing: Contrasting Styles of Argument in India and the West. Pp. 183–198 in Selected Lectures from the 7th International Conference on Mathematical Education. Sainte-Foy, Quebec: Les Presses de l’Universite Laval.
Kak, S. C. 1987. On the astronomy in ancient India. Indian Journal of History of Science 22: 205–221.
———. 1993. Astronomy of the Vedic Altars. Vistas in Astronomy 36: 117–140.
Mackie, E. W. 1977. The Megalithic Builders. Oxford: Phaidon.
Seidenberg, A. 1983. The geometry of the Vedic Rituals. Pp. 95–126 in Agni, The Vedic Ritual of the Fire Altar, vol. II, F. Staal, ed. Berkeley: Asian Humanities Press.
Sen, S. N. and A. K. Bag. 1983. The Sulbasutras. New Delhi: Indian National Science Academy.
Staal, F. 1978. “The Ignorant Brahmin of the Agnicayana,” Annals of the Bhandarkar Oriental Research Institute, Diamond Jubilee Number, pp. 337–348.
Thibaut, G. 1875. On the Sulbasutra. Journal of the Asiatic Society of Bengal 44, 3: 227–275.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Joseph, G.G. (2015). Geometry of Vedic Altars. In: Williams, K., Ostwald, M. (eds) Architecture and Mathematics from Antiquity to the Future. Birkhäuser, Cham. https://doi.org/10.1007/978-3-319-00137-1_10
Download citation
DOI: https://doi.org/10.1007/978-3-319-00137-1_10
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-319-00136-4
Online ISBN: 978-3-319-00137-1
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)









