Pseudodifferential Operators on Manifolds with Foliated Boundaries

Abstract

Let X be a compact manifold with boundary ∂X endowed with a fibration

1991 Mathematics Subject Classification: 58J28, 58J32, 58J40.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

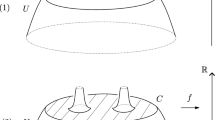
1 Manifolds with Fibred Boundaries

Let X be a compact manifold with boundary ∂X endowed with a fibration

Let $x \in {\mathcal{C}}^{\infty }(X)$ be a boundary defining function and let ${g}_{\Phi }$ be a complete Riemannian metric on X ∖ ∂X which in a collar neighborhood of ∂X is of the form

$${g}_{\Phi } = \frac{d{x}^{2}} {{x}^{4}} + \frac{{\Phi }^{{_\ast}}h} {{x}^{2}} + \kappa ,$$

(1)

where κ is a symmetric 2-tensor restricting to give a metric on each fibre of $\Phi$ and h is a Riemannian metric on Y. To study geometric operators (Laplacian, Dirac operators) associated to such metrics, Mazzeo and Melrose introduced a calculus of pseudodifferential operators: the $\Phi$-calculus. The starting point is the Lie algebra of $\Phi$-vector fields:

$${\mathcal{V}}_{\Phi }(X) =\{ \xi \in \Gamma (TX)\;\vert \;\xi x \in {x}^{2}{\mathcal{C}}^{\infty }(X),\;{\Phi }_{ {_\ast}}({\left.\xi \right \vert }_{\partial X}) = 0\}.$$

In local coordinates, such a vector $\xi \in {\mathcal{V}}_{\Phi }(X)$ takes the form:

$$\xi = a{x}^{2} \frac{\partial } {\partial x} +\sum\limits_{i}{b}^{i}x \frac{\partial } {\partial {y}^{i}} +\sum\limits_{j}{c}^{j} \frac{\partial } {\partial {z}^{j}},\quad a,{b}^{i},{c}^{j} \in {\mathcal{C}}^{\infty }(X).$$

Since it is a Lie algebra, we can consider its universal enveloping algebra to define $\Phi$-differential operators. Mazzeo and Melrose defined more generally $\Phi$-pseudodifferential operators. They are useful to study mapping properties, for instance to determine when a $\Phi$-differential operator is Fredholm.

2 Manifolds with Foliated Boundaries

Question 1.

What can we do when the fibration $\Phi$ is replaced by a smooth foliation $\mathcal{F}$ on ∂X?

The notion of $\mathcal{F}$-vector fields is easy to define:

$${\mathcal{V}}_{\mathcal{F}}(X) =\{ \xi \in \Gamma (TX)\;\vert \;\xi x \in {x}^{2}{\mathcal{C}}^{\infty }(X),\;{\left.\xi \right \vert }_{ \partial X} \in \Gamma (T\mathcal{F})\}.$$

This is still a Lie algebra, so we can define $\mathcal{F}$-differential operators. However, since pseudodifferential operators are not local, we expect global aspects of the foliation $\mathcal{F}$ to come into play. One approach consists in using groupoid theory, namely, since ${\mathcal{V}}_{\mathcal{F}}(X)$ is in fact a Lie algebroid, we can integrate it to get a Lie groupoid $\mathcal{G}$. We can then use the general approach of Nistor-Weinstein-Xu to construct a pseudodifferential calculus. We will instead proceed differently by assuming the foliation can be ‘resolved’ by a fibration. This restricts the class of foliations that can be considered, but will allow us to develop further the underlying analysis.

We will assume the foliation arises as follows:

• 1. $\partial X = \partial \widetilde{X}/\Gamma$, where $\Gamma$ is a discrete group acting freely and properly discontinuously on $\partial \widetilde{X}$, a possibly non-compact manifold;

• 2. There is a fibration $\Phi : \partial \widetilde{X} \rightarrow Y$ with $Y$ a compact manifold;

• 3. The group $\Gamma$ acts Y in a locally free manner (that is, if $\gamma \in \Gamma$ and $\mathcal{U}\subset Y$ an open set are such that y ⋅γ = y for all $y \in \mathcal{U}$, then γ is the identity element) and so that $\Phi (p \cdot \gamma ) = \Phi (p) \cdot \gamma$ for all $p \in \partial \widetilde{X}$ and $\gamma \in \Gamma$;

• 4. The images of the fibres of $\Phi$ under the quotient map $q : \partial \widetilde{X} \rightarrow \partial X$ give the leaves of the foliation $\mathcal{F}$.

Example 1.

The Kronecker foliation on the 2-torus with lines of irrational slope θ arise in this way. One takes $\partial \widetilde{X} = \mathbb{R} \times \mathbb{R}/\mathbb{Z}$ with the fibration $\Phi$ given by the projection on the right factor $Y = \mathbb{R}/\mathbb{Z}$, and the group $\Gamma$ to be the integers with action given by

$$(x,[y]) \cdot k = (x + k,[y - k\theta ]),\;[y] \cdot k = [y - k\theta ],\;k \in \mathbb{Z}.$$

The identification with the standard definition of the Kronecker foliation is then given by the map

$$\begin{array}{lccc} \Psi :&(\mathbb{R} \times \mathbb{R}/\mathbb{Z})/\mathbb{Z}& \rightarrow &{\mathbb{T}}^{2} = \mathbb{R}/\mathbb{Z} \times \mathbb{R}/\mathbb{Z} \\ & [x,[y]] & \mapsto & ([x],[y + \theta x])\end{array}$$

Example 2.

Seifert fibrations (circle foliations on a compact 3-manifold) typically arise in this way, except when the space of leaves is a bad orbifold.

For such foliations, we can define $\mathcal{F}$-operators as follows. We let M = ∂X ×[0, ε) _x  ⊂ X be a collar neighborhood of ∂X and consider $\widetilde{M} = \partial \widetilde{X} \times [0,\epsilon {)}_{x}$ with $\Gamma$ acting on $\widetilde{M}$ in obvious way so that $\widetilde{M}/\Gamma = M$. On $\widetilde{M}$, we consider the space of $\Gamma$-invariant $\Phi$-operators ${\Psi }_{\Phi ,\Gamma }^{{_\ast}}(\widetilde{M})$ with support away from x = ε. Given $\widetilde{P} \in {\Psi }_{\Phi ,\Gamma }^{k}(\widetilde{M})$, we can make it act on $f \in {\mathcal{C}}^{\infty }(M)$ by requiring that $\widetilde{P}({q}^{{_\ast}}f) = {q}^{{_\ast}}\widetilde{P}(f)$, where $q :\widetilde{ M} \rightarrow M$ is the quotient map. This is meaningful because $\widetilde{P}$ acts on $\Gamma$ invariant functions to give again $\Gamma$-invariant functions. We denote by ${q}_{{_\ast}}\widetilde{P}$ the operator acting on ${\mathcal{C}}^{\infty }(M)$ obtained from $\widetilde{P}$ in this way.

Definition 1.

An $\mathcal{F}$-pseudodifferential operator $P \in {\Psi }_{\mathcal{F}}^{m}(X)$ is an operator of the form

$$P = {q}_{{_\ast}}{P}_{1} + {P}_{2},\quad {P}_{1} \in {\Psi }_{\Phi ,\Gamma }^{m}(\widetilde{M}),\;{P}_{ 2} \in \dot{ {\Psi }}^{m}(X).$$

From the $\Phi$-calculus, we deduce relatively easily that $\mathcal{F}$-operators are closed under composition, that they map smooth functions to smooth functions and that they are bounded when acting on appropriate Sobolev spaces. One can also introduce a notion of principal symbol σ _m (P) as well as a notion of normal operator ${N}_{\mathcal{F}}(P)$ defined by ‘restricting’ the operator P to the boundary. This leads to a simple criterion to describe Fredholm operators. An operator $P \in {\Psi }_{\mathcal{F}}^{m}(X)$ is Fredholm (when acting on suitable Sobolev spaces) if and only if its principal symbol σ _m (P) and its normal operator ${N}_{\mathcal{F}}(P)$ are invertible.

3 An Index Theorem for Some Dirac-Type Operators

Assume now that the the foliation $\mathcal{F}$ is also such that $\partial \widetilde{X}$ is compact and the group $\Gamma$ is finite. In particular, the leaves of $\mathcal{F}$ must be compact. Let ${g}_{\mathcal{F}}$ be a metric such that ${q}^{{_\ast}}({\left.{g}_{\mathcal{F}}\right \vert }_{M})$ takes the form (1) near $\partial \widetilde{X}$. Suppose X is even dimensional and that X, $\widetilde{X}$ and Y are spin manifolds. Let ${D}_{\mathcal{F}}$ be the induced Dirac operator. Suppose its normal operator ${N}_{\mathcal{F}}({D}_{\mathcal{F}})$ is invertible, which is the case for instance when the induced metric on the leaves of the foliation $\mathcal{F}$ has positive scalar curvature. Under the decomposition $S = {S}^{+} \oplus {S}^{-}$ of the spinor bundle, the Dirac operator can be written as

$${D}_{\mathcal{F}} = \left (\begin{array}{cc} 0 &{D}_{\mathcal{F}}^{-} \\ {D}_{\mathcal{F}}^{+} & 0 \end{array} \right ).$$

Since ${N}_{\mathcal{F}}({D}_{\mathcal{F}})$ is invertible, the operator ${D}_{\mathcal{F}}^{+}$ is Fredholm.

Theorem 1.

The index of ${D}_{\mathcal{F}}^{+}$ is given by

$$\text{ ind}({D}_{\mathcal{F}}^{+}) =\int\limits_{X}\widehat{A}(X,{g}_{\mathcal{F}}) - \frac{1} {\vert \Gamma \vert }\int\limits_{Y }\widehat{A}(Y,h)\widehat{\eta }(\widetilde{{D}}_{0}) + \frac{\rho } {2},$$

where $\widetilde{{D}}_{0}$ is a family of Dirac operators on the fibres of $\Phi : \partial \widetilde{X} \rightarrow Y$ associated to ${q}^{{_\ast}}({\left.{D}_{\mathcal{F}}\right \vert }_{M})$ and $\rho = \frac{\eta (\widetilde{{D}}_{\delta })} {\vert \Gamma \vert } - \eta ({D}_{\delta })$ is a difference of two eta invariants with $\widetilde{{D}}_{\delta }$ the Dirac operator on $(\partial \widetilde{X}, \frac{{\Phi }^{{_\ast}}h} {{\delta }^{2}} + \kappa )$ and D _δ the Dirac operator on $(\partial X,{q}_{{_\ast}}(\frac{{\Phi }^{{_\ast}}h} {{\delta }^{2}} + \kappa ))$ . Both $\widetilde{{D}}_{\delta }$ and D _δ are invertible for δ > 0 small enough and ρ does not depend on δ.

The strategy to prove this theorem is to take an adiabatic limit.