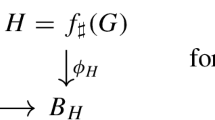Generalized Blow-Up of Corners and Fiber Products

Abstract

Consider the category of manifolds with corners and interior b-maps f : X → Y.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Consider the category of manifolds with corners and interior b-maps f : X → Y. These are required to pull back smooth functions to be smooth, and pull back each principal ideal¹ ${\mathcal{I}}_{H} = {C}^{\infty }(Y ) \cdot {\rho }_{H}$ of functions vanishing on a boundary hypersurface $H \in {\mathcal{M}}_{1}(Y )$ to a product

$$ {f}^{{\ast}}{\mathcal{I}}_{H} \subset {\prod \limits }_{G\in {\mathcal{M}}_{1}(X)}{\mathcal{I}}_{G}^{\alpha (H,G)}\quad \alpha (\cdot ,\cdot ) \in \mathbb{N} $$

(1)

of similar ideals in C ^∞(X). One reason to consider this category is that it contains blow-up.

Recall that the blow-up of a codimension k boundary face² $F \in {\mathcal{M}}_{k}(Y )$ is the space $[Y ;F] = Y \setminus F \cup {S}_{+}NF$, where S ₊ NF denotes the inward pointing spherical normal bundle. It has a “blow-down” map β : [Y ; F] → Y and is equipped with the smooth functions generated by β^∗ C ^∞(Y ) as well as the quotients ${\rho }_{{H}_{i}}/{\rho }_{{H}_{j}}$ (where finite) of boundary defining functions for hypersurfaces through F.

While this theory is well-known, we give a new description of the data defined by a b-map that allows for significant clarification and generalization of boundary blow-up, which we use to discuss the existence and resolution of fiber products of manifolds with corners. This new description is the theory of monoidal complexes and their refinements.

The boundary faces of a manifold have natural ‘b-normal’ spaces

$${}^{\mathrm{b}}NF {\subset }^{\mathrm{b}}{T}_{ F}X,\quad F \in {\mathcal{M}}_{{\ast}}(X)$$

with natural inclusions ${}^{\mathrm{b}}{N}_{p}F {\subset }^{\mathrm{b}}{N}_{p}G$ whenever p ∈ G ⊂ F. At each point these are spanned by the ‘radial’ vector fields with respect to the face in question. As a result such a bundle has a global canonical frame³ $\{{\rho }_{i}{\partial }_{{\rho }_{i}}\}$ by which it can be trivialized, identifying the fibers with a fixed vector space ^b NF which has well-defined lattice structure $\mathrm{{span}}_{\mathbb{Z}}\{{\rho }_{i}{\partial }_{{\rho }_{i}}\}$. Taking the inward pointing lattice points defines a ‘smooth,’ which is to say freely generated, monoid

$${\sigma }_{F} =\mathrm{{ span}}_{{\mathbb{Z}}_{+}}\{{\rho }_{i}{\partial }_{{\rho }_{i}}\},$$

and the collection of these along with the inclusions ${i}_{GF} : {\sigma }_{G}\hookrightarrow {\sigma }_{F}$ for G ⊆ F define what we call the ‘basic monoidal complex’ of X:

$${\mathcal{P}}_{X} =\{ ({\sigma }_{F},\ {i}_{GF})\;;\;G \subseteq F \in \mathcal{M}(X)\}.$$

A b-map f : X → Y has a tangent differential which at a face $F \in \mathcal{M}(X)$ restricts to a well-defined monoid homomorphism (i.e. additive map)

$${f}_{\natural } : {\sigma }_{F} \rightarrow {\sigma }_{G}$$

where G is the boundary face of largest codimension in Y such that f(F) ⊂ G. Indeed, viewed as a matrix, the coefficients of this map are just the relevant exponents $\alpha (\cdot ,\cdot ) \in {\mathbb{Z}}_{+}$ in (1). The collection of these homomorphisms patch together to form a morphism

$${f}_{\natural } : {\mathcal{P}}_{X} \rightarrow {\mathcal{P}}_{Y }$$

of monoidal complexes which is fundamental to our discussion.

In general, the monoidal complexes and their morphisms capture only the combinatorial relationships between boundary faces of X, those of Y , and the order of vanishing of boundary defining functions with respect to these faces. However, in the case of blow-up, this is enough to completely specify the domain X = [Y ; F] in terms of the range Y. Indeed, in this case the blow-down map has additional properties, namely

$$\beta : X \setminus \partial X \rightarrow Y \setminus \partial Y \ \text{ is a diffeomorphism,}$$

(2)

and

$${ }^{\mathrm{b}}{\beta }_{ {\ast}} {: }^{\mathrm{b}}{T}_{ p}X {\rightarrow }^{\mathrm{b}}{T}_{ \beta (p)}Y \ \text{ is an isomorphism for all}\ p,$$

(3)

and the morphism ${\beta }_{\natural } : {\mathcal{P}}_{X} \rightarrow {\mathcal{P}}_{Y }$ forms what we call a ‘smooth refinement’ of ${\mathcal{P}}_{Y }$.

Abstracting this, we call a smooth proper map between manifolds satisfying (1), (2) and (3) a generalized blow-down map. Such are substantially more general than standard blow-down maps, and one of our main results is a complete characterization of these maps.

FormalPara Theorem 1.

A generalized blow-down map f : X → Y determines a smooth refinement ${\mathcal{P}}_{X} \rightarrow {\mathcal{P}}_{Y }$ of the monoidal complex on Y , and conversely for any smooth refinement $\mathcal{R}\rightarrow {\mathcal{P}}_{Y }$ there is a unique (up to diffeomorphism) manifold $X = [Y ;\mathcal{R}]$ with ${\mathcal{P}}_{X} = \mathcal{R}$ and a generalized blow-down map $f : X = [Y ;\mathcal{R}] \rightarrow Y$.

We call $[Y ;\mathcal{R}]$ the ‘generalized blow-up’ of Y by the refinement $\mathcal{R}$, and we show that the important question of lifting of b-maps under generalized blow-ups of the domain and/or range can be addressed at the level of monoidal complexes.

Finally this theory is applied to the problem of fiber products. Recall that, in any category, the fiber product of two maps f _i : X _i  → Y , i = 1, 2 is an object X with maps h _i : X → X _i such that ${f}_{1} \circ {h}_{1} = {f}_{2} \circ {h}_{2}$, and has the universal property that for any other maps g _i : Z → X _i such that ${g}_{2} \circ {f}_{2} = {g}_{1} \circ {f}_{1}$ there is a unique map h : Z → X through which they factor.

In the category of sets there is a unique fiber product

$${X}_{1} {\times }_{Y }{X}_{2} =\{ ({p}_{1},{p}_{2})\;;\;{f}_{1}({p}_{1}) = {f}_{2}({p}_{2})\} \subset {X}_{1} \times {X}_{2},$$

(4)

however, in the setting of manifolds, (4) is not smooth and fiber products do not generally exist. For manifolds without boundary, there is a well-known sufficient condition for existence, namely that f ₁ and f ₂ be transversal, meaning that whenever ${f}_{1}({p}_{1}) = {f}_{2}({p}_{2}) = q \in Y$, then

$${({f}_{1})}_{{\ast}}({T}_{{p}_{1}}{X}_{1}) + {({f}_{2})}_{{\ast}}({T}_{{p}_{2}}{X}_{2}) = {T}_{q}Y.$$

(5)

In this case (4) is a smooth manifold and the h _i are smooth maps.

The natural analog of (5) in the setting of manifolds with corners is ‘b-transversality,’ namely the requirement that

$${{(}^{\mathrm{b}}{f}_{ 1})}_{{\ast}}{(}^{\mathrm{b}}{T}_{{ p}_{1}}{X}_{1}) + {{(}^{\mathrm{b}}{f}_{ 2})}_{{\ast}}({}^{\mathrm{b}}{T}_{{ p}_{2}}{X}_{2}) {= }^{\mathrm{b}}{T}_{ q}Y.$$

(6)

Under this condition, (4) is not necessarily a manifold, but it is a union of what we call ‘interior binomial subvarieties.’ These are objects generalizing manifolds with corners, with smooth interiors and boundary faces of the same type.

As for a manifold, there is a natural monoidal complex ${\mathcal{P}}_{D}$ defined over the boundary faces of a binomial subvariety D ⊂ X, the difference being that the monoids may not be smooth (freely generated). If they are smooth, then D has a natural structure of a smooth manifold (though it need not be smoothly embedded in X), and if they are not, we show that D can be resolved, giving a smooth manifold $[D;\mathcal{R}] \rightarrow D$ for every smooth refinement $\mathcal{R}\rightarrow {\mathcal{P}}_{D}$.

In the case of fiber products, the monoids in ${\mathcal{P}}_{D}$ are of the form

$${\sigma }_{{F}_{1}} {\times }_{{\sigma }_{G}}{\sigma }_{{F}_{2}},\quad {F}_{i} \in \mathcal{M}({X}_{i}),\;{f}_{i}({F}_{i}) \subset G$$

(7)

which leads to our second main theorem.

FormalPara Theorem 2.

If f _i : X _i → Y are b-maps of manifolds with corners which satisfy (6), and if each of the monoids (7) is freely generated, then there exists a smooth fiber product in the category of manifolds with corners.

In case the monoids (7) are not freely generated, our theory leads to the following ‘resolved’ version of the fiber product.

FormalPara Theorem 3.

For every smooth refinement $\mathcal{R}$ of the complex ${\mathcal{P}}_{{X}_{1}{\times }_{Y }{X}_{2}}$ , there is a smooth manifold with corners $[{X}_{1} {\times }_{Y }{X}_{2}\;;\;\mathcal{R}]$ with maps to X _i commuting with the f _i : X _i → Y. If h _i : Z → X _i , i = 1,2 are smooth maps commuting with the f _i for some other manifold Z, then there exists a generalized blow-up $[Z;\mathcal{S}] \rightarrow Z$ and a unique map $h : [Z;\mathcal{S}] \rightarrow [{X}_{1} {\times }_{Y }{X}_{2}\;;\;\mathcal{R}]$ such that the maps form a commutative diagram.