Oppositions and Opposites

Abstract

A formal theory of oppositions and opposites is proposed on the basis of a non-Fregean semantics, where opposites are negation-forming operators that shed some new light on the connection between opposition and negation. The paper proceeds as follows.

After recalling the historical background, oppositions and opposites are compared from a mathematical perspective: the first occurs as a relation, the second as a function. Then the main point of the paper appears with a calculus of oppositions, by means of a non-Fregean semantics that redefines the logical values of various sorts of sentences. A number of topics are then addressed in the light of this algebraic semantics, namely: how to construct value-functional operators for any logical opposition, beyond the classical case of contradiction; Blanché’s “closure problem”, i.e. how to find a complete structure connecting the sixteen binary sentences with one another.

All of this is meant to devise an abstract theory of opposition: it encompasses the relation of consequence as subalternation, while relying upon the use of a primary “proto-negation” that turns any relatum into an opposite. This results in sentential negations that proceed as intensional operators, while negation is broadly viewed as a difference-forming operator without special constraints on it.

1 The Historical Background of Logical Oppositions

To begin with, everyone knows the “famous square of opposition”, but what it consists in is less clear. Moreover, almost everyone wrongly equates this polygon with the entire theory of opposition. Let us see this into detail.

1.1 Aristotle’s Square?

The theory of opposition is to be traced back from Aristotle’s logical corpus [1–3], where the Stagirite wanted to examine the whole list of necessary conclusions that could be derived from any pair of sentences varying with respect to their quantity (universal or particular) or quality (affirmative or negative). But contrary to the current expression of “Aristotelian square”, Aristotle never used and wouldn’t have accepted the logical square as a proper diagram for logical oppositions.¹

One main reason why this theory hardly went beyond traditional logic is that Aristotle sticked to two sorts of opposition, viz. contradiction and contrariety. The former follows the laws of contradiction and excluded middle: two contradictory sentences cannot be true together and cannot be false together, while the latter follows the second law only (two contrary propositions can be false together). Furthermore, why bother with a theory of opposition if the only proper task of logic is to state what follows from what in a consequence relation? Be that as it may, the history of logic can testify to the relative poverty of developments about logical opposition taken in isolation. Despite a special attention to opposition in the medieval works (Abelardus, Buridan, Burley, Ockam, Paul of Venice, Peter of Spain, William of Sherwood), all seems to show that the theory of opposition is nothing but a minor section within the area of logic.

1.2 Beyond and Beneath the Square

Nevertheless, a certain revival of the subject-matter occurred during the fifties under the impetus of two French philosophers: Augustin Sesmat [18] and Robert Blanché [5], who independently gave rise to an extension of the well-known Aristotelian square of opposition AEIO. In a nutshell, Blanché claimed that the ambiguous meaning of possibility in the Aristotelian modal syllogistics justifies a further distinction between pure or one-sided and two-sided possibility (contingency): the former means that a possible proposition is not impossible but can be necessary, whereas the latter means that a possible proposition is neither impossible nor necessary. Blanché added that possibility and existential quantification share a common feature in the so-called “reflexive” or natural (informal) reading: their sentential expression is expected to exclude necessity and universality, respectively, so that Blanché and Sesmat favored the use of triangles rather than the Aristotelian square (including the unnatural one-sided possibility I). (See Fig. 1.)

Fig. 1

The logical squares and triangles of contraries for quantified and modal sentences

Opposition essentially proceeds by means of the classical (or standard) negation ∼, given the dual relation between universal and existential quantifiers (∼∀∼↔∃) or between necessity and possibility (∼□∼↔◊). It entails that the above square of quantification assumes a relation of logical consequence from ∀ to ∃. That this relation fails whenever the subject term is empty has been largely discussed in the literature under the name of “existential import”, contributing to the decline of traditional logic; but it could be replied that such a failure is not so much due to the logical square as to its lexicalization. Indeed, the logical square can be seen to be fully valid when only negative sentences are used to express the vertices O and I.²

As opposition is closely related to negation, a care for symmetry led Blanché to supplement his triangle of contraries with an opposite triangle of subcontraries whose sixth uppermost edge U is an unnatural expression of determinacy; U corresponds to the contradictory of two-sided possibility Y=∼U and eventually extends the debated square into a logical hexagon of oppositions AUEIYO. (See Fig. 2.)

Fig. 2

The two logical triangles and in Blanché’s logical hexagon

However, a strict combination of the two above triangles should not lead to the right-sided hexagon as presented with its arrowed lines; these correspond to the fourth opposition of subalternation. At the same time, Aristotle never mentioned the latter in his logical works about opposition, and Jean-Yves Béziau supported this point in [4] in order to leave subalternation aside and reduce the hexagon to a more restricted star of logical oppositions. (See Fig. 3.)

Fig. 3

Béziau’s logical star of oppositions

1.3 Is Subalternation an Opposition?

Why not to include subalternation among the logical oppositions? It is usually assumed that logical opposition refers to incompatibility and means that two opposite sentences cannot be true together. Now given that such is the case in a subalternation, where the subaltern is necessarily true whenever its superaltern is, it naturally follows that Aristotle could not include it among his theory of opposition because the latter is closely related to negation.

But if so, why not to exclude subcontrariety by the same token? Two subcontrary propositions cannot be false together but can be true together; and if a necessary condition for being an opposite is to differ in truth-value, then subalternation also fulfills this requirement since a subaltern can be true whereas its superaltern is false. [4] follows Aristotle’s stringent view of opposition as incompatibility, however, which states that two opposite sentences can never be true together. While noting that subcontraries are merely “verbal” oppositions according to [3, 4] still includes them into the class of oppositions whether for indirect or constructive reasons: indirect, in the sense that subcontraries amount to contradictories of contraries and are thus defined in terms of direct or genuine opposites; constructive, in the sense that refusing subcontrariety leads to incomplete polygons that cannot yield a full geometrical presentation of logical oppositions.

In the light of these preliminaries, the paper wants to give a broader analysis of logical oppositions. Rather than restricting opposition to a relation of incompatibility between two propositions, a more comprehensive presentation should include some other sorts of syntactic object (beyond quantified sentences) and relation (beyond incompatibility). For this purpose, let us abstract from the Aristotelian context and construct a purely formal theory of logical opposition.

2 Opposition and Opposites

To begin with, it is worthwhile noticing that no opposition can occur without opposites: any two concepts, terms, propositions or whatever else express an opposition if and only if either of these is the opposite of the other one. However, no genuine theory of opposites has ever been proposed in support of the current theory of opposition. In order to do justice to this logical primacy of opposites over oppositions, let us consider the difference between the two related concepts from a mathematical point of view.

2.1 Two Mathematical Notions

Take the opposition between black and white as an example. It is well known that these stand into a relation of contrariety, which entails that black is the contrary of white just as white is the contrary of black. Furthermore, such an opposition between concepts can be transferred to the sentential level by saying that the related sentences “This table is black” and “This table is white” cannot be true together but can be false together (whenever the table is neither white nor black). The mathematical difference between an opposition and an opposite is that the former is a relation, the latter a function. In the sentence “Tom and Jim are mutual brothers”, brotherhood is the expression of a relation between the two individuals Tom and Jim. In logical symbols:³

$$(\exists \mathrm{x})(\exists \mathrm{y}) \mathrm{B}\bigl(\mathrm{T}(\mathrm{y}),\mathrm{J}(\mathrm{x})\bigr) $$

If this sentence is true, then it is the case that both Jim is Tom’s brother and Tom is Jim’s brother; this means that the two-place relation of brotherhood can be translated into a function of being brother of. It results in two synonymous sentences as follows:

By analogy, the same logical reformulation can be applied to the higher-order sentence “The sentences α and ψ are mutual contradictories” once quantification over sentential variables is allowed:

$$(\exists\alpha)(\exists\psi) \mathrm{C}(\alpha,\psi) $$

Again, this entails that ψ is the contradictory of α and, conversely, that α is the contradictory of ψ:

Oppositions and opposites can be further described in a syntactic and semantic way.

Syntactically speaking, opposition is a sentence-forming relation attached to predicate variables if its arguments are concepts, or sentence variables if its arguments are sentences; it is usually presented as a two-place predicate, but more than two arguments can be related by it.⁴ As to the opposite, it is a one-place function that yields another concept if attached to a concept, or another sentence if attached to a sentence. Only concepts and sentences are the syntactic objects concerned with oppositions and opposites: it does not make sense to say that a given individual is logically opposed to another one, so that we restrict the theory of opposition to predicate or sentence variables as its arguments.

Semantically speaking, a relation of opposition proceeds as a mapping from V×V to V (where V is a set of truth-values). In the sentence “Black and white are contrary to each other”, for instance, contrariety is a relation that is attached to a pair of propositions like {this table is black, this table is white} and makes the whole sentence true in V. By contrast, a function of opposite is a mapping from V to V that turns the truth-value associated to a sentence into another one in V. In the sentence “ψ is the contrary of α”, contrariety is attached to the truth-value of α and results into the truth-value of ψ. The entire sentence is true only if either α is false whenever ψ is true, or α and ψ are both false.

2.2 Opposition and Truth-Values

Nevertheless, such a purely formal presentation could be blamed for not taking the sentential content into account: formal logic is topic-neutral, but the traditional precondition for logical opposition is that opposite sentences to differ with respect to quality or quantity while being about the same subject and predicate. Thus “Every raven is black” and “Some raven is not black” are properly opposed to each other by differing only with respect to quality and quantity, the former affirming blackness of every raven and the latter negating it of some of these. Consequently, a purely formal characterization fails by reducing the relation of opposition to a relation between contentless truth-values. We challenge the content-dependent approach of opposition in the following, and the motivation for a purely formal theory of oppositions and opposites will be detailed in the next section.

More generally, a logical opposition is meant to be a relation between a sentence α and its opposite ψ. Letting OP stand for the relation of opposition and O for the opposite-forming function (or operator), it thus follows from it this general logical form:

$$\mathrm{OP}(\alpha,\psi) = \mathrm{OP}\bigl(\alpha,\mathrm{O}(\alpha)\bigr) $$

2.3 Towards a Calculus of Logical Oppositions

That an opposition is taken to be logical should also mean that it deals with some given calculus upon values.

Truth-values are the expected values for a logic of opposition, and the appropriate calculus will be discussed later on. Let us recall that Aristotle also mentioned several additional oppositions between concepts outside his logical works, especially in [1]: “double” and “half” are said to be opposed by correlation, but nothing logical occurs in this opposition and the same holds for the oppositions by contrariety (“black” and “white”) and privation (“blind” and “sighted”). It could strike one as surprising to say now that opposition by contrariety is not a logical opposition, given that it is a crucial component of the logical square. But again, contrariety is a logical relation only when applied to sentences rather than concepts: only the former can be said to be true or false.

What of its calculus? In standard sentential logic, some oppositions are expressed by truth-functions, i.e. binary connectives that assign truth-values to complex sentences in V. For instance, conjunction is a two-place sentential function that assigns truth to a whole sentence whenever its two arguments are also true, and falsity otherwise. Negation is the only one-place function (or operator) at hand in standard logic, since it turns any true single sentence into a false one and conversely.

Can it be said that each logical connective corresponds to a relation of opposition, and negation to an opposite-forming function? It seems so, while noting at the same time that standard logic cannot give a complete calculus for oppositions and opposites.

On the one hand, to each relation of opposition corresponds one of the sixteen standard connectives.⁵ (See Fig. 4.)

Fig. 4

The four logical oppositions and their corresponding four binary connectives

This can be easily depicted by means of the standard truth-tables, where the various truth-value assignments for any combination of sentential arguments characterize the resulting oppositional relation between these. Thus α and ψ are opposed to each other through the truth-conditions of the standard connectives. (See Fig. 5.)

Fig. 5

The four binary connectives and their truth-tables

On the other hand, nothing is said here about the remaining twelve connectives of standard logic. Which opposition is established by an arbitrary standard connective ⊕ upon its arguments α and ψ in the whole sentence α⊕ψ cannot be answered unless a mechanical procedure is found for this purpose. A least information is given by the above logical square, however: subcontraries have been previously said to be the contradictories of contraries, and this is shown by the opposition between the contrary pairs {α,ψ} and the subcontrary pairs {∼α,∼ψ}. This entails two things: ∼α and ∼ψ are the contradictories of α and ψ, respectively; classical negation ∼ is a contradictory-forming operator, since the relation OP(α,∼α) is a contradiction.

Let us symbolize the four traditional oppositions with capital letters, such that {CT,CD,SCT,SB} is the set of logical oppositions OP including the four elements of contrariety (CT), contradiction (CD), subcontrariety (SCT), and subalternation (SB). Two questions remain unanswered thus far.

Firstly, classical negation ∼ is a contradictory-forming operator in the relation CD(α,∼α); but what is O for the other three relations? O is a unary operator, but standard logic includes only one such non-trivial function that is classical negation; this means that another theory has to be constructed to identify the other opposite-forming operators.

Secondly, every relation of opposition is symmetrical except for subalternation, given that $\operatorname{SB}(\alpha,\psi) \neq \mathrm{SB}(\psi,\alpha)$. How to account for this peculiarity?

A non-standard semantics will be presented in the next section, in order to answer these questions and even more.

3 Question-Answer Semantics

A first step towards the formalization of oppositions has been suggested by Alessio Moretti’s n-opposition theory (N.O.T.) in his so-called “Aristotelian P^Q-semantics” [11], where P refers to the number of answers and Q to the number of questions in a question-answer game.

3.1 The Legacy of N.O.T.

This game was meant to characterize the Aristotelian theory of opposition by means of a combinatorial set of ordered questions and answers.

Thus every given opposition results from a set of two ordered answers to questions about the compossibility of two arbitrary sentences. Let Q₁: “Can α and ψ be both false?”, Q₂: “Can α and ψ both true?”, and let P=1 and P=0 the two sorts of answers to be given accordingly: “yes” or “no”, respectively. It results in a combinatorial set of four ordered pairs of answers, namely: [1|0], [0|0], [0|1], and [1|1]. Moretti argues that each of these pairs characterizes a logical opposition: contrariety, contradiction, subcontrariety, and subalternation.

While giving rise to a new relevant research field, this semantics suffers from two main defaults: on the one hand, a calculus for the P^Q-semantics is still to be found since no operator has been suggested to turn any paired value into another one; on the other hand, the characterization of subalternation as [1|1] is too broad since it includes the biconditional α↔ψ and cannot explain why ψ cannot be false once α is true in the relation SB(α,ψ).

Another question-answer game is purported to fulfill these two requirements: Question-Answer semantics (thereafter: QAS), which proceeds as an algebraic semantic frame.

3.2 Disjunctive Normal Forms and Logical Values

First and foremost, QAS is a non-Fregean semantics: the sense of any sentence α is an ordered finite set of n questions Q(α)=〈q ₁(α),…,q _n (α)〉 (where n≥1) about this sentence; its reference is not a variable truth-value but another sort of constant logical value, viz. an ordered finite set of answers A(α)=〈a ₁(α),…,a _n (α)〉 to the corresponding questions.⁶

Just as in Moretti’s semantics, there are m ⁿ different logical values for a specific set of sentences (where m is the number of the different sorts of answers available for each of the n questions) and, accordingly, 2⁴=16 logical values for any two-place sentential function α⊕ψ. The n=4 ordered questions relate to the Disjunctive Normal Form of any such complex sentence, so that the following expresses the sense of a binary sentence by the truth-conditions of its arguments α and ψ : Q ₁: “Can “α and ψ be both true?”, Q ₂: “Can α be true and ψ be false?”, Q ₃: “Can α be false and ψ be true?”, and Q ₄: “Can α and ψ be both false?”. Symbolizing again a yes-answer by 1 and a no-answer by 0, we thus obtain a set of 16 logical values that refer to the meaning of a binary sentence Φ=α⊕ψ. Its logical value A(Φ)=〈a ₁(Φ),…,a _n (Φ)〉 results in the following combinatorial set (omitting the brackets for sake of convenience):

• (1) A(⊥)=0000 (antilogy);

• (2) A(α∧ψ)=1000 (conjunction);

• (3) A(α↛ψ)=0100 (negated conditional);

• (4) A(α↚ψ)=0010 (negated reverted conditional);

• (5) A(α↓ψ)=0001 (rejection, or negated disjunction);

• (6) A(α)=1100 (truth of α);

• (7) A(α↮ψ)=0110 (negated biconditional);

• (8) A(∼α)=0011 (negated truth of α);

• (9) A(α↔ψ)=1001 (biconditional);

• (10) A(ψ)=1010 (truth of ψ);

• (11) A(∼ψ)=0101 (negated truth of ψ);

• (12) A(α∨ψ)=1110 (disjunction);

• (13) A(α←ψ)=1101 (reverted conditional);

• (14) A(α→ψ)=1011 (conditional);

• (15) A(α↑ψ)=0111 (incompatibility, or negated conjunction);

• (16) A(⊤)=1111 (tautology).

It is well known that the half of these values stand for the classical negation of the remaining half: (1)=∼(16), (2)=∼(15), (3)=∼(14), (4)=∼(13), (5)=∼(12), (6)=∼(8), (7)=∼(9), and (10)=∼(11). This means that one half of the above list already results from the application of one contradictory-forming operator to one complex sentence from the other half.

3.3 Piaget’s INRC Group and Opposites

Jean Piaget showed in [14] that some further opposite-forming operators also help to turn a binary sentence into another one in addition to the function of classical negation. According to his so-called “theory of reversibility”, here is the INRC Group that proceeds as follows in the line of Klein’s Vierergruppe. For every binary sentence Φ of standard logic and its logical value A(Φ)=abcd, there are four sorts of higher-order operators to be applied as follows:

Identity:

A(I(Φ))=abcd

Inversion:

A(N(Φ))=a′b′c′d′

Reciprocity:

A(R(Φ))=dcba

Correlation:

A(C(Φ))=d′c′b′a′

Just as the operator of inversion N corresponds to the truth-function of standard negation, the operator of identity I corresponds to the trivial truth-function of affirmation, turning its argument into itself. And just as the truth-function of affirmation is to be strictly distinguished from a yes-answer in QAS, the truth-function of classical negation applied to sentences differs from the metalinguistic operation of denial: denying a given answer a _i (Φ)=x (where x=1 or 0) results in x′ and means that the initial yes- or no-answer is reverted into a no- or yes-answer. Actually, denial is logically prior to negation in the sense that it helps to define the truth-functional operation of standard negation in QAS, where the latter consists in denying each component a _i (Φ) of a logical value A(Φ) through the operator N.

3.4 Non-truth-functional, but Value-Functional Operators

In addition to the truth-functional affirmation I and negation N, the remaining two operators of reciprocity R and correlation C don’t appear within the standard theory of truth-functions.

A conjecture is to the effect that these are non-truth-functional versions of negation, or non-classical negations whose properties can be made value-functional within our non-Fregean semantics, i.e. a Boolean algebra of non-Fregean logical values.

For one thing, the set {I,N,R,C} includes a group of four commutative and involutive opposite-forming operators whose relative product results in another operator. That is, for any such operations X, Y, Z we have XY=YX=Z and XX=YY=ZZ=I. This accounts for the standard law of double negation, when X=N: NN(Φ)=Φ, and the same holds for the remaining three operators. (See Fig. 6.)

Fig. 6

Piaget’s matrix for the INRC Group

Furthermore, the properties of INRC help to answer to our preceding three questions about OP.

Firstly, it turns out that R proceeds alternatively as a contrary-, contradictory- or subcontrary-forming operator, depending upon which value its argument Φ is given: R is a contrary-forming operator when the logical value of Φ contains only one yes-answer, a contradictory-forming operator when applying to two yes-answers, a subcontrary-forming operator upon three yes-answers, and even collapsing with I when its argument includes only yes- or no-answers (i.e. when α is either a tautology or an antilogy).⁷

Secondly, SCT can be seen as a sort of mixed double negation applied to both the whole sentence and its arguments: the definition of subcontraries as “contradictories of contraries” amounts to the equation SCT(α,ψ)=CT(N(α),N(ψ)), where the relation of contrariety CT includes two complex arguments with contradictory-forming operators N.⁸ It is in this sense that subcontrariety occurs as an “indirect” opposition: its arguments α and ψ can be both true, but its syntactic construction calls for negation-forming operators in O.

Thirdly, the asymmetry of SB entails that no operator O can be said to be a subalternation-forming operator per se: although OP(α,C(α))=SB(α,ψ) for some α, a necessary condition for subalternation is this relation of opposition to be ordered since OP(C(α),α)≠SB(ψ,α). Given that ordering cannot be accounted for by the operation itself, this means that something more must be added to the characterization of subalternation.

Actually, a Boolean algebra of logical oppositions shows that subalternation cannot be properly defined in usual terms of compossible truth-values. Let ∩ and ∪ be the Boolean operations of meet and join such that 1∩x=0∪x=x, 0∩x=0, 1∪x=1, and A(α)∘A(ψ)=〈a ₁(α)∘a ₁(ψ),…,a _n (α)∘a _n (ψ)〉 for any ∘∈{∩,∪}. Then we have the four possible cases of logical opposition OP(α,ψ) in QAS: α and ψ can be both true only if there is at least one common yes-answer about their truth-conditions, and they can be both false if they share at least one common no-answer. This can be expressed algebraically as follows, where join and meet proceed pointwisely upon the elements of each logical value:

3.5 Consequence in Opposition

The fourth relation NCD is a weaker relation of mere non-contradiction, corresponding to the general case in which the two opposite sentences can be both true or both false. Subalternation generally appears as a subcase of non-contradiction, but it requires another condition to be satisfied.

Blanché states it in his own vocabulary of truth-cases and indeterminate sentences (those including three truth-cases, i.e. yes-answers):

The indeterminates are implied by the determinates whose truth-case they contain: since each has three truth-cases, the latter is thus implied by three determinates (…)⁹

In other words, SB(α,ψ) is true if and only if every truth-case for α is also a truth-case for ψ; but the converse needn’t hold, and this does account for the asymmetry of the relation of subalternation unlike that of non-contradiction. This characterization of subalternation as a containment relation between the truth-cases of α and ψ can be rephrased as follows:

$$\mathrm{OP}(\alpha,\psi) = \mathrm{SB}(\alpha,\psi) \qquad \mbox{iff} \qquad \mathbf{A}(\alpha)\cap\mathbf{A}(\psi) =\mathbf{A}(\alpha)\mbox{ and }\mathbf{A}(\alpha)\cup\mathbf{A}(\psi) =\mathbf{A}(\psi) $$

It clearly appears now why SB is an asymmetric relation: the truth of SB(α,ψ) entails that each truth-case of α is also a truth-case of ψ, whereas the truth of SB(ψ,α) would require the converse to hold and this cannot be the case unless α and ψ express one and the same sentence. Unlike the other three logical oppositions, subalternation should not be formed by a standard connective: while being frequently confused with the conditional →, the criterion of containment that characterizes SB makes it similar to the metalinguistic relation of entailment or consequence. In other words, a parallel can be made between the general properties of subalternation and Tarski’s logical consequence as truth-preservation. That is, for any α, ψ:

There are at least two reasons why NCD has never been mentioned thus far as a proper logical opposition. On the one hand, most of the literature on logical opposition merely focused upon the logical square and its limited stock of sentences where any two sentences that can be both true and both false happen to stand into a relation of subalternation. However, not every pair of such non-contradictories collapses into SB with some more complex logical polygons like Tadeusz Czeżowski’s hexagon [9], for instance.¹⁰ (See Fig. 7.)

Fig. 7

Czeżowski’s logical hexagon for binary sentences

Taking again the binary sentences of standard logic, the above relation between α and ψ is a case in point: these can be both true and both false, but not every truth-case of α is also a truth-case of ψ. On the other hand, the content-dependent view of logical opposition seems to reject that α and ψ could be properly opposed to each other; but again, our purely formal and embracing presentation of logical opposition wants to go beyond these preconditions and includes the cases in which any two sentences are compatible while differing by their content.

Let us explore further the algebraic properties of oppositions and opposites, by returning upon the binary connectives of standard logic and developing some new opposite-forming operators in the following.

4 A Theory of Opposites

It is recognized in [7] that [14] developed a famous problem of standard logic, namely: the interconnection between the standard connectives, and its visual presentation within an extended polygon of logical oppositions. Initially, a number of interpreted squares depicted the oppositions between binary sentences instead of quantifiers or modalities. It has been noted earlier that some of the related connectives embed the four standard relations of opposition, but they occur as arguments in these interpreted squares.

4.1 Functional Completeness

It is well known that functional completeness obtains in standard sentential logic: each logical connective can be defined in terms of basic ones by a number of intermediary steps. Thus incompatibility can be defined as a negated conjunction, for instance. But that does not mean that any such connective can be defined by any other one: although the single connective of incompatibility suffices to define any other connective, conjunction and negation are usually taken to be the two basic connectives for a definition of the remaining ones: rejection can be translated as a conjunction of negated sentences, disjunction as a negation of negated conjuncts, and so on.

At the same time, one hardly sees how any connective could be turned directly into any other one: how to turn rejection into tautology, for instance? This is not an impossible task, however: standard negation contributes to functional completeness, but its limited properties prevent one from having a direct definition between any two standard connectives. Such is the goal of the present section, in the light of the theory of opposites.

4.2 Blanché’s “Closure Problem”

Let us call by “closure problem” the following one: how to relate any elements of a exhaustive set to each other into a closed logical structure? To begin with, a logical hexagon cannot suffice to structure a complete set of relations between binary sentences: for every set of n sentences, the number of oppositions between these corresponds to the decreasing sequence (n−1)+(n−1)−1+⋯+1 or, equivalently, (n×(n−1))/2. Since there are n=16 elements in the set of binary sentences, a closed structure of their logical oppositions should include (16−1)+(15−1)+⋯+1=120 (or, equivalently, (16×15)/2=120) instances of relation OP(α,ψ).

Blanché noted in [6, 7] that [14] failed to find a closed structure in this respect:

This problem has hardly been addressed thus far and never, to our knowledge, in a fully satisfying way. A quadratic shape of the four junctions can be found in Bocheński, but the idea has not been pushed farther. More developed are Piaget and Gottschalk’s investigations. Unfortunately, they remain incomplete in that, while they organize the connectives into some well structured groups, these very groups remain isolated from each other without being into a whole structure.¹¹

Indeed, [7] split the various logical interconnections into four independent quadratic structures: the logical quaterns, supplemented with their logical values in QAS. (See Fig. 8.)

Fig. 8

Piaget’s four quaterns and their logical values in QAS

[6, 7] blamed these squares from being plainly wrong: not only are the contraries and subcontraries inverted in (A) and (B), but several sentences are opposed to themselves in (C) and (D). Actually, Blanché was wrong himself by taking these figures for logical squares of opposition: these are quaterns of opposites, where the relation obtaining between the edges does not count as much as the operators by means of which they are constructed. Here is a way to depict the difference of perspective between a square of opposition and a quatern of opposites. (See Fig. 9.)

Fig. 9

Logical square of oppositions, logical quatern of opposites

Despite this, [7] relevantly proposed a more structured polygon of oppositions that helps to link some of Piaget’s quaterns. This polygon is called by him a “double hexadic structure”, where two logical hexagons are connected in an indefinitely repeated sequence (see Fig. 10). As the whole structure includes a restricted set of 10 binary sentences, it cannot contain more than 45 relations of opposition instead of the expected 120 ones. Moreover, it can be seen that the “functional” counterpart of this polygon contains some blanks: not every relation OP can be constructed by means of an operator O in the right-sided structure, as witnessed by its unknown functions? (α⊕ψ).

Fig. 10

Blanché’s double helix of logical oppositions, their corresponding logical values in QAS, and their incomplete opposite-forming operators among INRC

Actually, a solution to the closure problem has been found after [7]: each of the 16 binary sentences can be related to each other within a more complex polygon than Blanché’s double hexadic structure. This solution has been discovered by Régis Pellissier in [12], illustrated by Dominique Luzeaux, Jean Sallantin and Christopher Dartnell in [10], and improved by Hans Smessaert in [20] with a closed structure that is a 3D tetraicosahedron (Fig. 11).¹²

Fig. 11

Pellissier’s tetraicosahedron of logical oppositions for binary sentences, and their corresponding logical values in QAS

Here is a complete list of the 120 relations OP(α,ψ) between any binary sentences α and ψ, according to the logical values of the binary sentences and the algebraic definitions of the oppositions in QAS.

• CT(α,ψ) (18 instances):

  

• CD(α,ψ) (8 instances):

  For every α: {α,N(α)}

• SCT(α,ψ) (18 instances):

  

• SB(α,ψ) (65 instances)¹³

  For every α: 〈⊥,α〉; 〈α,⊤〉

  

• NCD(α,ψ) (12 instances)

  

4.3 Global and Local Opposites

This is not the whole story, however, since the closure problem for oppositions can be extended to the case of opposites as follows: how to extend the exhaustive range of opposite-forming operators such that, for any two binary sentences α, ψ of standard logic, there is a O such that ψ=O(α)? Piaget could not have thought of the double hexadic structure suggested by Blanché, because the latter does not stand for a polygon of opposites (based on the operators O) but, rather, a polygon of oppositions (based on the relations OP). Actually, no operator from the INRC Group can be used to construct the relata of Blanché’s hexagons such that, for every side X of the square AEIO, O(X)=U and O(X)=Y.

A solution to this problem requires an extension of the set O to new opposite-forming functions beyond Piaget’s subset of the three non-trivial elements {N,R,C}. For this purpose, let us make a distinction between global and local operations.

A function O is said to be global if and only if it applies the same sort of transformation to every element a _i (α) of a logical value A(α). Thus N is a global operation that inverts every element of a _i (α) (from 1 to 0, and conversely); R is a global operation that proceeds by permutation for every such element; and C is a composed operation of inversion and permutation, following the equation C=NR. N and R are primitive with respect to C, since permutation and inversion are basic operations that help to define the operation of C (while the converse is not the case).

A function is said to be local if and only if it is not global, i.e. it applies the same sort of transformation to some element(s) a _i (α) of A(α) but not all. For every A(α)=abcd, we have an inversion function N^k _j (where k is the number of inverted elements a _i (α) in A(α), and j the jth case of the kth subset) such that, for any pair of binary sentences α, ψ, ψ=N^k _j (α). This results in a difference between inversion and contradiction, since only the Piagetian global inversion function N is still a contradictory-forming operator as depicted in the following:

• Global inversion: N=N⁴ ₁

  $$\mathbf{A}\bigl(\mathrm{N}(\alpha)\bigr) = \mathbf{A}\bigl(\mathrm{N}^{4}{}_{1}(\alpha)\bigr) = a'b'c'd'$$

• Local inversions:

  

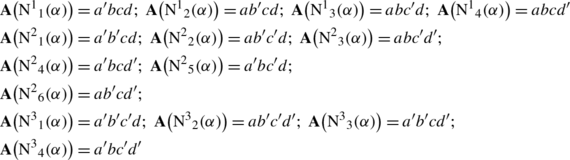
Accordingly, it can be seen that the generic operation of inversion can solve the closure problem for opposite-forming operators by means of local applications. Returning to Blanché’s double helix, the unknown functions are then to be replaced by new local functions in the right-sided polygon of opposites. (See Fig. 12.)

Fig. 12

A complete set of local opposite-forming operators N^k _j for Blanché’s double helix of logical oppositions

It must be noted that the use of local functions entails a complete relativization of the correspondences between opposites and oppositions: every relation of opposition OP can be constructed by means of any local opposition $\operatorname{O}^{k}{}_{j}$. While this holds only for some sentences α and some operators of INRC, in the sense that OP(Φ,R(Φ))=OP(Φ,N(Φ)) or OP(Φ,C(Φ))=OP(Φ,N(Φ)) only when Φ∈{α,ψ,∼α,∼ψ,⊥,⊤}, this is the case for every binary sentence Φ whenever O is a local function. The preceding case has been restricted to the localization of inversion N, but the same process can be safely applied to the other two local functions of reciprocity R and correlation C. Taking conjunction as an arbitrary starting point, here is a tetraicosahedron of opposites that exhaustively describes the way in which any relation of opposition OP(α⊕ψ,O(α⊕ψ)) can be constructed by means of any local operator N^k _j . (See Fig. 13.)

Fig. 13

A complete set of local functions N^k _j for Pellissier’s tetraicosahedron of binary connectives, where the basic argument is α∧ψ

Following Piaget’s matrix for the group of global functions INRC, each of these functions equates with the relative product of two other ones $\operatorname{O}^{k}{}_{j} \times \operatorname{O}^{k}{}_{j}$. Here is a more fine-grained matrix for this group of commutative local functions, such that XY=YX. (See Fig. 14.)

Fig. 14

A matrix for the commutative group of local functions N^k _j

The preceding patently shows how opposition proceeds from negation. But it is not clear which sort of negation one talks about in this theory of logical opposites. Actually, the enlarged group $\operatorname{O}^{k}{}_{j}$ contains a set of negation-forming operators without any special constraint: it can be considered as a set of “proto-negations”, i.e. unary operators that give rise to proper negations without being logical negations themselves (see Sect. 5.5). But what do they amount to exactly, if so?

5 Opposition and Negation

It is taken to be granted that opposition is closely related to negation, since the relation OP(α,N(α)) relies upon the opposite-forming operator N. Moreover, it can be shown that N corresponds to the classical negation: OP(α,N(α))=CD(α,ψ). But what about the other opposite-forming operators beyond N?

5.1 A Theory of Negations?

Hartley Slater famously claimed in [19] that there cannot be true contradictions, insofar as every such negation should result in a relation of incompatible truth-values. It has been variously replied that paraconsistent negation needn’t rely upon dialetheia, and [4] developed this objection by arguing that a modal hexagon implicitly includes three distinct negations in the classical (I), paracomplete (II), and paraconsistent (III) hexagons. (See Fig. 15.)

Fig. 15

Three sorts of logical negation within three hexagons of opposition for alethic modalities: classical negation (I), paracomplete negation (II), and paraconsistent negation (III)

Following [20], QAS helps to algebraize the language of modal atomic sentences ♣α by means of an alternative question-answer game: instead of questions about the truth-conditions of α⊕ψ, Smessaert’s Modal Quantified Algebra MQA2 considers modalities ♣ as generalized quantifiers and asks questions about how often an atomic sentence α is true or false. It results in an ordered set of four alternative questions Q ₁: “Is α always false?”, Q ₂: “Is α sometimes (but not always) false?”, Q ₃: “Is α sometimes (but not always) true?”, and Q ₄: “Is α always true?”, together with their 2⁴=16 ordered answers:

• (1) A(⊥)=0000;

• (2) A(□∼α)=1000;

• (3) A(∼α∧∼□∼α)=0100;

• (4) A(α∧∼□α)=0010;

• (5) A(□α)=0001;

• (6) A(∼α)=1100;

• (7) A(∼□α∧∼□α)=0110;

• (8) A(α)=0011;

• (9) A(□∼α∨□α)=1001;

• (10) A(□∼α∨(α∧∼□α))=1010;

• (11) A((∼α∧∼□∼α)∨□α)=0101;

• (12) A(∼□α)=1110;

• (13) A(∼α∨□α)=1101;

• (14) A(□∼α∨α)=1011;

• (15) A(∼□∼α)=0111;

• (16) $\mathbf{A(}\top) = 1111$

These logical values of the modal sentences shed some light upon the connection between logical negations and oppositions. Here are the algebraic counterparts of the above hexagons, where each modal sentence is replaced by its logical value in QAS. (See Fig. 16.)

Fig. 16

The three logical hexagons and their corresponding logical values in QAS

Now according to [4], (I) is a classical logical hexagon because it essentially exemplifies the classical negation through the relation of contradiction CD(□α,∼□α)=CD(□α,N(□α)); (II) expresses the paracomplete negation through the contrary relation CT(α,□∼α), provided that □ stands for the necessity from S4; and (III) exemplifies the paraconsistent negation through the relation of subcontrariety SCT(α,∼□α), assuming that □ is the necessity from S5. How to account for such a correlation between oppositions and negations?

5.2 Non-standard Negations Are Local Opposites

To begin with, it is argued in [4] that a negation is paracomplete whenever a sentence and its paracomplete negation can be both false, paraconsistent if these can be both true. Such criteria match with the main theorems of intuitionistic and paraconsistent logics as well as the definitions of contrariety and subcontrariety.

Moreover, a difference made between the three preceding hexagons is that only the first negation in (I) can be constructed by means of a Piaget’s opposite-forming operator. Two remarks can be addressed to this comparison between oppositions and negations, however. For one thing, each of the aforementioned negations can be constructed by means of a local opposite function instead of the global ones: thus

At the same time, negation needn’t be equated with a modal unary operator: although [4] identified paracomplete and paraconsistent negations with the contrary and subcontrary relations of the hexagons (II) and (III), it can be replied that a proper paracomplete negation of any sentence α needn’t be rendered as □∼α, just as its proper paraconsistent negation needn’t be ∼□α. Actually, a paracomplete negation is any opposite-forming operator O such that α and O(α) cannot be both true, and a paraconsistent negation is such that these can be both true. In the semantics of QAS, this means that the negations of α are variously defined in terms of their compatible answers a _i (α):

• Classical negation: ∼

  $$\mathrm{OP}(\alpha,\psi) =\mathrm{OP}(\alpha,{\sim}\alpha) = \mathrm{CD}(\alpha,\psi) \qquad \mbox{iff} \qquad \mathbf{a}_{i}(\alpha) = 1 \Leftrightarrow \mathbf{a}_{i}({\sim}\alpha) = 0$$

• Paracomplete negation: ¬

  $$\mathrm{OP}(\alpha,\psi) =\mathrm{OP}(\alpha,\neg\alpha) = \mathrm{CT}(\alpha,\psi) \qquad \mbox{iff} \qquad \mathbf{a}_{i}(\alpha) = 1 \Rightarrow \mathbf{a}_{i}(\neg\alpha) = 0$$

• Paraconsistent negation: −

  $$\mathrm{OP}(\alpha,\psi) =\mathrm{OP}(\alpha,-\alpha) = \mathrm{SCT}(\alpha,\psi) \qquad \mbox{iff} \qquad \mathbf{a}_{i}(\alpha) = 0 \Rightarrow \mathbf{a}_{i}(-\alpha) = 1$$

Therefore, each of the three preceding hexagons actually contains the three sorts of negation among their oppositional relations since each of the contrary or subcontrary relations relies upon the use of an opposite-forming operator O, such that the opposites α and O(α) cannot be both true or both false. This entails that there can be more than three exemplifications of negation in the modal hexagons, in the sense that there can be more than three ways not to be both true or false. Hence the seven modal hexagons that can be added to the preceding three ones, thus yielding a combined tetraicosahedron of modalities.¹⁴ (See Fig. 17.)

Fig. 17

A complete set of local functions N^k _j for Pellissier’s tetraicosahedron of alethic modalities, where the basic argument is □α

Again, the connection made between negation and modalities is merely convenient but not crucial: the syntactic translation of negations holds beyond the sole fragment of modal sentences and equally holds for the preceding language of binary non-modal sentences.

5.3 Non-standard Negations Are Intensional Functions

The main difference between contradiction and the three other relations of opposition is that only the former is a truth-function: to each truth-value α corresponds only one truth-value for the bijection N(α), whereas there can be several values associated to the injection R(α).

This accounts for the non-truth-functional behavior of the non-standard negations constructed by means of R, insofar as these proceed as intensional rules by associating a set of values to an initial value. This helps to explain why paracomplete and paraconsistent negations are formed by means of R without being identifiable with it; the validity of RR = I shows evidence of this difference, since the iteration of a paracomplete negation does not result in the corresponding affirmation: ¬¬α⊭α, i.e. not SB(¬¬α,α).

More generally, the intensional application of ∼ (or −) to α maps α to the set of formulas that cannot be true (or false) together with α. This equally holds for ∼, but with the crucial difference that the classical negation ∼ maps to a single value and accounts for its involutivity.

But just as the intensional modalities in a possible-world semantics, R can be extensionalized by changing the set of truth-values into a set of alternative logical values. This has been done with QAS, so that this non-Fregean semantics turns O into a set of intensional functions similar with the modal operators of a Fregean (truth-functional) semantics.

Using opposites as negations, contrary-forming operators proceed as paracomplete negations of either modal or non-modal sentences, e.g. in the relation OP(α↚ψ,α↓ψ)=OP(α↚ψ,N² ₃(α↚ψ))=OP(α↚ψ,¬(α↚ψ)) or in OP(□α,∼α∧∼□α)=OP(□α,N² ₆(□α))=OP(α↚ψ,¬(α↚ψ)); subcontrary-forming operators proceed as paraconsistent negations, e.g. in the relation OP(α→ψ,α↮ψ)=OP(α→ψ,N³ ₃(α→ψ))=OP(α→ψ,−(α→ψ)) or in OP(∼□∼α,∼α∨□α)=OP(∼□∼α,N² ₅(∼□∼α))=OP(∼□∼α,−(∼□∼α)).

It is worthwhile recalling that, except for the contradictory-forming operator N⁴ ₁, no single operator O (whether global or, a fortiori, local) results in only one relation of opposition: the nature of OP(α,O(α)) crucially depends upon the value of the argument α it applies upon. To compare with the preceding examples, N² ₃ is not a contrary- but subcontrary-forming operator when applied to α∨ψ or ∼α∧∼□∼α. And conversely, N² ₅ is not a subcontrary- but contrary-forming operator when applied to α↚ψ or □∼α.

Finally, some sentences are such that their logical values prevent them from standing into a contrary or subcontrary relation; this relies upon the number of inversions applied by the local function N^k _j . Letting i be this number such that i(x)=x′ (where x∈{0,1}), here are the resulting oppositions OP(α,O(α) for the 16 sentences A(α)=〈a ₁(α),a ₂(α),a ₃(α),a ₄(α)〉:

• i=1: OP(α,O(α))=SB(α,ψ) for every α

• i=2: OP(α,O(α))=CT(α,ψ)×2, SCT(α,ψ)×2, NC(α,ψ)×4, SB(α,ψ)×8

• i=3: OP(α,O(α))=CT(α,ψ)×6, SCT(α,ψ)×6, SB(α,ψ)×4

• i=4: OP(α,O(α))=SB(α,ψ)×2, CD(α,ψ) for every α

This characterization of SB accounts for the peculiar fact that CD and SB don’t differ when α=⊥ and ψ=⊤. For SB does not state that its two opposite terms can be true and false together, which would be incompatible with CD. Rather, SB states that every truth-case (or yes-answer) of the superaltern α is also a truth-case (or yes-answer) of the subaltern ψ. But given that this definition of SB doesn’t require for the superaltern to include at least one truth-case (or yes-answer), the same situation appears here as with the empty class: its set of truth-cases (or yes-answers) is empty and, thus, is included into every other set of truth-cases (or yes-answers); hence A(⊥) is included into A(ψ) for every ψ. Consequently, ⊥ and ⊤ satisfy both CD and SB without entailing any paradoxical situation but a peculiar case in which two opposites satisfy two different relations of opposition.

5.4 Subalternation and Double Negations

Subalternation has not been mentioned yet in this section about negation, although it always occurs in the above oppositions and irrespective of i. Now assuming that O proceeds as an operator of negation, why not to conclude from it that subalternation equally results from the relation of a sentence and one of its negations?

Actually, the functional approach to oppositions through opposite-forming operators justifies the general reluctance to consider subalternation as a proper opposition: the latter concept is closely related to negation, whereas subalternation is used to preserve truth and proceeds as a sort of mixed double negation or weak affirmation. This clearly appears in the light of Piaget’s INRC Group of global operators O, where correlation C helps to construct subalternation and is defined as the product of inversion N and reciprocity R: C=NR=RN; C is a subalternation-forming operator, N a contradictory-forming operator that behaves like a classical negation, and R an operator whose behavior crucially depends upon the value of its argument. Let y(α) be the number of yes-answers to Q(α); it results in a number of distinctive unary operators formed by R according to y(α):

• Affirmation

  R(α)=α with y(α)=0, or y(α)=2 and a ₁(α)=a ₄(α), or y(α)=4

• Classical negation

  R(α)=∼α with y(α)=2 and a ₁(α)≠a ₄(α)

• Paracomplete negation

  R(α)=¬α with y(α)=1

• Paraconsistent negation

  R(α)=−α with y(α)=3

According to the nature of the unary operator formed by R, it is easily verified that the relation of subalternation SB needn’t result from the operator C=NR:

$$\begin{array}{@{}l@{\qquad}l} \mathrm{OP}\bigl(\alpha,\mathrm{C}(\alpha)\bigr) = \mathrm{OP}(\alpha,{\sim}\alpha)& \mbox{when }y(\alpha) = 0,\mbox{ or } y(\alpha) =2\mbox{ and } \\ &\mathbf{a}_1(\alpha )=\mathbf{a}_4(\alpha )\\ \mathrm{OP}\bigl(\alpha,\mathrm{C}(\alpha)\bigr) = \mathrm{OP}(\alpha,{\sim}{\neg}\alpha)& \mbox{when }y(\alpha) =1\\ \mathrm{OP}\bigl(\alpha,\mathrm{C}(\alpha)\bigr) = \mathrm{OP}(\alpha,{\sim}{\sim}\alpha) = \mathrm{OP}(\alpha,\alpha)& \mbox{when }y(\alpha) = 2\mbox{ and }\mathbf{a}_{{1}}(\alpha) \neq \mathbf{a}_{{4}}(\alpha)\\ \mathrm{OP}\bigl(\mathrm{C}(\alpha),\alpha\bigr) = \mathrm{OP}({\sim} -\alpha,\alpha)& \mbox{when }y(\alpha) = 3\\ \mathrm{OP}\bigl(\alpha,\mathrm{C}(\alpha)\bigr) = \mathrm{OP}({\sim}\alpha,\alpha)& \mbox{when }y(\alpha) = 4 \end{array}$$

These constructions betray two exceptions in Piaget’s matrix INRC (see Sect. 3).

Firstly, the contradictory-forming operator N can also yield a relation of subalternation when applied to ⊥ (i.e. with y(α)=0) or ⊤ (i.e. with y(α)=4). It means that two opposite sentences can stand into a relation of subalternation without being non-contradictory to each other, in the sense that they are contradictories when y(α)=0 or y(α)=4. This special feature has not been taken seriously by Blanché, but it should not be neglected in a complete formal theory of oppositions and opposites.

Secondly, the cases where y(α)=2 and a ₁(α)=a ₄(α) are such that NR(α)=NI(α)=N(α), so that C(α)=N(α) with these two values.

Apart from these peculiarities, subalternation typically results from the standard negation of a non-standard negation (or the converse).

Finally, the intensional aspect of the non-standard negations •={¬,−} entails that these cannot be safely commuted; they can be so only with the extensional, standard negation ∼. That is:

$$\mbox{For every }\bullet \in \{{\neg},-\}: {\sim}{\bullet}\alpha = \bullet{\sim}\alpha,\mbox{ but }{\neg}{-}\alpha \neq {-}{\neg}\alpha$$

5.5 A Theory of “Proto-negations”!

All of this could relevantly shed some new light on the connection between opposition and negation.

On the one hand, the view of subalternation as a mixed double negation could relevantly justify the usual rejection of subalternation by whoever considers opposition to be essentially related to negation while excluding the opposite operator of affirmation. But such a mixed double negation needn’t lead to a plain affirmation, depending upon the value of its arguments.

On the other hand, a reference to Piaget’s INRC Group has shown that any opposition somehow resorts to negation through the application of opposite-forming operators: although subcontrariety and subalternation admit their opposites α and ψ to be true together, ψ results from the application of a kind of “proto-negation” O to α such that O(α)=ψ. Whether global or local, the family of O turns the Disjunctive Normal Form of any sentence into another one and this seems to be how opposition is always related to negation as change: opposition essentially works as a change- or difference- rather than an incompatibility- or falsity-forming operator in the light of QAS, turning yes-answers into no-answers (or conversely) in every case (with N⁴ ₁=N) or in some case(s) (with R or C, or any N^k _j , where k≠4).

6 Conclusion and Prospects

Let us recapitulate the main theses of this paper:

• (i) Opposition is a relation OP(α,ψ) between two opposite terms α and ψ, the second of which results from the first one by applying an opposite-forming operator O such that O(α)=ψ; the properties of OP and O can be investigated within such a non-Fregean semantics as QAS, where the logical value of a sentence is an ordered set of answers to corresponding questions about it.

• (ii) With respect to the theory of binary sentences α⊕ψ, the logical value of a sentence characterizes its Disjunctive Normal Form; Piaget’s INRC Group roughly expresses the various properties of O, where the operation N is a contradictory-forming operator corresponding to the standard negation.

• (iii) The case of correlation C has led to the result that subalternation is a special subcase of opposition: the compossibility of truth and falsity for its opposite terms is a necessary, but not sufficient condition for it. The definition of subalternation in terms of yes-answers-containment shows that opposition includes the Tarskian relation of entailment among its components.

• (iv) It is possible to turn any given sentence into any other one by means of O, provided that O includes a more fine-grained set of local functions. For this purpose, Piaget’s three global operations N, R, C have been collapsed into a unique set of 16 local operations N^k _j which correspond to proto-negations: they are the basic operations by means of which logical negations can be constructed.

• (v) Following Béziau’s translation of logical negations within modal logic, it has been shown that the connection between negations and oppositions is sufficient for an algebraic definition of standard and non-standard negations. Subcontrariety and subalternation deserve to be included among the proper range of oppositions, in the sense that they essentially proceed from the application of opposite-forming operators to their argument(s).

A number of problems remains to be investigated within this new theory of opposites, among which the following ones: Is there an informal meaning for the opposite-forming operators O? Can the various features of O be generalized for an arbitrary logical value? What about the counterparts of local reciprocity R^k _j or local correlation C^k _j , in addition to the functions of local inversion N^k _j ? How to characterize the logical value of any structured sentence, in addition to the binary or modal unary sentences; what is the logical value of a modal binary sentence like □(α∧ψ), for instance? What of many-valued oppositions? Non-standard negations have been defined within the standard frame of a Boolean algebra, but what about the converse; that is: how to define classical negation within a non-standard frame; does this require the use of a non-Boolean algebra?

A lot is still to be accomplished before giving a more substantial role to this introductory theory of opposites within the area of logic.