Abstract
Parametric Timed Games (PTG) are an extension of the model of Timed Automata. They allow for the verification and synthesis of real-time systems, reactive to their environment and depending on adjustable parameters. Given a PTG and a reachability objective, we synthesize the values of the parameters such that the game is winning for the controller. We adapt and implement the On-The-Fly algorithm for parameter synthesis for PTG. Several pruning heuristics are introduced, to improve termination and speed of the algorithm. We evaluate the feasibility of parameter synthesis for PTG on two large case studies. Finally, we investigate the correctness guarantee of the algorithm: though the problem is undecidable, our semi-algorithm produces all correct parameter valuations “in the limit”.
This work was partially supported by CNRS international PhD programme, the CNRS International Research Network CLoVe and Innovationsfonden Danmark’s DIREC project SIoT (Secure Internet of Things).
You have full access to this open access chapter, Download conference paper PDF


1 Introduction
The seminal model of Timed Automata (TA) [1] equips finite automata with real-valued clocks, to verify real-time reactive systems. Numerous extensions of TA have been proposed. Timed Games (TG) [18] distinguish controllable and uncontrollable actions, to study the interaction of a controller with its environment (e.g. the plant, an attacker, or a system-under-test). Here, we focus on reachability objectives, which require a strategy for the controller to schedule controllable actions such that — no matter which and when uncontrollable actions are executed by the environment — a desirable state is reached.
Since precise timing constraints are not always known, one might replace concrete values by symbolic parameters, to study a whole family of timed systems. This leads to the model of Parametric Timed Automata (PTA) [2]. The problem is to find (some or all) values for the parameters such that the system satisfies a desired property. Most problems on PTA are undecidable [3], in particular the reachability problem. Several decidable fragments are known, e.g. by restricting the number of clocks or the positions of the parameters, as in L/U PTA [14].
This paper tackles the parameter synthesis problem for Parametric Timed Games (PTG) [15] with reachability objectives. We provide the first implementation of a semi-algorithm for PTG parameter synthesis. It operates on-the-fly, i.e. it starts solving the game while the symbolic state space is being generated. To avoid the generation of the full, potentially infinite, state space, we also implement several state space reductions. These improve the termination and efficiency of parameter synthesis. In particular, we lift inclusion/subsumption from TA to PTG, generalize coverage pruning and losing state propagation from TG to PTG, and we port cumulative pruning from PTA to PTG.
Interestingly, unlike the situation in PTA [5] and TG [10], the algorithm for PTG is not guaranteed to terminate, even if the symbolic state space is finite. But we claim that if the algorithm terminates, it produces the precise constraints under which there exists a winning strategy. If the algorithm does not terminate, the stronger guarantee holds, that (in the limit) it produces all valid parameter valuations, provided the waiting list is handled fairly.
The implementation allows us to study the feasibility of parameter synthesis for larger case studies in PTG. In particular, we synthesize parameters for the correctness of a game version of the Bounded Retransmission Protocol [13] and a parametric version of the Production Cell [10, 19]. We measure the effectiveness of the individual pruning heuristics on these case studies. It appears that the state space reduction techniques are essential for feasible parameter synthesis.
Related Work. For TG, Maler et al. [18] proposed a strategy synthesis algorithm based on classical reachability games, handling the uncountable set of clock values using symbolic regions. Cassez et al. [10] improved the efficiency of TG strategy synthesis by an on-the-fly algorithm, and working with symbolic zones, represented by DBMs as implemented in UPPAAL Tiga [8]. Previous work on PTG initially focused on decidable subcases, like the case for bounded integers [16] and the fragment of L/U PTG [15, 17]. The latter two papers also provide semi-algorithms for general PTG, either based on backward fixed points [17], or an on-the-fly algorithm [15], directly extending the work on Timed Games [10]. That paper leaves an implementation of the algorithm (and hence an evaluation on larger case studies) as future work. Our implementation extends the infrastructure of Imitator [4], which so far could only handle PTA. The symbolic data structure is based on Parma’s convex Polyhedra Library [7].
Contributions. (1) We provide the first implementation of a parameter synthesis algorithm for PTG (Sec. 4), and integrate this on-the-fly algorithm in the Imitator toolset [4] (Sec. 6).
(2) We devise and implement several pruning heuristics to speed up parameter synthesis (Sec. 5).
(3) We evaluate the feasibility of parameter synthesis for PTG on two large case studies, and measure the effect of the various pruning techniques (Sec. 6).
(4) We carefully introduce the model (Sec. 2) and solution principles (Sec. 3), pointing out several semantic subtleties, and find that the semi-algorithm yields all valid parameters in the limit (Sec. 4).
2 Model of Parametric Timed Games
A Parametric Timed Game (PTG) is a structure based on timed automata (TA). Similarly to classical automata, it is composed of locations connected by discrete transitions. Moreover, it is equipped with clocks. Locations are associated a condition on clock valuations (invariant) that must be satisfied while staying in the location. An action in a timed automaton is either to take a discrete transition or to let some time pass. Discrete transitions have a guard that must be satisfied in order to take the transition. In a parametric setting, these conditions use linear terms over clocks and parameters. Parameters hold an unspecified value, and remain constant during a run. A discrete transition also has a subset of clocks which are reset when the transition is taken.
In a two-player timed game, discrete transitions are partitioned between controllable transitions and uncontrollable environment transitions.
Definition 1 (PTG)
A Parametric Timed Game is a tuple of the form \(G = (L, X, P, Act , T _c, T _u, \ell _0, Inv)\) such that
-
\(L\), \(X\), \(P\), \(Act \) are sets of locations, clocks, parameters, transition labels.
-
\(T = T _c \cup T _u\) is the set of transitions in \(L\times \mathcal {G} (X,P) \times Act \times \mathcal {P}(X) \times L\), partitioned into sets \(T _c\) of controllable and \(T _u\) of uncontrollable transitions of the form
 ;
;  ,
,  are source and target locations; \(g \in \mathcal {G} (X,P)\) is the guard (see Def. 4);
are source and target locations; \(g \in \mathcal {G} (X,P)\) is the guard (see Def. 4);  is the label; Y is the set of clocks to reset.
is the label; Y is the set of clocks to reset. -
 is the initial location.
is the initial location. -
\(Inv\; : \; L\rightarrow \mathcal {G} (X,P)\) associates an invariant with each location.
Example 1
Fig. 1 shows the example of a coffee machine. The controller represents the coffee machine and the environment represents the user. Uncontrollable transitions are depicted as dashed arcs. From  , the user can
, the user can  . It resets clock
. It resets clock  that will measure the time since the demand. The machine is then
that will measure the time since the demand. The machine is then  . Action
. Action  can happen after
can happen after  (parameter featuring the time to pour the coffee) and no later than
(parameter featuring the time to pour the coffee) and no later than  after the request. While the coffee is being prepared, the user may
after the request. While the coffee is being prepared, the user may  . Adding sugar does not interrupt the pouring of the coffee and lasts
. Adding sugar does not interrupt the pouring of the coffee and lasts  . The coffee cannot be served while sugar is being added. A situation that may arise is that sugar is being added to the coffee when the time limit
. The coffee cannot be served while sugar is being added. A situation that may arise is that sugar is being added to the coffee when the time limit  is met, making it impossible for the coffee to be served on time. To avoid this issue,
is met, making it impossible for the coffee to be served on time. To avoid this issue,  is disabled after waiting
is disabled after waiting  .
.
Our goal is to synthesize the constraints on parameters  to
to  for the coffee to be timely served. Hence, the initial location is set to
for the coffee to be timely served. Hence, the initial location is set to  , with both clocks at 0. One possible solution to the problem is
, with both clocks at 0. One possible solution to the problem is  .
.
2.1 Semantics of Parametric Timed Games
A state of a PTG consists of a location and a valuation of clocks and parameters.
Definition 2 (valuations)
A clock valuation is a function \(v _X\in \mathbb {R}_{\ge 0}^{X}\) assigning a positive real value to each clock. A parameter valuation \(v _P\in \mathbb {Q}_{\ge 0}^{P}\) assigns a positive rational value to each parameter. A valuation of the game \(G \) is a pair \(v = (v _X,v _P)\). The set of all valuations of the game is denoted \(V= \mathbb {R}_{\ge 0}^{X} \times \mathbb {Q}_{\ge 0}^{P}\).
A guard is a constraint that can be satisfied by some valuations of the game.
Definition 3 (linear terms)
A linear term over \(P\) is a term defined by the following grammar:  where \(k \in \mathbb {Q}\) and
where \(k \in \mathbb {Q}\) and  .
.
Definition 4 (guards)
The set of guards \(\mathcal {G} (X,P)\) is the set of formulas defined inductively by the following grammar:

where  , \({\sim }\in \{ <; \le ; =; \ge ; > \}\) and \(plt \), \(plt '\) are linear terms over \(P\).
, \({\sim }\in \{ <; \le ; =; \ge ; > \}\) and \(plt \), \(plt '\) are linear terms over \(P\).
We now introduce the notion of zone which will be used to solve a PTG.
Definition 5 (zones)
The set of parametric zones \(\mathcal {Z}(X,P)\) is the set of formulas defined inductively by the following grammar:

where  , \({\sim } \in \{ <; \le ; =; \ge ; > \}\) and \(plt \) and \(plt '\) are linear terms over \(P\).
, \({\sim } \in \{ <; \le ; =; \ge ; > \}\) and \(plt \) and \(plt '\) are linear terms over \(P\).
Function \(v _P\) is naturally extended to linear terms on parameters, by replacing each parameter in the term with its valuation. With \(v \models \phi \), we denote that valuation \(v = (v _X, v _P)\) satisfies a guard or a zone \(\phi \), which is defined in the expected manner. Zones, guards and invariants can also be seen as a convex set in the space of valuations of the game by considering those valuations that satisfy the condition.
Transitions modify clock valuations by letting time pass or resetting clocks.
Definition 6 (time delays)
Let \(v = (v _X,v _P)\) be a valuation of the game and \(\delta \ge 0\) a delay.
-
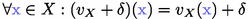
-
\(v +\delta = (v _X+\delta , v _P)\)
Definition 7 (clock resets)
Let \(v = (v _X,v _P)\) be a valuation of the game and \(Y \subseteq X\). \(v _X[Y:=0]\) is the valuation obtained by resetting the clocks in Y, i.e. :
-
 and
and 
-
\(v [Y:=0]= (v _X[Y:=0], v _P)\)
We can now define the semantics of a Parametric Timed Game.
Definition 8 (state)
A state of a PTG is a pair  where
where  is a location and \(v \) a valuation of the game satisfying its invariant:
is a location and \(v \) a valuation of the game satisfying its invariant:  . The state space is then
. The state space is then 
From a state in this state space, timed and discrete transitions can happen.
Definition 9 (timed and discrete transitions)
Let \( \delta \in \mathbb {R}_{\ge 0}\) be a time delay. A timed transition is a relation \({\rightarrow ^{\delta }} \in \mathbb {S}\times \mathbb {S}\) s.t.  iff
iff  and
and  .
.
Let  be a transition. A discrete transition is a relation \({\rightarrow ^{t}} \in \mathbb {S}\times \mathbb {S}\) s.t.
be a transition. A discrete transition is a relation \({\rightarrow ^{t}} \in \mathbb {S}\times \mathbb {S}\) s.t.  iff \(v \models g \) and \( v ' = v [Y:=0]\).
iff \(v \models g \) and \( v ' = v [Y:=0]\).
Let \(\vec {0}\) be the clock valuation where all clocks have value 0. The set of possible initial states of the PTG is  .
.
Definition 10 (run)
A run of the PTG G is a finite or infinite sequence of states \(s _0 s _1 s _2 \ldots \) s.t. \(s _0 \in \xi _0\) and \(\forall i \in \mathbb {N}, \; s _{2i} \rightarrow ^{\delta }s _{2i+1} \rightarrow ^{t}s _{2i+2}\). \(\mathcal {R} (G )\)denotes the set of runs, and \(\mathcal {R} (G )(s )\) the set of those starting from state \(s \).
A run alternates between (potentially null) delays and discrete transitions, avoiding runs that let only time pass. However, there might still be Zeno runs where infinitely many discrete transitions are taken in a finite amount of time. When there is no ambiguity, we omit \(G \) in the notations.
Example 2
Let us consider again the coffee machine in Fig. 1. Assume the parameter valuations are:  ,
,  ,
,  and
and  . Let
. Let  . We get the sequence:
. We get the sequence: 
Definition 11 (history)
A history is a finite prefix of a run. The set of histories of game \(G \) is denoted \(\mathcal {H}(G )\), and those starting in state \(s \) by \(\mathcal {H} (G )(s )\).
The notion of coverage allows for capturing all states that can occur up to some time, without a discrete transition.
Definition 12 (coverage)
Let \(s , s ' \in \mathbb {S}\) and \(\delta \ge 0\) such that \( s \rightarrow ^{\delta }s '\). The coverage of the timed transition is the set of intermediate states traversed: \( Cover ( s \rightarrow ^{\delta } s ') = \{s '' \in \mathbb {S}\; | \; \exists \delta ' : 0\le \delta ' \le \delta \; \wedge \; s \rightarrow ^{\delta '} s ''\}\,.\)
The coverage of state \(s \) is the set of states obtained from \(s \) with timed transitions only: \( Cover (s ) = \{s ' \in \mathbb {S}\; | \; \exists \delta \ge 0 \; s \rightarrow ^{\delta }s ' \}\,.\)
The coverage of a run \(r = s _0 s _1 s _2 \ldots \) is the union of the coverage of its timed transitions. When finite, it includes the coverage of its last state \(ls(r )\) : \( Cover (r ) = \Big ( \mathop {\bigcup }\limits _{i\in \mathbb {N}}\; Cover (s _{2i} \rightarrow ^{\delta }s _{2i+1}) \Big ) \cup Cover \big (ls(r )\big )\,.\)
Definition 13 (reachability objective and winning runs)
Let \({R} \subseteq L\) be a reachability objective. The set of winning runs \(\varOmega _{Reach}({R} )\) is the subset of runs that visit \({R} \): 
Example 3
In the coffee machine, the objective is to reach from the initial location  the location
the location  . The reachability objective is thus
. The reachability objective is thus  , and the set of winning runs is
, and the set of winning runs is 
2.2 Strategies in Parametric Timed Games
We introduce a definition of a strategy that deviates from [10], where at each moment, a player decides to either wait, or take a discrete transition. So their strategy returns values in \(T \cup \{wait\}\). The problem with their strategy is that it is not always clear what should happen: for instance, given a delay \(\delta \), a history \(h=s _0\rightarrow ^{\delta }s _1\) and a strategy \(\sigma \), where \(\sigma (h)=wait\) for \(0<\delta \le 1\) and \(\sigma (h)=t\) for \(\delta > 1\), it is not clear when transition t happens: there is no minimal \(\delta >1\). Although this works formally, it is less clear what the allowed behaviour of the winning player is precisely. For that reason, in our definition of strategy, players must decide in advance which delay they will take. This makes the definition more constructive, clarifying what move the winning player will actually take (i.e. perform an action or decide to wait for some particular time) and in the end simplifies the definition of what is winning.
Furthermore, following [10], the definition of strategy is asymmetric for controller and environment: If both wish to do a discrete transition, we provide priority to the environment; this corresponds to the safest situation from a software controller point of view. Another subtle asymmetry is that the controller cannot assume that the environment will take some uncontrollable transition, even when waiting any longer would violate the location invariant. While this is in line with the formal definition of strategy in TG [10], experiments with UPPAAL Tiga [8] reveal that in that tool, an uncontrollable discrete transition is actually forced when reaching the boundary of violating an invariant.
Definition 14 (strategy)
A controller strategy \(\sigma _c\) (resp. environment strategy \(\sigma _e\)) models decision-making. It is a function, depending on a history, deciding either to wait some amount of time (possibly infinite) or to take a discrete transition: \(\sigma _c : \mathcal {H} \rightarrow \mathbb {R}_{\ge 0}^{\infty } \cup T _c\), \(\sigma _e: \mathcal {H} \rightarrow \mathbb {R}_{\ge 0}^{\infty } \cup T _u\) s.t. \(\forall h \in \mathcal {H}\) and \(\sigma \in \{\sigma _c,\sigma _e\}\),
-
1.
If

then
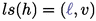 such that \(v \models g\) and
such that \(v \models g\) and 
-
2.
If \(( \sigma (h) = \delta \in \mathbb {R}_{\ge 0})\) and the transition \(\rightarrow ^{\delta }\) is available in ls(h)
then \(\sigma (h \rightarrow ^{\delta } s ) \in T \)
where \(h \rightarrow ^{\delta } s \) denotes the history obtained by adding the delay \(\delta \) at the end of h.
A strategy can return a discrete transition if its guard is satisfied and the resulting state satisfies the destination invariant (1). To respect the alternation between timed and discrete transitions, we require that a strategy which returns a finite delay \(\delta \ge 0\) on a history returns a discrete transition after the delay (if the run did not stop by violating an invariant)(2).
A controller strategy \(\sigma _c\) and an environment strategy \(\sigma _e\) can be combined into a global strategy \(\sigma _{(\sigma _c,\sigma _e)}\) as follows. If both players try to take a transition, we consider that the controller cannot guarantee his transition will be taken, thus the environment chooses. If one player decides on a discrete transition while the other decides to wait, the discrete transition is taken. If both players decide to wait, we wait for the smallest delay.
Definition 15 (global strategy)
Let \(\sigma _c\) be a controller strategy and \(\sigma _e\) an environment strategy. For all \(h \in \mathcal {H}\), the global strategy \(\sigma _{(\sigma _c,\sigma _e)}\) is defined by:
-
\(\sigma _e(h) = t _u \in T _u \implies \sigma _{(\sigma _c,\sigma _e)}(h) = t _u\)
-
\(\sigma _c(h) = t _c \in T _c \wedge \sigma _e(h) = \delta \ge 0 \implies \sigma _{(\sigma _c,\sigma _e)}(h) = t _c\)
-
\(\sigma _c(h) = \delta \ge 0 \wedge \sigma _e(h) = \delta ' \ge 0 \implies \sigma _{(\sigma _c,\sigma _e)}(h) = min (\delta , \delta ')\)
Example 4
Let us look at possible strategies in location  of the running example. The machine can choose
of the running example. The machine can choose  while the user can select
while the user can select  . If both want to do an action, the strategy chooses
. If both want to do an action, the strategy chooses  , thus giving priority to the user. If only one of them wants to take an action and the other waits, the action is taken. Hence, the machine can do
, thus giving priority to the user. If only one of them wants to take an action and the other waits, the action is taken. Hence, the machine can do  if the user is waiting. This is the expected behavior of a coffee machine and its user.
if the user is waiting. This is the expected behavior of a coffee machine and its user.
The global strategy induces a unique run, introducing null delays between two discrete transitions to guarantee the alternation with timed transitions.
Definition 16 (run induced by a global strategy)
Let an initial state \(s _0\) and a global strategy \(\sigma \) be given. The run induced by strategy \(\sigma \) is the unique \(r _{\sigma } = s_0 s_1 s_2 \ldots \) obtained by:
-
If i is even, the next transition is a timed transition :
-
If \(\sigma (\langle s_0, \ldots , s_i \rangle )=t \in T \) a delay 0 is added: \(s_i\rightarrow ^0 s_{i+1} \rightarrow ^t s_{i+2}\)
-
If \(\sigma (\langle s_0, \ldots , s_i \rangle )\) returns a delay \(\delta \ge 0\) and there is a unique state \(s \) such that \(s_i \rightarrow ^{\delta }s \) (invariant not violated), then \(s_{i+1}=s \).
-
Otherwise, the invariant is violated and the run ends.
-
-
If i is odd, the next transition is a discrete transition. By the properties of a strategy \(\sigma (\langle s_0, \ldots , s_i \rangle )\) returns a transition \(t \) such that there is a unique state \(s \) where \(s _i \rightarrow ^{t } s \). Then, \(s_{i+1} = s \).
Definition 17 (winning strategy)
A controller strategy \(\sigma _c\) is said to be winning from a state \(s \in \mathbb {S}\) w.r.t. a reachability objective \({R} \) if and only if all runs starting in \(s \) and adhering to \(\sigma _c\) are winning w.r.t. the objective. State \(s \) is said to be winning if there exists a winning strategy from it.
Run \(r \) is adhering to a controller strategy \(\sigma _c\) if there exists an environment strategy \(\sigma _e\), such that \(r = r _{\sigma _{(\sigma _c,\sigma _e)}}\).
The question we now aim to answer is: Given a Parametric Timed Game \(G \) and a Reachability Objective \({R} \), is there a winning controller strategy from the initial state? The question depends on the value of the parameters. So, more precisely, we are interested in the question: For which parameter valuations is the corresponding initial state winning?
3 Solving the Game
In this section, we introduce necessary elements for solving a game. We first describe the symbolic state space on which the algorithm operates. Then we characterize the set of winning states as a nested fixed point.
3.1 Parametric Zone Graph
Since clock valuations assign real numbers, the timed transition system of a PTG has an uncountable number of states. Zones (cf. Def. 5) are a practical tool to regroup these states in more manageable sets. Recall that zones (like guards and invariants) are conjunctions of simple constraints on valuations, and can be viewed as sets of valuations. Our algorithms operate on symbolic states  , which consist of a location and a zone. We require that
, which consist of a location and a zone. We require that  . For instance, the set of initial states of a PTG \(\xi _0\) (cf. Def. 10) can be described by the symbolic state
. For instance, the set of initial states of a PTG \(\xi _0\) (cf. Def. 10) can be described by the symbolic state  .
.
In the notation, we identify a symbolic state  with its semantics as the set of concrete states: \(\{(l,v) \mid v \vDash Z\}\subseteq \mathbb {S}\). We will write \(\xi .\ell \) to denote the (common) location of a symbolic state \(\xi \). Zones are closed under the following operations, which we extend to symbolic states:
with its semantics as the set of concrete states: \(\{(l,v) \mid v \vDash Z\}\subseteq \mathbb {S}\). We will write \(\xi .\ell \) to denote the (common) location of a symbolic state \(\xi \). Zones are closed under the following operations, which we extend to symbolic states:
-
Intersection between sets
-
Temporal successors: \( \xi ^{\nearrow } = \{ s ' \in \mathbb {S}\mid \exists s \in \xi , s \rightarrow ^{\delta }s ' \} \)
-
Temporal predecessors: \( \xi ^{\swarrow } = \{ s ' \in \mathbb {S}\mid \exists s \in \xi , s ' \rightarrow ^{\delta }s \}\)
-
Discrete successors: \(Succ(t , \xi ) = \{ s ' \in \mathbb {S}\mid \exists s \in \xi , s \rightarrow ^{t } s ' \} \)
-
Discrete predecessors: \(Pred(t , \xi ) = \{ s ' \in \mathbb {S}\mid \exists s \in \xi , s ' \rightarrow ^{t } s \} \)
-
Projection onto parameters: \( \xi {\downarrow _P} = \{ v _P\mid \exists v _X, \ell , \, (\ell , (v _X,v _P))\in \xi \}\)
These operations can be implemented by standard operations on convex polyhedra [7]. We also use union, set complement and set difference, which can return non-convex shapes. These are represented as unions of zones, still denoting sets of concrete states. All previous operations are extended to unions of zones.
Our algorithms operate on the Parametric Zone Graph (PZG). The PZG of a PTG is not guaranteed to be finite, so our algorithms are in fact semi-algorithms.
Definition 18 (Parametric Zone Graph)
Given a PTA of the form  , its Parametric Zone Graph is defined as the tuple \((\varXi , \xi _0^{\nearrow } , \Rightarrow ^t _c,\Rightarrow ^t _u)\), where \(\varXi \subseteq 2^\mathbb {S}\); \(\forall \xi ,\xi '\in \varXi \) we have \(\xi \Rightarrow ^t_c \xi '\) if \(\xi ' = Succ(t ,\xi )^{\nearrow } \) and \(t \in T_c\); and \(\xi \Rightarrow ^t_u \xi '\) if \(\xi ' = Succ(t ,\xi )^{\nearrow } \) and \(t \in T_u\).
, its Parametric Zone Graph is defined as the tuple \((\varXi , \xi _0^{\nearrow } , \Rightarrow ^t _c,\Rightarrow ^t _u)\), where \(\varXi \subseteq 2^\mathbb {S}\); \(\forall \xi ,\xi '\in \varXi \) we have \(\xi \Rightarrow ^t_c \xi '\) if \(\xi ' = Succ(t ,\xi )^{\nearrow } \) and \(t \in T_c\); and \(\xi \Rightarrow ^t_u \xi '\) if \(\xi ' = Succ(t ,\xi )^{\nearrow } \) and \(t \in T_u\).
3.2 Alternating Fixed Point Property
The algorithm works by alternating between exploring new states and back-propagating winning-state information from discovered winning states, starting from target states. The exploration relies on a fixed point property of the set \(Reach(\xi _0)\), defined as all symbolic states in some run from an initial state in \(\xi _0\):
Lemma 1
(from [15]). \(Reach(\xi _0)\) is the smallest set \(S\) containing \( \xi _0^{\nearrow } \) such that \(\forall t \in T,\; Succ(t ,S)^{\nearrow } \subseteq S\).
Similarly, the set of winning states \(W({R} )\) of the PTG with reachability objective \({R} \) can be computed as a fixed point. Intuitively, we can win the game if we can take a temporal transition (without being diverted by an uncontrollable action leading us to a non-winning state) to a state that is either directly winning, or has a controllable transition to a winning state. We formalize this with three operators on sets of states. Let \(W\) be the set of winning states of the game.
We call \( WinningMoves (S) = \{ s \in \mathbb {S}\mid \exists t \in T_c, s ' \in S, \; s \rightarrow ^{t } s ' \}\) the set of states that have access to a controllable action leading to \(S\). When applied to \(W\), it gives us the states with a controllable action to reach \(W\), from which we have a winning strategy. \( WinningMoves (S)\) is increasing in \(S\). It can be computed using the previous operators as \( WinningMoves (S) = \bigcup _{t _c \in T _c} Pred(t_c, S)\,.\)
We call \( Uncontrollable (S) = \{ s \in \mathbb {S}\mid \exists t \in T_u, s ' \notin S, \; s \rightarrow ^{t } s ' \}\) the set of states where an uncontrollable action leads to a state outside \(S\). When applied to \(W\), it gives us the states where the environment can derail us into a state outside \(W\), from which we have no winning strategy. \( Uncontrollable (S)\) is decreasing in \(S\). It can be computed from the operators from the previous subsection by \( Uncontrollable (S) = \bigcup _{t _u \in T _u} Pred(t_u, \mathbb {S}\backslash S)\,.\)
Finally, we call \( SafePred (S_1, S_2)\) the set of states that can reach \(S_1\) by a temporal transition while avoiding \(S_2\). Since it aims to be applied to reach winning moves while avoiding uncontrollable actions, if a state is in the intersection of \(S_1\) and \(S_2\), priority is given to the environment and the state is not considered safe. \( SafePred (S_1,S_2) = \{ s \in \mathbb {S}\mid \exists s ' \in S_1, s \rightarrow ^{\delta }s ' \wedge Cover ( s \rightarrow ^{\delta }s ') \cap S_2 = \emptyset \}\). \( SafePred (S_1, S_2)\) is increasing in \(S_1\) and decreasing in \(S_2\).
Thanks to the work of Cassez et al. [10], \( SafePred \) can be computed between zones using the precedent operations and extended to union of zones:
Lemma 2
(from [10] for TG, [17] for PTG).
We can now formulate the fixed point property followed by \(W\).
Lemma 3
\(W({R} )\) is the smallest set \(S\) containing \({R} \) such that \( SafePred ( S\cup WinningMoves (S) , Uncontrollable (S)) \subseteq S\,.\)
Proof
See [12, App. B]
4 Algorithm and Correctness

We can now introduce the algorithm for parameter synthesis for PTG. Alg. 1 explores the state space and creates a map of symbolic states connected by a discrete transition through the operation \( Succ(t _s, \_ )^{\nearrow } \). Simultaneously, any newly found winning states in a symbolic state \(\xi \), starting from the target locations, are propagated by marking the predecessors of \(\xi \) for an update. To update a symbolic state \(\xi \), we compute \( SafePred ({ Win \cup WinningMoves ( Win )},\) \( Uncontrollable ( Win ))\) within \(\xi \) and add the result to \( Win [\xi ]\). If new winning states are found, we mark \(\xi \) predecessors for an update.
The algorithm is non-deterministic: it does not describe how we choose between explore and update, and which symbolic state in the waiting lists to explore or update. These choices are left abstract on purpose, as optimization opportunities. A fair strategy would be to join \( WaitingExplore \) and \( WaitingUpdate \) in a single queue, whose head determines which operation to apply next. In our implementation, we prioritized back-propagation from \( WaitingUpdate \).
4.1 Invariants and Correctness
Recall that the algorithm works on a zone graph. We are looking for subsets of winning states within symbolic states. The same state may appear in different symbolic states and may not have the same status in each instance. Therefore, the set \(W_{temp}\), the winning states found by the algorithm so far, and \(W\), the set of all winning states, also take into account the symbolic state considered. Formally, \(W\) consists of all pairs \((\xi , s )\) where \(s \) is a winning state contained in the symbolic state \(\xi \), and \(W_{temp}= \mathop {\bigcup }\limits _{\xi \in Explored } \{\xi \} \times Win[\xi ]\).
Theorem 1
These invariants hold during the execution of the algorithm:
-
1.
\( \xi _0^{\nearrow } \in Explored \).
-
2.
\(\forall \xi \in Explored , t \in T , \xi '\), if \(\xi \Rightarrow ^{t }\xi '\), then \(\xi ' \in { WaitingExplore \cup Explored }\)
-
3.
\(\forall \xi \in Explored \), if \(\xi .l \in {R} \), \(\{\xi \} \times \xi \subseteq W_{temp}\).
-
4.
\(W_{temp}\subseteq W\).
-
5.
\(\forall \xi \in Explored \), we have either \(\xi \in WaitingUpdate \) or \( SafePred ( W_{temp}\cup WinningMoves (W_{temp}) , \, Uncontrollable (W_{temp}) ) \cap (\{ \xi \} \times \xi ) \subseteq W_{temp}\).
Proof
See [12, App. B].
Invariant 4 guarantees that even if the algorithm times out the winning states found by the algorithm are indeed winning. Furthermore, if the algorithm terminates and the waiting lists are empty, we can apply the fixed point properties of \(Reach(\xi _0)\) and \(W\), and \(W_{temp}\) corresponds exactly to \(W\) over the explored symbolic states that cover \(Reach(\xi _0)\).
Theorem 2
Alg. 1 is correct (when it terminates).
Proof
See [12, App. B].
Example 5
For the coffee machine, the PZG is only finite after applying inclusion subsumption (Sec. 5). However, even on this finite PZG, Alg. 1 does not terminate, but keeps reporting solutions at Line 29. In fact, it produces increasingly more general solutions, including  (for any \(n>0\)). If we bound these parameters in the initial specification, for instance
(for any \(n>0\)). If we bound these parameters in the initial specification, for instance  , our algorithm synthesizes the extra constraints
, our algorithm synthesizes the extra constraints  , as expected.
, as expected.
Theorem 3
Provided the waiting lists are treated fairly, any explored winning state is discovered as winning by the algorithm eventually.
Proof
(sketch). For a classical TG, we can represent the underlying TA as a finite classical automaton (e.g. the region graph). On this automaton, we can define a (finite) turn-based reachability game equivalent to the initial TG. Hence, we can use the notion of discrete distance to target in a reachability game, corresponding to the smallest number of discrete transitions in which a controller can ensure to reach a target. This is equivalent to solving a Min-Cost Reachability game as studied in [9] where delay transitions have weight 0 and discrete transitions have weight 1. The game graph is finite and the weights non-negative, so the discrete distance to target of a winning state is positive and finite.
While the same construction is not necessarily finite in a PTG, any state of a PTG is a state \((\ell , (v _P, v _X))\) of the TG, where all parametric linear terms in guards have been replaced by their valuation through \(v _P\). Therefore, this result extends to winning states of a PTG.
Let s be an explored winning state of the PTG and n its distance to target. We only need to explore states reachable in n discrete transitions from s. By invariant 2 from Thm. 1, when all states reachable in k discrete transitions are explored, all states reachable in \(k+1\) discrete transitions are either already explored or in the exploration waiting list. Assuming fairness of the waiting lists, at some time they have all been explored. Therefore, at some time, all states reachable from s in n discrete steps have been explored.
When all states reachable in n discrete steps have been explored, all target states within are discovered. Those are states with distance to target 0. For \(0\le k<n\), when all winning states reachable in less than \(n-k\) discrete transitions from s and with a distance to target less than k are discovered, then all winning states reachable in less than \(n-(k+1)\) discrete transitions from s and with a distance to target less than \(k+1\) are discoverable by update. Using the invariant (5) of Thm. 1, those states are either already discovered as winning or they are in the update waiting list. Assuming fairness of the waiting lists, at some time they have all been discovered winning. Applying this recurrence until \(k=n\), we get that there is a time where s is discovered winning.
We can guarantee: (1) All winning parameter valuations reported in Line 29 are correct, since the algorithm satisfies the invariants of Thm. 1. (2) Every winning parameter valuation will eventually be reported, provided the waiting lists are treated fairly. Hence, Alg. 1 is “sound and complete in the limit” [5].
5 Optimizations

We present four optimizations to the algorithm presented in Section 4. All of them adapt optimizations from previous works, three of them (coverage pruning, inclusion checking and losing state propagation) from Cassez et al. [10] and one of them (cumulative pruning) from André et al. [5]. We start by updating the exploration procedure to include the optimizations, as shown in Alg. 2.
5.1 Pruning
First, we present some pruning techniques, as these only require slight modifications in the exploration procedure. To this end, we introduce the notion of a controller deadlock state. A state is a controller deadlock state if it has no controllable transitions. We define it as the following predicate on symbolic states:
Now, we introduce the two kinds of pruning:
-
Cumulative Pruning: If the projected parameters of a zone in a new symbolic state are included in the current set of winning parameters, we can safely prune the successors of this state. Indeed, if the only possible parameters in the zone already are determined to be winning, no new winning parameter can be found by exploring the successors of this state. This check can be seen in Lines 3 and 4 of Alg. 2.
-
Coverage Pruning: If a symbolic state is either winning or a controllable deadlock state, its successors can safely be pruned. Indeed, if the symbolic state is winning, we gain nothing from exploring further. Dually, a controller deadlock state can never become winning, since the controller has no action to do. This check can be seen in Lines 10 and 11 of Alg. 2.
5.2 Inclusion checking
Originally, checking if a symbolic state \(\xi '\) has been explored already is done by checking if \(\xi '\in Explored \). The optimization by inclusion checking instead checks if \(\exists \xi '' \in Explored : \xi '\subseteq \xi ''\). If this is the case, the newly discovered symbolic state can safely be discarded since its superset has already been explored. Of course, the new dependency that \(\xi \) depends on \(\xi ''\) still must be added. This optimization is done in the exploration procedure (Lines 14 to 18 of Alg. 2).
5.3 Losing state propagation
Losing state propagation is inspired by Cassez et al. [10] for TG. The idea is that instead of only discovering and propagating winning states, we will now also do the same for losing states, starting from controller deadlock states. A map Lose will maintain the currently known losing states for a given symbolic state. Thus, each symbolic state \(\xi \) can now be partitioned into three:
-
Winning: \(Win[\xi ]\),
-
Losing: \(Lose[\xi ]\)
-
Unknown: \(\xi \setminus (Win[\xi ]\cup Lose[\xi ])\).
To initially mark a state as losing, we use the controller deadlock predicate again while also making sure that the state is not winning, as shown in Alg. 2, Lines 8 and 9. On Lines 19 and 20, we partition the \( WaitingUpdate \) list into two lists for propagating winning and losing states respectively.
While pruning and inclusion checking only required the modification of the exploration procedure, the propagation of losing states influences all of the procedures of the original algorithm. We go through them now.
Update procedure. We create a new procedure for updating losing states, which can be seen in Alg. 3. As the dual of the original update procedure, it is almost identical. Instead of \( Uncontrollable \), we compute \( Controllable \), i.e. the union of zones where the controller can lead to a non-losing state. Similarly, instead of \( WinningMoves \), we compute \( LosingMoves \) which is the set of states where the environment can lead to a losing state. We then compute \( NewLosing \) which is the set of states where the environment can lead us to a losing state while avoiding states where only controllable transitions are enabled (\( Controllable \setminus LosingMoves \)). Finally, we update \(Lose[\xi ]\) and \( WaitingUpdate _L\) accordingly.

Terminate function. The terminate function is modified to allow for early termination if all possible information is already known, i.e. \( \xi _0^{\nearrow } \setminus (Win[ \xi _0^{\nearrow } ]\cup Lose[ \xi _0^{\nearrow } ]) = \emptyset \). Indeed, if for all valuations we have determined that we either win or lose, the algorithm can safely terminate. This is shown in Alg. 4.

The final algorithm is then modified to include the new procedures and data structures introduced. As a result, in the main loop we now have to choose between three waiting lists instead of two: \( WaitingExplore \), \( WaitingUpdate _W\) and \( WaitingUpdate _L\).
6 Implementation and Experimental Evaluation
To evaluate the termination behavior and efficiency of the semi-algorithm and the optimizations, we implement them in the Imitator toolset and measure the performance on some realistic case studies.
6.1 Implementation
We have implemented our proposed algorithm and optimizations in the Imitator model checker [4], which features a wide repertoire of synthesis algorithms for PTA. We have extended its input language to PTG and added our PTG parameter synthesis algorithm, including the optimizations described in Sec. 5. The source code (in OCaml) is available on githubFootnote 1.
In Imitator, the user specifies a model consisting of parameters, clocks and a network of parametric timed automata. The user can analyse the model using an analysis or synthesis query. Imitator selects the corresponding algorithm to use, after which it outputs the result of the query.
Our extension enables the user to specify edges in a PTA as (un)controllable, effectively turning it into a PTG. Along with this we add a new property Win and a corresponding algorithm AlgoPTG. In order to synthesize parameters for a PTG one must use property := #synth Win(state_predicate), using a predicate to define which states are winning. Usually, this predicate is simply accepting, meaning that any state in an accepting location of the PTG is winning.
In Alg. 1 we left the choice between exploration and back-propagation to be non-deterministic. In the implementation back-propagation is prioritized over exploration whenever possible (i.e. when \( WaitingUpdate \) is non-empty). This seems to yield the fastest results in practice.
6.2 Experiment Design
We selected two large case studies, one PTA and one TG, and extended them to PTGs by adding (un)controllable actions, and clock parameters, respectively. An artifact containing instructions to run all the experiments is available online [11].
Production Cell. This case study [19] has two conveyor belts (1 / 2), a robot with two arms (A / B) and a press. Plates arrive at conveyor belt 1 and are taken to the press by robot arm A, where they are processed for some time. Robot arm B takes processed plates and removes them through conveyor belt 2.
We model systems with 1–4 plates in Imitator. In the goal location, every plate made it safely to conveyor belt 2. If two plates collide before they are picked up by arm A, the game is lost immediately. We assume that the rotation speed of the robot arm, the speed of the conveyor belt and the time to press are known constants. The aim is to synthesize a parameter MINWAIT, the minimum time interval between two plates arriving at the conveyor belt. The maximum time interval between two plates is fixed by an additional constant MAXWAIT.
Our PTG model is largely inspired by the TG model of Cassez et al. [10]. Besides adding parameters, we check for collisions between plates rather than defining a maximum waiting time frame. For 2–4 plates, we create a winning and a losing configuration of the constants; for 1 plate a collision is not possible. The losing configurations are created by setting MAXWAIT too small, which will deadlock the system for any value of MINWAIT.
The Imitator model for the 1-plate configuration can be seen in [12, App. C].
Bounded Retransmission Protocol. The BRP provides reliable communication over an unreliable channel. We create a PTG from a PTA model of the BRP [6], in turn based on a TA model [13], by making message loss uncontrollable.
In the BRP, a sender sends message frames to a receiver, tagged with an alternating bit, through a lossy channel. The receiver acknowledges all frames. If the sender does not receive an acknowledgement in time, it retransmits the message at most k times, after which the sender gives up. The goal location indicates the successful transmission of the message, or the abort by the sender.
Experimental Setup. All experiments were run on a single core of a computer with an Intel Core i5-10400F CPU @ 2.90GHz with 16GB of RAM running Ubuntu 20.04.6 LTS. For each implementation (basic, inclusion checking, cumulative pruning, coverage pruning, losing state propagation) we run the experiments 5 times and report the average time and state space size. A timeout of 2 hours is used.
6.3 Experimental Results
We present the results of the experiments in Table 1. We do not include the runs without optimizations as they all timed out. This indicates that inclusion checking is the most vital optimization and should always be enabled.
Indicated in green cells are the best results for each row. We can clearly see that coverage pruning has the biggest effect of all the optimizations in our experiments. Losing state propagation seems to not provide much benefit in these experiments, as the overhead overshadows any positive effect it might have had.
7 Conclusion
We provide the first implementation of parameter synthesis for Parametric Timed Games with reachability objectives, based on an on-the-fly algorithm [10, 16]. It appears that without additional pruning heuristics, the algorithm cannot handle the case studies, Bounded Retransmission Protocol and Production Cell. Inclusion subsumption is a minimal requirement to achieve any result.
Contrary to previous algorithms for PTA [5] and TG [10], the parameter synthesis algorithm does not terminate, even if the parametric zone graph is finite. But we found that in the limit all parameter values will be enumerated.
We added additional pruning techniques (coverage pruning and cumulative pruning) to further reduce the search space. These techniques generally increased the speed. We also experimented with propagating losing states, but in our examples the overhead of checking and propagating losing states was not compensated by any pruning potential. Future work could study under which circumstances the propagation of losing states could be beneficial, but also strengthen the detection of (partially) losing states. Another venue for future work is to study other objectives, like safety games or liveness conditions.
Notes
- 1.
https://github.com/imitator-model-checker/imitator, branch: develop
References
Rajeev Alur and David L. Dill. A theory of timed automata. Theoretical Computer Science, 126(2):183–235, 1994.
Rajeev Alur, Thomas A. Henzinger, and Moshe Y. Vardi. Parametric real-time reasoning. In STOC, pages 592–601. ACM, 1993.
Étienne André. What’s decidable about parametric timed automata? Int. J. Softw. Tools Technol. Transf., 21(2):203–219, 2019.
Étienne André. IMITATOR 3: Synthesis of timing parameters beyond decidability. In CAV (1), volume 12759 of Lecture Notes in Computer Science, pages 552–565. Springer, 2021.
Étienne André, Jaime Arias, Laure Petrucci, and Jaco van de Pol. Iterative bounded synthesis for efficient cycle detection in parametric timed automata. In TACAS, LNCS 12651, pages 311–329. Springer, 2021.
Étienne André, Dylan Marinho, and Jaco van de Pol. A benchmarks library for extended parametric timed automata. In TAP@STAF, volume 12740 of Lecture Notes in Computer Science, pages 39–50. Springer, 2021.
Roberto Bagnara, Patricia M. Hill, and Enea Zaffanella. The parma polyhedra library: Toward a complete set of numerical abstractions for the analysis and verification of hardware and software systems. Sci. Comp. Prog., 72(1-2):3–21, 2008.
Gerd Behrmann, Agnès Cougnard, Alexandre David, Emmanuel Fleury, Kim Guldstrand Larsen, and Didier Lime. Uppaal-tiga: Time for playing games! In CAV, volume 4590 of Lecture Notes in Computer Science, pages 121–125. Springer, 2007.
Thomas Brihaye, Gilles Geeraerts, Axel Haddad, and Benjamin Monmege. To reach or not to reach? Efficient algorithms for total-payoff games. In CONCUR, volume 42 of LIPIcs, pages 297–310. Schloss Dagstuhl - Leibniz-Zentrum für Informatik, 2015.
Franck Cassez, Alexandre David, Emmanuel Fleury, Kim G. Larsen, and Didier Lime. Efficient on-the-fly algorithms for the analysis of timed games. In Martín Abadi and Luca de Alfaro, editors, CONCUR 2005 – Concurrency Theory, pages 66–80, Berlin, Heidelberg, 2005. Springer Berlin Heidelberg.
Mikael B. Dahlsen-Jensen, Jaco van de Pol, Laure Petrucci, and Baptiste Fievet. Artifact for "On-The-Fly Algorithm for Reachability in Parametric Timed Games". Zenodo, https://doi.org/10.5281/zenodo.10046945, October 2023.
Mikael Bisgaard Dahlsen-Jensen, Baptiste Fievet, Laure Petrucci, and Jaco van de Pol. On-the-fly algorithm for reachability in parametric timed games (extended version). arXiv, https://doi.org/10.48550/arxiv.2401.11287, 2024.
P. R. D’Argenio, J. P. Katoen, T. C. Ruys, and J. Tretmans. The bounded retransmission protocol must be on time! In Ed Brinksma, editor, Tools and Algorithms for the Construction and Analysis of Systems, pages 416–431, Berlin, Heidelberg, 1997. Springer Berlin Heidelberg.
Thomas Hune, Judi Romijn, Mariëlle Stoelinga, and Frits W. Vaandrager. Linear parametric model checking of timed automata. J. Log. Algebraic Methods Program., 52-53:183–220, 2002.
Aleksandra Jovanovic, Sébastien Faucou, Didier Lime, and Olivier H. Roux. Real-time control with parametric timed reachability games. In IFAC WODES, pages 323–330. Elseviers, 2012.
Aleksandra Jovanovic, Didier Lime, and Olivier H. Roux. Synthesis of bounded integer parameters for parametric timed reachability games. In ATVA, volume 8172 of Lecture Notes in Computer Science, pages 87–101. Springer, 2013.
Aleksandra Jovanović, Didier Lime, and Olivier Henri Roux. A game approach to the parametric control of real-time systems. International Journal of Control, pages 1–12, January 2018.
Oded Maler, Amir Pnueli, and Joseph Sifakis. On the synthesis of discrete controllers for timed systems. In Ernst W. Mayr and Claude Puech, editors, STACS 95, pages 229–242, Berlin, Heidelberg, 1995. Springer Berlin Heidelberg.
Helmut Melcher and Klaus Winkelmann. Controller synthesis for the “production cell” case study. In Proceedings of the Second Workshop on Formal Methods in Software Practice, FMSP ’98, page 24-33, New York, NY, USA, 1998. ACM.
Acknowledgment
We thank Étienne André for his help with integrating our algorithm in the Imitator tool set.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2024 The Author(s)
About this paper
Cite this paper
Dahlsen-Jensen, M.B., Fievet, B., Petrucci, L., de Pol, J.v. (2024). On-The-Fly Algorithm for Reachability in Parametric Timed Games. In: Finkbeiner, B., Kovács, L. (eds) Tools and Algorithms for the Construction and Analysis of Systems. TACAS 2024. Lecture Notes in Computer Science, vol 14572. Springer, Cham. https://doi.org/10.1007/978-3-031-57256-2_10
Download citation
DOI: https://doi.org/10.1007/978-3-031-57256-2_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-57255-5
Online ISBN: 978-3-031-57256-2
eBook Packages: Computer ScienceComputer Science (R0)


 ;
;  ,
,  are source and target locations;
are source and target locations;  is the label; Y is the set of clocks to reset.
is the label; Y is the set of clocks to reset. is the initial location.
is the initial location.
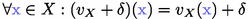
 and
and 

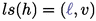 such that
such that 
