Abstract
This work studies the key-alternating ciphers (KACs) whose round permutations are not necessarily independent. We revisit existing security proofs for key-alternating ciphers with a single permutation (KACSPs), and extend their method to an arbitrary number of rounds. In particular, we propose new techniques that can significantly simplify the proofs, and also remove two unnatural restrictions in the known security bound of 3-round KACSP (Wu et al., Asiacrypt 2020). With these techniques, we prove the first tight security bound for t-round KACSP, which was an open problem. We stress that our techniques apply to all variants of KACs with non-independent round permutations, as well as to the standard KACs.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
The key-alternating ciphers (see Eq. (1)) generalize the Even-Mansour construction [EM97] over multiple rounds. They can be viewed as abstract constructions of many substitution-permutation network (SPN) block ciphers (e.g. AES [DR02]). In addition, there are various variants of the key-alternating ciphers.
This work only considers the case of independent round keys, and reducing their independence is a relatively parallel topic. That is, we are concerned with different variants of KACs on round permutations, while the round keys are always independent and random. For convenience, we simply use KAC to represent the standard KAC with independent permutations, and refer to all the other variants as KAC -type constructions. In particular, KACSP is a KAC-type construction in which all the round permutations are identical.
In a t-round KAC or KAC-type construction, the number of different round permutations, denoted \(t'\), is an important parameter. Clearly, we have \(t' = t\) in the case of KAC and \(t'=1\) in the case of KACSP. When \(t' < t\), it means that there are different rounds using the same permutation. For a given construction, we name the round permutations as follows. In particular, the name \(P_{k}\) will be assigned to each round permutation in order from round 1 to round t, where \(k \in \{1,\dots ,t'\}\). For round i, we check if there exists \(j < i\) such that round j uses the same permutation as round i. If so, we use the same name as the permutation in round j; otherwise, we use the name \(P_{k}\), where \(k \in \{1,\dots , t'\}\) is the smallest integer not used in previous rounds. For simplicity, we sometimes only use the permutation names to denote a construction, such as \(P_{1}P_{2}P_{3}\)-construction (i.e. 3-round KAC), \(P_{1}P_{1}P_{1}\)-construction (i.e. 3-round KACSP), \(P_{1}P_{1}P_{2}\)-construction, etc.
We now give a more formal definition of KAC and KACSP constructions. Let \(x \in \{0,1\}^n\) denote the plaintext, \(\kappa _0, \kappa _1, \dots , \kappa _t \in \{0,1\}^{n \times (t+1)}\) denote the \(t+1\) round keys, and \(P_{1}, \dots , P_{t}\) denote the permutations over \(\{0,1\}^n\), then the outputs of t-round KAC and t-round KACSP are computed as follows.
Related Works. Bogdanov et al. [Bog+12] were the first to study the provable security of t-round KAC (for \(t \ge 2\)), and showed that it is secure up to \(\mathcal {O}(2^{\frac{2}{3}n})\) queries. On the other hand, they presented a simple distinguishing attack using \(\mathcal {O}(2^{\frac{t}{t+1}n})\) queries, and conjectured that this attack cannot be improved intrinsically. Thus, their result is optimal for 2-round KAC. After a series of papers [Ste12, LPS12, CS14, HT16], the above conjecture was proved. Roughly, it says that unless \(\varOmega (2^{\frac{t}{t+1}n})\) queries are used, one cannot distinguish t-round KAC from a truly random permutation with non-negligible advantage, where the round permutations are public and random.
Another line of research focuses on the variants of KAC constructions, where round permutations and keys may not be independent of each other. [DKS12] was the first to study the minimalism of Even-Mansour cipher, and showed that several of its single-key variants could achieve the same level of security as it. Later, Chen et al. [Che+18] proved that a variant of 2-round KAC still enjoys security close to \(\mathcal {O}(2^{\frac{2}{3}n})\) when only n-bit key and a single permutation are used. Next, [WYCD20] generalized Chen et al.’s technique and proved a tight security bound (with two unnatural restrictions) for 3-round KACSP. Recently, Tessaro and Zhang [TZ21] showed that \((t-2)\)-wise independent round keys are sufficient for t-round KAC to achieve the tight security bound, where \(t \ge 8\).
Our Contributions. This work focuses on the provable security of KAC or KAC-type constructions in random permutation model. Our main contribution is to prove the tight security bound \(\mathcal {O}(2^{\frac{t}{t+1}n})\) for t-round KACSP.
We revisit the security proofs in [Che+18, WYCD20]. The idea of their proofs is not hard to understand, but the analysis is quite laborious. In particular, the security bound of [WYCD20] (see Theorem 1) has two unnatural restrictions, making the result far from elegant. The first is the existence of an error function \(\zeta (\cdot )\), and the second is that it requires \(28q_e^2/2^n \le q_p \le q_e/5\), where \(q_p\) and \(q_e\) denote the number of two types of queries made by the distinguisher respectively.
We propose new techniques that can significantly simplify proofs, thus making the security proofs of KAC-type constructions easier to understand and read. One of the key techniques is a general transformation, which reduces our task to bounding only one probability in the form of (9) (even for t-round constructions). Note that [WYCD20] needs to bound at least 3 such probabilities. We stress that the transformation is general and may also be used to simplify other security proofs. To increase the number of constructive methods, we introduce a new notion of recycled-edge which is different from the shared-edge used in [Che+18, WYCD20]. Roughly speaking, recycled-edge is to reuse existing permutation queries made by distinguisher to save resources, while shared-edge is to reuse the permutation queries generated on-the-fly. We point out that recycled-edge has the following features compared to shared-edge. First, the analysis of recycled-edge is easier, which is another important reason why our proof is simpler. Second, the recycled-edge has wider applicability and is less sensitive to constructions.
Moreover, we provide new ideas to remove the two unnatural restrictions in the security bound of [WYCD20]. For the first restriction, our approach is to consider the security proof in two disjoint cases, and provide separate proofs for each case. It should be pointed out here that these two proofs will be almost identical, except for slightly different calculations. For the second restriction, our approach is to increase the number of variablesFootnote 1 so that we can better exploit the power of multivariate hypergeometric distribution used in the calculation. Our main finding here is that the improvements in security bound are largely influenced by computational rather than conceptual factors. This is a key to addressing the security bound of t-round KACSP. More details about our new techniques can be found in Sect. 3.
With the above new techniques, we first obtain a neat security bound for the 3-round KACSP (see Theorem 2), and discuss its proof in detail in Sect. 4. We then generalize the proof to the general t-round KACSP (see Theorem 3), using almost the same techniques. It should be emphasized that our proof techniques apply to KAC and all kinds of KAC-type constructions. For example, we also apply the proof techniques to other variants of 3-round KAC (see Thms. 17 and 18 in the full version [Yu+23] of this paper).
2 Preliminaries
2.1 Notation
Let \(N=2^n\) and \(\mathcal {P}_n\) be the set of all permutations over \(\{0,1\}^n\). For a permutation \(P \in \mathcal {P}_n\), we let \(P^{-1}\) denote its inverse permutation. If A is a finite set, then \(\left| A \right| \) and \(\overline{A}\) represent the cardinality and complement of A, respectively. Given a set of n-bit strings A and a fixed \(k \in \{0,1\}^n\), we will use \(A \oplus k\) to denote the set \(\{a \oplus k: a \in A\}\). For a finite set S, let \(x\leftarrow _\$S\) denote the act of sampling uniformly from S and then assigning the value to x. The falling factorial is usually written by \((a)_b=a(a-1)\dots (a-b+1)\), where \(1 \le b \le a\) are two integers. For a set of pairs \(\mathcal {Q}_{}=\{(x_1,y_1),\dots , (x_q,y_q)\}\), where \(x_i\)’s (resp. \(y_i\)’s) are distinct n-bit strings, and a permutation \(P\in \mathcal {P}_n\), we say that \(P_{}\) extends the set \(\mathcal {Q}_{}\), denoted as \(P_{} \downarrow \mathcal {Q}_{}\), if \(P_{}(x_i)=y_i\) for \(i=1,2,\dots ,q\). In particular, we write \(\textsf{Dom}(\mathcal {Q}_{}):= \{x_1,\dots ,x_q\}\) (resp. \(\textsf{Ran}(\mathcal {Q}_{}):= \{y_1,\dots ,y_q\}\)) as the domain (resp. range) of \(\mathcal {Q}_{}\).
2.2 Random Permutation Model, Transcripts and Graph View
Random Permutation Model. This work studies the security of KAC or KAC-type constructions under the random permutation model. The model can be viewed as an enhanced version of black-box indistinguishability with additional access to the underlying permutations, making security analysis more operable.
Given a t-round KAC or KAC-type construction, the task of distinguisher \(\mathcal {D} \) is to tell apart two worlds, the real world and the ideal world. In the real world, the distinguisher can interact with \(t'+1\) oracles \((E_K, P_1,\dots , P_{t'})\), where \(E_K\) is the t-round target cipher (denoted as E) computed based on \(t'\) independent random permutations \(P_1, \dots , P_{t'}\) and a key K. In the ideal world, there are also \(t'+1\) oracles but the first oracle \(E_K\) is replaced by an independent random permutation \(P_0\). That is, what interact with the distinguisher \(\mathcal {D} \) are \(t'+1\) independent random permutations \((P_0, P_1,\dots , P_{t'})\). Furthermore, we allow the distinguisher to be adaptive and query each permutation oracle in both directions. We can then define the super-pseudorandom permutation (\(\textsf{SPRP}\)) advantage of distinguisher \(\mathcal {D} \) on t-round \(E_K\) (with \(t'\) different permutations) as follows.
where all oracles can be queried bidirectionally. In particular, we refer to the queries on the first oracle (i.e. \(E_K\) or \(P_0\)) as construction queries and to the set formed by them and their answers as \(\mathcal {Q}_{0}\). Similarly, the queries on the other \(t'\) oracles are called permutation queries and the resulting sets are denoted as \(Q_{i}\), where \(i = 1,\dots , t'\).
Transcripts. Formally, the interaction between \(\mathcal {D} \) and \(t'+1\) oracles can be represented by an ordered list of queries, which is often called transcript. Each query in the transcript is in the form of (i, b, u, v), where \(i \in \{0, 1, \dots , t'\}\) represents the oracle being queried, b indicates whether it is a forward query or backward query, u is the query value and v is the corresponding answer. We can assume wlog that the adversary \(\mathcal {D} \) is deterministic and does not make redundant queries, since it is computationally unbounded. That means the output of \(\mathcal {D} \) is entirely determined by its transcript, which can also be encoded (requiring a description of \(\mathcal {D} \)) into \(t'+1\) unordered lists of queries.
In addition, we are more generous to the distinguisher \(\mathcal {D} \) in the analysis, so that it will receive the actual key used in the real world (after all queries are done but before a decision is made). To maintain consistency, \(\mathcal {D} \) would also receive a dummy key in the ideal world (even the key is not used). This modification is justified since it only increases the advantage of \(\mathcal {D} \). From the perspective of \(\mathcal {D} \), a transcript \(\tau \in \mathcal {T}\) has the form of \(\tau =(\mathcal {Q}_{0}, \mathcal {Q}_{1},\dots ,\mathcal {Q}_{t'}, K)\), and can be rewritten as the following unordered lists.
where \(y_j = E_K(x_j)\) or \(y_j = P_{0}(x_j)\) (depending on which world) for all \(j \in \{1, \dots , q_e \}\) and \(v_{i,j} = P_i (u_{i,j})\) for all \(i \in \{1, \dots , t' \}\) and \(j \in \{1, \dots , q_i\}\), and where \(K\in \{0,1\}^{(t+1)n}\) is a \((t+1)n\)-bit key.
Statistical Distance of Transcript Distributions. We already know that the output of \(\mathcal {D} \) is a deterministic function on transcript. For any fixed distinguisher \(\mathcal {D} \), its advantage is obviously bounded by the statistical distance of transcript distributions in two worlds. That is, it is usually to determine the upper bound of the value (3) as follows,
where \(\Vert \cdot \Vert \) represents the statistical distance, and \(\mathcal {T}_{\textsf{real}}\) (resp. \(\mathcal {T}_{\textsf{ideal}}\)) denotes the transcript random variable generated by the interaction of \(\mathcal {D} \) with the real (resp. ideal) world. We let \(\mathcal {T}\) denote the set of attainable transcripts \(\tau \) such that \(\textrm{Pr} [\mathcal {T}_{\textsf{ideal}} = \tau ] >0\). It is worth noting that although the set \(\mathcal {T}\) depends on \(\mathcal {D} \), the probabilities \(\textrm{Pr} [\mathcal {T}_{\textsf{ideal}} = \tau ]\) and \(\textrm{Pr} [\mathcal {T}_{\textsf{real}} = \tau ]\) (for any \(\tau \in \mathcal {T}\)) are independent of \(\mathcal {D} \), since they are inherent properties of the two worlds. The task of bounding (5) is to figure out two (partial) distributions, of which the one for ideal world is simple and easy to deal with. Thus, the main effort in various proofs is essentially to study the random value \(\mathcal {T}_{\textsf{real}}\).
Crucial Probability in the Real World. The basis of studying \(\mathcal {T}_{\textsf{real}}\) is the probability \(\textrm{Pr} [\mathcal {T}_{\textsf{real}} = \tau ]\), which can be reduced to a conditional probability with intuitive meaning (see Eq. (7)). For any fixed transcript \(\tau =(\mathcal {Q}_{0}, \mathcal {Q}_{1},\dots ,\mathcal {Q}_{t'}, K) \in \mathcal {T}\), it has
The central task of calculating \(\textrm{Pr} [\mathcal {T}_{\textsf{real}} = \tau ]\) is to evaluate Eq. (7)Footnote 2, since the value of Eq. (6) can be solved trivially for any KAC or KAC-type construction. In this work, we will use a graph view (basically taken from [CS14] and to be defined in next part), then Eq. (7) can be interpreted as the probability that all the paths between \(x_j\) and \(y_j\) (where \((x_j, y_j) \in \mathcal {Q}_{0}\)) are completed, when each random permutation \(P_{i}\) extending the corresponding set \(\mathcal {Q}_{i}\).
Graph View. It is often more convenient to work with constructions and transcripts in a graph view. Here we take only the t-round KAC or KAC-type construction as an example, and other constructions are similar. For a given construction, all the information of transcript \(\tau =(\mathcal {Q}_{0}, \mathcal {Q}_{1},\dots ,\mathcal {Q}_{t'}, K) \in \mathcal {T}\) can be encoded into a round graph \(G(\tau )\). First, one can view each set \(\mathcal {Q}_{i}\) as a bipartite graph with shores \(\{0,1\}^n\) and containing \(q_i\) (resp. \(q_e\), in the case of \(\mathcal {Q}_{0}\)) disjoint edges. To have maximum generality, we here keep the value of \(K = (\kappa _0, \dots , \kappa _t)\) in graph \(G(\tau )\)Footnote 3, where each mapping of XORing round key \(\kappa _i\) is viewed as a full bipartite graph (i.e. it contains \(2^n\) disjoint edges).
More specifically, graph \(G(\tau )\) contains \(2(t+1)\) shores, each of which is identified with a copy of \(\{0,1\}^n\). The \(2(t+1)\) shores are indexed as \(0, 1, 2, \dots , 2t+1\). We use the ordered pair \(\langle i, u \rangle \) to represent the string u in shore i, where \(i \in \{0,1,\dots , 2t+1\}\) and \(u \in \{0,1\}^n\). For convenience, we simply use u to denote a string if it is clear from the context which shore the u is in. In particular, the vertices in shore 0 and shore \(2t+1\) are often called plaintexts and ciphertexts, respectively. More care should be taken when \(t' < t\), as this means that the target construction uses the same permutation in different rounds. For any \(i \ne j \in \{1,\dots ,t\}\) that round i and round j use the same permutation, the shores \(2i-1\) and \(2j-1\) are actually the same, and the shores 2i and 2j are also the same. That is, \(\langle 2i-1,u \rangle =\langle 2j-1,u \rangle \) and \(\langle 2i,v \rangle =\langle 2j,v \rangle \) for all \(u,v \in \{0,1\}^n\).
We define the even-odd edges between shore 2i and shore \(2i+1\) as \(E_{(2i,2i+1)} := \{(v, v \oplus \kappa _i): v \in \{0,1\}^n \}\) and call them key-edges, where \(i \in \{ 0, \dots , t\}\). The key-edges \(E_{(2i,2i+1)}\) correspond to the step of XORing round key \(\kappa _{i}\) in the KAC or KAC-type construction, and form a perfect matching of bipartite graph.
For \(i \in \{1, \dots , t\}\), we use the odd-even edges between shore \(2i-1\) and shore 2i to represent the queries made to the permutation in round i, and call them permutation-edges. Naturally, the term \(P_{k}\)-permutation-edge is used to indicate the round permutation associated with it, where \(k\in \{1,\dots ,t'\}\). Based on the definition of strings above, more care should also be taken when \(t' < t\). For any \(i \ne j \in \{1,\dots ,t\}\) that round i and round j use the same permutation, the bipartite graph between the shore \(2i-1\) and 2i, and the bipartite graph between the shore \(2j-1\) and 2j are the same one. More specifically, we define the permutation-edges between shore \(2i-1\) and 2i as \(E_{(2i-1,2i)} := \{\langle u, P_{k}, v\rangle : (u,v) \in \mathcal {Q}_{k} \}\)Footnote 4 for \(i = 1, \dots , t\), where \(P_{k}\) (\(1 \le k \le t'\)) is the name of round permutation between shore \(2i-1\) and 2i (see the naming in Sect. 1). That is, we distinguish strings and permutation-edges by the round permutation associated with them, rather than by shores.
In addition, we should keep in mind that there are implicit permutation-edges (i.e., \(\{\langle x_i, \mathcal {Q}_{0}, y_i\rangle : (x_i,y_i) \in \mathcal {Q}_{0} \}\), although not drawn) directly from shore 0 to shore \(2t+1\) according to the construction queries in \(\mathcal {Q}_{0}\), i.e. these edges are from the plaintexts \(x_i\)’s to the corresponding ciphertexts \(y_i\)’s. Throughout this work, we use symbols related to x (e.g., \(x_i\) and \(x_i'\)) and y (e.g., \(y_i\) and \(y_i'\)) to denote plaintexts (i.e., strings in shore 0) and ciphertexts (i.e., strings in shore \(2t+1\)), respectively.
Basic Definitions about Graph. We say shore i is to the left of shore j if \(i < j\), and view paths as oriented from left to right. For convenience, the index of the shore containing vertex u is written as \(\textsf{Sh}(u)\). A vertex u in a shore i is called right-free, if no edge connects u to any vertex in shore \(i+1\). A vertex v in a shore j is called left-free, if no edge connects v to any vertex in shore \(j-1\). Notice that right-free vertices and left-free vertices must be located on the odd and even shores, respectively.
We write \(\textsf{R}(u)\) for the rightmost vertex in the path of \(G(\tau )\) starting at u, and \(\textsf{L}(v)\) for the leftmost vertex in the path of \(G(\tau )\) ending at v. For any odd \(i \in \{0, \dots , 2t+1\}\) and \(i < j \in \{0, \dots , 2t+1\}\), we let \(U_{ij}\) denote the set of paths that starts at a left-free vertex in shore i and reaches a vertex in shore j. Similarly, for any \(i < j \in \{0, \dots , 2t+1\}\), we use \(Z_{ij}\) to denote the set of paths that starts at a vertex in shore i and reaches a vertex in shore j. That is, the only difference between \(Z_{ij}\) and \(U_{ij}\) is that the starting vertices on shore i in the former need not be left-free.
Path-Growing Procedure. In this work, we usually imagine the crucial probability (7) as connecting all \(x_j\) with \(y_j\) through a (probabilistic) path-growing procedure, where \((x_j,y_j) \in \mathcal {Q}_{0}\). Note that all the key-edges already exist, so we only need to generate edges from odd shores to the next shore. Given \(G(\tau )\) and a vertex u, we define the following procedure to generate a path \((u, w_1, \dots , w_r)\) from u.
Let \(w_0 =u\). For i from 1 to r, if \(w_{i-1}\) is not right-free and adjacent to some vertex z in shore i, then let \(w_i = z\); otherwise, sample \(u_i\) uniformly at random from all left-free vertices in shore i, and let \(w_i = u_i\).
For convenience, we let \(u \rightarrow v\) denote the event that u is connected to v through the above path-growing procedure and write \(\textrm{Pr} _{G}[u \rightarrow v] = \textrm{Pr} _{G}[w_r = v]\), where v is a vertex in shore \(\textsf{Sh}(u)+r\). We are now ready to give the key lemma of [CS14] (adapted slightly to fit here) as follows.
Lemma 1
(Lemma 1 of [CS14]). Given any \(G(\tau )\) as described above, let u be any right-free vertex in shore 1 and v be any left-free vertex in shore 2t, then it has
where the sum is taken over all sequences \(\sigma =(i_0,\dots ,i_s)\) with \(1=i_0<\dots <i_s=2t+1\) (where \(i_0, i_1,\dots ,i_{s}\) are required to be odd integers), and \(|\sigma |=s\).
2.3 Two Useful Lemmas
The H-coefficient technique [CS14] is a very popular tool for bounding the statistical distance between two distributions (e.g. Eq. (5)). Its core idea is to properly partition the set of attainable transcripts \(\mathcal {T}\) into two disjoint sets, the good transcripts set \(\mathcal {T}_1\) and the bad transcripts set \(\mathcal {T}_2\). If for any \(\tau \in \mathcal {T}_1\), we are able to obtain a lower bound (e.g. \(1 - \varepsilon _1\)) on the ratio \(\textrm{Pr} [\mathcal {T}_{\textsf{real}} = \tau ]/ \textrm{Pr} [\mathcal {T}_{\textsf{ideal}} = \tau ]\). And we can also obtain an upper bound (e.g. \(\varepsilon _2\)) on the value of \(\textrm{Pr} [\mathcal {T}_{\textsf{ideal}} \in \mathcal {T}_2]\). The statistical distance is then bounded by \(\varepsilon _1 + \varepsilon _2\). All of the above are formalized in the following lemma.
Lemma 2
(H-Coefficient Technique, [CS14]). Let E denote the target t-round KAC or KAC-type construction, and \(\mathcal {T}=\mathcal {T}_1 \cup \mathcal {T}_2\) be the set of attainable transcripts. Assume that there exists a value \(\varepsilon _1 > 0\) such that
holds for any \(\tau \in \mathcal {T}_1\), and there exists a value \(\varepsilon _2 >0 \) such that \(Pr[\mathcal {T}_{\textsf{ideal}} \in \mathcal {T}_2] \le \varepsilon _2\). Then for any information-theoretic distinguisher \(\mathcal {D} \), it has \(\textbf{Adv} _{E,t}^{\textsf{SPRP}}(\mathcal {D} ) \le \varepsilon _1+\varepsilon _2\).
To apply Lemma 2, the main task is usually to determine the value of \(\varepsilon _1\). As we have argued in the previous section, it is essentially to calculate the crucial probability (7). The following lemma re-emphasizes this fact.
Lemma 3
(Lemma 2 of [Che+18]). Let E denote the target t-round KAC or KAC-type construction, and \(\tau =(\mathcal {Q}_{0},\mathcal {Q}_{1},\dots ,\mathcal {Q}_{t'},K) \in \mathcal {T}\) be an attainable transcript, where K is the \((t+1)n\)-bit key. We denote \(p(\tau )=\textrm{Pr} _{P_{1},\dots ,P_{t'} \leftarrow _\$ \mathcal {P}_n} [(E_K \downarrow \mathcal {Q}_{0}) \mid (P_{1} \downarrow \mathcal {Q}_{1}) \wedge \cdots \wedge (P_{t'} \downarrow \mathcal {Q}_{t'})]\), then
3 Technical Overview
This section outlines the techniques used in security proofs of this work. We first review the known proof method, then propose a general transformation to simplify it, and finally give new proof strategies to further simplify security proofs and remove unnatural restrictions in the known result.
3.1 Proof Method of [Che+18]
The proof method for KAC-type constructions was originally proposed by Chen et al. [Che+18] in their analysis of the minimization of 2-round KAC. We note that [WYCD20] also follows this method and further refines it into an easy-to-use framework. Our approach is more closely inspired by that of [WYCD20] than by [Che+18].
At a high level, the proof method uses the H-coefficient technique (see Theorem 2), so the values of \(\varepsilon _1\) and \(\varepsilon _2\) need to be determined for good and bad transcripts, respectively. We focus here only on the main challenge, the value of \(\varepsilon _1\), which is equivalent to the crucial probability (7) (see Lemma 3).
For a given construction and transcript (represented equivalently in graph view), we call a set of pairs of strings \(A^\equiv = \{(\langle 0,a_1\rangle , \langle 2t+1,b_1\rangle ), \dots ,(\langle 0,a_m \rangle , \langle 2t+1,b_m \rangle )\}\) a uniform-structure-group, if \(\textsf{Sh}(\textsf{R}(a_1)) = \cdots = \textsf{Sh}(\textsf{R}(a_m)) < \textsf{Sh}(\textsf{L}(b_1)) = \cdots = \textsf{Sh}(\textsf{L}(b_m))\). Clearly, all pairs in \(A^\equiv \) have a uniform structure in graph view, i.e., the numbers and locations of missing permutation-edges are the same for each pair of strings \((\langle 0,a_i\rangle , \langle 2t+1,b_i\rangle )\). We now give the general problem abstracted in [WYCD20], but slightly different to fit better here.
Definition 1
(Completing A Uniform-Structure-Group, [WYCD20]). Consider a t-round KAC or KAC-type construction E, and fix arbitrarily an attainable transcript \(\tau =(\mathcal {Q}_{0}, \mathcal {Q}_{1},\dots ,\mathcal {Q}_{t'}, K)\). Let \(\mathcal {Q}_{0}^\equiv = \{(x_{i_1},y_{i_1}), (x_{i_2},y_{i_2}), \dots , (x_{i_s},y_{i_s})\} \subseteq \mathcal {Q}_{0}\) be a uniform-structure-group of plaintext-ciphertext pairsFootnote 5, then the problem is to evaluate the probability that \(\mathcal {Q}_{0}^\equiv \) is completed (i.e. all plaintext-ciphertext pairs in \(\mathcal {Q}_{0}^\equiv \) are connected), written as
For 3-round KACSP, [WYCD20] showed that the set \(\mathcal {Q}_{0}\) can be divided into six disjoint uniform-structure-groups \(\mathcal {Q}_{0,1}^\equiv ,\mathcal {Q}_{0,2}^\equiv ,\mathcal {Q}_{0,3}^\equiv ,\mathcal {Q}_{0,4}^\equiv ,\mathcal {Q}_{0,5}^\equiv ,\mathcal {Q}_{0,6}^\equiv \), and the crucial probability (7) can be decomposed into six probabilities (in the form of (9)) associated with them. Then, all that remains is to find a good lower bound on the probability (9).
It is shown in [WYCD20] that there exists a general framework for the task. To state it, we should first look at a useful concept called \(\textsf{Core}\).
Definition 2
(\(\textsf{Core}\), [WYCD20]). For a complete path from \(x_j\) to \(y_j\), we refer to the set of permutation-edges that make up the path as the \(\textsf{Core}\) of \((x_j,y_j)\), and denote it as \(\textsf{Core}(x_j,y_j)\). That is,
Similarly, when a uniform-structure-group \(\mathcal {Q}_{0}^\equiv \) is completed, we can also define its \(\textsf{Core}\) , i.e. the set of permutation-edges used to connect all plaintext-ciphertext pairs in \(\mathcal {Q}_{0}^\equiv \), denoted as \(\textsf{Core}(\mathcal {Q}_{0}^\equiv )\). That is,
In order to illustrate the definition of \(\textsf{Core}\) more clearly, we also provide several concrete examples in the full version [Yu+23, Appendix B].
Note that the probability (9) is equivalent to counting all possible permutations \(P_{1},\dots ,P_{t'}\) that complete \(\mathcal {Q}_{0}^\equiv \) and also satisfy the known queries \(\mathcal {Q}_{1}, \cdots , \mathcal {Q}_{t'}\). The idea of the general framework is to classify all such possible permutations \(P_{1},\dots ,P_{t'}\), according to the number of new edges added to each round permutation (relative to the known \(\mathcal {Q}_{1}, \cdots , \mathcal {Q}_{t'}\)) in \(\textsf{Core}(\mathcal {Q}_{0}^\equiv )\). Since the goal is to obtain a sufficiently large lower bound, a constructive approach can be used. In particular, for each sequence of the numbers of newly added edges in round permutations, we should construct as many permutations \(P_{1},\dots ,P_{t'}\) as possible that complete \(\mathcal {Q}_{0}^\equiv \) and satisfy these parameters. Summing up a sufficient number of sequences will give a desired lower bound.
More precisely, we let \( \mathcal {P}_{C}=\{ (P_1,\dots ,P_{t'}) \in \mathcal {P}_n^{t'}: (E_K \downarrow \mathcal {Q}_{0}^ \equiv ) \wedge (P_{1} \downarrow \mathcal {Q}_{1}) \wedge \dots \wedge (P_{t'} \downarrow \mathcal {Q}_{t'}) \} \) denote the set of all permutations that complete \(\mathcal {Q}_{0}^ \equiv \) and extend respectively \(\mathcal {Q}_{1},\dots ,\mathcal {Q}_{t'}\), and let \( \mathcal {C}=\{ \textsf{Core}(\mathcal {Q}_{0}^ \equiv ): \mathcal {Q}_{0}^ \equiv \textit{ is completed by a sequence} \textit{of round permutations} (P_1,\dots ,P_{t'}) \in \mathcal {P}_{C}\}\) denote the set of all possible \(\textsf{Core}\)s. For each \(\widetilde{C} \in \mathcal {C}\), we can determine a tuple of numbers \((\vert \widetilde{C}_{1}\vert , \vert \widetilde{C}_{2}\vert ,\dots ,\vert \widetilde{C}_{t'}\vert )\), where \(\vert \widetilde{C}_j\vert \) represents the number of edges newly added to \(\mathcal {Q}_{j}\) in the \(\widetilde{C}\). Then, we can give a more general form than the framework in [WYCD20] (i.e., setting \(t'=1\)) as follows,
As mentioned earlier, Eq. (10) essentially turns the task into constructing as many \(\textsf{Core}\)s as possible for different tuples \((m_1, \dots , m_{t'})\), and then summing their results. In general, the framework can be carried out in three steps. The first step is to design a method that, for each given tuple \((m_1, \dots , m_{t'})\), ensures to generate \(\textsf{Core}\)s \(\widetilde{C}\) satisfying \(\vert \widetilde{C}_{1}\vert = m_1, \dots , \vert \widetilde{C}_{t'}\vert = m_{t'}\). The second step is then to count the possibilities that can be generated by the first step. And the third step is to perform a summation calculation, where a trickFootnote 6 of hypergeometric distribution (pioneered by [Che+18]) will be used.
Note. It should be pointed out here that all proofs in this work are conducted under the guidance of this framework (i.e., Eq. (10)). In particular, we showed that the key task of H-coefficient technique (i.e., Lemma 2) is to bound the probability (7) in the real world, which can then be reduced to bound the probabilities of the form (9). Therefore, the framework provides a high-level intuition that we can always accomplish the above task in three steps (for any KAC or KAC-type constructionFootnote 7): constructing \(\textsf{Core}\)s with specific cardinalities, counting the number of \(\textsf{Core}\)s and performing a summation calculation. When analyzing different constructions, such as the KACs (setting \(t'=t\)) and KACSPs (setting \(t'=1\)), the subtle difference mainly lies in step 1, where the available constructive methods will be slightly different. In contrast, the detailed analysis and calculations in steps 2 and 3 are similar.
3.2 A General Transformation
We propose a general transformation to simplify the above proof method of [Che+18], such that only one probability (9) needs to be bounded. As we shall see, it does cut out a lot of tedious work and significantly simplify the proof. We apply this transformation to the security proofs of various constructions in this work.
For each pair \((x_j,y_j)\), there are \(r_j := \big (\textsf{Sh}(\textsf{L}(y_j)) - \textsf{Sh}(\textsf{R}(x_j)) + 1 \big )/2\) undefined edges between \(x_j\) and \(y_j\), where \(r_j \in \{1,\dots ,t\}\) for a good transcriptFootnote 8. We call \(r_j\) the actual distance between \(x_j\) and \(y_j\). We say that \((x_i,y_i)\) is farther than \((x_j,y_j)\) if \(r_i > r_j\); or closer if \(r_i < r_j\); or equidistant, otherwise. Clearly, all pairs in a uniform-structure-group are equidistant.
The idea of our general transformation is quite natural. First note that the set \(\mathcal {Q}_{0}\) usually contains pairs with various actual distances, leading to the existence of multiple uniform-structure-groups. Just by intuition, the farther pair \((x_i,y_i)\) feels more “hard” (conditionally, in fact) to connect than the closer pair \((x_j,y_j)\), given the same available resources. After all, the former tends to consume more resources (e.g. new edges), so fewer edges can be freely defined. Assuming this argument holds, we can define a set \(\widehat{\mathcal {Q}_{0}}\) satisfying \(\vert \widehat{\mathcal {Q}_{0}} \vert = \left| \mathcal {Q}_{0} \right| \) and in which all pairs have the maximal actual distance t. That is, all the easier pairs in \(\mathcal {Q}_{0}\) are replaced with the hardest ones, thus making \(\widehat{\mathcal {Q}_{0}}\) itself a uniform-structure-group. Then, for the same known queries \(\mathcal {Q}_{1},\dots ,\mathcal {Q}_{t'}\), it should have
Clearly, if we can obtain a good lower bound for \(p_{\tau }(\widehat{\mathcal {Q}_{0}})\), it holds for the target crucial probability as well. The advantage of this treatment is that we only need to bound a single probability (9), namely \(p_{\tau }(\widehat{\mathcal {Q}_{0}})\). Of course it comes at a price, so we need to keep the probability loss within an acceptable range. In short, this transformation can be seen as sacrificing a small amount of accuracy for great computational convenience.
All that remains is to find a method to transform closer pairs into farther ones, and make sure that they are less likely to be connected. We first point out that the direct transformation does not necessarily hold, although it is intuitively sound. Taking KAC as an example, we can know from the well-known Lemma 1 that the direct transformation does hold in the average case. However, it does not hold in the worst case, since counterexamples are not difficult to construct.
We next show that the direct transformation can be proved to hold, if a simple constraint is added on the replaced farther pairs. First of all, we say that a vertex u is connected to a vertex v in the most wasteful wayFootnote 9, if all growing permutation-edges in the path are new (i.e. not defined before then) and each of them is used exactly once. Similarly, we can also connect a group of pairs of nodes in the most wasteful way, where all growing permutation-edges in these paths are new and each of them is used exactly once. The following is a useful property: for a given group of pairs, the number of new edges added to each round permutation \(P_{j}\) is fixed (denoted as \(m_j\)), among all possible paths generated in the most wasteful way. These numbers \(m_1,\dots ,m_{t'}\) must be the maximum values (i.e. the number of missing edges between the group of pairs), determined by the construction and the number of pairs.
More formally, we give below the definition of the most wasteful way (in the contex of plaintext-ciphertext pairs for ease of notation; other cases can be defined similarly).Footnote 10
Definition 3 (The Most Wasteful Way)
Consider a t-round KAC or KAC-type construction E, and fix arbitrarily the set of construction queries \(\mathcal {Q}_{0}\) and the key K. Let \(\mathcal {Q}_{k}'\) denote the set of all \(P_{k}\)-permutation-edges fixed so far, where \(k=\{1,\dots ,t'\}\). Let \(\tilde{\mathcal {Q}_{0}} = \{(x_{i_1},y_{i_1}),(x_{i_2},y_{i_2}), \dots ,(x_{i_s},y_{i_s})\} \subseteq \mathcal {Q}_{0}\) be a set of plaintext-ciphertext pairs to be connected, where \(\textsf{Sh}(\textsf{R}(x_{i_j})) < \textsf{Sh}(\textsf{L}(y_{i_j}))\) for all \(j \in \{1,\dots ,s\}\). We denote by \(m_k\) the total number of \(P_{k}\)-permutation-edges missing in the paths between all pairs in \(\tilde{\mathcal {Q}_{0}}\) (given \(\mathcal {Q}_{1}',\dots ,\mathcal {Q}_{t'}'\)), where \(k=\{1,\dots ,t'\}\).
Then, \(\tilde{\mathcal {Q}_{0}}\) is said to be connected in the most wasteful way (with respect to \(\mathcal {Q}_{1}',\dots ,\mathcal {Q}_{t'}'\)), if the \(\textsf{Core}\) of the completed \(\tilde{\mathcal {Q}_{0}}\) contains exactly \(m_k\) new \(P_{k}\)-permutation-edges compared to \(\mathcal {Q}_{k}'\) for all \(k \in \{1,\dots ,t'\}\).
At this point, we are ready to describe our transformation from \(\mathcal {Q}_{0}\) to \(\widehat{\mathcal {Q}_{0}}\): all pairs in \(\mathcal {Q}_{0}\) whose actual distance is less than t are replaced with new pairs whose actual distance is equal to t, and it is required that these replaced new pairs must be connected in the most wasteful way. The correctness of this transformation can be verified by repeatedly using the general Lemma 4, the proof of which is given in the full version [Yu+23, Appendix E.1].
Lemma 4 (The Closer The Easier)
Consider a t-round (\(t \ge 2\)) KAC or KAC-type construction E, and fix arbitrarily the sets of known queries \(\mathcal {Q}_{1},\dots ,\mathcal {Q}_{t'}\) and the key K.
Let \(A^\equiv = \{(x_1,y_1),\dots ,(x_s,y_s)\}\) be a uniform-structure-group of s plaintext-ciphertext pairs, where \(\textsf{Sh}(\textsf{R}(x_1)) = \cdots = \textsf{Sh}(\textsf{R}(x_s)) = 3\) and \(\textsf{Sh}(\textsf{L}(y_1)) = \cdots = \textsf{Sh}(\textsf{L}(y_s)) = 2t\). That is, the actual distance of each pair in \(A^\equiv \) is \(t-1\).
Let \(B^\equiv = \{(x_1',y_1'),\dots ,(x_s',y_s')\}\) be a uniform-structure-group of s plaintext-ciphertext pairs, where \(\textsf{Sh}(\textsf{R}(x_1')) = \cdots = \textsf{Sh}(\textsf{R}(x_s')) = 1\) and \(\textsf{Sh}(\textsf{L}(y_1')) = \cdots = \textsf{Sh}(\textsf{L}(y_s')) = 2t\). That is, the actual distance of each pair in \(B^\equiv \) is t.
Assume that \(s \cdot t \le \vert \mathcal {Q}_{i_2} \vert / 2\) and \(\vert U_{04} \vert \le \vert \mathcal {Q}_{i_2} \vert / 2 \), where \(\mathcal {Q}_{i_2}\) denotes the set of known queries to the second round permutation \(P_{i_2}\) (where \(i_2 \in \{1,\dots ,t'\}\)). If we both connect \(A^\equiv \) and \(B^\equiv \) in the most wasteful way, then the closer \(A^\equiv \) is relatively easier. That is, for sufficiently large n, we have
where \(E_K \downarrow _w A^\equiv \) (resp. \(E_K \downarrow _w B^\equiv \)) denotes the event that \(A^\equiv \) (resp. \(B^\equiv \)) is completed in the most wasteful way.
The Lemma 4 tells us that the closer pairs are easier to connect than the farther pairs, even if they are both in the wasteful way. Also note that the ordinary probability of connecting given pairs must be greater than when only the most wasteful way is allowed, since there may be other ways of connecting (e.g. reusing edges). Thus, our general transformation replaces the closer uniform-structure-group (whose connections are unrestricted) by a farther one that can only be connected in the most wasteful way, the connecting probability of course becoming smaller (i.e. Eq. (11) holds). We should also stress that the assumptions \(s \cdot t \le \vert \mathcal {Q}_{i_2} \vert / 2\) and \(\vert U_{04} \vert \le \vert \mathcal {Q}_{i_2} \vert / 2 \) are quite loose, and their only effect on the security proof is to add a few conditions to the definition of good transcripts. For convenience, we can simply ignore the assumptions, except that there is a negligible deviation in the value of \(\varepsilon _2\). To see this more clearly, we first point out that the number of pairs that need to be replaced s is often much smaller than \(\vert \mathcal {Q}_{i} \vert \) and the number of rounds t is a constant. In particular, the largest s encountered in the security proof for a t-round construction is \(s =\mathcal {O}( \vert \mathcal {Q}_{i} \vert / N^{1/(t+1)})\). Second, since the expectation of \(\vert U_{04} \vert \) is \(\vert \mathcal {Q}_{1} \vert \cdot \vert \mathcal {Q}_{i_2} \vert / N\), the well-known Markov’s inequality is sufficient to give a good upper bound on the probability \(\textrm{Pr} [\vert U_{04} \vert > \vert \mathcal {Q}_{i_2} \vert / 2]\).
Finally, we illustrate how the general transformation can be applied in practical security proofs. The process is quite simple. Given a good transcript \(\tau =(\mathcal {Q}_{0}, \mathcal {Q}_{1},\dots ,\mathcal {Q}_{t'}, K)\), we first partition the set \(\mathcal {Q}_{0}\) into disjoint uniform-structure-groups, such as \(\mathcal {Q}_{0,1}^\equiv , \dots , \mathcal {Q}_{0,k}^\equiv \). Typically, there is only one uniform-structure-group, say \(\mathcal {Q}_{0,k}^\equiv \), whose actual distance is t and \(\vert \mathcal {Q}_{0,k}^\equiv \vert = \vert \mathcal {Q}_{0}\vert \cdot \big (1 - \mathcal {O}(\frac{1}{N^{t+1}}) \big ) \). That is, only about \(s = \mathcal {O}(\frac{1}{N^{t+1}}) \cdot \vert \mathcal {Q}_{0} \vert \) plaintext-ciphertext pairs need to be replaced by the general transformation. We write wlog that \(\mathcal {Q}_{0} = \{(x_1,y_1), \dots , (x_q,y_q)\}\) and \(\mathcal {Q}_{0,k}^\equiv = \{ (x_{s+1},y_{s+1}), \dots , (x_{q},y_{q})\}\). We first arbitrarily choose s right-free vertices \(u_1,\dots ,u_s\) in the shore 1, and s left-free vertices \(v_1,\dots ,v_s\) in the shore 2t (this always works since both s and \(\vert \mathcal {Q}_{i} \vert \) are much smaller than N). Then, we define \((x_{q+i},y_{q+i}) := (u_i \oplus \kappa _0, v_i \oplus \kappa _t)\) for \(i = 1, \dots , s\), and denote the set they form as \(\mathcal {Q}_{0}^*\). Next, we set \(\widehat{\mathcal {Q}_{0}} = \mathcal {Q}_{0,k}^\equiv \cup \mathcal {Q}_{0}^*\), i.e. \(\widehat{\mathcal {Q}_{0}} = \{(x_{s+1},y_{s+1}),\dots ,(x_{q},y_{q}), (x_{q+1}, y_{q+1}), \dots , (x_{q+s},y_{q+s})\}\). It is easy to see that \(\widehat{\mathcal {Q}_{0}}\) is indeed a uniform-structure-group with actual distance t. Please note that all the known queries \(\mathcal {Q}_{1},\dots ,\mathcal {Q}_{t'}\) remain unchanged throughout. Also, don’t forget that the last s pairs (i.e. \(\mathcal {Q}_{0}^*\)) must be connected in the most wasteful way. Lastly, the property of general transformation (see Eq. (11)) allows us to focus only on the lower bound of the new probability
where \(E_K \downarrow _w \mathcal {Q}_{0}^*\) denotes the event that the plaintext-ciphertext pairs in \(\mathcal {Q}_{0}^*\) are connected in the most wasteful way.
3.3 New Proof Strategies
Although we are guided by the proof method of [Che+18], the low-level proof strategies are quite different.
We introduce a new notion of recycled-edge, while [WYCD20] only uses the shared-edge. Intuitively, our use of a recycled-edge means that an edge is recycled from the known queries (i.e. from \(\mathcal {Q}_{1},\dots ,\mathcal {Q}_{t'}\)) to build the path, so that one less new edge is added. Thus, recycled-edges serve the same purpose as shared-edges, i.e. to reduce the use of new edges when growing paths (relative to the most wasteful way). The difference between them is that the former reuses known edges, while the later reuses the newly added edges. We point out that recycled-edge has the following features compared to shared-edge. First, the analysis of recycled-edges is easier because each of recycled-edge involves only one path, whereas each shared-edge involves multiple paths. Second, the recycled-edge is less sensitive to the construction, and its analysis is relatively uniform in different constructions. In particular, it exists in the KAC construction where edges cannot be shared as in [WYCD20].
We provide new ideas to remove the two unnatural restrictions in the security bound of [WYCD20] (i.e., Theorem 1). The first restriction is the existence of an error term \(\zeta (q_e)\), making it impossible to obtain a uniform bound for all \(q_e\)’s. To get a good bound, [WYCD20] needs to choose an appropriate c for different values of \(q_e\). In particular, it is unnatural that their bound does not converge to 0 as the number of queries \(q_e\) decreases to 0. Our observation is that this problem may be due to the nature of the hypergeometric distribution, whose variance is not a monotonic function. This leads to the fact that the tail bound obtained by Chebyshev’s inequality (see Lemma 16 in the full version [Yu+23]) is also not monotonic, and thus only works well for part of the \(q_e\)’s, e.g. \(q_e = \omega (N^{1/2})\). A natural solution is to give a different proof for the range of \(q_e = \mathcal {O}(N^{1/2})\). But one thing to note here is that we need to get a beyond-birthday-bound (i.e. \(\mathcal {O}(N^{1/2+\epsilon })\)-bound for \(\epsilon > 0\)), so that the bound is negligible for all \(q_e = \mathcal {O}(N^{1/2})\). We found that the proof for \(q_e = \omega (N^{1/2})\) can be adapted to the case of \(q_e = \mathcal {O}(N^{1/2})\) just by modifying several constants defined in the proof (e.g., the values of M and \(M_0\) in Sect. 4). Therefore, the security proofs in this work usually consider two cases, one is large \(q_e = \omega (N^{1/2})\) and the other is small \(q_e = \mathcal {O}(N^{1/2})\). Their proofs are almost identical except for slightly different calculations.
The second restriction is that it requires \(q_p \le q_e/5\), where \(q_p\) and \(q_e\) are the number of permutation queries and construction queries respectively. This is an unnatural limitation on the access ability of distinguisher. After a lot of effort and calculation, we found that under the proof method of [Che+18], the main factor affecting the final security bound is the number of variables. Each variable is used to represent the number of new edges reduced in a \(\textsf{Core}\) (relative to the most wasteful way), and is denoted by \(h_i\) in our proofs. That is, more variables usually means a more accurate bound. It is important to note here that each variable actually corresponds to a constructive method of reducing new edges, and the results generated by these different methods are required to be disjoint. On the other hand, there seems to be an upper bound on the number of constructive methods of reducing new edges. Therefore, a big challenge is to perform a fine-grained analysis that allows us to find an appropriate number of variables to meet both requirements (i.e., accuracy and feasibility).
4 Improved Security Bound of \(P_{1}P_{1}P_{1}\)-Construction
4.1 Comparison of the Results
Known Result. Wu et al. [WYCD20] were the first to prove a tight security bound for the \(P_{1}P_{1}P_{1}\)-construction, and their proof was quite laborious.
Theorem 1
(\(P_{1}P_{1}P_{1}\)-Construction, Theorem 1 of [WYCD20]). Consider the \(P_{1}P_{1}P_{1}\)-construction. Assume that \( n\ge 32 \) is sufficiently large, \( \frac{ 28(q_e)^2 }{ N } \le q_p\le \frac{ q_e}{5}\) and \(2 q_p+5 q_e\le \frac{N}{2}\), then for any \(6 \le c \le \frac{ N^{1/2} }{ 8 }\), the following upper bound holds:
where \(\zeta (q_e)= {\left\{ \begin{array}{ll} \frac{32}{c^2}, &{} \text {for } q_e\le \frac{c}{6}N^{1/2} \\ \frac{9N}{q_e^2}, &{} \text {for } q_e\ge \frac{7c}{6}N^{1/2} \end{array}\right. }\) and \(\mathcal {D} \) can be any distinguisher making \(q_e\) construction queries and \(q_p\) permutation queries.
It can be seen that the above security bound has two unnatural restrictions. The first is the error term \(\zeta (q_e)\), where the entire range of \(q_e\) cannot be covered by a single value c. In particular, this term is non-negligible for small values of \(q_e\), such as \(q_e=\mathcal {O}(N^{1/2})\), making the security bound quite counter-intuitive. The second is the requirement on \(q_e\) and \(q_p\), that is, \(28(q_e)^2 /N \le q_p\le q_e/5\), which is not a reasonable limit on the ability of distinguisher.
Our Result. Using the general transformation and new proof strategies outlined in Sect. 3, we obtain a neat security bound for the \(P_{1}P_{1}P_{1}\)-construction and the proof is much simpler.
Theorem 2
(\(P_{1}P_{1}P_{1}\)-Construction, Improved Bound). Consider the \(P_{1}P_{1}P_{1}\)-construction. For any distinguisher \(\mathcal {D} \) making \(q_e\) construction queries and \(q_p\) permutation queries, the following upper bound holds:

where \(q:= \max \{q_e,q_p\}\).
In contrast to Theorem 1, our bound does give a negligible bound for all \(q=\mathcal {O}(N^{1/2})\) (which is better than \(\mathcal {O}(N^{2/3})\)-bound but slightly worse than \(\mathcal {O}(N^{3/4})\)-bound), and has no restriction on the values of \(q_e\) and \(q_p\). In fact, the bound for \(q=\mathcal {O}(N^{1/2})\) can be easily improved to \(\mathcal {O}(N^{3/4 - \epsilon })\)-bound for any \(\epsilon > 0\), by modifying M to \(q / N^{1/2 - \epsilon }\) and \(M_0\) to \(q / N^{1/4 + \epsilon }\), where M and \(M_0\) are two constants to be defined in the proof. Even if we focus only on the large \(q=\omega (N^{1/2})\), our bound is better than Eq. (13) (for which the optimal \(c=6\) is set). Most importantly, the proof of Theorem 2 is simpler and can be found in Sect. 4.2.
Remarks. It should be pointed out that the tightness of our bound is with respect to attacks achieving constant probability, i.e., an adversary needs \(q=\varOmega (N^{3/4})\) queries to distinguish \(P_{1}P_{1}P_{1}\)-construction from random with a high advantage. The curve of our bound (i.e., roughly \((q^4 / N^{3})^{\frac{1}{4}}\)) is not as sharp as the tigher bound (i.e., roughly \(q^4 / N^{3}\)) achieved in the study of KACs (e.g., [HT16]).
We here show that the exact threshold of the two bounds in Theorem 2 can be determined. In fact, there are values of q that satisfy both bounds (for these q’s, we can choose the better one at the time of use). More specifically, the first bound holds for all \(q>=N^{1/2+\epsilon }\) for any \(\epsilon >0\), and the second bound holds for all \(q\le N^{11/20}/2\). Thus, any value in the interval \([N^{1/2+\epsilon }, N^{11/20}/2]\) (e.g., \(N^{0.53}\)) can be safely chosen as the threshold.
The main reason that leads us to discuss two cases is the Eq. (35) in the full version [Yu+23], where the magnitudes of MN and \(q^2\) need to be compared. For more details, please refer to the calculation below Eq. (34) in the full version [Yu+23], which shows the analysis for all \(q \ge N^{1/2+\epsilon }\). If we set \(M= \frac{q}{N^{9/20}}\) there, then it can be verified that the second bound holds for \(q \le N^{11/20}/2\).
4.2 Proof of Theorem 2
As discussed in Sect. 3, we will consider two disjoint cases separately to remove the first restriction, namely the case \(q=\omega (N^{1/2})\) and the case \(q=\mathcal {O}(N^{1/2})\). For each case, the proof is guided by the proof method of [Che+18], thus using the H-coefficient technique (see Lemma 2) at a high level. Following the technique, we define the sets of good and bad transcripts, and then determine the values of \(\varepsilon _1\) and \(\varepsilon _2\), respectively. When calculating the value of \(\varepsilon _1\), we apply the general transformation (see Eq. (11)) so that only a single probability need to be considered. Finally, we address this single probability using the general framework (see Eq. (10)) combined with our new proof strategies.
Preparatory Work. First, we point out the simple fact that for every distinguisher \(\mathcal {D} \) that makes \(q_e\) construction queries and \(q_p\) permutation queries, there exists a \(\mathcal {D} '\) making q construction queries and q permutation queries with at least the same distinguishing advantage, where \(q= \max \{q_e,q_p\}\). We can just let \(\mathcal {D} '\) simulate the queries of \(\mathcal {D} \), and then perform additional \(q - q_e\) construction queries and \(q - q_p\) permutation queries, which obviously increases its advantage. For computational convenience, we consider the distinguisher \(\mathcal {D} '\) that makes q construction queries and q permutation queries in the analysis. That is, for each attainable transcript \(\tau =(\mathcal {Q}_{0},\mathcal {Q}_{1},K) \in \mathcal {T}\), it has \(\left| \mathcal {Q}_{0} \right| =\left| \mathcal {Q}_{1} \right| =q\).
To illustrate the key probability (7) of a good transcript, we can assume that there is no path of length 7 starting from \(x_i \in \textsf{Dom}(\mathcal {Q}_{0})\) in shore 0 or ending at \(y_i \in \textsf{Ran}(\mathcal {Q}_{0})\) in shore 7 (otherwise, it would be a bad transcript). Then, as in [WYCD20], the set \(\mathcal {Q}_{0}\) can be partitioned into the following 6 uniform-structure-groups.
-
Denote WLOG that \( \mathcal {Q}_{0,1}^\equiv = \{ (x_1,y_1), \dots , (x_{\alpha _2} , y_{\alpha _2} ) \} \subset \mathcal {Q}_{0} \), where \( \textsf{Sh}( \textsf{R}(x_i) ) = 5 \) and \( \textsf{Sh}( \textsf{L}(y_i) ) =6 \) for \(i = 1, \dots , \alpha _2\). That is, the actual distance of \(\mathcal {Q}_{0,1}^\equiv \) is 1 and \(\vert \mathcal {Q}_{0,1}^\equiv \vert = \alpha _2\). We also denote by \( \textsf{R}(\mathcal {Q}_{0,1}^\equiv ) = \{ \textsf{R}(x_i): i =1, \dots , \alpha _2 \}, \textsf{L}(\mathcal {Q}_{0,1}^\equiv ) = \{ \textsf{L}(y_i): i =1, \dots , \alpha _2 \}\).
-
Denote WLOG that \( \mathcal {Q}_{0,2}^\equiv = \{ (x_{\alpha _2+1},y_{\alpha _2+1}), \dots , (x_{\alpha _2+\beta _2} , y_{\alpha _2+\beta _2} ) \} \subset \mathcal {Q}_{0} \), where \( \textsf{Sh}( \textsf{R}(x_i) ) = 1 \) and \( \textsf{Sh}( \textsf{L}(y_i) ) =2 \) for \(i = \alpha _2 + 1, \dots , \alpha _2+\beta _2\). That is, the actual distance of \(\mathcal {Q}_{0,2}^\equiv \) is 1 and \(\vert \mathcal {Q}_{0,2}^\equiv \vert = \beta _2\). We also denote by \( \textsf{R}(\mathcal {Q}_{0,2}^\equiv ) = \{ \textsf{R}(x_i): i =\alpha _2 + 1, \dots , \alpha _2+\beta _2 \}, \textsf{L}(\mathcal {Q}_{0,2}^\equiv ) = \{ \textsf{L}(y_i): i =\alpha _2 + 1, \dots , \alpha _2+\beta _2 \}\).
-
Denote WLOG that \( \mathcal {Q}_{0,3}^\equiv = \{ (x_{\alpha _2+\beta _2+1},y_{\alpha _2+\beta _2+1}), \dots , (x_{\delta _2} , y_{\delta _2} ) \} \subset \mathcal {Q}_{0} \), where \( \textsf{Sh}( \textsf{R}(x_i) ) = 3 \) and \( \textsf{Sh}( \textsf{L}(y_i) ) =4 \) for \(i = \alpha _2+\beta _2+1, \dots , \delta _2\). That is, the actual distance of \(\mathcal {Q}_{0,3}^\equiv \) is 1 and \(\vert \mathcal {Q}_{0,3}^\equiv \vert := \gamma _2 = \delta _2 - \alpha _2 - \beta _2\). We also denote by \( \textsf{R}(\mathcal {Q}_{0,3}^\equiv ) = \{ \textsf{R}(x_i): i =\alpha _2+\beta _2+1, \dots , \delta _2 \}, \textsf{L}(\mathcal {Q}_{0,3}^\equiv ) = \{ \textsf{L}(y_i): i =\alpha _2+\beta _2+1, \dots , \delta _2 \}\).
-
Denote WLOG that \( \mathcal {Q}_{0,4}^\equiv = \{ (x_{\delta _2+1},y_{\delta _2+1}), \dots , (x_{\delta _2+\alpha _1} , y_{\delta _2+\alpha _1} ) \} \subset \mathcal {Q}_{0} \), where \( \textsf{Sh}( \textsf{R}(x_i) ) = 3 \) and \( \textsf{Sh}( \textsf{L}(y_i) ) =6 \) for \(i = \delta _2+1, \dots , \delta _2+\alpha _1\). That is, the actual distance of \(\mathcal {Q}_{0,4}^\equiv \) is 2 and \(\vert \mathcal {Q}_{0,4}^\equiv \vert = \alpha _1\). We also denote by \( \textsf{R}(\mathcal {Q}_{0,4}^\equiv ) = \{ \textsf{R}(x_i): i =\delta _2+1, \dots , \delta _2+\alpha _1 \}, \textsf{L}(\mathcal {Q}_{0,4}^\equiv ) = \{ \textsf{L}(y_i): i =\delta _2+1, \dots , \delta _2+\alpha _1 \}\).
-
Denote WLOG that \( \mathcal {Q}_{0,5}^\equiv = \{ (x_{\delta _2+\alpha _1+1}, y_{\delta _2+\alpha _1+1}), \dots , (x_{\delta _2+\delta _1} , y_{\delta _2+\delta _1} ) \} \subset \mathcal {Q}_{0} \), where \( \textsf{Sh}( \textsf{R}(x_i) ) = 1 \) and \( \textsf{Sh}( \textsf{L}(y_i) ) = 4 \) for \(i = \delta _2+\alpha _1+1, \dots , \delta _2+\delta _1\). That is, the actual distance of \(\mathcal {Q}_{0,5}^\equiv \) is 2 and \(\vert \mathcal {Q}_{0,5}^\equiv \vert := \beta _1 = \delta _1 - \alpha _1\). We also denote by \( \textsf{R}(\mathcal {Q}_{0,5}^\equiv ) = \{ \textsf{R}(x_i): i =\delta _2+\alpha _1+1, \dots , \delta _2+\delta _1 \}, \textsf{L}(\mathcal {Q}_{0,5}^\equiv ) = \{ \textsf{L}(y_i): i =\delta _2+\alpha _1+1, \dots , \delta _2+\delta _1 \}\).
-
Denote WLOG that \( \mathcal {Q}_{0,6}^\equiv = \{ (x_{\delta _2+\delta _1+1},y_{\delta _2+\delta _1+1}), \dots , (x_{ q } , y_{ q } ) \} \subset \mathcal {Q}_{0} \), where \( \textsf{Sh}( \textsf{R}(x_i) ) = 1 \) and \( \textsf{Sh}( \textsf{L}(y_i) ) =6 \) for \(i = \delta _2+\delta _1+1, \dots , q\). That is, the actual distance of \(\mathcal {Q}_{0,6}^\equiv \) is 3 and \(\vert \mathcal {Q}_{0,6}^\equiv \vert = \delta _0 = q - \delta _1 - \delta _2\). We also denote by \( \textsf{R}(\mathcal {Q}_{0,6}^\equiv ) = \{ \textsf{R}(x_i): i =\delta _2+\delta _1+1, \dots , q \}, \textsf{L}(\mathcal {Q}_{0,6}^\equiv ) = \{ \textsf{L}(y_i): i =\delta _2+\delta _1+1, \dots , q \}\).
It is easy to see that the crucial probability
In [WYCD20], the probability (14) was decomposed into several conditional probabilities, which were quite cumbersome to analyze.
Applying General Transformation. We use the general transformation (see Eq. (11)) here to reduce the task to bounding only one probability. The basic idea is to replace the uniform-structure-groups whose actual distance is less than 3 (i.e. \(\mathcal {Q}_{0,1}^\equiv ,\mathcal {Q}_{0,2}^\equiv ,\mathcal {Q}_{0,3}^\equiv ,\mathcal {Q}_{0,4}^\equiv ,\mathcal {Q}_{0,5}^\equiv \)) with a new uniform-structure-group whose actual distance is 3, and make the connecting probability smaller.
First note that when \(q = \mathcal {O}(N^{3/4})\), the expectation of \(\alpha _2,\beta _2,\gamma _2\) is \(q^3 / N^2 = \mathcal {O}(q / N^{1/2})\), and the expectation of \(\alpha _1,\beta _1\) is \(q^2 / N = \mathcal {O}(q / N^{1/4})\). Then, we denote \(s = \delta _1+\delta _2=\alpha _1+\beta _1+\alpha _2+\beta _2+\gamma _2=\mathcal {O}(q / N^{1/4})\) as the number of pairs to be replaced. As discussed in Sect. 3, we take arbitrarily s vertices in shore 0 from the set \(\{0,1\}^n \setminus \textsf{Dom}(\mathcal {Q}_{0}) \setminus \textsf{Dom}(\mathcal {Q}_{1}) \oplus \kappa _0\) and denote them as \(x_{q+1},\dots , x_{q+s}\). We also take arbitrarily s vertices in shore \(2t+1\) from the set \(\{0,1\}^n \setminus \textsf{Ran}(\mathcal {Q}_{0}) \setminus \textsf{Ran}(\mathcal {Q}_{1}) \oplus \kappa _3\) and denote them as \(y_{q+1},\dots , y_{q+s}\). Then, we define the new uniform-structure-group \(\mathcal {Q}_{0}^*:= \{(x_i,y_i): i = q+1,\dots , q+s\}\) and set \(\widehat{\mathcal {Q}_{0}}:= \mathcal {Q}_{0,6}^\equiv \cup \mathcal {Q}_{0}^*\), where the pairs in \(\mathcal {Q}_{0}^*\) must be connected in the most wasteful way. Using Lemma 4 several times, we can know that
4.2.1 Case 1: \(q = \omega (N^{1/2})\)
We mainly focus on the large values of \(q= \omega (N^{1/2})\), and the other case of \(q= \mathcal {O}(N^{1/2})\) is similar. Let \(M = \frac{q}{N^{1/2}}\) and \(M_0 = \frac{q}{N^{1/4}}\). We first give the definition of good and bad transcripts.
Definition 4
(Bad and Good Transcripts, \(P_{1}P_{1}P_{1}\)-Construction). For an attainable transcript \( \tau = ( \mathcal {Q}_{0}, \mathcal {Q}_{1}, K ) \in \mathcal {T}\), we say that \(\tau \) is bad if \(K \in \bigcup _{i =1}^5 \textsf{BadK}_i\); otherwise \(\tau \) is good. The definitions of \(\textsf{BadK}_i\) are shown below:
We can determine the value of \(\varepsilon _2 = \frac{ 12 q }{ N^{3/4} } + \frac{ 3 q^2 }{ N^{3/2} } + \frac{ 8 q ^4 }{ N^3 } + \frac{ 6 q^6 }{ N^5 }\) from the following lemma, the proof of which can be found in the full version [Yu+23, Appendix E.2].
Lemma 5
(Bad Transcripts, \(q = \omega (N^{1/2})\)). For any given \(\mathcal {Q}_{0}, \mathcal {Q}_{1}\) such that \(\left| \mathcal {Q}_{0} \right| =\left| \mathcal {Q}_{1} \right| =q\), we have
The following lemma gives a lower bound on Eq. (15) for any good transcript.
Lemma 6
(Good Transcripts, \(q = \omega (N^{1/2})\)). Fix arbitrarily a good transcript \( \tau = ( \mathcal {Q}_{0}, \mathcal {Q}_{1}, K ) \in \mathcal {T}\) as defined in Definition 4. Let \(\mathcal {Q}_{0,6}^\equiv \) and \(\mathcal {Q}_{0}^*\) be as described in Eq. (15), then we have
Before giving the proof of Lemma 6, we first show how to obtain the final security bound from the above two lemmas. First note that (16) is also a lower bound on the crucial probability (7), i.e. \(p(\tau )\) in Lemma 3 when \(t=3,t'=1\). Then it is not difficult to determine the value of \(\varepsilon _1 = \frac{ 57 q }{ N^{3/4} } + \frac{ 122 q^2 }{ N^{3/2} } + \frac{ 78 q }{ N } + \frac{ 32\,N }{ q^2 } \). According to the H-coefficient technique (see Lemma 2), we can obtain
which is the result of large \(q=\omega (N^{1/2})\) in Theorem 2.
Proof
(Proof of Lemma 6). Let \(\mathcal {Q}_{0}^\equiv = \widehat{\mathcal {Q}_{0}} := \mathcal {Q}_{0,6}^\equiv \cup \mathcal {Q}_{0}^*\) and \(t =3, t' = 1\), then the target probability is exactly an instantiation of the general problem (9). We apply the general framework (10) to bound it, so roughly in three steps.
The first step is to generate \(\textsf{Core}\)s with specific numbers of new edges. We will use four variables (denoted as \(h_1,h_2,h_3,h_4\)) to obtain a sufficiently accurate security bound, so four constructive methods of reducing new edges are needed.
The first method we use is called recycled-edge-based method, which exploits recycled-edges to reduce a specified number of new edges when building paths. Intuitively, when we construct a path connecting plaintext-ciphertext pair \((x_i,y_i)\) with an actual distance of 3, the choice of the permutation-edge between shore 3 and 4 is quite free and can be “recycled” from the known edges in \(\mathcal {Q}_{1}\) for use. Thus, we can construct the path with one less new edge. Furthermore, most of the known edges in \(\mathcal {Q}_{1}\) (about the proportion of \(1 - \mathcal {O}(1 / N^{1/4})\)) can be used as recycled-edges. More details about the recycled-edge-based method can be found in the full version [Yu+23, Appendix C.1].
The other three methods we use are shared-edge-based methods, each of which exploits a different type of shared-edges to reduce a specified number of new edges when building paths. Intuitively, we consider two plaintext-ciphertext pairs together and let them share exactly 1 permutation edge. The two paths can then be connected with one less new edge than the most wasteful way. In particular, this work only considers shared-edges of this type, each of which saves 1 new edge for 2 paths. To distinguish, we refer to a shared-edge as (i, j)-shared-edge, where i and j represent the rounds that the shared-edge lies in two paths respectively. Note that the positions of the two paths are interchangeable, so (i, j)-shared-edges and (j, i)-shared-edges are essentially the same type. More details about the shared-edge-based methods can be found in the full version [Yu+23, Appendix C.2].
Recalling the Eq. (15), our task is to connect the q pairs of \(\widehat{\mathcal {Q}_{0}} = \mathcal {Q}_{0,6}^\equiv \cup \mathcal {Q}_{0}^*\) using a specified number of new edges, where \(\mathcal {Q}_{0}^*\) is connected in the most wasteful way. Let \(h_1,h_2,h_3,h_4\) be four integer variables in the interval [0, M], where \(M = \frac{q}{N^{1/2}}\) is a constant determined by q. We combine the recycled-edge-based method, the shared-edge-based methods and the most wasteful way to accomplish the task in five steps.
-
1.
Select \(h_1\) distinct pairs from \(\mathcal {Q}_{0,6}^\equiv \), and connect each of these pairs using the recycled-edge-based method.
-
2.
Apart from the \(h_1\) pairs selected in Step 1, select \(2h_2\) appropriate pairs from \(\mathcal {Q}_{0,6}^\equiv \), and connect these pairs using the (1, 2)-shared-edge-based method.
-
3.
Apart from the \(h_1+2h_2\) pairs selected in Steps 1 and 2, select \(2h_3\) appropriate pairs from \(\mathcal {Q}_{0,6}^\equiv \), and connect these pairs using the (1, 3)-shared-edge-based method.
-
4.
Apart from the \(h_1+2h_2+2h_3\) pairs selected in Steps 1–3, select \(2h_4\) appropriate pairs from \(\mathcal {Q}_{0,6}^\equiv \), and connect these pairs using the (2, 3)-shared-edge-based method.
-
5.
Connect the remaining \(\delta _0 - h_1- \sum _{i=2}^{4} 2h_i \) pairs in \(\mathcal {Q}_{0,6}^\equiv \) and the s pairs in \(\mathcal {Q}_{0}^*\) in the most wasteful way.
Clearly, the above procedure must generate a \(\textsf{Core}(\widehat{\mathcal {Q}_{0}})\) containing exactly \(3q - \sum _{i=1}^{4} h_i\) new edges, and all the pairs of \(\mathcal {Q}_{0}^*\) are connected in the most wasteful way.
As mentioned in Sect. 3, the main factor affecting the final security bound is the number of variables. A simple explanation is that more variables make the multivariate hypergeometric distribution used in the calculations more tunable. That is why we define four variables \(h_1,h_2,h_3,h_4\) here (i.e., to improve the accuracy), and it can be verified that these four methods necessarily produce different types of paths (i.e., to ensure the plausibility). Note that even considering only the shared-edge-based methods, our strategy is simpler than [WYCD20]. In particular, a single selection operation of theirs may generate three different types of shared-edges, whereas each of our selection operations will only generate shared-edges of the same type.
The second step is to evaluate the number of \(\textsf{Core}\)s that can be generated in the first step. According to the above procedure of connecting q plaintext-ciphertext pairs of \(\widehat{\mathcal {Q}_{0}}\), we determine the number of possibilities for each step as follows. In the following, \(\textsf{RC}_i(j)\) denotes the Range (set) of all possible Candidate values for the to-be-assigned nodes in shore j (according to the constructive method used in Step i).
-
1.
Since \(\vert \mathcal {Q}_{0,6}^\equiv \vert = \delta _0\), it has \(\left( {\begin{array}{c}\delta _0\\ h_1\end{array}}\right) \) possibilities to select \(h_1\) distinct pairs from \(\mathcal {Q}_{0,6}^\equiv \). After the \(h_1\) pairs are chosen, we use the recycled-edge-based method to connect them by first determining a set \(\textsf{RC}_1(3)\) (the analysis of which is referred to the \(\textsf{RC}(3)\) in full version [Yu+23, Appendix C.1]) and choosing \(h_1\) different
 from it, and then assigning one
from it, and then assigning one  to each pair. In total, the possibilities of Step 1 is at least \(\left( {\begin{array}{c}\delta _0\\ h_1\end{array}}\right) \cdot (\vert \textsf{RC}_1(3) \vert )_{h_1}\).
to each pair. In total, the possibilities of Step 1 is at least \(\left( {\begin{array}{c}\delta _0\\ h_1\end{array}}\right) \cdot (\vert \textsf{RC}_1(3) \vert )_{h_1}\). -
2.
For simplicity, we can define a set of plaintext-ciphertext pairs \(Z \subset \mathcal {Q}_{0,6}^\equiv \) (see Eq. (17) for the definition of Z), so that the \(2(h_2+h_3+h_4)\) distinct pairs in Step 2–4 can all be selected from Z. Then in Step 2, we have \(\left( {\begin{array}{c}\left| Z \right| \\ h_2\end{array}}\right) \cdot \left( {\begin{array}{c}\left| Z \right| -h_2\\ h_2\end{array}}\right) \) possibilities to sequentially select \(h_2\) distinct pairs from Z twice, where the first (resp. second) selected \(h_2\) pairs will be constructed as the upper-paths (resp. lower-paths)Footnote 11 in the (1, 2)-shared-edge-based method. We then use the (1, 2)-shared-edge-based method to connect these \(2h_2\) pairs. According to the discussion in the full version [Yu+23, Appendix C.2], the core task of (1, 2)-shared-edge-based method is to determine two sets denoted by \(\textsf{RC}_2(2)\) and \(\textsf{RC}_2(4)\). By simple counting, the possibilities of Step 2 is at least \(\frac{(\left| Z \right| )_{2h_2}}{ h_2!} \cdot (\vert \textsf{RC}_2(2) \vert )_{h_2} \cdot (\vert \textsf{RC}_2(4) \vert )_{h_2} \), where \(\frac{(\left| Z \right| )_{2h_2}}{ h_2!}=\left( {\begin{array}{c}\left| Z \right| \\ h_2\end{array}}\right) \cdot \left( {\begin{array}{c}\left| Z \right| -h_2\\ h_2\end{array}}\right) \cdot h_2!\).
-
3.
For Step 3, we can select \(2h_3\) distinct pairs from Z after removing the \(2h_2\) pairs chosen in Step 2. Then, we have \(\left( {\begin{array}{c}\left| Z \right| -2h_2\\ h_3\end{array}}\right) \cdot \left( {\begin{array}{c}\left| Z \right| -2h_2-h_3\\ h_3\end{array}}\right) \) possibilities to sequentially select \(h_3\) distinct pairs from the rest of Z twice (similar to Step 2, the first and second selected \(h_3\) pairs will play different roles). After the \(2h_3\) pairs are chosen, we use the (1, 3)-shared-edge-based method to connect them. According to an analysis similar to that in the full version [Yu+23, Appendix C.2], the core task of (1, 3)-shared-edge-based method is also to determine two sets denoted by \(\textsf{RC}_3(4)\) and \(\textsf{RC}_3(2)\). By simple counting, the possibilities of Step 3 is at least \(\frac{(\left| Z \right| -2h_2)_{2h_3}}{ h_3!} \cdot (\vert \textsf{RC}_3(2) \vert )_{h_3} \cdot (\vert \textsf{RC}_3(4) \vert )_{h_3} \).
-
4.
For Step 4, we can select \(2h_4\) distinct pairs from Z after removing the \(2(h_2+h_3)\) pairs chosen in Step 2 and Step 3. Then, we have \(\left( {\begin{array}{c}\left| Z \right| -2h_2 -2h_3\\ h_4\end{array}}\right) \cdot \left( {\begin{array}{c}\left| Z \right| -2h_2 -2h_3-h_4\\ h_4\end{array}}\right) \) possibilities to sequentially select \(h_4\) distinct pairs from the rest of Z twice (similar to Step 2, the first and second selected \(h_4\) pairs will play different roles). After the \(2h_4\) pairs are chosen, we use the (2, 3)-shared-edge-based method to connect them. According to an analysis similar to that in the full version [Yu+23, Appendix C.2], the core task of (2, 3)-shared-edge-based method is to determine two sets denoted by \(\textsf{RC}_4(4)\) and \(\textsf{RC}_4(2)\). By simple counting, the possibilities of Step 4 is at least \(\frac{(\left| Z \right| -2h_2-2h_3)_{2h_4}}{ h_4!} \cdot (\vert \textsf{RC}_4(2) \vert )_{h_4} \cdot (\vert \textsf{RC}_4(4) \vert )_{h_4} \).
-
5.
Step 5 is to connect the remaining \( (\delta _0 - h_1 - \sum _{i=2}^{4} 2h_i )\) pairs in \( \mathcal {Q}_{0,6}^\equiv \) and the s pairs in \(\mathcal {Q}_{0}^*\) in the most wasteful way. According to the analysis in the full version [Yu+23, Appendix C.3], we can determine a set \(\textsf{RC}_5(2)\) and choose \((\delta _0 - h_1 - \sum _{i=2}^{4} 2h_i ) +s = q- h_1 - \sum _{i=2}^{4} 2h_i\) different
 from it, and assign one
from it, and assign one  to each pair; then determine a set \(\textsf{RC}_5(4)\) and choose \(q- h_1 - \sum _{i=2}^{4} 2h_i\) different
to each pair; then determine a set \(\textsf{RC}_5(4)\) and choose \(q- h_1 - \sum _{i=2}^{4} 2h_i\) different  from it, and then assign one
from it, and then assign one  to each pair. In total, the possibilities of Step 5 is at least \((\vert \textsf{RC}_5(2) \vert )_{q- h_1 - \sum _{i=2}^{4} 2h_i} \cdot (\vert \textsf{RC}_5(4) \vert )_{q- h_1 - \sum _{i=2}^{4} 2h_i}\).
to each pair. In total, the possibilities of Step 5 is at least \((\vert \textsf{RC}_5(2) \vert )_{q- h_1 - \sum _{i=2}^{4} 2h_i} \cdot (\vert \textsf{RC}_5(4) \vert )_{q- h_1 - \sum _{i=2}^{4} 2h_i}\).
All that’s left is to give a lower bound on the cardinality for Z and each \(\textsf{RC}_j(i)\) mentioned above. Let \(\varLambda _1\) denote the set of \(h_1\) pairs selected from \(\mathcal {Q}_{0,6}^\equiv \) in Step 1. We first give the definition of set Z belowFootnote 12, and denote by \(\left| Z \right| =q_0\).
From the \(\textsf{BadK}_4\) in Defn. 4, we can know that
Based on the analysis in the full version [Yu+23, Appendix C.1–C.3], we proceed to lower-bound the cardinality of each \(\textsf{RC}_j(i)\) as follows.
since \(\left| S_1 \right| = \left| U_{05} \right| \le M_0, \left| S_2 \right| = \left| U_{27} \right| \le M_0\) hold in any good transcript (see \(\textsf{BadK}_5\) in Defn. 4).
where U (resp. V) denotes the domain (resp. range) of all \(P_{1}\)-input-output-pairs fixed so far (i.e., after Step 1) and \(3 \cdot (2h_1)=6h_1\) is the maximum numberFootnote 13 of new values generated by Step 1 that fall within the constraints of \(\textsf{RC}_2(2)\). This is exactly the consequence of updating U, V discussed in the full version [Yu+23, Appendix C.2]. Due to the similarity, we directly give the remaining lower bounds without explanation.
Let \( \# \textsf{Core}s_{i} \) denote the number of \(\textsf{Core}s(\widehat{\mathcal {Q}_{0}})\) containing exactly i new edges (relative to \(\mathcal {Q}_{1}\)). Combining all the above, we finally obtain that
The third step is to perform the summation calculation. Since the lower bound on \(\# \textsf{Core}s_{ 3q -\sum _{i=1}^{4} h_i}\) is known, we are now ready to calculate the final result. From the Eqs. (10) and (28), we have
By lower-boundingFootnote 14 the Eq. (29), we end up with
which completes the proof. \(\square \)
4.2.2 Case 2: \(q = \mathcal {O}(N^{1/2})\)
The entire proof is almost the same as in the case \(q = \omega (N^{1/2})\), except for a slight modification to the calculations related to M and \(M_0\). As mentioned before, for any positive \(\epsilon >0\), if we set \(M=q / N^{1/2 - \epsilon }\) and \(M_0=q / N^{1/4 + \epsilon }\), then we can get a \(\mathcal {O}(N^{3/4 - \epsilon })\)-bound.
For simplicity, we here set \(M = \frac{q}{N^{9/20} }\) and \(M_0 = \frac{q}{N^{3/10}}\), i.e. \(\epsilon =\frac{1}{20}\). We omit the details of proof and only list the following two technical lemmas.
Lemma 7
(Bad Transcripts, \(q = \mathcal {O}(N^{1/2})\)). For any given \(\mathcal {Q}_{0}, \mathcal {Q}_{1}\) such that \(\left| \mathcal {Q}_{0} \right| =\left| \mathcal {Q}_{1} \right| =q\), we have
Lemma 8
(Good Transcripts, \(q = \mathcal {O}(N^{1/2})\)). Fix arbitrarily a good transcript \( \tau = ( \mathcal {Q}_{0}, \mathcal {Q}_{1}, K ) \in \mathcal {T}\) as defined in Definition 4. Let \(\mathcal {Q}_{0,6}^\equiv \) and \(\mathcal {Q}_{0}^*\) be as described in Eq. (15), then we have
According to the H-coefficient technique (see Lemma 2), we can obtain
which is the result of small \(q=\mathcal {O}(N^{1/2})\) in Theorem 2.
5 Tight Security Bound of t-Round \(\textsf{KACSP}\)
In this section, we generalize the proof of 3-round KACSP to the general t-round KACSP. The proof idea is basically the same, except the notation is heavier.
Theorem 3
(t-Round KACSP). Consider the t-round KACSP \((\text {where } t \ge 4)\), denoted as \(P_{1}^{(t)}\)-construction. For any distinguisher \(\mathcal {D} \) making \(q_e\) construction queries and \(q_p\) permutation queries, the following upper bound holds:

where \(q:= \max \{q_e,q_p\}\).
Note that the value of \(t = \mathcal {O}(1)\) is a constant. Therefore, the above bound does show that unless \(\mathcal {D} \) makes \(q = \varOmega (N^{t/(t+1)})\) queries, its advantage of distinguishing \(P_{1}^{(t)}\) from a truly random permutation is negligible (for sufficiently large n). In other words, t-round KACSP has the same security level as the t-round KAC.
Proof
(Proof of Theorem 3). As discussed in Sect. 4.2, we also consider that the distinguisher makes q construction queries and q permutation queries in the analysis. That is, for each attainable transcript \( \tau = ( \mathcal {Q}_{0}, \mathcal {Q}_{1}, K ) \in \mathcal {T}\), it has \(\left| \mathcal {Q}_{0} \right| = \left| \mathcal {Q}_{1} \right| =q\). Furthermore, we let \(\textsf{AD}_{t-i} \subset \mathcal {Q}_{0}\) denote the set of pairs \((x_i,y_i) \in \mathcal {Q}_{0}\) whose actual distance is i, where \(i=1,\dots ,t\). We also let \(\delta _{i} := \left| \textsf{AD}_{i} \right| \). For convenience, we simply use \(\mathcal {Q}_{0,t}^\equiv \) to denote \(\textsf{AD}_{0}\) since it is a uniform-structure-group.
Applying General Transformation. First of all, we also use the general transformation (see Eq. (11)) here to reduce the task to bounding only one probability. The basic idea is to replace the uniform-structure-groups whose actual distance is less than t with a new uniform-structure-group whose actual distance is t, and make the connecting probability smaller.
Note that the expectation of \(\delta _{i}\) is \(\mathcal {O}(q / N^{i/(t+1)})\) and we can wlog assume that \(q = \mathcal {O}(N^{t/(t+1)})\) (otherwise the security bound is invalid). Then, we denote \(s = \sum _{i=1}^{t-1} \delta _{i} = \mathcal {O}(q / N^{1/(t+1)})\) as the number of pairs to be replaced. As discussed in Sect. 3, it is easy to construct a new uniform-structure-group \(\mathcal {Q}_{0}^*:= \{(x_i,y_i): i = q+1,\dots , q+s\}\) and set \(\widehat{\mathcal {Q}_{0}}:= \mathcal {Q}_{0,t}^\equiv \cup \mathcal {Q}_{0}^*\), where the pairs in \(\mathcal {Q}_{0}^*\) must be connected in the most wasteful way. Using Lemma 4 several times, we can know that the crucial probability
Thus, Eq. (30) becomes the target probability for which we need a lower bound.
5.1 Case 1: \(q = \omega (N^{1/2})\)
As in Sect. 4.2, we mainly focus on the large values of \(q= \omega (N^{1/2})\), and the other case of \(q= \mathcal {O}(N^{1/2})\) is similar. We also first give the definition of good and bad transcripts.
Let \(\textsf{R}_{t-1} = \{\textsf{R}(x_i): (x_i,y_i)\in \textsf{AD}_{t-1} \}\) and \(\textsf{L}_{t-1} = \{\textsf{L}(y_i): (x_i,y_i)\in \textsf{AD}_{t-1} \}\) denote the set of all rightmost and leftmost vertices of the pairs whose actual distance is 1, respectively. Next, we define \(t-1\) constants \(M_j=\frac{q}{N^{j/(t+1)}}\) related to the value of q, where \(j=1,2,\dots ,t-1\).
Definition 5
(Bad and Good Transcripts, \(P_{1}^{(t)}\)-Construction). For an attainable transcript \( \tau = ( \mathcal {Q}_{0}, \mathcal {Q}_{1}, K ) \in \mathcal {T}\), we say that \(\tau \) is bad if \(K \in \bigcup _{i=1}^5 \textsf{BadK}_i\); otherwise \(\tau \) is good. The definitions of \(\textsf{BadK}_i\) are shown below:
We can determine the value of \(\varepsilon _2 = \frac{5t q }{ N^{t/(t+1)}} + \frac{ 2t^2 q^{t+1} }{ N^t } \) from the following lemma, the proof of which can be found in the full version [Yu+23, Appendix E.3].
Lemma 9
(Bad Transcripts, \(q = \omega (N^{1/2})\)). For any given \(\mathcal {Q}_{0}, \mathcal {Q}_{1}\) such that \(\left| \mathcal {Q}_{0} \right| =\left| \mathcal {Q}_{1} \right| =q\), we have
The following lemma gives a lower bound on Eq. (30) for any good transcript.
Lemma 10
(Good Transcripts, \(q = \omega (N^{1/2})\)). Fix arbitrarily a good transcript \( \tau = ( \mathcal {Q}_{0}, \mathcal {Q}_{1}, K ) \in \mathcal {T}\) as defined in Definition 5. Let \(\mathcal {Q}_{0,t}^\equiv \) and \(\mathcal {Q}_{0}^*\) be as described in Eq. (30), then we have
The proof of Lemma 10 is given in the full version [Yu+23, Appendix E.4]. We next show how to obtain the final security bound from the above two lemmas. First note that (31) is also a lower bound on the crucial probability (7), i.e. \(p(\tau )\) in Lemma 3 when \(t'=1\). Then it is not difficult to determine the value of \(\varepsilon _1\). According to the H-coefficient technique (see Lemma 2), we can obtain
which is the result of large \(q=\omega (N^{1/2})\) in Theorem 3.
5.2 Case 2: \(q = \mathcal {O}(N^{1/2})\)
The entire proof is almost the same as in the case \(q = \omega (N^{1/2})\), except for a slight modification to the calculations related to \(M_1\) and \(M_{t-1}\) and we here set \(M_1 = \frac{q}{N^{3/10}}\) and \(M_{t-1} = \frac{q}{N^{9/20} }\). We omit the details of proof and only list the following two technical lemmas.
Lemma 11
(Bad Transcripts, \(q = \mathcal {O}(N^{1/2})\)). For any given \(\mathcal {Q}_{0}, \mathcal {Q}_{1}\) such that \(\left| \mathcal {Q}_{0} \right| =\left| \mathcal {Q}_{1} \right| =q\), we have
Lemma 12
(Good Transcripts, \(q = \mathcal {O}(N^{1/2})\)). Fix arbitrarily a good transcript \( \tau = ( \mathcal {Q}_{0}, \mathcal {Q}_{1}, K ) \in \mathcal {T}\) as defined in Definition 5. Let \(\mathcal {Q}_{0,t}^\equiv \) and \(\mathcal {Q}_{0}^*\) be as described in Eq. (30), then we have
According to the H-coefficient technique (see Lemma 2), we can obtain
which is the result of small \(q=\mathcal {O}(N^{1/2})\) in Theorem 2.
6 Remarks on Other Variants of KACS
Our proof technology in this work applies to various KAC-type constructions as well as the standard KAC construction. Our general transformation also works and the proof idea is similar. The core task is to find enough constructive methods of reducing new edges, so that the final security bound is sufficiently accurate.
We also find that the more rounds means more methods, so it seems easier to find enough methods in constructions with more rounds. This is somewhat counter-intuitive. It might be interesting to figure out whether this phenomenon is an artifact of the proof technology, or because larger constructions inherently have more security redundancy.
Notes
- 1.
Each variable represents the number of new edges that can be saved by some constructive method, usually denoted by \(h_i\) in the proofs.
- 2.
- 3.
Although this leads to a somewhat redundant notation, it is still relatively easy to understand. For a concrete example, you can refer to Fig. 1 in the full version [Yu+23, Appendix C].
- 4.
Due to the uniqueness, we will interchangeably use the permutation-edge \(\langle u, P_{k}, v\rangle \) and the input-output pair (u, v) under \(P_{k}\).
- 5.
Recall that \(x_i\)’s and \(y_i\)’s are by default in shore 0 and shore \(2t+1\) respectively, so we use the simplified notation here.
- 6.
The terms arising from a (multivariate) hypergeometric distribution are introduced to help calculate a lower bound on the target probability, see the full version [Yu+23, Eq. (30)] for an example.
- 7.
In fact, the idea of this framework is quite general and it can be easily generalized to other constructions.
- 8.
The definition of good transcripts usually excludes the case where \(r_j = 0\). Please note that we keep all key-edges in the graph view here for maximum generality.
- 9.
Intuitively, this kind of paths require the most new-edges and do not share any edges with other paths. In the words of [WYCD20], the most wasteful way actually means sampling an exclusive element for each inner-node. It had also been shown in [WYCD20] that such samples are easy to analyze. More concrete examples and analysis can be found in the security proofs, such as the Fig. 1 and Appendix C.3 in the full version [Yu+23].
- 10.
It can be verified that the Examples 2 and 4 in full version [Yu+23, Appendix B] are both connected in the most wasteful way (we purposely assume \(\mathcal {Q}_{1}=\mathcal {Q}_{2}=\emptyset \) over there to ensure that each permutation-edge fixed in the path(s) is new compared to \(\mathcal {Q}_{1}\) and \(\mathcal {Q}_{2}\)).
- 11.
In Fig. 1 of the full version [Yu+23, Appendix C], the paths between \((x_2,y_2)\) and \((x_2',y_2')\) are called the upper-path and lower-path, respectively.
- 12.
See Appendix D of the full version [Yu+23] for an analysis of the constraints on Z, which are the sum of constraints from the three shared-edge-based methods.
- 13.
Note that Step 1 will generate \(2h_1\) new permutation-edges, so there will be \(2h_1\) new elements added to U and V respectively (compared to \(\textsf{Dom}(\mathcal {Q}_{1})\) and \(\textsf{Ran}(\mathcal {Q}_{1})\)). It can be seen that there are only three constraints related to U and V in Eq. (20), \(6h_1\) is obviously the maximum number of changes. We need to point out that this is actually an overestimation. For example, newly added permutation-edges in Step 1 of the form \(\langle x_i\oplus \kappa _0, P_{1}, * \rangle \) cause the set \( U \oplus \kappa _1\) to add new elements (i.e., \(x_i \oplus \kappa _0 \oplus \kappa _1\)) which are already included in \(\textsf{Dom}(\mathcal {Q}_{0}) \oplus \kappa _0 \oplus \kappa _1\). A finer analysis could provide more accurate results, but this simplified treatment is sufficient here since we are not seeking to optimize the constant coefficients in security bounds. Also, we use this easily verifiable overestimation in the evaluation of Eqs. (21)–(26) below.
- 14.
Although the calculation involves a large number of terms, it is actually simple and regular; the details can be found in the full version [Yu+23].
References
Bogdanov, A., Knudsen, L.R., Leander, G., Standaert, F.-X., Steinberger, J., Tischhauser, E.: Key-alternating ciphers in a provable setting: encryption using a small number of public permutations. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 45–62. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_5 (cited on p. 2)
Chen, S., Lampe, R., Lee, J., Seurin, Y., Steinberger, J.P.: Minimizing the two-round even-Mansour cipher. J. Cryptol. 4, 1064–1119 (2018). https://doi.org/10.1007/s00145-018-9295-y (cited on pp. 2, 3, 8, 9, 11, 15, 17)
Chen, S., Steinberger, J.: Tight security bounds for key-alternating ciphers. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 327–350. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_19 (cited on pp. 2, 6, 8)
Dunkelman, O., Keller, N., Shamir, A.: Minimalism in cryptography: the even-Mansour scheme revisited. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 336–354. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_21 (cited on p. 2)
Daemen, J., Rijmen, V.: The advanced encryption standard process. In: The Design of Rijndael. Information Security and Cryptography. Springer, Berlin, Heidelberg (2002).https://doi.org/10.1007/978-3-662-04722-4 (cited on p. 1)
Even, S., Mansour, Y.: A construction of a cipher from a single pseudorandom permutation. J. Cryptol. 3, 151–162 (1997). https://doi.org/10.1007/s001459900025 (cited on p. 1)
Hoang, V.T., Tessaro, S.: Key-alternating ciphers and key-length extension: exact bounds and multi-user security. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9814, pp. 3–32. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_1 (cited on pp. 2, 17)
Lampe, R., Patarin, J., Seurin, Y.: An asymptotically tight security analysis of the iterated even-Mansour cipher. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 278–295. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34961-4_18 (cited on p. 2)
Steinberger, J.P.: Improved security bounds for key-alternating ciphers via Hellinger distance. In: IACR Cryptology ePrint Archive, p. 481 (2012). http://eprint.iacr.org/2012/481 (cited on p. 2)
Tessaro, S., Zhang, X.: Tight security for key-alternating ciphers with correlated sub-keys. In: Tibouchi, M., Wang, H. (eds.) ASIACRYPT 2021. LNCS, vol. 13092, pp. 435–464. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-92078-4_15 (cited on p. 2)
Wu, Y., Yu, L., Cao, Z., Dong, X.: Tight security analysis of 3-round key-alternating cipher with a single permutation. In: Moriai, S., Wang, H. (eds.) ASIACRYPT 2020. LNCS, vol. 12491, pp. 662–693. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-64837-4_22 (cited on pp. 2, 3, 9, 10, 12, 15, 16, 18, 21)
Yu, L., Wu, Y., Yu, Y., Cao, Z., Dong, X.: security proofs for key-alternating ciphers with non-independent round permutations. In: IACR Cryptology ePrint Archive, Paper 2023/1355 (2023). https://eprint.iacr.org/2023/1355 (cited on pp. 3, 6, 10, 11, 12, 13, 15, 17, 19, 21, 22, 23, 24, 25, 27, 28)
Acknowledgements
We would like to thank the anonymous reviewers of TCC 2023 for their valuable comments. Yu Yu is supported by the National Natural Science Foundation of China (Grant Nos. 62125204 and 92270201), the National Key Research and Development Program of China (Grant No. 2018YFA0704701), and the Major Program of Guangdong Basic and Applied Research (Grant No. 2019B030302008). Yu Yu also acknowledges the support from the XPLORER PRIZE. This work is supported in part by the National Key Research and Development Program of China (Grant No. 2022YFB2701400) and in part by the National Natural Science Foundation of China (Grant No. 62132005, 62172162).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 International Association for Cryptologic Research
About this paper
Cite this paper
Yu, L., Wu, Y., Yu, Y., Cao, Z., Dong, X. (2023). Security Proofs for Key-Alternating Ciphers with Non-Independent Round Permutations. In: Rothblum, G., Wee, H. (eds) Theory of Cryptography. TCC 2023. Lecture Notes in Computer Science, vol 14369. Springer, Cham. https://doi.org/10.1007/978-3-031-48615-9_9
Download citation
DOI: https://doi.org/10.1007/978-3-031-48615-9_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-48614-2
Online ISBN: 978-3-031-48615-9
eBook Packages: Computer ScienceComputer Science (R0)



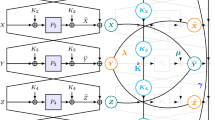

 from it, and then assigning one
from it, and then assigning one  to each pair. In total, the possibilities of Step 1 is at least
to each pair. In total, the possibilities of Step 1 is at least  from it, and assign one
from it, and assign one  to each pair; then determine a set
to each pair; then determine a set  from it, and then assign one
from it, and then assign one  to each pair. In total, the possibilities of Step 5 is at least
to each pair. In total, the possibilities of Step 5 is at least 