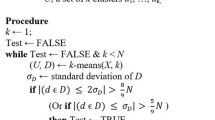Mutual k-Nearest Neighbor Graph for Data Analysis: Application to Metric Space Clustering

Abstract

In this paper, we delve into the Mutual k-Nearest Neighbor Graph ($m$k$NN G$) and its significance in clustering and outlier detection. We present a rigorous mathematical framework elucidating its application and highlight its role in the success of various clustering algorithms. Building on Brito et al.’s findings, which link the connected components of the $m$k$NN G$ to clusters under specific density bounds, we explore its relevance in the context of a wide range of density functions.

1 Introduction

Clustering demands a nuanced understanding of data and a varied toolset tailored to each unique problem. Successfully clustering hinges on formalizing intuitions into clear theorems. We aim to develop a robust mathematical framework for $m$k$NN G$ clustering use and explain the success of algorithms that use this principle.

Our literature review underscores the recurring emphasis on the $m$k$NN$ concept, and our study provides insights into its application in clustering.

This paper bridges intuition and mathematics, advancing clustering techniques. We offer a robust exploration of the Mutual k-Nearest Neighbor Graph, laying groundwork for improved clustering and outlier detection. The formalization is covered in Sect. 3.

2 The $m$k$NN$ Graph in Clustering

Gowda and Krishna were, to our knowledge, the first to propose using the m$k$NN relationship for agglomerative clustering in [8]. Starting with $k=1$, fine-grained clusters are created and merged with increasing k values until only one cluster remains. This was later refined with probabilistic arguments in [5] under a density hypothesis; a detailed discussion on this is deferred to Sect. 3.

The approach in [11] offers a unique m$k$NN relationship, where each point connects to exactly k-neighbors, proceeding from closest to farther pairs. Once a point connects to its allotted neighbors, it’s excluded from further links. Unlike other m$k$NN methods, distant points could form a mutual $k$NN relationship. Due to the necessity of computing, storing, and sorting distance pairs, this method is super-quadratic in memory and storage. The clustering approach identifies dense clusters first, claiming to detect clusters of varying densities.

In [2], the authors introduce CMUNE, emphasizing linkage based on m$k$NN. Dense areas are identified by measuring common points in their k-nearest neighbor neighborhoods. Seed points from these dense regions then connect unclustered points, excluding those in sparse areas. Further refinements are discussed in [1].

In [9], a regressor based on the m$k$NN relationship is introduced. For a given query x and value of K, it outputs the expected value of values linked to the Mutual K-nearest neighbors of x. If the m$k$NN result for x is empty, indicating an outlier, the regressor doesn’t produce a value.

[17] details the construction of an m$k$NN graph, drawing parallels with earlier works [5, 8]. The aim is cluster detection via the graph’s connected components. Spurious connections, possibly arising from noise or outliers, are pruned by weighting the graph’s edges based on an affinity measure. Edges below a set affinity threshold are discarded, and clusters are recognized from the graph’s residual components.

In [14], a survey on using m$k$NN for cluster detection is presented. The authors’ proposed algorithm hinges on two concepts: extending the m$k$NN relation to point groups and incorporating density considerations.

[1] unveils DenMune, a clustering algorithm leveraging m$k$NN to discern centrality and density, as required in the Density Peak-like algorithm [13]. Points are categorized into strong, weak, and noise points based on their reverse $k$NN count ($\mathcal {R} _\mathcal {X} ^k({\boldsymbol{x}})$). The DenMune algorithm operates through a voting framework where points garner votes via their membership in the $k$NN of other points. High-vote recipients are tagged as dense or seed points, while noise points are excluded. Post noise-point removal, the points segregate into dense (seeds) and low-density (non-seeds). Clusters primarily form around seed points, with the low-density points accommodated subsequently. Remaining weak points are then aligned to the most suitable cluster. Remarkably, the authors use m$k$NN consistently for both density estimation and membership assessment.

A salient feature of the literature review is the dual application of the $m$k$NN$ test: determining cluster membership and performing three-tier density estimation (dense, weakly-dense, sparse) as illustrated in [1]. While some algorithms appear intricate, they yield compelling experimental results. Our goal is to present a theoretically sound understanding of these heuristics, introducing a streamlined tool for clustering tasks.

3 Data Model

We consider a N-sized D-dimensional dataset $\mathcal {X} =\{{{\boldsymbol{x}}}_1,\cdots ,{{\boldsymbol{x}}}_{N}\}$ from domain $\Omega \subseteq \mathbbm {R}^D$. From the perspective of the continuous domain $\Omega$, a statistical generative model defines the dataset $\mathcal {X}$ as a N-sized i.i.d sample of a probability density function (pdf) $f_\mathcal {X}:\Omega \rightarrow \mathbbm {R}^+$ with respect to the Lebesgue measure on $\Omega$. $\{{{\boldsymbol{x}}}_i\}_{i=1}^{N}$ is then one realization of a set of N independent random variables $\{{\textsf{X}}_i\}_{i=1}^{N}$ identically distributed according to this pdf ($\textsf{X}_i \sim f_\mathcal {X}$, $i\in \mathopen {[\![}N\mathclose {]\!]}$)

Let $\Xi \subseteq \Omega$ be the support of $f_\mathcal {X}$ defined as the closure of the set where $f_\mathcal {X}$ is non-zero ($\Xi = \textsf{supp}(f_\mathcal {X})=\overline{\{{\boldsymbol{x}}\in \Omega ~|\!\!|~f_\mathcal {X} ({\boldsymbol{x}})\ne 0\}}$). The fact that $\Xi$ is not connected indicates the presence of localized structures in the domain $\Omega$ such as (continuous) clusters. (Continuous) clustering is therefore defined as the labeling of connected components of the set $\Xi$. By (discrete) extension, given $\mathcal {X}$ as a sample of $\Xi$, clustering is the decision for every pair $({\boldsymbol{x}}_i,{\boldsymbol{x}}_j)\in \mathcal {X} \times \mathcal {X}$ whether both data belong to the same connected component of $\Xi$ or not (see Definition 3).

Assuming now that $(\Omega ,\textsf{d})$ is a metric space equipped with distance function $\textsf{d}: \Omega \times \Omega \rightarrow \mathbbm {R}$, then neighborhood systems may be defined over $\mathcal {X}$.

Definition 1

(Mutual ${\textbf {k}}$-nearest neighbor relationship). If ${\boldsymbol{x}}_j\in {\mathcal {V}}^k_\mathcal {X} ({\boldsymbol{x}}_i)$ and ${\boldsymbol{x}}_i\in {\mathcal {V}}^k_\mathcal {X} ({\boldsymbol{x}}_j)$ then ${\boldsymbol{x}}_i$ and ${\boldsymbol{x}}_j$ are said to be mutual k-nearest neighbors.

Based on the mutual k-nearest neighbor relationship, one can then build the non-directed mutual k-nearest neighbor (m$k$NN) graph $G_k=(\mathcal {X},\mathcal {E} _k)$ where data $\mathcal {X}$ serves as nodes and an edge $({\boldsymbol{x}}_i,{\boldsymbol{x}}_j)\in \mathcal {E} _k$ exists if ${\boldsymbol{x}}_i$ and ${\boldsymbol{x}}_j$ are mutual k-nearest neighbors. In this paper, we wish to argue for the interest in exploiting the m$k$NN graph and use data clustering as a natural application domain where using the m$k$NN is beneficial.

Here, we are particularly interested in the connectivity of $G_k$ given dataset $\mathcal {X}$.

Definition 2

(${\textbf {k}}_{{\textbf {D,N}}}$). Given a dataset $\mathcal {X} \subset \Omega$, $k_{D,N}$ is the smallest integer k such $G_k$ is connected.

Authors in [5] provide us with Theorem 1 bridging the continuous and discrete domains.

Theorem 1

(rephrased from [5], Thm 2.1).

Let the i.i.d sample $\mathcal {X} =\{{{\boldsymbol{x}}}_1,\cdots ,{{\boldsymbol{x}}}_{N}\}\subset \Omega \subseteq \mathbbm {R}^D$ come from a distribution P with support $\Xi \subseteq \Omega$ and density $f_\mathcal {X}$. Assume that $\Xi$ is connected and grid compatible, and that for constants $a_1$ and $a_2$, we have, on $\Xi$, $0<a_1\le f_\mathcal {X} ({\boldsymbol{x}})\le a_2$. Then, there exists a constant c such that, almost surely, $k_{D,N}\le c\log N$, for large enough N.

The proof of the theorem is detailed in [5]. Constants $0<a_1\le a_2$ make sure that values of $f_\mathcal {X}$ have finite non-zero extremes. Similarly, the grid compatibility criterion makes sure that $\Xi$ contains a (dominated) connected cover of cubes of finite side length, each with a sufficient intersection with $\Xi$. Theorem 1 relates the connectivity of the mutual $k$NN graph (via $k_{D,N}$) and the continuity (via grid compatibility) of the local density (via constants $a_1$ and $a_2$ and “large enough N”). According to this theorem, the mutual $k$NN graph is connected in parts where the density of the dataset allows to estimate a support that is grid compatible and where this density is bounded away from 0 and Infinity.

That is, the size $k\ge k_{D,N}$ to consider for $G_k$ to be connected (and therefore this discrete structure to represent faithfully the connected continuous domain) is bounded by a sub-linear function of N. As the local density at ${\boldsymbol{x}}_i$ may be estimated by $\hat{f}_\mathcal {X} ({\boldsymbol{x}}_i)=\frac{k}{\textsf{vol}({\mathcal {V}}^k_\mathcal {X})}$, Theorem 1 states formally that as long as this local estimated density is large enough, $G_k$ remains connected. We will exploit that interpretation to use the m$k$NN graph to perform data clustering. Since we rely on the formal model given by Theorem 1, we give data clustering a formal and simple definition.

Definition 3

(Data cluster). Given dataset $\mathcal {X}$, data clusters are defined as connected components of the mutual nearest neighbor graph $G_k$ built on $\mathcal {S}$, as the result of the data filtering operation

Theorem 1 provides guarantees that data clusters defined as above asymptotically represent the connected subsets of the support of the continuous density $f_\mathcal {X}$. However, since no parametric model is used for $f_\mathcal {X}$, this definition accommodates arbitrary distributions, i.e arbitrary clusters shapes and arrangements.

4 Data Analysis with the Mutual k-Nearest Neighbor Graph

Theorem 1 formally relates the local estimated density of $\mathcal {X}$ to the m$k$NN graph connectivity. This creates a natural link to clustering operations. Reversing the argument, we state that parts of low estimated density represent potential fords thru which spurious (weak) connections in the m$k$NN graph may appear. Hence we propose to remove these spurious low-density parts matching the “bounded away from 0 and Infinity” continuous counterpart argument. By construction, the resulting data subset guarantees a minimal local density, which by Theorem 1 guarantees m$k$NN graph connectivity. Starting from dataset $\mathcal {X}$, we propose a generic clustering algorithm below.

Algorithm 1

. Data clustering based on m$k$NN graph

Data Filtering. Filtering low-density regions is a staple in the denoizing domain. In many contexts, sparse regions within datasets are interpreted as low-likelihood samples, which are typically smoothed over by MSE-based regression models. However, in this study, our primary concern revolves around the density $f_\mathcal {X}$, especially under the parameters delineated in Theorem 1 and subsequent discussions.

From this perspective, the objective becomes highlighting areas where the estimated density not only reaches a minimal threshold ($a_1$) but also stands as statistically reliable, backed by adequate local samples. Notably, due to the intrinsic property $\int _\Omega f_\mathcal {X} =1$, identifying “low-density” zones becomes a comparative exercise, relative to the entire dataset’s distribution. Such an approach closely aligns with the objective of outlier detection; an outlier’s definition invariably hinges on its relation to the surrounding data [4, 10].

Given this, our preliminary strategy entails employing outlier detection for data filtration, sidestepping traditional methods like KDE [15] which tends to falter in sparsely populated datasets. It’s worth noting that contemporary density estimation techniques, such as generative normalizing flows [12], might find applicability in this scenario.

From the input dataset $\mathcal {X}$, the filtration process yields $\mathcal {S}$. This step intriguingly presents a dual relationship with its successor. Even though filtering frequently mandates a predefined k value, techniques spanning outlier detection to density estimation can potentially help pinpoint an optimal k.

Complexity: The construction of a compressed cover tree to solve the $k$NN exhibits a time complexity of $O(c_m(\mathcal{X})^8c((\mathcal{X})^2N\log (N))$, where $c_m$ and c represent expansion constants pertinent to the dataset. When tasked with deriving the k nearest neighbor table for a novel point, q, the time complexity is set at $O(c(\mathcal{X}\cup {q})^2\log (k)[c_m(\mathcal{X})^{10}\log N+c(\mathcal{X}\cup {q})k])$. This infers that formulating the k nearest neighbor table remains a sub-quadratic challenge. The detailed analysis can be found in the recent PhD thesis [6]. With the $N\times k$ k-nearest neighbor table established, the determination of whether the k-nearest neighbor relationship is mutual or otherwise is achievable through a single table traversal, bearing a complexity of $O(Nk^2)$. Hence, the derivation of the mutual k-nearest neighbor graph retains a subquadratic nature.

5 Illustrative Experiments

5.1 k-Means Convex Model

To illustrate visually the ability of our toolset to naturally handle clusters of arbitrary shapes, we visualize the process with the 2D “Two Moons” dataset generated by sklearn ($N=10'000$, $\sigma _{\text {noise}}=0.1$). Due to its convex Gaussian model, k-means cannot separate this data into 2 clusters (Fig. 1[top left]) whereas our procedure (e.g with $k=10$ and $\tau _{\text {LOF}}=1.1$, Fig. 1 [others]) robustly splits the dataset.

One can easily picture the underlying dendrogram from the evolution of the partition. At $k=1000$, connectivity overrules low density regions and the m$k$NN then shows a unique connected component, leading to a high FP rate.

Fig. 1.

Two Moons partitions. [top left] k-means partition. [others] our procedure fixing $\tau _{\text {LOF}}=1.1$ and evolving $k\in \{1,4,5,6,7,10,1000\}$ in reading order

Figure 2 pinpoints the fact that this behavior is prevented by the initial filtering. If we remove this step, a large connected component appears in the m$k$NN graph from $k=4$.

Fig. 2.

Two Moons partitions without prior filtering and evolving $k\in \{1,2,4,5\}$ in reading order

5.2 Density-Based Clustering Model

Now, one strong bias brought by the sklearn “Two Moons” dataset is that the two clusters are of approximate equal densities. When modifying the generation to obtain contrasted densities, one falls in a setup known to be adverse to the density-based clustering algorithms, of which DBSCAN [7] is a major representative.

Fig. 3.

Adapted Two Moons dataset with varying densities. [left] k-means partition. [center] DBSCAN partition. [right] m$k$NN-based partition

As shown in Fig. 3, k-means fails again to identify proper clusters due to its convex model. DBSCAN appears very difficult to tune for such data since the high density pushes towards a small Eps radius which creates an empty ball, not passing the MinPts threshold in low density regions. In contrast, such a setup is accepted by our m$k$NN procedure with the same parameters as before.

Discussion: The filtering step, to be useful, should retain most data from the original dataset. Finding the proper filtering value is a problem in itself, it should be related to fords detection, as discussed earlier. There are many hidden parameters in the clustering procedure we outline in Algorithm 4, derived from the theorems. This dependency goes also to the bounds of density function and the $\alpha$ value in the grid-compatibility constant in Theorem 1. Rather than giving a clustering algorithm, we have discussed the grounding of successful clustering strategies, proposing tools to build a dedicated connectivity-based clustering algorithm for datasets adhering to precise hypothesis.

We were able to replicate clustering experiments, as reported in [1] with a simpler procedure more amenable to analysis. Also following the conclusions of the cited research, the proposed tools are useful in low-dimensional datasets. They propose to use non-linear embeddings to two dimensions, using for example t-SNE [16]. As analyzed in [3], handling high dimensional datasets is riddle with problems derived from the phenomenon of concentration of measure which generates the so-called curse of dimensionality, one of its many forms is the phenomenon of hubness and the increase of the in-degree in metric graphs, with consequences in the connectivity of the $m$k$NN G$.

Further and maybe most importantly, no vector computation is required. Hence, this toolset may operate in metric spaces that are not necessarily vector spaces and where the data is given by similarity, known to respect the metric conditions. Again, this is to be contrasted with the popular k-means algorithm operating in vector spaces, as illustrated in Fig. 1.