Keywords

1 Introduction

Epicardial adipose tissue (EAT) is the fat inside the pericardium, and recent findings indicate its positive correlation with the risk of coronary artery disease, cardiovascular disease, etc. [1]. However, due to technical limitations and anatomy complexity, the manual segmentation of EAT or pericardium in medical images is time-consuming. Nowadays, deep neural networks have shown great performance in many medical image segmentation applications. Most efficient deep learning-based methods for pericardium or EAT segmentation [2] are trained with loss functions such as the Dice loss [3] and the cross-entropy loss [4]. Some researchers have explored utilizing the shape information in segmentation networks to improve or guide deep neural networks for better accuracy [5, 6]. A recent review paper on anatomy-aided deep learning for medical image segmentation [7] indicates many ways to use shape information. For pericardium segmentation, the pericardium shape could be an informative input. To involve that in segmentation networks, it is needed to find a way to model or represent the shape information. The Fourier series and Fourier transform are powerful tools for shape representation in many computer vision applications. By applying them, shape information could be represented by the Fourier descriptors (FDs) in the frequency domain for further analysis. Especially, with the Fourier series, a few descriptors are enough to represent the shape of the pericardium. Thus, in this paper, we propose a method that uses the shape information represented by the FDs in the loss function as well as pre-processing with polar coordinate transformation to improve segmentation performance.

1.1 Related Work

Loss Functions. The most widely used losses for segmentation are distribution-based losses and region-based losses [5, 6]. Distribution-based losses guide the training process by minimizing the dissimilarity between the ground truth distribution and the predicted distributions, e.g. the cross-entropy loss [4] and its variations. Region-based losses guide the training process by minimizing the false predictions or maximizing the overlap regions between the predicted segmentation and the ground truth region, e.g. the Dice loss [3]. Besides these two types of losses, boundary-based losses have shown interesting effects on medical image segmentation. These losses usually work as a regularization term with a distribution-based or region-based loss [6]. The idea of boundary-based losses is to reduce the distance between two segmented regions, e.g. the boundary loss [8] and the Hausdorff distance loss [9]. However, these losses need to be trained with a region-based loss such as Dice loss to maintain the training stability. There is more study on minimizing distance or using distance map loss penalty [10]. The boundary-based losses incorporate the boundary information due to their theoretical concept, while boundary information is not identical to shape information. Recently, Kervadec et al. [11] introduced loss functions based on a few global shape descriptors such as the volume of segmentation, the location of the centroid, the average distance to the centroid, and the length of the contour. Their experiments show that simple shape descriptors are effective for segmentation. Although their shape descriptor loss did not outperform the cross-entropy loss, it shows the potential.

Fourier Series and Fourier Transformation for Shape Representation. The Fourier descriptor is widely used to encode shape features and has been applied to image/shape retrieval [12, 13]. It is a contour-based shape descriptor obtained by representing a closed contour using the Fourier Series. In signal processing, the Fourier series creates new descriptors to represent the frequency domain knowledge. Some works applied 2D Fourier transform for the frequency domain analysis of images. Usually, the 2D Fourier transform is used in 2D images to generate hand-crafted features for further processing. The frequency features could be used for image classification, image registration [14], and the Fourier domain training framework [15]. Fourier space losses proposed by Fuoli et al. [16] improve the accuracy in high-frequency content for image super-resolution by working directly in the frequency domain. Experiments showed that by combining spatial domain and frequency domain losses, the image quality is improved. A more integrated way is to apply a frequency domain representation within the neural network. Han et al. [17] introduced a Fourier convolutional neural network for image classification. They designed the Fourier convolutional layers that apply the 2D Fourier transform with small random kernel sizes to study the frequency domain knowledge. To sum up, the frequency domain knowledge for image analysis and shape analysis is of great significance and has shown its ability in many applications.

1.2 Contribution

To leverage shape information, we introduce a novel Fourier descriptor loss (FD loss) that utilizes Fourier descriptors in relation to the Euclidean distance between boundary points and a point within the boundary. And we validate it on the pericardium segmentation. To improve the segmentation performance and simplify FD loss calculation, we apply pre-processing steps including selecting the region of interest and a polar coordinate transformation. The experimental results show that the pre-processing leads to better segmentation for all the tested losses. As an alternative to the commonly-used Dice loss, we investigate how the FD loss works individually and as a regularizer in combination with Dice loss. When working individually, FD loss does not outperform the Dice loss or cross-entropy loss, but it shows visually competitive results. When working as a regularizer with the Dice loss, the compound loss shows improved segmentation accuracy and higher convergence speed. In addition, as the FDs represent the frequency domain knowledge, we show the effect of FD loss with fewer FDs and the effect of FD loss with the weighted frequency content of a contour for improving its smoothness.

Fig. 1.
figure 1

Visualizing the computation of distances between boundary sample points and the centroid for Fourier descriptor loss calculation.

Full size image

2 Methodology

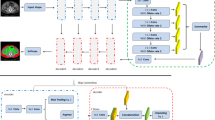
Let \(I:\varOmega \subset \mathbb {R}^{2} \rightarrow \mathbb {R}\) denotes a training image with spatial domain \(\varOmega \), and \(g:\varOmega \rightarrow \{0,1\}\) denotes a binary ground truth of the image. Similarly, \(s:\varOmega \rightarrow \{0,1\}\) is a binary predicted segmentation of the image. The FD loss is formulated based on the distance between sample points on the boundary and the centroid of the segmentation. Thus, with the spatial domain \(\varOmega \), \(\delta G\) denotes a representation of the boundary of the ground truth region G and \(\delta S\) denotes the boundary of the segmentation region defined by the network output. Figure 1 shows how to compute the distance between the sample points on the boundary and the centroid. We denote the ground truth map as g(x, y) where x, y are the Cartesian coordinates of pixels. And we denote the map \(\tilde{g}(r,\theta )\) in polar coordinates with the centroid origin \(O(x_c,y_c)\) as shown in Fig. 1, where \(r(x,y) = \sqrt{(y-y_c)^2 + (x-x_c)^2}\), and \(\theta (x,y) = angle(y-y_c, x-x_c)\). Thus, we have \(g(x,y) \text { and } \tilde{g}(r,\theta ) = 1\) if inside the boundary while \(g(x,y) \text { and } \tilde{g}(r,\theta ) = 0\) if outside the boundary. Similarly, we have \(s(x,y) \text { and } \tilde{s}(r,\theta ) = 1\) if inside the boundary while \(s(x,y) \text { and } \tilde{s}(r,\theta ) = 0\) if outside the boundary. We define the shape signature of the target by the distance between the sample points on the boundary and the centroid. Assume we have K sample points on the boundary. Thus, the distance between the kth sample point on the boundary of the ground truth and the centroid is defined as: \(d_k(\delta G) = \int _{0}^{r} \tilde{g}(\rho ,k\frac{2\pi }{K}) \textrm{d}\rho \). For calculation, we approximate it as \(d_k(\delta G) = \sum _{r=0} \tilde{g}(r,k\frac{2\pi }{K})\). Similarly, for the kth sample points on the output segmentation: \(d_k(\delta S) = \sum _{r=0} \tilde{s}(r,k\frac{2\pi }{K})\). Applying this to all sample points, we obtain sequences of distance measurements \(D(\delta G)= d_0(\delta G), d_1(\delta G), ..., d_{K-1}(\delta G)\), and \(D(\delta S)= d_0(\delta S), d_1(\delta S), ..., d_{K-1}(\delta S)\). With K sample points, the FDs are defined as the discrete Fourier series of the sequence of distance measurements:

$$\begin{aligned} c_n = \sum _{k=0}^{K-1}d_k e^{-jnk\frac{2\pi }{N}} \end{aligned}$$
(1)

Thus, we obtain N complex FDs from \(D(\delta G)\) and \(D(\delta S)\). In practice, we usually make \(N = K\) for the FD calculation. The FD loss is defined as the L1 norm of the dissimilarity between the FDs of ground truth and predicted segmentation.

$$\begin{aligned} \mathcal {L}_{FD} = \sum _{n=0}^{N-1}|c_n^{G} - c_n^{S}| \end{aligned}$$
(2)

Due to the limitation of this type of FD, we exclude non-convex shapes with strong curvatures. One advantage of the Fourier series is that we can always reconstruct the original shapes with the inverse Fourier transform and miss very little information about the original shapes. In addition, we could remove some FDs to capture only the significant features. When training with the FD loss function, images are transformed into polar coordinates with a fixed origin of the reference labels. Before applying the polar coordinate transformation, we extract a region of interest (ROI) in a circular shape from the original 2D image based on the reference labels. Then, as shown in Fig. 2, polar coordinates transformation applies to the circular ROI. For better visibility, we enlarge the polar-coordinate-transformed images to the same size as the original images. With the polar-coordinate-transformed images, the distance between the sample points on the boundary and the centroid can be calculated by measuring the number of pixels inside the boundary along the horizontal axis.

Fig. 2.
figure 2

Demonstration of pre-processing steps, including FD loss calculation and polar coordinate transformation. Figure (a) shows the original image in Cartesian coordinates, while Figure (b) displays the pre-processed image used for training, validation, and testing, enabling FD loss computation

Full size image

3 Experiments

Our experimental objective is threefold: (a) To demonstrate the impact of FD loss both as an individual loss and as a regularizer. (b) To assess the effectiveness of the pre-processing steps employed. (c) To investigate the influence of the number and weights of Fourier descriptors on the performance. All of our experiments focus on pericardium segmentation in low-dose CT scans.

3.1 Data

Chest computed tomography (CT) scanning from the Risk Or Benefit IN Screening for CArdiovascular Diseases (ROBINSCA) dataset [18] is used for experiments in this work. It is performed using a second-generation dual-source computed tomography system. This is a multi-center dataset with CT screening performed at the Gelre Hospital, the Bronovo Hospital, and the University Medical Center Groningen. The labels of the region inside the pericardium are annotated by an experienced radiologist using the open-source medical imaging processing software 3D Slicer [19]. As 2D boundary information is used in the loss calculation, we process 3D images as a stack of independent 2D images, which are fed into the network. All the images are resized to \(256 \times 256\) pixels for further processing. For our experiments, 154 CT scans (11000 slices) were annotated for further training (9000 slices), validation (1000 slices), and testing (1000 slices).

3.2 Implementation Details

We employed the U-net++ with backbone VGG16 by Zhou et al. [20] as the deep learning architecture in our experiments. U-net++ is a nested U-net architecture for medical image segmentation that is widely used in related segmentation tasks. To train our model, we employed the Adam optimizer with a learning rate of 0.001 and early stopping with patience of 30. And the batch size is 8. For implementation, we used Keras and TensorFlow and ran the experiments on an NVIDIA RTX 6000 GPU.

For evaluation, we employed the common Mean Intersection of Union (MIU), Dice Similarity Coefficient (DSC), and Sensitivity (SEN), which are defined as follows,

$$\begin{aligned}&MIU = \frac{1}{N} \frac{P(Y \bigcap \hat{Y})}{ P(Y \bigcup \hat{Y}) }, DSC = \frac{1}{N} \frac{2 \cdot P(Y \bigcap \hat{Y})}{P(Y)+P(\hat{Y})}, SEN = \frac{1}{N} \frac{P(Y \bigcap \hat{Y})}{P(Y)}&\\ \end{aligned}$$

where N indicates the number of slices, Y denotes the ground truth, \(\hat{Y}\) denotes the predictions, and \(P(\cdot )\) denotes the number of pixels.

3.3 Results

Quantitative Evaluation. To show the effect of the FD loss, we compared it to two commonly used loss functions, the Dice loss and the cross-entropy loss, with both original data and pre-processed data. Table 1 lists the results of the corresponding experiments. Overall, with pre-processing, all the losses show improved performance. The FD loss individually can not outperform the Dice loss or cross-entropy loss, but its performance is competitive and convincing visually as shown in Fig. 3. Boundary-based losses are often used as a regularizer with distributed-based losses or region-based losses [5], so as the FD loss. We tested the compound loss with both the Dice loss and the FD loss. As the value range of the FD loss is larger than that of the Dice loss, a weight of 0.01 is applied to the FD loss. With the compound loss, we obtained results of MIU: 96.79%, DSC: 98.20%, and SEN: 98.55%, which outperforms both Dice loss and cross-entropy loss. In addition, the convergence speed of the compound loss (converge at the 13th epoch) is much higher than the Dice loss (converge at the 30th epoch). With Fig. 3, we visualize the pericardium segmentation results of various loss functions in a CT slice. We can see that the manual labeling is not perfect with noise and mislabelled pixels on the pericardium boundary. In the example manual label, there are some pixels mislabelled as the region inside the pericardium around the right boundary. In the segmentation results of the Dice loss in Fig. 3(c), some pixels in that region still are mislabelled. With the FD loss, both Fig. 3(d) and Fig. 3(e) have better segmentation results in that region.

Table 1. Performance of losses with U-net++ backbone VGG16.
Full size table
Fig. 3.
figure 3

The figure illustrates the visualization of different segmentation results within the pericardium region: (a) Manual label, (b) Cross-entropy loss, (c) Dice loss, (d) FD loss, and (e) Compound loss (FD + Dice).

Full size image

Effect with Fewer Fourier Descriptors in the Fourier Descriptor Loss. The key to the FD loss is the shape descriptors. By default, we utilize the same number of descriptors as sample points on the contour, which is, in our case, 256. For loss calculation, we use the absolute values of the FDs. Due to the symmetric relation of the FDs, by default, every shape is represented by 128 real number FDs. As FDs represent the shape information in the frequency domain, we could control the shape information in the loss function by controlling descriptors. By removing high-frequency descriptors, the shape information in small scales which could be the noise is neglected. In addition, the computation cost is reduced. In Table 2, we show the experiment results of the FD loss with 128, 64, 32, 16, and 8 descriptors. The results indicate that more descriptors do not lead to better segmentation. With our data, 64 descriptors result in the best performance. We also tested the compound loss of the 64 descriptor loss and the dice loss, which lead to 96.69% in MIU, 98,15% in DCS, and 98.56% in SEN.

Table 2. Performance of FD loss with fewer FDs.
Full size table

Weighing Fourier Descriptors in the Fourier Descriptor Loss. As the FDs represent shape information in the frequency domain, by weighing the descriptors we could weigh the shape representations of the corresponding frequency. There may be some shape representations that are more important for segmentation. As the low-frequency descriptors represent the global shape, we apply higher weights to them to get the global shape better considered. We applied Sigmoid-based weights to the FDs \(c_n\). The Sigmoid function is define as \( \sigma (x) = \frac{\textrm{1} }{\textrm{1} + e^{-x} } \). Assume we have N FDs, with a selected range of [a, b], for the nth FD, the corresponding weight is \(\sigma (a-\frac{a-b}{N}*n)\). Thus, the loss becomes

$$\begin{aligned} \mathcal {L}_{FD}^\sigma = \sum _{n=0}^{N-1}\sigma (a-\frac{a-b}{N}*n)|c_n^{G} - c_n^{S}| \end{aligned}$$
(3)

With a positive a and a negative b, we apply higher weights to low-frequency descriptors while lower weights to high-frequency descriptors. As shown in Table 3, with \([a,b]=[4,-4]\), we obtained better results (MIU: 96.18% [+0.62%], DSC: 97.40% [+0.72%], SEN: 98.21% [+0.5%]).

Table 3. Performance of FD loss with Sigmoid-weighted Fourier descriptors.
Full size table

4 Conclusions and Future Work

We have presented a method of FD loss and polar coordinate transformation for pericardium segmentation. The pre-processing with polar coordinate transformation overall leads to better segmentation for all losses. A recent work by Alblas et al. [21] for artery vessel wall segmentation also showed better results with polar coordinate transformation. Compared to other boundary-based losses such as the boundary loss [8] and Hausdroff distance loss [9] which need to be trained with a region-based loss, the FD loss can be trained individually. Although, when working individually, FD loss can not outperform region-based losses like the Dice loss and cross-entropy loss. It has shown the potential to improve both the performance and convergence speed when working as a regularizer of the Dice loss. Due to the physical meaning and invertibility of FDs, our loss has more interpretability. As we worked with medical images, the labels of the pericardium were annotated manually. There are unavoidable noise and mislabeled pixels around the boundary in the manual labels. Compared to the manual labels, the predicted segmentation is smoother with less noise along the boundary.

A main limitation of the method is that it can not apply to non-convex shapes with strong curvatures. The centroid must locate inside the shape for further polar coordinate transformation. The cause of the limitation is the application of the Fourier series to the shape signature along the boundary. There may be alternative ways to avoid this limitation by using a 2D Fourier transform. In this work, we focus on 2D CT slices as the manual labels were annotated in 2D manners.

For future work, it is possible to explore a similar approach in 3D cylinder coordinates since many medical images are 3D images. Although the Fourier transforms only apply to 1D or 2D signals, a recent work by Wiesner et al. [22] shows a similar transform in 3D for encoding the cell shape. All in all, we have shown the potential of FD loss and polar coordinate transformation in pericardium segmentation with shape/boundary-based formulation, but the generalization of this method is an open field for further research.