Keywords

1 Introduction

A classical result by Erdős and Pósa [5] states that there is a function \(f : \mathbb {N} \rightarrow \mathbb {N}\) such that, for every k, every graph G contains either k pairwise vertex-disjoint cycles or a set T of at most f(k) vertices such that \(G - T\) is acyclic. The generalization of Erdős and Pósa’s result for digraphs and directed cycles was conjectured by Younger [13] and proved by Reed et al. [7].

We say that H is a minor of G if H is obtained from a subgraph of G by a sequence of edge contractions. If H is a digraph and we restrict the contractions in the previous definition to butterfly contractions [6], we get the definition of a butterfly minor. We say that a graph H has the Erdős-Pósa (EP) property for minors if there is a function \(f : \mathbb {N} \rightarrow \mathbb {N}\) such that, for every k, every graph G contains either k pairwise vertex-disjoint copies of H as a minor or a set T of at most f(k) vertices such that H is not a minor of \(G - T\). By changing graph into digraph and minor into butterfly minor, the previous definition can be adapted into the EP property for butterfly minors in digraphs. In this view, if H is the undirected graph with a unique vertex and a unique loop on it and D is the digraph obtained from H by orienting its loop edge, then Erdős and Pósa proved that H has the EP property for minors while Reed et al. proved that D has the EP property for butterfly minors.

The results of Erdős and Pósa and Reed et al. were generalized by Robertson and Seymour [8] for undirected graphs and by Amiri et al. [1] for digraphs. Robertson and Seymour [8] proved that an undirected graph G has the EP property for minors if, and only if, G is planar. Amiri et al. [1] proved that a strong digraph D has the EP property for butterfly minors if, and only if, D is a butterfly minor of a cylindrical grid (see Fig. 1). The results of Robertson and Seymour [8] and Amiri et al. [1] are similar since an undirected graph is planar if, and only if, it is a minor of some grid [9]. Contrary to the undirected case, not all planar digraphs are butterfly minors of a cylindrical grid. In this paper, we provide a structural characterization of planar digraphs that are butterfly minors of a cylindrical grid. In particular, such characterization leads to a linear-time algorithm that decides whether a weakly 3-connected strong digraph has the EP property for butterfly minors.

Fig. 1.
figure 1

The \((4\times 4)\)-grid (left), the \((3\times 6)\)-cylindrical grid \(C_{3,6}\) (middle), and the directed wall (right) obtained from \(C_{3,6}\) by removing the three red arcs. (Color figure online)

Full size image

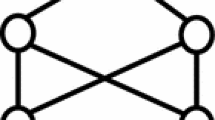
Although planarity is a necessary condition for a digraph to be a butterfly minor of a cylindrical grid, it is not sufficient. For example, the two planar digraphs of Fig. 2 are not butterfly minors of any cylindrical grid. To see this, first note that they are planar, weakly 3-connected, and have essentially a unique (up to the outerface) embedding in the plane, according to Whitney’s Theorem [12]. Note also that, in a cylindrical grid, any embedding is such that there is a point in the plane around which all directed cycles go, and in the same direction. We refer to this as being concentric and with same orientation. Now, in the digraph L of Fig. 2, the matching between the two directed triangles forces that, in any planar embedding, either the two triangles are not concentric or they have opposite orientations. On the other hand, the digraph R of Fig. 2 is acyclic but it is not a minor of any cylindrical grid. To see why, note that, if R was a butterfly minor of a cylindrical grid, then, because R is acyclic, it would also be a butterfly minor of a directed wall, which is the digraph obtained by cutting a cylindrical grid along “parallel” arcs (see Fig. 1). Note that, in an embedding of a directed wall similar to the one given in Fig. 1, no arc goes down. This means that some relative positions of the vertices of R in a directed wall are forced. Namely, the two sources \(v_4\) and \(v_5\) of R must be below each of their out-neighbors, vertex \(v_1\) must be below its three out-neighbors, and the universal sink \(v_0\) must be above every other vertex. It can then be checked that these positions must lead to some crossing arcs. This second example shows that sources and sinks may play an important role in the fact that a planar digraph may or may not be a butterfly minor of a cylindrical grid. In a way, our main result tells that the above two examples fully characterize the reasons why a planar digraph cannot be a butterfly minor of a cylindrical grid.

Fig. 2.
figure 2

Two planar digraphs L (left) and R (right) which are not butterfly minors of any cylindrical grid.

Full size image

To formally state our main result, we need a few definitions. Given a digraph \(D=(V,A)\) and \(\emptyset \ne X\subset V(D)\), the set of arcs between X and \(V{\setminus } X\) is denoted by \((X,V{\setminus } X)\). We say that \((X,V{\setminus } X)\) is a dicut if there are no arcs from \(V{\setminus } X\) to X. A dijoin path P of D is a directed path in D whose arc-set intersects the arc-set of every dicut of D. A plane digraph is a planar digraph together with a planar embedding. Recall also that, given a plane digraph H, \(H^*\) denotes its dual. That is, the dual digraph \(H^*\) of H (with a fixed planar embedding) is the digraph that has a vertex for each face of the embedding of H and \(H^*\) has an arc \(e^*=\{u,v\}\) for each two faces u and v in the embedding of H that are separated from each other by an arc \(e \in E\). Moreover, each dual arc \(e^*\) is oriented by a 90\(^{\circ }\) clockwise turn from the corresponding primal arc e. For instance, if a face of a plane digraph H is “surrounded” by a directed cycle oriented clockwise (resp., counter-clockwise), then the corresponding vertex of \(H^*\) is a source (resp., a sink).

We can now state our main result.

Theorem 1

A digraph D is a butterfly minor of a cylindrical grid if, and only if, D has a plane spanning supergraph H with neither sources nor sinks such that \(H^*\) admits a dijoin path.

To get further intuition about Theorem 1, consider the definition of a feedback arc set \(F \subseteq A\) of a digraph \(D=(V,A)\), which is any subset of arcs such that \(D-F\) is acyclic. Given a plane digraph D, it is known that every directed cycle of D is associated to a dicut in \(D^*\). This implies that a set of arcs is a feedback arc set of D if, and only if, the corresponding set of its dual edges intersects the arc-set of every dicut of \(D^*\) [2]. Therefore, the fact that \(D^*\) admits a dijoin path means that such path intersects the arcs of a feedback arc set of D “in the same direction”, i.e., intersects the drawing of each directed cycle of D, with each intersection occurring in the same orientation. This is equivalent to being concentric and with the same orientation. This condition (\(D^*\) admits a dijoin path) allows avoiding the kind of planar digraphs as exemplified by the digraph L in Fig. 2. In turn, the difficulties exemplified in digraph R in Fig. 2 are dealt with by the existence of a supergraph H with neither sources nor sinks.

Structure of the Paper and Algorithmic Applications. We first prove that if D is a plane digraph with neither sources nor sinks such that \(D^*\) has a dijoin path, then D is a butterfly minor of a cylindrical grid (Theorem 4). Observe that this gives us the sufficiency part of Theorem 1. We then show that if D is a butterfly minor of a cylindrical grid, then D has a planar embedding such that \(D^*\) admits a dijoin path (Theorem 5). Observe that D might still have sources and sinks, so the remainder of the proof consists in adding arcs to D in order kill all sources and sinks (Lemma 2).

Theorems 4 and 5 have the following important corollary:

Corollary 1

Any digraph D without sources or sinks is a butterfly minor of a cylindrical grid if and only if D admits a planar embedding s.t. \(D^*\) has a dijoin path.

Note that the planar digraph R in Fig. 2 is acyclic. So, whatever be its planar embedding, the dual is strongly connected, i.e., \(R^*\) has no dicuts. Therefore, every planar embedding of R is such that \(R^*\) has a trivial dijoin path (the empty path). Therefore, unfortunately, there is no hope that the condition on sources and sinks can be removed from Corollary 1.

Note that any strongly connected digraph (or strong) D satisfies the conditions of Corollary 1. Together with the result of Amiri et al. [1], this implies that:

Corollary 2

Any strong digraph D has the EP property for butterfly minors if, and only if, D admits a planar embedding such that \(D^*\) has a dijoin path.

By Whitney’s Theorem [12], any weakly 3-connected planar digraph D has a unique (up to the outerface) planar embedding (computable in linear time). Since deciding whether the dual of a plane digraph admits a dijoin path can be done in linear time, then our result has the following algorithmic application:

Corollary 3

Deciding whether a weakly 3-connected strong digraph has the EP property for butterfly minors can be done in linear time.

Section 2 is devoted to defining the main notions and to present previously known results used in this paper. Section 3 is devoted to digraphs with neither sources nor sinks. Section 4 is devoted to obtaining the supergraph with neither sinks nor sources.

2 Preliminaries

Planar Digraphs and Duality. In this section, we present a number of simple known facts concerning planar graphs and their duals. The interested reader can find formal definitions and proofs for such facts in most books on graph theory (e.g., [11]).

Given a digraph \(D=(V,A)\) and \(e \in A\), let \(D{\setminus } e=(V,A {\setminus } \{e\})\) and let D/e be the digraph obtained from D after contracting the arc e.

Observation 1

Let \(D=(V,A)\) be a plane digraph, and \(e \in A\) be any arc of D. Then, \((D{\setminus } e)^*=D^*/e^*\) and \((D/e)^*=D^*{\setminus } e^*\).

A dicut of a digraph \(D=(V,A)\) is a partition \((X, V{\setminus } X)\) of the vertex-set such that X is a non empty proper subset of V and there are no arcs from \(V{\setminus } X\) to X. The arc-set of \((X, V{\setminus } X)\) is the set of arcs from X to \((X, V{\setminus } X)\). A dijoin \(X\subseteq A(D)\) of D is a set of arcs intersecting all dicuts’ arc-sets of D. A dijoin path (resp., dijoin walk) of D is a dijoin inducing a directed path (resp., directed walk) in D. That is, a dijoin path/walk P of D is a directed path/walk whose arc-set intersects the arc-set of every dicut of D.

Observation 2

A digraph D admits a dijoin path if, and only if, the decomposition of D into strongly connected components has a single source component and a single sink component.

Observation 3

Let \(D=(V,A)\) be a digraph with a dijoin path P, and \(e \in A {\setminus } A(P)\). Then, P is a dijoin path of \(D {\setminus } e\).

Observation 4

Let \(D=(V,A)\) be a digraph with a dijoin path P, and \(e \in A\). Let \(P'\) be obtained from P by contracting e if \(e \in A(P)\), and \(P'=P\) otherwise. Then, \(P'\) is a dijoin walk of D/e.

Observation 5

Let \(D=(V,A)\) be a digraph with a dijoin path P, and \(v \in V\) be an isolated vertex. Then, P is a dijoin path of \(D {\setminus } v\).

Observation 6

Every digraph with a dijoin walk admits a dijoin path.

Butterfly Models and Cylindrical Grids. We now present the formal definition of butterfly models. Let G and H be two digraphs. A (butterfly) model of G in H is a function \(\eta :V(G)\cup A(G) \rightarrow \mathcal{S}(H)\), where \(\mathcal{S}(H)\) denotes the set of all subdigraphs of H, such that:

  • for every \(v \in V(G)\), \(\eta (v)\) is a subdigraph of H being the orientation of some tree such that \(V(\eta (v))\) can be partitioned into \((\{r_v\},I_v,O_v)\) where

    • \(\eta (v)[O_v \cup \{r_v\}]\) is an out-arborescence rooted in \(r_v\) (thus in which all non-root vertices have in-degree 1), called the out-tree of v,

    • \(\eta (v)[I_v \cup \{r_v\}]\) is an in-arborescence rooted in \(r_v\) (thus in which all non-root vertices have out-degree 1), called the in-tree of v;

  • for every two distinct \(u,v \in V(G)\), \(\eta (u)\) and \(\eta (v)\) are vertex-disjoint;

  • for every \((x,y) \in A(G)\), \(\eta (xy)\) is a directed path of H from the out-tree of x to the in-tree of y, with internal vertices disjoint from every vertex of \(\eta (u)\) for every \(u \in V(G)\), and from every internal vertex of \(\eta (uv)\) for every \((u,v) \in A(G){\setminus } \{(x,y)\}\).

Throughout this work, given a model of G in H, we will refer to the arcs \(e \in A(H) \cap \bigcup _{f \in A(G)} A(\eta (f))\) as the blue arcs of the model, and to the arcs \(e \in A(H) \cap \bigcup _{v \in V(G)} A(\eta (v))\) as the black arcs. A vertex of H incident to at least one black arc will be referred to as a black vertex.

A model of G in H is minimal if, for every \(v \in V(G)\) and for every leaf w of \(\eta (v)\), w is incident to some blue arc. Note that, up to removing the leaves that do not satisfy this property from \(\eta (v)\), we can always assume to be working on a minimal model.

Butterfly contracting an arc \((u,v) \in A(D)\) of some digraph D consists in contracting the arc (u, v) if \(d^-(v)=1\) or \(d^+(u)=1\). A digraph G is a butterfly minor of some digraph H if G can be obtained from H by deleting arcs, deleting vertices, and butterfly contracting arcs. Note that if G is a butterfly minor of H, then G can be obtained by first removing some arcs, then removing isolated vertices, and finally performing butterfly contractions.

Observation 7

[1]. A digraph G is a butterfly minor of some digraph H if, and only if, G has a butterfly model in H.

We now deal with cylindrical grids. Let \(n,m\in \mathbb {N}^*\). The cyclindrical grid \(C_{n,2m}\) can be seen as a set of n concentric directed cycles having the same direction and linked through 2m directed paths that alternate directions (see Fig. 3). Formally, \(C_{n,2m}\) is the digraph with vertex-set \(\{(i,j) \mid 0\le i< n, 0 \le j < 2m\}\), and with the following arc-set. For every \(0 \le i < n\) and \(0 \le j < 2m\), we have \(((i,j),(i,j+1 \mod m))\in A(C_{n,2m})\), and the directed cycle induced by \(\{(i,j)\mid 0 \le j <m\}\) is called the \(i^{th}\) column of \(C_{n,2m}\). For every \(0\le i < n-1\) and \(0 \le j < m\), we have \(((i,2j),(i+1,2j))\in A(C_{n,2m})\) and \(((i,2j+1),(i-1,2j+1))\in A(C_{n,2m})\). Moreover, for every \(0 \le j <2m\), the directed path induced by \(\{(i,j)\mid 0 \le i <n\}\) is called the \(j^{th}\) row of \(C_{n,2m}\).

Fig. 3.
figure 3

A planar embedding of the cylindrical grid \(C_{6,6}\). The red directed path \(Q^*_{6,6}\) is the dijoin path defined and used in Sect. 4. (Color figure online)

Full size image

Throughout this work, we consider that any \(C_{n,2m}\) is embedded in the plane so that its first column coincides with the outerface (see Fig. 3). Hence, we may naturally refer to left/right and top/bottom such that the first (last) column is the leftmost (rightmost) and the first (last) row is the bottommost (topmost). The arcs of a column are referred to as vertical arcs. Note that all vertical arcs are going up. The arcs of a row are the horizontal arcs. Moreover, the arcs of even (resp., odd) rows are horizontal to the right (resp., to the left).

Since \(C_{n,2m}\) is strong, we get that \(C^*_{n,2m}\) is a DAG. Moreover, \(C^*_{n,2m}\) has a unique sink \(t^*\), corresponding to the outerface of the given embedding of \(C_{n,2m}\), and a unique source \(s^*\), corresponding to the face of \(C_{n,2m}\) bounded by the last column of \(C_{n,2m}\). Note that if \(P^*\) is any directed path from \(s^*\) to \(t^*\) in \(C^*_{n,2m}\), then \(P^*\) is a dijoin path, i.e., it intersects all dicuts of \(C^*_{n,2m}\) (or, equivalently, \(P^*\) “crosses” all directed cycles of \(C_{n,2m}\)).

Fig. 4.
figure 4

Green rows and columns are added. Blue arcs belong to the images of some arcs of G by \(\eta \). Grey subtrees (with black vertices and arcs) are the images of some vertices of G by \(\eta \). (Color figure online)

Full size image

Let \(\eta \) be a butterfly model of a digraph G in \(C_{n,2m}\). We will deal with \(\eta \) through a few operations. Due to lack of space, we only present them informally.

  • Adding one column between columns i and \(i+1\) in \(\eta \) consists in considering the new model \(\eta '\) of G in the cylindrical grid \(C_{n+1,2m}\) obtained as follows. Roughly, the left part of the model (between columns 0 to i) does not change, one new column is added (with abscissa \(i+1\)), and the right part of the model (between former columns \(i+1\) to n) is translated by one column to the right. The horizontal arcs of the model that were going from former columns i to \(i+1\) are subdivided once, i.e., they are now directed paths that go from column i to column \(i+2\). Note that no vertical arcs of the added column belong to the new model \(\eta '\) of D. See Fig. 4 for an illustration.

  • Adding two rows between rows j and \(j+1\) in \(\eta \) consists in considering the new model \(\eta '\) of G in the cylindrical grid \(C_{n,2(m+1)}\) defined as follows. All the elements of the model below row j, or in row j, remain the same, all elements of the model above row j are translated up from two rows, and all vertical arcs from former row j to former row \(j+1\) are subdivided twice, i.e., they are now vertical directed paths with three arcs from row j to row \(j+3\). Note that no horizontal arcs of the two added rows belong to the new model \(\eta '\) of D. See Fig. 4 for an illustration.

Fig. 5.
figure 5

Construction of \(D_{P^*}(s,t)\). On the left, a dijoin path \(P^*\) is represented by dashed red arcs. On the right, the obtained digraph \(D_{P^*}(s,t)\) is depicted. (Color figure online)

Full size image

3 Digraphs with Neither Sources nor Sinks

Let D be a plane digraph such that \(D^*\) has a dijoin path \(P^*\) with arcs \((e^*_1,\cdots ,e^*_p)\). Let \(D_{P^*}(s,t)\) be obtained from D as follows (see Fig. 5 to follow the construction). For every \(i\in \{1,\cdots , p\}\), let \(e_i=(u_i,w_i)\) be the arc of D corresponding to \(e^*_i\). Subdivide \(e_i\) into three arcs \((u_i,t_i),(t_i,s_i)\), and \((s_i,w_i)\). Then, remove \((t_i,s_i)\), and, for every \(i\in \{1,\cdots ,p\}\), identify the vertices \(t_1,\cdots ,t_p\) into one vertex t, and the vertices \(s_1,\cdots ,s_p\) into one vertex s. Finally, add an arc from s to t. Note that \(V(D_{P^*}(s,t))=V(D) \cup \{s,t\}\) and, for every \(v \in V(D)\), the in-degree (resp., out-degree) of v in D is the same as in \(D_{P^*}(s,t)\). Since \(P^*\) is a dijoin path of \(D^*\), the set \(\{e_i\}_{i\le m}\) is a feedback arc set of D [2]. Therefore:

Observation 8

Let D be a plane digraph such that \(D^*\) has a dijoin path \(P^*\). If D has neither sources nor sinks, then \(D_{P^*}(s,t)\) is a planar DAG having s as unique source and t as unique sink.

A visibility representation of a graph G is a mapping of V(G) into non-intersecting horizontal segmentsFootnote 1 \(\{h_u\}_{u\in V(G)}\), together with a mapping \(\{t_e\}_{e\in E(G)}\) of the edges into vertical segments such that for every \(uv\in E(G)\), we get that \(t_{uv}\) has endpoints in \(h_u\) and \(h_v\), and \(t_{uv}\) does not cross \(h_w\) for every \(w\ne u,v\).

Theorem 2

([4]). Every planar graph admits a visibility representation.

Here, we apply the approach presented in [10] to our context in order to obtain a butterfly model of a planar digraph D into a cylindrical grid, if one exists. For this, we slightly adapt their definitions to our purposes.

We consider a visibility representation \((\{h_u\}_{u\in V},\{t_e\}_{e\in A})\) of \(D=(V,A)\) to be drawn on the plane, and, given two horizontal (vertical) segments \(s_1,s_2\), we write \(s_1\le s_2\) if the y-coordinate (x-coordinate) of \(s_1\) is smaller than the one of \(s_2\). Now, given a DAG \(D=(V,A)\), we say that a visibility representation \((\{h_u\}_{u\in V},\{t_e\}_{e\in A})\) of D is increasing if \(h_u\le h_v\) for every arc \((u,v)\in A\) (in other words, the arcs are all directed upwards).

In [10], in order to construct a visibility representation, the authors show that they can obtain an orientation D of a graph G that is acyclic, has exactly one source s and exactly one sink t, and \((s,t)\in A(D)\) (they call such a digraph a PERT-digraph). After they obtain this orientation, they use a total order \((v_1,\ldots ,v_n)\) of V(G) that meets the orientation D, and then construct a visibility representation such that \(s_1< s_2< \ldots < s_n\), where \(s_i\) denotes the y-coordinate of \(h_{v_i}\), for every \(i\in \{1,\ldots , n\}\). Observe that, because the order meets the orientation, we get that this is an increasing visibility representation. Their representation also has the property that the x-coordinate of arc (s, t) is smaller than the x-coordinate of every other edge of G. In short, even though they use a different terminology, the results presented in [10] actually show that the theorem below holds. The interested reader can check this is true by observing, in their algorithm W-VISIBILITY, that after they obtain the desired orientation D (line 2), they only work on D itself; also, the increasing order over the y-coordinates is ensured in line 5.1 of their algorithm.

Theorem 3

([10]). Let D be a planar DAG with unique source s and unique sink t, and such that \((s,t)\in A(D)\). Then, D admits an increasing visibility representation such that each horizontal segment has a distinct y-coordinate, and the x-coordinate of the segment of (s, t) is smaller than the x-coordinate of the segment of every other arc of D.

Theorem 4

Let \(D=(V,A)\) be a digraph without sources or sinks. If D has a planar embedding such that \(D^*\) admits a dijoin path \(P^*\), then D has a butterfly model in \(C_{n,2m}\) for some \(n,m\in \mathbb {N}^*\).

Sketch of the Proof. By Observation 8, \(D_{P^*}(s,t)\) is a DAG with a unique source s, a unique sink t, and \((s,t) \in A(D_{P^*}(s,t))\). By Theorem 3, there exists an increasing visibility representation of \(D_{P^*}(s,t)\). Let \(V(D_{P^*}(s,t)) = \{s=v_1,\ldots ,t=v_n\}\) be ordered increasingly according to their y-coordinates on the representation and suppose, without loss of generality, that the y-coordinate of \(h_{v_1}=h_s\) is 0 and the difference between the y-coordinates of \(h_{v_i}\) and \(h_{v_{i-1}}\) is 2 (their value on the constructed increasing visibility representation are all different, so we just need to adjust it). Observe that, in this case, the y-coordinate of \(h_{v_i}\) is \(2i-2\). We will build a model of D in some cylindrical grid as follows.

For each \(v_i\in V(D)\) (hence \(i\notin \{1,n\}\)), let \(h'_{v_i}\) be the segment equivalent to \(h_{v_i}\), but in the upper row. In other words, \(h'_{v_i}\) has y-coordinate \(2i-1\), and leftmost and rightmost x-coordinates equal to the ones of \(h_{v_i}\). The idea of the proof is to relate \(v_i\) with the path formed by the union of paths associated to \(h'_{v_i}\) and \(h_{v_i}\) in the cylindrical grid. Since all arcs of D point upwards, we get that the subpath associated to \(h'_{v_i}\) (i.e., in row \(2i-1\)) corresponds to the out-tree of \(v_i\), while the subpath associated to \(h_{v_i}\) (i.e., in row \(2i-2\)) corresponds to the in-tree of \(v_i\).    \(\square \)

Note that Theorem 4 allows us to prove the “if” part of Theorem 1.

Theorem 5

If a digraph \(D=(V,A)\) has a butterfly model in \(C_{n,2m}\) for some \(n,m\in \mathbb {N}^*\), then D has a planar embedding such that \(D^*\) admits a dijoin path.

Proof

Consider the planar embedding of \(C_{n,2m}\) such that the outerface contains its first column (see Fig. 3) and let \(P^*\) be any directed path from the single source of \(C^*_{n,2m}\) to its single sink. Note that \(P^*\) is a dijoin path of \(C^*_{n,2m}\).

By Observation 7, D is a butterfly minor of \(C_{n,2m}\). Let \(s_1,\cdots ,s_q\) be the sequence of operations allowing to get D from \(C_{n,2m}\) where these operations are ordered in such a way that first arcs are removed, then isolated vertices are removed and, finally, butterfly contractions are performed. For every \(0 \le i \le q\), let \(G_i\) be the digraph obtained after the \(i^{th}\) operation (so \(G_0=C_{n,2m}\) and \(G_q=D\)). We show, by induction on \(0 \le i \le q\), how to obtain a directed path \(P_i\) which is a dijoin path of \(G^*_i\). In particular, it holds for \(i=0\) by taking \(P_0=P^*\).

Let \(i \ge 1\). If \(s_i\) consists in removing an arc \(e_i\) of \(G_{i-1}\) then, if \(e^*_i \in A(P_{i-1})\), let \(P'_{i}=P_{i-1} / e^*_i\), and let \(P'_{i}=P_{i-1}\) otherwise. By Observations 1 and 4, \(P'_{i}\) is a dijoin walk of \(G^*_i\) and, by Observation 6, \(G^*_i\) admits a dijoin path \(P_i\). If \(s_i\) consists in removing an isolated vertex, then, by Observation 5, \(P_i=P_{i-1}\) is a dijoin path of \(G^*_i\). And if \(s_i\) is a butterfly contraction of the arc \(e_i \in A(G_{i-1})\), where \(e^*_i \notin A(P_{i-1})\), then Observations 1 and 3 ensure us that \(P_i=P_{i-1}\) is a dijoin path of \(G^*_i\).

Finally, let us consider the case when \(s_i\) consists in butterfly contracting an arc \(e_i=(u,v) \in A(G_{i-1})\) such that \(e^*_i \in A(P_{i-1})\). Let us assume that \(d^-(v)=1\) (the case when \(d^+(u)=1\) is symmetric). Observe that \(d^+(v)>0\) as otherwise \(e^*_i\) would be a loop, contradicting that \(P_{i-1}\) is a directed path. Then, let \(\{f_1,\cdots ,f_q\}\) be the set of out-arcs of v ordered clockwise in the embedding of D in the plane. Then, let \(P'_i\) be the directed walk obtained by replacing \(e^*_i\) in \(P_{i-1}\) by the directed walk consisting of the arcs \(f^*_1,f^*_2,\cdots ,f^*_q\). Note that \(P'_i\) is a dijoin walk in \(G^*_{i}\). Indeed, consider the set of arcs K of a dicut of \(G^*_{i}\). If K is also a dicut in \(G^*_{i-1}\), then \(e^*_i \notin K\) and \(P'_i\) intersects K since \(P_{i-1}\) is a dijoin path and so intersects K. Otherwise, \(e^*_i \in K\) which implies that \(\{f^*_1,f^*_2,\cdots ,f^*_q\} \cap K \ne \emptyset \), and so \(P'_i\) intersects K. Finally, by Observation 6, \(G^*_i\) admits a dijoin path \(P_i\).

      \(\square \)

Theorems 4 and 5 prove the following corollary which corresponds to Theorem 1 in the case of digraphs with neither sources nor sinks (and in particular, Corollary 3 is a special case of the following corollary).

Corollary 4

A digraph D without sources or sinks is a butterfly minor of a cylindrical grid if, and only if, D admits a planar embedding such that \(D^*\) has a dijoin path. Moreover, if D is weakly 3-connected, then this can be decided in linear time.

Proof

Due to the weakly 3-connectivity of D, and by Whitney’s Theorem, D has a unique (up to the outerface) planar embedding (and a unique dual). Given such an embedding, checking the existence of a dijoin path can be done in linear time by Observation 2.    \(\square \)

Recall that a strong digraph D has the EP property for butterfly minors if and only if D is a butterfly minor of a cylindrical grid [1]. Together with our result, we get:

Corollary 3

Deciding whether a weakly 3-connected strong digraph D has the EP property for butterfly minors can be done in linear time.

4 Digraphs with Sources and Sinks

We have seen that if D is a butterfly minor of a cylindrical grid, then D has a planar embedding such that \(D^*\) admits a dijoin path (Theorem 5). As we want to show that this holds for a spanning supergraph with neither sources nor sinks, it remains to “kill” sources and sinks in D. This is done in this section.

Given a cylindrical grid \(C_{n,2m}\) with the canonical planar embedding described previously, let \(Q^*_{n,2m}\) be the directed path of the dual \(C^*_{n,2m}\) whose arcs correspond exactly to all arcs of \(C_{n,2m}\) that go from the last (topmost) row to the first (bottommost) row. Note that \(Q^*_{n,2m}\) is a dijoin path of \(C^*_{n,2m}\) (see Fig. 3). The next lemma states that if a digraph D has a model in a cylindrical grid, then it is possible to get a model such that \(Q^*_{n,2m}\) only crosses blue arcs of this model.

Lemma 1

If a digraph D has a butterfly model \(\eta \) in \(C_{n,2m}\), then D has a butterfly model in \(C_{n',2m'}\) for some \(n'\ge n\) and \(m'\ge m\) such that no black arcs of this model are dual of an arc of \(Q^*_{n',2m'}\).

Lemma 2

If a digraph \(D=(V,A)\) has a butterfly model in \(C_{n,2m}\), then D has a spanning supergraph with neither sources nor sinks that has a butterfly model in \(C_{n',2m'}\) for some \(n'\ge n\) and \(m'\ge m\).

Sketch of the Proof. If D has no sources nor sinks, then we are done, so suppose otherwise. In what follows, given a source s in D (resp., a sink t), we describe a process that builds a model for an in-arc that we add to s (resp., an out-arc that we add to t), so that the obtained supergraph has also a model in a cylindrical grid and has one less source (resp., sink). By iteratively applying such process, we get the desired conclusions.

Let us consider a butterfly model \(\eta \) of D with a dijoin path \(P^*\) as in Lemma 1, and suppose that D has a source s (the case of a sink is symmetric). We will add a new arc (z, s) for some \(z \in V(D)\), and a directed path Q (finishing in the in-tree of the model of s) for modelling this arc in the existing model \(\eta \). The difficulty is to find the vertex of an out-tree in which we can start Q from. First let us add two columns between any two consecutive columns and let us add two rows between any two consecutive rows. We also add one column to the left and one column to the right of the cylindrical grid.

Let \(r_s\) be the root of \(\eta (s)\). Note that, by assuming \(\eta \) to be minimal, we get that the in-tree of the model of s in \(\eta \) is reduced to its root. Let \(a_1\) be the vertex below \(r_s\) and \(b_1\) the vertex below \(a_1\). Since we have just added two rows between any two rows, and because the in-tree of s is reduced to \(r_s\), we get that \(a_1,b_1\) are not part of the model of any vertex nor arc. Let Q initially contain just the arc \((a_1,r_s)\) (this will actually be the last arc of Q). Let us assume that Q has been built up to some vertex \(a_h\), i.e., \(Q=(a_h,a_{h-1},\cdots ,a_1,r_s)\), and additionally assume that the vertex \(b_h\) below \(a_h\) is not part of the model of any vertex nor arc (this is the case for \(h=1\)). Let w be the vertex below \(b_h\).

  • If w is not part of the model of any vertex nor arc, then let \(a_{h+1}=b_h\) and let \(b_{h+1}=w\), and we continue to build Q.

  • If w is in the out-tree of some vertex, then add \((w,b_h),(b_h,a_h)\) to the end of Q to be done.

  • If w is part of the in-tree of some vertex a (and not of its out-tree, i.e., w is not the root of the model of a), then assume that the row of \(a_h\) goes to the right (the other case is symmetric). Let x be the left neighbor of \(a_h\), y be the vertex below x (and to the left of \(b_h\)), and z the vertex below y (and to the left of w). Note that, since w is part of the model and \(b_h\) is not, then the rows of \(b_h\) and \(a_h\) are rows that have been added just before starting the process. In particular, this implies that either both x and y belong to the model of some \(e\in V(D)\cup A(D)\), or neither x nor y is part of any model. We can then prove that the former case is not possible because it would contradict the fact that w is part of the in-tree (and not of the out-tree) of the model of a. In the latter case, we set \(a_{h+1}=x\) and \(b_{h+1}=y\) and go on.

  • If w is part of the model of some arc \(e=(u,v) \in A(D)\). We apply similar arguments and omit the proof because of space constraints.

The above process is not ensured to finish because if might happen that vertices \(a_h\) and \(b_h\) are already on the outerface of the model \(\eta \). The next two cases allow to ensure that our process will actually terminate. For this purpose, we use the dijoin path \(P^*\).

  • If \((b_h,a_h)\) crosses the dijoin path \(P^*\) and \(P^*\) does not cross any blue arc, then let us consider the closest row under \(P^*\) that contains a vertex of the model. W.l.o.g., let us assume that this row goes to the right and let x be the rightmost vertex of this row that is part of the model of some vertex \(v^*\) of D. By minimality of the model and because x has no out-neigbour in the model of any vertex or arc, then, x must be the root of \(\eta (v^*)\) (which is actually an in-tree). Now, we add to \(\eta (v^*)\): the up-going arc (x, y) (y being the up-neighbor of x), and the horizontal directed path Y starting from y to the leftmost vertex of this row (then y becomes the new root of \(\eta (v^*)\) and the path Y will be considered as its out-tree). To conclude this case, add at the beginning of Q, the directed path from the path Y of \(\eta (v^*)\) (added in previous paragraph) to \(b_h\).

  • If \((b_h,a_h)\) crosses \(P^*\) which crosses some blue arc, then we apply similar arguments and omit the proof because of space constraints.    \(\square \)

Further Work. An interesting question is whether there exists a structural condition on the sources and sinks of a digraph D that corresponds to being a butterfly minor of a cylindrical grid (avoiding to invoke a supergraph without sources or sinks). This may help to answer the question of the computational complexity of deciding if a strong digraph D has the EP property when D is not weakly 3-connected. Since the class of digraphs that are butterfly minors of a cylindrical grid is closed under taking butterfly minors, it would also be interesting to characterize the minimal forbidden butterfly minors for this class.