Efficient Constructions for the Győri-Lovász Theorem on Almost Chordal Graphs

Abstract

In the 1970s, Győri and Lovász showed that for a k-connected n-vertex graph, a given set of terminal vertices $t_1, \dots , t_k$ and natural numbers $n_1, \dots , n_k$ satisfying $\sum _{i=1}^{k} n_i = n$, a connected vertex partition $S_1, \dots , S_k$ satisfying $t_i \in S_i$ and $|S_i| = n_i$ exists. However, polynomial time algorithms to actually compute such partitions are known so far only for $k \le 4$. This motivates us to take a new approach and constrain this problem to particular graph classes instead of restricting the values of k. More precisely, we consider k-connected chordal graphs and a broader class of graphs related to them. For the first class, we give an algorithm with $\mathcal {O}(n^2)$ running time that solves the problem exactly, and for the second, an algorithm with $\mathcal {O}(n^4)$ running time that deviates on at most one vertex from the required vertex partition sizes.

1 Introduction

Partitioning a graph into connected subgraphs is a fundamental task in graph algorithms. Such connected partitions occur as desirable structures in many application areas such as image processing [8], road network decomposition [9], and robotics [17].

From a theoretical point of view, the existence of a partition into connected components with certain properties also gives insights into the graph structure. In theory as well as in many applications, one is interested in a connected partition that has a given number of subgraphs of chosen respective sizes. With the simple example of a star-graph, it is observed that not every graph admits a connected partition for any such choice of subgraph sizes. More generally speaking, if there exists a small set of t vertices whose removal disconnects a graph (separator), then any connected partition into $k>t$ subgraphs has limited choice of subgraph sizes. Graphs that do not contain such a separator of size less than k are called k-connected.

On the other hand, Győri and Lovász independently showed that k-connectivity is not just necessary but also sufficient to enable a connected partitioning into k subgraphs of required sizes, formally stated by the following result.

Győri-Lovász Theorem ([4, 7]). Let $k\ge 2$ be an integer, $G=(V,E)$ a k-connected graph, $t_1,\ldots , t_k\in V$ distinct vertices and $n_1,\ldots ,n_k\in \mathbb {N}$ such that $\sum _{i=1}^kn_i= |V|$. Then G has disjoint connected subgraphs $G_1, \ldots G_k$ such that $|V(G_i)|=n_i$ and $t_i\in V(G_i)$ for all $i\in [k]$.

The caveat of this famous theorem is that the constructive proof of it yields an exponential time algorithm. Despite this result being known since 1976, to this day we only know polynomial constructions for restricted values of k. Specifically, in 1990 Suzuki et al. [15] provided such an algorithm for $k=2$ and also for $k=3$ [14]. Moreover in 1994 Wada et al. [16] also provided an extended result for $k=3$. Nakano et al. [10] gave a linear time algorithm for the case where $k=4$, G is planar and the given terminals are located on the same face of a plane embedding of G, while in 2016 Hoyer and Thomas [5] provided a polynomial time algorithm for the general case of $k=4$. And so far, this is where the list ends, thus for $k\ge 5$ it remains open whether there even exists a polynomial time construction.

Towards a construction for general k, we consider restricting the class of k-connected graphs instead of the values of k. More precisely, we consider (generalizations of) chordal k-connected graphs. A graph is called chordal, if it does not contain an induced cycle of length more than three. The restriction to chordal graphs is known to often yield tractability for otherwise NP-hard problems, for example chromatic number, clique number, independence number, clique covering number and treewidth decomposition [13]. Apart from the interest chordal graphs have from a graph theoretic point of view, their structural properties have also been proven useful in biology when it comes to studying multidomain proteins and network motifs (see e.g. [11, 12]).

Our Contribution. To the best of our knowledge, this paper is the first to pursue the route of restricting the Győri-Lovász Theorem to special graph classes in order to develop a polynomial construction for general values of k on a non-trivial subclass of k-connected graphs. We believe that in general considering the structure of the minimal separators of a graph is promising when it comes to developing efficient algorithms for the Győri-Lovász Theorem.

We give a constructive version of the Győri-Lovász Theorem for chordal k-connected graphs with a running time in $\mathcal {O}(|V|^2)$. Observe here that this construction works for all values of k. Then we show how this result can be generalized in two directions.

First, we generalize our result to the vertex weighted version of the Győri-Lovász Theorem (as proven independently by Chandran et al. [2], Chen et al. [3] and Hoyer [5]), specifically deriving the following theorem.

Theorem 1

Let $k\ge 2$ be an integer, $G=(V,E,w)$ a vertex-weighted k-connected chordal graph with $w :V \rightarrow \mathbb {N}$ and $w_{ max }:=\max _{u\in V}w(u)$, $t_1,\ldots , t_k \in V$ distinct vertices, and $w_1,\ldots ,w_k \in \mathbb {N}$ with $w_i \ge w(t_i)$ for all $i \in [k]$ and $\sum _{i=1}^k w_i = w(V)$. A partition $S_1,\dots ,S_k$ of V, such that $G[S_i]$ is connected, $t_i \in S_i$ and $w_i - w_{ max }< w(S_i) < w_i + w_{ max }$, for all $i \in [k]$, can be computed in time $\mathcal {O}(|V|^2)$.

We further use this weighted version to derive an approximate version of the Győri-Lovász Theorem for a larger graph class. Specifically we define $\text {I}_j^i$ to contain all graphs that occur from two distinct chordless $C_j$’s that have at least i vertices in common. We focus on $\text {I}_4^2$-free combined with HH-free graphs. More specifically, we consider the subclass of k-connected graphs that contain no hole or house as an induced subgraph (see preliminaries for the definitions of structures such as hole, house etc.) and that does not contain two distinct induced $C_4$ that share more than one vertex. We call this class of graphs $\text {HHI}_4^2$-free . Note that $\text {HHI}_4^2$-free , apart from being a strict superclass of chordal graphs, is also a subclass of HHD-free graphs (that is house, hole, domino-free graphs), a graph class studied and being used in a similar manner as chordal graphs as it is also a class where the minimum fill-in set is proven to be polynomially time solvable [1] (see also [6] for NP-hard problems solved in polynomial time on HHD-free graphs). Taking advantage of the fact that given an $\text {HHI}_4^2$-free graph, the subgraph formed by its induced $C_4$ has a treelike structure, we are able to derive the following result.

Theorem 2

Let $k\ge 2$ be an integer, $G=(V,E,w)$ a vertex-weighted k-connected $\text {HHI}_4^2$-free graph with $w :V \rightarrow \mathbb {N}$ and $w_{ max }:=\max _{u\in V}w(u)$, $t_1,\ldots , t_k \in V$ distinct vertices, and $w_1,\ldots ,w_k \in \mathbb {N}$ with $w_i \ge w(t_i)$ for all $i \in [k]$ and $\sum _{i=1}^k w_i = w(V)$. A partition $S_1,\dots ,S_k$ of V, such that $G[S_i]$ is connected, $t_i \in S_i$ and $w_i - 2w_{ max }< w(S_i) < w_i + 2w_{ max }$, for all $i \in [k]$, can be computed in time $\mathcal {O}(|V|^4)$.

Notice that the above theorem implies a polynomial time algorithm with an additive error of 1 for the unweighted case.

2 Preliminaries

All graphs mentioned in this paper are undirected, finite and simple. Given a graph G and a vertex $v\in V(G)$ we denote its open neighborhood by $N_G(v):=\{u\in V(G) \mid uv\in E(G)\}$ and by $N_G[v]$ its closed neighborhood, which is $N(v)\cup \{v\}$. Similarly we denote by $N_G(S):=\bigcup _{v\in S}N_G(v){\setminus }S$ the open neighborhood of a vertex set $S\subseteq V(G)$ and by $N_G[S]:=N_G(S)\cup S$ its closed neighborhood. We omit the subscript G when the graph we refer to is clear from the context. A vertex $v\in V(G)$ is universal to a vertex set $S \subset V(G)$ if $S\subseteq N(v)$. Let G be a graph and $S\subseteq V(G)$. The induced subgraph from S, denoted by G[S], is the graph with vertex set S and all edges of E(G) with both endpoints in S.

A graph G is chordal if any cycle of G of size at least 4 has a chord (i.e., an edge linking two non-consecutive vertices of the cycle). A vertex $v\in V(G)$ is called simplicial if N[v] induces a clique. Based on the existence of simplicial vertices in chordal graphs, the following notion of vertex ordering was given. Given a graph G, an ordering of its vertices $(v_1,\ldots ,v_n)$ is called perfect elimination ordering (p.e.o.) if $v_i$ is simplicial in $G[\{v_i,v_{i+1},\ldots , v_n\}]$ for all $i\in [n]$. Given such an ordering $\sigma : V(G)\rightarrow \{1,\ldots ,n\}$ and a vertex $v\in V(G)$ we call $\sigma (v)$ the p.e.o. value of v. Rose et al. [13] proved that a p.e.o. of any chordal graph can be computed in linear time.

Let $e=\{u,v\}$ be an edge of G. We denote by G/e the graph $G'$, that occurs from G by the contraction of e, that is, by removing u and v from G and replacing it by a new vertex z whose neighborhood is $\left( N(u)\cup N(v)\right) {\setminus }\{u,v\}$.

A graph G is connected if there exists a path between any pair of distinct vertices. Moreover, a graph is k-connected for some $k\in \mathbb {N}$ if after the removal of any set of at most $k-1$ distinct vertices G remains connected. Given a graph G and a vertex set $S \subseteq V(G)$, we say that S is a separator of G if its removal disconnects G. We call S a minimal separator of G if the removal of any subset $S' \subseteq V(G)$ with $|S'|<|S|$ results in a connected graph.

We now define some useful subgraphs, see also Fig. 1 for illustrations. An induced chordless cycle of length at least 5 is called a hole. The graph that occurs from an induced chordless $C_4$ where exactly two of its adjacent vertices have a common neighbor is called a house. When referring to the induced $C_3$ part of a house we call it roof while the induced $C_4$ is called body. Two induced $C_4$ sharing exactly one edge form a domino. A graph that contains no hole, house or domino as an induced subgraph is called HHD-free. We call a graph that consists of two $C_4$ sharing a vertex, and an edge that connects the two neighbors of the common vertex in a way that no other $C_4$ exists a double house.

Lastly, let $G=(V,E)$ be a k-connected graph, let $t_1,\ldots , t_k\in V$ be k distinct vertices, and let $n_1,\ldots , n_k$ be natural numbers satisfying $\sum _{i=1}^kn_i= |V|$. We call $S_1,\ldots S_k \subseteq V(G)$ a GL-Partition of G if $S_1,\ldots S_k$ forms a partition of V(G), such that for all $i \in [k]$ we have that $G[S_i]$ is connected, $t_i \in S_i$ and $|S_i|=n_i$. When there exists an $l\in \mathbb {N}$, such that for such a partition only $n_i-l\le |S_i|\le n_i+l$ holds instead of $|S_i|=n_i$, we say that $S_1,\ldots ,S_k$ is a GL-Partition of G with deviation l.

Fig. 1.

Specific subgraphs used throughout the paper, from left to right: house, double house, domino and hole example

3 GL-Partition for Chordal Graphs

We present a simple, implementable algorithm with quadratic running time that computes GL-Partitions in chordal graphs. We then show that a slight modification of our algorithm is sufficient to compute a GL-Partition on a vertex weighted graph, thus proving Theorem 1.

3.1 GL-Partition for Unweighted Chordal Graphs

For simplicity, we first prove the restricted version of Theorem 1 to unweighted graphs. We use a p.e.o. to compute a vertex partition, as described formally in Algorithm 1. This algorithm receives as input a k-connected chordal graph $G=(V,E)$, terminal vertices $t_1,\ldots ,t_k \in V$, and natural numbers $n_1,\ldots ,n_k$ satisfying $\sum _{i=1}^kn_i=n$, and outputs connected vertex sets $S_1,\ldots ,S_k \subseteq V$ such that $|S_i|=n_i$ and $t_i \in S_i$. In the beginning of the algorithm we initialize each set $S_i$ to contain only the corresponding terminal vertex $t_i$, and add vertices iteratively to the non-full sets ($S_i$’s that have not reached their demanded size). We say a vertex v is assigned if it is already part of some $S_i$ and unassigned otherwise. At each iteration, the unassigned neighborhood of the union of the previously non-full sets is considered, and the vertex with the minimum p.e.o. value is selected to be added to a non-full set. In case there is more than one non-full set in the neighborhood of this vertex, it is added to the one with lowest priority, where the priority of each set is defined to be the largest p.e.o. value of its vertices so far. The algorithm terminates once all vertices are assigned, in $\mathcal {O}({|V|}^2)$ time.

For the correctness of Algorithm 1 it is enough to show that the unassigned neighborhood $V'$ of all non-full sets is not empty in each iteration of the while-loop, since this implies that we enlarge a non-full set (in the algorithm denoted by $S_{j'}$) by one vertex (in the algorithm denoted by $v'$) while maintaining the size of all remaining sets. That is, in each iteration we make progress in the sense that $|\bigcup _{i \in [k]} S_i|$ increases while maintaining the invariant $|S_i| \le n_i$ for all $S_i$’s. Note that $v' \in N(S_{j'})$ which in turn implies that $G[S_i]$ is always connected for all $i \in [k]$. Finally, by $\sum _{i=1}^k n_i=n$ and through the way we update I we ensure that the algorithm (or while-loop) terminates as $\bigcup _{i \in [k]} S_i = V$ only if we have $|S_i| = n_i$ for all $S_i$’s.

Towards proving the required Lemmata for the correctness of Algorithm 1 we make the following observation for the p.e.o. of a graph.

Lemma 1

Let $\sigma$ be a p.e.o of a graph $G=(V,E)$ and $P=\{v_1,v_2,\ldots ,v_k\}$ a vertex set of G that induces a simple path with endpoints $v_1$ and $v_k$. Then $\sigma (v_i)>\min \{\sigma (v_1),\sigma (v_k)\}$ for all $i=2,\ldots ,k-1$.

Lemma 2

In each iteration of the while-loop in Algorithm 1 we have $V' \ne \varnothing$.

Proof

We first define the z-connecting neighborhood of a vertex v to be the neighbors of v that are included in some induced path connecting v to z.

We prove that every non-full set $S_i$ contains a vertex in its neighborhood $N(S_i)$ that is unassigned, which implies that $V' \ne \varnothing$. Assume for a contradiction that at some iteration of our algorithm there is an non-full set $S_i$ whose neighborhood is already assigned to other sets. Let v be the vertex of $S_i$ of maximum $\sigma$ value among its vertices and z be the vertex of maximum $\sigma$ value among the unassigned vertices. Note that $vz\not \in E(G)$. Let $\mathcal {P}$ be the set of all simple induced paths of G with endpoints z and v. Consider now the following cases:

• 1. If $\sigma (z)>\sigma (v)$, we get from Lemma 1 that every internal vertex of each path in $\mathcal {P}$ has higher $\sigma$ value than v. Note that no vertex of $S_i$ is an internal vertex of some path in $\mathcal {P}$, since all of them have smaller $\sigma$ value than v by the selection of v. Denote the z-connecting neighborhood of v by C. Let a, b be two vertices in C and assume that $a,b\in S_j$ for some j. Assume also that during our algorithm, a is added to $S_j$ before b. Since all vertices of $S_i$ have smaller $\sigma$ value than both a and b, and a is added to $S_j$ before b, the moment b is added to $S_j$, $S_i$ has already been formed. Consider now the iteration that this happens. Since $b\in N(v)$, $G[S_i\cup \{b\}]$ is connected. Moreover since $\sigma (a)>\sigma (v)$ and $S_i$ is not full, b should be added to $S_i$ instead of $S_j$. As a result each set apart from $S_i$ contains at most one such neighbor of v, and hence $|C|<k$. Observe that $G{\setminus } C$ has no induced path connecting z and v which in turn implies that $G{\setminus } C$ has no $z-v$ path in general. However, this contradicts the k-connectivity of G.

• 2. If $\sigma (z)<\sigma (v)$, since z is the unassigned vertex of the highest $\sigma$ value among all unassigned vertices, and by Lemma 1 all vertices in $\mathcal {P}$ have greater $\sigma$ value than z, all of its v-connecting neighbors in $\mathcal {P}$ are already assigned in some set. Denote the set of v-connecting neighbors of z by C. Assume now that there are two vertices of C, a and b, that are contained in some $S_j$ and assume also without loss of generality that a was added to $S_j$ before b. Note that since $\sigma (z)<\sigma (b)$ at each iteration of our algorithm z is considered before b to be added to some set if the induced graph remains connected. As a result, after a is added to $S_j$, the induced subgraph $G[S_j \cup \{z\}]$ is connected and hence z should be added to $S_j$ before b. This means that each set contains at most one v-connecting neighbor of z and therefore $|C|<k$. Since $G{\setminus } C$ has no induced path connecting z and v, there is no z-v-path in $G {\setminus } C$, which contradicts the k-connectivity.

Corollary 1

At each iteration of Algorithm 1, unless all vertices are assigned, the neighborhood of each non-full set contains at least one unassigned vertex.

In the weighted case we use the above corollary of Lemma 2. In particular, it follows from Corollary 1 that as long as we do not declare a set to be full, we ensure that we are able to extend it by a vertex in its neighborhood that is unassigned. Note that in the weighted case we do not know in advance how many vertices are in each part.

3.2 GL-Partition for Weighted Chordal Graphs

With a slight modification of Algorithm 1 we can compute the weighted version of a GL-Partition . In particular, we prove Theorem 1.

The input of our algorithm differs from the unweighted case by having a positive vertex-weighted graph $G=(V,E,w)$ and instead of demanded sizes $n_1, \dots , n_k$ we have demanded weights $w_1, \dots , w_k$ for our desired vertex sets $S_1, \dots , S_k$, where $\sum _{i=1}^{k} w_i = w(V)$. Note also that $w(S_i)$ is not allowed to deviate more than $w_{ max }= \max _{v \in V} w(v)$ from $w_i$, i.e. $w_i - w_{ max }< w(S_i) < w_i + w_{ max }$.

Again we set each terminal vertex $t_i$ to a corresponding set $S_i$, and enlarge iteratively the non-full weighted sets ($S_i$’s that are not declared as full). One difference to the previous algorithm is that we declare a set $S_i$ as full weighted set, if together with the next vertex to be potentially added its weight would exceed $w_i$. After that, we decide whether to add the vertex with respect to the currently full weighted sets. Similar to Algorithm 1 we interrupt the while-loop if $S_1,\dots ,S_k$ forms a vertex partition of V and the algorithm terminates. However, to ensure that we get a vertex partition in every case, we break the while-loop when only one non-full weighted set is left and assign all remaining unassigned vertices to it.

Observe that we can make use of Corollary 1, since Algorithm 2 follows the same priorities concerning the p.e.o. as Algorithm 1. Basically, it implies that as long we do not declare a set as full weighted set and there are still unassigned vertices then those sets have unassigned vertices in their neighborhood.

We conclude this section by extending the above algorithms to graphs having distance k/2 from being chordal. In particular this corollary is based on the observation that an edge added to a graph does not participate in any of the parts those algorithms output if both of its endpoints are terminal vertices.

Corollary 2

Let G be a k-connected graph which becomes chordal after adding k/2 edges. Given this set of edges, a GL-Partition (also its weighted version) can be computed in polynomial time but without fixed terminals.

4 GL-Partition for $\text {HHI}_4^2$-free

This section is dedicated to the proof of Theorem 2. The underlying idea for this result is to carefully contract edges to turn a k-connected $\text {HHI}_4^2$-free graph into a chordal graph that is still k-connected. Note that we indeed have to be very careful here to find a set of contractions, as we need it to satisfy three seemingly contradicting properties: removing all induced $C_4$, preserving k-connectivity, and contracting at most one edge adjacent to each vertex. The last property is needed to bound the maximum weight of the vertices in the contracted graph. Further, we have to be careful not to contract terminal vertices.

The computation for the unweighted case of the partition for Theorem 2 is given in Algorithm 3 below, which is later extended to the weighted case as well. Note that we can assume that $n_i\ge 2$ since if $n_i=1$ for some $i\in [k]$ we simply declare the terminal vertex to be the required set and remove it from G. This gives us a $(k-1)$-connected graph and $k-1$ terminal vertices.

Before starting to prove the Lemmata required for the correctness of Algorithm 3 we give a structural insight which is used in almost all proofs of the following Lemmata.

Lemma 3

Given an $\text {HHI}_4^2$-free graph G and an induced $C_4$, $C\subseteq V(G)$, then any vertex in $V(G){\setminus }C$ that is adjacent to two vertices of C is universal to C. Moreover, the set of vertices that are universal to C induces a clique.

Lemma 4

Let G be an $\text {HHI}_4^2$-free graph. If G contains a double house as a subgraph then at least one of the two $C_4$ in it has a chord.

Fig. 2.

Illustrations for the vertex namings used in proofs, from left to right: Lemma 4, Lemma 7 and Lemma 8

The following lemma captures the essence of why the algorithm provided in this section cannot be applied also on HHD-free graphs, since it holds for $\text {HHI}_4^2$-free graphs but not for HHD-free graphs. Think for example of a simple path P of length 5 and a vertex disjoint induced chordless $C_4$, C. Consider also each vertex of P being universal to C. Observe that this graph is HHD- but not $\text {HHI}_4^2$-free . Every two non adjacent vertices of C together with the endpoints of P create an induced chordless $C_4$. Adding a chord connecting the two endpoints of P creates a hole and hence the resulting graph is not HHD-free.

Lemma 5

Let G be an $\text {HHI}_4^2$-free graph and $C=\{v_1,v_2,v_3,v_4\}$ an induced $C_4$ in G. Then the graph $G'$ created by adding the chord $v_1v_3$ to G is $\text {HHI}_4^2$-free and has one less induced $C_4$ than G.

An essential property of the graph class we work on is being closed under contraction, since our algorithm is based on contracting edges iteratively until the resulting graph becomes chordal. Before proving this property though, although “after an edge contraction a new cycle is created” is intuitively clear, we formally define what it means for a $C_4$ to be “new”.

Definition 1

Let G be a graph, $uv\in E(G)$ and $G'=G/uv$. Let also w be the vertex of $G'$ that is created by the contraction of uv. We say that an induced cycle C containing w in $G'$ is new if $N_C(w)\not \subseteq N_G(v)$ and $N_C(w)\not \subseteq N_G(u)$.

Lemma 6

$\text {HHI}_4^2$-free graphs are closed under contraction of an edge of an induced $C_4$.

In order to prove that the contractions of our algorithm do not affect the connectivity, we first study the possible role of vertices on an induced $C_4$ in minimal separators in $\text {HHI}_4^2$-free graphs.

Lemma 7

Let G be a k-connected $\text {HHI}_4^2$-free graph for $k\ge 5$. Then no three vertices of an induced $C_4$ belong in the same minimal separator.

Proof

Let G be a k-connected $\text {HHI}_4^2$-free graph for $k\ge 5$ and $v_1,v_2,v_3,v_4$ vertices that induce a $C_4$, C. Assume that $v_1,v_2,v_3$ belong in the a same minimal separator S and hence, $(G{\setminus }\{v_1,v_2,v_3\})$ is only $k-3$ connected. Let also u and w be two distinct vertices belonging in different connected components of $G{\setminus } S$.

Consider now the chordal graph $G'$ created, by adding $v_2v_4$ to C and one chord to each other induced $C_4$ of G. By Lemma 5 this is possible by adding exactly one chord to each induced $C_4$ of G - in particular each addition does not create new induced $C_4$. Since $G'$ is chordal each minimal separator induces a clique, and hence $v_1,v_2,v_3$ cannot be part of the same minimal separator in $G'$ because they do not induce a triangle in $G'$. Thus $G'{\setminus } S$ remains connected.

Let $P_1$ be a $u-w$ path in $G'{\setminus } S$ that contains a minimal number of added edges. Let $z_1z_3\in E(P_1)$ be one of the added edges, such that $z_3$ is closer to u on $P_1$ than $z_1$. Note that $z_1$ and $z_3$ are part of some induced $C_4$, $C'=\{z_1,z_2,z_3,z_4\}$ in G. Since $z_1z_3$ cannot be replaced by neither $z_1z_2,z_2z_3$, nor $z_1z_4,z_4z_3$ (otherwise we get a path with strictly less added edges than $P_1$) it follows that $z_2,z_4\in S$.

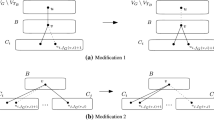
We will use the $u-w$ paths through S in G to reach a contradiction. Since S is a minimal $u-w$ separator in G, there are two internally vertex disjoint $u-w$ paths $P_2$ and $P_3$, with $P_2\cap S=\{z_2\}$ and $P_3\cap S=\{z_4\}$. Let $w_2$ be the neighbor of $z_2$ on $P_2$ closer to w, $w_1$ the respective neighbor of $z_1$ on $P_1$ and $w_3$ the respective neighbor of $z_4$ on $P_3$. Let also $u_1$, $u_2$, $u_3$ be the corresponding neighbors of these paths closer to u. See the illustration in Fig. 2 for these namings, keeping in mind that it could be $w_1\in \{w_2,w_3\}$ or $u_1\in \{u_2,u_3\}$ or also $w_1=w_2=w_3=w$ or $u_1=u_2=u_3=u$.

We claim that, in G, $z_3$ is adjacent to a vertex on $P_2^{[w_2,w]}$ or $P_3^{[w_3,w]}$. Assume otherwise, and assume that $P_2^{[w_2,w]}$, $P_3^{[w_3,w]}$ are induced paths in G (shortcut them otherwise). If $w_2=w_3$ then notice that $w_2=w=w_3$. In order for $z_3,z_2,z_4,w$ not to induce a $C_4$ with three common vertices to C, $z_3$ has to be adjacent to w which is on $P_2^{[w_2,w]}$. If $w_2\ne w_3$ then assume without loss of generality that $w_2\ne w$. In order to not be a hole, there has to be a chord in the cycle build by $P_2^{[w_2,w]}$, $P_3^{[w_3,w]}$ with $z_4,z_3,z_2$. By assumption, this chord cannot be from $z_3$, so it has to involve $z_4$ or $z_2$. Since $P_2^{[w_2,w]}$ and $P_3^{[w_3,w]}$ are induced and $w_2\ne w$, either $w_2$ is adjacent to $z_4$, or $w_3\ne w$ is adjacent to $z_2$. Both cases create a $C_4$ that has three vertices in common with C, ($w_2,z_2,z_3,z_4$, and $w_3,z_2,z_3,z_4$, resp.) and since $z_4z_2\notin E(G)$, the added chord for these $C_4$ has to be $w_2z_3$, resp. $w_3z_3$, leading again to $z_3$ being adjacent to some vertex on $P_2^{[w_2,w]}$ or $P_3^{[w_3,w]}$.

Thus we conclude that $z_3$ is adjacent to a vertex x on $P_2^{[w_2,w]}$ or $P_3^{[w_3,w]}$ in G. This however allows to create a path from u to w with (at least) one added edge less than $P_1$ in G (since $P_2, P_3$ do not contain any added edges). Specifically, if x is on $P_2$ we get $P_1'=P_1^{[u,z_3]}xP_2^{[x,w]}$ and if $x\in P_3$, $P_1'=P_1^{[u,z_3]}xP_3^{[x,w]}$.

Since $C'$ was an arbitrary cycle we conclude that $v_1,v_2,v_3$ cannot be part of the same minimal separator in G.

Lemma 8

Let G be an $\text {HHI}_4^2$-free k-connected graph and $C=\{v_1,v_2,v_3,v_4\}$ be an induced $C_4$. The graph $G'=G/v_1v_2$ is still k-connected.

Now, we finally look specifically at Algorithm 3, and first show that its subroutine creating $G''$ works correctly.

Lemma 9

Given an $\text {HHI}_4^2$-free graph G, the vertices selected in line 6 of Algorithm 3 indeed exist as long as an induced $C_4$ exists.

Proof

Let G be an $\text {HHI}_4^2$-free graph and $\mathcal {C}$ the set of all induced $C_4$ in G, consider the bipartite graph T constructed through the following procedure: Its vertices are partitioned into two sets B, and S referred to as big and small vertices of T, respectively. Each big vertex represents an induced $C_4$ of $\mathcal {C}$ while each small vertex represents a vertex of G participating in at least two induced $C_4$. Each small vertex is adjacent to the big vertices which represent a $C_4$ this vertex participates in. We claim that with this definition T is indeed a tree (actually a forest). Assume now for a contradiction that T contains a cycle and let C be one of the shortest such cycles in T.

First, consider the case that C has length $l\ge 6$. Since T is bipartite, due to its construction, l is even and the vertices of $C=\{s_1,b_1,s_2,b_2,\ldots ,s_{l/2},b_{l/2}\}$ alternate between big and small. We denote by $P_{b_i}^{s_w,s_z}$ a shortest path containing edges from the $C_4$ represented by the big vertex $b_i$ with endpoints the vertices represented by $s_w$ and $s_z$. Due to C, the cycle $P_{b_1}^{s_1,s_{l/2}}\ldots P_{b_l/2}^{s_{l/2-1},s_{l/2}}$ exists in G as a subgraph. Note that since we have assumed that C is a minimal length cycle of T it is also chordless. Hence, in order for a hole not to be an induced subgraph of G at least one chord must exist connecting two vertices corresponding to two small ones of T. This however would create a double house as a subgraph with the two $C_4$ forming it being the two that correspond to big vertices of T. By Lemma 4 this means that one of the $C_4$ is not induced, a contradiction to the construction of T. Notice also that in the case where $l=6$ we directly find a double house and reach a contradiction using the same arguments.

Moreover the assumption that $l=4$, leads us to a contradiction to the fact that two $C_4$ have at most one vertex in common. Hence, T is a forest and the vertices mentioned in line 6 are the ones belonging only to a cycle represented by one leaf belonging in B.

Lemma 10

Given an $\text {HHI}_4^2$-free graph G, lines 1–10 of Algorithm 3 transforms G into a weighted chordal graph $G''$, with the same connectivity as G and such that each vertex from G is involved in at most one edge contraction to create $G''$.

At last, notice that we can easily alter Algorithm 3 to also work for weighted graphs, with the simple change of setting the weights of a vertex in $G''$ in line 10 to the sum of the weights of the original vertices it was contracted from. With this alteration, we can conclude now the proof of Theorem 2 with the following.

Lemma 11

Algorithm 3 works correctly and runs in time $\mathcal {O}(|V|^4)$.

Proof

By Lemma 10, $G''$ is a chordal graph with maximum vertex weight $2w_{ max }$. Further, observe that we did not merge terminal vertices with each other, thus we can properly run Algorithm 2 on it. By the correctness of this algorithm (Theorem 1), we know that $S_1,\dots ,S_k$ in line 11 is a GL-partition for $G''$ with deviation $2w_{ max }$. Since reversing edge-contraction does not disconnect these sets, the unfolded sets $S_1,\dots ,S_k$ are thus also a GL-partition for G with deviation $2w_{ max }$; note here that the only edges we added to create $G''$ are between terminal vertices, which are in separate sets $S_i$ by definition.

The most time consuming part of Algorithm 3 is the preprocessing to transform the input graph into a weighted chordal graph which requires $\mathcal {O}({|V|}^4)$ time in order to find all the induced $C_4$ (note that the induced $C_4$ are at most $(n-4)/3$ since they induce a tree).

Moreover, as is the case for chordal graphs, we can sacrifice terminals to enlarge the considered graph class.

Corollary 3

Let G be a k-connected graph which becomes $\text {HHI}_4^2$-free after adding k/2 edges. Then, given those edges, a GL-Partition of G with deviation 1 (also its weighted version with deviation $2w_{max}-1$) can be computed in polynomial time but without fixed terminals.