Reducing the Computational Complexity of the Eccentricity Transform of a Tree

Abstract

This paper proposes a novel approach to reduce the computational complexity of the eccentricity transform (ECC) for graph-based representation and analysis of shapes. The ECC assigns to each point within a shape its geodesic distance to the furthest point, providing essential information about the shape’s geometry, connectivity, and topology. Although the ECC has proven valuable in numerous applications, its computation using traditional methods involves heavy computational complexity. To overcome this limitation, we present a method that computes the ECC of a tree, significantly reducing the computational complexity from $\mathcal{O}(n^2log(n))$ to $\mathcal{O}(b)$, where n and b are the numbers of vertices and branching points in the tree, respectively. Our method begins by computing the ECC for tree structures, which are simpler representations of shapes. Subsequently, we introduce the concept of a 3D curve that corresponds to a smooth shape without holes, enabling the computation of the ECC for more complex shapes. By leveraging the 3D curve representation, our method provides an upper-bound approximation of the ECC, which can be effectively utilized in various applications. The proposed approach not only preserves the valuable properties of the ECC but also significantly reduces the computational burden, making it a more efficient and practical solution for graph-based representation and analysis of shapes in both 2D and 3D contexts.

Supported by the Vienna Science and Technology Fund (WWTF), project LS19-013.

1 Introduction

The eccentricity transform (ECC) is a function that assigns to each point within a shape its geodesic distance to the furthest point [10]. In other words, it associates each point with the longest of the shortest paths connecting it to any other point within the shape [11]. The eccentricity transform is valuable for graph-based image analysis [1] due to its robustness to noise and minor segmentation errors [7], unique representation of a shape’s geometry, and the ability to reveal connectivity and topology [9]. Additionally, it is useful for 2D and 3D shape matching [5], enabling accurate comparisons between shapes [6]. Its invariance to translation, rotation, and scaling [5] allows for precise comparisons between shapes, while its capability to separate touching or overlapping objects enhances object detection and segmentation [12].

Calculation of the eccentricity transform for a shape can be computationally intensive. Using the Dijkstra algorithm, the complexity is $\mathcal{O}(n^2\,log(n))$ [5], where n is the number of vertices (pixels) in a 2D connected plane graph (2D image). However, under certain conditions, such as when a shape S has no holes, Ion [5] managed to reduce this complexity to $\mathcal{O}(|\partial S|\,n\,log(n))$, where $|\partial S|$ is the number of vertices (pixels) on the boundary of the shape S. In this study, we examine basic shapes with increasing complexity, including line segments, tree structures , and smooth shapes. Our primary approach is to compute the eccentricity transform without the need for distance propagation. Nevertheless, when direct computation is not feasible, one can employ efficient parallel and hierarchical approaches [4] to expedite the propagation of distances.

Presently, our research focuses on the Water’s Gateway to Heaven project¹, which involves high-resolution X-ray micro-tomography ($\mu CT$) and fluorescence microscopy. The image dimensions in this project exceed 2000 pixels per side, necessitating the use of the eccentricity transform to distinguish cells that are visually challenging to separate [2, 3]. Consequently, fast computation of the eccentricity transform with low complexity is essential.

In this study, we begin in Sect. 3 by computing the eccentricity of line segments and extending the method to develop an efficient algorithm for tree structures. Next, in Sect. 4, we introduce the concept of a 3D curve for a shape and expand the proposed method to compute the eccentricity in smooth shapes without holes. Finally, Sect. 5 presents the simulations and results of our investigation.

2 Definitions

Basic definitions and properties of the ECC are introduced following [8, 10]. Let the shape S be a closed set in $\mathbb {R}^{2}$ and $\partial S$ be its border. A path $\pi$ is the continuous mapping from the interval [0, 1] to S. Let $\Pi (p_1, p_2)$ be the set of all paths between two points $p_1,p_2 \in S$ within the set S. The geodesic distance $d(p_1, p_2)$ between two points $p_1,p_2 \in S$ is defined as the length $\lambda$ of the shortest path $\pi (p_1, p_2)$, such that $\pi \in S$, more formally

$$\begin{aligned} d(p_1,p_2)=min\{ \lambda (\pi (p_1,p_2)) | \pi \in \Pi \} \end{aligned}$$

(1)

where

$$\begin{aligned} \lambda (\pi )= \int _{0}^{1} \sqrt{1+{\mathop {\pi }\limits ^{\cdot }}^2(t)} \,dt \end{aligned}$$

(2)

where ${\mathop {\pi }\limits ^{\cdot }}$ is a parametrization of the path from $p_1= \,{\mathop {\pi }\limits ^{\cdot }}(0)$ to $p_2=\, {\mathop {\pi }\limits ^{\cdot }}(1)$. The eccentricity transform of a simply connected planar shape S is defined as, $\forall p \in S$

$$\begin{aligned} ECC_S(p)=max\{ d(p,q) | q \in S \}=max \{ d(p,q) | q \in \partial S \} \end{aligned}$$

(3)

i.e. to each point p it assigns the length of the shortest geodesics to the points farthest away from it. An eccentric point is defined as the point y that reaches a maximum in Eq. 3. Note that all eccentric points of a simply connected planar shape S lie on its border $\partial S$ [10].

3 Tree Structure

A tree structure is an undirected graph characterized by its acyclic nature and connectedness, which means that there are no cycles and any two vertices are connected by exactly one path. A tree can be constructed by combining line segments that are connected together at branching points . Each line segment represents an edge in the tree, connecting two vertices, while the branching points serve as junctions where multiple line segments meet. By connecting line segments in this manner, it is possible to create a hierarchical structure with a single root node at the top and multiple branches extending downwards, ultimately forming a tree structure that captures the relationships and connectivity among the various nodes in the graph.

Consequently, computing the eccentricity transform in a tree can be achieved by considering the combination of its line segments. By analyzing each line segment’s eccentricity and their connections at the branching points, the overall eccentricity transform for the entire tree structure can be determined. This approach simplifies the computation of the eccentricity transform for complex tree structures by breaking them down into smaller, more manageable segments, ultimately allowing for a more efficient calculation of the eccentricity values throughout the tree.

3.1 Line Segment

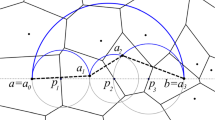
Consider a line segment, denoted by $l=(A,B)$, with endpoints A and B. In order to compute the eccentricity:

Proposition 1

The eccentric points of a line segment are its corresponding two endpoints.

Proof

Let us consider a line segment l with its two endpoints, A and B. Suppose that there exists a point $P \in l \backslash \{A,B\}$ such that Q is an eccentric point, meaning that Q is the farthest point away from P. If we move Q towards the corresponding endpoint, for instance point B, we obtain $\lambda (P,Q) < \lambda (P,B)$, which contradicts the original assumption.    $\square$

Proposition 2

The eccentricity of a point P on a line segment $l=(A,B)$ is:

$$\begin{aligned} \begin{aligned} ECC: P \in l&\mapsto \mathbb {R}^{+} \\ ECC(P)&= \max \{\lambda (A,P),\lambda (B,P)\} \end{aligned} \end{aligned}$$

(4)

where $\lambda (A,P)$ and $\lambda (B,P)$ represent the arc length of curves (A, P) and (B, P), respectively.

Proof

Based on Proposition.1, the two endpoints of a line segment are its eccentric points. Therefore, the eccentricity is the maximum value of these two endpoints to the point P (see Fig. 1a).    $\square$

It is important to note that the edges of a graph are not necessarily straight lines; in general, an edge can be a curve. Therefore, $\lambda (A,P)$ and $\lambda (B,P)$ typically represent the geodesic distance from point P to points A and B.

3.2 Branching Point

In a tree, vertices having only one incident edge are the leaves of the tree. We define a branching point as follows:

Definition 1 (Branching point)

A branching point in a tree is a vertex with a degree of more than two.

Consider a tree consisting of a branching point B and k number of leaves.

Proposition 3

The eccentricity of a point P in a tree T containing one branching point B and k leaves is:

$$\begin{aligned} ECC(P) = \max \{ \lambda (A,P) , \lambda (B,P) + D_{max} \} \end{aligned}$$

(5)

where $P \in l=(A,B)$ and $D_{max}$ is the maximum distance of other leaves to the branching point B as follows:

$$\begin{aligned} D_{max}=\{ \max \{ \lambda (B,V_i) \} | \forall i \in k, V_i \ne A \} \end{aligned}$$

(6)

Proof

With only one line segment $l = AB$, the eccentricity is computed based on Proposition 2. When adding another line segment BC that shares an endpoint with l, the eccentricity is computed as $ECC(P)=\max \{ \lambda (A,P), (\lambda (P,B) + \lambda (B,C) \}$. To prove the proposition, we can iteratively connect a branch into the branching point B and keep the maximum distance as the result of the comparison to the previous branch (see Fig. 1b). By doing this, the $\lambda (B,C)$ is substituted with $D_{max}$.    $\square$

Fig. 1.

computing the ECC. (a) a line segment, $ECC(P)=\lambda (A,P)$. (b) a branching point, $ECC(P)=\lambda (P,B)+\lambda (B,C)$.

3.3 Tree

Let $T = (V, E)$ represent a tree comprising leaves and branching points. The attribute of an edge e is its arc-length $\lambda (e)$ where $e=(u,v) \in E$, $u,v \in V$, and $\lambda (e)=\lambda (u,v)$. The eccentricity calculation is performed using a hierarchical structure constructed over the input tree as we call it hierarchical tree. There are two types of movements in the hierarchical tree: inward and outward. The former is considered a bottom-up movement, while the latter is regarded as top-down.

Bottom-Up Movement. In this fashion, in order to compute the eccentricity of vertices, a stack of smaller reduced trees is constructed over the given input tree. Consider the input tree T, which serves as the base of the hierarchy. At each level k of this hierarchy, vertices are categorized into two types: leaf vertices and branching vertices. Let $\mathcal {L}_k$ represent the set of all leaf vertices at level k, and let $\mathcal {B}_k$ represent the set of all branching vertices at the same level. All vertices connected to a given vertex v (the adjacent vertices of v) are identified by $\mathcal {N}_k(v)$ at level k. In order to propagate distances to the upper levels of the hierarchy, an intermediate distance, ID(v), is assigned to each vertex. Initially, all vertices have an intermediate distance of zero, i.e., $ID(v)=0$ for all $v \in V$. A distance value for each branching point $b \in \mathcal {B}_k$ incident to at least one leaf is then calculated as follows:

$$\begin{aligned} D(b)=max\{ \lambda (u,b)+ID(u)|\forall u \in \,\{ \mathcal {N}_k(b) \cap \mathcal {L}_k \} \, \} \end{aligned}$$

(7)

where $\mathcal {N}_k(b) \cap \mathcal {L}_k$ is a set of leaves that are adjacent to the branching point b. Subsequently, the leaves at the base level are contracted, leading to a smaller tree at the higher level, where the leaves of the smaller tree correspond to the branching points from the level below. This procedure is repeated, while the leaves are contracted in a bottom-up approach, ultimately leading us to the top of the hierarchy. At the top of the hierarchy, there is either one single vertex or two vertices. The longest path at the base of the hierarchical tree is the diameter of the tree, dim(T).

Proposition 4

The top of the hierarchical tree consists of a single vertex if and only if the length of the tree’s diameter at the base level is an even number.

Proof

Given that the tree’s diameter is an even number, dim(T) at the base level is expressed as 2k. The process of leaf contraction at each level leads to a subsequent smaller tree $T_1$ at the upper level, where $dim(T_1)$ equals $(2k)-2$. Upon repeated application of this reduction process at subsequent levels, we ultimately reach the apex, characterized by a single vertex where the diameter is equal to zero.

Proposition 5

The top of the hierarchical tree consists of two vertices if and only if the length of the tree’s diameter at the base level is an odd number.    $\square$

Proof

Similar to the previous proof, here $dim(T)=2k+1$ at the base level. Through the contraction of leaves at each level, the resulting smaller tree at the upper level has $dim(T)=(2k+1)-2$. Therefore, repeating this reduction at upper levels leads to a tree with diameter 1 at the top which is a tree consisting of two vertices.

When a single vertex is present at the top, the computed distance value represents that vertex’s eccentricity. However, when there are two vertices, labeled as $v_1$ and $v_2$, each with corresponding computed distance values $D_1$ and $D_2$, the eccentricity for these vertices is calculated as follows:

$$\begin{aligned} \begin{aligned} D_1 > D_2 \Rightarrow ECC(v_1)=max(D_1,D_2+\lambda (v_1,v_2)) \,\,\, and \,\,\,ECC(v_2)=D_1+\lambda (v_1,v_2)\\ D_1 = D_2 \Rightarrow ECC(v_1)=ECC(v_2)= D_1 + \lambda (v_1,v_2) \end{aligned} \end{aligned}$$

(8)

Top-Down Movement. The eccentricities of remaining vertices are iteratively computed in a top-down fashion. The tree at the top is successively expanded through outward movement until it reaches the base of the hierarchy, where each vertex is assigned its corresponding eccentricity value.

Consider a hierarchical tree with a single vertex at the top level $k+1$. Through a bottom-up approach, the eccentricity of the top vertex is determined based on Eq. (7) by taking the maximum value from the sum of intermediate values and the arc lengths of each leaf at level k. Let $v_m$ be the leaf at level k that corresponds to the maximum value. Additionally, let $D^\prime (b)$ be the maximum value of b where $v_m$ is eliminated from its adjacency:

$$\begin{aligned} D^\prime (b)=max\{ \lambda (u,b)+ID(u)|\forall u \in \,\{ \mathcal {N}_k(b) \cap \mathcal {L}_k \backslash v_m \} \, \} \end{aligned}$$

(9)

Employing a top-down approach, the eccentricities of the remaining vertices are iteratively computed. A leaf vertex at level $k+1$, whose eccentricity has already been determined, transmits its eccentricity to the corresponding branching point b at the lower level k. The eccentricity of each leaf $v \in \mathcal {L}_k,\backslash v_m$ at level k is computed as follows:

$$\begin{aligned} ECC(v) = \lambda (v,b)+ECC(b)\,, \,\,\,\, v\in \mathcal {L}_k\,, \,\,\, b \in \mathcal {B}_k \end{aligned}$$

(10)

To calculate the eccentricity of the leaf vertex $v_m$, a comparison is made between the value derived from Eq. (9) and the value of $ECC(b)-\lambda (v,b)$. Subsequently, the eccentricity of the vertex $v_m$ is computed as follows:

$$\begin{aligned} ECC(v_m)= max\{ D^\prime (v_m)+ \lambda (v_m,b)\,,\,ECC(b)-\lambda (v_m,b) \} \forall b \in \,\{ \mathcal {N}_k(b) \cap \mathcal {L}_k \} \end{aligned}$$

(11)

Figure 2a shows an instance of a hierarchical tree featuring three levels and a single vertex at its apex. The bottom-up movement is depicted on the left side, whereas the top-down progression is illustrated on the right. Intermediate distances are visually represented within a box, while the eccentricity of vertices is denoted by a number enclosed in a red circle. In the event that two vertices reside at the top following the computation of their eccentricities, the calculation of the eccentricity for the remaining vertices aligns with the methodology previously described (see Fig. 2b). The specifics of this method are outlined in Algorithm 1.

The algorithm’s complexity is determined by the number of branching points in the tree.

Fig. 2.

Computing the ECC in a hierarchical tree. (a) One vertex and (b) two vertices at the top level.

4 Shape

Calculating the eccentricity of trees can potentially enable us to extend the proposed method for more complex shapes. In a tree, the leaves are recognized as the eccentric points of the structure. However, what constitutes the eccentric points in an arbitrary shape? If we are unable to identify the eccentric points, is it possible to at least estimate them and compute the eccentricity of a shape? To address this question, we propose the following method, which may offer an upper bound for the eccentricity value of a given shape.

4.1 3D Curve of a Shape

The medial axis (MA) of a shape is a collection of center points of all maximally inscribed circles (or spheres in 3D) . These circles touch the shape’s boundary at two or more points, with their centers forming the MA, also known as the topological skeleton. This axis captures connectivity of the shape, providing a compact and informative representation. Conversely, the distance transform assigns a value to each point within the shape, representing the shortest distance from that point to the shape’s boundary.

The proposed method combines the MA and distance transform to effectively reconstruct the original shape. First, the radius of the maximally inscribed circle (or sphere in 3D) is obtained for each point on the MA using distance transform values. Then, these circles (or spheres) grow at each point on the MA, and their union is taken to reconstruct the shape. The reconstructed shape may not be an exact replica of the original, particularly if derived from a noisy or imperfect representation. However, it preserves the shape’s essential topology and connectivity, providing a reasonable approximation.

In this paper, a shape is represented by its MA and corresponding distance transform values, resulting in what we refer to as the 3D curve of the shape. The MA can be sensitive to non-smooth shapes or shapes with small irregularities, noise, or perturbations, which may produce many small branches or spurious structures. As a result, we focus on examining smooth shapes without any holes.

Fig. 3.

Computing the 3D curve of the snake shape.

Figure 3a displays a 2D binary image of a snake. Figure 3b presents the corresponding MA of the snake, while Fig. 3c calculates the shape’s distance transform. Figure 3d depicts the resulting 3D curve of the shape. Finally, Fig. 3e demonstrates how the original shape is reconstructed by combining the MA and the 3D curve.

4.2 Smooth Shapes Without Holes

Computing the eccentricity transform of a smooth shape without knowledge of the eccentric points can be a daunting task. However, by decomposing the shape into its corresponding 3D curve, it may be feasible to directly compute an approximation of the eccentricity.

By projecting the arc length onto the X-axis [13], a straightened version of the 3D curve is computed, resulting in a tree structure. Algorithm 1 computes the ECC of the MA. For the remaining points not on the MA of the shape, each point of the shape computes its corresponding distance to the MA. Afterward, the eccentricity of the resulting point is computed along the MA (geodesic distance) to find the corresponding eccentric point on the MA. Finally, the distance transform of the computed eccentric points is added to the previous distances. However, due to the concavity of a shape, the computed eccentricity using the proposed method is generally an overestimate of the true eccentricity of the original shape. This is because the method computes the geodesic distance along the MA, and the concavity of the shape can lead to the distance being overestimated in some regions [10]. As a result, the computed eccentricity represents an upper-bound for the eccentricity transform of the smooth shape.

5 Simulation and Result

The effectiveness of the proposed method for computing the eccentricity transform was evaluated through a simulation of a snake shape, as depicted in Fig. 4. The medial axis of the shape was first computed, and for each point on the medial axis, its corresponding eccentric point was computed (see Fig. 4a). The color of each point in Fig. 4a corresponds to the value of its corresponding eccentric point. The thickness of the smooth shape was then determined using the distance transform (Fig. 4b). The resulting upper bound of the eccentricity transform is presented in Fig. 4c, while the ground truth was computed and shown in Fig. 4d. Table 1 shows the computational error by comparing the ground truth with the upper bound of the eccentricity.

Table 1. Comparing the ECC of ground truth with the computed upper bound.

Fig. 4.

Computation of the eccentricity transform.

The presented results demonstrate that the proposed method offers a promising approach for achieving more accurate eccentricity computation. Notably, the method is capable of being computed with $\mathcal{O}(b)$ complexity when b is the number of branching points of the tree of the medial axis.

6 Conclusion

This paper introduces an innovative approach for computing the eccentricity transform of a tree. The proposed method achieves $\mathcal{O}(n)$ complexity, where n is the number of branching points. By utilizing the introduced 3D curve representation, the paper extends the method to compute the eccentricity of smooth shapes without holes. This allows for a faster computation of an upper bound for the eccentricity, which is useful in many applications in 2D and 3D shape analysis, such as shape matching, classification, and recognition. The main result of this paper demonstrates that the proposed algorithm provides a reliable estimation of the actual eccentricity, and it closely approximates the ground truth. Moreover, the reduced computational complexity of the proposed approach promises efficient processing of more complex shapes in future work, which is crucial for real-world applications where computational resources and time are limited.