Keywords

1 Introduction

Large Language Models (LLMs) represent the de-facto solution for dealing with complex Natural Language Processing (NLP) tasks such as sentiment analysis [45], question [19], and many others [34]. The ever-increasing popularity of such data-driven approaches is widely caused by their performance improvements against their counterparts. Indeed, Neural Network (NN) based approaches have shown uncanny performance over different NLP tasks such as grammar acceptability of a sentence [43] and text translation [40]. However, following the quest for higher performance, research efforts gave birth to ever more complex NN architectures such as BERT [15], GPT [12], and T5 [35].

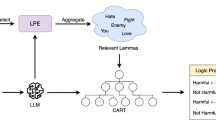
Although being powerful and, empirically, reliable, LLM suffer from a performance vs. transparency trade-off [11, 47]. Indeed, LLM are black-box models, as they rely on the optimisation of their numerical sub-symbolical components, which are mostly unreadable by humans. The black-box nature of LLMs hinder their applicability to some scenarios where transparency represents a fundamental requirement, e.g., NLP for medical analysis [29, 39], etc. Therefore, there exists the need to identify relevant mechanisms capable of opening such LLM black-boxes and diagnose their reasoning process, and presenting it in a human-understandable fashion. Towards this aim, a few different explainability approaches, focusing mostly on Local Post-hoc explainer (LPE) mechanisms, have been recently proposed. An LPE represents a popular solution to explain the reasoning process by highlighting how different portions of the input sample impact differently the produced output, by assigning a relevance score to each input component. These approaches apply to single instances of input sample, thus being local, and to optimised LLM—thus being post-hoc.

Despite a broad variety of LPE approaches, the state of the art lacks a fair comparison among them. A common trend for proposals of novel explanation mechanisms is to highlight its advantages through a set of tailored experiments. This hinders comparison fairness, making it very difficult to identify the best approach for obtaining explanations of NLP models or even to know if such a best approach exists. This is why we present a framework for comparing several well-known LPE mechanisms for text classification in NLP. Aiming at obtaining comparison fairness, we rely on aggregating the local explanations obtained by each local post-hoc explainer into a set of global impact scores. Such scores identify the set of concepts that best describe the underlying NLP model from the perspective of each LPE. These concepts, along with their aggregated impact scores, are then compared for each LPE against other LPE counterparts. The comparison between the aggregated global impact scores rather than the single explanations is justified by the locality of LPE approaches. Indeed, it is reasonable for local explanations of different LPEs to differ somehow, depending on the approach design, therefore making it complex to compare the quality of two LPEs over the same sample. However, it is also expected for the aggregated global impacts to be aligned between different LPE as they are applied to the same NN, which leverages the same set of relevant concepts for its inference. Therefore, when comparing the aggregated impact scores of different LPE, we expect them to be correlated—at least up to a certain extent.

We perform our comparison between LPE explanations across the social domains available in the Moral Foundation Twitter Corpus (MFTC) [20]. MFTC represents an example of a challenging task, as it is proposed to tackle moral values classification. Moral values are inherently subjective to human readers, therefore introducing possible disagreement inside annotations and making the overall optimisation pipeline sensitive to small changes. Moreover, identifying moral values represents a sensitive task, as it requires a deep and safe understanding of complex concepts such as harm and fairness. Consequently, we believe MFTC to represent a suitable option for analysing the behaviour of LPEs over different scenarios. Moreover, relying on MFTC enables a comparison between extracted relevant concepts and a set of humanly tailored impact scores, namely Moral Foundations Dictionary (MFD) [21]. Therefore, allowing us to study the extent of correlation between LPE-extracted concepts and humanly salient concepts. Surprisingly, our experiments show how there are setups where the explanations of different LPEs are far from being correlated, highlighting how explanation quality is highly dependent on the chosen eXplainable Artificial Intelligence (xAI) approach and the respective scenario at hand. There are huge discrepancies in the results of different state-of-the-art local explainers, each of which identifies a set of relevant concepts that largely differs from the others—at least in terms of relative impact scores. Therefore, we stress the need for identifying a robust approach to compare the quality of explanations and the approaches for their extraction. Moreover, the comparison between the distribution of LPEs’ impact scores and the set of human-tailored impact scores shows how there exists almost always no correlation between salient concepts extracted from the NN model and concepts relevant for humans. The obtained results highlight the fragility of xAI approaches for NLP, caused mainly by the complexity of large NN models, their inclination to the extreme fitting of data—with no regard for concept meaning—and the lack of sound techniques for comparing xAI mechanisms.

2 Background

2.1 Explanation Mechanisms in NLP

The set of explanations extraction mechanisms available in the xAI community are often categorized along two main aspects [2, 17]: (i) local against global explanations, and (ii) self-explaining against post-hoc approaches. In the former context, local identifies the set of explainability approaches that given a single input, i.e., sample or sentence, produce an explanation of the reasoning process followed by the NN model to output its prediction for the given input [32]. In contrast, global explanations aim at expressing the reasoning process of the NN model as a whole [18, 22]. Given the complexity of the NN models leveraged for tackling most NLP tasks, it is worth noticing how there is a significant lack of global explainability systems, whereas a variety of local xAI approaches are available [31, 37].

About the latter aspect, we define post-hoc as those set of explainability approaches which apply to an already optimized black-box model for which it is required to obtain some sort of insight [33]. Therefore, a post-hoc approach requires additional operations to be performed after that the model outputs its predictions [14]. Conversely, inherently explainable, i.e., self-explaining, mechanisms aim at building a predictor having a transparent reasoning process by design, e.g., CART [30]. Therefore, a self-explaining approach can be seen as generating the explanation along with its prediction, using the information emitted by the model as a result of the process of making that prediction [14].

In this paper, we focus on local post-hoc explanation approaches applied to NLP. Here, it represents a popular solution to explain the reasoning process by highlighting how different portions, i.e., words, of the input sample impact differently the produced output, by assigning a relevance score to each input component. The relevance score is then highlighted using some saliency map to ease the visualisation of the obtained explanation. Therefore, it is also common for local post-hoc explanations to be referred to as saliency approaches, as they aim at highlighting salient components.

2.2 Moral Foundation Twitter Corpus Dataset

In our experiments, we select the MFTC dataset as the target classification task. The MFTC dataset is composed of 35,108 tweets – sentences –, which can be considered as a collection of seven different datasets. Each split of MFTC corresponds to a different context. Here, tweets corresponding to the dataset samples are collected following a certain event or target. As an example, tweets belonging to the Black Lives Matter (BLM) split were collected during the period of Black Lives Matter protests in the US. The list of all MFTC subjects is the following: (i) All Lives Matter (ALM), (ii) BLM, (iii) Baltimore protests (BLT), (iv) hate speech and offensive language (DAV), (v) presidential election (ELE), (vi) MeToo movement (MT), (vii) hurricane Sandy (SND). In our experiments we also considered training and testing the NN model over the totality of MFTC tweets. This was done to analyse the LPEs behaviour over an unbiased task, as the average morality of each MFTC split is influenced by the corresponding collection event.

Each tweet in MFTC is labelled, following the same moral theory, with one or more of the following 11 moral values: (i) care/harm, (ii) fairness/cheating, (iii) loyalty/betrayal, (iv) authority/subversion, (v) purity/degradation, (vi) non-moral. Ten of the 11 available moral values are obtained as a moral concept and its opposite expression—e.g., fairness refers to the act of supporting fairness and equality, while cheating refers to the act of refraining from cheating or exploiting others. Given morality subjectivity, each tweet is labelled by multiple annotators, and the final moral labels are obtained via majority voting.

Finally, similar to previous works [28, 36], we preprocess the tweets before using them as input samples for our LLM training. We preprocess the tweets by removing URLs, emails, usernames and mentions, as well as correcting common spelling mistakes and converting emojis to their respective lemmas using the Ekphrasis packageFootnote 1 and the Python Emoji packageFootnote 2, respectively.

3 Methodology

In this section, we present our methodology for comparing LPE mechanisms. We first propose an overview of the proposed approach in Sect. 3.1. Subsequently, the set of LPE mechanisms adopted in our experiments are presented in Sect. 3.2, and the aggregation approaches leveraged to obtain global impact scores from LPE outputs are described in Sect. 3.3. Finally, in Sect. 3.4 we present the metrics used to identify the correlation between LPEs.

3.1 Overview

Given the complexity of measuring different LPE approaches over single local explanations, we here consider measuring how much LPEs correlate with each other over a set of fixed samples. The underlying assumption of our framework is that various LPE techniques aim at explaining the same NN model used for prediction. Therefore, while explanations may differ over local samples, it is reasonable to assume that reliable LPEs when applied over a vast set of samples—sentences or set of sentences—should converge to similar (correlated) results. Indeed, the underlying LLM considers being relevant for its inference always the same set of concepts—lemmas. A lack of correlation between different LPE mechanisms would hint that there exists a conflict between the set of concepts that each explanation mechanisms consider as relevant for the LLM, thus making at least one, if not all, of the explanations unreliable.

Being interested in analysing the correlation between a set of LPEs over the same pool of samples, we first define \(\epsilon _{NN}\) as a LPE technique applied to a NN model at hand. Being local, \(\epsilon _{NN}\) is applied to the single input sample \(\textbf{x}_{i}\), producing as output one impact score for each component (token) of the input sample \(l_{k}\). Throughout the remainder of the paper, we consider \(l_{k}\) to be the lemmas corresponding to the input components. Mathematically, we define the output impact score for a single token or its corresponding lemma as \(j \left( l_{k}, \epsilon _{NN} (\textbf{x}_{i}) \right) \). Depending on the given \(\epsilon _{NN}\), the corresponding impact score j may be associated with a single label – i.e., moral value –, making j a scalar value, or with a set of labels, making j a vector—one scalar value for each label. To enable comparing different LPE, we define the aggregated impact scores of a LPE mechanism over a NN model and a set of samples \(\mathcal {S}\) as \(\epsilon _{NN}(\mathcal {S})\). In our framework we obtain \(\epsilon _{NN}(\mathcal {S})\) aggregating \(\epsilon _{NN}(\textbf{x}_{i}) \text { for each } \textbf{x}_{i} \in \mathcal {S}\) using an aggregation operation \(\mathcal {A}\), mathematically:

$$\begin{aligned} \epsilon _{NN}\left( \mathcal {S}\right) = \mathcal {A} \left( \left\{ \epsilon _{NN}(\textbf{x}_{i}) \textit{ for each } \textbf{x}_{i} \in \mathcal {S} \right\} \right) . \end{aligned}$$
(1)

Defining a correlation metric \(\mathcal {C}\), we obtain from Eq. (1) the following for describing the correlation between two LPE techniques:

$$\begin{aligned} \begin{aligned} \mathcal {C} \left( \epsilon _{NN}\left( \mathcal {S}\right) , \epsilon '_{NN}\left( \mathcal {S}\right) \right) = \mathcal {C} \big (&\mathcal {A} \left( \left\{ \epsilon _{NN}(\textbf{x}_{i}) \textit{ for each } \textbf{x}_{i} \in \mathcal {S} \right\} \right) , \\&\mathcal {A} \left( \left\{ \epsilon '_{NN}(\textbf{x}_{i}) \textit{ for each } \textbf{x}_{i} \in \mathcal {S} \right\} \right) \big ) \end{aligned} \end{aligned}$$
(2)

where \(\epsilon _{NN}\) and \(\epsilon '_{NN}\) are two LPE techniques applied to the same NN model.

3.2 Local Post-hoc Explanations

In our framework, we consider seven different LPE approaches for extracting local explanations \(j \left( l_{k}, \epsilon _{NN} (\textbf{x}_{i}) \right) \) from an input sentence \(\textbf{x}_{i}\) and the trained LLM—identified as NN. The seven LPEs are selected in order to represent as faithfully as possible the state-of-the-art of xAI approaches in NLP. Subsequently, we briefly describe each of the seven selected LPE. However, a detailed analysis of these LPEs is out of the scope of this paper and we refer interested readers to [14, 32, 38].

Gradient Sensitivity Analysis. The Gradient Sensitivity analysis (GS) probably represents the simplest approach for assigning relevance scores to input components. GS relies on computing gradients over inputs components as \(\dfrac{\delta f_{c}(\textbf{x}_{i})}{\delta \textbf{x}_{i,k}}\), which represents the derivative of the output with respect to the the \(k^{th}\) component of \(\textbf{x}_{i}\). Following this approach local impact scores of an input component can be thus defined as:

$$\begin{aligned} j \left( l_{k}, \epsilon _{NN} (\textbf{x}_{i}) \right) = \dfrac{\delta f_{\tau _{m}}(\textbf{x}_{i})}{\delta \textbf{x}_{i,k}}, \end{aligned}$$
(3)

where \(f_{\tau _{m}}(\textbf{x}_{i})\) represents the predicted probability distribution of an input sequence \(\textbf{x}_{i}\) over a target class \(\tau _{m}\). While simple, GS has been shown to be an effective approach for understanding approximate input components relevance. However, this approach suffers from a variety of drawbacks, mainly linked with its inability to define negative contributions of input components for a specific prediction—i.e., negative impact scores.

Gradient \(\times \) Input Aiming at addressing few of the limitations affecting GS, the Gradient \(\times \) Input (GI) approach defines the relevance scores assignment as GS multiplied – element-wise – with \(\textbf{x}_{i,k}\) [25]. Therefore, mathematically speaking, GI impact scores are defined as:

$$\begin{aligned} j \left( l_{k}, \epsilon _{NN} (\textbf{x}_{i}) \right) = \textbf{x}_{i,k} \cdot \dfrac{\delta f_{\tau _{m}}(\textbf{x}_{i})}{\delta \textbf{x}_{i,k}}, \end{aligned}$$
(4)

where notation follows the one of Eq. (3). Being very similar to GS, GI inherits most of its limitations.

Layer-Wise Relevance Propagation. Building on top of gradient-based relevance scores mechanisms – such as GS and GI –, Layer-wise Relevance Propagation (LRP) proposes a novel mechanism relying on conservation of relevance scores across the layers of the NN at hand. Indeed, LRP relies on the following assumptions: (i) NN can be decomposed into several layers of computation; (ii) there exists a relevance score \(R_{d}^{(l)}\) for each dimension \(\textbf{z}_{d}^{(l)}\) of the vector \(\textbf{z}^{(l)}\) obtained as the output of the \(l^{th}\) layer of the NN; and (iii) the total relevance scores across dimensions should propagate through all layers of the NN model, mathematically:

$$\begin{aligned} f(\textbf{x}) = \sum _{d \in L}R_{d}^{(L)} = \sum _{d \in L-1}R_{d}^{(L-1)} = \dots = \sum _{d \in 1}R_{d}^{(1)}, \end{aligned}$$
(5)

where, \(f(\textbf{x})\) represents the predicted probability distribution of an input sequence \(\textbf{x}\), and L the number of layers of the NN at hand. Moreover, LRP defines a propagation rule for obtaining \(R_{d}^{(l)}\) from \(R^{(l+1)}\). However, the derivation of such propagation rule is out of the scope of this paper and thus we refer interested readers to [8, 10]. In our experiments, we consider as impact scores the relevance scores of the input layer, namely \(j \left( l_{k}, \epsilon _{NN} (\textbf{x}_{i}) \right) = R_{d}^{(1)}\).

Layer-Wise Attention Tracing. Since LLMs rely heavily on self-attention mechanisms [42], recent efforts propose to identify input components relevance scores analysing solely the relevance scores of attentions heads of LLM models, introducing Layer-wise Attention Tracing (LAT) [1, 44]. Building on top of LRP, LAT propose to redistribute the inner relevance scores \(R^{(l)}\) across dimensions using solely self-attention weights. Therefore, LAT defines a custom redistribution rule as:

$$\begin{aligned} R_{i}^{(l)} = \sum _{\textit{k s.t. i is input for neuron k}} \sum _{h} \textbf{a}^{(h)} R_{k, h}^{(l+1)}, \end{aligned}$$
(6)

where, h corresponds to the attention head index, while \(\textbf{a}^{(h)}\) are the corresponding learnt weights of the attention head. Similarly to LRP, we here consider as impact scores the relevance scores of the input layer, namely \(j \left( l_{k}, \epsilon _{NN} (\textbf{x}_{i}) \right) = R^{(1)}\).

Integrated Gradient. Motivated by the shortcomings of previously proposed gradient-based relevance score attribution mechanisms – such as GS and GI –, Sundararajan et al. [41] propose a novel Integrated Gradient approach. The proposed approach aims at explaining the input sample components relevance by integrating the gradient along some trajectory of the input space, which links some baseline value \(\textbf{x}'_{i}\) to the sample under examination \(\textbf{x}_{i}\). Therefore, the relevance score of the input \(k^{th}\) component of the input sample \(\textbf{x}_{i}\) is obtained following

$$\begin{aligned} j \left( l_{k}, \epsilon _{NN} (\textbf{x}_{i}) \right) = \left( \textbf{x}_{i,k} - \textbf{x}'_{i,k}\right) \cdot \int _{a=0}^{1} \dfrac{\delta f(\textbf{x}'_{i} + t \cdot (\textbf{x}_{i} - \textbf{x}'_{i}))}{\delta \textbf{x}_{i,k}} \, dt, \end{aligned}$$
(7)

where \(\textbf{x}_{i,k}\) represents the \(k^{th}\) component of the input sample \(\textbf{x}_{i}\). By integrating the gradient along an input space trajectory, the authors aim at addressing the locality issue of gradient information. In our experiments we refer to the Integrated Gradient approach as HESS, as for its implementation we rely on the integrated hessian library available for hugging face modelsFootnote 3.

SHAP. SHapley Additive exPlanations (SHAP) relies on Shapley values to identify the contribution of each component of the input sample toward the final prediction distribution. The Shapley value concept derives from game theory, where it represents a solution for a cooperative game, found assigning a distribution of a total surplus generated by the players coalition. SHAP computes the impact of an input component as its marginal contribution toward a label \(\tau _{m}\), computed deleting the component from the input and evaluating the output discrepancy. Firstly defined for explaining simple NN models [31], in our experiments we leverage the extension of SHAP supporting transformer models such as BERT [26], available in the SHAP python libraryFootnote 4.

LIME. Similarly to SHAP, Local Interpretable Model-agnostic Explanations (LIME) relies on input sample perturbation to identify its relevant components. Here, the predictions of the NN at hand are explained via learning an explainable surrogate model [37]. More in detail, to obtain its explanations LIME constructs a set of samples from the perturbation of the input observation under examination. The constructed samples are considered to be close to the observation to be explained from a geometric perspective, thus considering small perturbation of the input. The explainable surrogate model is then trained over the constructed set of samples, obtaining the corresponding local explanation. Given an input sentence, we here consider obtaining its perturbed version via words – or tokens – removal and words substitution. In our experiments, we rely on the already available LIME python libraryFootnote 5.

3.3 Aggregating Local Explanations

Once local explanations of the NN model are obtained for each input sentence – i.e., tweet –, we aggregate them to obtain a global list of concept impact scores. Before aggregating the local impact scores, we convert the words composing local explanations into their corresponding lemmas – i.e., concepts – to avoid issues when aggregating different words expressing the same concept—e.g., hate and hateful. As there exists no bullet-proof solution for aggregating different impact scores, we adopt four different approaches in our experiments, namely:

  • Sum. A simple summation operation is leveraged to obtain the aggregated score for each lemma. While simple this aggregation approach is effective when dealing with additive impact scores such as SHAP values. However, it suffers from lemma frequency issues, as it tends to overestimate frequent lemmas having average low impact scores. Global impact scores are here defined as \(J(l_{k}, \epsilon _{NN}) = \sum _{i=1}^{N} j \left( l_{k} , \epsilon _{NN} \left( \textbf{x}_{i}\right) \right) \). Therefore, we here define \(\mathcal {A}\) as

    $$\begin{aligned} \mathcal {A} \left( \left\{ \epsilon _{NN}(\textbf{x}_{i}) \textit{ for each } \textbf{x}_{i} \in \mathcal {S} \right\} \right) = \left\{ \sum _{i=1}^{N} j \left( l_{k} , \epsilon _{NN} \left( \textbf{x}_{i}\right) \right) \textit{ for each } l_{k} \in \mathcal {S} \right\} . \end{aligned}$$
    (8)

  • Absolute sum. We here consider summing the absolute values of the local impact scores – rather than their true values – to increase the awareness of global impact scores towards lemmas having both high positive and high negative impact over some sentences. Mathematically, we obtain aggregated scores as \(J(l_{k}, \epsilon _{NN}) = \sum _{i=1}^{N} \vert j \left( l_{k} , \epsilon _{NN} \left( \textbf{x}_{i}\right) \right) \vert \).

    $$\begin{aligned} \mathcal {A} \left( \left\{ \epsilon _{NN}(\textbf{x}_{i}) \textit{ for each } \textbf{x}_{i} \in \mathcal {S} \right\} \right) = \left\{ \sum _{i=1}^{N} \vert j \left( l_{k} , \epsilon _{NN} \left( \textbf{x}_{i}\right) \right) \vert \textit{ for each } l_{k} \in \mathcal {S} \right\} . \end{aligned}$$
    (9)

  • Average. Similar to the sum operation, we here consider obtaining aggregated scores averaging local impact scores, thus avoiding possible overshooting issues arising when dealing with very frequent lemmas. Mathematically, we define \(J(l_{k}, \epsilon _{NN}) = \frac{1}{N} \cdot \sum _{i=1}^{N} j \left( l_{k} , \epsilon _{NN} \left( \textbf{x}_{i}\right) \right) \).

    $$\begin{aligned} \mathcal {A} \left( \left\{ \epsilon _{NN}(\textbf{x}_{i}) \textit{ for each } \textbf{x}_{i} \in \mathcal {S} \right\} \right) = \left\{ \frac{1}{N} \cdot \sum _{i=1}^{N} j \left( l_{k} , \epsilon _{NN} \left( \textbf{x}_{i}\right) \right) \textit{ for each } l_{k} \in \mathcal {S} \right\} . \end{aligned}$$
    (10)

  • Absolute average. Similarly to absolute sum, we here consider to average absolute values of local impact scores for better-managing lemmas having a skewed impact as well as tackling frequency issues. Global impact scores are here defined as \(J(l_{k}, \epsilon _{NN}) = \frac{1}{N} \cdot \sum _{i=1}^{N} \vert j \left( l_{k} , \epsilon _{NN} \left( \textbf{x}_{i}\right) \right) \vert \).

    $$\begin{aligned} \mathcal {A} \left( \left\{ \epsilon _{NN}(\textbf{x}_{i}) \textit{ for each } \textbf{x}_{i} \in \mathcal {S} \right\} \right) = \left\{ \frac{1}{N} \cdot \sum _{i=1}^{N} \vert j \left( l_{k} , \epsilon _{NN} \left( \textbf{x}_{i}\right) \right) \vert \textit{ for each } l_{k} \in \mathcal {S} \right\} . \end{aligned}$$
    (11)

Being aware that the selection of the aggregation mechanism may influence the correlation between different LPEs, in our experiments we analyse LPEs correlation over the same aggregation scheme. Moreover, we also consider analysing how aggregation impacts the impact scores correlation over the same LPE, highlighting how leveraging the absolute value of impact score is highly similar to adopting its true value—see Sect. 4.3.

3.4 Comparing Explanations

Each aggregated global explanation J depends on a corresponding label \(\tau _{m}\) – i.e., moral value – since LPEs produce either a scalar impact value for a single \(\tau _{m}\) or a vector of impact scores for each \(\tau _{m}\). Therefore, recalling Sect. 4.3, we can define the set of aggregated global scores depending on the label they refer to as following:

$$\begin{aligned} \mathcal {J}_{\tau _{m}} \left( \epsilon _{NN}, \mathcal {S}\right) = \left\{ J \left( l_{k}, \epsilon _{NN} \right) \vert \tau _{m} \textit{ for each } l_{k} \in \mathcal {S} \right\} . \end{aligned}$$
(12)

\(\mathcal {J}_{\tau _{m}} \left( \epsilon _{NN}, \mathcal {S}\right) \) represents a distribution of impact scores over the set of lemmas – i.e., concepts – available in the samples set for a specific label. To compare the distributions of impact scores extracted using two LPEs – i.e., \(\mathcal {J}_{\tau _{m}} \left( \epsilon _{NN}, \mathcal {S}\right) \) and \(\mathcal {J}_{\tau _{m}} \left( \epsilon '_{NN}, \mathcal {S}\right) \) – we use Pearson correlation, which is defined as the ratio between the covariance of two variables and the product of their standard deviations, and it measures their level of linear correlation. The selected correlation metric is applied to the normalised impact scores. Indeed, different LPEs produce impact scores which may differ relevantly in terms of their magnitude. Normalising the impact scores, we map impact scores to a fixed interval, allowing for a direct comparison of \(\mathcal {J}_{\tau _{m}}\) over different \(\epsilon _{NN}\). Mathematically, we refer to the normalised global impact scores as \(\Vert \mathcal {J}_{\tau _{m}} \Vert \). Therefore, we define the correlation score between two sets of global impact scores for a single label as:

$$\begin{aligned} \begin{aligned} \rho \left( \Vert \mathcal {J}_{\tau _{m}} \left( \epsilon _{NN}, \mathcal {S}\right) \Vert , \Vert \mathcal {J}_{\tau _{m}} \left( \epsilon '_{NN}, \mathcal {S}\right) \Vert \right) = \rho \big (&\Vert \left\{ J \left( l_{k}, \epsilon _{NN} \right) \vert \tau _{m} \textit{ for each } l_{k} \in \mathcal {S} \right\} \Vert , \\&\Vert \left\{ J \left( l_{k}, \epsilon _{NN} \right) \vert \tau _{m} \textit{ for each } l_{k} \in \mathcal {S} \right\} \Vert \big ) \end{aligned} \end{aligned}$$
(13)

where \(\rho \) refers to the Pearson correlation used to compare couples of \(\mathcal {J}_{\tau _{m}} \left( \epsilon _{NN}, \mathcal {S}\right) \). Throughout our analysis we experimented with similar correlation metrics, such as Spearman correlation and simple vector distance – similarly to [27] –, obtaining similar results. Therefore, to avoid redundancy we here show only the Pearson correlation results. Throughout our experiments, we consider a simple min-max normalisation process, scaling the scores to the range \(\left[ 0,1\right] \).

As our aim is to obtain a measure of similarity between LPEs applied over the same set of samples, we can average the correlation scores \(\rho \) obtained for each label \(\tau _{m}\) over the set of labels \(\mathcal {T}\). Therefore, we mathematically define the correlation score of two LPEs, putting together Eqs. (2), (12) and (13) as:

$$\begin{aligned} \mathcal {C} \left( \epsilon _{NN}\left( \mathcal {S}\right) , \epsilon '_{NN}\left( \mathcal {S}\right) \right) = \frac{1}{M} \cdot \sum _{m=1}^{M} \rho \left( \Vert \mathcal {J}_{\tau _{m}} \left( \epsilon _{NN}, \mathcal {S}\right) \Vert , \Vert \mathcal {J}_{\tau _{m}} \left( \epsilon '_{NN}, \mathcal {S}\right) \Vert \right) \end{aligned}$$
(14)

where M is the total number of labels, i.e., moral principles, belonging to \(\mathcal {T}\).

4 Experiments

In this section, we present the setup and results of our experiments. We present the model training details and its obtained performance in Sect. 4.1. We then focus on the comparison between the available LPEs, showing the correlation between their explanations in Sect. 4.2. Section 4.3 analyses how correlation scores are affected by the selected aggregation mechanism \(\mathcal {A}\). Finally, in Sect. 4.4 we analyse the extent to which LPEs explanations are aligned with human notions of moral values.

4.1 Model Training

We follow state-of-the-art approaches for dealing with morality classification task [9, 24]. Thus, we treat the morality classification problem as a multi-class multi-label classification task, leveraging BERT as the LLM to be optimised [15]. We define one NN model for each MFTC split and optimise its parameters over the 70% of tweets, leaving the remaining 30% for testing purposes. However, conversely from recent approaches, we here do not rely on the sequential training paradigm, but rather train each model solely on the MFTC split at hand. Indeed, in our experiments, we do not aim at obtaining strong transferability between domains, but rather we focus on analysing LPEs behaviour.

We leverage the pre-trained bert-base-uncased model – available in the Hugging Face python libraryFootnote 6 – as the starting point of our training process. Each model is trained for 3 epochs using a standard binary cross entropy loss [46], a learning rate of \(5 \times 10^{-5}\), a batch size of 16 and a maximum sequence length of 64. We keep track of the macro F1-score for each model to identify its performance over the test samples. Table 1 shows the performance of the trained BERT model.

Table 1. BERT performance over MFTC datasets.
Full size table

4.2 Are Local Post-hoc Explainers Aligned?

We analyse the extent to which different LPEs are aligned in their process of identifying impactful concepts for the underlying NN model. With this aim, we train a BERT model over a specific dataset (following the approach described in Sect. 4.1) and compute the pairwise correlation \(\mathcal {C} \left( \epsilon _{NN}\left( \mathcal {S}\right) , \epsilon '_{NN}\left( \mathcal {S}\right) \right) \) (as described in Sect. 3) for each pair of LPE in the selected set. To avoid issues caused by model overfitting over the training set, which would render explanations unreliable, we apply each \(\epsilon _{NN}\) over the test set of the selected dataset.

Using the pairwise correlation values we construct the correlation matrices shown in Figs. 1 and 2, which highlight how there exist a very weak correlation score between most LPEs over different datasets. Here, it is interesting to notice how, there exists few specific couples or clusters of LPE which highly correlate with each other. For example, GS, GI and LRP show moderate to high correlation score, mainly due to their reliance on computing the gradient of the prediction to identify impactful concepts. However, this is not the case for all LPE couples relying on similar approaches. For example, GI and gradient integration – HESS in the matrices – show little to no correlation, although they both are gradient-based approach for producing local explanations. Similarly, SHAP and LIME show no correlation even if they both rely on input perturbation and are considered the state-of-the-art.

Fig. 1.
figure 1

\(\mathcal {C} \left( \epsilon _{NN}\left( \mathcal {S}\right) , \epsilon '_{NN}\left( \mathcal {S}\right) \right) \) using average aggregation (left) and absolute average aggregation (right) as \(\mathcal {A}\) over the BLM dataset.

Full size image
Fig. 2.
figure 2

\(\mathcal {C} \left( \epsilon _{NN}\left( \mathcal {S}\right) , \epsilon '_{NN}\left( \mathcal {S}\right) \right) \) using average aggregation (left) and absolute average aggregation (right) as \(\mathcal {A}\) over the ELE dataset.

Full size image

Figures 1 and 2 highlight how the vast majority of LPE pairs show very small to no correlation at all, exposing how there exists a disagreement between the selected approaches. This finding represents a fundamental result of our study, as it highlights how there is no accordance between LPE even when they are applied to the same model and dataset. The reason behind such large discrepancies among LPE might be various, but mostly bear down to the following:

  • Few of the LPE considered in the literature do not represent reliable solutions for identifying the reasoning principles of LLMs.

  • Each of the uncorrelated LPEs highlight a different set or subset of reasoning principles of the underlying model.

Therefore, our results show how it is also complex to identify a set of fair and reliable metrics to spot the best LPE or even reliable LPEs, as they seem to gather uncorrelated explanations. Similar results to the ones shown in Figs. 1 and 2 are obtained for all dataset splits and are made available at https://tinyurl.com/QU4RR3L.

4.3 How Does Impact Scores Aggregation Affect Correlation?

Since our LPE correlation metric is dependent on \(\mathcal {A}\), we here analyse how the selection of different aggregation strategies impacts the correlation between LPEs. To understand the impact of \(\mathcal {A}\) on \(\mathcal {C}\), we plot the correlation matrices for a single dataset, varying the aggregation approach, thus obtaining the four correlation matrices shown in Fig. 3.

Fig. 3.
figure 3

\(\mathcal {C} \left( \epsilon _{NN}\left( \mathcal {S}\right) , \epsilon '_{NN}\left( \mathcal {S}\right) \right) \) using different aggregations over the ALM dataset.

Full size image

From Figs. 3c and 3d it is possible to notice how there exists a strong correlation between different LPEs. This results seems to be in contrast with the results found in Sect. 4.2. However, the reason behind the strong correlation achieved when relying on summation aggregation is not caused by the actual correlation between explanations, but rather on the susceptibility of summation to tokens frequency. Indeed, since the summation aggregation approaches do not take into account the occurrence frequency of lemmas in \(\mathcal {S}\), they tend to overestimate the relevance of popular concepts. Intuitively, using this aggregations, a rather impactless lemma appearing 5000 times would obtain a global impact higher than a very impactful lemma appearing only 10 times. These results highlight the importance of relying on average based aggregation approaches when considering to construct global explanations from the LPE outputs.

Figure 3 also highlights how leveraging the absolute value of LPEs incurs in higher correlation scores. The reason behind such a phenomenon is to be found in the impact scores distributions. Indeed, while true local impact scores are distributed over the set of real numbers \(\mathbb {R}\), computing the absolute value of local impacts j shifts their distribution to \(\mathbb {R}^{+}\), shrinking possible differences between positive and negative scores. Moreover, it is also true that LPE outputs rely much more heavily on scoring positive contributions using positive impact scores, and tends to give less focus to negative impact scores. Therefore, it is generally true that the output of LPEs is unbalanced towards positive impact scores, making negative impact scores mostly negligible.

4.4 Are Local Post-hoc Explainers Aligned with Human Values?

As our experiments show the huge variability in the response by available state-of-the-art LPE approaches, we check whether there exists at least one LPE that is aligned with human interpretation of values. To do so, we compare the set of global impact scores \(\mathcal {J}\) extracted by each LPE against two sets of lemmas which are considered to be relevant for humans. The set of humanly-relevant lemmas, along with their impact scores are obtained from the MFD and the extended Moral Foundations Dictionary (eMFD). The MFD is a dictionary of relevant lemmas for the set of moral values belonging to MFTC. Such a dictionary is generated manually by picking relevant words from a large list of words for each foundation value [21]. Meanwhile, eMFD represents an extension of MFD constructed from text annotations generated by a large sample of human coders.

Similar to the comparison of Sect. 4.2, we rely on Pearson correlation, measuring the correlation coefficient \(\mathcal {C}\) between each LPE and MFD or eMFD, treating MFD as if it was a distribution of relevant concepts. Figure 4 shows the results for our study over the BLT dataset for different aggregation mechanisms.

Fig. 4.
figure 4

\(\mathcal {C} \left( \epsilon _{NN}\left( \mathcal {S}\right) , \textit{MFD}\right) \) using different aggregations over the BLT dataset.

Full size image

Alarmingly, the results show how there exists no positive correlation between any of the LPE approaches and both MFD and eMFD. Although it is possible that the trained model learns relevant concepts that are specific to the target domain – i.e., BLT in Fig. 4 – it is concerning how strongly uncorrelated LPE and human interpretation of values are. Indeed, while BERT may focus on a few specific concepts which are not human-like, it is assumed and proven to be effective in learning human-like concepts over the majority of NLP tasks. Especially if we consider our BERT model to be only fine-tuned on the target domain, it is very unreasonable to assume these results to be caused by BERT learning concepts that are not aligned with human values. Rather, it is fairly reasonable to deduce that the considered LPEs are far from being completely aligned to the real reasoning process of the underlying BERT model, thus incurring in such high discrepancy with human-labeled moral values.

5 Conclusion and Future Work

We propose a new approach for the comparison among state-of-the-art local post-hoc explanation mechanisms, aiming at identifying the extent to which their extracted explanations correlate. We rely on a novel framework for extracting and comparing global impact scores from local explanations obtained from LPEs, and apply such a framework over the MFTC dataset. Our experiments show how most LPEs explanations are far from being mutually correlated when LPEs are applied over a large set of input samples. These results highlight what we called the “quarrel” among state-of-the-art local explainers, apparently caused by each of them focusing on a different set or subset of relevant concepts, or imposing a different distribution on top of them. Further, we compare the impact scores distribution obtained from each LPEs with a set of human-made dictionaries. Our experiments alarmingly show how there exists no correlation between LPE outputs and the concepts considered to be salient by humans. Therefore, our experiments highlight the current fragility of xAI approaches for NLP.

Our proposal is a solid starting point for the exploration of the reliability and soundness of xAI approaches in NLP. In our future work, we aim at investigating more in-depth the issue of robustness of LPE approaches, adding novel LPEs to our comparison such as [16], and aiming at identifying if it is possible to rely on them to build a surrogate of the model from a global perspective. Moreover, we also consider as a promising research line the possibility of building on top of LPE approaches so as to obtain reliable global explanations of the underlying NN model. Finally, in the future we aim at extending the in-depth analysis of LPEs to domains different from NLP, such as computer vision [4, 5, 13], graph processing [6, 23], and neuro-symbolic approaches [3, 7].