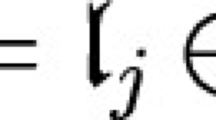Homogeneous Hypersurfaces in Symmetric Spaces

Abstract

A hypersurface of a Riemannian manifold is called homogeneous if it is an orbit of an isometric action on the ambient manifold. Homogeneous hypersurfaces have remarkable geometric properties, providing the simplest examples of hypersurfaces with constant mean curvature. Thus, they are crucial for the investigation of more general types of submanifolds in ambient spaces with large isometry groups.

In this survey article, we present an introduction to some of the basic geometric, topological, and algebraic features of homogeneous hypersurfaces, describing what is known about their classification problem in symmetric spaces and explaining the main tools needed for their study in the context of symmetric spaces of noncompact type.

1 Introduction

Minimal, and more generally, constant mean curvature hypersurfaces play a fundamental role in Riemannian submanifold geometry. As solutions to variational problems involving areas and volumes, they arise naturally in various contexts such as physics, biology, or optimal design. Their mathematical investigation has a long history and constitutes one of the most important trends in current research in geometric analysis. Some fundamental techniques in their study, such as the use of barriers, the maximum principle, or the bifurcation results, are based on the good knowledge that we have of certain examples of hypersurfaces with constant mean curvature and with a high degree of symmetry (hyperplanes, spheres, cylinders, catenoids, horospheres, etc.). Thus, one of the first natural steps in the investigation of submanifolds of a given Riemannian space is to determine some classes of constant mean curvature hypersurfaces that are invariant under a large group of isometries of the ambient space. When such group is large enough to act transitively on the hypersurface, the latter is called a homogeneous hypersurface, and the isometric action on the ambient space is said to be of cohomogeneity one. This is the case of hyperplanes, spheres, and cylinders in the Euclidean space or of horospheres in the hyperbolic space, among other examples.

By definition, the investigation of homogeneous hypersurfaces only makes sense in spaces with a large isometry group. Therefore, homogeneous spaces constitute the natural context for this investigation. Indeed, apart from spaces of constant curvature, the theory of surfaces with constant mean curvature in homogeneous 3-manifolds has undergone important advances (see, for example, [71]).

For arbitrary dimensions, a particularly elegant class of homogeneous manifolds is that of symmetric spaces. Locally, symmetric spaces are characterized by the property that curvature is invariant under parallel transport. Globally, the defining property of symmetric spaces is the existence of isometric central inversions around any point, which readily imply the existence of a transitive group of isometries. Symmetric spaces were classified by Élie Cartan [21] into several infinite families, some exceptional examples, and their products. Of course, this includes the space forms but also the isotropic (or two-point homogeneous) Riemannian manifolds, various (compact and noncompact) Grassmannians, compact Lie groups with bi-invariant metrics, and different moduli spaces of algebraic structures: real structures of a complex vector space, complex structures on a real vector space, positive definite symmetric matrices, etc. Symmetric spaces constitute a distinguished class in Berger’s classification of holonomy groups [17] but also an appropriate setting for several problems of geometric analysis [54]. Their study also arises naturally in other areas such as number theory and algebraic geometry [58, 86, 101].

In view of the crucial role played by homogeneous hypersurfaces in the classical submanifold theory of space forms, we believe that the investigation of homogeneous hypersurfaces in symmetric spaces constitutes one of the first steps in the long-term program of developing a submanifold theory of symmetric spaces. The centrality of these spaces in Mathematics, along with their fascinating geometric, algebraic, and analytic properties, gives us a glimpse of a field yet to be explored.

The aim of this text is to provide a survey on homogeneous hypersurfaces, their generalizations, and their classification problem in symmetric spaces, with a focus on the noncompact setting. Thus, we will start by discussing the definition, general properties, and important topological and geometric properties of homogeneous hypersurfaces in Sect. 2. In Sect. 3, we will review the notion and fundamental geometric and algebraic aspects of symmetric spaces (Sects. 3.1–3.2), mainly of those of noncompact type (Sect. 3.3), and the algebraic theory of parabolic subalgebras (Sect. 3.4). Section 4 will be devoted to report on the classification problem of homogeneous hypersurfaces in symmetric spaces of compact type. Here, we will provide an introductory discussion to the problem in spheres through various interesting examples (Sect. 4.1), and then we will describe the classification on the other compact symmetric spaces, focusing on the rank one case (Sect. 4.2). In Sect. 5, we will review the classification problem in symmetric spaces of noncompact type of rank one (the hyperbolic spaces over the normed division algebras), whereas in Sect. 6 we will present what is known in the higher rank case. Finally, in Sect. 7, we provide a list of open problems.

2 Homogeneous Hypersurfaces

Let M be a Riemannian manifold and $\mathrm {Isom}(M)$ its isometry group, which is known to be a Lie group. A connected, injectively immersed submanifold P of M is called (extrinsically) homogeneous if for any $p,q\in P$ there exists an isometry $\varphi$ of M such that $\varphi (p)=q$ and $\varphi (P)=P$. Note that if $P=M$, we recover the standard notion of (intrinsic) homogeneity of a Riemannian manifold. By considering the subgroup of isometries of M that leave the submanifold P invariant, one easily sees that P is homogeneous if and only if P is an orbit of an isometric action on M, that is, there exists a subgroup H of $\mathrm {Isom}(M)$ such that $P=H\cdot p$, for some (and hence, for any) $p\in P$. Hereafter, by $H\cdot p$, we denote the orbit of an action $H\times M\to M$ of a group H through a point p of M, and by $H_p=\{h\in H:h\cdot p=0\}$, we denote the isotropy group (or stabilizer) at p. Of course, $H\cdot p\cong H/H_p$ is a bijection, which is indeed a diffeomorphism if the H-action on M is smooth, when endowing the set of left cosets $H/H_p=\{hH_p: h\in H\}$ with a natural differentiable structure. Moreover, P is properly embedded (equivalently, closed and embedded) in M if and only if $H=\{\varphi \in \mathrm {Isom}(M):\varphi (P)=P\}$ is closed in $\mathrm {Isom}(M)$ (in particular, an embedded Lie subgroup of $\mathrm {Isom}(M)$); this in turn means that P is an orbit of a proper isometric smooth action on M. See [65, Chapter 21], [69], and [72, §6] for further information on smooth, proper, and isometric actions.

The family of orbits of a smooth isometric action of a connected Lie group H on a Riemannian manifold M determines what is called a singular Riemannian foliation of M. This is a decomposition of M into connected, injectively immersed submanifolds (leaves) that are locally equidistant to each other and such that there is a collection of smooth vector fields on M spanning all tangent spaces to all leaves. In the case of a smooth isometric H-action on M, the collection $\{X^*:X\in {\mathfrak {h}}\}$ of Killing fundamental vector fields on M, induced by elements X in the Lie algebra ${\mathfrak {h}}$ of H, span all tangent spaces to all orbits. Here, $X^*$ is given by $X^*_p=\frac {d}{dt}\vert _{t=0} \operatorname {\mathrm {Exp}}(tX)\cdot p$, where $\operatorname {\mathrm {Exp}}\colon {\mathfrak {h}}\to H$ denotes the Lie group exponential map. Moreover, if $\gamma$ is a geodesic in M that is orthogonal at $\gamma (0)$ to one orbit, $H\cdot \gamma (0)$, then for any fundamental vector field $X^*$, we have $\frac {d}{dt}\langle \dot {\gamma },X^*\rangle =\langle \dot {\gamma },\nabla _{\dot {\gamma }} X^*\rangle =0$, since $\nabla X^*$ is skew-adjoint as $X^*$ is Killing. Hence, $\langle \dot {\gamma },X^*\rangle =0$, and thus, any geodesic orthogonal to one orbit remains orthogonal to any other orbit that it meets. This means that the orbits are locally equidistant to each other. Orbit foliations, that is, singular Riemannian foliations induced by isometric actions, are also called homogeneous foliations. See [1] for more information on these concepts and properties.

Although Lie group theory plays a fundamental role in the analysis of homogeneous submanifolds and isometric actions, from a geometric perspective, we are ultimately interested in the orbit foliations of smooth isometric actions, and not so much in the (possibly multiple) groups that give rise to the same orbit foliation. Thus, when discussing isometric actions, we will usually consider actions to be equivalent if they have the same orbits. More precisely, we will say that two isometric actions of groups $H_1$ and $H_2$ on M are orbit equivalent if there is an isometry $\varphi$ of M such that $\varphi (H_1\cdot p)=H_2\cdot \varphi (p)$ for all $p\in M$, that is, $\varphi$ maps the $H_1$-orbits to the $H_2$-orbits. Thus, two smooth isometric actions are orbit equivalent if and only if their orbit foliations are congruent in M.

From now on, unless otherwise stated, isometric actions will be assumed to be smooth and proper, and homogeneous submanifolds will be closed and embedded.

The cohomogeneity of an isometric action is the lowest codimension of its orbits. Thus, a (proper) action has cohomogeneity zero precisely when it is transitive. An orbit of an isometric action is called regular if its codimension agrees with the cohomogeneity and is called singular otherwise.

Remark 1

Among regular orbits, we can distinguish two types: principal orbits and exceptional orbits. Given an isometric H-action on M, the H-orbit through p is principal if the isotropy group at p, $H_p=\{h\in H:h\cdot p=p\}$, is contained in any other isotropy group $H_q$, $q\in M$, up to conjugation in H. A nonprincipal regular orbit is called exceptional. The union of all principal orbits constitutes an open dense subset of M. If M is simply connected and complete and H is connected, then there are no exceptional orbits. See [1, Chapter 3 and Corollary 5.35] for further details.

2.1 Homogeneous Hypersurfaces and Cohomogeneity One Actions

A homogeneous hypersurface of M is a regular orbit of a cohomogeneity one action on M. It is known that a cohomogeneity one action on a complete connected Riemannian manifold has exactly zero, one, or two singular orbits. Indeed, the space of orbits $M/H=\{H\cdot p: p\in M\}$ of a cohomogeneity one H-action is homeomorphic to ${\mathbb {R}}$, $\mathbb {S}^1$, $[0,\infty )$ or $[0,1]$, and nonprincipal orbits correspond to the boundary of such spaces [3]. Depending on the geometry and topology of the ambient manifold M, some of these possibilities may be excluded (see Remark 2).

Example 1

The following items provide very simple examples of cohomogeneity one actions with orbit spaces homeomorphic to ${\mathbb {R}}$, $\mathbb {S}^1$, $[0,\infty )$, and $[0,1]$, respectively:

• (a) The action of $({\mathbb {R}}^{n-1},+)$ on ${\mathbb {R}}^n$ by translations: $h\cdot p=p+(h,0)$, where $h\in {\mathbb {R}}^{n-1}$, $p\in {\mathbb {R}}^{n}$. All orbits are regular (parallel hyperplanes).

• (b) The action of ${\mathsf {SO}}_2$ on a torus of revolution around the z-axis in ${\mathbb {R}}^3$, given by $A\cdot p=(A(p_1,p_2),p_3)$, where $A\in {\mathsf {SO}}_2$ and $p=(p_1,p_2,p_3)\in {\mathbb {R}}^3$. All orbits are regular (circles).

• (c) The standard action of ${\mathsf {SO}}_n$ on ${\mathbb {R}}^n$ by rotations around the origin. The origin is precisely the only singular orbit, whereas the concentric spheres about it are the regular orbits.

• (d) The action of ${\mathsf {SO}}_{n}$ on the unit sphere $\mathbb {S}^n$ of ${\mathbb {R}}^{n+1}$: $A\cdot p{=}(A(p_1,\dots , p_n), p_{n+1})$, where $A\in {\mathsf {SO}}_{n}$ and $p=(p_1,\dots , p_{n+1})$. The north and south poles of $\mathbb {S}^n$ are the two singular orbits, and the parallels are the regular orbits.

None of these actions has exceptional orbits (and hence the boundary points of their orbit spaces correspond to singular orbits). Here, we have three actions with exceptional orbits:

• (e) The action (d) above descends to a cohomogeneity one action of ${\mathsf {SO}}_{n}$ on the real projective space ${\mathbb {R}} {\mathsf {P}}^n$. This action has the same orbit space, namely, $[0,1]$, but only one singular orbit (the image of the poles under the projection map $\pi \colon \mathbb {S}^n\to {\mathbb {R}} {\mathsf {P}}^n$) and one exceptional orbit (the projection of the equator).

• (f) The action of ${\mathsf {U}}_1$ on the infinite Möbius band ${\mathbb {R}}^2/\{(x,y)\sim (-x,y+2\pi )\}$, given by $e^{i\theta }\cdot [(x,y)]=[(x,y+2\theta )]$, has orbit space $[0,\infty )$ and exceptional orbit ${\mathsf {U}}_1\cdot [(0,0)]$.

• (g) The action in (f) descends to a ${\mathsf {U}}_1$-action on the Klein bottle ${\mathbb {R}}^2/\{(x,y)\sim (-x,y+2\pi )\sim (x+2\pi ,y)\}$ with orbit space $[0,1]$, two exceptional orbits ${\mathsf {U}}_1\cdot [(0,0)]$ and ${{\mathsf {U}}_1\cdot [(\pi ,0)]}$, and no singular orbit.

As exemplified by the previous actions, the singular Riemannian foliation induced by a cohomogeneity one action on a complete connected manifold M is of a very particular type. It is a decomposition of M into mutually equidistant, properly embedded leaves, all of them of codimension one (the regular orbits/leaves), except at most two (the singular orbits/leaves). Each regular orbit is a tube around any of the singular orbits. Here, by tube of radius r around a submanifold P of M, we mean the subset of M given by

$$\displaystyle \begin{aligned} P^r=\{\exp(r\xi):\xi\in\nu P, \,|\xi|=1\}, \end{aligned}$$

where $\exp$ is the Riemannian exponential map of M and $\nu P$ is the normal bundle of P. If P is a hypersurface, each connected component of $P^r$ is called a parallel or equidistant hypersurface to P. Locally and for small enough r, a tube $P^r$ of radius r around P is a hypersurface. If Q is a hypersurface of M, $\xi$ is a smooth unit normal vector field along Q, and $Q^r_\xi =\{\exp (r\xi _p):p\in Q\}$ is a submanifold of codimension higher than one in M, then $Q^r_\xi$ is said to be a focal submanifold of Q. Thus, if P is a submanifold of codimension greater than one, then P is a focal submanifold of any of its codimension one, immersed tubes $P^r$. Observe that a codimension one, immersed tube around a submanifold P of codimension k in M is diffeomorphic to $P\times \mathbb {S}^{k-1}$.

Remark 2

The existence of a cohomogeneity one H-action on a complete connected Riemannian manifold M imposes some topological restrictions on M; we refer to [1, §6.3], [20, Chapter IV, Theorems 8.1–8.2], and [6, §2.9.3] for more information. If $M/H$ is ${\mathbb {R}}$ or $\mathbb {S}^1$, then all orbits are mutually diffeomorphic and principal, and M is a fiber bundle over $M/H$ (which is trivial if $M/H\cong {\mathbb {R}}$) and with fiber a principal orbit. In particular, if M is simply connected, $M/H$ cannot be $\mathbb {S}^1$; indeed, if M is a Hadamard manifold, the only possibilities for $M/H$ are ${\mathbb {R}}$ and $[0,\infty )$ (see [5, p. 212]). If $M/H\cong [0,\infty )$, then M is diffeomorphic to a tubular neighborhood of the only nonprincipal H-orbit, say $H\cdot p$, and hence $M\cong (H\cdot p)\times _{H_p}V$ is a Euclidean space bundle over such nonprincipal orbit $H\cdot p$. If $M/H\cong [0,1]$, then there are two nonprincipal orbits, say $H\cdot p_+$ and $H\cdot p_-$, and M admits a decomposition as a union of two disk bundles

$$\displaystyle \begin{aligned} M\cong (H\times_{H_{p_+}} \mathbb{D}_-)\cup_{H/K}(H\times_{H_{p_-}} \mathbb{D}_+), \end{aligned}$$

where $H_{p_\pm }$ are the isotropy groups at $p_\pm$; K is the isotropy at a point of a principal orbit $H/K$; $\mathbb {D}_\pm$ are two disks centered at the origin of the normal spaces to $H\cdot p_\pm$ at $p_\pm$, respectively; and the union of the disk bundles is made along the principal orbit $H/K$. This decomposition into two disk bundles is fundamental for various constructions and classifications (see, for instance, [47, 50, 80]).

2.2 Geometric Properties of Homogeneous Hypersurfaces

Homogeneous hypersurfaces and, in general, orbits of cohomogeneity one actions have some nice geometric properties. Since the shape operators (at different points) of a homogeneous hypersurface P of M are conjugate by the differentials of isometries of M, their eigenvalues are independent of the point, that is, P has constant principal curvatures. As the orbits of an isometric action are locally equidistant and nearby orbits to a regular one are regular, the nearby (locally defined) equidistant hypersurfaces to a homogeneous hypersurface are also (open subsets of) homogeneous hypersurfaces and therefore also with constant principal curvatures. This implies that a homogeneous hypersurface P is isoparametric: the locally defined, nearby parallel hypersurfaces to P have constant mean curvature. Isoparametric hypersurfaces have a long history arising from a problem in geometric optics, with contributions by Levi-Civita, Segre, and Cartan in the 1930s, and with many beautiful results obtained over the last five decades. We refer to [26, 27, 34, 90, 98, 99] and the references therein for more information on this topic.

Actually, the classification of homogeneous hypersurfaces in Euclidean and real hyperbolic spaces follows from the respective Segre’s [87] and Cartan’s [22] classifications of isoparametric hypersurfaces in such spaces. For Euclidean spaces ${\mathbb {R}}^n$, this classification states that isoparametric hypersurfaces are open subsets of affine hyperplanes ${\mathbb {R}}^{n-1}$, spheres $\mathbb {S}^{n-1}$, or cylinders $\mathbb {S}^k\times {\mathbb {R}}^{n-k-1}$, $k=1,\dots , n-2$. Since homogeneous hypersurfaces are always isoparametric and the previous complete hypersurfaces of ${\mathbb {R}}^n$ are homogeneous, they also exhaust all homogeneous hypersurfaces in Euclidean spaces. Thus, up to orbit equivalence, the cohomogeneity one actions on a Euclidean space ${\mathbb {R}}^n$ are the standard actions of ${\mathbb {R}}^{n-1}$ (Example 1 (a)), of ${\mathsf {SO}}_n$ (Example 1 (c)), and of ${\mathsf {SO}}_{k+1}\times {\mathbb {R}}^{n-k-1}$. Cartan’s classification for hyperbolic spaces will be reviewed in Sect. 5.

We remark that whereas in spaces of constant curvature a hypersurface is isoparametric if and only if it has constant principal curvatures, this is not true in general. Examples of isoparametric hypersurfaces with nonconstant principal curvatures (and hence inhomogeneous hypersurfaces) have been found in several symmetric spaces, such as complex and quaternionic projective spaces [36, 39], and many symmetric spaces of noncompact type [29, 30, 35, 41]; see also Remarks 4, 5, 6, 7, and 8. Conversely, we do not know of any nonisoparametric hypersurface with constant principal curvatures in symmetric spaces, although there do exist examples for some particular conformally flat metrics [81]. There are also important spaces where isoparametric hypersurfaces are known to be homogeneous, such as the homogeneous 3-manifolds with 4-dimensional isometry group or the product of two round 2-spheres [40, 100], besides Euclidean and real hyperbolic spaces.

There is, however, an important characterization of isoparametric hypersurfaces that holds in any Riemannian manifold. Specifically, a hypersurface P of M is isoparametric if and only if P is (maybe only locally) a regular level set of an isoparametric function on (an open subset of) M. Here, a smooth function $f\colon M\to {\mathbb {R}}$ is called isoparametric if f is not constant on any open subset of M and it satisfies the system of partial differential equations

$$\displaystyle \begin{aligned} {} |\nabla f|{}^2=a\circ f,\qquad \Delta f= b\circ f, \end{aligned} $$

(1)

for some real functions a, b of real variable, with a smooth and b continuous. In other words, the norm of the gradient and the Laplacian of f are constant along the level sets of f. The collection of level sets of an isoparametric function is called an isoparametric family of hypersurfaces. We refer the reader to [1, §5.5], [6, §2.9.2], and [48] for more information on isoparametric functions.

We would like to emphasize that as homogeneous hypersurfaces are isoparametric, they are also given as level sets of isoparametric functions. This result, which would be only local in principle, is indeed global. More precisely, given a cohomogeneity one action on a complete and simply connected Riemannian manifold M, its orbit foliation is recovered as the collection of level sets of an isoparametric function on M, as follows from [1, Theorem 5.68]. Of course, the converse is not true due to the existence of inhomogeneous isoparametric families of hypersurfaces. If M is compact, any isoparametric family of hypersurfaces on M has at least a minimal hypersurface in the family, which is unique if M has positive Ricci curvature [49]. In particular, any cohomogeneity one action on a compact Riemannian manifold M has a minimal regular orbit.

The fact that homogeneous hypersurfaces (or, more generally, isoparametric hypersurfaces) arise as regular level sets of solutions to the equations (1) makes that these geometric objects appear naturally in relation to certain overdetermined problems of partial differential equations; see [59] for a survey. These include parabolic equations, as in the study of the heat flow [83,84,85] or of stationary isothermic surfaces [70, 82], and elliptic equations, as in some problems in mathematical physics [77] and in various overdetermined boundary value problems (including generalizations of the outstanding Schiffer conjecture [89]). Indeed, the homogeneity (respectively, isoparametricity) of geodesic spheres plays a crucial role in a partial symmetry result proved in [37] for overdetermined boundary value problems for semilinear elliptic equations on small domains of two-point homogeneous spaces (resp. harmonic spaces). Here, by symmetry result, we mean a Serrin-type theorem [88] showing that bounded solution domains to certain overdetermined problems must be balls (in the case of [37], such domains are assumed to be small perturbations of small geodesic balls).

Finally, we mention that not only homogeneous hypersurfaces have interesting geometric properties but also their focal submanifolds (i.e., the singular orbits of the corresponding cohomogeneity one actions). It was stated by Wang [102] and proved by Ge and Tang [49] that the focal submanifolds of an isoparametric family of hypersurfaces are minimal. However, if the hypersurfaces of such an isoparametric family have, in addition, constant principal curvatures, each one of their focal submanifolds has a stronger geometric property: their shape operators for all unit normal vectors are isospectral, i.e., they have the same principal curvatures and corresponding multiplicities [49]. This geometric property was called CPC (which stands for “constant principal curvatures”) in [11]. In particular, focal submanifolds of homogeneous hypersurfaces are CPC. Notice that any CPC submanifold is austere, that is, their principal curvatures counted with multiplicities are invariant under change of sign. The notion of austere submanifold was introduced by Harvey and Lawson [52, Definition 3.15]. Clearly, austere submanifolds are minimal. In spaces of constant sectional curvature, CPC submanifolds of codimension higher than one are precisely the focal submanifolds of isoparametric hypersurfaces (equivalently, of hypersurfaces with constant principal curvatures). This is not true in general as, in many spaces (e.g., nonflat complex space forms), tubes around certain totally geodesic (and hence CPC) submanifolds are not isoparametric and have nonconstant principal curvatures (cf. Sect. 5.3 and Remark 5). Recently, it was proved that focal submanifolds of isoparametric hypersurfaces need not be austere [41].

3 Symmetric Spaces

In this section, we provide a short introduction to Riemannian symmetric spaces, with special focus on those of noncompact type. There are several references for the reader interested in obtaining further information on this topic. Two classical references are Helgason’s book [53] and Loos’ books [67, 68]. As introductory texts, we refer to Eschenburg’s survey [45] and Ziller’s notes [105]. Some nice chapters on symmetric spaces can be found in the books by Berndt, Console, and Olmos [6], Besse [17], O’Neill [76], and Wolf [103].

3.1 Definition and Fundamental Properties

Let M be a connected Riemannian manifold. Given a point $p\in M$, we can consider the geodesic ball $B_p(r)$ centered at p of radius r, for $r>0$ small enough. On such ball, we can define the smooth map $\sigma _p\colon B_p(r)\to B_p(r)$ that sends $q=\exp _p(v)$ to $\sigma _p(q)=\exp _p(-v)$, where $v\in T_pM$, $|v|<r$. This map $\sigma _p$ is nothing but a geodesic reflection about p. It is clearly an involution, i.e., $\sigma _p^2= \operatorname {\mathrm {id}}$.

A Riemannian symmetric space is a connected Riemannian manifold M such that, for any $p\in M$, the geodesic reflection $\sigma _p$ at p is defined globally on M and is an isometry of M. Thus, symmetric spaces are characterized by the existence of central symmetries around any point. From this definition, one can easily see that symmetric spaces are complete (geodesics can be extended by using geodesic reflections) and homogeneous (given $p_1$, $p_2\in M$, by completeness, there is a geodesic segment joining them, and if q is its midpoint, then $\sigma _q(p_1)=p_2$).

We fix from now on an arbitrary point $o\in M$, which is sometimes called the origin or the base point of M. The homogeneity and the connectedness of M imply that the Lie group $G=\mathrm {Isom}(M)^0$, the connected component of the identity of the isometry group $\mathrm {Isom}(M)$ of M, acts transitively on M. Let $K=\{g\in G:g(o)=o\}$ be the isotropy group at the origin o, which can be shown to be a compact Lie group. Hence, M is diffeomorphic to the set of left cosets $G/K=\{gK:g\in G\}$ endowed with some natural differentiable structure. Note that under the diffeomorphism $M\cong G/K$, the origin o corresponds to the coset eK, where e is the identity of G. See [65, Chapter 21] for more information on homogeneous spaces.

The map $s\colon G\to G$, $s(g)=\sigma _o g\sigma _o$, is a well-defined involutive Lie group automorphism of G. It satisfies $G_s^0\subset K\subset G_s$, where $G_s=\{g\in G:s(g)=g\}$ and $G_s^0$ denotes its connected component of the identity. Its differential $\theta =s_*\colon {\mathfrak {g}} \to {\mathfrak {g}}$ is an involutive Lie algebra automorphism, the so-called Cartan involution associated with the symmetric space (of course, $\theta$ depends on the choice of o). The Lie algebra ${\mathfrak {k}}$ of the isotropy group K is precisely the $(+1)$-eigenspace of $\theta$. If we denote by ${\mathfrak {p}}$ the $(-1)$-eigenspace of $\theta$, then ${\mathfrak {g}}={\mathfrak {k}}\oplus {\mathfrak {p}}$ is the eigenspace decomposition of $\theta$, called the Cartan decomposition of ${\mathfrak {g}}$. Since $\theta$ is an automorphism, it is easy to check that $[{\mathfrak {k}},{\mathfrak {k}}]\subset {\mathfrak {k}}$, $[{\mathfrak {k}},{\mathfrak {p}}]\subset {\mathfrak {p}}$, and $[{\mathfrak {p}},{\mathfrak {p}}]\subset {\mathfrak {k}}$.

Consider the smooth map $\phi \colon G\to M$, $\phi (g)=g(o)$. Its differential $\phi _{*e}$ at the identity element e induces a vector space isomorphism ${\mathfrak {p}}\cong T_oM$. Moreover, the linearization of the isotropy action $K\times M\to M$, $k\cdot p=k(p)$, at o turns out to be an isometric linear action $K\times T_oM\to T_oM$, $k\cdot v=k_{*o}v$. This is called the isotropy representation of $M\cong G/K$ at o. The isotropy representation turns out to be equivalent to the adjoint representation of K on ${\mathfrak {p}}$, namely, the action $K\times {\mathfrak {p}}\to {\mathfrak {p}}$ given by $k\cdot X= \operatorname {\mathrm {Ad}}(k)X$. We will also call this action the isotropy representation of M.

The curvature tensor R of a symmetric space M at the base point o admits a simple description as

$$\displaystyle \begin{aligned} {} R(X,Y)Z=-[[X,Y],Z], \qquad X,Y,Z\in{\mathfrak{p}}\cong T_oM. \end{aligned} $$

(2)

It turns out that the curvature tensor of a symmetric space is parallel with respect to the Levi-Civita connection, $\nabla R=0$. Riemannian manifolds with this property are called locally symmetric, and the complete ones turn out to be quotients of symmetric spaces by discrete group actions.

Formula (2) leads to a very simple characterization of the totally geodesic submanifolds of symmetric spaces: they are (up to congruence in M) of the form $S=\exp _o {\mathfrak {s}}$, where ${\mathfrak {s}}$ is a subspace of ${\mathfrak {p}}\cong T_oM$ such that $[[{\mathfrak {s}},{\mathfrak {s}}],{\mathfrak {s}}]\subset {\mathfrak {s}}$. Such a subspace ${\mathfrak {s}}$ of ${\mathfrak {p}}$ is called a Lie triple system. However, determining such Lie triple systems is a very difficult problem, and indeed the classification of totally geodesic submanifolds is still an outstanding problem; see [9, 10], and [64] for important recent contributions. In the particular case when ${\mathfrak {s}}$ is abelian, then the associated totally geodesic submanifold is flat by (2). Among all the abelian subspaces of ${\mathfrak {p}}$, the maximal ones have the same dimension. The associated totally geodesic submanifolds are called maximal flats of the symmetric space. The common dimension of such maximal flats is called the rank of the symmetric space.

Remark 3

It is rather common to express symmetric spaces as quotient manifolds $G/K$ where G is not necessarily exactly $\mathrm {Isom}(M)^0$. For instance, the complex hyperbolic space ${\mathbb {C}} H^n$ is usually presented as ${\mathsf {SU}}_{1,n}/{\mathsf {S}}({\mathsf {U}}_1{\mathsf {U}}_n)$ instead of $(\mathsf {SU}_{1,n}/\mathbb {Z}_{n+1})/({\mathsf {S}}({\mathsf {U}}_1{\mathsf {U}}_n)/\mathbb {Z}_{n+1})$. The common practice is to present a symmetric space in terms of a so-called symmetric pair $(G,K)$, where K is compact, there is an involutive automorphism s of G such that $G_s^0\subset K\subset G_s$, and G acts almost effectively on $M=G/K$ (i.e., there is at most a discrete subgroup of elements of G that act trivially on $G/K$). Of course, if M is a symmetric space, then $(\mathrm {Isom}(M)^0,\mathrm {Isom}(M)^0_o)$ is a symmetric pair. These subtleties will not play an important role in this article.

3.2 Types of Symmetric Spaces

A symmetric space $M\cong G/K$ is called (isotropy) irreducible if the restriction of its isotropy representation to the connected component of the identity of K is irreducible. This is equivalent to the property that the Riemannian universal cover $\widetilde {M}$ of M (which is again a symmetric space) is not a nontrivial product of symmetric spaces, unless $\widetilde {M}={\mathbb {R}}^n$ is a Euclidean space.

Recall that the Killing form of a Lie algebra ${\mathfrak {g}}$ is the symmetric bilinear form $\mathcal {B}\colon {\mathfrak {g}}\times {\mathfrak {g}}\to {\mathbb {R}}$ given by $\mathcal {B}(X,Y)= \operatorname {\mathrm {tr}}( \operatorname {\mathrm {ad}}(X)\circ \operatorname {\mathrm {ad}}(Y))$, where $\operatorname {\mathrm {ad}}(X)=[X,\cdot ]$. It is not difficult to check that ${\mathfrak {k}}$ and ${\mathfrak {p}}$ are orthogonal subspaces with respect to $\mathcal {B}$. A symmetric space $M\cong G/K$ is said to be of compact type, of noncompact type, or of Euclidean type if $\mathcal {B}\vert _{{\mathfrak {p}}\times {\mathfrak {p}}}$ is negative definite, positive definite, or identically zero, respectively. If M is irreducible, Schur’s lemma implies that $\mathcal {B}\vert _{{\mathfrak {p}}\times {\mathfrak {p}}}$ is proportional to the inner product on ${\mathfrak {p}}\cong T_oM$ induced by the symmetric metric of M. According to the sign of the proportionality constant, M falls into one of the three possible types. If M is not irreducible, there is no guarantee that it is of one of the three types.

If M is of compact type, then G is a compact semisimple Lie group, and M is compact and has nonnegative sectional curvature. If M is of noncompact type, then it turns out that G is a noncompact real semisimple Lie group (with no compact factors), and M is a Hadamard manifold (it is diffeomorphic to a Euclidean space and has nonpositive sectional curvature). If M is of Euclidean type, its Riemannian universal cover is a Euclidean space ${\mathbb {R}}^n$. In general, the Riemannian universal cover of a symmetric space M splits as a Riemannian product of symmetric spaces $\widetilde {M}=M_+\times M_-\times M_0$, where $M_+$ is of compact type, $M_-$ is of noncompact type, and $M_0$ is a Euclidean space.

There is a notion of duality between the classes of symmetric spaces of compact type and of noncompact type. Specifically, there is a one-to-one correspondence between symmetric spaces of noncompact type and simply connected symmetric spaces of compact type. This duality can be made explicit in terms of the Lie algebras and groups involved, although here we will not enter into details. Dual symmetric spaces have the same rank and equivalent isotropy representations, and hence, duality preserves irreducibility. However, it is important to remark that both types of symmetric spaces have very different topological and geometrical properties.

Example 2

We illustrate the notion of duality through some examples:

• (a) The real hyperbolic space ${\mathbb {R}} H^n\cong {\mathsf {SO}}_{1,n}^0/{\mathsf {SO}}_n$ is of noncompact type and has two dual symmetric spaces of compact type: the sphere $\mathbb {S}^n\cong {\mathsf {SO}}_{n+1}/{\mathsf {SO}}_n$ and the real projective space ${\mathbb {R}} {\mathsf {P}}^n\cong {\mathsf {SO}}_{n+1}/{\mathsf {O}}_n$. These spaces have rank one.

• (b) The other rank one (nonflat) symmetric spaces are the projective and the hyperbolic spaces over the division algebras of the complex numbers ${\mathbb {C}}$, the quaternions ${\mathbb {H}}$, and the octonions $\mathbb {O}$. Thus, the complex spaces ${\mathbb {C}} {\mathsf {P}}^n={\mathsf {SU}}_{n+1}/{\mathsf {S}}({\mathsf {U}}_1{\mathsf {U}}_n)$ and ${\mathbb {C}} {\mathsf {H}}^n={\mathsf {SU}}_{1,n}/{\mathsf {S}}({\mathsf {U}}_1{\mathsf {U}}_n)$, the quaternionic spaces ${\mathbb {H}} {\mathsf {P}}^n={\mathsf {Sp}}_{n+1}/{\mathsf {Sp}}_1{\mathsf {Sp}}_n$ and ${\mathbb {H}} {\mathsf {H}}^n={\mathsf {Sp}}_{1,n}/{\mathsf {Sp}}_1{\mathsf {Sp}}_n$, and the Cayley planes $\mathbb {O} {\mathsf {P}}^2=\mathsf {F}_4/{\mathsf {Spin}}_9$ and $\mathbb {O} {\mathsf {H}}^2=\mathsf {F}_4^{-20}/{\mathsf {Spin}}_9$ constitute three pairs of dual symmetric spaces of rank one.

• (c) Any compact Lie group K endowed with a bi-invariant metric is a symmetric space of compact type. An associated symmetric pair is $(K\times K,\Delta K)$, where $\Delta K=\{(k,k):k\in K\}$. Its dual symmetric space of noncompact type is of the form $K^{\mathbb {C}}/K$, where $K^{\mathbb {C}}$ denotes the complexification of K. For example, ${\mathsf {SO}}_n$ (and also its universal cover ${\mathsf {Spin}}_n$) and ${\mathsf {SO}}_n({\mathbb {C}})/{\mathsf {SO}}_n$ are dual to each other, $n\geq 3$.

• (d) The compact space ${\mathsf {SU}}_n/{\mathsf {SO}}_n$ of special Lagrangian subspaces of ${\mathbb {C}}^n$ is dual to the noncompact space ${\mathsf {SL}}_n({\mathbb {R}})/{\mathsf {SO}}_n$ of all positive definite symmetric matrices of determinant 1 and order n.

For the complete list of irreducible symmetric spaces (up to coverings), we refer to [53, pp. 516, 518]. See [103] for a discussion of locally symmetric spaces of compact type.

3.3 Symmetric Spaces of Noncompact Type: Root Space and Iwasawa Decompositions

Symmetric spaces of noncompact type constitute a rich family of Hadamard manifolds that generalize the hyperbolic spaces. We refer to [4, 34], [44, Chapter 2], [53, Chapter VI], and [60, Chapter VI, §4-5] for more information on different aspects of these spaces.

Let $M\cong G/K$ be a (not necessarily irreducible) symmetric space of noncompact type. Let ${\mathfrak {g}}={\mathfrak {k}}\oplus {\mathfrak {p}}$ be the Cartan decomposition of the Lie algebra ${\mathfrak {g}}$ of G determined by the choice of a base point $o\in M$. The Killing form $\mathcal {B}$ of ${\mathfrak {g}}$ makes ${\mathfrak {k}}$ and ${\mathfrak {p}}$ orthogonal, restricts to a positive definite inner product on ${\mathfrak {p}}$ by definition of noncompact type, and turns out to be negative definite when restricted to ${\mathfrak {k}}$. Thus, by changing its sign on ${\mathfrak {k}}$, we get a positive definite inner product on ${\mathfrak {g}}$. This inner product $\mathcal {B}_\theta$ can alternatively be defined by $\mathcal {B}_\theta (X,Y)=-\mathcal {B}(\theta X,Y)$, for each X, $Y\in {\mathfrak {g}}$, where $\theta$ is the Cartan involution.

Let ${\mathfrak {a}}$ be an arbitrary maximal abelian subspace of ${\mathfrak {p}}$. Recall that $\dim {\mathfrak {a}}$ is the rank of M. The endomorphisms $\operatorname {\mathrm {ad}}(H)=[H,\cdot ]$ of ${\mathfrak {g}}$, where $H\in {\mathfrak {a}}$, turn out to be self-adjoint with respect to $\mathcal {B}_\theta$, and they commute with each other (since $\operatorname {\mathrm {ad}}$ is a Lie algebra homomorphism and ${\mathfrak {a}}$ is abelian). Thus, such endomorphisms of ${\mathfrak {g}}$ diagonalize simultaneously. Their common eigenspaces are called the restricted root spaces, and their nonzero eigenvalues (which are linear in $H\in {\mathfrak {a}}$) are called the restricted roots of ${\mathfrak {g}}$. More precisely, for each linear functional $\lambda \in {\mathfrak {a}}^*$, consider the subspace of ${\mathfrak {g}}$ given by

$$\displaystyle \begin{aligned} {\mathfrak{g}}_\lambda=\{X\in{\mathfrak{g}}: [H,X]=\lambda(H)X \text{ for all }H\in{\mathfrak{a}}\}. \end{aligned}$$

Then, any ${\mathfrak {g}}_\lambda \neq 0$ is a restricted root space, and any $\lambda \neq 0$ with ${\mathfrak {g}}_\lambda \neq 0$ is a restricted root. Note that $0\neq {\mathfrak {a}}\subset {\mathfrak {g}}_0$. Let us denote by

$$\displaystyle \begin{aligned} \Sigma=\{\lambda\in{\mathfrak{a}}^*:\lambda\neq 0, \, {\mathfrak{g}}_\lambda\neq 0\} \end{aligned}$$

the set of restricted roots of ${\mathfrak {g}}$. Hence, we can write the $\mathcal {B}_\theta$-orthogonal direct sum decomposition

$$\displaystyle \begin{aligned} {\mathfrak{g}}={\mathfrak{g}}_0\oplus\bigg(\bigoplus_{\lambda\in\Sigma}{\mathfrak{g}}_\lambda\bigg), \end{aligned}$$

known as the restricted root space decomposition of ${\mathfrak {g}}$. The multiplicity $m_\lambda$ of a restricted root $\lambda$ is the dimension of its root space, $m_\lambda =\dim {\mathfrak {g}}_\lambda$. In what follows, we will omit the word “restricted”.

Roots and root space decompositions enjoy several nice properties, such as the following:

• (a) $[{\mathfrak {g}}_\lambda ,{\mathfrak {g}}_\mu ]\subset {\mathfrak {g}}_{\lambda +\mu }$, for any $\lambda$, $\mu \in \Sigma \cup \{0\}$.

• (b) $\theta {\mathfrak {g}}_\lambda ={\mathfrak {g}}_{-\lambda }$, for any $\lambda \in \Sigma \cup \{0\}$. Hence, $\lambda \in \Sigma$ if and only if $-\lambda \in \Sigma$.

• (c) ${\mathfrak {g}}_0={\mathfrak {k}}_0\oplus {\mathfrak {a}}$, where ${\mathfrak {k}}_0={\mathfrak {g}}_0\cap {\mathfrak {k}}=N_{{\mathfrak {k}}}({\mathfrak {a}})=Z_{{\mathfrak {k}}}({\mathfrak {a}})$ is both the normalizer and the centralizer of ${\mathfrak {a}}$ in ${\mathfrak {k}}$.

Moreover, the finite subset $\Sigma$ of ${\mathfrak {a}}^*$ formed by the roots has various symmetry properties. Firstly, we can endow ${\mathfrak {a}}^*$ with an inner product given by $\langle \lambda ,\mu \rangle =\mathcal {B}_\theta (H_\lambda ,H_\mu )$, for any $\lambda$, $\mu \in {\mathfrak {a}}^*$, and where $H_\lambda \in {\mathfrak {a}}$ is defined by the relation $\mathcal {B}_\theta (H_\lambda ,H)=\lambda (H)$ for all $H\in {\mathfrak {a}}$. With this inner product, one can show that $\Sigma$ is an abstract root system on the Euclidean space $({\mathfrak {a}}^*,\langle \cdot ,\cdot \rangle )$. This means (see [60, §II.5]):

• (a) ${\mathfrak {a}}^*= \operatorname {\mathrm {span}}\Sigma$.

• (b) The number $a_{\alpha \beta } =2\langle \alpha ,\beta \rangle / \langle \alpha ,\alpha \rangle$ is an integer for any $\alpha ,\beta \in \Sigma$.

• (c) $\beta -a_{\alpha \beta }\,\alpha \in \Sigma$, for any $\alpha ,\beta \in \Sigma$.

This system is called nonreduced if there is $\lambda \in \Sigma$ such that $2\lambda \in \Sigma$. In this case, $2\lambda$ is called a nonreduced root. Root systems can be classified, and this is indeed the basis for the classification of real semisimple Lie algebras and of symmetric spaces.

The information of a root system can be codified in a smaller set of roots. By considering an open halfspace of ${\mathfrak {a}}^*$ containing exactly half of the roots in $\Sigma$ (recall that $\Sigma$ is invariant under the reflection about the origin), we can declare as positive those roots lying in such halfspace. If we denote by $\Sigma ^+$ this set of positive roots, we then have $\Sigma =\Sigma ^+\sqcup (-\Sigma ^+)$. Among the elements of $\Sigma ^+$, there are some that cannot be expressed as sum of exactly two positive roots. These are called the simple roots, and we denote by $\Lambda$ its collection. It turns out that $\Lambda$ is a basis for ${\mathfrak {a}}^*$, and hence, its cardinality $|\Lambda |$ is precisely the rank of M. Any root $\lambda$ in $\Sigma$ turns out to be a linear combination of elements of $\Lambda$ with integer coefficients, all of them nonnegative (when $\lambda \in \Sigma ^+$) or all of them nonpositive (when $\lambda \in -\Sigma ^+$).

The set $\Lambda$ of simple roots allows to construct the Dynkin diagram of $\Sigma$ (and, ultimately, of the symmetric space M). This is a graph consisting in as many nodes as elements in $\Lambda$. Two nodes are joined by a simple (respectively, double or triple) edge whenever the angle between the corresponding simple roots is $2\pi /3$ (respectively, $3\pi /4$ or $5\pi /6$). Finally, if the system is nonreduced, any simple root whose double is also a root is represented by a double node (two concentric circles). We refer to [6, pp. 336-340] for a list of all possible connected Dynkin diagrams, together with the multiplicities of the simple (and nonreduced) roots and with the associated irreducible symmetric spaces of noncompact type. There is also a theory of roots for symmetric spaces of compact type, and both theories behave well under duality, cf. [68, pp. 119, 146].

The sum of the root spaces associated with positive roots,

$$\displaystyle \begin{aligned} {\mathfrak{n}}=\bigoplus_{\lambda\in\Sigma^+}{\mathfrak{g}}_\lambda, \end{aligned}$$

is a nilpotent Lie subalgebra of ${\mathfrak {g}}$, by the properties of the root space decomposition. Since ${\mathfrak {a}}$ normalizes ${\mathfrak {n}}$, we have that ${\mathfrak {a}}\oplus {\mathfrak {n}}$ is a solvable Lie subalgebra of ${\mathfrak {g}}$. The Iwasawa decomposition theorem for Lie algebras ensures that

$$\displaystyle \begin{aligned} {\mathfrak{g}}={\mathfrak{k}}\oplus{\mathfrak{a}}\oplus{\mathfrak{n}} \end{aligned}$$

is a vector space direct sum (but it is not orthogonal, and none of the addends is an ideal of ${\mathfrak {g}}$). Let A and N denote the connected subgroups of G with Lie algebras ${\mathfrak {a}}$ and ${\mathfrak {n}}$, respectively. Then AN is the connected subgroup of G with Lie algebra ${\mathfrak {a}}\oplus {\mathfrak {n}}$. The Iwasawa decomposition at the Lie group level states that the multiplication map

$$\displaystyle \begin{aligned} K\times A\times N\to G, \qquad (k,a,n)\mapsto kan, \end{aligned}$$

is a diffeomorphism and the Lie groups A, N, and AN are diffeomorphic to Euclidean spaces.

Recall the smooth map $\phi \colon G\to M$, $\phi (g)=g(o)$, from Sect. 3.1. By the Iwasawa decomposition, its restriction to AN is a diffeomorphism $\phi \vert _{AN}\colon AN\to M$. Let us denote by ${\mathsf {g}}$ the symmetric Riemannian metric of M, and consider its pullback metric $(\phi \vert _{AN})^*{\mathsf {g}}$ on AN. This metric, which will be denoted by $\langle \cdot ,\cdot \rangle$ in what follows, happens to be left-invariant on the Lie group AN. Therefore, we have that any symmetric space of noncompact typeMis isometric to a certain solvable Lie groupANendowed with a particular left-invariant metric. This in particular implies, as we had already advanced, that a symmetric space of noncompact type M is diffeomorphic to a Euclidean space. By formula (2), one can actually show that such an M is nonpositively curved and hence it is a Hadamard manifold. This enables us to regard any of these spaces as an open ball endowed with certain metric, similarly as with the ball model of the real hyperbolic space.

For certain problems, it can be useful to regard a symmetric space of noncompact type M as an open dense subset of a larger compact topological space $M\sqcup M(\infty )$ that is homeomorphic to a closed ball. The ideal boundary$M(\infty )$ of M is defined to be the set of points at infinity of M, namely, the equivalence classes of complete, unit-speed geodesics of M under the relation $\gamma _1\sim \gamma _2$ if $\{d(\gamma _1(t),\gamma _2(t)):t\geq 0\}$ is bounded. One can endow $M\sqcup M(\infty )$ with the so-called cone topology, so that $M\sqcup M(\infty )$ becomes homeomorphic to a closed ball whose interior corresponds to M and whose boundary is $M(\infty )$. Two geodesics are called asymptotic if they converge to the same point at infinity, i.e., if they belong to the same equivalence class. If $M=G/K$, the action of G on M can be naturally extended to $M(\infty )$ by taking $g\cdot [\gamma ]:=[g\cdot \gamma ]$.

Symmetric spaces of noncompact type, as particular instances of Hadamard manifolds, admit certain codimension one foliations by the so-called horospheres. Specifically, given any complete, unit-speed geodesic $\gamma$ in M, one can consider the Busemann function$f_\gamma \colon M\to {\mathbb {R}}$ given by $f_\gamma (p)=\lim _{t\to +\infty }\bigl (d(p,\gamma (t))-t\bigr )$. The horosphere foliation determined by $\gamma$ is the regular Riemannian foliation of M given by the collection of level sets of the Busemann function $f_\gamma$. It is known that any horosphere foliation of a symmetric space of noncompact type M is homogeneous: it is the orbit foliation of the cohomogeneity one action on M given by the codimension one subgroup of AN with Lie algebra $({\mathfrak {a}}\ominus \ell )\oplus {\mathfrak {n}}$, for some specific one-dimensional subspaces $\ell$ of ${\mathfrak {a}}$; see [42, Remark 5.4] for more information.

By making use of the solvable model of a symmetric space of noncompact type, one can provide an explicit formula for the Levi-Civita connection on $AN\cong M$ and also relate the left-invariant metric $\langle \cdot ,\cdot \rangle =(\phi \vert _{AN})^*{\mathsf {g}}$ on AN to the inner product $\mathcal {B}_\theta$. These tools, along with a careful analysis of root space decompositions, are very useful in the investigation of submanifold geometry of symmetric spaces of noncompact type. We refer to [34] for further details.

3.4 Parabolic Subgroups and Subalgebras, and Boundary Components

The investigation of cohomogeneity one actions on symmetric spaces of noncompact type that we will review in Sect. 6 depends on a number of concepts and notation related to the theory of the so-called parabolic subalgebras of real semisimple Lie algebras. Here, we present a quick introduction to this topic. We refer to [6, §13.2], [18, §I.1], [44, §2.17], and [60, §VII.7] for more information.

Geometrically speaking, we say that a Lie subgroup Q of G is parabolic if $Q=G$ or Q is the stabilizer $G_x$ of a point at infinity $x\in M(\infty )$. From the algebraic viewpoint, it can be proved that a Lie subalgebra ${\mathfrak {q}}$ of ${\mathfrak {g}}$ is the Lie algebra of a parabolic subgroup Q of G precisely if it contains a subalgebra of ${\mathfrak {g}}$ conjugate to ${\mathfrak {k}}_0\oplus {\mathfrak {a}}\oplus {\mathfrak {n}}$ (recall that ${\mathfrak {k}}_0=N_{\mathfrak {k}}({\mathfrak {a}})$). In this case, we say that ${\mathfrak {q}}$ is a parabolic subalgebra of ${\mathfrak {g}}$.

Our interest in parabolic subalgebras arises from their explicit description in terms of roots and root spaces, which we explain now. Up to conjugacy in G, a parabolic subalgebra of ${\mathfrak {g}}$ can be constructed from the choice of a subset $\Phi \subset \Lambda$ of simple roots of ${\mathfrak {g}}$. Let $\Sigma _\Phi =\Sigma \cap \operatorname {\mathrm {span}} \Phi$ be the root subsystem generated by $\Phi$, and consider the positivity notion on $\Sigma _\Phi$ induced by that of $\Sigma$, that is, $\Sigma _\Phi ^+=\Sigma ^+\cap \Sigma _\Phi$. Define the following subalgebras of ${\mathfrak {g}}$:

$$\displaystyle \begin{aligned} {\mathfrak{l}}_\Phi={\mathfrak{g}}_0\oplus\bigg(\bigoplus_{\lambda\in\Sigma_\Phi}{\mathfrak{g}}_\lambda\bigg),\qquad {\mathfrak{a}}_\Phi=\bigcap_{\alpha\in\Phi}\ker\alpha, \qquad {\mathfrak{n}}_\Phi=\bigoplus_{\lambda\in\Sigma^+\setminus\Sigma^+_\Phi}{\mathfrak{g}}_\lambda, \end{aligned}$$

which are reductive (in the sense of it being invariant with respect to a Cartan involution of ${\mathfrak {g}}$, cf. [62]), abelian, and nilpotent, respectively. The subalgebra ${\mathfrak {l}}_{\Phi }$ is the centralizer and the normalizer of ${\mathfrak {a}}_{\Phi }$ in ${\mathfrak {g}}$ and normalizes ${\mathfrak {n}}_{\Phi }$. Thus, ${\mathfrak {q}}_{\Phi }={\mathfrak {l}}_{\Phi }\oplus {\mathfrak {n}}_{\Phi }$ is a subalgebra of ${\mathfrak {g}}$ containing ${\mathfrak {k}}_0\oplus {\mathfrak {a}}\oplus {\mathfrak {n}}$. We say that ${\mathfrak {q}}_{\Phi }$ is the parabolic subalgebra of ${\mathfrak {g}}$ associated with the subset $\Phi \subset \Lambda$. The decomposition ${\mathfrak {q}}_{\Phi }={\mathfrak {l}}_{\Phi }\oplus {\mathfrak {n}}_{\Phi }$ is known as the Chevalley decomposition of ${\mathfrak {q}}_{\Phi }$. The subalgebra ${\mathfrak {m}}_{\Phi }={\mathfrak {l}}_{\Phi }\ominus {\mathfrak {a}}_{\Phi }$ (hereafter, $\ominus$ denotes orthogonal complement with respect to the inner product $\mathcal {B}_\theta$) is a reductive subalgebra of ${\mathfrak {g}}$ that normalizes ${\mathfrak {a}}_{\Phi }\oplus {\mathfrak {n}}_{\Phi }$. Hence, we have a decomposition ${\mathfrak {q}}_{\Phi }={\mathfrak {m}}_{\Phi }\oplus {\mathfrak {a}}_{\Phi }\oplus {\mathfrak {n}}_{\Phi }$, which is known as the Chevalley decomposition of ${\mathfrak {q}}_{\Phi }$. By a result of Borel and Tits [19], any parabolic subalgebra of a real semisimple Lie algebra ${\mathfrak {g}}$ is conjugate to one of the subalgebras ${\mathfrak {q}}_{\Phi }$, for some $\Phi \subset \Lambda$.

The orthogonal projection ${\mathfrak {k}}_{\Phi }=\pi _{{\mathfrak {k}}}({\mathfrak {m}}_{\Phi })$ of ${\mathfrak {m}}_{\Phi }$ onto ${\mathfrak {k}}$ turns out to be a maximal compact subalgebra of ${\mathfrak {m}}_{\Phi }$. It can be written as

$$\displaystyle \begin{aligned} {\mathfrak{k}}_{\Phi}={\mathfrak{q}}_{\Phi}\cap{\mathfrak{k}}={\mathfrak{l}}_{\Phi}\cap{\mathfrak{k}}={\mathfrak{m}}_{\Phi}\cap{\mathfrak{k}}={\mathfrak{k}}_0\oplus\left(\bigoplus_{\lambda\in\Sigma_{\Phi}^{+}}{\mathfrak{k}}_{\lambda}\right), \end{aligned}$$

where ${\mathfrak {k}}_{\lambda }=\pi _{{\mathfrak {k}}}({\mathfrak {m}}_\lambda )={\mathfrak {k}}\cap ({\mathfrak {g}}_\lambda \oplus {\mathfrak {g}}_{-\lambda })$. Similarly, the projection ${\mathfrak {b}}_{\Phi }=\pi _{{\mathfrak {p}}}({\mathfrak {m}}_{\Phi })$ of ${\mathfrak {m}}$ onto ${\mathfrak {p}}$ is a Lie triple system, which is also given by

$$\displaystyle \begin{aligned} {\mathfrak{b}}_{\Phi}={\mathfrak{m}}_{\Phi}\cap{\mathfrak{p}}={\mathfrak{a}}^{\Phi}\oplus\left(\bigoplus_{\lambda\in\Sigma_{\Phi}^{+}}{\mathfrak{p}}_{\lambda}\right), \end{aligned}$$

where ${\mathfrak {a}}^{\Phi }={\mathfrak {a}}\ominus {\mathfrak {a}}_{\Phi }=\bigoplus _{\alpha \in \Phi }{\mathbb {R}} H_{\alpha }$ and $\mathfrak {p}_\lambda =\pi _{{\mathfrak {p}}}({\mathfrak {m}}_\lambda )={\mathfrak {p}}\cap ({\mathfrak {g}}_\lambda \oplus {\mathfrak {g}}_{-\lambda })$. Associated with ${\mathfrak {b}}_{\Phi }$, one can consider the semisimple Lie algebra ${\mathfrak {s}}_{\Phi }=[{\mathfrak {b}}_{\Phi },{\mathfrak {b}}_{\Phi }]\oplus {\mathfrak {b}}_{\Phi }$. The previous decomposition is a Cartan decomposition for ${\mathfrak {s}}_{\Phi }$, and ${\mathfrak {a}}^{\Phi }$ is a maximal abelian subspace of ${\mathfrak {b}}_{\Phi }$. The root subsystem $\Sigma _{\Phi }$ can be identified with a set of roots for ${\mathfrak {s}}_{\Phi }$ by restricting the roots of $\Sigma _{\Phi }$ to ${\mathfrak {a}}^{\Phi }$. The corresponding root spaces of ${\mathfrak {s}}_{\Phi }$ coincide with those of ${\mathfrak {g}}$. More precisely, we have the root space decomposition

$$\displaystyle \begin{aligned} {\mathfrak{s}}_{\Phi}=({\mathfrak{s}}_{\Phi}\cap{\mathfrak{k}}_0)\oplus{\mathfrak{a}}^{\Phi}\oplus\left(\bigoplus_{\lambda\in\Sigma_{\Phi}}{\mathfrak{g}}_{\lambda}\right). \end{aligned}$$

It is possible to give results analogous to the previous Lie algebra decompositions for the group G and the symmetric space M. For this, consider the connected Lie subgroups $A_\Phi$, $N_\Phi$, and $S_\Phi$ of G with Lie algebras ${\mathfrak {a}}_\Phi$, ${\mathfrak {n}}_\Phi$, and ${\mathfrak {s}}_\Phi$, respectively. If we define $L_\Phi =Z_G({\mathfrak {a}}_\Phi )$ as the centralizer of ${\mathfrak {a}}_\Phi$ in G, then $L_\Phi$ is a Lie subgroup of G that normalizes $N_\Phi$. The subgroup $Q_\Phi =N_{G}({\mathfrak {q}}_{\Phi })=L_\Phi N_\Phi$ is the parabolic subgroup of G associated with $\Phi$. The decomposition $Q_\Phi =L_\Phi N_\Phi$ is known as the Chevalley decomposition of $Q_{\Phi }$.

Define $K_{\Phi }=Z_K{({\mathfrak {a}}_{\Phi })}$, which is a Lie subgroup of G with Lie algebra ${\mathfrak {k}}_\Phi$. It is a maximal compact subgroup of $L_\Phi$ which normalizes $S_\Phi$. The subgroup $M_\Phi =K_\Phi S_\Phi$ is a reductive subgroup of G with Lie algebra ${\mathfrak {m}}_{\Phi }$. Moreover, the multiplication map $A_\Phi \times N_\Phi \times M_\Phi \rightarrow Q_\Phi$ is a diffeomorphism, known as the Langlands decomposition of the parabolic subgroup $Q_\Phi$.

Consider now the orbit $B_\Phi$ of the isometric action of $M_{\Phi }$ through o. Since ${\mathfrak {b}}_\Phi$ is a Lie triple system,

$$\displaystyle \begin{aligned} B_{\Phi}=M_\Phi\cdot o=S_\Phi\cdot o\cong M_\Phi/K_\Phi\cong S_\Phi/(K_\Phi\cap S_\Phi) \end{aligned}$$

is a totally geodesic submanifold of M, called the boundary component of M associated with the subset of simple roots $\Phi$. Intrinsically, $B_\Phi$ turns out to be a symmetric space of noncompact type and rank $|\Phi |$. In fact, since $S_\Phi$ is a connected semisimple Lie group and $K_\Phi \cap S_\Phi$ a maximal compact subgroup of $S_\Phi$, $(S_\Phi ,K_\Phi \cap S_\Phi )$ is a symmetric pair for $B_\Phi$. The Langlands decomposition of $Q_\Phi$ induces a diffeomorphism at the manifold level, given by

$$\displaystyle \begin{aligned} A_\Phi\times N_\Phi\times B_\Phi\rightarrow M, \qquad (a,n,m\cdot o)\mapsto (anm)\cdot o. \end{aligned}$$

This diffeomorphism is known as the horospherical decomposition of the symmetric space M corresponding to the subset $\Phi \subset \Lambda$ of simple roots.

The horospherical decomposition can be restated in terms of an isometric action on M with some interesting geometric properties. The connected solvable Lie group $A_\Phi N_\Phi$ acts freely and isometrically on M, and its orbits are mutually congruent minimally embedded submanifolds of M. Moreover, the totally geodesic submanifold $B_\Phi$ of M intersects each $A_\Phi N_\Phi$-orbit exactly once and perpendicularly. These properties are fundamental in a geometric extension procedure of submanifolds from $B_\Phi$ to M called canonical extension (see [35]). Its application to the extension of cohomogeneity one actions will be discussed in Sect. 6.

4 Homogeneous Hypersurfaces in Compact Symmetric Spaces

In this section, we give an overview of the classification problem of homogeneous hypersurfaces in compact symmetric spaces. We will mostly focus on the spherical case (Sect. 4.1), since it admits a more elementary approach and showcases very interesting geometric properties. Then, in Sect. 4.2, we will consider the case of the other compact symmetric spaces, with special focus on the rank one setting.

4.1 Homogeneous Hypersurfaces of Round Spheres

The classification of homogeneous hypersurfaces in round spheres had to wait more than 30 years after Segre’s and Cartan’s works on Euclidean and real hyperbolic spaces. The classification in round spheres was achieved by Hsiang and Lawson [55] and revisited by Takagi and Takahashi [95], who calculated the principal curvatures of such homogeneous hypersurfaces. Their works provide a very interesting family of examples, which surprisingly turns out to be characterized by a subclass of symmetric spaces, as we will comment on below. But before explaining their results, let us consider some examples.

Recall that a homogeneous hypersurface is isoparametric with constant principal curvatures, and hence, the multiplicities of such principal curvatures are constant. We will denote by g the number of distinct constant principal curvatures. Notice also that cohomogeneity one actions on $\mathbb {S}^n$, $n\geq 2$, must have orbit space of type $[0,1]$, in view of Remark 2. The simplest example of cohomogeneity one action on spheres was given in Example 1 (d) as the standard action of ${\mathsf {SO}}_{n}$ on the unit sphere $\mathbb {S}^n$. Note that its regular orbits (the parallels) are totally umbilical ($g=1$) and there are exactly two singular orbits (the poles). Observe that a geodesic of $\mathbb {S}^n$ normal to one orbit (and hence to all orbits) intersects the singular orbits at points separated by distance $\pi$. Let us see how this generalizes to more interesting examples.

Example 3

Consider the action of $H={\mathsf {U}}_1\times {\mathsf {U}}_1$ on ${\mathbb {C}}^2\cong {\mathbb {R}}^4$ given by $(e^{i\theta _1},e^{i\theta _2})\cdot (z_1,z_2)=(e^{i\theta _1}z_1,e^{i\theta _2}z_2)$. Since it is an isometric action for the Euclidean metric on ${\mathbb {R}}^4$, it leaves the unit sphere of ${\mathbb {R}}^4$ invariant, so it induces an isometric action on the unit sphere $\mathbb {S}^3$. It is easy to calculate that the isotropy groups at points of the form $(z_1,0)$ or $(0,z_2)$ are isomorphic to ${\mathsf {U}}_1$, whereas the stabilizers at any other point are trivial. Thus, there are exactly two singular orbits, $H\cdot (1,0)$ and $H\cdot (0, 1)$, which are totally geodesic circles in $\mathbb {S}^3$, and the remaining orbits are principal and diffeomorphic to tori $\mathbb {S}^1\times \mathbb {S}^1$. Among these tori, exactly one turns out to be minimal, namely, $H\cdot \bigl (\frac {1}{\sqrt {2}},\frac {1}{\sqrt {2}}\bigr )$: the Clifford torus. The principal orbits have $g=2$ distinct principal curvatures. Any normal geodesic to the orbit foliation (e.g., $\gamma (t)=(\cos t, \sin t)\in {\mathbb {C}}^2$) intersects the singular orbits at four equidistributed points ($(\pm 1, 0)$ and $(0,\pm 1)$). This action of ${\mathsf {U}}_1\times {\mathsf {U}}_1\cong {\mathsf {SO}}_2\times {\mathsf {SO}}_2$ on $\mathbb {S}^3$ can easily be generalized to a cohomogeneity one action of ${\mathsf {SO}}_{k+1}\times {\mathsf {SO}}_{n-k}$ on $\mathbb {S}^n$, $k=1,\dots , n-2$, with totally geodesic singular orbits $\mathbb {S}^{k}$ and $\mathbb {S}^{n-k-1}$ and principal orbits $\mathbb {S}^{k}\times \mathbb {S}^{n-k-1}$ with $g=2$.

Example 4

Let $\mathrm {Herm}_3^0({\mathbb {R}})$ denote the vector space of real symmetric matrices of order 3 and trace 0, endowed with the standard inner product $\langle X,Y\rangle = \operatorname {\mathrm {tr}} XY$. Hence, $\mathrm {Herm}_3^0({\mathbb {R}})$ is a Euclidean space ${\mathbb {R}}^5$. The smooth action of $H={\mathsf {SO}}_3$ on $\mathrm {Herm}_3^0({\mathbb {R}})$ by conjugation, $A\cdot X=AXA^t$, is clearly isometric. We consider its induced isometric action on the unit sphere $\mathbb {S}^4$ of $\mathrm {Herm}_3^0({\mathbb {R}})\cong {\mathbb {R}}^5$. The subset $\Sigma =\{X\in \mathbb {S}^4:X\text{ is diagonal}\}$ is the trace of a geodesic in $\mathbb {S}^4$ that intersects all H-orbits in $\mathbb {S}^4$ by the spectral theorem. One can easily compute the stabilizers at the points of $\Sigma$. These stabilizers are larger when $X\in \Sigma$ has two equal entries in the diagonal, which happens when X has diagonal entries $\frac {1}{\sqrt {6}},\frac {1}{\sqrt {6}},-\frac {2}{\sqrt {6}}$ or $-\frac {1}{\sqrt {6}},-\frac {1}{\sqrt {6}},\frac {2}{\sqrt {6}}$ (reordered in any way). Notice that these six points are equidistributed along the great circle $\Sigma$. For these six points X in $\Sigma$, we have $H_X\cong {\mathsf {S}}({\mathsf {O}}_2\times {\mathsf {O}}_1)\cong {\mathsf {O}}_2$. The other points X in $\Sigma$ have finite isotropy group. Therefore, the regular orbits have dimension $\dim {\mathsf {SO}}_3=3$, and hence, we have a cohomogeneity one action on $\mathbb {S}^4$. There are two singular orbits (one passing through the diagonal matrices with diagonal entries $\frac {1}{\sqrt {6}},\frac {1}{\sqrt {6}},-\frac {2}{\sqrt {6}}$ and the other passing through the diagonal matrices with the opposite entries). These are diffeomorphic to real projective planes, $H/H_X\cong {\mathsf {SO}}_3/{\mathsf {O}}_3\cong {\mathbb {R}} {\mathsf {P}}^2$, which are minimally embedded in $\mathbb {S}^4$. One can show that the principal orbits of this action have $g=3$ principal curvatures.

Example 5

The previous action in Example 4 is the simplest one of a collection of four cohomogeneity one actions on the unit spheres $\mathbb {S}^4$, $\mathbb {S}^7$, $\mathbb {S}^{13}$, and $\mathbb {S}^{25}$ of the space $\mathrm {Herm}_3^0(\mathbb {F})$ of trace-free Hermitian matrices of order three with coefficients in some normed division algebra $\mathbb {F}\in \{{\mathbb {R}},{\mathbb {C}},{\mathbb {H}},\mathbb {O}\}$, with inner product $\langle X,Y\rangle =\mathrm {Re}( \operatorname {\mathrm {tr}} XY)$. The respective groups acting upon are ${\mathsf {SO}}_3$, ${\mathsf {SU}}_3$, ${\mathsf {Sp}}_3$, and ${\mathsf {F}}_4$. These actions produce homogeneous hypersurfaces with $g=3$ principal curvatures (all of them with the same multiplicity $m\in \{1,2,4,8\}$) which are tubes around certain minimal embeddings of the projective planes ${\mathbb {R}} {\mathsf {P}}^2$, ${\mathbb {C}} {\mathsf {P}}^2$, ${\mathbb {H}} {\mathsf {P}}^2$, and $\mathbb {O} {\mathsf {P}}^2$, respectively. Of particular interest is the octonionic case, as it provides one of the simplest models of the exceptional Lie group ${\mathsf {F}}_4$, as well as of the Cayley projective plane $\mathbb {O}{\mathsf {P}}^2$. Indeed, ${\mathsf {F}}_4$ can be defined as the automorphism group of the Jordan algebra $\mathrm {Herm}_3(\mathbb {O})$ with multiplication $X\circ Y=\frac {1}{2}(XY+YX)$. Similarly as in Example 4, the minimally embedded Cayley projective planes are obtained as the orbits through $\operatorname {\mathrm {diag}}(\frac {1}{\sqrt {6}},\frac {1}{\sqrt {6}},-\frac {2}{\sqrt {6}})$ and $\operatorname {\mathrm {diag}}(-\frac {1}{\sqrt {6}},-\frac {1}{\sqrt {6}},\frac {2}{\sqrt {6}})\in \mathrm {Herm}_3^0(\mathbb {O})$ of the action of the automorphism group ${\mathsf {F}}_4$ on the unit sphere $\mathbb {S}^{25}$ of $\mathrm {Herm}_3^0(\mathbb {O})$. For more information on these actions, we refer the reader to the discussion in [78, §3.3.3], which is based on [2, §3], [6, p. 86], and [51, pp. 289–292].

The homogeneous hypersurfaces described in the examples above were characterized by Cartan [23] as the only (complete) isoparametric hypersurfaces in round spheres with up to $g=3$ distinct principal curvatures. Whereas the examples with $g\in \{1,2\}$ arise in spheres $\mathbb {S}^n$ of any dimension ($n\geq 3$ if $g=2$), examples with $g=3$ are restricted to four possible dimensions $n\in \{4,7,13,25\}$. Cartan [24] also initiated the study of isoparametric hypersurfaces with $g=4$ and was able to produce two examples in $\mathbb {S}^5$ and $\mathbb {S}^9$. These are recovered in the following two constructions:

Example 6

Let $\mathcal {M}_{2\times k}(\mathbb {F})$ denote the vector space of $2\times k$ matrices with entries in $\mathbb {F}\in \{{\mathbb {R}},{\mathbb {C}},\mathbb {H}\}$, endowed with the standard inner product $\langle X,Y\rangle = \operatorname {\mathrm {tr}} XY^*$, where $(\cdot )^*$ denotes conjugate transpose. In order to settle ideas, assume $\mathbb {F}={\mathbb {R}}$. Consider the isometric action of $H={\mathsf {SO}}_2\times {\mathsf {SO}}_k$ on $\mathcal {M}_{2\times k}({\mathbb {R}})$ by $(A,B)\cdot X=AXB^*$ and then its restriction to the unit sphere $\mathbb {S}^{2k-1}$ of $\mathcal {M}_{2\times k}({\mathbb {R}})\cong {\mathbb {R}}^{2k}$. The geodesic of $\mathbb {S}^{2k-1}$ given by

$$\displaystyle \begin{aligned} \gamma(t)=\begin{pmatrix} \cos t & 0 & 0 &\dots &0 \\ 0 & \sin t & 0&\dots &0 \end{pmatrix} \end{aligned}$$

intersects all H-orbits in $\mathbb {S}^{2k-1}$ and always perpendicularly (again, it suffices to check this at one point, say for $t=0$). One can compute the stabilizers of the points in this geodesic, obtaining that for any $t\notin \{\ell \frac {\pi }{4}:\ell \in \mathbb {Z}\}$, $\gamma (t)$ belongs to a principal orbit of codimension one in $\mathbb {S}^{2k-1}$. Moreover, for any $\ell \in \mathbb {Z}$, $\gamma \bigl (\ell \frac {\pi }{2}\bigr )$ belongs to a singular orbit of dimension k, and $\gamma \bigl (\frac {\pi }{4}+\ell \frac {\pi }{2}\bigr )$ belongs to a singular orbit of dimension $2k-3$. Again, the singular points along the normal geodesic $\gamma$ are equidistributed. The homogeneous hypersurfaces arising from this action turn out to have $g=4$ principal curvatures with multiplicities 1, 1, $k-2$, and $k-2$. Cartan’s example with $g=4$ in $\mathbb {S}^5$ corresponds to $k=3$. The discussion for $\mathbb {F}\in \{{\mathbb {C}},{\mathbb {H}}\}$ is analogous by considering the actions of ${\mathsf {U}}_2\times {\mathsf {U}}_k$ on the unit sphere $\mathbb {S}^{4k-1}$ of $\mathcal {M}_{2\times k}(\mathbb {C})$ and of ${\mathsf {Sp}}_2\times {\mathsf {Sp}}_k$ on the unit sphere $\mathbb {S}^{8k-1}$ of $\mathcal {M}_{2\times k}(\mathbb {H})$. In these cases, the distribution of singular points along a normal geodesic is the same as in the real case, but now the $g=4$ principal curvatures of the homogeneous hypersurfaces have multiplicities 2, 2, $2k-3$, $2k-3$ for the complex case and 4, 4, $4k-5$, $4k-5$ for the quaternionic case.

Example 7

Consider the action by conjugation of ${\mathsf {SO}}_5$ on its Lie algebra ${\mathfrak {so}}_5$ of skew-symmetric matrices, namely, $A\cdot X=AXA^t$. When ${\mathfrak {so}}_5$ is endowed with the standard inner product $\langle X,Y\rangle =- \operatorname {\mathrm {tr}} XY$, this action is isometric and hence induces an isometric action on the unit sphere $\mathbb {S}^{9}$ of ${\mathfrak {so}}_5$. The geodesic of $\mathbb {S}^9$ given by the block diagonal matrices

$$\displaystyle \begin{aligned} \gamma(t)=\frac{1}{\sqrt{2}}\operatorname{\mathrm{diag}}\left( \begin{pmatrix} 0 & \cos t \\ -\cos t & 0 \end{pmatrix}, \begin{pmatrix} 0 & \sin t \\ -\sin t & 0 \end{pmatrix}, 0\right) \end{aligned}$$

intersects all orbits and always perpendicularly. Similarly as in Example 6, $\gamma$ meets the two singular orbits at $t\in \{\ell \frac {\pi }{4}:\ell \in \mathbb {Z}\}$, and these singular orbits have dimension 6. The principal orbits are homogeneous hypersurfaces of $\mathbb {S}^9$ with $g=4$ principal curvatures, all of them with multiplicity 2.

All the actions above fit into a general construction: they are induced by isotropy representations of symmetric spaces of rank 2. This is, roughly speaking, what Hsiang and Lawson proved in [55] for arbitrary cohomogeneity one actions on round spheres.

Let us recall from Sect. 3 that if $M\cong G/K$ is a symmetric space, where K is the isotropy in G of some point $o\in M$, then K acts on the tangent space $T_oM$ by the differential of the isometries in K. That is, we have a smooth action $K\times T_oM\to T_oM$ given by $k\cdot v=k_{*o}v$. This action is equivalent to the adjoint representation of K on ${\mathfrak {p}}$, that is, $K\times {\mathfrak {p}}\to {\mathfrak {p}}$, $k\cdot X= \operatorname {\mathrm {Ad}}(k)X$. Each one of these actions is called the isotropy representation of M.

Since K is made of isometries of M, the isotropy representation is an isometric action on $T_oM\cong {\mathfrak {p}}$. Hence, it restricts to an isometric action on the unit sphere $\mathbb {S}^{\dim M-1}$ of $T_oM\cong {\mathfrak {p}}$. Any maximal abelian subspace ${\mathfrak {a}}$ of ${\mathfrak {p}}$ turns out to intersect all the orbits of the isotropy representation and always perpendicularly (see [6, §2.3.2] for a proof). Hence, ${\mathfrak {a}}\cap \mathbb {S}^{\dim M-1}$ is a totally geodesic submanifold of $\mathbb {S}^{\dim M-1}$ that intersects all the orbits of the restricted action to the unit sphere of $T_oM\cong {\mathfrak {p}}$ perpendicularly. By dimension reasons, if we want this restricted action on $\mathbb {S}^{\dim M-1}$ to be of cohomogeneity one, we just need to impose that ${\mathfrak {a}}\cap \mathbb {S}^{\dim M-1}$ has dimension 1 or, equivalently, that $\dim {\mathfrak {a}}=2$. But $\dim {\mathfrak {a}}$ is, by definition, the rank of the symmetric space M. Hence, we are led to the conclusion that the restriction of the isotropy representation of a symmetric space M to the unit sphere of the tangent space is of cohomogeneity one precisely when M has rank two. Up to orbit equivalence, these actions exhaust all cohomogeneity one actions on spheres, by Hsiang and Lawson’s theorem.

Theorem 1 (Homogeneous Hypersurfaces in Round Spheres)

Any homogeneous hypersurface of a round sphere is congruent to a principal orbit of the action obtained by restriction to the unit sphere of the isotropy representation of a symmetric space of rank two.

For the whole list of symmetric spaces, see [53, pp. 516, 518], or [38, Table 2] for the list of the rank 2 symmetric spaces of compact type.

Example 8

The compact symmetric spaces whose isotropy representations induce the examples considered above in this section are the following:

• (1) Example 1 (d): $M=\mathbb {S}^n\times \mathbb {S}^1\cong ({\mathsf {SO}}_{n+1}/{\mathsf {SO}}_n) \times \mathbb {S}^1$, since in this case $K={\mathsf {SO}}_n$ and $T_oM=T_{v}\mathbb {S}^n\times {\mathbb {R}}$.

• (2) Example 3: $M=\mathbb {S}^{k+2}\times \mathbb {S}^{n-k+1}$.

• (3) Example 4: $M={\mathsf {SU}}_3/{\mathsf {SO}}_3$.

• (4) Example 5: M is ${\mathsf {SO}}_6/{\mathsf {SU}}_3$, ${\mathsf {SU}}_6/{\mathsf {Sp}}_3$, or the exceptional space ${\mathsf {E}}_6/{\mathsf {F}}_4$.

• (5) Example 6: M is ${\mathsf {SO}}_{2+k}/{\mathsf {SO}}_2{\mathsf {SO}}_k$, namely, the Grassmannian of oriented 2-planes of ${\mathbb {R}}^{2+k}$ or ${\mathsf {U}}_{2+k}/{\mathsf {U}}_2{\mathsf {U}}_k\cong {\mathsf {SU}}_{2+k}/{\mathsf {S}}({\mathsf {U}}_2{\mathsf {U}}_k)$ or ${\mathsf {Sp}}_{2+k}/{\mathsf {Sp}}_2{\mathsf {Sp}}_k$, that is, the Grassmannians of complex or quaternionic 2-planes of ${\mathbb {C}}^{2+k}$ or ${\mathbb {H}}^{2+k}$, respectively.

• (6) Example 7: M is the compact Lie group ${\mathsf {SO}}_5$ with a bi-invariant metric.

In each of the previous cases, we have indicated a compact symmetric space, but there is also a noncompact symmetric space with equivalent isotropy representation, by duality. For instance, in item (3), M could be taken as ${\mathsf {SL}}_3({\mathbb {R}})/{\mathsf {SO}}_3$. In this case, its Cartan decomposition ${\mathfrak {g}}={\mathfrak {k}}\oplus {\mathfrak {p}}$ is nothing but the decomposition of ${\mathfrak {g}}={\mathfrak {sl}}_3({\mathbb {R}})$ into the sum of the subspace of skew-symmetric matrices ${\mathfrak {k}}={\mathfrak {so}}_3$ and the subspace ${\mathfrak {p}}=\mathrm {Herm}_3^0({\mathbb {R}})$ of trace-free symmetric matrices, and the isotropy representation $K\times {\mathfrak {p}}\to {\mathfrak {p}}$ agrees directly with the ${\mathsf {SO}}_3$-action by conjugation on $\mathrm {Herm}_3^0({\mathbb {R}})$ described in Example 4.

In the examples discussed in this section, we could see the following remarkable fact: a normal geodesic to the orbit foliation intersects the singular orbits in exactly 2g equidistributed points, where g agrees with the number of distinct principal curvatures of each one of the principal orbits. This is something that holds for any cohomogeneity one action on a round sphere (and more generally, for any isoparametric family, by Münzner’s seminal work [74]).

The number g of principal curvatures of homogeneous hypersurfaces in spheres, their multiplicities, and their actual values were calculated by Takagi and Takahashi [95]. Their description can be done in terms of the restricted root system $\Sigma$ associated with the symmetric space M of noncompact type whose isotropy representation induces the action. Let $X\in {\mathfrak {a}}\cap \mathbb {S}^{\dim M-1}$ be a point in a geodesic of $\mathbb {S}^{\dim M-1}$ that is orthogonal to the orbits of the isotropy representation $K\times {\mathfrak {p}}\to {\mathfrak {p}}$. Assume that X lies in a principal orbit. Let $\xi$ be a unit normal vector to the hypersurface $K\cdot X$, i.e., $\xi$ spans $T_X({\mathfrak {a}}\cap \mathbb {S}^{\dim M-1})$. Then, the principal curvatures of $K\cdot X$ are of the form $\mu _\alpha =-\alpha (\xi )/\alpha (X)$, for each positive root $\alpha \in \Sigma ^+$. Note that if $\alpha , 2\alpha \in \Sigma ^+$, then both roots have the same associated principal curvature, $\mu _\alpha =\mu _{2\alpha }$. Thus, the number g of principal curvatures of a homogeneous hypersurface is precisely the cardinality of the set of reduced positive roots. It is a standard fact of root systems that those of rank 2 have exactly 2, 3, 4 or 6 reduced roots (see [60, Figure 2.2 in p. 151]). This immediately gives that $g\in \{1,2,3,4,6\}$; the case $g=1$ arises since the symmetric space can have a flat factor (see Example 8 (1)), and then the associated root system is of rank 1. The multiplicities correspond to the multiplicities of the positive roots. Specifically, the multiplicity of the principal curvature $\mu _\alpha$ associated with the reduced positive root $\alpha$ is $m_\alpha =\dim {\mathfrak {g}}_\alpha \oplus {\mathfrak {g}}_{2\alpha }$. We refer to [6, §2.3.2 and §2.7] for more details and to [74, §2, Satz 1] or [78, Teorema 3.8] for an alternative description in the general setting of isoparametric hypersurfaces.

4.2 Homogeneous Hypersurfaces in the Other Compact Symmetric Spaces

In this subsection, we will review the classification problem of homogeneous hypersurfaces in compact symmetric spaces of nonconstant curvature. We will mainly focus on the rank one setting.

The simply connected Riemannian symmetric spaces of compact type and rank one are the sphere $\mathbb {S}^n$ and the projective spaces ${\mathbb {C}}{\mathsf {P}}^n$, ${\mathbb {H}}{\mathsf {P}}^n$, and $\mathbb {O}{\mathsf {P}}^2$ ($n\geq 2$). They can be described by a symmetric pair $(G,K)$ as specified in Table 1.

Table 1 Data for the sphere and the projective spaces

The classification problem for the complex projective space was solved by Takagi [96].

Theorem 2 (Homogeneous Hypersurfaces in Complex Projective Spaces)

A homogeneous hypersurface in a complex projective space ${\mathbb {C}}{\mathsf {P}}^n$ is congruent to one of the following:

• (1) A geodesic sphere

• (2) A tube around a totally geodesic${\mathbb {C}}{\mathsf {P}}^k$in${\mathbb {C}}{\mathsf {P}}^n$, $k\in \{1,\dots ,n-1\}$

• (3) A tube around a totally geodesic ${\mathbb {R}}{\mathsf {P}}^{n}$ in ${\mathbb {C}}{\mathsf {P}}^n$

• (4) A tube around the Segre embedding of ${\mathbb {C}}{\mathsf {P}}^1\times {\mathbb {C}}{\mathsf {P}}^k$ into ${\mathbb {C}}{\mathsf {P}}^n$ with $n=2k+1$ odd, $k\geq 1$

• (5) A tube around the Plücker embedding of the complex Grassmannian ${\mathsf {G}}_2({\mathbb {C}}^5)$ into ${\mathbb {C}}{\mathsf {P}}^9$

• (6) A tube around the half spin embedding of ${\mathsf {SO}}_{10}/{\mathsf {U}}_5$ into ${\mathbb {C}}{\mathsf {P}}^{15}$

A remarkable observation, similar to the discussion above in spheres and which follows from the work of Takagi [96] and later by Podestà and Thorbergsson [79], is that a homogeneous hypersurface in the complex projective space ${\mathbb {C}}{\mathsf {P}}^n$ is congruent to the quotient of a principal orbit of the isotropy representation of a Hermitian symmetric space of rank two. We will develop this idea a bit further before commenting on the different items of the classification given by Theorem 2.

Let $M\cong G/K$ be a Hermitian symmetric space of rank two. Being Hermitian means that M has a complex structure that is invariant under each geodesic symmetry. Then, M has even dimension, and we write $\dim M=2n+2$. Consider the base point $o\cong eK$. The isotropy representation of M is the action $K\times T_o M\to T_o M$, $(k,v)\mapsto k_{*e}v$. Since $T_o M\cong {\mathbb {R}}^{2n+2}\cong {\mathbb {C}}^{n+1}$ and the elements of K act as linear holomorphic isometries of ${\mathbb {C}}^{n+1}$, this action can be restricted to an action on the unit sphere $\mathbb {S}^{2n+1}\subset {\mathbb {C}}^{n+1}$. As discussed in the previous subsection, this action on the unit sphere is of cohomogeneity one. Moreover, the action on ${\mathbb {C}}^{n+1}$ is polar and with totally real section, that is, there exists a totally real plane in ${\mathbb {C}}^{n+1}$ that intersects all the orbits of the isotropy representation, and, at the points of intersection, the plane and the orbits are orthogonal. Since this action maps complex lines of ${\mathbb {C}}^{n+1}$ to complex lines of ${\mathbb {C}}^{n+1}$, it descends to a cohomogeneity one action on the projectivization ${\mathsf {P}}({\mathbb {C}}^{n+1})\cong {\mathbb {C}}{\mathsf {P}}^n$.

In order to obtain the classification in Theorem 2, it is therefore enough to consider the classification of (possibly reducible) Hermitian symmetric spaces of rank two and calculate their induced isotropy representations on the corresponding projectivization of the tangent space at the point where the isotropy is considered. See [53, X.6], taking into account the possible coincidences between different classes.

Tubes around totally geodesic ${\mathbb {C}}{\mathsf {P}}^k$, $k\in \{0,\dots ,n-1\}$, are principal orbits of the action of ${\mathsf {U}}_{k+1}\times {\mathsf {U}}_{n-k}$. This action comes from the isotropy representation of the reducible symmetric space ${\mathbb {C}}{\mathsf {P}}^{k+1}\times {\mathbb {C}}{\mathsf {P}}^{n-k}=({\mathsf {SU}}_{k+2}\times {\mathsf {SU}}_{n-k+1})/({\mathsf {S}}({\mathsf {U}}_1\times {\mathsf {U}}_{k+1})\times {\mathsf {S}}({\mathsf {U}}_1\times {\mathsf {U}}_{n-k}))$. If $k=0$, we recover geodesic spheres.

The real oriented two-plane Grassmannian ${\mathsf {G}}_2^+({\mathbb {R}}^{n+3})={\mathsf {SO}}_{n+3}/{\mathsf {SO}}_2\times {\mathsf {SO}}_{n+1}$ induces an action of ${\mathsf {SO}}_{n+1}$ on ${\mathbb {C}}{\mathsf {P}}^n$ with two singular orbits: a totally geodesic real projective space ${\mathbb {R}}{\mathsf {P}}^n$ and the complex quadric ${\mathsf {Q}}^{n-1}=\{[z]\in {\mathbb {C}}{\mathsf {P}}^n:{z_0^2+\dots +z_n^2=0}\}$.

Similarly, the complex two-plane Grassmannian ${\mathsf {G}}_2({\mathbb {C}}^{k+3})={\mathsf {SU}}_{k+3}/{\mathsf {S}}({\mathsf {U}}_2{\mathsf {U}}_{k+1})$ induces an action on ${\mathbb {C}}{\mathsf {P}}^{2k+1}$, one of whose singular orbits is the Segre embedding of ${\mathbb {C}}{\mathsf {P}}^1\times {\mathbb {C}}{\mathsf {P}}^k$ in ${\mathbb {C}}{\mathsf {P}}^{2k+1}$. This is an embedding of a product of projective spaces onto another projective space of suitable dimension, where homogeneous coordinates are multiplied out. In our case, this embedding is given by the map ${\mathbb {C}}{\mathsf {P}}^1\times {\mathbb {C}}{\mathsf {P}}^k\to {\mathbb {C}}{\mathsf {P}}^{2k+1}$, $([z_0:z_1],[w_0:\dots :w_k])\mapsto [z_0w_0:\dots :z_0w_k:z_1w_0:\dots :z_1w_k]$.

The Plücker embedding is another classical embedding into a complex projective space. In this case, we embed a Grassmannian of k-planes into the projectivization of the space of k-forms. For ${\mathsf {G}}_2({\mathbb {C}}^5)$ into ${\mathsf {P}}(\Lambda ^2{\mathbb {C}}^5)\cong {\mathbb {C}}{\mathsf {P}}^9$, this embedding is defined by $\operatorname {\mathrm {span}}\{v_1,v_2\}\mapsto {[v_1\wedge v_2]}$. Tubes around this submanifold are homogeneous and correspond to the principal orbits of the cohomogeneity one action induced by the isotropy representation of the Hermitian symmetric space ${\mathsf {SO}}_{10}/{\mathsf {U}}_5$.

Finally, the Hermitian symmetric space ${\mathsf {E}}_6/{\mathsf {U}}_1{\mathsf {Spin}}_{10}$ induces a cohomogeneity one action on ${\mathbb {C}}{\mathsf {P}}^{15}$. One of the singular orbits of this action is the half spin embedding of the symmetric space ${\mathsf {SO}}_{10}/{\mathsf {U}}_5$. We refer to [25, §7.5] for further details on this embedding.

The classification problem in quaternionic projective space is attributed to D’Atri [28] and Iwata [56].

Theorem 3 (Homogeneous Hypersurfaces in Quaternionic Projective Spaces)

A homogeneous hypersurface in a quaternionic projective space ${\mathbb {H}}{\mathsf {P}}^n$ is congruent to one of the following:

• (1) A geodesic sphere

• (2) A tube around a totally geodesic${\mathbb {H}}{\mathsf {P}}^k$in${\mathbb {H}}{\mathsf {P}}^n$, $k\in \{1,\dots ,n-1\}$

• (3) A tube around a totally geodesic ${\mathbb {C}}{\mathsf {P}}^{n}$ in ${\mathbb {H}}{\mathsf {P}}^n$

The action of ${\mathsf {Sp}}_{k+1}\times {\mathsf {Sp}}_{n-k}$ on ${\mathbb {H}}{\mathsf {H}}^k$ is of cohomogeneity one, and its principal orbits are tubes around totally geodesic quaternionic projective spaces ${\mathbb {H}}{\mathsf {P}}^k$, $k\in \{0,\dots ,n-1\}$. If $k=0$, we retrieve geodesic spheres. The principal orbits of the action of ${\mathsf {U}}_{n+1}$ on ${\mathbb {H}}{\mathsf {P}}^n$ are tubes around a totally geodesic ${\mathbb {C}}{\mathsf {P}}^n$.

It can be shown [79] that a cohomogeneity one action on a quaternionic projective space is induced by the isotropy representation of a product of two quaternionic Kähler symmetric spaces of rank one or of an irreducible quaternionic Kähler symmetric space of rank two. Thus, an alternative way of getting the list of Theorem 3 is to look at the corresponding list of these spaces, which turns out to be ${\mathbb {H}}{\mathsf {P}}^{k+1}\times {\mathbb {H}}{\mathsf {P}}^{n-k}$ and ${\mathsf {SU}}_{n+3}/{\mathsf {S}}({\mathsf {U}}_2\times {\mathsf {U}}_{n+1})$.

We finish our review of homogeneous hypersurfaces in rank one symmetric spaces of compact type recalling the classification result for the Cayley projective plane given by Iwata [57].

Theorem 4 (Homogeneous Hypersurfaces in the Cayley Projective Plane)

A homogeneous hypersurface in the Cayley projective plane $\mathbb {O}{\mathsf {P}}^2$ is congruent to one of the following:

• (1) A geodesic sphere

• (2) A tube around a totally geodesic ${\mathbb {H}}{\mathsf {P}}^2$ in $\mathbb {O}{\mathsf {P}}^2$

A geodesic sphere can be seen as a principal orbit of the isotropy action of ${\mathsf {Spin}}_9$ on $\mathbb {O}{\mathsf {P}}^2$. This action has two singular orbits: a fixed point and a totally geodesic $\mathbb {S}^8=\mathbb {O}{\mathsf {P}}^1$. The second example in this classification is congruent to a principal orbit of the action of ${\mathsf {Sp}}_3{\mathsf {Sp}}_1$, which has two singular orbits: a totally geodesic ${\mathbb {H}}{\mathsf {P}}^2$ and a minimal $\mathbb {S}^{11}={\mathsf {Sp}}_3{\mathsf {Sp}}_1/{\mathsf {Sp}}_2{\mathsf {Sp}}_1$. As pointed out by Iwata, there are two more groups, up to conjugation, with the same orbits as ${\mathsf {Sp}}_3{\mathsf {Sp}}_1$. These are ${\mathsf {Sp}}_3{\mathsf {U}}_1$ and ${\mathsf {Sp}}_3$. Unlike the results presented here, Iwata’s classification was obtained up to conjugation by an element of ${\mathsf {F}}_4$, not up to orbit equivalence.

Remark 4

We would like to point out that there is a classification of isoparametric families of hypersurfaces in complex projective spaces ${\mathbb {C}}{\mathsf {P}}^n$, $n\neq 15$ [36], and in quaternionic projective spaces ${\mathbb {H}} {\mathsf {P}}^n$, $n\neq 7$ [39]. It follows from these classifications that there are inhomogeneous examples of isoparametric hypersurfaces in complex and quaternionic projective spaces. However, the classification problem of isoparametric hypersurfaces in the Cayley projective plane is still open [99].

All these results were generalized by Kollross [61], who classified cohomogeneity one actions on irreducible symmetric spaces of compact type up to orbit equivalence. Thus, homogeneous hypersurfaces in an irreducible symmetric space of compact type can be obtained via a case-by-case study of all these actions in each corresponding space.

Theorem 5 (Cohomogeneity One Actions on Irreducible Symmetric Spaces of Compact Type)

A cohomogeneity one action on an irreducible symmetric space of compact type is locally orbit equivalent to one of the following:

• (1) A Hermann action of cohomogeneity one

• (2) The action of $\{(g,\bar {g}):g\in {\mathsf {SU}}_3\}$ on ${\mathsf {SU}}_3$

• (3) An action induced by the isotropy representation of a symmetric space of rank two

• (4) One of the seven exceptions corresponding to the action of $H\times K$ on G or of the action of H on $G/K$ , where $(H,K,G)$ is a triple of Table 2

  Table 2 Seven exceptional cohomogeneity one actions on symmetric spaces of compact type

Let H and K be compact Lie subgroups of G. In Theorem 5 and in the discussion below, the isometric action of a product group $H\times K$ on a compact Lie group G with bi-invariant metric is given by

$$\displaystyle \begin{aligned} (h,k)\cdot g=hgk^{-1},\qquad h\in H,\; k\in K,\; g\in G. \end{aligned}$$

The action of a subgroup H of G on a compact symmetric space $G/K$ is given by $h\cdot gK=hgK$.

Let G be a compact semisimple Lie group. A subgroup K of G is called a symmetric subgroup of G if its Lie algebra is a fixed point set of an involutive automorphism of the Lie algebra of G. Then $(G,K)$ is a symmetric pair and $G/K$ a symmetric space of compact type if equipped with a suitable metric.

A Hermann action is the action of $H\times K$ on G defined above, where H and K are symmetric subgroups of G. The natural action of H on $G/K$ is also called a Hermann action, and it turns out that the action of $H\times K$ on G is of cohomogeneity one if and only if so is the action of H on $G/K$ (or the action of K on $G/H$). Thus, classifying cohomogeneity one Hermann H-actions on $G/K$ and classifying cohomogeneity one Hermann $H\times K$-actions on G are equivalent problems. Indeed, there is a correspondence between Hermann actions on symmetric spaces of type II (or group type), that is, compact simple Lie groups, and Hermann actions on symmetric spaces of type III, that is, compact symmetric spaces with simple isometry group, and this correspondence preserves the cohomogeneity.

Not any Hermann action is of cohomogeneity one, but it is possible to determine explicitly which ones are by looking at the classification of symmetric spaces of compact type. Obvious examples that fall into this category are isotropy actions of symmetric spaces $G/K$ of rank one and the corresponding $K\times K$ actions on G. However, there are a few more examples as shown in [61, Theorem B].

In Theorem 5 (2), the action of $\{(g,\bar {g}):g\in {\mathsf {SU}}_3\}$ on ${\mathsf {SU}}_3$ is given by $(g,\bar {g})\cdot g'=gg'\bar {g}^{-1}$. Here, $\bar {g}$ denotes the complex conjugation of a matrix g, which induces an outer Lie group automorphism of ${\mathsf {SU}}_3$.

Finally, we describe the actions in Theorem 5 (3). Let $\widehat {G}/\widehat {K}$ be a simply connected symmetric space of rank 2. Then, the isotropy representation of $\widehat {G}/\widehat {K}$ can be regarded as a Lie group homomorphism $\rho = \operatorname {\mathrm {Ad}}\vert _{\widehat {K}}\colon \widehat {K}\to {\mathsf {SO}}(\widehat {{\mathfrak {p}}})\cong {\mathsf {SO}}_n$, where $\widehat {{\mathfrak {p}}}\cong T_{\widehat {o}}\widehat {G}/\widehat {K}$ and $n=\dim \widehat {G}/\widehat {K}$. If $\widehat {G}/\widehat {K}$ is Hermitian, then $\widehat {K}\cong K_h\cdot {\mathsf {U}}_1$, for some compact Lie group $K_h$, and we can regard the restriction of $\rho$ to $K_h$ as a homomorphism $\rho \vert _{K_h}\colon K_h\to {\mathsf {SU}}_n$, where $n=\dim _{\mathbb {C}} \widehat {G}/\widehat {K}$. If $\widehat {G}/\widehat {K}$ is quaternionic Kähler, then $\widehat {K}=K_q\cdot {\mathsf {Sp}}_1$, for some compact Lie group $K_q$, and we can regard the restriction of $\rho$ to $K_q$ as a homomorphism $\rho \vert _{K_q}\colon K_q\to {\mathsf {Sp}}_n$, where $n=\dim _{\mathbb {H}} \widehat {G}/\widehat {K}$. Then, the actions in item (3) of Theorem 5 correspond to the action of $H\times K$ on G and to the action of H on $G/K$, where $(H,K,G)$ is given in Table 3 and $\widehat {G}/\widehat {K}$ is a rank two symmetric space.

Table 3 Actions induced by isotropy representations of symmetric spaces of rank two

5 Homogeneous Hypersurfaces in Hyperbolic Spaces

In this section, we review the classification results of homogeneous hypersurfaces in rank one symmetric spaces of noncompact type. These are precisely the hyperbolic spaces over the normed real division algebras, namely, ${\mathbb {R}}{\mathsf {H}}^n$, ${\mathbb {C}} {\mathsf {H}}^n$, ${\mathbb {H}} {\mathsf {H}}^n$, and $\mathbb {O} {\mathsf {H}}^2$ ($n\geq 2$).

5.1 Homogeneous Hypersurfaces in Real Hyperbolic Spaces

The classification of homogeneous hypersurfaces in real hyperbolic spaces was solved in a classical paper by Cartan [22]. Actually, Cartan’s aim was to classify isoparametric hypersurfaces in Riemannian manifolds of constant curvature. He succeeded to get such classification in ${\mathbb {R}}{\mathsf {H}}^n$, but not in spheres, where the problem remained open for nearly a century. It follows from this classification that an isoparametric hypersurface in ${\mathbb {R}}{\mathsf {H}}^n$ is an open part of a homogeneous hypersurface. This implies the classification of homogeneous hypersurfaces in ${\mathbb {R}}{\mathsf {H}}^n$:

Theorem 6 (Homogeneous Hypersurfaces in Real Hyperbolic Spaces)

A homogeneous hypersurface in ${\mathbb {R}}{\mathsf {H}}^n$ is congruent to one of the following:

• (1) A geodesic sphere

• (2) A tube around a totally geodesic${\mathbb {R}}{\mathsf {H}}^k$, $k\in \{1,\dots ,n-2\}$, in${\mathbb {R}}{\mathsf {H}}^n$

• (3) A totally geodesic ${\mathbb {R}}{\mathsf {H}}^{n-1}$ or one of its equidistant hypersurfaces

• (4) A horosphere

Recall that the connected component of the identity of the isometry group of the real hyperbolic space ${\mathbb {R}}{\mathsf {H}}^n$ is ${\mathsf {SO}}^0_{1,n}$. A geodesic sphere is congruent to a principal orbit of the action of ${\mathsf {SO}}_{n}$ on ${\mathbb {R}}{\mathsf {H}}^n$. Similarly, a tube around a totally geodesic ${\mathbb {R}}{\mathsf {H}}^k$ in ${\mathbb {R}}{\mathsf {H}}^n$ is congruent to a principal orbit of the action of ${\mathsf {SO}}^0_{1,k}\times {\mathsf {SO}}_{n-k}$, $k\in \{1,\dots ,n-2\}$. If $k=0$, we recover the geodesic spheres, and if $k=n-1$, then ${\mathsf {SO}}^0_{1,n-1}$ acts with cohomogeneity one, but in this case, all orbits are principal; in particular, a totally geodesic ${\mathbb {R}}{\mathsf {H}}^{n-1}$ is also a homogeneous hypersurface. Finally, the horospheres are the orbits of the nilpotent part N of the Iwasawa decomposition of ${\mathsf {SO}}^0_{1,n}$ (see Sect. 3.3). It is remarkable that the horospheres are Euclidean spaces ${\mathbb {R}}^{n-1}$ embedded in ${\mathbb {R}}{\mathsf {H}}^{n}$ in a totally umbilical way [93, p. 14]; all horospheres of ${\mathbb {R}} {\mathsf {H}}^n$ are congruent to each other.

5.2 General Approach to Homogeneous Hypersurfaces in Hyperbolic Spaces

In the rest of this section, we address the classification problem for the remaining symmetric spaces of noncompact type and rank one. In this subsection, we review the algebraic structure theory of these spaces and explain the general approach for the classification of homogeneous hypersurfaces in this setting. In the subsequent subsections, we will describe the classification results separately for each family of spaces. We will use the notation introduced in Sect. 3.3.

Let $(G,K)$ be a symmetric pair representing the symmetric space $\mathbb {F}{\mathsf {H}}^n$, $\mathbb {F}\in \{{\mathbb {R}},{\mathbb {C}},{\mathbb {H}},\mathbb {O}\}$ ($n=2$ if $\mathbb {F}=\mathbb {O}$). Then, the root space decomposition of ${\mathfrak {g}}$, the Lie algebra of G, reads

$$\displaystyle \begin{aligned} {\mathfrak{g}}={\mathfrak{g}}_{-2\alpha}\oplus{\mathfrak{g}}_{-\alpha}\oplus{\mathfrak{g}}_0\oplus{\mathfrak{g}}_\alpha\oplus{\mathfrak{g}}_{2\alpha}, \end{aligned}$$

where ${\mathfrak {g}}_{2\alpha }={\mathfrak {g}}_{-2\alpha }=0$ in the case of the real hyperbolic space ${\mathbb {R}}{\mathsf {H}}^n$; the associated root system is otherwise nonreduced. Recall that ${\mathfrak {g}}_0={\mathfrak {k}}_0\oplus {\mathfrak {a}}$, where ${\mathfrak {a}}$ is one-dimensional. We denote by $K_0$ the connected subgroup of K whose Lie algebra is ${\mathfrak {k}}_0$. Then, the possibilities for G, K, and $K_0$ are summarized in Table 4.

Table 4 Data for each hyperbolic space

In this case, the nilpotent part of the Iwasawa decomposition of ${\mathfrak {g}}$ is simply ${\mathfrak {n}}={\mathfrak {g}}_\alpha \oplus {\mathfrak {g}}_{2\alpha }$. If ${\mathfrak {g}}_\alpha =0$, then ${\mathfrak {n}}$ is abelian. Otherwise, if ${\mathfrak {g}}_\alpha \neq 0$, it turns out that ${\mathfrak {g}}_{2\alpha }$ is the center of ${\mathfrak {n}}$ and the derived subalgebra of the nilpotent Lie algebra ${\mathfrak {n}}$, that is, $[{\mathfrak {n}},{\mathfrak {n}}]={\mathfrak {g}}_{2\alpha }$. We have $\dim {\mathfrak {g}}_{2\alpha }=\dim _{\mathbb {R}}\mathbb {F}-1$. In fact, ${\mathfrak {g}}_{2\alpha }$ can be interpreted as the imaginary part of $\mathbb {F}$; following this idea, there is a Clifford algebra representation $J\colon \mathrm {Cl}({\mathfrak {g}}_{2\alpha })\to \mathrm {End}({\mathfrak {g}}_\alpha )$ which turns ${\mathfrak {g}}_\alpha$ into a Clifford module. The restriction of J to ${\mathfrak {g}}_{2\alpha }$ gives rise to endomorphisms $J_Z$ of ${\mathfrak {g}}_\alpha$ that are defined by the relation

$$\displaystyle \begin{aligned} \langle [U,V],Z\rangle=\langle J_Z U,V\rangle,\qquad U, V\in{\mathfrak{g}}_\alpha, Z\in{\mathfrak{g}}_{2\alpha}. \end{aligned}$$

See [16] for further details. Moreover, ${\mathfrak {g}}_\alpha \cong \mathbb {F}^{n-1}$, and the action of $K_0$ on ${\mathfrak {g}}_\alpha$ is equivalent to the standard action.

We will now describe the possible types of cohomogeneity one actions that may arise on a rank one symmetric space of noncompact type and nonconstant curvature. The fact that the following types exhaust all actions follows from the various works of Berndt, Brück, and Tamaru [5, 12, 14]. In Sect. 6, we will describe a more general approach that holds for arbitrary rank.

• (1) If a cohomogeneity one action on $\mathbb {F}{\mathsf {H}}^n$ induces a regular foliation, then there are two options up to orbit equivalence [12]:

  • (a) The horosphere foliation, whose leaves are the orbits of the action of the nilpotent part of the Iwasawa decomposition of G, namely, the connected subgroup N with Lie algebra ${\mathfrak {n}}$

  • (b) The solvable foliation, whose leaves are the orbits of the subgroup S whose Lie algebra is ${\mathfrak {s}}={\mathfrak {a}}\oplus {\mathfrak {w}}\oplus {\mathfrak {g}}_{2\alpha }$, where ${\mathfrak {w}}$ is a real hyperplane of ${\mathfrak {g}}_\alpha$

• (2) In order to determine the cohomogeneity one actions on $\mathbb {F}{\mathsf {H}}^n$ that have a totally geodesic singular orbit, it is enough to determine which totally geodesic submanifolds of $\mathbb {F}{\mathsf {H}}^n$ have homogeneous tubes. Totally geodesic submanifolds of hyperbolic spaces have been classified. By calculating the stabilizer of each one of these submanifolds, as well as its slice representation (i.e., the linearized action on the normal space to the totally geodesic submanifold), one can conclude which ones give rise to cohomogeneity one actions [5].

• (3) Finally, it remains to study cohomogeneity one actions on $\mathbb {F}{\mathsf {H}}^n$ with a non-totally geodesic singular orbit. Berndt and Tamaru devised in [14] a procedure to address this case. In symmetric spaces of higher rank, this method is called the nilpotent construction, cf. Sect. 6.4. In brief, the classification of cohomogeneity one actions on $\mathbb {F}{\mathsf {H}}^n$ with a non-totally geodesic singular orbit reduces to the classification of the subspaces ${\mathfrak {w}}$ of ${\mathfrak {g}}_\alpha$ such that $N_{K_0}({\mathfrak {w}})$, the normalizer of ${\mathfrak {w}}$ in $K_0$, acts transitively on the unit sphere of ${\mathfrak {w}}^\perp ={\mathfrak {g}}_\alpha \ominus {\mathfrak {w}}$, the orthogonal complement of ${\mathfrak {w}}$ in ${\mathfrak {g}}_\alpha$, up to congruence by an element of $K_0$. In this case, the connected subgroup of $K_0AN\subset G$ whose Lie algebra is $N_{K_0}({\mathfrak {w}})\oplus {\mathfrak {a}}\oplus {\mathfrak {w}}\oplus {\mathfrak {g}}_{2\alpha }$ acts on $\mathbb {F}{\mathsf {H}}^n$ with cohomogeneity one. The subspaces ${\mathfrak {w}}\subset {\mathfrak {g}}_\alpha$ satisfying this condition have been classified in [14] for $\mathbb {F}\in \{{\mathbb {C}},\mathbb {O}\}$ and in [32] for $\mathbb {F}={\mathbb {H}}$.

5.3 Homogeneous Hypersurfaces in Complex Hyperbolic Spaces

The classification of homogeneous hypersurfaces in the complex case was obtained by Berndt and Tamaru in [14]. It can be stated as follows:

Theorem 7 (Homogeneous Hypersurfaces in Complex Hyperbolic Spaces)

A homogeneous hypersurface in ${\mathbb {C}}{\mathsf {H}}^n$ is congruent to one of the following:

• (1) A geodesic sphere

• (2) A tube around a totally geodesic${\mathbb {C}}{\mathsf {H}}^k$in${\mathbb {C}}{\mathsf {H}}^n$, $k\in \{1,\dots ,n-1\}$

• (3) A tube around a totally geodesic ${\mathbb {R}}{\mathsf {H}}^{n}$ in ${\mathbb {C}}{\mathsf {H}}^n$

• (4) A horosphere

• (5) A ruled homogeneous minimal Lohnherr hypersurface $W^{2n-1}_{\pi /2}$ or one of its equidistant hypersurfaces

• (6) A tube around a ruled homogeneous minimal Berndt–Brück submanifold$W^{2n-k}_\varphi$, for$k\in \{2,\dots , n-1\}$, $\varphi \in (0, \pi /2]$, where k is even if$\varphi \neq \pi /2$

Tubes around totally geodesic complex hyperbolic spaces ${\mathbb {C}}{\mathsf {H}}^k$, $k\in \{0,\dots ,n-1\}$, are congruent to the principal orbits of the action of ${\mathsf {S}}({\mathsf {U}}_{1,k}\times {\mathsf {U}}_{n-k})$. The particular case of $k=0$ corresponds to geodesic spheres. The principal orbits of the group ${\mathsf {SO}}^0_{1,n}$ produce tubes around a totally geodesic real hyperbolic space ${\mathbb {R}}{\mathsf {H}}^n$. Note that tubes around a totally geodesic ${\mathbb {R}}{\mathsf {H}}^k$, $k\in \{1,\dots ,n-1\}$, are not homogeneous because the normal space of ${\mathbb {R}}{\mathsf {H}}^k$ is a direct sum of a nontrivial totally real and a nontrivial complex subspace of a complex vector space and isometries of ${\mathbb {C}}{\mathsf {H}}^n$ are holomorphic. The group N gives rise to a horosphere foliation, whose orbits are isometric to generalized Heisenberg groups. All of the orbits of this action are principal and congruent to each other.

Item (5) in Theorem 7 corresponds to the solvable foliation, whereas example (6) corresponds to a nilpotent construction. We review them in more detail here. Let ${\mathfrak {w}}$ be a real subspace of ${\mathfrak {g}}_\alpha \cong {\mathbb {C}}^{n-1}$. We denote by J the complex structure of ${\mathfrak {g}}_\alpha \cong {\mathbb {C}}^{n-1}$. The Kähler angle of a nonzero $v\in {\mathfrak {w}}^\perp$ is the angle between Jv and ${\mathfrak {w}}^\perp$. We say that ${\mathfrak {w}}^\perp$ has constant Kähler angle $\varphi \in [0,\pi /2]$ if the Kähler angle of any nonzero vector of ${\mathfrak {w}}^\perp$ is $\varphi$. Examples of subspaces with constant Kähler angle are totally real subspaces, that is, $\langle J{\mathfrak {w}}^\perp ,{\mathfrak {w}}^\perp \rangle =0$, whose Kähler angle is $\pi /2$, and complex subspaces, that is, $J{\mathfrak {w}}^\perp ={\mathfrak {w}}^\perp$, whose Kähler angle is 0. Any angle $\varphi \in (0,\pi /2)$ can be achieved, and in this case, $\dim {\mathfrak {w}}^\perp =k$ is an even number. Two subspaces of ${\mathfrak {g}}_\alpha$ with the same dimension and Kähler angle are congruent by an isometry of $K_0$, and a basis of such a subspace can be written as

$$\displaystyle \begin{aligned} \{e_1,\cos{}(\varphi)Je_1+\sin{}(\varphi)Je_2,\dots,e_{2k-1},\cos{}(\varphi)Je_{2k-1}+\sin{}(\varphi)Je_{2k}\}, \end{aligned}$$

where $\{e_1,\dots ,e_{2k}\}$ is a ${\mathbb {C}}$-orthonormal subset in ${\mathfrak {g}}_\alpha \cong {\mathbb {C}}^{n-1}$.

It turns out that if ${\mathfrak {w}}^\perp$ has constant Kähler angle $\varphi$, then $N_{K_0}({\mathfrak {w}})$ acts transitively on the unit sphere of ${\mathfrak {w}}^\perp$. Berndt and Tamaru [14] showed that the connected subgroup of ${\mathsf {SU}}_{1,n}$ whose Lie algebra is $N_{K_0}({\mathfrak {w}})\oplus {\mathfrak {a}}\oplus {\mathfrak {w}}\oplus {\mathfrak {g}}_{2\alpha }$ acts on ${\mathbb {C}}{\mathsf {H}}^n$ with cohomogeneity one. We denote by $W^{2n-k}_\varphi$ the orbit through the origin $o\cong eK$ of this group, where k is its codimension. If ${\mathfrak {w}}$ is a hyperplane, then ${\mathfrak {w}}^\perp$ is one-dimensional and, thus, totally real. The corresponding action has exactly one minimal orbit, known as the Lohnherr hypersurface, and the rest of the orbits are equidistant hypersurfaces to it. If ${\mathfrak {w}}$ has codimension $k>1$, then there is exactly one singular orbit, known as a Berndt-Brück submanifold, and the rest of the orbits are tubes around it. Any Kähler angle is possible if $n\geq 3$. However, if $\varphi =0$, this construction reproduces the tubes around a totally geodesic ${\mathbb {C}}{\mathsf {H}}^k$, $k\in \{1,\dots ,n\}$, so it is removed from item (6) of Theorem 7 to avoid duplication.

Remark 5

Isoparametric hypersurfaces in ${\mathbb {C}}{\mathsf {H}}^n$ have been classified in [33]. It follows from this classification that a hypersurface in ${\mathbb {C}}{\mathsf {H}}^n$ is isoparametric if and only if it is an open part of a homogeneous hypersurface or of a tube around the orbit through the origin of the subgroup of $AN\subset {\mathsf {SU}}_{1,n}$ whose Lie algebra is ${\mathfrak {a}}\oplus {\mathfrak {w}}\oplus {\mathfrak {g}}_{2\alpha }$, where ${\mathfrak {w}}^\perp$ is a subspace of ${\mathfrak {g}}_\alpha$ with nonconstant Kähler angle. As a consequence, any isoparametric hypersurface in ${\mathbb {C}}{\mathsf {H}}^2$ is homogeneous, but there are infinitely many inhomogeneous examples in ${\mathbb {C}}{\mathsf {H}}^n$, $n\geq 3$.

5.4 Homogeneous Hypersurfaces in Quaternionic Hyperbolic Spaces

The classification of cohomogeneity one actions on quaternionic hyperbolic spaces ${\mathbb {H}}{\mathsf {H}}^n$ has recently been obtained in [32] by the first two authors and Rodríguez-Vázquez. The corresponding classification of homogeneous hypersurfaces can be read from there.

Theorem 8 (Homogeneous Hypersurfaces in Quaternionic Hyperbolic Spaces)

A homogeneous hypersurface in ${\mathbb {H}}{\mathsf {H}}^n$ is congruent to one of the following:

• (1) A geodesic sphere

• (2) A tube around a totally geodesic${\mathbb {H}}{\mathsf {H}}^k$in${\mathbb {H}}{\mathsf {H}}^n$, $k\in \{1,\dots ,n-1\}$

• (3) A tube around a totally geodesic ${\mathbb {C}}{\mathsf {H}}^n$ in ${\mathbb {H}}{\mathsf {H}}^n$

• (4) A horosphere

• (5) A homogeneous minimal hypersurface $P_1$ or one of its equidistant hypersurfaces

• (6) A tube around a homogeneous minimal submanifold $P_{{\mathfrak {w}}}$ in ${\mathbb {H}}{\mathsf {H}}^n$ , where ${\mathfrak {w}}^\perp$ is a protohomogeneous subspace of ${\mathfrak {g}}_\alpha$

Similar to the complex case, tubes around a totally geodesic quaternionic hyperbolic space ${\mathbb {H}}{\mathsf {H}}^k$, $k\in \{0,\dots ,n-1\}$, are homogeneous and are congruent to the principal orbits of the action of ${\mathsf {Sp}}_{1,k}\times {\mathsf {Sp}}_{n-k}$ on ${\mathbb {H}}{\mathsf {H}}^n$. If $k=0$, we again have geodesic spheres. Tubes around totally geodesic complex hyperbolic spaces ${\mathbb {C}}{\mathsf {H}}^n$ in ${\mathbb {H}}{\mathsf {H}}^n$ are also homogeneous and correspond to the principal orbits of the action of ${\mathsf {SU}}_{1,n}$. Although there are more totally geodesic submanifolds of ${\mathbb {H}}{\mathsf {H}}^n$, their tubes fail to be homogeneous. The action of N gives rise to a horosphere foliation, all whose orbits are congruent to each other. Examples (5) correspond to the leaves of the solvable foliation. This is constructed, as usual, as the action of the subgroup of $AN\subset {\mathsf {Sp}}_{1,n}$ whose Lie algebra is ${\mathfrak {a}}\oplus {\mathfrak {w}}\oplus {\mathfrak {g}}_{2\alpha }$, where ${\mathfrak {w}}$ is a hyperplane in ${\mathfrak {g}}_\alpha$. This foliation has exactly one minimal leaf, which we have denoted by $P_1$.

For the rest of the examples, we need to determine all subspaces ${\mathfrak {w}}$ of ${\mathfrak {g}}_\alpha \cong {\mathbb {H}}^{n-1}$ such that $N_{K_0}({\mathfrak {w}})$ acts transitively on the unit sphere of ${\mathfrak {w}}^\perp$ up to congruence by an element of $K_0\cong {\mathsf {Sp}}_1{\mathsf {Sp}}_{1,n-1}$. As we explained before, the subgroup of $K_0AN\subset {\mathsf {Sp}}_{1,n}$ whose Lie algebra is $N_{K_0}({\mathfrak {w}})\oplus {\mathfrak {a}}\oplus {\mathfrak {w}}\oplus {\mathfrak {g}}_{2\alpha }$ acts on ${\mathbb {H}}{\mathsf {H}}^n$ with cohomogeneity one. We will call the subspaces ${\mathfrak {w}}$ of ${\mathfrak {g}}_\alpha$ satisfying this condition protohomogeneous. In the particular case that ${\mathfrak {w}}$ is a hyperplane, we recover the solvable foliation, which corresponds to item (5) of Theorem 8.

The space ${\mathfrak {g}}_\alpha \cong {\mathbb {H}}^{n-1}$ is a right quaternionic vector space. It can be endowed with a quaternionic structure $\mathfrak {J}$, that is, a vector subspace of $\mathrm {End}_{\mathbb {R}}({\mathbb {H}}^{n-1})$ admitting a so-called canonical basis $\{J_1,J_2,J_3\}$ satisfying

$$\displaystyle \begin{aligned} J_i^2=-\operatorname{\mathrm{Id}},\quad J_i J_{i+1}=J_{i+2}=-J_{i+1}J_i\quad \text{ (indices modulo 3).} \end{aligned}$$

For a given subspace ${\mathfrak {w}}^\perp \subset {\mathfrak {g}}_\alpha$, each complex structure $J\in \mathfrak {J}$ determines a Kähler angle of a nonzero vector $v\in {\mathfrak {w}}^\perp$ in the sense we have considered for the complex case. We define the quaternionic Kähler angle of a nonzero $v\in {\mathfrak {w}}^\perp$ to be the triple $(\varphi _1(v),\varphi _2(v),\varphi _3(v))$ satisfying that there exists a canonical basis $\{J_1,J_2,J_3\}$ such that:

• (i) $\varphi _1(v)\leq \varphi _2(v)\leq \varphi _3(v)$.

• (ii) $\varphi _i(v)$ is the Kähler angle of v with respect to $J_i$, $i\in \{1,2,3\}$.

• (iii) $\langle \pi _{{\mathfrak {w}}^\perp }J_i v,\pi _{{\mathfrak {w}}^\perp }J_j v\rangle =0$ if $i\neq j$ and where $\pi _{{\mathfrak {w}}^\perp }\colon {\mathfrak {g}}_\alpha \to {\mathfrak {w}}^\perp$ denotes the orthogonal projection onto ${\mathfrak {w}}^\perp$.

• (iv) $\varphi _1(v)$ is minimum, and $\varphi _3(v)$ is maximum among the Kähler angles of v with respect to the complex structures $J\in \mathfrak {J}$.

A probably more telling way of defining the quaternionic Kähler angle is the following. We consider the symmetric bilinear form:

$$\displaystyle \begin{aligned} L_v\colon\mathfrak{J}\times\mathfrak{J}\to{\mathbb{R}},\quad (J,J')\mapsto\langle\pi_{{\mathfrak{w}}^\perp}Jv,\pi_{{\mathfrak{w}}^\perp}J'v\rangle. \end{aligned}$$

Then, the Kähler angle of a nonzero $v\in {\mathfrak {w}}^\perp$ is the ordered triple $(\varphi _1(v),\varphi _2(v), \varphi _3(v))$ satisfying that the eigenvalues of $L_v$ are precisely $\cos ^2(\varphi _i(v))\langle v,v\rangle$. The canonical basis $\{J_1,J_2,J_3\}$ used above to define the quaternionic Kähler angle is precisely a basis that diagonalizes $L_v$.

If ${\mathfrak {w}}^\perp$ is protohomogeneous, then ${\mathfrak {w}}^\perp$ has constant quaternionic Kähler angle. Protohomogeneous subspaces of ${\mathbb {H}}^n$ have been classified in [32] up to congruence by an element of ${\mathsf {Sp}}_1{\mathsf {Sp}}_n$ by making extensive use of the concept of quaternionic Kähler angle. The moduli space $\mathcal {M}_{k,n}$ of nonzero protohomogeneous subspaces of dimension k in ${\mathbb {H}}^n$, up to congruence in ${\mathsf {Sp}}_1{\mathsf {Sp}}_n$, is described in Table 5.

Table 5 Moduli space of protohomogeneous subspaces of dimension k in ${ \mathbb {H}}^n$

This classification includes well-known examples such as totally real subspaces (precisely those with quaternionic Kähler angle $(\pi /2,\pi /2,\pi /2)$), totally complex subspaces (with quaternionic Kähler angle $(0,\pi /2,\pi /2)$), quaternionic subspaces (with quaternionic Kähler angle $(0,0,0)$), subspaces of constant Kähler angle $\varphi \in (0,\pi /2)$ inside a totally complex vector subspace (with quaternionic Kähler angle $(\varphi ,\pi /2,\pi /2)$), complexifications of subspaces of constant Kähler angle $\varphi \in (0,\pi /2)$ in a totally complex subspace (with quaternionic Kähler angle $(0,\varphi ,\varphi )$), and subspaces of the form $\mathfrak {J}v$, $v\in {\mathbb {H}}^n$, $v\neq 0$ (with quaternionic Kähler angle $(0,0,\pi /2)$).

However, there are some other nonclassical examples. See [32] for an explicit construction of these subspaces. While two subspaces with different quaternionic Kähler angles cannot be congruent to each other, a remarkable consequence of this classification implies the existence of noncongruent subspaces of ${\mathbb {H}}^n$ with the same quaternionic Kähler angles. These correspond precisely to the intersections ${\mathfrak {R}}_3^+\cap {\mathfrak {R}}_3^-={\mathfrak {R}}_3^-$ and ${\mathfrak {R}}_4^+\cap {\mathfrak {R}}_4^-={\mathfrak {R}}_4^-$.

All the examples in Theorem 8 (6) are obtained as tubes around the orbit through the origin $o\cong eK$ of the connected subgroup of $AN\subset G={\mathsf {Sp}}_{1,n}$ whose Lie algebra is ${\mathfrak {a}}\oplus {\mathfrak {w}}\oplus {\mathfrak {g}}_{2\alpha }$ and where ${\mathfrak {w}}^\perp$ is protohomogeneous in ${\mathfrak {g}}_\alpha \cong {\mathbb {H}}^{n-1}$. The moduli space $\mathcal {M}_{k,n-1}$ determines the congruence classes of the singular orbits of the corresponding cohomogeneity one actions, which in turn determines the orbit equivalence classes of cohomogeneity one actions on ${\mathbb {H}}{\mathsf {H}}^n$.

In order to get a proper classification, we still need to exclude a few classes that intersect with previous items of Theorem 8. If ${\mathfrak {w}}^\perp$ has quaternionic Kähler angle $(0,0,0)$, then ${\mathfrak {w}}^\perp$ and also ${\mathfrak {w}}$ are quaternionic vector subspaces of ${\mathfrak {g}}_\alpha \cong {\mathbb {H}}^{n-1}$. In this case, we recover tubes around totally geodesic quaternionic hyperbolic spaces ${\mathbb {H}}{\mathsf {H}}^k$, $k\in \{1,\dots ,n-1\}$. As we explained before, we also have to exclude when ${\mathfrak {w}}$ is a hyperplane, as this gives the solvable foliation.

Remark 6

Consider the connected subgroup of ${\mathsf {Sp}}_{1,n}$ with Lie algebra ${{\mathfrak {a}}\oplus {\mathfrak {w}}\oplus {\mathfrak {g}}_{2\alpha }}$, where ${\mathfrak {w}}$ is an arbitrary proper subspace of ${\mathfrak {g}}_\alpha$. It follows from [30] that tubes around the orbit through the origin of that group are always isoparametric. These have constant principal curvatures if and only if ${\mathfrak {w}}^\perp$ has constant quaternionic Kähler angle. If follows from [32] that by taking direct sums of spaces in both $\mathfrak {R}_4^+$ and $\mathfrak {R}_4^-$ with the same constant quaternionic Kähler angles, we obtain subspaces ${\mathfrak {w}}^\perp$ that still have constant quaternionic Kähler angle but are not protohomogeneous. This yields examples of isoparametric hypersurfaces with constant principal curvatures in ${\mathbb {H}}{\mathsf {H}}^n$, $n\geq 8$, that are not homogeneous.

5.5 Homogeneous Hypersurfaces in the Cayley Hyperbolic Plane

Finally, we deal with the Cayley hyperbolic plane $\mathbb {O}{\mathsf {H}}^2$.

Theorem 9 (Homogeneous Hypersurfaces in the Cayley Hyperbolic Plane)

A homogeneous hypersurface in $\mathbb {O}{\mathsf {H}}^2$ is congruent to one of the following:

• (1) A geodesic sphere

• (2) A tube around a totally geodesic $\mathbb {O}{\mathsf {H}}^1$

• (3) A tube around a totally geodesic $\mathbb {H}{\mathsf {H}}^2$

• (4) A horosphere

• (5) A minimal homogeneous hypersurface $F_1$ or one of its equidistant hypersurfaces

• (6) A tube around the minimal submanifold $F_k$ of codimension $k\in \{2, 3, 6, 7\}$

• (7) A tube around the minimal submanifold$F_{4,\varphi }$of codimension 4 for some$\varphi \in [0,1]$

Geodesic spheres are principal orbits of the isotropy action of ${\mathsf {Spin}}_9$ on $\mathbb {O}{\mathsf {H}}^2$. Tubes around a totally geodesic $\mathbb {O}{\mathsf {H}}^1$ on $\mathbb {O}{\mathsf {H}}^2$ are congruent to the principal orbits of the action of ${\mathsf {Spin}}_{1,8}^0\subset {\mathsf {F}}_4^{-20}$, and tubes around a totally geodesic ${\mathbb {H}}{\mathsf {H}}^2$ are principal orbits of the action of ${\mathsf {Sp}}_{1,2}{\mathsf {Sp}}_1\subset {\mathsf {F}}_4^{-20}$. The group N, which is the nilpotent part of the Iwasawa decomposition of ${\mathsf {F}}_4^{-20}$, gives rise to the horosphere foliation in $\mathbb {O}{\mathsf {H}}^2$, whose leaves are congruent to each other. Example (5) of Theorem 9 corresponds to the solvable foliation, which is obtained by the action of the subgroup of ${\mathsf {F}}_4^{-20}$ whose Lie algebra is ${\mathfrak {a}}\oplus {\mathfrak {w}}\oplus {\mathfrak {g}}_{2\alpha }$, where ${\mathfrak {w}}$ is a hyperplane in ${\mathfrak {g}}_\alpha$. This action has a unique minimal orbit which is denoted by $F_1$.

Examples (6) and (7) correspond to the nilpotent construction. Berndt and Br̈uck classified in [5] all subspaces ${\mathfrak {w}}$ of ${\mathfrak {g}}_\alpha \cong \mathbb {O}$ such that $N_{K_0}({\mathfrak {w}})$ acts transitively on the unit sphere of ${\mathfrak {w}}^\perp$. It turns out that any proper subspace ${\mathfrak {w}}$ of ${\mathfrak {g}}_\alpha$ with $\dim {\mathfrak {w}}\neq 3$ satisfies this condition. Hyperplanes of ${\mathfrak {g}}_\alpha$ are ones of such spaces, but they correspond to item (5) and produce a foliation. The group $K_0\cong {\mathsf {Spin}}_7$ acts on $\mathbb {O}\cong {\mathbb {R}}^8$ by its irreducible 8-dimensional spin representation. This action induces an action on the Grassmannians ${\mathsf {G}}_k({\mathbb {R}}^8)$ of k-planes in ${\mathbb {R}}^8$. If $k\neq 4$, this action is transitive, and if $k=4$, this action is of cohomogeneity one (see the discussion for $\mathbb {O}{\mathsf {H}}^2$ in [14] and the references therein). This implies that any pair of subspaces of ${\mathfrak {g}}_\alpha$ of dimension $k\neq 4$ are congruent by an isometry of ${\mathsf {Spin}}_7$. The singular orbit of the action on $\mathbb {O}{\mathsf {H}}^2$ of the connected subgroup of ${\mathsf {F}}_4^{-20}$ with Lie algebra $N_{K_0}({\mathfrak {w}})\oplus {\mathfrak {a}}\oplus {\mathfrak {w}}\oplus {\mathfrak {g}}_{2\alpha }$ is denoted by $F_k$, where $k=\dim {\mathfrak {w}}^\perp =8-\dim {\mathfrak {w}}$. The moduli space of ${\mathsf {Spin}}_7$-congruence classes of subspaces of ${\mathfrak {g}}_\alpha$ of dimension 4 is in one-to-one correspondence with the orbit space ${\mathsf {G}}_4({\mathbb {R}}^8)/{\mathsf {Spin}}_7\cong [0,1]$. The congruence class corresponding to some $\varphi \in [0,1]$ produces a cohomogeneity one action on $\mathbb {O}{\mathsf {H}}^2$ whose singular orbit is denoted by $F_{4,\varphi }$.

Remark 7

As in the previous hyperbolic spaces, any tube around the orbit through the origin of the subgroup $S_{{\mathfrak {w}}}$ of $AN\subset {\mathsf {F}}_4^{-20}$ with Lie algebra ${\mathfrak {a}}\oplus {\mathfrak {w}}\oplus {\mathfrak {g}}_{2\alpha }$ is isoparametric. Moreover, in this case, it follows from [30] that each one of these tubes has constant principal curvatures. Thus, for $\dim {\mathfrak {w}}^\perp =5$, the corresponding tubes around $S_{{\mathfrak {w}}}\cdot o$ are inhomogeneous isoparametric hypersurfaces with constant principal curvatures. If $\dim {\mathfrak {w}}^\perp =4$, the constant principal curvatures of the homogeneous tubes around $F_{4,\varphi }$ are independent of $\varphi$. Thus, there is an infinite family of noncongruent homogeneous isoparametric hypersurfaces with the same constant principal curvatures counted with multiplicities.

6 Homogeneous Hypersurfaces in Symmetric Spaces of Noncompact Type and Arbitrary Rank

The aim of this section is to provide an overview of the methods of construction and classification of cohomogeneity one actions on symmetric spaces of noncompact type and arbitrary rank. As we commented in the previous section, the classification in rank one is nowadays complete. Although this is not the case for higher rank, there have been recent advances that give us not only some classifications in certain spaces but also, importantly, a panoramic view of the possible types of actions that may arise in any symmetric space of noncompact type.

We will start by explaining four construction techniques that can be regarded as building blocks for the classification problem. These techniques are the construction of codimension one subgroups of the solvable part AN of the Iwasawa decomposition (explained in Sect. 6.1), the actions with a totally geodesic singular orbit (Sect. 6.2), the canonical extension of actions from lower rank symmetric spaces (Sect. 6.3), and the nilpotent construction (Sect. 6.4). Then, in Sect. 6.5, we will report on a structural result that asserts that these four building blocks are enough to construct any cohomogeneity one action on any (not necessarily irreducible) symmetric space of noncompact type.

6.1 Homogeneous Codimension One Foliations

Since any symmetric space of noncompact type M is a Hadamard manifold, any cohomogeneity one action on M has at most one singular orbit. We will explain in this subsection that the case of actions without singular orbit is nowadays well understood.

It follows from the Iwasawa decomposition that the connected solvable subgroup AN of G with Lie algebra ${\mathfrak {a}}\oplus {\mathfrak {n}}$ acts freely and transitively on M. Thus, codimension one subgroups of AN give rise to homogeneous codimension one regular foliations on M. Berndt and Tamaru used this in [12] to propose two general methods for constructing cohomogeneity one actions with no singular orbits on a given symmetric space of noncompact type.

The first method produces a regular Riemannian foliation $\mathcal {F}_\ell$ for each one-dimensional subspace $\ell$ in ${\mathfrak {a}}$. Define ${\mathfrak {h}}_\ell$ to be the orthogonal complement of $\ell$ in ${\mathfrak {a}}\oplus {\mathfrak {n}}$, ${\mathfrak {h}}_\ell =({\mathfrak {a}}\ominus \ell )\oplus {\mathfrak {n}}$. This is a codimension one subalgebra of ${\mathfrak {a}}\oplus {\mathfrak {n}}$, so the corresponding connected subgroup $H_\ell$ of G acts on M with cohomogeneity one and no singular orbits. It turns out that the orbits of this action are congruent to each other. Foliations of M by horospheres (i.e., by the level sets of a Busemann function on M) are a particular type of such a construction [42, Remark 5.4], so we will refer to the $\mathcal {F}_\ell$ as foliations of horospherical type.

The second method gives us a foliation $\mathcal {F}_i$ for each simple root $\alpha _i\in \Lambda =\{\alpha _1,\dots ,\alpha _r\}$. Let $\ell$ be a one-dimensional subspace of a simple root space ${\mathfrak {g}}_{\alpha _i}$. It follows from the properties of root spaces that ${\mathfrak {h}}_i={\mathfrak {a}}\oplus ({\mathfrak {n}}\ominus \ell )$ is a codimension one subalgebra of ${\mathfrak {a}}\oplus {\mathfrak {n}}$, and so, its corresponding connected subgroup $H_i$ of G acts with cohomogeneity one on M. Actions arising in this way have a unique minimal orbit (namely, the orbit through o). We will refer to these $\mathcal {F}_i$ as foliations of solvable type.

It was shown in [12] for irreducible M and in [7] for the general case that every cohomogeneity one action on a symmetric space of noncompact type with no singular orbits is orbit equivalent to the action of some $H_\ell$ or $H_i$ as constructed before. Furthermore, the moduli space of such actions has been studied in [12] and [92]. Two actions of horospherical type $\mathcal {F}_\ell$ and $\mathcal {F}_{\ell '}$ are isometrically congruent precisely whenever there exists an isometry of M that induces a symmetry of the Dynkin diagram of ${\mathfrak {g}}$ taking $\ell$ to $\ell '$. Something similar happens for the foliations of solvable type: $\mathcal {F}_i$ and $\mathcal {F}_j$ are isometrically congruent if and only if there exists an isometry of M that induces a symmetry of the Dynkin diagram of ${\mathfrak {g}}$ taking $\alpha _i$ to $\alpha _j$. In particular, if $\ell$ and $\ell '$ are contained in the same root space, they yield congruent foliations. Thus, the moduli space of homogeneous codimension one foliations on a symmetric space of noncompact type up to orbit equivalence is isomorphic to $({\mathbb {R}} {\mathsf {P}}^r\sqcup \{1,\dots ,r\})/\text{Aut}(\text{DD}_M)$, where $r={\mathrm {rank}\;}(M)$ and $\text{Aut}(\text{DD}_M)$ denotes the subgroup of symmetries of the Dynkin diagram of ${\mathfrak {g}}$ which are induced by isometries of M.

6.2 Cohomogeneity One Actions with a Totally Geodesic Singular Orbit

Among the cohomogeneity one actions that have a singular orbit, it is natural to first determine those actions whose singular orbit is totally geodesic. Recall that if a cohomogeneity one action on a Euclidean or a real hyperbolic space has a singular orbit, this must be totally geodesic, although this is no longer the case for other hyperbolic spaces, as explained in Sect. 5.

In the article [13], Berndt and Tamaru derived the classification of the totally geodesic submanifolds F of any irreducible symmetric space of noncompact type M that arise as singular orbits of cohomogeneity one actions on M, i.e., the totally geodesic submanifolds F such that the tubes around them are homogeneous hypersurfaces. This is basically the only case where the use of duality of symmetric spaces can be applied. However, we recall that one cannot simply analyze case-by-case all possible totally geodesic submanifolds of M, since even nowadays there is no such a classification. Berndt and Tamaru appeal to the use of duality, along with Kollross’ classification [61] in the compact setting, as well as Leung’s classification [66] of a certain very particular type of totally geodesic submanifolds, called reflective submanifolds. A reflective submanifoldF of a symmetric space M is a totally geodesic submanifold of M such that the exponential of its normal space at some (and hence all) point, $F^\perp =\exp (\nu _p F)$, is also totally geodesic in M. Recall that, as totally geodesic submanifolds, both F and $F^\perp$ are themselves symmetric spaces.

Berndt and Tamaru proved that F is a totally geodesic singular orbit of a cohomogeneity one action on an irreducible M if and only if one of the following possibilities holds:

• (i) F is a reflective submanifold such that $F^\perp$ is a symmetric space of rank one (see [13, Theorem 3.3] for an explicit list).

• (ii) F is one of the five possible nonreflective totally geodesic submanifolds related to the exceptional Lie group ${\mathsf {G}}_2$ appearing in Table 6.

  Table 6 Nonreflective totally geodesic submanifolds related to $G_2$

It is important to mention that the lists provided in [13] are given up to congruence in M by isometries of the full isometry group $\mathrm {Isom}(M)$, cf. Problem 3 in Sect. 7.

Let us now assume that M is reducible. Put $M=M_1\times \dots \times M_s$ for its de Rham decomposition into irreducible symmetric spaces (of noncompact type). For each $i\in \{1,\dots , s\}$, we write $M_i\cong G_i/K_i$, and hence, ${\mathfrak {g}}={\mathfrak {g}}_1\oplus \dots \oplus {\mathfrak {g}}_s$ is the decomposition of the semisimple Lie algebra ${\mathfrak {g}}$ into its simple ideals. A fundamental observation made in the recent work [31] is that if a cohomogeneity one action on M with a totally geodesic singular orbit does not split nicely with respect to the previous decompositions (i.e., if it is not orbit equivalent to a product action), then there must exist two homothetic factors $M_j$ and $M_k$ of M of rank one, and the action is orbit equivalent to that of the connected subgroup of G whose Lie algebra is

$$\displaystyle \begin{aligned} {} {\mathfrak{g}}_{j,k,\tau}\oplus\bigg(\bigoplus_{\begin{subarray}{c}i=1\\i\neq j,k\end{subarray}}{\mathfrak{g}}_i\bigg), \qquad \text{with }\; {\mathfrak{g}}_{j,k,\tau}=\{X+\tau X:X\in {\mathfrak{g}}_j\}, \end{aligned} $$

(3)

where $\tau \colon {\mathfrak {g}}_j\to {\mathfrak {g}}_k$ is a Lie algebra isomorphism. In this case, the singular orbit is also homothetic to $M_j$ and $M_k$. This result ultimately follows from a classical theorem of Dynkin [43, Theorem 15.1, p. 235] which states that a maximal proper subalgebra of either ${\mathfrak {g}}$ splits nicely with respect to the decomposition of ${\mathfrak {g}}$ into simple ideals or it is of the form (3).

All in all, any cohomogeneity one action with a totally geodesic singular orbit on M is determined by one of the actions on an irreducible factor of M listed by Berndt and Tamaru in [13] or by a diagonal action on the product of two homothetic rank one factors of M, as in (3).

6.3 Canonical Extension of Actions on Boundary Components

Consider a subset $\Phi \subset \Lambda$ of simple roots and its associated boundary component $B_\Phi$. Since $S_\Phi$ is (up to a covering) the identity component of $\mathrm {Isom}(B_\Phi )$, any isometric action on $B_\Phi$ has the same orbits as some connected Lie subgroup $H_\Phi$ of $S_\Phi$. Consider the subgroup

$$\displaystyle \begin{aligned} H_{\Phi}^{\Lambda}=H_\Phi A_\Phi N_\Phi \end{aligned}$$

of G. Then, $H_{\Phi }^{\Lambda }$ acts on M with the same cohomogeneity of the action of $H_\Phi$ on $B_\Phi$. Indeed, each $H_{\Phi }^{\Lambda }$-orbit on M, say $H_{\Phi }^{\Lambda }\cdot p$, is nothing but the union of all $A_\Phi N_\Phi$-orbits through the points of $H_{\Phi }\cdot p$. Recall from Sect. 3.4 that all the $A_\Phi N_\Phi$-orbits have the same dimension. We say that $H_{\Phi }^{\Lambda }$ is the group obtained by canonical extension of $H_{\Phi }$ from the boundary component $B_{\Phi }$ to M. Furthermore, it was proved in [15, Proposition 4.2] that if the actions of two connected subgroups of $S_{\Phi }$ are orbit equivalent on $B_{\Phi }$ by an isometry in $S_{\Phi }$ (equivalently, by an isometry of $\mathrm {Isom}(B_\Phi )^0$), then their canonical extensions are orbit equivalent on M by an element of G.

As boundary components of M are symmetric spaces of noncompact type, it makes sense to study what happens if one applies this procedure twice. Consider the boundary component $B_\Phi$ associated with a subset of simple roots $\Phi \subset \Lambda$. Recall that we can naturally identify $\Phi$ with a set of simple roots for ${\mathfrak {s}}_{\Phi }$. Thus, a boundary component of $B_\Phi$ is determined by a subset $\Psi \subset \Phi \subset \Lambda$ and in fact coincides with the boundary component $B_\Psi$ of M associated with $\Psi$. One gets an inclusion of totally geodesic submanifolds $B_{\Psi }\subset B_{\Phi }\subset M$. Let $H_{\Psi }$ be a connected closed subgroup of $S_{\Psi }$ acting isometrically on $B_\Psi$. Then, its canonical extension $H_{\Psi }^{\Phi }$ is a connected closed subgroup of $S_\Phi$ acting isometrically on $B_\Phi$, so we can consider its canonical extension to M, which we denote by $(H_{\Psi }^{\Phi })^{\Lambda }$. This construction turns out to be the same as directly extending the action of $H_{\Psi }$ from $B_{\Psi }$ to the whole M, that is, $(H_{\Psi }^{\Phi })^{\Lambda }=H_{\Psi }^{\Lambda }$ (cf. [31, Lemma 4.2]). Roughly speaking, the composition of canonical extensions is a canonical extension.

Remark 8

The canonical extension method described above admits an interesting version that allows to enlarge submanifolds from boundary components to the whole symmetric space. This procedure preserves important geometric properties such as the constancy of the mean curvature or isoparametricity, as was shown in [35]. More recently, another remarkable extension method of submanifolds and actions in the context of symmetric spaces of noncompact type has been discovered [41]. In this case, the extension does not apply to boundary components, but to certain totally geodesic and flat submanifolds. As a by-product of this method, the first examples of inhomogeneous isoparametric hypersurfaces in any symmetric space of noncompact type and rank higher than two were obtained.

6.4 The Nilpotent Construction Method

Apart from the canonical extension, Berndt and Tamaru proposed in [15] another method for constructing cohomogeneity one actions from the parabolic subgroups of G. Although this procedure was originally formulated for an arbitrary subset of simple roots $\Phi \subset \Lambda$, it will be enough to consider subsets of cardinality $|\Phi |=|\Lambda |-1$, that is, those giving rise to maximal proper parabolic subgroups of G.

Let $\Phi =\Lambda \setminus \{\alpha _j\}$, for some $\alpha _j\in \Lambda$, and consider the dual vector $H^j\in {\mathfrak {a}}$ of $\alpha _j$, defined by $\alpha _i(H^j)=\delta _{ij}$. The subalgebra ${\mathfrak {n}}_{\Phi }$ admits a natural gradation $\bigoplus _{\nu \geq 1}{\mathfrak {n}}_{\Phi }^{\nu }$, where ${\mathfrak {n}}_{\Phi }^{\nu }=\bigoplus _{\lambda (H^j)=\nu }{\mathfrak {g}}_{\lambda }$. Note that $\lambda (H^j)=\nu$ if and only if $\lambda$ has coefficient $\nu$ in $\alpha _j$ when expressed as a sum of simple roots. Suppose that ${\mathfrak {v}}$ is a subspace of ${\mathfrak {n}}_{\Phi }^1$ of dimension $\dim {\mathfrak {v}}\geq 2$. Then, ${\mathfrak {n}}_{\Phi ,{\mathfrak {v}}}={\mathfrak {n}}_{\Phi }\ominus {\mathfrak {v}}$ is a subalgebra of ${\mathfrak {n}}_{\Phi }$. Denote by $N_{\Phi ,{\mathfrak {v}}}$ the corresponding connected Lie subgroup of $N_{\Phi }$. Assume the following conditions hold:

• (NC1) $N_{M_\Phi }({\mathfrak {n}}_{\Phi ,{\mathfrak {v}}})$ acts transitively on $B_\Phi =M_\Phi \cdot o$.

• (NC2) $N_{K_\Phi }({\mathfrak {n}}_{\Phi ,{\mathfrak {v}}})=N_{K_\Phi }({\mathfrak {v}})$ acts transitively on the unit sphere of ${\mathfrak {v}}$.

Then, the group

$$\displaystyle \begin{aligned} H_{\Phi,{\mathfrak{v}}}=N^0_{L_\Phi}({\mathfrak{n}}_{\Phi,{\mathfrak{v}}})N_{\Phi,{\mathfrak{v}}}=N^0_{M_\Phi}({\mathfrak{n}}_{\Phi,{\mathfrak{v}}})A_{\Phi}N_{\Phi,{\mathfrak{v}}} \end{aligned}$$

acts on M with cohomogeneity one and a singular orbit $H_{\Phi ,{\mathfrak {v}}}\cdot o$. Here, $N^0(\cdot )$ denotes the connected component of the identity of a normalizer. In this case, we say that the action of $H_{\Phi ,{\mathfrak {v}}}$ on M has been obtained by nilpotent construction from the choices of $\Phi$ and ${\mathfrak {v}}$. Moreover, it was proved in [15] that if two subspaces ${\mathfrak {v}}_1,{\mathfrak {v}}_2\subset {\mathfrak {n}}_{\Phi }^{1}$ giving rise to actions by nilpotent construction are conjugate by an element in $K_{\Phi }$, the actions of the corresponding groups $H_{\Phi ,{\mathfrak {v}}_1},H_{\Phi ,{\mathfrak {v}}_2}$ on M are orbit equivalent (via the same element).

Remark 9

Conditions (NC1)–(NC2) have geometric meaning. Condition (NC1) implies that the orbit $H_{\Phi ,{\mathfrak {v}}}\cdot o$ contains the boundary component $B_\Phi$, and hence its normal space can be identified with ${\mathfrak {v}}$, i.e., $\nu _o (H_{\Phi ,{\mathfrak {v}}}\cdot o)\cong {\mathfrak {v}}$. Then, condition (NC2) means that the slice representation of $H_{\Phi ,{\mathfrak {v}}}$ (i.e., the action of the group of differentials of the isometries in $H_{\Phi ,{\mathfrak {v}}}$ on $\nu _o (H_{\Phi ,{\mathfrak {v}}}\cdot o)\cong {\mathfrak {v}}$) is of cohomogeneity one on the Euclidean space $\nu _o (H_{\Phi ,{\mathfrak {v}}}\cdot o)\cong {\mathfrak {v}}$, with orbits given by the origin and concentric spheres. Since an isometric action has the same cohomogeneity as its slice representation, we see that both conditions (NC1)–(NC2) imply that $H_{\Phi ,{\mathfrak {v}}}$ acts on M with cohomogeneity one, as claimed above.

Remark 10

Subspaces of ${\mathfrak {n}}_{\Phi }^1$ satisfying condition (NC1) (respectively, (NC2)) have been called admissible (resp. protohomogeneous) in [32] and [91]. We observe that if M has rank one, then any proper subset $\Phi$ of $\Lambda =\{\alpha _1\}$ is necessarily the empty set, and hence, any proper boundary component is a point. Therefore, the admissibility condition (NC1) is trivially satisfied. Thus, for rank one spaces, the nilpotent construction amounts to the determination of protohomogeneous subspaces. For these spaces, $K_\Phi ^0=K_\emptyset ^0=K_0$, from where one can see that condition (NC2) is equivalent to the definition of protohomogenous subspace given in Sect. 5.

The complete determination of all possible subspaces ${\mathfrak {v}}$ satisfying conditions (NC1)–(NC2) for a specific symmetric space is usually a very difficult task. Indeed, as commented in Sect. 5, this was even hard in the case of the quaternionic hyperbolic spaces, where condition (NC1) did not play any role.

As before, it is important to determine what happens when one considers an action on a boundary component $B_\Phi$ obtained by nilpotent construction, and then one extends it to M. This turns out to be equivalent to an action obtained via nilpotent construction on M. More precisely, let $\alpha _j\in \Phi \subset \Lambda$. Let $H_\Phi$ be a subgroup of $S_\Phi$ obtained by the nilpotent construction method applied to the symmetric space $B_\Phi$. Then the subgroup $H_\Phi ^\Lambda$ of G obtained by canonical extension of the $H_\Phi$-action to M acts on M with the same orbits as the Lie group $H_{\Lambda \setminus \{\alpha _j\},{\mathfrak {v}}}=N^0_{L_{\Lambda \setminus \{\alpha _j\}}}({\mathfrak {n}}_{\Lambda \setminus \{\alpha _j\},{\mathfrak {v}}})N_{\Lambda \setminus \{\alpha _j\},{\mathfrak {v}}}$ obtained by nilpotent construction applied to M, for certain subspace ${\mathfrak {v}}$ of ${\mathfrak {n}}_{\Lambda \setminus \{\alpha _j\}}^1$ of $\dim {\mathfrak {v}}\geq 2$. For further details and a proof, see [31, Lemma 4.3].

6.5 The Classification of Cohomogeneity One Actions

A general procedure to classify cohomogeneity one actions on a given symmetric space of noncompact type $M\cong G/K$ (not necessarily irreducible) goes as follows. Assume we have a connected Lie subgroup H of G acting on M with cohomogeneity one. If the H-action produces a regular foliation, then the H-action is orbit equivalent to one of the actions described in Sect. 6.1, as explained in that subsection. Thus, let us suppose that the action of H has a singular orbit. The Lie algebra ${\mathfrak {h}}$ of H is contained in some maximal proper subalgebra ${\mathfrak {q}}$ of ${\mathfrak {g}}$. By a result of Mostow [73], there are two possibilities for ${\mathfrak {q}}$: it is either a maximal proper reductive subalgebra or a maximal proper parabolic subalgebra of ${\mathfrak {g}}$. Denote by Q the connected subgroup of G with Lie algebra ${\mathfrak {q}}$. Then:

• (a) If ${\mathfrak {q}}$ is a maximal proper reductive subalgebra of ${\mathfrak {g}}$, then Q acts with cohomogeneity one and the same orbits as the H-action, one of them being totally geodesic (which is the singular one if M is irreducible and $M\neq {\mathbb {R}}{\mathsf {H}}^n$), as shown in [15, Theorem 3.2].

• (b) If ${\mathfrak {q}}$ is a maximal proper parabolic subalgebra of ${\mathfrak {g}}$, then the H-action is orbit equivalent to an action obtained by canonical extension or by nilpotent construction, as proved by Berndt and Tamaru in [15, Theorem 5.8].

Using this approach, along with a careful analysis of the nilpotent construction, allowed for the classification of the cohomogeneity one actions on several symmetric spaces of noncompact type and rank 2, namely, on

$$\displaystyle \begin{aligned} {} \begin{gathered} {\mathsf{SL}}_3({\mathbb{R}})/{\mathsf{SO}}_3,\quad {\mathsf{SL}}_3({\mathbb{C}})/{\mathsf{SU}}_3,\quad {\mathsf{SL}}_3({\mathbb{H}})/{\mathsf{Sp}}_3, \quad {\mathsf{SO}}_5({\mathbb{C}})/{\mathsf{SO}}_5, \\ {\mathsf{G}}_2^2/{\mathsf{SO}}_4, \quad {\mathsf{G}}_2^{\mathbb{C}}/{\mathsf{G}}_2,\quad {\mathsf{SO}}^0_{2,n}/{\mathsf{SO}}_2{\mathsf{SO}}_n, \quad {\mathsf{SU}}_{2,n}/{\mathsf{S}}({\mathsf{U}}_2{\mathsf{U}}_n). \end{gathered} \end{aligned} $$

(4)

These classifications were obtained in the series of papers [8, 15, 91].

When trying to implement this approach in spaces of rank greater than 2, it turns out that one can apply a rank reduction procedure. Roughly speaking, if the H-action is orbit equivalent to the canonical extension of some action on a boundary component, we can apply the same procedure as before recursively until we get to an action that can no longer be retrieved by canonical extension. Thus, every cohomogeneity one action with a singular orbit can ultimately be obtained by nilpotent construction or by extending an action of cohomogeneity one with a totally geodesic singular orbit on a boundary component of M. In the latter case, as follows from the discussion in Sect. 6.2, the action being extended is of one of the following two types:

• (i) A cohomogeneity one action with a totally geodesic singular orbit on an irreducible boundary component $B_\Phi$ of M and hence orbit equivalent to one of the actions classified in [13] in terms of certain reflective submanifolds and some exceptions related to ${\mathsf {G}}_2$.

• (ii) A cohomogeneity one action with a diagonal totally geodesic submanifold on a reducible boundary component $B_{\{\alpha _j,\alpha _k\}}\cong B_{\{\alpha _j\}}\times B_{\{\alpha _k\}}\cong \mathbb {F}{\mathsf {H}}^{n}\times \mathbb {F}{\mathsf {H}}^{n}$, given by a connected Lie group with Lie algebra ${\mathfrak {s}}_{j,k,\tau }=\{X+\tau X\, : X\in {\mathfrak {s}}_{\{\alpha _j\}}\}$, where $\tau \colon {\mathfrak {s}}_{\{\alpha _j\}}\rightarrow {\mathfrak {s}}_{\{\alpha _k\}}$ is a Lie algebra isomorphism between the isometry Lie algebras of both factors of $B_{\{\alpha _j,\alpha _k\}}$.

As a consequence of all the facts sketched above in this section, we have recently obtained the following structural result in [31, Theorem A].

Theorem 10 (Cohomogeneity One Actions on Symmetric Spaces of Noncompact Type)

Let $M\cong G/K$ be a symmetric space of noncompact type, and let H be a connected closed subgroup of G. Then, H acts on M with cohomogeneity one if and only if the H-action is orbit equivalent to one of the following:

• (FH) An action inducing a regular codimension one foliation of horospherical type

• (FS) An action inducing a regular codimension one foliation of solvable type

• (CEI) The canonical extension of a cohomogeneity one action with a totally geodesic singular orbit on an irreducible boundary component

• (CER) The canonical extension of a cohomogeneity one diagonal action on a reducible boundary component of rank two with two homothetic factors

• (NC) An action obtained by nilpotent construction

Remark 11

Cases (CEI) and (NC) in the previous theorem may overlap. Indeed, the nilpotent construction method often produces actions that can be obtained by canonical extension. So far, the only spaces where the nilpotent construction is known to produce actions that cannot be obtained by any other methods are the hyperbolic spaces of nonconstant curvature, ${\mathsf {G}}_2^2/{\mathsf {SO}}_4$ and ${\mathsf {G}}_2^{\mathbb {C}}/{\mathsf {G}}_2$.

Remark 12

Although the moduli space of cohomogeneity one actions producing regular foliations has been completely determined (see Sect. 6.1), the study of the moduli space of actions with a singular orbit is much more involved. Note that in Sect. 6.3 we have only stated sufficient conditions for two canonical extensions to be orbit equivalent on M. Despite two actions not being orbit equivalent on a boundary component, it could happen that their canonical extensions could be orbit equivalent. It may also happen that two orbit equivalent actions could produce canonical extensions which are not orbit equivalent in M (if the equivalence in the boundary component $B_\Phi$ had been obtained by an isometry in $\mathrm {Isom}(B_\Phi )\setminus \mathrm {Isom}(B_\Phi )^0$). Thus, determining the orbit equivalence classes involves additional difficulties (see Problem 3 in Sect. 7).

As an application of Theorem 10, we derived in [31] the classification of cohomogeneity one actions on the family of spaces ${\mathsf {SL}}_{n+1}({\mathbb {R}})/{\mathsf {SO}}_{n+1}$. We recall that ${\mathsf {SL}}_{n+1}({\mathbb {R}})/{\mathsf {SO}}_{n+1}$ has rank n. The associated root space decomposition of ${\mathfrak {g}}={\mathfrak {sl}}_{n+1}({\mathbb {R}})$ satisfies ${\mathfrak {g}}_0={\mathfrak {a}}$ and $\dim {\mathfrak {g}}_\lambda =1$, for any root $\lambda \in \Sigma$.

Theorem 11 (Cohomogeneity One Actions on ${\mathsf {SL}}_{n+1}({\mathbb {R}})/{\mathsf {SO}}_{n+1}$)

Let$M\cong {\mathsf {SL}}_{n+1}({\mathbb {R}})/{\mathsf {SO}}_{n+1}$, $n\geq 1$, and let$\Lambda =\{\alpha _1,\dots ,\alpha _n\}$be a set of simple roots for${\mathfrak {sl}}_{n+1}({\mathbb {R}})$whose Dynkin diagram is

Any cohomogeneity one action on M is orbit equivalent to one of the following:

• (FH) The action of the connected subgroup of${\mathsf {SL}}_{n+1}({\mathbb {R}})$with Lie algebra$({\mathfrak {a}}\ominus \ell )\oplus {\mathfrak {n}}$, for some line$\ell$of${\mathfrak {a}}$.

• (FS) The action of the connected subgroup of${\mathsf {SL}}_{n+1}({\mathbb {R}})$with Lie algebra${\mathfrak {a}}\oplus ({\mathfrak {n}}\ominus {\mathfrak {g}}_{\alpha _j})$, for some simple root$\alpha _j\in \Lambda$.

• (CE) The canonical extension$H_\Phi ^\Lambda$of the action of the connected subgroup$H_\Phi$of${\mathsf {SL}}_{n+1}({\mathbb {R}})$on a boundary component$B_\Phi$, for one of the cases in Table7.

  Table 7 Actions on ${\mathsf {SL}}_{n+1}({ \mathbb {R}})/{\mathsf {SO}}_{n+1}$ obtained by canonical extension

Theorem 10 can also be used to address the classification problem on reducible symmetric spaces by allowing us to restrict our analysis to the classification problem on each irreducible factor. It turns out that actions of the types (FS), (CEI), and, importantly, (NC) split well with respect to the de Rham decomposition of a reducible symmetric space, so they are product actions. We emphasize that a result analogous to Theorem 12 below is not yet known for compact symmetric spaces (see Problem 5 in Sect. 7).

Theorem 12 (Cohomogeneity One Actions on Reducible Symmetric Spaces of Noncompact Type)

Let M be a symmetric space of noncompact type with de Rham decomposition$M=M_1\times \dots \times M_s$, where$M_i=G_i/K_i$, $i=1,\dots ,s$, and let$G=\prod _{i=1}^s G_i$. Then, a cohomogeneity one action on M is orbit equivalent to one of the following:

(Prod) :

The product action of a subgroup$H_j\times \prod _{\begin {subarray}{c}i=1\\i\neq j\end {subarray}}^s G_i$of G, where$H_j$is a connected Lie subgroup of$G_j$that acts with cohomogeneity one on the irreducible factor$M_j$.

(FH) :

The action of the connected subgroup of G with Lie algebra${\mathfrak {h}}=({\mathfrak {a}}\ominus \ell )\oplus {\mathfrak {n}}$, for some line$\ell$of${\mathfrak {a}}$.

(CER) :

The canonical extension of a cohomogeneity one diagonal action on a reducible boundary component of M of rank two with two homothetic factors.

Theorem 12 can be applied to derive explicit classifications on any product of symmetric spaces of noncompact type for which we already have the complete list of cohomogeneity one actions (namely, all rank one spaces studied in Sect. 5, the rank two spaces in (4), and the spaces ${\mathsf {SL}}_{n+1}({\mathbb {R}})/{\mathsf {SO}}_{n+1}$). As a very particular instance of these possible applications, we state the following classification of homogeneous hypersurfaces on any finite product of real hyperbolic spaces:

Theorem 13 (Homogeneous Hypersurfaces in Products of Real Hyperbolic Spaces)

A homogeneous hypersurface of $M={\mathbb {R}}{\mathsf {H}}^{n_1}\times \dots \times {\mathbb {R}}{\mathsf {H}}^{n_r}$ is congruent to one of the following:

(FH) :

A leaf of a regular codimension one foliation of horospherical type

(FS) :

An extrinsic product ${\mathbb {R}} {\mathsf {H}}^{n_j-1}\times \prod _{i\neq j}{\mathbb {R}}{\mathsf {H}}^{n_i}$ , where ${\mathbb {R}} {\mathsf {H}}^{n_j-1}$ is totally geodesic in ${\mathbb {R}}{\mathsf {H}}^{n_j}$ , or one of its equidistant hypersurfaces

(CEI) :

A tube around the extrinsic product ${\mathbb {R}} {\mathsf {H}}^k\times \prod _{i\neq j}{\mathbb {R}}{\mathsf {H}}^{n_i}$ , where ${\mathbb {R}} {\mathsf {H}}^k$ is totally geodesic in ${\mathbb {R}}{\mathsf {H}}^{n_j}$ , for some $k\in \{0,\dots ,n_j-2\}$

(CER) :

A tube around the extrinsic product $\Delta {\mathbb {R}} {\mathsf {H}}^{n_j}\times \prod _{i\neq j,k}{\mathbb {R}}{\mathsf {H}}^{n_i}$ , where

$$\displaystyle \begin{aligned} \Delta{\mathbb{R}} {\mathsf{H}}^{n_j}=\{(p,\varphi(p)):p\in{\mathbb{R}}{\mathsf{H}}^{n_j}\}\end{aligned}$$

is a totally geodesic real hyperbolic space diagonally embedded in ${\mathbb {R}}{\mathsf {H}}^{n_j}\times {\mathbb {R}}{\mathsf {H}}^{n_k}$ , for two indices j, k with $n_j=n_k$ and where $\varphi$ is a homothety between ${\mathbb {R}}{\mathsf {H}}^{n_j}$ and ${\mathbb {R}}{\mathsf {H}}^{n_k}$

Note that even in the simplest case of a product of two hyperbolic planes, $M={\mathbb {R}}{\mathsf {H}}^2\times {\mathbb {R}}{\mathsf {H}}^2$, the classification of homogeneous hypersurfaces did not seem to be previously known (see [46] for a recent alternative approach via isoparametric hypersurfaces). In this particular case, there are uncountably many cohomogeneity one actions up to orbit equivalence, due to the existence of actions of horospherical type, which are determined by the choice of a line $\ell$ in the 2-dimensional space ${\mathfrak {a}}$. Apart from these, there are exactly other three cohomogeneity one actions (up to orbit equivalence) if both factors of M are isometric and exactly five actions otherwise:

(FS):

Two of them producing foliations with the totally geodesic codimension one leaf ${\mathbb {R}}{\mathsf {H}}^1\times {\mathbb {R}}{\mathsf {H}}^2$ or ${\mathbb {R}}{\mathsf {H}}^2\times {\mathbb {R}}{\mathsf {H}}^1$, respectively (being both orbit equivalent if and only if both factors of M are isometric)

(CEI):

Other two with the totally geodesic singular orbits $\{o_1\}\times {\mathbb {R}}{\mathsf {H}}^2$ or ${\mathbb {R}} {\mathsf {H}}^2\times \{o_2\}$, respectively (again, both orbit equivalent when both factors are isometric)

(CER):

The diagonal action of ${\mathsf {SO}}_{1,2}^0\cong {\mathsf {SL}}_2({\mathbb {R}})$ on M, which has a diagonal totally geodesic ${\mathbb {R}}{\mathsf {H}}^2$ as singular orbit

It is interesting to compare this result with the situation in the compact dual of M, namely, the product of two round spheres $\mathbb {S}^2\times \mathbb {S}^2$. Here, by a result of Urbano [100] (who actually classified isoparametric hypersurfaces in this space), the only homogeneous hypersurfaces are dual analogs to the examples (CEI) and (CER) above. Again, it is important to recall that the generalization of Urbano’s classification of homogeneous hypersurfaces for products of several spheres of higher dimensions (i.e., the compact analog of Theorem 13) is still outstanding.

7 Open Problems

We include a list of open problems and questions related to the investigation of homogeneous hypersurfaces in symmetric spaces:

• (1) Analyze the nilpotent construction for each symmetric space of noncompact type. This, along with the structural result in Theorem 10, would allow to complete the classification of cohomogeneity one actions in this setting. Due to the difficulty of this problem, we can distinguish two main cases:

  • (a) For spaces whose isometry group is a split semisimple Lie group, we expect that the nilpotent construction leads to various linear algebraic problems (each one depending on a certain class of representations) whose solution may be achieved following the lines of the analogous problem for ${\mathsf {SL}}_n({\mathbb {R}})/{\mathsf {SO}}_n$.

  • (b) For the remaining spaces, the linear algebraic problems involved are more complicated, but we expect that the combination of Solonenko’s ideas in [91] with the ones used for ${\mathsf {SL}}_n({\mathbb {R}})/{\mathsf {SO}}_n$ in [31] may eventually lead to a complete classification.

• (2) Is there any cohomogeneity one action on a symmetric space of noncompact type, rank at least 2, and of non-(${\mathsf {G}}_2$)-type that can be obtained by nilpotent construction but not as a canonical extension?

• (3) Investigate the congruence problem of homogeneous hypersurfaces, or, equivalently, determine when two cohomogeneity one actions are orbit equivalent. Whereas for actions of foliation type this problem has already been solved in [92], an eventual positive answer to Question (2) would need a specific (but probably easy) investigation. However, the analysis of the other types of actions seems more difficult. In particular, one would need to address the following issues:

  • (a) Given a rank two reducible boundary component $B_\Phi \cong \mathbb {F}{\mathsf {H}}^n\times \mathbb {F}{\mathsf {H}}^n$ of M, determine when two different isomorphisms $\tau _1$ and $\tau _2$ between the isometry Lie algebras of the two homothetic factors $\mathbb {F}{\mathsf {H}}^n$ give rise to orbit equivalent canonical extensions of type (CER).

  • (b) Can two orbit equivalent cohomogeneity one actions with totally geodesic singular orbits on an irreducible boundary component produce non-orbit equivalent canonical extensions of type (CEI)? If the answer is affirmative, one would probably have to revisit Berndt and Tamaru’s classification of cohomogeneity one actions with totally geodesic singular orbits [13] in order to determine the moduli space of actions up to strong orbit equivalence (i.e., up to orbit equivalence by isometries in the connected component of the identity of the isometry group). This may entail an analysis of a strong congruence problem of Leung’s classification of reflective submanifolds [66].

• (4) Determine the extrinsic geometry of homogeneous hypersurfaces of symmetric spaces of noncompact type. As an application, one may obtain the classification of homogeneous minimal hypersurfaces.

• (5) Leaving aside the noncompact setting, classify cohomogeneity one actions on reducible symmetric spaces of compact type. See [63] for information on this problem.

• (6) Initiate the study of homogeneous hypersurfaces of locally symmetric spaces, both of compact and noncompact types.

• (7) Derive structure results for cohomogeneity one actions on symmetric spaces of mixed type, including noncompact spaces with Euclidean factors (e.g., ${\mathsf {GL}}_n^+({\mathbb {R}})/{\mathsf {SO}}_n$).

• (8) Obtain characterizations of (certain families of) homogeneous hypersurfaces by (both extrinsic and intrinsic) geometric properties, such as isoparametricity, constancy of principal curvatures, curvature adaptedness, or having an Einstein or Ricci soliton induced metric, cf. [42, 75]. Also, obtaining characterizations of the inhomogeneous isoparametric examples known in most symmetric spaces would be very interesting, in that this would probably entail the introduction of new techniques in submanifold geometry of symmetric spaces. Specifically, although isoparametric hypersurfaces of a product of two real hyperbolic planes turn out to be (open subsets of) homogeneous hypersurfaces [46], for a product of three hyperbolic planes, we know the existence of inhomogeneous examples [41].

• (9) In this survey, we assumed actions to be proper and homogeneous submanifolds to be closed and embedded. Under which circumstances and for which ambient spaces can one guarantee that nonproper cohomogeneity one actions have the same orbits as proper cohomogeneity one actions? Can one prove that on a simply connected ambient space there do not exist nonembedded or nonclosed homogeneous hypersurfaces?