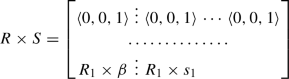Keywords

1 Introduction

The concept of fuzzy sets was founded by Zadeh [19]. Intuitionistic Fuzzy Sets (InFuSes) introduced by Atanassov [2] are appropriate for such a situation. But the intuitionistic fuzzy sets can only handle the incomplete information considering both the truth-membership (or simply membership) and falsity-membership (or non-membership) values. It does not handle the indeterminate and inconsistent information, which exists in belief system. Smarandache [16] introduced the concept of Neutrosophic Set (NeSe), which is a mathematical tool for handling problems involving imprecise, indeterminacy, and inconsistent data.

In our regular everyday life, we face situations that require procedures allowing certain flexibility in information processing capacity. Molodtsov [12] addressed soft set theory problems successfully. In their early work, soft set was described purely as a mathematical method to model uncertainties. The researchers can pick any kind of parameters of any nature they wish in order to facilitate the decision-making procedure as there is a varied way of picturing the objects.

Maji [10] have done further research on soft set theory. Presence of vagueness demanded Fuzzy Soft Set (FuSoSe) to come into picture. But satisfactory evaluation of membership values is not always possible because of the insufficiency in the available information (besides the presence of vagueness) situation. Evaluation of non-membership values is also not always possible for the same reason, and as a result, there exists an indeterministic part upon which hesitation survives. Certainly fuzzy soft set theory is not suitable to solve such problems. In those situations, Intuitionistic Fuzzy Soft Set theory (InFuSoSs) [11] may be more applicable. Now in the parlance of soft set theory, there is hardly any limitation to select the nature of the criteria, and as most of the parameters or criteria (which are words or sentences) are neutrosophic in nature, Maji [9] has been motivated to combine the concept of soft set and neutrosophic set to make the new mathematical model neutrosophic soft set and has given an algorithm to solve a decision-making problem.

The theory of a fuzzy matrix is very useful in the discussion of fuzzy relations. We can represent basic propositions of the theory of fuzzy relations in terms of matrix operations. Furthermore, we can deal with the fuzzy relations in the matrix form. In the study of the theory of fuzzy matrix, a canonical form of some fuzzy matrices has received increasing attention. For example, Kim and Roush [8] studied the Idempotent fuzzy matrices. Xin [18] introduced the idea for Convergence of powers of controllable fuzzy matrices. Padder and Murugadas [15] are presented the max-min opetarion on InFuMa. Broumi et al. [3] redefined the notion of neutrosophic set in a new way and put forward the concept of neutrosophic soft matrix and different types of matrices in neutrosophic soft theory. They have introduced some new operations and properties on these matrices. The minimal solution was done by Kavitha et al. [5], based on the notion of FuNeSoMa given by Arokiarani and Sumathi [1]. As time goes, some works on FuNeSoMa were done by Kavitha et al. [4,5,6,7]. The Monotone interval fuzzy neutrosophic soft eigenproblem, and Monotone fuzzy neutrosophic soft eigenspace structures in max-min algebra and Solvability of system of neutrosophic soft linear equations were investigated by Murugadas et al. [13, 14]. Also, two kinds of fuzzy neutrosophic soft matrices presented by Uma et al. [17].

In this chapter, we study and prove some properties of controllable and Idompotent FuNeSoMas. However, we have developed an algorithm for controllable and nilpotent FuNeSoMas and reduce a controllable FuNeSoMa to canonical form. One of these results enables us to construct an idempotent and controllable FuNeSoMa from a given one, and this is the main result in the chapter.

2 Preliminaries

For basic result refer [5, 16,17,18].

2.1 Main Results

Let \(R=\langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle \) and \(S=\langle s^{T}_{ij},s^{I}_{ij},s^{F}_{ij} \rangle \) be square FuNeSoMa with elements in [0,1].

  • \(R \vee S=[\langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle \vee \langle s^{T}_{ij},s^{I}_{ij},s^{F}_{ij} \rangle ],\)

  • \(R \wedge S=[\langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle \wedge \langle s^{T}_{ij},s^{I}_{ij},s^{F}_{ij} \rangle ],\)

  • \(R \ominus S=[\langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle \ominus \langle s^{T}_{ij},s^{I}_{ij},s^{F}_{ij} \rangle ],\)

$$\displaystyle \begin{aligned} \left. \langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle \ominus \langle s^{T}_{ij},s^{I}_{ij},s^{F}_{ij} \rangle:= \begin{cases} \langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle~~~ If ~~~\langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle > \langle s^{T}_{ij},s^{I}_{ij},s^{F}_{ij} \rangle\\ \langle 0,0,1 \rangle~~~~~~~ If ~~~ \langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle \leq \langle s^{T}_{ij},s^{I}_{ij},s^{F}_{ij} \rangle \end{cases}\!\!\!\!\!\! \right\} \end{aligned}$$

  • \(R \times S=[(\langle r^{T}_{i1},r^{I}_{i1},r^{F}_{i1} \rangle \wedge \langle s^{T}_{1j},s^{I}_{1j},s^{F}_{1j} \rangle ) \vee (\langle r^{T}_{i2},r^{I}_{i2},r^{F}_{i2} \rangle \wedge \langle s^{T}_{2j},s^{I}_{2j},s^{F}_{2j} \rangle ) \vee \ldots \vee \)

    \((\langle r^{T}_{in},r^{I}_{in},r^{F}_{in} \rangle \wedge \langle s^{T}_{nj},s^{I}_{nj},s^{F}_{nj} \rangle )],\)

  • \(R^{k+1}=R^{k}\times R,~~k=\{0,1,2,\ldots \},\)

  • \(R^{0}=I,\)

  • \(R^{\prime }=\langle r^{T}_{ji},r^{I}_{ji},r^{F}_{ji} \rangle \) the transpose of \(R,\)

  • \(\varDelta R=R\ominus R^{\prime } =\varDelta \langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle = \langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle \ominus \langle r^{T}_{ji},r^{I}_{ji},r^{F}_{ji} \rangle ,\)

  • \(\nabla R=R \wedge R^{\prime } = \nabla \langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle = \langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle \wedge \langle r^{T}_{ji},r^{I}_{ji},r^{F}_{ji} \rangle ,\)

  • \(R \leq S \) iff \((\langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle \leq \langle s^{T}_{ij},s^{I}_{ij},s^{F}_{ij} \rangle \forall ~ i,j \in \{1,2,\ldots ,n\}),\)

  • \(R \varPsi S \) iff \((\langle s^{T}_{ij},s^{I}_{ij},s^{F}_{ij} \rangle =\langle 0,0,1 \rangle \Rightarrow \langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle = \langle 0,0,1 \rangle ~~\forall i,j \in \{1,2,\ldots ,n\}),\)

FuNeSoMa R is said to be

  • Transitive if \(\langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle ^{2} \leq \langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle ;\)

  • Idempotent if \(\langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle ^{2}=\langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle ;\)

  • Nilpotent if \(\langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle ^{n}=\langle 0,0,1 \rangle ;\)

  • Symmetric if \(\langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle =\langle r^{T}_{ji},r^{I}_{ji},r^{F}_{ji} \rangle ;\)

  • ST iff for any index \(i,j, k \in \{1, 2,\ldots ,n\},\) with \(i \neq j, i \neq k, j \neq k,\) such that \(\langle r^{T}_{ik},r^{I}_{ik},r^{F}_{ik} \rangle > \langle r^{T}_{ki},r^{I}_{ki},r^{F}_{ki} \rangle \) and \( \langle r^{T}_{kj},r^{I}_{kj},r^{F}_{kj} \rangle > \langle r^{T}_{jk},r^{I}_{jk},r^{F}_{jk} \rangle ,\) we have \(\langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle > \langle r^{T}_{ji},r^{I}_{ji},r^{F}_{ji} \rangle ;\)

  • Strictly Lower (Upper) Triangular (SL(U)T) if \( \langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle =\langle 0,0,1 \rangle \forall i \leq j (i \leq j).\)

Theorem 1

Consider a NiFuNeSoMa N and Symmetric FuNeSoMa (SyFuNeSoMa) S. For a FuNeSoMa R given by \(R=N \vee S \exists \) a Pemutation FuNeSoMa (PeFuNeSoMa) \(P~~\ni \) \(T=\langle t^{T}_{ij},t^{I}_{ij},t^{F}_{ij} \rangle =\langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \times \langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle \times \langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle \) satisfies \(\langle t^{T}_{ij},t^{I}_{ij},t^{F}_{ij} \rangle \geq \langle t^{T}_{ji},t^{I}_{ji},t^{F}_{ji} \rangle \) for \(i > j.\)

Proof

\(\langle t^{T}_{ij},t^{I}_{ij},t^{F}_{ij} \rangle =\langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \times \langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle \times \langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle \)

\(=\langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \times (\langle n^{T}_{ij},n^{I}_{ij},n^{F}_{ij} \rangle \vee \langle s^{T}_{ij},s^{I}_{ij},s^{F}_{ij} \rangle ) \times \langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle \)

\(=(\langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \times \langle n^{T}_{ij},n^{I}_{ij},n^{F}_{ij} \rangle \times \langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle )\vee (\langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \times \langle s^{T}_{ij},s^{I}_{ij},s^{F}_{ij} \rangle \times \langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle ).\)

Since N is NiFuNeSoMa, \((\langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \times \langle n^{T}_{ij},n^{I}_{ij},n^{F}_{ij} \rangle \times \langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle )\) becomes strictly lower triangler for some PeFuNeSoMa \(P.\)

Thus since \((\langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \times \langle n^{T}_{ij},n^{I}_{ij},n^{F}_{ij} \rangle \times \langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle )\) is symmetric,

T satisfies \(\langle t^{T}_{ij},t^{I}_{ij},t^{F}_{ij} \rangle \geq \langle t^{T}_{ji},t^{I}_{ji},t^{F}_{ji} \rangle \) for \(i > j\) by choosing such a PeFuNeSoMa \(P.\)

Remark 1

If \(N=\langle n^{T}_{ij},n^{I}_{ij},n^{F}_{ij} \rangle \) is NiFuNeSoMa, then there exists a PeFuNeSoMa P such that \(\langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \times \langle n^{T}_{ij},n^{I}_{ij},n^{F}_{ij} \rangle \times \langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle \) is SL(U)T.

Remark 2

The NiFuNeSoMa, R has not less than a null row and atleast one null column.

Remark 3

If R is NiFuNeSoMa iff \(\langle r^{T}_{ii},r^{I}_{ii},r^{F}_{ii} \rangle ^{(k)}=\langle 0,0,1 \rangle ,\) to a little \(i \in I_n\)(Index) and little \(k \in I_n,\) for \(R^{k}:=[\langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle ^{(k)}].\)

Theorem 2

For any FuNeSoMa \(R,\ \langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle =\varDelta \langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle \vee \nabla \langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle .\)

3 Controllable Fuzzy Neutrosophic Soft Matrices

Here we establish some basic properties of FuNeSoMas. In the ensuing discussion, we pact only with SqFuNeSoMas.

Proposition 1

For a FuNeSoMa N. If \(\exists \) a PeFuNeSoMa \(P~ \ni ~\langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \times \langle n^{T}_{ij},n^{I}_{ij},n^{F}_{ij} \rangle \times \langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle \) is SL(U)T, then N is a NiFuNeSoMa.

Proof

Let

$$\displaystyle \begin{aligned} S=\langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \times \langle n^{T}_{ij},n^{I}_{ij},n^{F}_{ij} \rangle \times \langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle = \begin{bmatrix} \langle 0,0,1\rangle & \langle 0, 0,1\rangle\\ \ddots\\ * & \langle 0,0,1\rangle\\ \end{bmatrix} \end{aligned}$$

we can prove the direct multiplication that \(S^{2}\) is also SL(U)T, and consequently \(S^{3},S^{4},\ldots \) all powers of \(S.\) All diagonals are zero in \(S,S^{2},S^{3},\ldots , \) so by Remark 3, S is nilpotent. As \(\langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \times \langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle =\langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle \times \langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle =\langle 1,1,0 \rangle ,\) then multiplying S on the left by \(\langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle ,\) we get \(\langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle \times \langle s^{T}_{ij},s^{I}_{ij},s^{F}_{ij} \rangle \times \langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle =\langle n^{T}_{ij},n^{I}_{ij},n^{F}_{ij} \rangle ,\) so we find the \(N^{n},\)

that is \(\langle n^{T}_{ij},n^{I}_{ij},n^{F}_{ij} \rangle ^{n}=\langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle \times \langle s^{T}_{ij},s^{I}_{ij},s^{F}_{ij} \rangle \times \langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \times \langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle \times \langle s^{T}_{ij},s^{I}_{ij},s^{F}_{ij} \rangle \times \langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \times \ldots \times \langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle \times \langle s^{T}_{ij},s^{I}_{ij},s^{F}_{ij} \rangle \times \langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \)

\(=\langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle \times \langle s^{T}_{ij},s^{I}_{ij},s^{F}_{ij} \rangle ^{n} \times \langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \)

\(=\langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle \times \langle 0,0,1 \rangle \times \langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle = \langle 0,0,1 \rangle .\)

Theorem 3

A FuNeSoMa N is nilpotent iff \(\exists \) a PeFuNeSoMa \(\langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \ni \langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \times \langle n^{T}_{ij},n^{I}_{ij},n^{F}_{ij} \rangle \times \langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle \) is SL(U)T.

Note 1

Let \(\langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle \) be a FuNeSoMa, \(\langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \) is PeFuNeSoMa. Let \(T=\langle t^{T}_{ij},t^{I}_{ij},t^{F}_{ij} \rangle =\langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \times \langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle \times \langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle .\) The element which lies in the \((i,j)^{th}\) entry of R lies next in the \((h,k)^{th}\) of T iff \(\langle p^{T}_{hi},p^{I}_{hi},p^{F}_{hi} \rangle = \langle p^{T}_{kj},p^{I}_{kj},p^{F}_{kj} \rangle = \langle 1,1,0 \rangle .\)

Theorem 4

Let \(R=\langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle \) be a FuNeSoMa, \(P= \langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \) is PeFuNeSoMa. Then

$$\displaystyle \begin{aligned} & \langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \times (\varDelta \langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle) \times \langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle =\varDelta(\langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \\ & \quad \times \langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle)\times \langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle, \end{aligned} $$
(1)
$$\displaystyle \begin{aligned} & \langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \times(\nabla \langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle) \times \langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle =\nabla(\langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \\ & \quad \times \langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle\times \langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle). \end{aligned} $$
(2)

Definition 1

We say a FuNeSoMa R is controllabel from belove (above), if \(\exists \) a PeFuNeSoMa \(P~\ni ~\langle t^{T}_{ij},t^{I}_{ij},t^{F}_{ij} \rangle =\langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \times \langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle \times \langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle \) satisfies \(\langle t^{T}_{ij},t^{I}_{ij},t^{F}_{ij} \rangle \geq \langle t^{T}_{ji},t^{I}_{ji},t^{F}_{ji} \rangle ~ (\langle t^{T}_{ij},t^{I}_{ij},t^{F}_{ij} \rangle \leq \langle t^{T}_{ji},t^{I}_{ji},t^{F}_{ji} \rangle )\) a long as \(i > j.\)

A FuNeSoMa \(R=\langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle \) is said to be controlled from below (above), if \(\langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle \geq \langle r^{T}_{ji},r^{I}_{ji},r^{F}_{ji} \rangle (\langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle \leq \langle r^{T}_{ji},r^{I}_{ji},r^{F}_{ji} \rangle ) \)as long \( i > j.\)

Theorem 5

The next statements are analogous:

  • (1) \(\langle r^{T}_{ji},r^{I}_{ji},r^{F}_{ji} \rangle \) is CFB(A).

  • (2) There exists a PeFuNeSoMa \(\langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \) such that \(\varDelta (\langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \times \langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle \times \langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle )\) is SL(U)T.

  • (3) There exists a PeFuNeSoMa \(\langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \) such that \(\langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \times (\varDelta \langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle )\times \langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle )\) is SL(U)T.

  • (4)\(\varDelta \langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle \)

Corollary 1

\(\langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle \) is CFB iff \(\langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle \) is CFA.

Note 2

Let R and S be FuNeSoMas, and P is a PeFuNeSoM. Then \(R \varPsi S\) iff \(\langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \times \langle r^{T}_{ij},r^{I}_{ij},r^{F}_{ij} \rangle \times \langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle \varPsi \langle p^{T}_{ij},p^{I}_{ij},p^{F}_{ij} \rangle \times \langle s^{T}_{ij},s^{I}_{ij},s^{F}_{ij} \rangle \times \langle p^{T}_{ji},p^{I}_{ji},p^{F}_{ji} \rangle .\)

Proof: The proof is obvious.

Theorem 6

Let \(R, S\) be a FuNeSoMas, and \(\varDelta R \varPsi \varDelta S.\) If S is controllable, then R is controllable.

4 Reduction of Controllable Matrix to Canonical Form

Lemma 1

Let \(R=(\langle r^{T}_{ij}, r^{I}_{ij},r^{F}_{ij}\rangle )\) and \(S=(\langle s^{T}_{ij},s^{I}_{ij},s^{F}_{ij}\rangle )\) be \(n\times n\) FuNeSoMa of the form

$$\displaystyle \begin{aligned} R=\begin{bmatrix} \langle 0,0,1\rangle &\vdots & \langle0,0,1\rangle & \cdots & \langle 0,0,1\rangle \\ && \kern-1em \cdots\cdots\cdots\cdots\cdots\\ \alpha & \vdots & R_{1} \end{bmatrix}, \end{aligned}$$
$$\displaystyle \begin{aligned} S=\begin{bmatrix} \langle 0,0,1\rangle &\vdots & \langle 0,0,1\rangle & \cdots & \langle 0,0,1\rangle \\ && \kern-1em \cdots\cdots\cdots\cdots\cdots\\ \beta & \vdots & S_{1} \end{bmatrix}, \end{aligned}$$

where \(\alpha \) and \(\beta \) are \((n-1)\times 1\) FuNeSoMa and \(R_{1}\) and \(S_{1}\) are FuNeSoMa of order (n-1). Then

  1. (i)
  2. (ii)
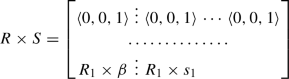
  3. (iii)

    R is NiFuNeSoMa iff \(R_{1}\) is nilpotent.

Remark 4

Let \(R=(\langle r^{T}_{ij},r^{I}_{ij}, r^{F}_{ij}\rangle ) \in FuNeSoMa_{n},\) and R have no less than one \(\langle 0, 0,1 \rangle \) row (say, the \(i^{th}\) row). Let \(i^{th}\) row \(\rightarrow \) I-row and vice versa and do the same for column; then we have

Lemma 2

R is NiFuNeSoMa iff \(R_{1}\) is NiFuNeSoMa. By Lemma 1, we have the following for NiFuNeSoMa \(R.\)

Algorithm 1

Step 1. Check \(R,\) for a null row and null column; if anyone is missing, then R fails to be nilpotent. End.

Check R for both zero row and zero column. If not, then R is not nilpotent. If R has both conditions, then do interchange as mentioned; then, we have

where \(\langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle _{1}=\langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle (1,i_{1})\). Next step

Step 2. Check R for both zero row and zero column. If not then \(R_{1}\) is not nilpotent, Stop.

If \(R_{1}\) satisfies desired conditions, i.e., in \(R_{1}\), the \(i_{2}^th\) row is a null row. The new form \(\langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle _{2}\times \langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle _{1}\times R\times \langle p^{T}_{ji}, p^{I}_{ji},p^{F}_{ji}\rangle _{1}\times \langle p^{T}_{ji}, p^{I}_{ji},p^{F}_{ji}\rangle _{2}\) from FuNeSoMa \(\langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle _{1}\times R\times \langle p^{T}_{ji}, p^{I}_{ji},p^{F}_{ji}\rangle _{1}\) by interchanging the \((i_{2}+1)\)-th row with II row and \((i_{2}+1)\)-th column with the II column such that

$$\displaystyle \begin{aligned} \langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle_{2}\times \langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle_{1}\times R\times \langle p^{T}_{ji}, p^{I}_{ji},p^{F}_{ji}\rangle_{1}\times \langle p^{T}_{ji}, p^{I}_{ji},p^{F}_{ji}\rangle_{2} \end{aligned}$$

where \(\langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle _{2}=\langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle (2, i_{2}+ 1)\). Next step.

Step 3. Check \(R_{2},\) for a null row and null column. If not, \(R_{2}\) is not nilpotent; thus, Lemma 2 implies \(R_{1}\) and R are not nilpotent, stop.

Else if in \(R_{1},\) the \(i_{3}^{th}\) row of \(R_{2}\) is null, the new FuNeSoMa of the form \( \langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle _{3}\times \langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle _{2}\times \langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle _{1}\times R\times \langle p^{T}_{ji}, p^{I}_{ji},p^{F}_{ji}\rangle _{1}\times \langle p^{T}_{ji}, p^{I}_{ji},p^{F}_{ji}\rangle _{2}\times \langle p^{T}_{ji}, p^{I}_{ji},p^{F}_{ji}\rangle _{3}\) from matrix \(\langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle _{2}\times \langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle _{1}\times R \times \langle p^{T}_{ji}, p^{I}_{ji},p^{F}_{ji}\rangle _{1}\times \langle p^{T}_{ji}, p^{I}_{ji},p^{F}_{ji}\rangle _{2}\) then changes the \((i_{3}+2)\)-th row with II row and \((i_{3}+2)\)-th column with the II column \(\ni \),

$$\displaystyle \begin{aligned} & \langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle_{3}\times \langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle_{2}\times \langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle_{1}\times R \times \langle p^{T}_{ji}, p^{I}_{ji},p^{F}_{ji}\rangle_{1} \\ & \quad \times \langle p^{T}_{ji}, p^{I}_{ji},p^{F}_{ji}\rangle_{2}\times \langle p^{T}_{ji}, p^{I}_{ji},p^{F}_{ji}\rangle_{3} \end{aligned} $$

where \(\langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle _{3}= \langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle (3, i_{3} + 2)\). Next step.

Continuing like this, finally we get

where \(\langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle _{m}=\langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle (m, i_{m} + m-1)\), \(m \in I_n.\)

In the event if \(R_{n}\) fails to satisfy both the condition, then R is not nilpotent.

Else,

$$\displaystyle \begin{aligned} R_{n}=\begin{bmatrix} \langle 0,0,1\rangle & \langle 0,0,1\rangle \\ \ddots\\ * & \langle 0,0,1\rangle \end{bmatrix} \end{aligned}$$

then by Lemma 2, R is nilpotent by the sequence of actions. Then, \(\langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle = \langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle _{t}\times \langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle _{t-1}\times \ldots \times \langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle _{2}\times \langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle _{1}.\)

We obtain,

$$\displaystyle \begin{aligned} \langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle\times R\times \langle p^{T}_{ji}, p^{I}_{ji},p^{F}_{ji}\rangle =\begin{bmatrix} \langle 0,0,1\rangle & \langle 0,0,1\rangle \\ \ddots\\ * & \langle 0,0,1\rangle \end{bmatrix} \end{aligned}$$

which indeed SLT. Algorithm to curtail CoFuNeSoMa to canonical form.

Algorithm 2

Step 1. By Algorithm 1, we can check if \(\varDelta R\) is nilpotent or not. Thus R is CoFuNeSoMa or not by Theorem 5.

Step 2. If R is CoFuNeSoMa, then by Step I, we get a permutation matrix P, i.e., \( \langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle \times (\varDelta R)\times \langle p^{T}_{ji}, p^{I}_{ji},p^{F}_{ji}\rangle \), which is SLT. So \(\langle p^{T}_{ij}, p^{I}_{ij},p^{F}_{ij}\rangle \times R\times \langle p^{T}_{ji}, p^{I}_{ji},p^{F}_{ji}\rangle \) is canonical form of \(R.\) Stop.

5 Conclusion

In this article the controllable fuzzy neutrosophic soft matrix is defined. Further, various properties of nilpotent and controllable fuzzy neutrosophic soft matrices are showed. We have developed an algorithm for controllable and nilpotent fuzzy neutrosophic soft matrices and reduced a controllable fuzzy neutrosophic soft matrix to canonical form.