A Systematic Approach to Smart Damping of Mechanical Systems Based on Inductive Electro-Mechanical Coupling

Abstract

Changing magnetic flux in conductive materials will induce electric currents: if the change of flux is – somehow – related to mechanical motions, the corresponding kinetic energy of the mechanical system may be converted into electric energy. Thus, such inductive coupling offers highly flexible opportunities to remove energy from the mechanical system and either store or dissipate it in an electrical subsystem. Consequently, the corresponding mechanical force will act as a damping force. This basic effect is a classical means to calm structural vibrations: however, it is found that common approaches are very diverse and strongly differ in their basic mechanisms. The main aim of this contribution is to give an overview and classify the various approaches by emphasizing systematical differences as well as common points. In this sense, this contribution is intended to be a first step to pave the way for interconnected arrays of such devices. Therefore, the necessary basic functionalities to build an inductive damping element are surveyed and different topologies are built from these basic functionalities. The first part focuses on models based on magnetic circuits, where a change of the magnetic flux is achieved by the modulation of air gaps and thus, the magnetic reluctance of the circuit. The second part deals with an alternative design based on an eddy current damping element, that consists of a permanent magnet moving in a conductive tube. Beyond this basic configuration, the influence of kinematic modulations is explored by equipping this element with geometric discontinuities. Eventually, this offers manifold opportunities to design the dissipative behavior and thus, to smartly model the damping characteristic. After stating the equations of motion, a numerical analysis is inevitable. Partly Finite Element analysis is used for validation and to complement the analytic derivations.

1 Introduction

The field of inductive damping of structural vibrations is best described from an energetic point of view. The kinetic energy of the structural vibration is converted into electric energy by electromagnetic induction. The electric energy is then dissipated by ohmic resistors and is thus extracted from the mechanical system. In order to convert kinetic energy into electric energy, the magnetic flux through some conductive material has to be modulated. This process can be divided into four basic functionalities: source of magnetic flux, transport of magnetic flux, modulation of magnetic flux and induction of electric current.

Fig. 1

Overview on functional elements of electromagnetic damping devices

For each of these functionalities different realizations are possible. The source of the magnetic flux can either be a permanent magnet or an electromagnet, the transport of the magnetic flux can be guided through the structure by use of high permeability iron cores or can be unguided. The modulation of the flux in a conductive material may be due to a change of the magnetic flux itself or due to a movement of a conductive material relative to a magnetic field. The induction can either occur in a coil (as a lumped element of the system) or in form of eddy currents, distributed over a part of the structure. Figure 1 shows a matrix which gives an overview on the different functionalities as well as symbolic design examples.

Based on this matrix, damping devices may systematically be created by (rather) freely combining different alternatives to implement the basic functionalities. For example, an inductive damping device may be constructed by combining a guided transport of the magnetic flux, a modulation of the flux by varying an air gap, an inductive coupling by means of a coil and providing dissipation using an ohmic resistor. For the source of the magnetic flux, basically two options are available: it may either be produced by a permanent magnet with a remanence of $B_R$ (cf. Fig. 2a) or by means of an electromagnet fed with a constant current $I_0$ (cf. Fig. 2b).

Fig. 2

Examples built from the matrix of basic functionalities using different realizations of the source of the magnetic flux: a permanent magnet, b electromagnet

In the past decades several investigations on inductive damping have been published. Behrens et al. [4] have introduced electromagnetic shunt damping. They proposed a plunger, consisting of permanent magnets, that is moving in a coil, which is connected to an impedance network.

Przybylowicz and Szmidt [8, 9] theoretically investigated a mechanical oscillator between two electromagnets. The magnetic flux is guided with iron cores through the mechanical oscillator and builds two independent magnetic circuits with an air gap. The length of the air gap is modulated by the mechanical movement and thus, eddy currents are induced in the iron core. The investigated model shows strongly nonlinear behavior.

Bae et al. [1, 2] studied the behavior of a cylindrical permanent magnet moving in a conductive tube. Sodano et al. [12, 13] investigated a model consisting of a cantilever beam with a conducting plate, that is moving in the magnetic field of a permanent magnet. Later on Sodano and Inman [14] proposed an active damping device where they used again a cantilever beam with a conductive plate. This time an electromagnet generates the magnetic field and a feedback control system is used to control the oscillations of the structure. Laborenz et al. [5, 6] experimented with eddy current damping to reduce the oscillations of steam turbine blades. They, as well, used a copper plate oscillating in the magnetic field of a permanent magnet.

Bae et al. [3] studied the use of an eddy current damper as a magnetically damped tuned mass damper to reduce oscillations of a beam structure. They showed, that the resonance amplitudes of the structure were decreased by applying eddy current damping to the tuned mass damper. Lian et al. [7] proposed an eddy current-tuned mass damper for wind turbines.

The objective of this contribution is to systematically analyze different realizations of inductive damping elements. Therefore models using different elements of the basic functionalities shown in Fig. 1 will be investigated. Furthermore, the possibility to modify inductive damping systems with additional nonlinearities to show a specific behavior is presented.

2 Analysis of Models Based on Magnetic Circuits

In this section the equations of motions for the proposed models shown in Fig. 2 will be derived and the static and dynamic behavior will be analyzed. The derivation of the equations of motion is exemplary shown for the system with permanent magnet, illustrated in Fig. 2a.

To describe an inductive damping model mathematically, the system can be divided into three subsystems, as shown in Fig. 3. Here, the electrical and the mechanical subsystem do not interact directly but will be coupled by the magnetic field which acts as a mediator.

Fig. 3

Separate physical sub-domains involved in an inductive damping device

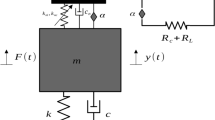
The mechanical system in this case is a simple single degree of freedom (DoF) oscillator with mass m and stiffness k (cf. Fig. 4a). The position of the mass is described by the coordinate x. The mass is excited harmonically by an external force F(t). Furthermore the magnetic force $F_{mag}$ acts on the mass. Another static force $F_0$ is introduced in order to compensate static magnetic forces and thus to ensure, that the system will have a static resting position at $x=0$. For instance, such a force could easily be realized by preloading the spring. Eventually, the equation of motion for the mechanical system follows from Newton’s law and is given by

$$\begin{aligned} m \ddot{x} + k x = F(t) + F_{mag} -F_0. \end{aligned}$$

(1)

The electric subsystem is a simple electrical network, featuring an ohmic resistor R and the induced voltage $U_{emf}$. The current flowing in the circuit is denoted by I. The equation of motion follows from Kirchhoff’s law and reads

$$\begin{aligned} U_{emf} + R I =0. \end{aligned}$$

(2)

Fig. 4

a Mechanical subsystem. b Electrical subsystem

Assuming magnetostatic conditions the magnetic problem can be described by the simplified form of Ampère’s law [16], reading

$$\begin{aligned} \oint _\Gamma \textbf{H} \cdot \,\textrm{d}\textbf{l} = I_{enc}, \end{aligned}$$

(3)

where $\textbf{H}$ is the magnetic field, $I_{enc}$ is the current enclosed by the loop $\Gamma$ and $\,\textrm{d}\mathbf {\ell }$ is an infinitesimal element of the curve $\Gamma$. Furthermore, the conservation law of the magnetic flux holds according to

$$\begin{aligned} \oint _S \textbf{B} \cdot \,\textrm{d}\textbf{a} = 0, \end{aligned}$$

(4)

where $\textbf{B}$ is the magnetic flux density and $\,\textrm{d}\textbf{a}$ is the outer normal unit vector of the closed surface S. The magnetic flux density $\textbf{B}$ is connected to the magnetic field $\textbf{H}$ by the constitutive relation

$$\begin{aligned} \textbf{H} = \textbf{H}(\textbf{B}). \end{aligned}$$

(5)

Furthermore, the magnetic flux through a surface S is defined by

$$\begin{aligned} \Phi = \int _S \textbf{B} \cdot \,\textrm{d}\textbf{a}. \end{aligned}$$

(6)

Fig. 5

Magnetic subsystem

The magnetic subsystem for the proposed inductive damping device with a permanent magnet is shown in Fig. 5. Applying Ampère’s law to the illustrated loop $\Gamma$ yields

$$\begin{aligned} H_m \ell _m + H_{\text {\textit{fe}}} \ell _{\text {\textit{fe}}} + H_{d} (\ell _d-x) = N I, \end{aligned}$$

(7)

where $H_m$ is the magnetic field in the permanent magnet, $\ell _m$ is the length of the permanent magnet, $H_{\text {\textit{fe}}}$ is the field in the iron core, $\ell _{\text {\textit{fe}}}$ is the length of the iron core, $H_d$ is the field in the air gap and $\ell _d$ is the nominal length of the air gap, N is the number of turns of the coil and I is the current flowing through the coil. From the conservation of the magnetic flux, it may be followed that all individual parts of the structure are crossed by the same flux and thus

$$\begin{aligned} \Phi _m = \Phi _{\text {\textit{fe}}} = \Phi _d = \Phi \end{aligned}$$

(8)

holds. Assuming equal cross sections A of the individual parts yields

$$\begin{aligned} \Phi = B A, \end{aligned}$$

(9)

which states that the magnetic flux density in all parts is equal. The constitutive relations for the magnetic fields in the permanent magnet ($H_m$), the air gap ($H_d$) and the iron core ($H_{\text {\textit{fe}}}$) are given by

$$\begin{aligned} H_m = \frac{1}{\mu _0}(B-B_R), \quad H_d = \frac{1}{\mu _0} B \quad \text {and} \quad H_{\text {\textit{fe}}} = \frac{1}{\mu _{\text {\textit{fe}}}(B)}B, \end{aligned}$$

(10)

where $\mu _0$ is the magnetic permeability of free space and $\mu _{\text {\textit{fe}}}(B)$ is the permeability of the iron. The permeability of the magnet is assumed to be $\mu _0$, as this is approximately the case for neodymium magnets. For this study hysteresis losses of the B–H characteristic are neglected because most of the energy storage of the magnetic field occurs in the air gap, and thus hysteresis losses are assumed to be small [15]. The assumed B–H characteristic is shown in Fig. 6: the slope of the characteristic decreases sharply after the magnetic flux density reaches a magnitude $B_{sat}$, as the material saturates.

Fig. 6

B–H characteristic of the material for the iron core (adapted from [15])

Eventually, the magnetic flux of the system is described by

$$\begin{aligned} \left( (\ell _m + \ell _d -x) + \frac{\mu _0}{\mu _{\text {\textit{fe}}}(B)} \ell _{\text {\textit{fe}}} \right) \Phi =\mu _0 N A I + \ell _m \Phi _R, \end{aligned}$$

(11)

where $\Phi _R=B_R A$ is the magnetic flux of the remanence. The link of the mechanical and the magnetic subsystems may be expressed using Maxwell’s stress tensor

$$\begin{aligned} \mathbf {\textbf{T}} = \textbf{B}\otimes \textbf{H}-\frac{1}{2}(\textbf{B}\cdot \textbf{H})\mathbf {\textbf{I}}, \end{aligned}$$

(12)

where $\mathbf {\textbf{I}}$ is the unit dyadic tensor [11]. Accordingly, the total magnetic force acting on an object reads

$$\begin{aligned} \textbf{F} = \oint _S \mathbf {\textbf{T}} \cdot \,\textrm{d}\textbf{a}, \end{aligned}$$

(13)

where S is the surface of the object and $\,\textrm{d}\textbf{a}$ is the outer normal unit vector of the surface. For the considered model, the magnetic force results in

$$\begin{aligned} F_{mag} = A\frac{B^2}{2 \mu _0} = \frac{\Phi ^2}{2 A \mu _0}. \end{aligned}$$

(14)

The relation between the electric and the magnetic subsystem is given by the flux linkage of the coil, and thus

$$\begin{aligned} U_{emf} = \frac{\,\textrm{d}\Psi }{\,\textrm{d}t}, \quad \text {where} \quad \Psi = N \Phi . \end{aligned}$$

(15)

For the proposed model, $\Psi$ is not explicitly time-dependent and therefore

$$\begin{aligned} U_{emf} = N\frac{\,\textrm{d}\Phi }{\,\textrm{d}t} = N \left( \frac{\partial {\Phi }}{\partial {x}}\dot{x} +\frac{\partial {\Phi }}{\partial {I}}\dot{I} \right) \end{aligned}$$

(16)

applies. Summarizing, the equations of motion for the system in Fig. 2a read

$$\begin{aligned} m \ddot{x} + k x -\frac{\Phi ^2}{2 A \mu _0}&= F(t)-F_0 \end{aligned}$$

(17)

$$\begin{aligned} N \left( \frac{\partial {\Phi }}{\partial {x}} \dot{x} +\frac{\partial {\Phi }}{\partial {I}} \dot{I} \right) + R I&= 0 \end{aligned}$$

(18)

$$\begin{aligned} \left( (\ell _m + \ell _d -x) + \frac{\mu _0}{\mu _{\text {\textit{fe}}}(\Phi /A)} \ell _{\text {\textit{fe}}} \right) \Phi&= \mu _0 N A I + \ell _m \Phi _R. \end{aligned}$$

(19)

Using the mechanical eigenfrequency

$$\begin{aligned} \omega _0 = \sqrt{\frac{k}{m}} \end{aligned}$$

(20)

for vanishing electro-magnetic coupling (i.e. $\Phi = 0$), the time t is re-scaled to the dimensionless time $\tau = \omega _0 t$. Consequently, the differential operators transform according to $\dot{(\cdot )}=\omega _0 (\cdot )'$, where $(\cdot )'$ denotes the derivation with respect to $\tau$. Furthermore the dimensionless parameters

$$\begin{aligned} \kappa&= \frac{\ell _m}{b},&\delta _0&= \frac{\ell _d}{b},&\beta&= \frac{\ell _{\text {\textit{fe}}}}{b}, \end{aligned}$$

(21)

$$\begin{aligned} \nu&= \frac{N \Phi _R \omega _0}{R I_0},&\gamma&= \frac{\Phi _R^2}{2 \ell _d k A \mu _0 },&h(\varphi )&= \frac{\mu _0}{\mu _{\text {\textit{fe}}}\left( \Phi _R \varphi /A\right) }, \end{aligned}$$

(22)

$$\begin{aligned} \rho&= \frac{b\mu _0 N I_0}{\Phi _R},&f(\tau )&= \frac{1}{\ell _d k}F\left( \tau /\omega _0\right) ,&f_0&= \frac{1}{\ell _d k}F_0 \end{aligned}$$

(23)

as well as the scaled coordinates

$$\begin{aligned} \text{ displacement: } \quad \xi&= \frac{x}{\ell _d},&\text{ flux: } \quad \varphi&= \frac{\Phi }{\Phi _R} ,&\text{ current: } \quad \iota&=\frac{I}{I_0} \end{aligned}$$

(24)

are introduced, where b is the width of the iron core and $I_0$ is some reference current. Inserting these parameter into the Eqs. (17)–(19) results in the dimensionless equations of motion of the system with permanent magnet (cf. Fig. 2a)

$$\begin{aligned} \xi ''+\xi -\gamma \varphi ^2&=f(t)-f_0 \end{aligned}$$

(25)

$$\begin{aligned} \nu \left( \frac{\partial \varphi }{\partial \xi } \xi ' + \frac{\partial \varphi }{\partial \iota }\iota ' \right) + \iota&= 0 \end{aligned}$$

(26)

$$\begin{aligned} (\kappa +\rho \iota )-\big (\kappa +\delta _0(1-\xi )+\beta h(\varphi )\big )\varphi&= 0 . \end{aligned}$$

(27)

Apart from the difference in the source term of the magnetic flux, the mechanical and electrical subsystems for the damping device using an electromagnet as depicted in Fig. 2b are equivalent. For this case, Ampère’s law yields

$$\begin{aligned} H_{\text {\textit{fe}}} \ell _{\text {\textit{fe}}} + H_{d} \left( \ell _d-x\right) = N I + N_0 I_0, \end{aligned}$$

(28)

where $N_0$ is the number of turns of the electromagnet and $I_0$ is a constant current feeding the electromagnet. Following the same steps as for the system with a permanent magnet, the dimensionless equation of motion of the system with electro-magnet (cf. Fig. 2b) are found as

$$\begin{aligned} \xi ''+\xi -\gamma \varphi ^2&=f(t)-f_0 \end{aligned}$$

(29)

$$\begin{aligned} \nu \left( \frac{\partial \varphi }{\partial \xi } \xi ' + \frac{\partial \varphi }{\partial \iota }\iota ' \right) + \iota&= 0 \end{aligned}$$

(30)

$$\begin{aligned} (\rho _0+\rho \iota )-\left( \delta _0(1-\xi )+\beta h(\varphi )\right) \varphi&= 0, \end{aligned}$$

(31)

where $\rho _0$ is the source term of the magnetic flux, given by

$$\begin{aligned} \rho _0 = \frac{b\mu _0 N_0 I_0}{\Phi _r}. \end{aligned}$$

(32)

2.1 Static Analysis

In Fig. 7 the magnetic flux $\varphi$ of the considered models is shown as a function of the relative static displacement $\xi$.¹ Since a static solution is assumed ($\xi '=0$) no currents are induced and therefore, $\iota =0$ holds. Notice that a relative displacement of $\xi =1$ means, that the air gap is closed. The figure compares solutions with as well as those without accounting for magnetic saturation. For the system with permanent magnet, the influence of saturation is very small, as the magnetic flux is restricted due to the remanence of the permanent magnet. In contrast, the system with electromagnet shows a strong influence of saturation as the flux increases for small air gaps. Therefore, for the system with an electromagnet, saturation effects must be taken into account, if small air gaps occur.

Fig. 7

Magnetic flux of models with permanent magnet (pm) and electromagnet (em) with and without the effect of saturation

As the magnetic forces act equivalent to a nonlinear spring with negative stiffness, the static solution may become unstable for certain parameters. Figure 8 shows stability charts for both models for parameter variations of the source term of the magnetic flux ($\kappa$ respectively $\rho _0$) and the coupling parameter of the mechanical and the magnetic subsystem $\gamma$. While the system with a permanent magnet only shows instabilities for higher values of $\gamma$, the system with an electromagnet becomes unstable already for much lower values. As the stiffness of the magnetic force is dependent on the slope of the magnetic forces against $\xi$, the system becomes unstable if $\gamma \frac{\,\textrm{d}\varphi ^2}{\,\textrm{d}\xi }>1$ applies [10].

Fig. 8

Stability charts of magneto-mechanical coupling against flux source for a system with permanent magnet, b system with electromagnet [10]

2.2 Dynamic Analysis

For a harmonic excitation with $f(t) = \hat{f} \sin (\eta \tau )$, a dynamic analysis of the system is carried out using a simple shooting method. The maximal amplitudes of the occurring oscillations are shown in Fig. 9a. Both systems—the one with permanent magnet as well as the system with electromagnet—show a shift of the resonance frequency. This is caused by the magnetic forces acting as a spring with negative stiffness. Furthermore, in both cases resonance amplitudes are limited. The resonance amplitudes of the system featuring an electromagnet are much lower and thus, the damping is higher. While for the system with a permanent magnet higher amplitudes of the excitation force will lead to system failure, as the deflection reaches the length of the air gap, the frequency responses of the system with an electromagnet for higher excitation force levels are depicted in Fig. 9b. The system shows strongly nonlinear behavior for higher amplitudes. Even higher amplitudes of the force lead to instabilities and therefore are not computable by the used simple shooting method.

Fig. 9

a Frequency responses of the models with excitation force amplitude $\hat{f}= 0.02$. Red: system with permanent magnet—Green: system with electromagnet—Gray: system without magnets. b Frequency response of the system with electromagnet for different excitation force amplitudes $\hat{f}$

2.3 Numerical Validation

To validate the obtained results, a numerical model has been set up. To compensate the one-sided magnetic pull and to get a more efficient damping, the model has been expanded to a symmetric model, as depicted in Fig. 10a.

Fig. 10

a Model for numerical validation. b MEC-network of the model

To describe the model analytically, the method of magnetic equivalent circuits (MEC) is used. The method converts the continuous model into lumped parameters connected by nodes and thus, forming a network, similar to an electric network. The method is equivalent in assumptions to the one presented in the previous subsection, but it brings the advantage of being able to analyze more complex systems with multiple connected magnetic circuits. To transform the continuous model into a MEC, Ampère’s law (Eq. (3)) is split into individual sections

$$\begin{aligned} \oint _\Gamma \textbf{H} \cdot \,\textrm{d}\mathbf {\ell } = \sum _{d\in D_\Gamma } \int _{\ell _d} \textbf{H} \cdot \,\textrm{d}\mathbf {\ell } = \sum _{d\in D_\Gamma } F_d, \end{aligned}$$

(33)

where $D_\Gamma$ is the set of names of the individual parts. $F_d$ is commonly referred to as magnetomotive force (MMF) drop. Accordingly the currents inside the loop $\Gamma$ are called MMF sources and are denoted as

$$\begin{aligned} I_{enc,\Gamma } = \sum _{s\in S_\Gamma } N_s I_s = \sum _{s\in S_\Gamma } F_s, \end{aligned}$$

(34)

where $S_\Gamma$ is a set, containing the names of the MMF sources. Ampère’s law in the theory of MECs is referred to as Kirchhoff’s MMF law, which states that the sum of MMF drops in a closed loop equals the sum of MMF sources, i.e.

$$\begin{aligned} \sum _{d\in D_\Gamma } F_d = \sum _{s\in S_\Gamma } F_s. \end{aligned}$$

(35)

Additionally the flux conservation law (Eq. (4)) was used in the previous chapter. This is found in Kirchhoff’s flux law, which states that the sum of fluxes into respectively out of any node must vanish. It is left to define Ohm’s law for magnetic equivalent circuits, which is found by manipulating the MMF drops to a form

$$\begin{aligned} F_d = R_d \Phi _d, \end{aligned}$$

(36)

where $R_d$ is called a reluctance of the associated section of the structure. A detailed description of the method is provided in [15].

For the presented model, the MEC network is shown in Fig. 10b. As the previous study showed, that for the considered system with permanent magnet saturation doesn’t have an influence on the magnetic flux, saturation is not taken into account for this study. Thus, the MEC model provides a linear algebraic equation to calculate the magnetic flux, given by

$$\begin{aligned} \textbf{R}_N \boldsymbol{\Phi }_N = \textbf{F}_N. \end{aligned}$$

(37)

In Eq. (37), $\textbf{R}_N$ is the network reluctance matrix, $\textbf{F}_N$ is a column matrix containing the external MMF sources and $\boldsymbol{\Phi }_N$ is the column matrix of the network fluxes. The equations of motion for the mechanical and the electric system read

$$\begin{aligned} m \ddot{x} + k x - \frac{1}{\mu _0 A}(\Phi _{2}^2-\Phi _{1}^2)&= F(t) \end{aligned}$$

(38)

$$\begin{aligned} \textbf{C} \dot{x} + \textbf{L} \dot{\textbf{I}} + \textbf{R} \textbf{I}&= 0, \end{aligned}$$

(39)

where m is the oscillating mass, k is the stiffness of the spring, F(t) is a harmonic force, $\mu _0$ is the vacuum permeability, A is the cross section of the iron cores. The matrices $\textbf{C}$ (coupling), $\textbf{L}$ (inductance) and $\textbf{R}$ (electric resistance) are calculated with

$$\begin{aligned} \textbf{C} = N\frac{\,\textrm{d}\boldsymbol{\Phi }}{\,\textrm{d}x} \quad \text {and} \quad \textbf{L} = N\frac{\,\textrm{d}\boldsymbol{\Phi }}{\,\textrm{d}\textbf{I}} \quad \text {and} \quad \textbf{R} = \begin{bmatrix} R &{} 0 \\ 0 &{} R \end{bmatrix}, \end{aligned}$$

(40)

where N is the number of turns of the coils, R is the ohmic resistance of the coils and $\boldsymbol{\Phi }=[\Phi _1 \; \Phi _2]^T$ is a column matrix containing the magnetic fluxes linked with the coils. The dynamic flexibility of the nonlinear set of equations is calculated using the Harmonic Balance Method (HBM).² During the calculation the derivatives of the fluxes are evaluated numerically. The results are depicted in Fig. 11a.

Fig. 11

a Dynamic flexibility of the symmetric model shown in Fig. 10a. Red circles: time dependent FEA—Blue line: MEC network shown in Fig. 10b—Green line: modified MEC with leakage paths (cf. Fig. 11b)—Gray line: system without magnets. b MEC network with additional elements to model leakage

For the validation process a finite element analysis (FEA) using the commercial program COMSOL Multiphysics has been carried out. The mesh for the analysis is depicted in Fig. 12a. In Fig. 12b the calculated flux is shown for a stationary analysis. A dynamic FEA is carried out using the moving mesh formulation of the software coupled with an ordinary differential equation for the mechanical subsystem. The dynamic flexibility, calculated with the FEA, is also shown in Fig. 11a. A significant difference to the result of the proposed MEC system exists. This can be explained by leakage effects, i.e. not all the magnetic flux follows the predefined path. Therefore the MEC model has been modified as illustrated in Fig. 11b with additional leakage paths. The dynamic flexibility of the enhanced model is also depicted in Fig. 11a. The FEA and the MEC analysis with the expanded model are in good agreement and thus, it is confirmed, that leakage is the main cause for the differences in the models. Consequently, the guidance of the magnetic flux through a structure has to be designed very carefully. Furthermore, flux leakage does effect the damping efficiency dramatically and therefore must be minimized in order to efficiently calm structural vibrations.

Fig. 12

a Mesh of the FEA model. b Simulation result from static FEA. Color Gradient: magnetic flux density—White lines: magnetic field lines

3 Analysis of Models Based on Eddy Currents

Another inductive damping device may be derived from the matrix in Fig. 1 by producing the modulation of the flux by moving a magnet in the vicinity of a conductive material. As a source of the magnetic flux, a permanent magnet is chosen and the transport is unguided. The induction is distributed over the conductive material. One representation of this set of realizations of the functionalities is shown in Fig. 13a and has been analyzed e.g. by Bae et al. [1]. Since the analytic calculation of eddy currents is rather complex and only applicable for simple geometries, a mixed formulation will be derived. Still, a short summary of the basic procedure as used in e.g. [1, 5, 12] is given.

Fig. 13

a Model of eddy current damper as proposed by Bae et al. [1]. b Model of a single DoF oscillator featuring position-dependent inductive damping

3.1 Analytic Description of Eddy Currents

According to Ohm’s law, the eddy current density $\textbf{J}$ is given by

$$\begin{aligned} \textbf{J} = \sigma \textbf{E}, \end{aligned}$$

(41)

where $\sigma$ is the electric conductivity of the material and $\textbf{E}$ is the electromotive force. If no electric charge accumulations exist, the electromotive force in a homogeneous conducting rigid object, moving translationally at the velocity $\textbf{v}$ in a constant magnetic field $\textbf{B}$, is given by

$$\begin{aligned} \textbf{E} = \textbf{v} \times \textbf{B}. \end{aligned}$$

(42)

The electromagnetic force on the object due to eddy currents can be calculated by

$$\begin{aligned} \textbf{F} = \int _V \textbf{J} \times \textbf{B} \,\textrm{d}V, \end{aligned}$$

(43)

which is known as the Lorentz force equation [11]. Neglecting the magnetic field induced by the eddy currents, the magnetic field is a prescribed quantity and can be calculated with Biot-Savart’s law. Inserting Eqs. (41) and (42) into Eq. (43) the force due to eddy currents yields

$$\begin{aligned} \textbf{F} = \int _V \sigma \left( \textbf{v} \times \textbf{B} \right) \times \textbf{B} \,\textrm{d}V. \end{aligned}$$

(44)

From this, the part of the force acting against the movement of the object and thus, as a damping force can be found as

$$\begin{aligned} F_{d} = v \int _V \sigma B_\perp ^2 \,\textrm{d}V. \end{aligned}$$

(45)

Herein v is the magnitude of the velocity and $B_\perp$ is the magnitude of the part of the magnetic flux density that is perpendicular to the velocity of the moving object. It can be concluded, that the damping force due to the eddy currents is linear in the velocity. This linearity in the velocity allows a numerical calculation of the damping force for a specific velocity. Afterwards a damping parameter can be calculated by dividing the damping force by this velocity. Further analysis may be carried out, using lumped models with the evaluated damping parameter. Note, that as the magnetic field of the induced eddy currents is neglected in this derivation, the method is only suitable, for (rather) low velocities.

3.2 Nonlinear Eddy Current Damping Element

The analysis in the previous subsection revealed that the damping force of a magnet moving in a conductive tube is proportional to the velocity, thus it behaves identical to linear viscous damping. In this section, the model of a permanent magnet moving in a conductive tube, as proposed by Bae et al. [1], is upgraded with geometric discontinuities for position-dependent damping behavior. Therefore a gap is introduced in the conductive tube as shown in the system in Fig. 13b.

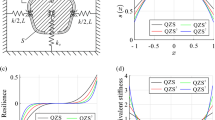
To calculate the position-dependent damping parameter, a FEA model of the magnet in the conductive tube with a gap has been set up. In a time dependent study the magnet was moved with constant velocity $v_0$ through the conductive tube and the damping force $F_d$ was calculated at each position. Afterwards, the resulting damping force $F_d$ has been divided by the velocity $v_0$ to obtain the damping parameter. Furthermore, it has been normalized to a maximum value of one and stretched, so that the maximum damping value is reached at $\xi =\pm 1$. The resulting normalized position dependent damping parameter is depicted in Fig. 14a. For the FEA again the moving mesh formulation has been used to adapt the mesh during the simulation. Figure 14b shows the FEA model at a specific time step.

Fig. 14

a Normalized damping coefficient of position dependent eddy current damping. Red circles: result of FEA—Blue line: fitted curve used for dynamic analysis. b Model of the eddy current damper with geometric discontinuities and position-dependent inductive damping. White lines: magnetic field lines—Gray gradient (in air): magnitude of magnetic flux density—Colored gradient (on conductive tube): magnitude of eddy current density

Fig. 15

a Frequency response and b dynamic flexibility of proposed nonlinear model for different levels of the excitation force

For the analysis of the system depicted in Fig. 13b, the normalized damping parameter has been fitted with the curve shown in Fig. 14a. The equations of motion for the system are given by

$$\begin{aligned} m \ddot{x} + d(x) \dot{x} + k x = \hat{F} \sin (\Omega t), \end{aligned}$$

(46)

where m is the mass of the moving object, d(x) is the position dependent damping coefficient (not normalized), k is the stiffness of the spring, $\hat{F}$ is the amplitude of an external harmonic force and $\Omega$ is its frequency. The position of the moving object is described by x. To minimize the number of parameters, the equation of motion is converted into dimensionless form. Based on the characteristics $\omega _0 = \sqrt{k/m}$ and thus $\tau = \omega _0 t$, the non-dimensional parameters $\eta = {\Omega }/{\omega _0}$ and $\hat{f}= {\hat{F}}/{(k \ell )}$ are introduced. Moreover, the scaled coordinate $\xi = \frac{x}{\ell }$ will be used, where $\ell$ is the reference length used for the stretch of the damping parameter. Introducing the re-scaled parameters and coordinates the damping term may be transformed as

$$\begin{aligned} d(x) = d_0 \delta \left( \frac{x}{\ell }\right) = d_0 \delta (\xi ) \quad \text {and} \quad \frac{d_0}{m} = 2 D \omega _0 \end{aligned}$$

(47)

where D is the damping factor and $\delta (\xi )$ is the normalized damping parameter, as depicted in Fig. 14a. The dimensionless equation of motion is given by

$$\begin{aligned} \xi '' + 2 D \delta (\xi ) \xi ' + \xi = \hat{f} \sin (\eta \tau ). \end{aligned}$$

(48)

To solve the nonlinear differential equations, again a simple shooting method is used. For the analysis, the maximum value of the damping parameter has been set to $D=1$. Figure 15a shows the frequency response of the nonlinear damped single degree of freedom device. The graph of the dynamic flexibility is depicted in Fig. 15b. It shows that for higher excitation levels the resonance peak becomes lower, and thus the position dependent damping allows for an amplitude dependent damping behavior. While small oscillations remain mainly unaffected, large oscillations are efficiently suppressed. This behavior might be favorable in situations, where for a better efficiency of a system a low damping ratio is necessary, but still large vibrations must be prevented.

3.3 Nonlinear Magnetically Damped Tuned Mass Damper

The proposed nonlinear damping device could as well be used as a magnetically damped tuned mass damper (TMD). A basic model of this is shown in Fig. 16. The equations of motion are given by

Fig. 16

Single degree of freedom oscillator with a magnetically damped tuned mass damper

$$\begin{aligned} \begin{bmatrix} M+m &{} m \\ m &{} m \end{bmatrix} \begin{bmatrix} \ddot{x} \\ \ddot{z} \end{bmatrix} + \begin{bmatrix} 0 &{} 0 \\ 0 &{} d_0 \delta (z/\ell ) \end{bmatrix} \begin{bmatrix} \dot{x} \\ \dot{z} \end{bmatrix} + \begin{bmatrix} k_0 &{} 0 \\ 0 &{} k \end{bmatrix} \begin{bmatrix} x \\ z \end{bmatrix} = \begin{bmatrix} \hat{F} \sin (\Omega t) \\ 0 \end{bmatrix}, \end{aligned}$$

(49)

where x is the coordinate describing the position of the primary mass M and $k_0$ is the stiffness of the spring connecting it with the environment. z is the coordinate describing the position of the TMD with the mass m and k is the stiffness of the spring connecting it with the primary mass. $d_0$ is the damping coefficient and $\delta (z/\ell )$ is the normalized position dependent damping parameter with the reference length $\ell$ as discussed in the previous subsection. To minimize the number of parameters, the scaled quantities

$$\begin{aligned} \omega _0&= \sqrt{\frac{k_0}{M}},&\omega _{T}&= \sqrt{\frac{k}{m}},&D_{T}&= \frac{d_0}{2 m \omega _{T}},&\mu&= \frac{m}{M},&\nu&= \frac{\omega _{T}}{\omega _{0}}, \end{aligned}$$

(50)

$$\begin{aligned} \hat{f}&= \frac{\hat{F}}{k_0} \ell ,&\tau&= \omega _0 t,&\eta&= \frac{\Omega }{\omega _0},&\xi&= \frac{x}{\ell },&\zeta&= \frac{z}{\ell } \end{aligned}$$

(51)

are introduced. The dimensionless equations of motion read

$$\begin{aligned} \begin{bmatrix} 1+\mu &{} \mu \\ \mu &{} \mu \end{bmatrix} \begin{bmatrix} \xi '' \\ \zeta '' \end{bmatrix} + \begin{bmatrix} 0 &{} 0 \\ 0 &{} 2\,\mu \nu D_{T} \delta (\zeta ) \end{bmatrix} \begin{bmatrix} \xi ' \\ \zeta ' \end{bmatrix} + \begin{bmatrix} 1 &{} 0 \\ 0 &{} \mu \nu ^2 \end{bmatrix} \begin{bmatrix} \xi \\ \zeta \end{bmatrix} = \begin{bmatrix} \hat{f} \sin (\eta \tau ) \\ 0 \end{bmatrix}. \end{aligned}$$

(52)

The dynamic flexibility charts for different excitation levels for the TMD and for the primary mass are shown in Fig. 17. The values of the parameters used for the analysis are $\mu =0.1$, $\nu =1$ and $D_{T}=0.2$.

Fig. 17

Dynamic flexibility of the system with nonlinear damped TMD for different excitation levels. a Primary mass. b TMD

Due to the presence of damping in the TMD, the resonance amplitudes are limited. However, near the designed operating point (here: $\eta \approx 1$) the system behaves similar to a weakly damped TMD which may show very effective vibration compensation. Thus, this nonlinear damper might combine the benefits of weakly damped TMDs with the operational safety of optimally damped TMDs, which have smaller resonance amplitudes, than weakly damped TMDs.

4 Conclusion

In a first step, basic functional elements of inductive damping devices were identified and classified into a matrix. Using this schematic, a systematic derivation of possible damping designs may be obtained by re-combining several options.

Based on this matrix, two basic designs were derived and analyzed in more detail. All analyzed models show the possibility to efficiently reduce the vibration amplitude of an oscillating structure, modeled as a single degree of freedom oscillator. From the analysis of the systems, modulating the magnetic flux due to mechanical movement and guiding the flux through the structure, it was concluded, that saturation has a major influence on systems based on electromagnets, if only small air gaps occur in the structure. Furthermore, it was shown, that flux leakage paths must be implemented in an analysis, as they strongly decrease the damping performance.

The analysis of the considered eddy current damping elements showed, that neglecting the field of the eddy currents, the resulting damping force is proportional to the velocity. As the analytic calculation of eddy currents is only favorable for simple geometries, a coupled numeric-analytic analysis was presented, where the damping coefficient is calculated using FEA and the result is integrated into a lumped parameter mechanical model. Using this procedure, the damping parameter of a position dependent eddy current damper was evaluated and the dynamic behavior of the system was analyzed. It was shown, that the proposed model is capable of reducing predominantly large oscillations. Furthermore, the position-dependent damping element was used in a TMD. The system with the TMD behaved similar to a weakly damped TMD for small oscillations, but limited resonance amplitudes effectively.