Vibration Reduction by Energy Transfer Using Shape Adaption

Abstract

Within the Priority Programme Calm, Smooth and Smart, a new approach for deliberately introduced damping through variation of stiffness was presented. The proposed approach is a novel way of combining the concepts of damping and absorption inherently in a structure. By dynamically adapting the stiffness of a slender, beam-like structure through the use of shape adaption in the cross-section, energy is transferred from critical low-frequency modes into a specifically designed, higher frequency absorber mode, which can then be damped in an optimal way. Experimental studies were first conducted to examine the suitability of shape adaption for the proposed approach. Various investigations were carried out regarding application of the presented concept with different time laws for free and forced oscillations. In addition, thorough analytical and numerical studies were conducted to understand the internal energy transfers and provide the basis for decoupling of active and semi-active effects related to the reduction of vibrations. Another focus was on the synthesis of a structural layout that enables a defined stiffness change to be induced and an absorber mode (defined in shape and eigenfrequency) to be integrated into the structure.

1 General Approach

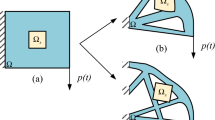
The approach is illustrated in Fig. 1 with an exemplary structure. The slender, beam-like structure consists of specially designed compliant ribs with selective compliance, interconnected by a hull structure. By actuating the compliant ribs, the structure can be modified from the configuration with shape I to shape II. This shape adaption of the cross-sections – which in turn modifies the beam’s second moment of area – enables a dynamic adaption of the beam’s bending stiffness.

Fig. 1

Approach for vibration reduction by stiffness variation using shape adaption

In the bottom part of Fig. 1, a possible time law for the two stiffness states is shown. The stiffness change is determined by the vibration mode – which is typically a critical, low-frequency bending mode (see Fig. 1, black curve). At zero-crossings of this mode’s amplitude, the stiffness is increased by adapting the cross-sections to shape II and returned to the original stiffness with shape I at the extremal points (see Fig. 1, gray curve).

The reduction of vibrations is – besides the present damping – based on two mechanisms. In the quarter cycles between zero points and maxima of the vibration mode, the higher stiffness causes a certain amplitude reduction. This effect – not directly visible in Fig. 1 – can be understood as a counterforce and is called active effect in the following. The second effect is a transfer of part of the kinetic energy subtracted from the critical vibration mode into a specifically designed, higher frequency absorber mode. This effect, called semi-active effect in the following, is illustrated by the blue curve. The high frequency of the absorber mode enables a faster amplitude decay through structural damping, which can potentially be enhanced by dampers particularly designed for this range.

In Sect. 2, a proof-of-concept is presented by an experiment with a shape-adaptive structure. The influence of shape adaption on the structural stiffness and the dynamics of the system is shown. In Sect. 3, the analysis of the two effects introduced above (active and semi-active) is discussed in detail. In Sect. 4, a method is presented for determining a spatially reasonable distribution of stiffness changes by actuation of the ribs and to perform parameter studies with respect to different types of cross-sectional modifications and absorber modes.

2 Experimental Study with a Shape-Adaptive Structure

In contrast to active methods, where actuators act directly on the degrees of freedom of the vibrating system, and passive methods, in which the system’s inherent damping is supplemented by additional dissipative elements without further energy requirements, semi-active approaches are defined as methods that influence the system parameters [12].

The literature offers numerous semi-active approaches for vibration reduction. Many of these relate to adaptive dampers, e.g. for wind and earthquake protection of buildings [26] or for car suspension systems [30]. Variable stiffness is often employed in tunable absorbers, e.g. with the use of shape memory alloys [28], piezo actuators [18], magnetostrictive [10] or magnetorheological materials [8]. Cyclical variations in stiffness are found less frequently. In most of the contributions, as for instance in [21] and [27], discrete spring-mass systems are considered. With shape adaption – a research field that is driven primarily by the aerospace sector [1] – there are some obvious benefits, such as the suitability for stiffness adjustment of continuous structures and the possibility of intermediate values in the stiffness change. Cyclical stiffness variations for vibration reduction based on shape adaption have, however, hardly been investigated. For this reason, the experimental setup [22] presented below was developed at the beginning of the project to evaluate the general feasibility of this approach.

2.1 Experimental Setup

The test object is shown in Fig. 2. It is a cantilever steel plate with elongating piezo patch actuators attached to it. When actuated, the piezo patches cause the plate’s cross-section to bend (see Fig. 2, bottom right) and thus the second moment of area with respect to the x-axis is changed.

Between the fixation and the first piezo patch, a shaker can be attached for forced vibrations in y-direction. The response of the structure is measured with a laser Doppler vibrometer capturing displacement and velocity at the end of the plate.

Fig. 2

Setup with a shape-adaptive structure

The fixation is designed in a way that the curvature of the plate is free to change. Under the subsequent assumption of a constant cross-sectional curvature along the beam, the second moment of area $I_x$ of the deformed configuration can be calculated with the outer and inner radius ($r_1,r_2$) and the angle of curvature $\vartheta$ by

$$\begin{aligned} I_x= \int \limits _{-\vartheta /2}^{\vartheta /2}~ \int \limits _{r_1}^{r_2} (r\cdot \cos \vartheta -s)^2 \cdot r~dr~d\vartheta \end{aligned}$$

(1)

The stiffening factor $\mu (\vartheta )$, i.e. the ratio between $I_x$ of the initial and the deformed geometry, is given by

$$\begin{aligned} \begin{aligned} \mu (\vartheta )&= \frac{12}{wh^3}\left( A(\vartheta )w^3h+B(\vartheta )\frac{wh^3}{12}\right) \\ A(\vartheta )&=\frac{1}{\vartheta ^2}\left( \frac{1}{2}(1+\frac{\sin \vartheta }{\vartheta }) - 4\frac{\sin ^2(\vartheta /2)}{\vartheta ^2} \right) \\ B(\vartheta )&= \frac{3}{2}(1+\frac{\sin \vartheta }{\vartheta })-8\frac{\sin ^2(\vartheta /2)}{\vartheta ^2} \end{aligned} \end{aligned}$$

(2)

At maximum measured curvature, a value of approx. 2 is obtained for $\mu$. The experimental bending measurements also yield a doubling of the bending stiffness at small deflection. As already mentioned above, it is naturally possible to realize intermediate values for $\mu$ depending on the voltage on the piezos.

2.2 Wavelet-based Analysis

The stiffness variation obviously implies a non-linear, time-variant system. A classical frequency response function offers only limited suitability for the analysis of such systems.

To reveal the time-variant dynamics of the structure, continuous wavelet transform is therefore applied. The wavelet-based spectra of the input excitation E and output response R are given by

$$\begin{aligned} E(a,b) = \frac{1}{\sqrt{a}} \int \limits _{-\infty }^{\infty } e(t)\psi ^* \left( \frac{t-b}{a}\right) dt,\quad R(a,b) = \frac{1}{\sqrt{a}} \int \limits _{-\infty }^{\infty } r(t)\psi ^* \left( \frac{t-b}{a}\right) dt \end{aligned}$$

(3)

with b and a as operators for locality in time and frequency, respectively, and $\psi (t)$ as the analyzing wavelet function. The time-variant frequency response, defined as the $H_1$ estimator is

$$\begin{aligned} H_1(a,b) = \frac{G_{RE}(a,b)}{G_{EE}(a,b)} \end{aligned}$$

(4)

with the wavelet-based cross-power spectra $G_{RE}$ and auto-power spectra $G_{EE}$:

$$\begin{aligned} \begin{aligned} G_{RE}(a,b)&=R(a,b)E^*(a,b) \\ G_{EE}(a,b)&=E(a,b)E^*(a,b) \end{aligned} \end{aligned}$$

(5)

Equation 4 is a two-dimensional function representing a set of frequency response functions for all specific values of time. For a more detailed consideration of this topic and an extension to wavelet-based coherence, please refer to [9].

With the presented method, the time variant characteristics of the structure shown in Fig. 2 were investigated. The structure was excited with band-limited white noise and simultaneously, the piezo patches were actuated with square and sine signals. For clarification, it should be mentioned here that the piezos were actuated very slowly to achieve a good resolution of the results. This investigation here is therefore not to be confused with a stiffness variation time law based on a modal amplitude as shown in Fig. 1.

Fig. 3

Time-variant frequency response function due to actuation with a square-wave signal (left) and a sinusoidal signal (right)

The wavelet-based input-output analysis is shown in Fig. 3. The results clearly show the varying natural frequency of the system. The stiffness variation provides two limits at the natural frequency, specified in Fig. 3 with deformed conf. at maximum voltage and initial conf. with switched off piezos. It can also be seen that a square-wave signal allows a relatively sharp transition between those frequencies, while the sinusoidal actuation leads to a continuous adaption of the natural frequencies with all intermediate values. This offers a considerable advantage over variable systems as in [21, 27], which, as mentioned above, allow only two stiffness states.

2.3 Vibration Reduction Analysis

The analysis carried out in the previous section demonstrates that a time-variant structural behavior with a defined change in stiffness is possible via shape adaption. This section describes the application to vibration reduction.

First, this requires the definition of a suitable time law for the stiffness variation. Preliminary studies on simplified systems (see also Sect. 3) have revealed that a cyclic stiffness increase at the zero-crossing and recovery of the original stiffness value at the maximum of the modal amplitude (see Fig. 1, gray curve) is best suited. In the experiment, this time law is realized by a feedback control based on the y-displacement at the beam end. Thereby, several signal shapes are conceivable. Figure 4 shows three of these variants, which all have their starting point at the zero-crossing and end point at the maximum, but with increasingly smoother shapes (in the following called square, rounded square and sine actuation). For the square signal, the voltage V on the piezos can be stated in simplified form as

$$\begin{aligned} V = {\left\{ \begin{array}{ll} \text {max,} &{} \text {if }~|u_k| > |u_{k-1}| \\ \text {off,} &{} \text {else} \end{array}\right. } \end{aligned}$$

(6)

with $u_k$ as the measured displacement at a timestep k. This requires an ideal (damped) sinusoidal displacement curve like the blue one in Fig. 4. However, superposition with higher-frequency components occurs due to the (desired) internal energy transfer (see Fig. 1 blue curve), resulting in additional zero-crossings and maxima in the displacement curve. With application of (6), this leads to frequent and abrupt stiffness increases mostly not related to the modal amplitude of the vibration mode, which turned out to be highly counterproductive in the experiment and in the numerical calculations. Filter techniques have also proven to be unsuitable, as the resulting time delay severely impairs the results.

Fig. 4

Possible time laws for actuation of the piezos

The following procedure was eventually implemented: the high-frequency components are filtered out of the measured displacement and velocity, but not for direct control of the piezo voltage according to a time law like (6). Instead, these data sets serve for an estimation of the next quarter period based on previous cycles. If a displacement zero-crossing is detected together with an exceedance of an adaptive velocity threshold, the actuation with one of the signal shapes in Fig. 4 is triggered. The actuation is then no longer influenced by the current measurement but is executed until the end of the estimated quarter period.

Alternatively, the possibility for multiple sensors and real-time transformation into the relevant modal amplitudes as a basis for the actuation signals should be mentioned, which is planned for upcoming experimental studies.

The presented method to modify the stiffness was applied in different test scenarios, including free vibration after initial deflection, sweep over the range of the first natural frequency and with random excitation forces. For comparison, the structure in the initial configuration (low stiffness) and with permanently activated piezos (high stiffness) was considered. Additional damping elements were not employed.

A first interesting result was observed in the comparison of the three investigated signal shapes of Fig. 4. The best results are achieved with sinusoidal actuation, followed by rounded square and square. Particularly in contrast to stiffness switching with a square signal, the sinusoidal adaption of the structure does not act as an impulse on the structure and thus excitation by the actuators is reduced. Besides, a long dwell time on the maximum stiffness is not that significant, but rather the difference between maximum and minimum stiffness – which is identical for all shapes. This observation, however, is very dependent on the structure, type and position of the actuators and should therefore not be understood in a generalized way.

In all tested cases and also for all signal types, improved performance was achieved by applying the variable stiffness concept compared to the time-invariant structure. Figure 5 shows two exemplary results. For free vibration (see Fig. 5a, comparing constant low stiffness $k_l$ to stiffness variation with a sine signal $k_s$), the amplitude decay is considerably faster. For harmonic loads (see Fig. 5b, comparing $k_l$, $k_s$ and constant high stiffness $k_h$ under swept sine excitation), the resonance of $k_s$ is clearly less intense and it is evident that there is no typical resonance peak. The response curve is rather flat, which is due to the fact that the energy is transferred to higher-frequency modes.

Fig. 5

Experimental results for a free vibration and b sweep excitation

3 Energetic Considerations

An important aspect in the evaluation of the presented method are energetic considerations. On the one hand, the internal energy transfer to a higher mode (see Fig. 1, blue curve) needs to be investigated. On the other hand, efficiency must be evaluated. In the approach discussed here, actuators are involved and, as already mentioned, there is definitely an active component which is generally associated with high energy requirements.

The realization of the stiffness variation evidently has a significant influence on this consideration. Several approaches can be found in the literature on vibration reduction by cyclically modified stiffness, including piezoceramic actuators switched from open-circuit to short-circuit state [4], controllable magnetorheological dampers [17], tension-controlled strings [25], connection of the main structure with an elastic brace whose stiffness is controlled by a control valve [29, 31] or employment of a Voigt element with an adaptive damper [16]. Adaption of spring stiffness values is also frequently found, e.g. by manipulating the effective length of a spring [27], connecting and detaching a secondary system [15, 21] or changing the shape in which the springs are arranged [20].

In all mentioned publications, the respective approaches are considered semi-active. A decisive advantage of semi-active methods often emphasized is their low energy consumption compared to active methods [16, 17, 21, 29, 31]. However, justifications based on energetic calculations or quantitative comparisons with other methods are not provided. Almost all approaches are either based on adaptive dampers or include devices that dissipate energy through e.g. friction or electrical resistance. While this is certainly reasonable in terms of vibration reduction, it makes it more difficult to separate the different effects.

The experiment presented in the last section could also hardly be considered for such energetic observations. Although the excitation of higher modes can be shown in a numerical simulation, a separation of active and semi-active components is practically impossible. In addition, the actuators cover almost the entire free area and cannot be controlled individually. A parameter variation and determination of the origin of the internal energy transfer is therefore not feasible.

For this reason, discretized systems similar to [21, 27] were chosen for fundamental energetic considerations. A detailed study in this regard is given in [24]. The following section will provide a brief overview of this topic.

3.1 Single-Degree-of-Freedom System with Variable Stiffness

The system considered in this section is inspired by [27]. In this contribution, the stiffness of a spring can be increased by a motor-controlled arm blocking some of the spring coils. Equivalent to the time law based on a modal amplitude shown in Sect. 1, the time law in [27] is defined as increase of stiffness between zero points and maxima and vice versa – in this case related to the measured displacement of the mass. In the above-mentioned publication, the system is treated as a single spring-mass oscillator, which is also considered in this section. For the sake of explanation, the system is further assumed to be undamped.

Fig. 6

Spring-mass oscillator with variable stiffness

The corresponding single-degree-of-freedom system is given in Fig. 6, together with an exemplary displacement curve of a free oscillation. The stiffening device is realized by scaling the basic stiffness $k_0$ with a factor $\gamma$, ranging between 1 and the quotient of high to low stiffness given in [27]. Thus, no energy expenses due to e.g. deformation of the structure are considered at this point.

Under these assumptions, the potential energy change at the points of the stiffness switches results in

$$\begin{aligned} \Delta U = \dfrac{1}{2} \Delta k u^2 \end{aligned}$$

(7)

Considering Eq. 7, two facts stand out: the potential energy remains constant when increasing the stiffness, as the displacement u is zero. As a consequence, the amplitude decreases after the stiffness switch; however – considering the undamped system – no energy has been lost so far. Switching back to $k_0$ at the next zero point would thus result in virtually no variation of the system’s dynamics afterwards.

The second point concerns the stiffness decrease at the maximum of the displacement. In this case, there is a drop of energy, defined by the stiffness difference of the two states $\Delta k = k_0(1-\gamma )$. The energy is extracted from the system by the stiffening device performing negative work on the system. By definition, it is still a semi-active procedure, since a system parameter is varied. A corresponding actuator, however, has to perform the same work as given in (7), which de facto does not distinguish it from active vibration reduction. In such cases where an amplitude reduction is based on negative work instead of damping – as shown in Fig. 6 – the corresponding energy loss is called active component here and in the following.

3.2 Serial System with Variable Stiffness

The preliminary study of the last section is now extended by considering damping and dividing the spring into two sections. As mentioned, the system’s spring in [27] can be separated by an arm, which is represented here by two springs with basis stiffness values $k_{01}$ and $k_{02}$. The (comparatively small) mass of the physical spring is represented by $m_1$.

The corresponding system is illustrated in Fig. 7. As displayed, both springs can now be scaled with a factor $\gamma _1$ or $\gamma _2$, respectively. Thus the high stiffness of the total system corresponds to

$$\begin{aligned} k_h = \dfrac{\gamma _1 \gamma _2 k_{01} k_{02}}{\gamma _1 k_{01} + \gamma _2 k_{02}} \end{aligned}$$

(8)

First, the case of [27] is considered in which an increase in stiffness is performed by completely blocking the left spring. Therefore, the corresponding scaling factor $\gamma _1$ tends towards infinity. With Eq. 8 and $\gamma _1 \rightarrow \infty$, the high stiffness is consequently equal to $k_{02}$. Alternatively, both springs can be scaled with the same factor $\gamma _1 = \gamma _2 = \gamma = k_h/k_l$, which is in accordance with the single-degree-of-freedom system in Sect. 3.1. The case of scaling one of the spring stiffness values is called local case here; scaling the whole system is called global case.

Fig. 7

Serial system with variable stiffness

The curves in Fig. 7 show a free oscillation with the local case. After releasing the blocked spring, a noticeable high-frequency oscillation of $u_1$ can be observed, which already resembles the modal amplitude of the absorber mode in Fig. 1. In this quarter cycle, the proportionality of $u_1$ to $u_2$

$$\begin{aligned} u_1 = \dfrac{k_2}{k_1 + k_2} u_2 \end{aligned}$$

(9)

which otherwise results from the low inertia of $m_1$, can obviously no longer apply. However, Eq. 9 is valid for any high stiffness quarter cycle and the equation of motion derived for the second degree of freedom is identical in the local and global case before and after the stiffness increase:

$$\begin{aligned} m_2 \ddot{u}_2 + \dfrac{k_1 k_2}{k_1 + k_2} u_2 = 0 \end{aligned}$$

(10)

Consequently, the loss of vibration energy (without damping) over two extremal points $t_1$ and $t_2$ is for both cases

$$\begin{aligned} \Delta E (t_1, t_2) = \dfrac{1}{2} k_h (u_2^2 (t_2^-) - u_2^2 (t_1^-)) \end{aligned}$$

(11)

The generalized energy balance independent of the half-cycle can be formulated for the global case as

$$\begin{aligned} \dfrac{\Delta E_a (t_1, t_2)}{E(t_1)} = \dfrac{k_l - k_h}{k_h} \end{aligned}$$

(12)

The same relative value of energy is periodically extracted from the second degree of freedom, reflecting the active component introduced in the last section. In the local case, the relative energy extraction is exactly the same, but is transferred to the first degree of freedom. This energy transfer is stated here as the semi-active component $\Delta E_s$. If damping is now included ($E_p$) and hence – in the best case – the high-frequency oscillation of $u_1$ is damped out until the next stiffness increase, the relative energy loss in each half cycle and thus the total energy level at the end of the observation will be the same in both cases:

$$\begin{aligned} \begin{aligned} \dfrac{\Delta E_{\textrm{local}} (t_1, t_2)}{E(t_1)}&= \dfrac{\Delta E_s (t_1, t_2)}{E(t_1)} + \dfrac{\Delta E_p (t_1, t_2)}{E(t_1)} = \\ \dfrac{\Delta E_{\textrm{global}} (t_1, t_2)}{E(t_1)}&= \dfrac{\Delta E_a (t_1, t_2)}{E(t_1)} + \dfrac{\Delta E_p (t_1, t_2)}{E(t_1)} \end{aligned} \end{aligned}$$

(13)

The specific situation of a completely blocked degree of freedom is of course not the general case. Hence, the example of modifying the second spring with finite values for $\gamma _2$ is discussed below. Due to this adjustment, it is no longer possible to reduce the vibration without an active component. The stiffness change now implies negative work and the energy loss is determined by all three components $\Delta E_a$, $\Delta E_p$ and $\Delta E_s$. To compare the two variants – local and global stiffness variation – Fig. 8 shows the energy lost through damping for three pairs with increasing intensity of the stiffness variation. Each pair of same color results in the same total energy at the end of the observation, with the dotted lines representing the global case and the solid lines representing the corresponding local case.

Fig. 8

Energy loss by damping, compared for global (dashed curves) and local (solid curves) case

With increasing value for $\gamma _2$, the damped energy also increases significantly in the local case. In the global case, the dissipated energy even decreases with increasing $\gamma$. This phenomenon can be best explained by considering the system in modal space. With the matrix of eigenvectors $\boldsymbol{\Phi }$ of the generalized eigenvalue problem with the stiffness matrix $\textbf{K}$ and the mass matrix $\textbf{M}$

$$\begin{aligned} \textbf{K} \boldsymbol{\Phi } = \textbf{M} \boldsymbol{\Phi } \boldsymbol{\Lambda } \end{aligned}$$

(14)

applied for modal transformation

$$\begin{aligned} \tilde{\textbf{K}} = \boldsymbol{\Phi }^T \textbf{K} \boldsymbol{\Phi } = \boldsymbol{\Lambda } \end{aligned}$$

(15)

it is evident that globally scaling each spring stiffness with $\gamma$ leads to exactly the same set of eigenvectors:

$$\begin{aligned} \gamma \textbf{K} \boldsymbol{\Phi } = \textbf{M} \boldsymbol{\Phi } \bar{\boldsymbol{\Lambda }} \end{aligned}$$

(16)

The eigenvalues $\lambda _i$ as the diagonal entries of $\boldsymbol{\Lambda }$ are all scaled according to $\gamma$

$$\begin{aligned} \bar{\lambda }_i = \gamma \lambda _i \end{aligned}$$

(17)

and thus also the total modal stiffness matrix $\tilde{\textbf{K}}$ is scaled with the same factor as the physical one. The modal basis $\boldsymbol{\Phi }$ however remains constant and likewise the relation of the entries in $\tilde{\textbf{K}}$. The mutual relationship of the modal amplitudes is not affected and the modal oscillators do not show any additional response. Without further external excitation, the first modal amplitude remains dominant in the present case and again, the system can be considered as a single-degree-of-freedom system. The active component can be expressed with the modal amplitudes $\tilde{\textbf{u}}$ at a point t of stiffness decrease

$$\begin{aligned} \Delta E_a = \dfrac{1}{2}(1-\gamma ) \tilde{\textbf{u}}^T (t) \tilde{\textbf{K}} \tilde{\textbf{u}}(t) \end{aligned}$$

(18)

which basically corresponds to Eq. 7.

This consideration no longer applies in the case presented here, nor in general, when performing local changes in stiffness. The entries in the stiffness matrix are changed individually and consequently, there are two modal bases (and possibly corresponding intermediate states). When switching from high to low stiffness, the vector of the modal amplitudes ${\tilde{\textbf{u}}}_\textbf{h}$ must be transformed into the new space

$$\begin{aligned} {\tilde{\textbf{u}}}_\textbf{l} = \boldsymbol{\Phi _l}^{-1} \boldsymbol{\Phi _h} {\tilde{\textbf{u}}}_\textbf{h} \end{aligned}$$

(19)

which can contribute to the transfer of energy to higher modes.

With this observation, the damping shown in Fig. 8 shall be discussed once more. The second mode is not or hardly excited in the global case. Accordingly, there is no damping with respect to the second mode and the dissipated energy shown in Fig. 8 takes place exclusively in mode 1. Since more energy is extracted with increasing factor $\gamma$, the energy dissipated by damping over the observed period even decreases, as mentioned above.

In the local case, the same energy is extracted from the first mode as in the corresponding global case. However, only a part of it can be attributed to the active component, which is associated with negative work by the actuator. Most of the energy is transferred to the second mode, making use of the available dissipation capacity. Since the energy stored in the first modal oscillator is identical for each color pair, the damping in this mode is also identical. The difference between a dashed curve and a solid curve thus corresponds to the semi-active component, which is achieved by local stiffness variation.

Finally, two points remain to be named for continuous structures with stiffness changes performed by shape adaption. On the one hand, the actuator must be explicitly considered in the calculation of the active component. The extracted energy is not directly reflected in the system energy, but via the force and stroke applied by the actuator. On the other hand, it should be noted that shape adaption always leads to a change of the modal basis. Accordingly, there will always be an internal energy transfer and thus a semi-active component. This also applies to the test structure presented in Sect. 2. With the observations outlined in this section – and those of the next section – this transfer can be enhanced allowing for a more efficient implementation.

4 Synthesis of Shape-Adaptive Beams

In the last two sections, the focus was on the analysis of the dynamics associated with variable stiffness. For practical relevance, a method is presented in this section to design structures for the required stiffness change.

As described in the introduction section, beam-like structures are considered in the context of this project with the stiffness change being achieved by shape adaption. Shape adaption is generally associated with compliant mechanisms [6]. Thereby, the deformability of the structure is exploited in order to achieve predefined kinematics without requiring sliding or rolling components of conventional mechanisms. The design of such mechanisms is typically approached by structural optimization procedures [7]. Most of those approaches to synthesize compliant mechanisms for shape adaption are however limited to planar structures and do not take into account their dynamic behavior.

A versatile approach for shape adaption of three-dimensional structures is the belt-rib concept presented in [3] and extended by a synthesis method in [2]. Compliant inner rib structures are employed here to deform the surrounding outer envelope. Related concepts are still being developed to this day, mostly in the field of wing structures for e.g. the modification of aerodynamic characteristics [19]. As it is well suited for the adaption of beam-like exterior structures, a design method based on compliant ribs was also developed within this project with special emphasis on structural dynamics and realization of stiffness variations.

4.1 Surrogate Model

The energetic considerations in Sect. 3.2 have demonstrated that a homogeneous increase in the stiffness of a structure is not optimal or efficient. For three-dimensional, continuous structures, the dynamic behavior is much more complex and difficult to predict. The initial focus of the design is therefore not on maximizing stiffness changes, but on the pre-definition of an efficient model that can represent the dynamics of the 3D structure under stiffness variations and allows for parameter studies. This surrogate model [23] is presented in the following.

Fig. 9

Shape-adaptive beam with surrogate model

An exemplary target structure is shown in Fig. 9. It consists of the outer hull structure, the ribs to be defined and possibly additional stiffening elements. The corresponding surrogate model of the ribs, on which the design of a stiffness matrix is based, is shown on the right-hand side. The surrogate model is a reduced order model defined at master nodes that are connected to the hull structure. The structural target behavior is realized by an inverse modal transformation performed on the reduced model. The general objective is to modify the critical bending mode and, if necessary, to embed a particular absorber mode. The model should also provide the possibility to parameterize the cross-sectional deformation, absorber mode and placement of the ribs in an efficient way.

The first step is the definition of the master (m) and slave (s) degrees of freedom (DoFs). All DoFs at which loads are applied and the coupling points with the ribs are placed in the set of the m-DoFs, the others in the set of the s-DoFs. The global stiffness matrix is rearranged on basis of these two sets and a transformation matrix $\textbf{T}$ is calculated

$$\begin{aligned} \textbf{K} = \begin{bmatrix} \textbf{K}_{mm} &{} \textbf{K}_{ms}\\ \textbf{K}_{sm} &{} \textbf{K}_{ss} \end{bmatrix}, \quad \textbf{T} = \begin{bmatrix} \textbf{I} \\ - {\textbf{K}_{ss}}^{-1} \textbf{K}_{sm} \end{bmatrix} \end{aligned}$$

(20)

which is the basis of the well-known Guyan reduction [13]. Since the dynamic behavior is relevant, $\textbf{T}$ can be extended by eigenvectors derived from the generalized eigenvalue problem of the slave stiffness and mass matrix [5].

The following calculation only takes place on the partition $\textbf{K}_{mm}$ and is therefore independent of the expensive inversion $\textbf{K}_{ss}^{-1}$ in the transformation matrix $\textbf{T}$.

The criterion here is not the specification of a desired displacement, but the manipulation of a certain eigenvalue of the stiffness matrix. Thus, it is a matter of finding a stiffness matrix for each rib i which is essentially ruled by the corresponding desired deformation mode $\boldsymbol{\varphi _d}$. This desired mode (or modes, if the absorber mode is included) has to be specified and may be considered as several linear combinations of the cross-sectional modes in the parameter study. The matrix of eigenvectors $\boldsymbol{\Phi }$ and eigenvalues $\boldsymbol{\Lambda }$ of a rib’s master DoF subspace $\mathbf {k_i}$ are then determined and compared with the desired mode:

$$\begin{aligned} \textbf{a} = \boldsymbol{\Lambda }^{-1} (\boldsymbol{\Phi }^T \mathbf {k_i} \boldsymbol{\varphi _d}) \end{aligned}$$

(21)

Via $\textbf{a}$, the least influence on the matrix due to a modal adjustment can be determined. In the corresponding column of $\boldsymbol{\Phi }$, the eigenvector is replaced by $\boldsymbol{\varphi _d}$. Since the orthogonality of $\boldsymbol{\Phi }$ is lost through the mode replacement, this condition must first be restored, which is performed by a cholesky decomposition and qr-factorization, yielding the new modal basis $\boldsymbol{\Psi }$

$$\begin{aligned} \mathbf {k_i} = \textbf{C}\textbf{C}^*, \quad \textbf{C}^T \boldsymbol{\Phi } = \textbf{QR}, \quad \boldsymbol{\Psi } = (\textbf{C}^T)^{-1}\textbf{Q} \end{aligned}$$

(22)

After normalization of $\boldsymbol{\Psi }$, the modified modal stiffness values are obtained

$$\begin{aligned} \bar{\boldsymbol{\Lambda }} = \boldsymbol{\Psi }^T \mathbf {k_i} \boldsymbol{\Psi } \end{aligned}$$

(23)

By scaling the modal stiffness value of the desired mode (and absorber mode), the adaption of the structure is eventually specified. Finally, the current adapted subspace ${\bar{\textbf{k}}}_\textbf{i}$ of the stiffness matrix is recalculated with the modified eigenvalues and modal basis

$$\begin{aligned} {\bar{\textbf{k}}}_\textbf{i} = \boldsymbol{\Psi } \bar{\boldsymbol{\Lambda }} \boldsymbol{\Psi }^T \end{aligned}$$

(24)

and is returned to $\textbf{K}_{mm}$.

4.2 Application of the Surrogate Model

As stated in the last section, the presented calculation is independent of the pre-solved part in (20). As only the master DoFs change, the transformation matrix $\textbf{T}$ remains valid and does not have to be recalculated. Thus, parameter studies can be carried out with little expense by the reduced matrices

$$\begin{aligned} \tilde{\textbf{K}} = \textbf{T}^T \textbf{K} \textbf{T},\quad \tilde{\textbf{M}} = \textbf{T}^T \textbf{M} \textbf{T} \end{aligned}$$

(25)

The main parameters to be considered are the form of the actuation, the form of the absorber mode and the number and placement of the ribs. A detailed parameter study would be too extensive at this point, but referring to the considerations in Sects. 2 and 3, one example shall be discussed here. Figure 10 shows three results for a free oscillation case. In the three instances, all parameters such as the form of actuation were identical, except for the distribution of 5 possible ribs along the beam. The fastest amplitude reduction can be observed in the configuration with maximum number of ribs (blue curve). However, it is outperformed by the black configuration – only having two ribs – after a little over half of the observation time.

Fig. 10

Parameter assessment based on the surrogate model

Both parameter settings reveal a performance decline after an initially strong amplitude reduction, which reminds of the experimental observations in Sect. 2.3. The impulse excitation by the stiffness variation has a negative effect and should therefore be terminated below a certain velocity limit.

With reference to Sect. 3.2, the following can further be deduced: with only two ribs (black) as opposed to five (blue), less actuators and thus significantly less energy is required for a comparable result. The ribs in the blue case are distributed over the entire length of the beam, providing an almost global increase in stiffness. In the black case, the ribs are locally positioned at two points, leaving space for vibrations within the structure and enhancing the highlighted semi-active component by internal energy transfer. However, considering the gray curve with also two ribs, it is evident that a local application of few ribs is no assurance of good performance, which justifies the employment of such preliminary investigations.

Subsequently to such a study and the identification of suitable parameters, these serve as a basis for the design of the rib structures, which will not be covered here. The relevant literature offers a variety of approaches, and the interested reader is referred to e.g. [14] or [11].

5 Conclusions and Outlook

This report has summarized the subjects that were addressed within an approach for vibration reduction by stiffness variation. Shape adaption was employed to vary the structures’ stiffness, which proved to be a powerful approach since it allows to modify the stiffness of continuous beam structures and there is no limitation to pure on-off switches, as there is with classical stiffness switching concepts. The stiffness is varied cyclically, with an increase in stiffness between zero points and maxima of the modal amplitude to be reduced. Two mechanisms are involved in the reduction of vibrations – on the one hand an active component through negative work of the actuator and on the other hand a semi-active one by energy transfer into higher frequency modes. Experimental investigations revealed the desired, time-variant behavior of the structure due to shape adaption and provided a general feasibility assessment of the proposed approach. Analytical studies of structures with few degrees of freedom examined the energetic aspects, whereby a correlation between the efficient, semi-active component and local stiffness variations was identified. For the design of shape-adaptive structures, a numerical model based on an inverse modal transformation was presented with which computationally efficient parameter studies can be performed.

Upcoming studies mainly refer to the distribution of stiffness variation in spatial and temporal sense. The importance of a local stiffness variation has already been shown in Sects. 3 and 4, but the development of a general strategy or optimization approaches for the spatial distribution of stiffness changes over a structure is still pending. Temporal optimization of the stiffness variations has not yet been operated at all (except for signal shapes). When several areas for stiffness modification are available, as is the case with the belt-rib concept, they can be actuated independently of each other, which is particularly promising for the reduction of modes other than the first one.