Edge-Based Graph Neural Networks for Cell-Graph Modeling and Prediction

Abstract

Identification and classification of cell-graph features using graph-neural networks (GNNs) has been shown to be useful in digital pathology. In this work, we consider the role of edge labels in cell-graph modeling, including histological modeling techniques, edge aggregation in GNN architectures, and edge label prediction. We propose EAGNN (Edge Aggregated GNN), a new GNN model that aggregates both node and edge label information to take advantage of topological information about cellular data and facilitate edge label prediction. We introduce new edge label features that improve histological modeling and prediction. We evaluate our EAGNN model for the task of detecting the presence and location of the basement membrane in oral mucosal tissue, as a proof-of-concept application.

1 Introduction

To capture intra-cellular and high-level histological relationships in whole-slide images (WSI) of tissue samples, cell-graph models have been considered [13]. In a cell-graph, properties of cells and interactions between them are represented by labelled nodes and edges. Graph neural networks (GNNs) are a specific class of machine learning (ML) algorithm which have been applied to cell-graph models to locate and classify complex histological features [4, 16, 20]. In this work, we consider the role of edge labels in cell-graph modeling and GNN-based model analysis including: (i) histological modeling using edge labels, (ii) edge aggregation in GNNs, and (iii) edge label classification algorithms.

Our study will mainly focus on new GNN algorithms for aggregating node and edge data, with a view to making edge label predictions in a cell-graph model. We also propose new types of edge features, going beyond the simple geometric distance label found in the literature. These new edge labels are shown to be effective for improved histological analysis by means of ML ablation studies. We evaluate the new GNN models and edge features on a representative digital pathology task of predicting the presence and location of the basement membrane (BM) in hematoxylin and eosin (H &E) stained oral mucosa samples. Structural properties of the BM play an important role in classifying oral diseases such as chronic graft-versus-host disease (oral cGvHD) [23].

1.1 Contributions of This Work

The main contributions of this work are as follows:

• 1. We propose EAGNN as a novel message passing model¹ for predicting cell-graph properties. EAGNN aggregates both node and edge label data to yield edge label predictions.

• 2. We propose two new types of edge classification algorithm, which can be used on the backend of EAGNN to make edge label predictions.

• 3. We propose three new edge label features for cell-graph analyses: (a) cell density difference, (b) cell entropy difference, and (c) neighborhood overlap similarity.

• 4. We evaluate different combinations of EAGNN with edge classifiers and edge label features for the prediction of BM location in oral mucosa images. We show that EAGNN can significantly outperform simple node-based aggregation across a wide variety of performance measures.

The organisation of this work is as follows. In Sect. 2 we consider background and related research on GNNs for learning cell-graph models. In Sect. 3 we discuss message passing GNNs and graph data aggregation. In Sect. 4 we define the EAGNN model with edge label aggregation and edge classification algorithms. In Sect. 5 we evaluate EAGNN on the task of predicting BM integrity in healthy and diseased oral tissue images and compare it with simple node-based aggregation. In Sect. 6 we discuss some limitations of this study and address the possible directions to overcome them. Finally, in Sect. 7 we present some conclusions.

2 Background and Related Work

Mapping the structural features of tissues is key to understanding and making a diagnosis of disease severity in digital pathology, for example the BM. An accurate estimation of the BM location and integrity is an important feature in health and disease, but a challenging task. Several studies have considered this problem [6, 25, 26]. However, most of these methods depend upon pixel level information that fails to capture histological and topological relationships between the BM and various cells locally present in the tissue. In this study, we used cell-graphs and graph-based ML techniques to map oral mucosal tissue and locate the BM in healthy and diseased situations.

Generally in the literature on digital pathology, node labels alone have been used for cell-graph modeling and GNN training [1]. To our knowledge, [17] is the only work that has considered the use of cellular interactions in a cell graph for identifying the BM. However the GNN model used in [17] does not utilize the topological information encoded in graph edges during the learning process. Other GNN case studies also utilize edge features such as distance [2, 5, 21, 22] or edge weights [9] for digital pathology. However, in all these approaches the edge features are simple one-dimensional real-valued features. The use of multi-dimensional edge features for optimal cell-graph representation and prediction is currently heavily under-explored.

3 Graph Neural Networks for Cell-Graph Learning

3.1 Cell-Graphs as Labelled Graph Structures

A cell-graph is a mathematical model of histological tissue features that can represent nuclei and the interactions between nuclei. This model is motivated by the hypothesis that cells in a tissue organize to perform a specific function [27].

Formally, a cell-graph: $G = \left( \mathcal {V}, \ \mathcal {E}, \ l_{\mathcal {V}}: \mathcal {V} \rightarrow \mathbb {R}^D, \ l_{\mathcal {E}}: \mathcal {E} \rightarrow \mathbb {R}^{P} \right) ,$ is a labelled undirected graph where $\mathcal {V} = \{ v_1 ,\ldots , v_n\}$ is a finite set of nodes, and n is the size of the graph. Furthermore, $\mathcal {E} = \{ e_1 ,\ldots , e_m\}$ is a finite set of edges, and each edge $e \in \mathcal {E}$ is an unordered pair of nodes $e = \{ v_i, v_j\}$. A node $v_j$ is termed an immediate neighbour of $v_i$ if there exists an edge $\{ v_j, v_i\} \in \mathcal {E}$. We let $\mathcal {N}(v)$ denote the set of all immediate neighbours of v. The degree of a node v is the size of its immediate neighbour set, $deg(v) = \vert \mathcal {N}(v) \vert$. The functions $l_{V}$ and $l_{\mathcal {E}}$ are node and edge labelling functions of D and P features respectively.

To apply methods of linear algebra to graph learning problems, an edge set $\mathcal {E}$ can be encoded by an adjacency matrix $\textbf{A} \in \mathbb {R}^{n \times n}$ of real values, where n is the graph size. The matrix values $\textbf{A}_{uv}$ and $\textbf{A}_{vu}$ are both set to 1.0 if there exists an edge between node u and node v in $\mathcal {E}$, otherwise both are set to 0.0. Moreover, the node labelling $l_{\mathcal {V}}$ can be encoded as a node feature matrix $\textbf{X} \in \mathbb {R}^{n \times D}$ in which case the matrix row $\textbf{X}_v \in \mathbb {R}^{D}$ represents the feature vector for node v. Similarly, the edge labelling $l_{\mathcal {E}}$ can be encoded as an edge feature tensor $\textbf{E} \in \mathbb {R}^{n \times n \times P}$. For each pair of connected nodes $\{u, v \} \in E$ the entry $\textbf{E}_{uv} \in \mathbb {R}^{P}$ represents the P-dimensional feature vector of the edge between node u and node v. As a simplifying notation, for any edge feature $1 \le p \le P$ the matrix $\textbf{E}_{p} \in \mathbb {R}^{n \times n}$ denotes the projection of $\textbf{E}$ onto the single edge feature p.

3.2 Graph Neural Networks

A general spatial-based GNN has a layered architecture, where at each layer k, a low-dimensional ($d_{k}$-dimensional) representation $\textbf{h}^{k}_{u} \in \mathbb {R}^{d_{k}}$ of the graph structure around node u is computed. Computation at each layer k normally consists of two stages. Firstly, for each node u, an $AGGREGATE^{k}$ operation produces an integrated representation $\textbf{h}^{k}_{\mathcal {N}(u)}$ of all immediate neighbors $v \in \mathcal {N}(u)$ of u using the representations $\textbf{h}^{k-1}_{v}$ from layer $k-1$ and is represented as,

$$\begin{aligned} \textbf{h}^{k}_{\mathcal {N}(u)} = AGGREGATE^{k}\left( \lbrace \textbf{h}^{k-1}_{v},\forall v \in \mathcal {N}(u) \rbrace \right) . \end{aligned}$$

(1)

Secondly, for each node u, a $COMBINE^{k}$ operation updates the representation $\textbf{h}^{k}_{u}$ of u by combining its previous representation $\textbf{h}^{k-1}_{u}$ on layer $k-1$ with the aggregated representation $\textbf{h}^{k}_{\mathcal {N}(u)}$ of all its immediate neighbours $\mathcal {N}(u)$, using a nonlinear function, $\textbf{h}^{k}_{u} = COMBINE^{k}\left( \textbf{h}^{k-1}_{u}, \textbf{h}^{k}_{\mathcal {N}(u)}\right)$.

This iterative computation over layers $0 \le k \le K$ is initialized by setting $\textbf{h}^{0}_{u} = \textbf{X}_{u}$. Spatial variants of GNNs [3, 10, 18] implement aggregation by matrix multiplication as:

$$\begin{aligned} \textbf{H}^{k}_{agg} = \textbf{A} \textbf{H}^{k-1}\textbf{W}^{k}_{0} \end{aligned}$$

(2)

where $\textbf{H}^{k}_{agg} \in \mathbb {R}^{n \times d_{k}}$ is the tensor matrix (i.e. stack) of all aggregations $\textbf{h}^{k}_{\mathcal {N}(u)}$, $\textbf{A} \in \mathbb {R}^{n \times n}$ is the adjacency matrix, $\textbf{H}^{k-1} \in \mathbb {R}^{n \times d_{k-1}}$ is the tensor matrix of representations $\textbf{h}^{k-1}_{v}$ on the $k-1$-th layer, and $\textbf{W}^{k}_{0} \in \mathbb {R}^{d_{k-1} \times d_{k}}$ is a matrix of learnable parameters. The combine operation is formulated as:

$$\begin{aligned} \textbf{H}^{k} = \sigma \left( \textbf{H}^{k}_{agg} + \textbf{H}^{k-1} \textbf{W}^{k}_{1} \right) \end{aligned}$$

(3)

where $\textbf{W}^{k}_{1} \in \mathbb {R}^{d_{k-1} \times d_{k}}$ is a second matrix of learnable parameters, and $\sigma$ is a nonlinear function applied pointwise, such as ReLU [11]. Finally, after K layers, a low-dimensional node embedding $\textbf{Z} \in \mathbb {R}^{n \times d_{K}}$ is obtained as a tensor matrix, $\textbf{Z} = \textbf{H}^{K}$. A widely used spatial GNN using node aggregation alone is GraphSAGE [14].

To solve edge classification problems, we need a low-dimensional edge embedding $\textbf{Z}_e \in \mathbb {R}^{k}$ of each edge e. The simplest approach to embed an edge e is to combine the final embeddings of both of its nodes.

4 A GNN Model for Node and Edge Aggregation

Our proposed GNN architecture is depicted in Fig. 1, and can be divided into two stages, node embedding layers and an edge classifier. The node embedding layers derive latent node representation from a cell-graph.

Fig. 1.

The overview of the proposed GNN architecture which consists of two EAGNN layers and a classifier. The model extracts node and edge features from a cell-graph, and outputs a score to classify each edge as a BM crossing one or not.

4.1 Node Embedding Layers

Inspired by EGNN(C) [12], we propose an EAGNN layer which incorporates multiple edge features to embed nodes. The major difference between the proposed EAGNN layer and EGNN(C) is the way that edge features are normalised before aggregation. This feature normalization method is explained in detail in Sect. 5.1.

Following the matrix multiplication as in Eq. 2, we formulate the aggregation operation of the proposed model at layer k, named $EAgg^{k}$, as follows:

$$\begin{aligned} EAgg^{k}(\textbf{E}_{p}, \textbf{H}^{k-1}) = \textbf{E}_{p} \textbf{H}^{k-1} \textbf{W}_{0} \end{aligned}$$

(4)

Then, we combine the previous node representation using the combine operation formulated in Sect. 3.2. We perform these aggregation and combining operations for each edge feature, and concatenate them. Therefore, the formula for the kth EAGNN layer is given by:

$$\begin{aligned} \textbf{H}^{k} = \sigma \bigg [\mathbin \Vert ^{P}_{p=1}\left( \textbf{E}_{p} \textbf{H}^{k-1} \textbf{W}^{k-1}_{0} + \textbf{H}^{k-1} \textbf{W}^{k-1}_{1} \right) \bigg ] \end{aligned}$$

(5)

where $\mathbin \Vert$ denotes the concatenation operator. As a non-linear function $\sigma$ we employ the ELU function [7]. Note that this non-linear function is not used in the final layer K of the node embedding layers. As described in Fig. 1, we used two EAGNN layers in our case study of BM identification: our evaluation suggests that two layers are sufficient for this task. After two embedding layers, the node representation $\textbf{z}_{u}$ is given by $\textbf{z}_{u} = \textbf{H}_{u}^{2}$ for node u.

4.2 Edge Classifiers

Once the node embedding layers have computed the node representations, an edge classifier can partition all edges into two non-overlapping classes A, B. For each edge $e = \{u, v\} \in \mathcal {E}$, the edge classifier computes a score $S_{uv} \in [0, 1]$ which represents the estimated likelihood that e falls into class A or class B. The estimated likelihood score $S_{uv}$ is compared with a class threshold criterion $\theta$, which represents the decision boundary between A and B.

We propose here three methods of edge classification: multiplication (MUL), negative multiplication (NegMUL) and bidirectional concatenation + multilayer perceptron (BC+MLP). The simplest classifier among the three variants is the MUL classifier. It multiplies the embedding vector of node u and node v followed by the sigmoid function: $S_{uv} = sigmoid(\textbf{z}_{u} \textbf{z}_{v}^{T}).$ Similarly to the MUL classifier, the NegMul classifier multiplies the embedding vectors of a pair of nodes, but unlike MUL it subtracts the output from 1, $S_{uv} = 1 - sigmoid(\textbf{z}_{u} \textbf{z}_{v}^{T}).$

In contrast with the classifiers MUL and NegMUL, the BC+MLP classifier, which is depicted in Fig. 1, uses a shallow neural network approach to compute a score $S_{uv}$ for each edge. A neural network approach to edge classification also needs to combine the embedding vectors. There are several ways to combine a pair of node representations, such as element-wise product or summation. Concatenation of node embedding vectors is a simple and effective approach, since it preserves all node information [8]. As shown in Fig. 1, the BC+MLP classifier concatenates the node embeddings $\textbf{z}_u, \textbf{z}_v$ of nodes u, v in both directions $(\textbf{z}_{uv} = \textbf{z}_{u} \mathbin \Vert \textbf{z}_{v}, \ \textbf{z}_{vu} = \textbf{z}_{v} \mathbin \Vert \textbf{z}_{u})$ to obtain a final score in an orientation-invariant way. The node embedding concatenations $\textbf{z}_{uv}, \textbf{z}_{vu}$ are sequentially fed into an MLP to analyse the relationship between the nodes u, v. The scores generated from the MLP layers are combined and passed through the sigmoid activation function to obtain the final score $S_{uv}$² bounded in [0, 1]. A class threshold criterion $\theta$ can be chosen as a parameter, and compared with $S_{uv}$ to determine class membership.

5 Evaluation of the EAGNN Model

In this section we compare the performance of EAGNN against the widely used GraphSage GNN which is based on node aggregation alone. The evaluation task is prediction of the BM location and integrity in cell-graph models of oral mucosa samples.

5.1 An Oral Mucosa Cell-Graph Dataset

For supervised training and evaluation of the EAGNN model, a dataset of ground truth cell-graphs was compiled from digitized images of H &E stained oral tissue samples. To compile the dataset, we extracted 42 tiles from WSI of oral mucosal biopsies from nine patients receiving haematopoetic cell transplantation [23]. On each tile, histology experts manually annotated the cell type and x, y centroid co-ordinates for each cell nucleus. Focusing on the cell types $T = \{ \textit{epithelial}, \ \textit{fibroblast and endothelial}, \ \textit{inflammatory}, \ \textit{lymphocyte} \}$, each nucleus was then modeled by a graph node $v_i \in V$ and labelled by its cell type $N_{type} (v_i) \in T.$

The location and extent of the BM in each tile was manually annotated using cubic splines. An undirected edge set $\mathcal {E}$ for $\mathcal {V}$ was generated using the Delaunay triangulation method and all edges $e = \{ u, v\}$ having a Euclidean length greater than 300 pixels (150 microns) were deleted³

For accurate GNN-based prediction of the BM, besides cell type $N_{type}$, additional node and edge labels were shown to improve the quality of BM prediction.

Additional Node Labels

• 1. Cell Density: We define the (local) cell density at node $v \in \mathcal {V}$ as the average distance between v and its immediate neighbours $u \in \mathcal {N}(v)$.

  $$\begin{aligned} N_{den}(v) = \frac{1}{|\mathcal {N}(v)|}\mathop {\sum }\limits _{u \in \mathcal {N}(v)} d(v, u) . \end{aligned}$$

  (6)

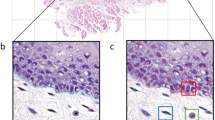
• 2. Cell Entropy: For defining the (local) cell entropy of a node $v \in \mathcal {V}$, we first calculate the probability $p_{v}(\tau )$ of finding the cell type $\tau \in T$ in its immediate neighbourhood using Eq. 7. Cell entropy is defined using the Shannon entropy measure in Eq. 8 and vizualised in Fig. 2.

  $$\begin{aligned} p_v(\tau ) = \frac{\vert \{ u \in N(v) \ \textit{or } u = v : N_{type}( u ) = \tau \} \vert }{|\mathcal {N}(v)|} \end{aligned}$$

  (7)
  $$\begin{aligned} N_{\textit{ent}}(v) = -\mathop {\sum }\limits _{\tau \in T} p_v(\tau ) \times \ln {p_v(\tau )} \end{aligned}$$

  (8)

Fig. 2.

Examples of nodes and their entropy values. The center node is highlighted with a rectangular box. The neighboring nodes are highlighted with a white circle and yellow edges. Cell types are represented by four colours: epithelial (red), fibroblast and endothelial (blue), inflammatory (green) and lymphocyte (yellow). (Color figure online)

Additional Edge Labels. For GNN-based prediction of the BM, the use of edge labels significantly increased the accuracy of our model. We make use of five edge labels defined below using edge feature tensor representation (c.f. Sect. 3.1).

• 1. Node Distance: For each edge $\{ u, v \} \in \mathcal {E}(d)$ we use the Euclidean distance between the endpoints as the distance label: $\mathbf {\ \hat{E}^{dis}}_{u,v} \ = \ d(u, v).$

• 2. Cell Density Difference: Recalling the cell density definition of Eq. 6, we can define the difference in cell density along edge $\{u, v\} \in \mathcal {E}(d)$ by: $\ \mathbf {\hat{E}^{den}}_{{u,v}} \ = \ N_{den}[v] - \ N_{den}[u]$

• 3. Cell Entropy Difference: Similarly to the cell density difference, we can define the cell entropy difference⁴ along an edge $\{u, v\} \in \mathcal {E}(d)$ by: $\ \mathbf {\hat{E}^{ent}}_{u,v} \ = \ |N_{ent}[v] - \ N_{ent}[u]|$

• 4. Neighbourhood Overlap Similarity: This measure aims to quantify the overlap between the neighbourhoods of two nodes, which is useful for tasks like edge and community detection [15]. To define the (relativized) overlap between two nodes u and v we use the Sorenson similarity index defined by: $\ \mathbf {\hat{E}^{nei}}_{{u,v}} = \frac{2 |\mathcal {N}(u) \ \cap \ \mathcal {N}(v)|}{deg (u) \ + \ deg (v)}$

• 5. BM Crossing: For each edge $\{ u, v \} \in \mathcal {E}(d)$ we define the binary valued BM crossing measure: $\mathbf {\hat{E}^{bm}}_{u,v} = 1$ if $\{u,v\}$ crosses the BM, otherwise $\mathbf {\hat{E}^{bm}}_{u,v} = 0$.

Edge Feature Normalization. To incorporate the edge features we multiply them with the node features during the convolution operations of each EAGNN layer. In order to maintain the feature scale during the matrix multiplication, we normalize the edge feature values. There are several ways to normalize the edge feature values, including the Doubly Stochastic Normalization method proposed in [12]. However the Doubly Stochastic Normalization method assumes all the edge feature values to be non-negative which is not true in our case especially while considering the cell density difference. We normalize the edge feature values by rows as proposed in [24]. The row normalization for feature $1 \le p \le P$ and edge $\left( u, v\right) \in \mathcal {E}(d)$ is defined by:

$$\begin{aligned} \textbf{E}_{uvp}^\textbf{X} = \frac{\mathbf {\hat{E}}_{uvp}^\textbf{X}}{\sum _{v' \in \mathcal {N}(u)}|\mathbf {\hat{E}}_{uv'p}^\textbf{X}|} . \end{aligned}$$

(9)

5.2 Training Setup

The cell-graph dataset was divided into two subsets: training (70%) and test data (30%). Some of the training dataset was reserved as a validation set (15%). Table 1 show the population sizes of edge classes in the data set indicating data bias to non-crossing edges. The GNN models were trained by backpropagation to minimize the mean of the binary cross entropy loss function for each mini-batch. The loss function was given by: $\mathbf {loss = - \frac{1}{N}\sum _{i=1}^{N}[l_{i}log(y_{pred}) + (1-l_{i})log(1-y_{pred})]}$, where N is the number of samples in a mini-batch, $l_{i} \in \{0,1\}$ and $y_{pred} \in [0,1]$ are the label and the prediction for sample i respectively. We trained the models for 100 epochs with a batch size of 32. Each batch had 16 BM crossing edges and 16 BM non-crossing edges to avoid the bias derived from data imbalance. To optimize learnable parameters, we used Adam with an initial learning rate set to 0.001 which was scheduled to drop by 0.1 after every 40 epochs. To avoid overfitting on the training data, we used dropout with probability 0.5 for EAGNN layers and BC+MLP classifier, 0.3 for GraphSAGE, and the weight-decay parameter was set to 0.0001.

Table 1. Population sizes of edge classes in the oral mucosa cell-graph dataset.

Table 2. Comparison of GNN models, edge classifiers, aggregated node features (NF) and edge features (EF) for BM prediction on the oral mucosa cell-graph dataset. (NF specifies aggregated node features: $N_1 = N_{type}$, $N_2 = N_{den}$, and $N_3 = N_{ent}$. EF specifies aggregated edge features: $E_1 = \hat{E}^{dis}$, $E_2 = \hat{E}^{den}$, $E_3 = \hat{E}^{ent}$, and $E_4 = \hat{E}^{nei}$.)

5.3 Discussion

To compensate for data imbalances in the ground truth dataset, we evaluated EAGNN performance on the BM prediction problem using five standard metrics: precision, recall, F1 score, ROC-AUC and accuracy.

Fig. 3.

Comparison of EAGNN and GraphSage predictions for intact and degraded BM tissue samples. The blue line is the BM annotation. The green, yellow and red lines represent true positive, false negative and false positive edge predictions respectively. (Color figure online)

Table 2 summarizes the performance of EAGNN combined with three different types of edge classifiers in comparison with GraphSAGE [14]. The combination GraphSAGE+MUL (row 2) is the baseline architecture which was used in [17] for BM prediction. The combination of EAGNN with the BC+MLPs edge classifier outperforms the other methods in 4 out of 5 metrics. GraphSAGE with BC+MLP resulted in high recall and relatively low precision, while EAGNN with BC+MLP resulted in high precision and relatively low recall. This is caused by the selection of the class threshold criterion $\theta$. Tuning the parameter $\theta$ w.r.t F1 score, helped to balance the trade-off between precision and recall. The optimum balance was $\theta = 0.7$.

Figure 3 shows the BM prediction results for the best and worst performing models: EAGNN+BC+MLP $(NF = N_1, EF = E_{1234})$ and GraphSAGE+MUL $(NF =N_1)$ respectively⁵. The figure shows BM prediction results for both models on an intact BM (Fig. 3 a, b) and a degraded BM (Fig. 3 c, d) from the test set. Figure 3 c shows that GraphSAGE+Mul erroneously classifies non-crossing edges close to the BM as crossing-edges, as shown by the many red lines. We term this tendency a “halo effect”. Notice that EAGNN+BC+MLP does not exhibit this halo effect as the false positives in Fig. 3 d are primarily in the region of broken BM.

6 Limitations

There exist several limitations to this study. One is the limitation of our dataset and prediction task: BM identification. Further cell-graph datasets and prediction tasks are needed to establish the wider value of the edge aggregation, classification and labelling methods proposed here.

Another general limitation is the data imbalance problem inherent in many medical datasets, due to low disease frequency, small sample sizes and the effort of annotation. A specific example of this limitation is the class imbalance problem between BM crossing and non-crossing edges. Since the BM is a thin protein interface localised between the epithelial and connective tissue, non-crossing BM edges constitute a large majority of the edges in each cell graph, as shown in Table 1. Figure 3 shows the difference in F1-scores for BM crossing edges between a healthy tissue sample where the BM is intact and a degraded sample where the BM is broken. This specific imbalance could be addressed by using the focal loss function [19] to reduce class imbalance.

7 Conclusions

In this work, we have proposed a new GNN model EAGNN that aggregates both node and edge label information and is suitable for edge label prediction. We have presented a digital pathology case study of BM prediction showing that aggregation of both node and edge label information can take advantage of the topological information in cell-graphs. In our case study, EAGNN significantly outperformed the widely used GraphSAGE GNN model under several performance measures. Furthermore, we have introduced new edge label features including cell entropy gradient and neighbourhood overlap similarity and shown that these improve the accuracy of BM prediction. Future directions of research include improving EAGNN performance and data augmentation methods to reduce the data imbalance.