Stochastic Gradual Covering Location Models

Abstract

Most location models assume that the parameters are given and fixed. Demand for services is known, and the distance to the facility is given. Real-world parameters are not fixed but follow a probability distribution such as a normal distribution. Therefore, stochastic models estimate the results (cost, profit, cover) more accurately.

In cover models, facilities need to be located in an area to provide service to a set of demand points. Demand points that are within a given distance are covered. Two main objectives are investigated in the literature: provide as much cover as possible with a given number of facilities and minimize the number of facilities required to provide full cover. In gradual cover models, up to a certain distance, the demand point is fully covered, and beyond a greater distance, it is not covered at all. Between these two extreme distances, the demand point is partially covered.

In this chapter, we summarize gradual cover models emphasizing on models that have stochastic parameters. We also propose a new model analyzing a stochastic version of the directional graduate cover.

1 Introduction

Most location models assume that the parameters are given and fixed. Demand for services is “known,” and the distance to the facility is given. If an ambulance or a fire truck needs to get to a customer within 10 min, the time is translated to a distance, for example, 3 miles, even though the travel speed may depend on traffic conditions and is not a constant. A customer is considered covered within 3 miles even though only a proportion of the customers are “covered.”

Customers are assumed to be located at “demand points” even though in most applications customers reside in neighborhoods that are defined by regions. Not all customers residing in a neighborhood have the same distance to the facility. Francis et al. (2009, 2000) analyzed the selection of a point that represents a set of demand points or an area. Drezner and Drezner (1997) showed that the squared distance between a demand point located at a center of a circular area and a facility should be increased proportionally to the circle’s area.

It is probably easier to formulate and solve models with known parameters, but in reality, stochastic models estimate the results (cost, profit, cover) more accurately. Real-world parameters are not fixed but follow a probability distribution such as a normal distribution.

2 Cover Models

Facilities need to be located in an area to provide service to a set of demand points. Demand points that are within a given distance are covered, meaning that they are getting the services under consideration (Church & ReVelle, 1974; ReVelle et al., 1976). Two main objectives are investigated in the literature: (i) provide as much cover as possible with a given number of facilities and (ii) minimize the number of facilities required to provide full cover. Such models are used for cover provided by emergency facilities such as ambulances, police cars, or fire trucks. They are also used to model cover by transmission towers such as cell phone towers, TV or radio transmission towers, and radar coverage, among others. For a review of cover models, see Plastria (2002), García and Marín (2015), Snyder (2011), Church and Murray (2018). Drezner et al. (2011, 2012) applied the cover concept to competing facilities. Each competing facility has a “sphere of influence” (Launhardt, 1885; Fetter, 1924; Lösch, 1954; Christaller, 1966; ReVelle, 1986), and customers patronize a facility up to a certain distance.

A different covering model where facilities “cooperate” in providing cover was proposed in Berman et al. (2010). Each facility emits a signal (such as light posts in a parking lot, warning sirens) whose strength declines according to a distance decay function. A point is covered if the combined signal from all facilities exceeds a certain threshold. For example, a parking spot is covered if the total light received at that spot exceeds a given threshold. Recent papers on the cooperative cover are Morohosi and Furuta (2017), Karatas (2017), Wang and Chen (2017), Bagherinejad et al. (2018).

3 Gradual Cover Models

In the gradual cover models, up to a certain distance $R_1$, the demand point is fully covered and beyond a greater distance $R_2$, it is not covered at all. Between these two extreme distances, the demand point is partially covered. Suppose that the cover distance in traditional cover models is 3 miles. At a distance of 2.99 miles, the demand point is fully covered while at a distance of 3.01 miles, it is not covered at all. This assumption may be convenient for analyzing and solving covering problems. However, in reality, cover does not drop abruptly but the decline in cover is gradual.

Various notations are defined in gradual cover models. To be consistent throughout this chapter, we define the following variables:

Notation

D :

Cover distance by non-gradual cover models.

d :

Distance between a facility and a demand point.

$R_1$ :

Full coverage for distance $d\le R_1$.

$R_2$ :

No coverage for distance $d\ge R_2$.

R :

= $\frac {R_1+R_2}{2}$.

$\Delta R$ :

= $R_2-R_1$.

r :

radius of a circle centered at the demand point.

Church and Roberts (1984) were the first to propose the gradual cover model (also referred to as partial cover). The facilities must be located within a finite set of potential locations. Drezner et al. (1998) investigated the gradual cover model in the plane for locating competing facilities. They model the partial cover by a logit function. The network version with a step-wise cover function is discussed in Berman and Krass (2002). The network and discrete models with a general non-increasing cover function were analyzed in Berman et al. (2003b). The single-facility planar model with a linearly decreasing cover function between $R_1$ and $R_2$ was optimally solved in Drezner et al. (2004) by the Big Triangle Small Triangle (BTST) optimization method (Drezner & Suzuki, 2004). It can also be solved by the Big Square Small Square (BSSS) method (Hansen et al., 1981). Location of several facilities can be solved optimally by the Big Cube Small Cube method (Schöbel & Scholz, 2010). Reasonable run time can be achieved for locating up to three facilities. Additional references include Karasakal and Karasakal (2004), Eiselt and Marianov (2009), Drezner and Drezner (2014), Berman et al. (2019).

3.1 Estimating Partial Cover of a Demand Point Covered by Several Facilities

An important issue in gradual cover models is the estimation of the total cover when a demand point is covered by several facilities. In traditional non-gradual cover models where a demand point is either fully covered by a facility, or not covered at all, the rule is straightforward. A demand point is covered if and only if it is covered by at least one facility.

This issue is discussed in Berman et al. (2019). They proposed several “axioms” and observations that we term properties, and we added Property 7:

Property 1::

The total cover is between 0 and 1.

Property 2::

If the partial coverage from a facility increases unilaterally, the joint coverage cannot decrease.

Property 3::

Adding facilities that provide no coverage cannot change the joint coverage received by a demand point.

Property 4::

The joint coverage is not lower than the partial coverage received from any one facility.

Property 5::

If a demand point receives positive coverage from only one facility, then the joint coverage equals to the individual coverage.

Property 6::

If a demand point is covered fully from any one facility, then the joint coverage is full as well.

Property 7::

If all the distances between the demand point and the facilities do not increase, the total cover of the demand point cannot decrease.

We prove the following theorem based on Property 7:

Theorem 1

The optimal locations of the facilities that maximize the total cover are in the convex hull of the demand points.

Proof

By a theorem in Wendell and Hurter (1973), for any location outside the convex hull of a set of points, there is a location in the convex hull that is closer to each of the points generating the convex hull. Therefore, for any location outside the convex hull of the demand points, there is a location in the convex hull with a better value of the objective function because all distances are shorter. If there is a facility outside the convex hull, a better location for that facility exists in the convex hull. The theorem follows by mathematical induction. □

Let $c_j$ be the partial cover of a demand point by facility j for $j=1,\ldots ,p$. Eiselt and Marianov (2009) proposed a total partial cover of $\min \left \{\sum \limits _{j=1}^p c_{j}, 1 \right \}$. Partial cover can be interpreted as the probability of cover. Assuming that the partial covers are not correlated, the total partial cover is: $1-\prod \limits _{j=1}^p\left (1-c_{j}\right )$ (Berman et al., 2003a; Drezner & Wesolowsky, 1997; Drezner & Drezner, 2008). The directional gradual cover discussed in Sect. 3.4 leads to a different rule for the total cover of several facilities.

3.2 Step-Wise Gradual Cover

Church and Roberts (1984) and Berman and Krass (2002) proposed a step-wise decline in cover. A sequence of $k>1$ distances $R_1<R_2<\ldots ,R_k$ is defined with associated partial covers $p_1=1>p_2>\ldots >p_k=0$. Up to a distance $R_1$ cover is full ($p_1=1$). For distances $R_i< d\le R_{i+1}$ for $1\le i\le k-1$, the cover is $p_{i+1}$, and for $d>R_k$ cover is zero.

3.3 Linear Decline Gradual Cover

The simplest model for gradual cover is a linear decline in cover between $R_1$ and $R_2$ as suggested in Drezner et al. (2004). For $d\le R_1$ cover is full (cover of one), and for $d\ge R_2$ cover is zero. For $R_1\le d\le R_2$, the partial cover is $\frac {R_2-d}{\Delta R}$. When $R_2\rightarrow R_1 (\Delta R\rightarrow 0)$, the linear decline model converges to the non-gradual cover model.

3.4 The Directional Gradual Cover

Drezner et al. (2019a) proposed a different approach to estimate partial cover defined as “directional gradual cover.” This model is distinguished from the others based on the assumption that each customer point is not a point, but an area. As in gradual cover models, up to distance $R_1$ a point is fully covered and beyond a distance $R_2$ it is not covered at all. Each demand point is replaced by a circle of radius $\frac {\Delta R}2=\frac {R_2-R_1}2$ and a facility covers points within a distance $R=\frac {R_1+R_2}2$ that can be different for different facilities. The intersection area between the disk centered at the demand point and the disk of the coverage radius $\frac {R_1+R_2}2$ centered at the facility is calculated. The ratio between the intersection area and the area of the disk centered at the demand point is the partial cover of that demand point.

The proportion of cover (for complete details, see Drezner et al. (2019a)) is:

(1)

where $\theta =\arccos \frac {d^2-R_1R_2}{d(R_2-R_1)};~~~\phi =\arccos \frac {d^2+R_1R_2}{d(R_1+R_2)}.$ For $d=R_1$: $\theta =\arccos (-1)=\pi$, and $\phi =\arccos (1)=0$, and therefore $c(d)=1$. For $d=R_2$: $\theta =\phi =\arccos (1)=0$, and $c(d)=0$.

Drezner et al. (2019a) tested discrete problems where there is a given set of potential locations for the facilities. Drezner et al. (2020a) investigated the objective of maximizing the minimum cover among the demand points rather than the total cover. Drezner et al. (2021) investigated maximizing the total cover when the facilities can be located anywhere in the plane.

In gradual cover models, it is not obvious how to estimate the total cover if a demand point is partially covered by several facilities as discussed in Sect. 3.1. In the directional gradual cover (Drezner et al., 2019a), if a demand point is partially covered by two or more facilities, the total cover (area) depends on the distances between the facilities and the demand point, and on the directions of the facilities from the demand point.

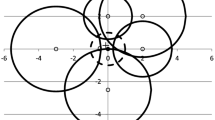
Demand points are usually not mathematical points but represent communities that occupy an area and not all the residents at the demand “point” are located at the same point. Therefore, facilities at different directions cover different parts of the area represented by the demand point. For example, consider one demand point and three facilities depicted in Fig. 1. Facilities 1 and 2 cover some of the northern part of the community and facility 3 covers part of the southern part of the community. Suppose that only facilities 1 and 2 exist in the area. The facilities are located to the north of the demand point, and there is an overlap between the covered areas. Therefore, the total cover is the area covered by facility 2 and facility 1 does not contribute to the total cover. If one facility (either 1 or 2) is located to the north and facility 3 to the south, there is usually a smaller overlap if at all. Since all facilities’ disks in Fig. 1 do not cover the demand point itself, the total area is the sum of the areas because there is no overlap. By any other gradual cover model, the total cover is calculated by the partial covers, and the total cover is the same regardless of the directions of the facilities.

Fig. 1

Three facilities and one demand point

When the radius of the demand point is zero, the directional gradual cover function is a discontinuous curve and the model is equivalent to the traditional non-gradual cover. The demand point is either fully covered or not covered at all.

3.5 Random Limits of Gradual Cover

Drezner et al. (2010) modified the linear decline model by a model where $R_1$, the lowest distance when partial cover starts to decline from full cover, and $R_2$, the upper limit of the distance beyond which there is no cover at all are random variables. They assumed that cover declines linearly between the random values of $R_1$ and $R_2$. Other decline functions can also be investigated in a similar fashion. We summarize the formulations reported in that paper.

Let the cover radius used in the non-gradual covering model be D. Let $\phi _1(d)$ and $\phi _2(d)$ be the density function of the probability that $R_1$ and $R_2$, respectively, are at distance d. Each demand point may have different values for $R_1$ and $R_2$. Let $c(d)$ be the expected cover at distance d. If $d\le R_1$, the cover is one. If $d\ge R_2$, the cover is zero. For $R_1\le d\le R_2$ the cover is $\frac {R_2-d}{R_2-R_1}$. Therefore, the expected cover at distance d, $c(d)$, is

$$\displaystyle \begin{aligned} \begin{array}{rcl} {}c(d)& =&\displaystyle Pr(d\le R_1)+\int\limits_{0}^d\int\limits_d^{\infty}\frac{z-d}{z-y}\phi_1(y)\phi_2(z)dzdy \end{array} \end{aligned} $$

(2)

Note that in (2) it is assumed that $\phi _1(d)$ and $\phi _2(d)$ are independent distributions. If they are correlated, then $\phi _1(y)\phi _2(z)$ should be replaced with a bi-variate distribution. The expected cover $c(d)$ can be calculated by numerical integration.

They analyzed the case where both distributions are uniform on both sides of a radius D and obtained an explicit formula for $c(d)$. Consider the following uniform distributions for a given $D>0$ (the traditional non-gradual cover radius) and a range $\sigma \le D$ for each one. Consequently, $R_1=D-\sigma$, and $R_2=D+\sigma$.

$$\displaystyle \begin{aligned} \phi_1(d)=\left\{\begin{array}{ll}\frac 1 \sigma &|~R_1\le d\le D\\\\0&|~\mbox{Otherwise}\end{array}\right.;~~~~~~~ \phi_2(d)=\left\{\begin{array}{ll}\frac 1 \sigma &|~D\le d\le R_2\\\\0&|~\mbox{Otherwise}\end{array}\right. \end{aligned}$$

The function $c(d)$ is (for complete details, see Drezner et al. (2010)):

(3)

where $u=\frac {D-d}{\sigma }$ and $w=\frac {d-D}{\sigma }$. Note that $0\le u,w\le 1$.

In Fig. 2, we depict the expression for the expected partial cover $c(d)$ by Eq. (3) for $R_1=1$ and $R_2=3$. By the linear decline gradual cover proposed in Drezner et al. (2004) with fixed values of $R_1$ and $R_2$, the graph has a line connecting $d=1$ and $c(d)=1$ with $d=3$ and $c(d)=0$ rather than the depicted curve. When $\sigma \rightarrow 0$, the random limit model converges to the non-gradual cover model.

Fig. 2

Different gradual cover functions for $R_1=1$ and $R_2=3$

3.6 The Logit Gradual Cover Function

Drezner et al. (1998) suggested a logit function

$$\displaystyle \begin{aligned} \frac{1}{1+e^{\alpha+\beta d+\gamma d^2}}\end{aligned}$$

for the partial cover. Drezner et al. (2020b) applied a simpler version of the logit function with only one parameter $\alpha$:

$$\displaystyle \begin{aligned} {} \frac{1+e^\alpha}{e^\alpha+e^{\alpha \frac{d}{R}}}~. \end{aligned} $$

(4)

These logit functions do not restrict the cover to be partial only between $R_1$ and $R_2$. A relatively large value of $\alpha$ is required as depicted in Figure 1 in Drezner et al. (2020b). In Fig. 2 below, a value $\alpha =10$ was used so that the cover up to $R_1$ is very close to 1 and the partial cover for a distance greater than $R_2$ is very small.

When $\alpha \rightarrow \infty$, the model converges to the traditional non-gradual cover model. For $d< R$, $e^{\alpha \frac {d}{R}}<<e^\alpha$ and becomes negligible compared to $e^\alpha$. Consequently, the ratio is close to 1. For $d> R$, $e^{\alpha \frac {d}{R}}>>e^\alpha$ and $e^\alpha$ becomes negligible compared to $e^{\alpha \frac {d}{R}}$. Consequently, the ratio is close to 0.

3.7 An Inverse Cumulative Normal Distribution

Berman et al. (2019) considered the situation that an ambulance, police car, and fire truck needs to reach a demand point within a given time threshold. The time it takes to reach a demand point at distance d has a probability distribution that can be assumed normal by the central limit theorem. The mean of the distribution is $\mu$ at which the probability of reaching the demand point in time is 0.5. The standard deviation of the normal distribution, $\sigma$, reflects the variability of the travel time. When $\sigma \rightarrow 0$, the inverse cumulative normal model converges to the non-gradual cover model. There is a likely time to reach the demand point within the given threshold. Therefore, the probability of not reaching a demand point within the time threshold is the cumulative normal distribution and the probability of reaching it is the inverse cumulative normal.

Budge et al. (2010) performed an empirical study of over 7000 ambulance trips in the city of Calgary in Alberta, Canada, and developed a graph of the probability, which is a measure of coverage, that an ambulance will reach a patient within a given time as a function of the distance (the “Golden Half Hour”). The probability graph developed in their study is almost identical to the inverse cumulative normal curve.

3.8 Correlated Binomial

The distribution of ambulance trips in Budge et al. (2010) can be interpreted as a binomial distribution of events. Success is when the ambulance arrived on time and failure if it did not. The limit of a binomial distribution is a normal distribution. The underlying assumption of a binomial distribution is that the events are not correlated. What if the events are correlated? Drezner and Farnum (1993) developed a “generalized binomial distribution” (GBD) for correlated Bernoulli processes. See also Drezner (2019).

An initial probability of success p is given. An association factor $\theta$, which is similar to the correlation coefficient, is given. Suppose that in the first k events, the number of successes is s. The probability of success in the next event is $(1-\theta )p+\theta \frac {s}k$. $\theta =0$ yields the “standard” binomial distribution where the probability of success is p regardless of the number of successes so far. On the other extreme, for $\theta =1$, if the first event is a success, all subsequent events are successes regardless of the value of p. The probability distribution when $\theta =1$ consists of two values success with probability of p and failure with probability $1-p$. It is not a bell shape distribution as is obtained by uncorrelated binomial.

When $\theta >0$, if the proportion of successes so far is greater than p, the probability of success in the next event is greater than p. If the rate of successes is below p, the probability of success is less than p. For example, in sport events, a “good” team that has a good record of successes so far in the season is more likely to succeed in the next game. Drezner and Farnum (1993) showed that the mean of the distribution is np, the same as the binomial distribution, but the variance is $p(1-p)\frac {n-\frac 1{B(n,2\theta )}}{1-2\theta }$. They found that in baseball games $\theta =0.397$. For complete details, see Drezner and Farnum (1993).

Drezner (2006) further investigated the limit of the GBD. It is proven that for $\theta \le 0.5$ the limit of the GBD, as the number of trials increases to infinity, is the normal distribution. For $\theta >0.5$, it can be bi-modal. It was also found, by analyzing real data, that the grade distribution of 1023 multiple choice exams yielded $\theta = 0.5921$ and the number of wins of NBA teams at the end of the season yielded $\theta =0.5765$; both are not a normal distribution. The percentage of “wins” for both exam scores and NBA teams are not random but depend on the skill of the individual. Bhootra et al. (2015) investigated the performance of mutual funds by the GBD and found that the performance of mutual funds is not random, but the skill of the managers plays an important role in their performance.

An interesting gradual decline function is the inverse of the limit of the cumulative GBD. For $\theta \le 0.5$, the function is the inverse cumulative normal distribution, but for $\theta >0.5$, the distribution can be bi-modal. For $\theta =1$, the distribution is either success or failure, which is actually the traditional non-gradual cover function. There is no gradual cover; the cover drops abruptly from full cover to no cover. In Fig. 2, the partial cover function is depicted for $\theta =0.9$.

3.9 Comparing Gradual Cover Functions

In Fig. 2, gradual decline in cover functions are depicted for $R_1=1$ and $R_2=3$. In the original non-gradual cover models, there is an abrupt decline in cover at a certain distance (distance of $R=2$ in the figure) from full cover to no cover. Church and Roberts (1984) and Berman and Krass (2002) proposed a step-wise decline in cover discussed in Sect. 3.2. Such approach still has discontinuities in the cover as a function of the distance. Drezner et al. (2004) proposed a linear decline in cover between $R_1$ and $R_2$, discussed in Sect. 3.3. This model is continuous but has a discontinuous derivative at $d=R_1$ and at $d=R_2$. Drezner et al. (2010) proposed that $R_1$ and $R_2$ are random variables rather than fixed values. Their model is discussed in Sect. 3.5. This partial cover function is continuous with a continuous derivative. By the directional cover, described in Sect. 3.4, it is close to linear decline and is the only function in Fig. 2 that is not equal to 0.5 at $d=2$. This is because the intersection area between the circles when the circle of radius R passes through the demand point is not half of the circle’s area. The logit-based gradual cover, discussed in Sect. 3.6, is based on Eq. (4). For $\alpha =10$, which was used in the figure, the shape of the partial cover function resembles the random function shape. This shape also resembles the inverse normal distribution function discussed in Sect. 3.7 for a standard deviation $\sigma =\frac {R-r}6$. The correlated binomial model, discussed in Sect. 3.8, is the inverse cumulative distribution of a possibly bi-modal distribution for $\theta >0.5$. The graph depicted in the figure is calculated by a simulation using $\theta =0.9$. The density function is bi-modal and the derivative of the curve has a sharper decline near the two modes and a shallow decline near $d=2$, which is the low point of the density function between the two modes.

3.10 Summary and Discussion of Gradual Cover Models

In the original gradual cover model, there is an abrupt decline from full cover to partial cover. In reality, cover does not drop abruptly. Earlier models of gradual cover attempted to rectify it by defining a decline of coverage by a step-wise or a linear function (Sects. 3.2, 3.3). More recently (see Sect. 3.4), it is assumed that every demand “point” is actually a neighborhood and not all customers are at the same distance from a facility.

Subsequent models discussed in Sects. 3.5–3.8 assume that the parameters of the gradual cover models are random rather than having fixed values. Such an assumption is closer to reality and provides more flexibility. For example, in Sect. 3.5, it is assumed that the start of partial cover $R_1$ and the start of no cover $R_2$ are random variables. In Sect. 4, we propose and test a new model assuming that the parameters of the directional gradual cover (Sect. 3.4) are random variables, which makes the model yet closer to reality.

4 The Stochastic Directional Gradual Cover Model

In this section, we propose a stochastic formulation for the directional gradual cover model. We incorporate standard gradual cover approaches into the directional cover model. As in the directional gradual cover, the demand point is defined by a circle of radius r. The facility does not cover a point in the plane by a disk of radius D, but there are two radii $R_1\le D\le R_2$ so that a point is fully covered within the circle of radius $R_1$, and not covered at all outside the circle of radius $R_2$. A point in the ring between $R_1$ and $R_2$ is partially covered. Each point in the circle of radius r centered at the demand point is covered at a proportion between 0 and 1. The cover of a demand point is the integral over the circle centered at the demand point, where the integrand at any point in the circle is its partial cover.

In Fig. 3, a typical cover of one demand point by one facility is depicted. The intersection area within a radius $R_1$ is fully covered. The area beyond $R_2$ is not covered. The intersection area with the ring between $R_1$ and $R_2$ is partially covered. In the original directional gradual cover (Drezner et al., 2019a), $R_1=R_2$, the ring is a circle, and there is no area with partial cover.

Fig. 3

Stochastic directional gradual cover

The partial cover between $R_1$ and $R_2$ can be defined in many ways. For example, the gradual cover can be defined by a reverse cumulative of a distribution: (i) a normal distribution centered at D with $R=D+3\sigma$ and $r=D-3\sigma$ discussed in Sect. 3.7, (ii) a beta distribution, and (iii) a logit distribution (Drezner et al., 2020b) discussed in Sect. 3.6. We opted in the computational experiments to define it as declining linearly between $R_1$ and $R_2$, which is a reverse cumulative of the uniform distribution, as proposed in Drezner et al. (2004) and discussed in Sect. 3.3. It is as easy to implement it by any gradual cover function as long as an explicit formula for the gradual decline is available.

Suppose that k facilities are located in the area. Each point in the plane may be partially covered by several facilities. Let the proportions of cover of a point (not necessarily the demand point) by facility $1\le j\le k$ be $0\le p_j\le 1$. This proportion $p_j$ can be calculated by a linear decline between $R_1$ and $R_2$, or any other rule. Interpreting these proportions as uncorrelated probabilities leads to a total cover of the point, P:

$$\displaystyle \begin{aligned} {} P=1-\prod_{j=1}^k(1-p_j) \end{aligned} $$

(5)

Note that if $p_j=0$, facility j does not affect the total cover, and if $p_j=1$ for some j, the total cover is full at 100% regardless of the other proportions.

4.1 Calculating the Total Cover

The total cover of a demand point is calculated by a two-dimensional integral in the disk centered at the demand point. The partial cover at each point (the integrand) in the disk is calculated by Eq. (5).

In the original directional cover model (Drezner et al., 2019a), the cover area of a demand point is the union of intersection areas between the circles centered at the facilities and the circle centered at the demand point. If at least one facility provides full cover, the total cover is full. Facilities that do not provide any cover can be removed from consideration. If, for example, there are five facilities that provide partial cover, it seems intractable to develop an explicit formula for the union of the five areas. It is possible to calculate the proportion of the circumference of a circle c with a radius $0\le \rho \le r$, centered at the demand point that is covered. Each circle centered at a facility covers part of the circumference between two angles $\theta _1$ and $\theta _2$, which are the intersection points between the circle centered at the facility and circle c. The proportion of cover is the union of these parts of the circumference.

The total cover area of a demand point of radius r can be found by integration. Consider a circle of radius $\rho$ for $0\le \rho \le r$ centered at the demand point. Let $\gamma (\rho )$ be the proportion of the circumference of the circle of radius $\rho$ that is covered. The total cover area A is

$$\displaystyle \begin{aligned} {} A=\int\limits_0^r2\pi \rho\gamma (\rho)d\rho~, \end{aligned} $$

(6)

and the joint cover of a demand point of radius r is

$$\displaystyle \begin{aligned} {} Cover=\frac{A}{\pi r^2}=\frac 1{\pi r^2}\int\limits_0^r2\pi \rho\gamma (\rho)d\rho~. \end{aligned} $$

(7)

Note that if the circumference of every circle of radius $\rho$ is covered, $\gamma (\rho )=1$, then $Cover=1$ by Eq. (7).

Drezner et al. (2019a) applied this calculation and evaluated the total covered area by Gaussian numerical quadrature based on Legendre polynomials. (Abramowitz & Stegun, 1972). For complete details, see Drezner et al. (2019a).

In the stochastic directional gradual cover, it is not simple to calculate the proportion of a circumference of a circle that is covered. The “circle” centered at the facility is actually a ring with various proportions of covers in the ring. There is no clear way to evaluate the intersection between the ring and the circumference of the circle. It is calculated by an integral for every facility and the union is not straightforward to calculate.

In the stochastic directional cover, as depicted in Fig. 3, it is not sufficient to calculate the union of the covered areas because some of the areas are partially covered and Eq. (5) need to be applied to each individual point. We therefore propose to evaluate the total cover numerically by the hexagonal pattern in the circle centered at the demand point as detailed in Drezner et al. (2021, 2019b). The points in the hexagonal pattern are defined by two sequences (all the combinations of the two lists for x and y):

$x=0,\pm 1,\pm 2,\ldots ;~~~y=0,\pm \sqrt {3},\pm 2\sqrt {3},\ldots$, and

$x=\pm \frac {1}{2},\pm \frac 32,\pm \frac 52,\ldots ;~~~y=\pm \frac {\sqrt {3}}2,\pm \frac {3\sqrt {3}}2\pm \frac {5\sqrt {3}}2,\ldots$.

These points cover the plane with hexagons centered at each point with sides as perpendicular bisectors to six adjacent points. The area of each hexagon is $\frac {\sqrt {3}}2$. All the points satisfying $x^2+y^2\le M$ for some M are selected. For example, $M=220$ results in $N=805$ points. To get N hexagons that cover a disk of radius r, we multiply the coordinates by a factor K so that $\frac {\sqrt {3}}2NK^2=\pi r^2$. Leading to a factor of $K=r\sqrt {\frac {2\pi }{N\sqrt {3}}}$ to get an hexagonal pattern in a circle of radius r centered at the origin (0, 0). Note that few hexagons have parts outside the circle and a small part of the area of the disk is not covered, but the total area of the hexagons is equal to the circle’s area. The perimeter of the covered area is a little ragged. Drezner et al. (2019b) investigated applying different areas for hexagons that are close to the circle’s perimeter and are either trimmed by the perimeter or have extra area bordered by the perimeter, and the results hardly changed. Therefore, such a refinement is not suggested.

There are many values of the number of hexagonal points that can be selected. We propose to select 805 points in the hexagonal pattern (see Fig. 4) that lead to a good estimate of the integral (Drezner et al., 2021). The partial cover for each point is calculated by Eq. (5), the sum S of the partial covers for all 805 points is calculated, and the partial cover of the demand point is $\frac {S}{805}$.

Fig. 4

Hexagonal pattern of 805 points

For example, consider a disk of radius 1 centered at the origin (demand point). The disk is partially covered by a facility located at (2,0). For a radius $D\le 1$, there is zero cover. As D increases, partial cover increases up to $D=3$. For $D\ge 3$, there is full cover. The area can be calculated exactly by Eq. (1). In Table 1, the exact area is compared with the hexagonal numerical integration for $N=805$ points for various values of $1\le D\le 3$. The average difference is 0.005. In one case, the difference exceeds 0.01 and in all other cases, it is below 0.01.

Table 1 Comparing exact proportion of the area to the hexagonal result

4.2 Investigating the Stochastic Directional Gradual Cover

Any solution method that was applied for (heuristically) solving directional gradual cover models can be applied for the stochastic model. Rather than calculating the value of the objective function numerically by the directional objective, it is calculated by the stochastic objective. The “black box” providing the total partial cover by the directional model is replaced by a black box providing total partial cover by the stochastic objective. For example, Drezner et al. (2019a) applied the ascent algorithm, Tabu search (Glover & Laguna, 1997), and simulated annealing (Kirkpatrick et al., 1983). Drezner et al. (2020a) applied the same heuristics but generated good starting solutions. Drezner et al. (2021) constructed a genetic algorithm (Holland, 1975; Goldberg, 2006) and solved the continuous case by SNOPT (Gill et al., 2005) and Nelder-Mead (Nelder & Mead, 1965; Dennis & Woods, 1987).

The justification for using gradual decline in cover rather than abrupt drop in cover is that it provides better estimates for the actual cover observed in real applications. The question is not whether one model provides greater coverage than another but which one estimates the cover more accurately. We believe that in reality, cover is stochastic in nature and does not drop abruptly. Therefore, stochastic gradual cover estimates the total cover more accurately because it imitates reality better. There are examples that total cover by one approach is greater than the total cover by another approach for facilities located at the same location. However, this does not mean that one model provides more “actual” cover than the other.

Consider locating one facility to cover four demand points, each with a weight of 1, located on the vertices of a square of side length of 1. By the non-gradual cover objective, if $D<0.5$, a maximum of one demand point is covered for a total cover of 1. The four circles of radius D centered at the demand points do not intersect. For $0.5\le D<\frac {\sqrt {2}}2$, the total cover is 2 because the only four intersections are of two circles of radius D. For $D\ge \frac {\sqrt {2}}2$, all four circles intersect and cover the center of the square, and locating a facility there covers all 4 demand points for a total cover of 4.

For the gradual cover model with the linear decline, it is fair to compare the non-gradual results with D being at the center of the segment connecting $R_1$ and $R_2$. For $D=0.499$, we investigate the range of $R_1=0.499-\sigma$ to $R_2=0.499+\sigma$. Since $R_1\ge 0$ by definition, then $\sigma \le 0.499$. If we locate the facility at the center of the square, all four distances are equal to $\frac {\sqrt {2}}2$. The partial cover of each demand point is $\frac {0.499+\sigma -\frac {\sqrt {2}}2}{2\sigma }$ and the total cover is $4\frac {0.499+\sigma -\frac {\sqrt {2}}2}{2\sigma }=2+\frac {0.998-\sqrt {2}}{\sigma }$. This total cover is greater than 1 for $\sigma >\sqrt {2}-0.998\approx 0.416$, which is better than the non-gradual optimal solution. However, for $\sigma <0.416$, the non-gradual solution is better.

A different question is whether the gradual cover objective for a given location of the facility is higher or lower than the non-gradual cover. It is easy to construct examples both ways. Consider the example of four demand points on the vertices of a square of side 1 and a facility located at the center of the square. For $D=0.499$ with $R_1=0.499-\sigma$ and $R_2=0.499+\sigma$ discussed above, for $\sigma >0.416$, the gradual cover is higher than the non-gradual cover (which is 0). However, for $D>\frac {\sqrt {2}}2$, non-gradual cover is 4 while partial cover is less than 4 when $R_1<\frac {\sqrt {2}}2$.

We compared the combined cover by the stochastic directional gradual cover model calculated for given locations of facilities to the directional cover and non-gradual cover model. For the comparison, we generated problems with $n=100$ demand points and up to 100 facilities by a pseudo-random number generator.

In order to allow for future comparisons, the problems were generated by the pseudo-random number generator described in Drezner et al. (2019c). It is based on the pseudo-random number generator proposed in Law and Kelton (1991). A sequence $r_k$ of integer numbers in the open range (0, 100,000) is generated. A starting seed $r_1$, which is the first number in the sequence, and a multiplier $\lambda$, which is an odd number not divisible by 5, are selected. We used $\lambda =12{,}219$. The sequence is generated by the following rule for $k\ge 1$:

$$\displaystyle \begin{aligned} r_{k+1}=\lambda r_k-\left\lfloor\frac{\lambda r_k}{100{,}000}\right\rfloor\times 100{,}000. \end{aligned}$$

The random number between 0 and 10 is $\frac {r_k}{10,000}$.

For demand points (with coordinates between 0 and 10), the x coordinates were generated by $r_1=97$, and for the y-coordinates, we used $r_1=367$. For the weights, we used $r_1=12{,}347$ and $w_i=1+\frac {r_i}{100,000}$ so $1<w_i<2$. Facilities were generated by $r_1=23{,}431$ for the x-coordinates and $r_1=56{,}407$ for the y-coordinates.

The points are depicted in Fig. 5, and the first 10 points are listed in Table 2. For the non-gradual cover model, a facility covers a demand point within a distance of 3. For directional cover models, each demand point is defined by a circle of radius $r=1$. For the directional cover (Drezner et al., 2019a), the facility covers points within a distance of 3. For the stochastic directional model, the facility covers a point in a range between 2 and 4. At a distance of 2, the cover is full and at a distance of 4, there is no cover. Cover declines linearly between 2 and 4.

Fig. 5

The 100 demand points and 20 facilities

Table 2 The first 10 pseudo-randomly generated points

The comparison of the proportion cover of all 100 demand points by p facilities for the traditional cover model that is termed non-gradual, the directional gradual cover (Drezner et al., 2019a), the stochastic directional gradual cover model proposed in this chapter, are reported in Table 3. The best covers for each p are marked in boldface. Note that these are not the optimal solutions but the values of the objective function at facilities locations that were randomly generated and depicted in Table 2. The procedures were coded in FORTRAN using double precision arithmetic and were compiled by an Intel 11.1 FORTRAN compiler using one thread with no parallel processing. The programs were run on a desktop with the Intel i7-6700 3.4GHz CPU processor and 16GB RAM. We do not report the run times because they are mostly less than a millisecond.

Table 3 Comparing non-gradual, directional, and stochastic directional covers

Since the demand points are basically located randomly and uniformly in the square, the proportion of cover does not vary by much. The majority of the best proportion of cover was found by the non-gradual cover approach, especially for $p\ge 12$. The average was the highest (not by much) for the directional model.

We found the proportions for $p=1,2,\ldots , 100$. The non-gradual model provided full cover for $p\ge 16$, the directional cover model yielded full cover for $p\ge 54$, and the stochastic directional cover model for $p\ge 75$.