Lipschitz Geometry of Real Semialgebraic Surfaces

Abstract

We present here basic results in Lipschitz Geometry of semialgebraic surface germs. Although bi-Lipschitz classification problem of surface germs with respect to the inner metric was solved long ago, classification with respect to the outer metric remains an open problem. We review recent results related to the outer and ambient bi-Lipschitz classification of surface germs. In particular, we explain why the outer bi-Lipschitz classification is much harder than the inner classification, and why the ambient Lipschitz Geometry of surface germs is very different from their outer Lipschitz Geometry. In particular, we show that the ambient Lipschitz Geometry of surface germs includes all of the Knot Theory.

8.1 Introduction

Lipschitz classification of semialgebraic surfaces has become in recent years one of the central questions of the Metric Geometry of Singularities. It was stimulated by the finiteness theorems of Mostowski, Parusinski and Valette (see [15, 16, 20]). They proved that there are finitely many Lipschitz equivalence classes in any semialgebraic family of semialgebraic sets. Lipschitz classification is intermediate between Smooth (too fine) and Topological (too coarse) classifications. For example, smooth classification of most singularities is not finite. It may be even infinite dimensional for non-isolated singularities.

Here we review recent developments in Lipschitz Geometry of semialgebraic surfaces (two-dimensional real semialgebraic sets). Since we are mainly interested in singularities of semialgebraic surfaces, our main object is a semialgebraic surface germ $(X,0)$ at the origin of ${\mathbb R}^n$. Note that most results presented in this paper remain true for subanalytic sets, and for the sets definable in a polynomially bounded o-minimal structure.

A connected semialgebraic set $X\subset {\mathbb R}^n$ inherits from ${\mathbb R}^n$ two metrics: the outer metric$dist(x,y) = |y-x|$ and the inner metric$idist(x,y) =$ length of the shortest path in X connecting x and y. Note that $dist(x,y)\le idist(x,y)$. A semialgebraic set is called Lipschitz Normally Embedded if these two metrics are equivalent (see Definition 8.2.3).

For the surface germs, there are three natural equivalence relations:

• 1. Inner Lipschitz equivalence: $(X,0)\sim _i (Y,0)$ if there is a homeomorphism

  $h:(X,0)\to (Y,0)$ bi-Lipschitz with respect to the inner metric.

• 2. Outer Lipschitz equivalence: $(X,0)\sim _o (Y,0)$ if there is a homeomorphism

  $h:(X,0)\to (Y,0)$ bi-Lipschitz with respect to the outer metric.

• 3. Ambient Lipschitz equivalence:

  $(X,0)\sim _a (Y,0)$ if there is an orientation preserving bi-Lipschitz homeomorphism $H:({\mathbb R}^n,0)\to ({\mathbb R}^n,0)$ such that $H(X)=Y$.

Inner Lipschitz Geometry of surface germs is relatively simple. The building block of the inner Lipschitz classification of surface germs is a $\beta$-Hölder triangle (see Definition 8.2.1). A surface germ $(X,0)$ with an isolated singularity and connected link is inner Lipschitz equivalent to a $\beta$-horn (see Definition 8.2.2). If the singularity is not isolated, classification is made by the theory of Hölder Complexes (see [1]). A Hölder Complex is a triangulation (decomposition into Hölder triangles) of a surface germ. Canonical Hölder Complex (see Definition 8.2.10) is a complete invariant of the inner Lipschitz equivalence of surface germs.

Outer Lipschitz Geometry of surface germs is much more complicated. For example, the germs of all irreducible complex curves are inner Lipschitz equivalent to $({\mathbb C},0)$, while the outer Lipschitz classification of the germs of complex plane curves is described by their sets of essential Puiseux pairs (see [12, 17]). Even for the union of two normally embedded Hölder triangles, the outer Lipschitz Geometry is not simple (see [3]).

A special case of a surface germ is the union of a Hölder triangle T and a graph of a Lipschitz semialgebraic function f defined on T. The outer Lipschitz equivalence of two such surface germs is equivalent to the Lipschitz contact equivalence of the two functions. This relates outer Lipschitz Geometry of surface germs with the Lipschitz Geometry of functions. A complete invariant of the contact equivalence class of a Lipschitz function f defined on a Hölder triangle T, called a “pizza,” is defined in [9]. Informally, a pizza is a decomposition of T into “slices,” Hölder sub-triangles $\{T_i\}$ of T, such that the order of f on each arc $\gamma \subset T_i$ depends linearly on the order of contact of $\gamma$ with a boundary arc of $T_i$.

For the general surface germs, Lipschitz classification with respect to the outer metric is still an open problem.

The study of Lipschitz Normally Embedded, or simply Normally Embedded, sets was initiated by Kurdyka and Orro [14]. Kurdyka proved that any semialgebraic set admits a “pancake decomposition,” a finite partition into normally embedded subsets. Using this partition, Kurdyka and Orro proved that any semialgebraic set admits a semialgebraic “pancake metric” equivalent to the inner metric. Normal Embedding theorem of Birbrair and Mostowski states that, for any semialgebraic set X, there is a semialgebraic and bi-Lipschitz with respect to the inner metric embedding $\varPsi : X \to {\mathbb R}^m$, where $m\ge 2\dim (X)+1$ (see [10]). Lipschitz Normal Embedding of complex analytic sets is addressed in the paper by Anne Pichon in the present volume.

The set of semialgebraic arcs in $(X,0)$ parameterized by the distance to the origin is called the Valette link$V(X)$ of the germ $(X,0)$ (see Definition 8.3.6). The tangency order of arcs (see Definition 8.3.9) defines a non-archimedean metric on $V(X)$.

A pancake decomposition is called minimal if it is not a refinement of another pancake decomposition. A natural question related to Lipschitz Normal Embedding of surface germs is uniqueness of a minimal pancake decomposition. The answer is negative even for a Hölder triangle. Gabrielov and Sousa in [13] gave examples of Hölder triangles having several combinatorially non-equivalent minimal pancake decompositions.

Relations between the ambient and outer equivalence of surface germs were studied in [2, 5, 6]. In the paper [2] the authors presented several outer Lipschitz and ambient topologically equivalent families of surface germs in ${\mathbb R}^3$ and ${\mathbb R}^4$, which are pairwise ambient Lipschitz non-equivalent. In [5, 6], several “Universality Theorems” were formulated. Informally, these theorems state that, even when the link of a surface germ is topologically a trivial knot, the classification problem of the ambient Lipschitz equivalence of such surface germs “contains all of the knot theory.”

8.2 Inner Lipschitz Equivalence

Definition 8.2.1

For $1\le \beta \in \mathbb Q$, the standard $\beta$-Hölder triangle $T_\beta$ is the germ at the origin of ${\mathbb R}^2$ of the surface $\{x\ge 0, \; 0\le y \le x^\beta \}$ (see Fig. 8.1a). A $\beta$-Hölder triangle is a surface germ inner Lipschitz equivalent to $T_\beta$.

Fig. 8.1

A $\beta$-Hölder triangle and a $\beta$-horn

Definition 8.2.2

For $1\le \beta \in \mathbb Q$, the standard $\beta$-horn $C_\beta$ is the germ at the origin of ${\mathbb R}^3$ of the surface $\{z\ge 0, \; x^2+y^2 = z^{2\beta }\}$ (see Fig. 8.1b). A $\beta$-horn is a surface germ inner Lipschitz equivalent to $C_\beta$.

Definition 8.2.3

A semialgebraic set X is called Lipschitz Normally Embedded (LNE) if the inner and outer metrics on X are equivalent: $dist(x,y)\le idist(x,y)\le C\,dist(x,y)$ for some constant $C>0$ and all $x,y\in X$.

For example, the germ of an algebraic curve $\{x^3=y^2\}$ is not LNE, while the standard $\beta$-horn $C_\beta$ is LNE.

Theorem 8.2.4

Given the germ$(X,0)$of a semialgebraic surface with isolated singularity and connected link, there is a unique rational number$\beta \geq 1$such that$(X,0)$is inner Lipschitz equivalent to the standard$\beta$-horn$C_\beta$.

Birbrair’s theory of Hölder Complexes (see [1]) is a generalization of Theorem 8.2.4 for the surface germs with non-isolated singularities.

Definition 8.2.5

A Formal Hölder Complex is a pair $(G,\beta )$, where G is a graph and $\beta : E_G\to \mathbb Q_{\ge 1}$ is a function, where $E_G$ the set of edges of G.

Definition 8.2.6

A Geometric Hölder Complex corresponding to a Formal Hölder Complex $(G,\beta )$ is a surface germ $(X,0)$ such that

• 1. For small $\varepsilon >0$, the intersection of X with the $\varepsilon$-ball $B_\varepsilon$ is homeomorphic to the cone over G, and the intersection of X with the $\varepsilon$-sphere $S_\varepsilon$ is homeomorphic to G.

• 2. For any edge $g\in E_G$, the subgerm of $(X,0)$ corresponding to g is a $\beta (g)$-Hölder triangle.

Theorem 8.2.7

For any surface germ$(X,0)\subset {\mathbb R}^n$, there exists a Formal Hölder Complex$(G,\beta )$such that$(X,0)$is a Geometric Hölder Complex corresponding to$(G,\beta )$.

Remark 8.2.8

For a given surface germ $(X,0)$, the Formal Hölder Complex $(G,\beta )$ in Theorem 8.2.7 is not unique. The simplification procedure described below reduces it to the unique Canonical Hölder Complex corresponding to $(X,0)$.

Definition 8.2.9

We say that a vertex $v_0$ of the graph G is non-critical if it is adjacent to exactly two edges $g_1$ and $g_2$ of G, and these edges connect $v_0$ with two different vertices of G. A vertex $v_0$ of G is called a loop vertex if it is adjacent to exactly two different edges $g_1$ and $g_2$ of G, and these edges connect $v_0$ with the same vertex $v_1$ of G. The other vertices of G (neither non-critical nor loop vertices) are called critical.

Definition 8.2.10

An Abstract Hölder Complex $(G,\beta )$ is Canonical if

• 1. All vertices of G are either critical or loop vertices;

• 2. For any loop vertex v of G adjacent to the edges $g_1$ and $g_2$, one has $\beta (g_1)=\beta (g_2)$.

Now we define a simplification procedure, reducing an Abstract Hölder Complex $(G,\beta )$ to a Canonical one.

We start with eliminating non-critical vertices. Let $v_0$ be a non-critical vertex of G, connected with the vertices $v_1$ and $v_2$ of G by the edges $g_1$ and $g_2$. Then we remove the vertex $v_0$ from the set of vertices of G, and replace the edges $g_1$ and $g_2$ of G with the single edge $g_0$ connecting $v_1$ with $v_2$. Let $G'$ be the graph obtained from G by this operation. We define an abstract Hölder complex $(G',\beta ')$, setting $\beta '(g_0)=\min (\beta (g_1),\beta (g_2))$ and $\beta '(g)=\beta (g)$ for all edges g of $G'$ other than $g_0$ (see Fig. 8.2a).

Fig. 8.2

Simplification of Hölder complexes

We repeat this operation until there are no non-critical vertices. After that, we take care of the loop vertices of G.

Let $(G,\beta )$ be an Abstract Hölder Complex without non-critical vertices. If a loop vertex $v_0$ of G is connected by the edges $g_1$ and $g_2$ with the same vertex $v_1$, such that $\beta (g_1)\ne \beta (g_2)$, we define an Abstract Hölder Complex $(G,\beta ')$, replacing $\beta _1=\beta (g_1)$ and $\beta _2=\beta (g_2)$ with $\beta '(g_1)=\beta '(g_2)=\min (\beta _1,\beta _2)$ (see Fig. 8.2b). We repeat this operation for all loop vertices of G.

The main results of the paper [1] are the following:

Theorem 8.2.11 (Inner Lipschitz Classification Theorem)

The surface germs $(X,0)$ and $(X',0)$ are Lipschitz equivalent with respect to the inner metric if, and only if, the corresponding Canonical Hölder Complexes are combinatorially equivalent.

Theorem 8.2.12 (Realization Theorem)

Let$(G,\beta )$be an Abstract Hölder Complex. Then there exists a surface germ$(X,0)$such that$(X,0)$is a Geometric Hölder Complex corresponding to$(G,\beta )$.

Remark 8.2.13

The theory of Hölder Complexes implies that a germ $(X,0)$ of an irreducible complex curve, considered as a real surface germ, is inner Lipschitz equivalent to the germ $({\mathbb C},0)$. Otherwise $(X,0)$ is inner Lipschitz equivalent to the union of finitely many germs $({\mathbb C},0)$ pinched at the origin.

8.3 Normal Embedding Theorem, Lipschitz Normally Embedded Sets

Examples of Lipschitz Normally Embedded (LNE) Surface Germs

• 1. The standard $\beta$-horn $C_\beta$ is LNE.

• 2. A germ of an irreducible complex curve is LNE if, and only if, it is smooth.

There are many examples of not normally embedded surface germs. On the other hand, we have the following result:

Theorem 8.3.1 (See [7, 10])

Let $X\subset {\mathbb R}^m$ be a connected semialgebraic set. Then there exist a normally embedded semialgebraic set $\tilde {X}\subset {\mathbb R}^q$ , where $q\le 2\dim X+1$ , and an inner bi-Lipschitz homeomorphism $p:X\to \tilde {X}$ . This map is called a normal embedding of X.

Definition 8.3.2

A subset $\tilde {X}\subset {\mathbb R}^m$ is called Lipschitz Normally Embedded if there exists a bi-Lipschitz homeomorphism $\varPsi : \tilde {X}_{inner} \rightarrow \tilde {X}_{outer}$.

Here $\tilde {X}_{inner}$ means the space $\tilde {X}$ equipped with the inner metric, and $\tilde {X}_{outer}$ means $\tilde {X}$ equipped with the outer metric. The difference with Definition 8.2.3 is that in Definition 8.3.2 we do not a priori suppose that $\varPsi$ is the identity map.

Proposition 8.3.3

The two definitions of Lipschitz Normally Embedded sets are equivalent.

Pancake decomposition of Kurdyka [14] implies that there exists a decomposition of any semialgebraic set X into LNE semialgebraic subsets.

Theorem 8.3.4

There is a decomposition of any semialgebraic set X into subsets $X_i$ such that

• 1. $\cup X_i= X$.

• 2. $X_i$ are semialgebraic LNE sets.

• 3. $\dim (X_i \cap X_j)< \min (\dim X_i,\dim X_j)$for$i\ne j$.

Remark 8.3.5

Using pancake decomposition, Kurdyka and Orro defined the so-called pancake metric (see [7, 14]). It is a semialgebraic metric equivalent to the inner metric.

Definition 8.3.6 (See [19])

An arc in ${\mathbb R}^n$ is (a germ at the origin of) a mapping $\gamma :[0,\epsilon )\rightarrow {\mathbb R}^n$ such that $\gamma (0)=0$. Unless otherwise specified, arcs are parameterized by the distance to the origin, i.e., $|\gamma (t)|=t$. We usually identify an arc $\gamma$ with its image in ${\mathbb R}^n$. The Valette link of a germ $(X,0)$ is the set $V(X)$ of all arcs $\gamma \subset X$.

Theorem 8.3.7 (See [19])

Let$(X,0)$and$(Y,0)$be germs of semialgebraic sets in${\mathbb R}^n$. If these germs are semialgebraically (inner, outer or ambient) Lipschitz equivalent, then there exists a bi-Lipschitz map$h:X\to Y$(or$h:{\mathbb R}^n\to {\mathbb R}^n$such that$h(X)=Y$in the case of ambient equivalence) preserving the distance to the origin, i.e., such that$h(X\cap S_\varepsilon )=Y\cap S_\varepsilon$for small$\varepsilon >0$.

Definition 8.3.8

Let $f\not \equiv 0$ be (a germ at the origin of) a Lipschitz function defined on an arc $\gamma$. The order$ord_\gamma f$ of f on $\gamma$ is the exponent $q\in \mathbb Q$ such that $f(\gamma (t))=c t^q+o(t^q)$ as $t\to 0$, where $c\ne 0$. If $f\equiv 0$ on $\gamma$, we set $ord_\gamma f=\infty$.

Definition 8.3.9

The tangency order of arcs $\gamma$ and $\gamma '$ is $tord(\gamma ,\gamma ')=ord_{\gamma } |\gamma (t)-\gamma '(t)|$. The tangency order of an arc $\gamma$ and a set of arcs $Z\subset V(X)$ is $tord(\gamma ,Z)=\sup _{\lambda \in Z} tord(\gamma ,\lambda )$. The tangency order of two subsets Z and $Z'$ of $V(X)$ is $tord(Z,Z')=\sup _{\gamma \in Z} tord(\gamma ,Z')$. Similarly, $itord(\gamma ,\gamma ')$, $itord(\gamma ,Z)$ and $itord(Z,Z')$ are the tangency orders with respect to the inner metric.

Remark 8.3.10

If $(X,0)$ is a germ of a semialgebraic curve, i.e., $X=\cup \gamma _i$ is a finite family of semialgebraic arcs, then the outer Lipschitz Geometry of $(X,0)$ is completely determined by the tangency orders $tord(\gamma _i,\gamma _j)$ (see [4]).

Proposition 8.3.11

A surface germ$(X,0)$is LNE if, and only if, for any two arcs$\gamma _1$and$\gamma _2$in X one has$tord(\gamma _1,\gamma _2)=itord(\gamma _1,\gamma _2)$.

Proposition 8.3.12

Let$(X,0) \in {\mathbb R}^n$be a surface germ inner Lipschitz equivalent to a$\beta$-horn. The Grassmannian$G(n,2)$can be considered as the space of all orthogonal projections$\rho :{\mathbb R}^n\to {\mathbb R}^2$. Then there exists an open dense semialgebraic subset$\widetilde {G} \subset G(n,2)$such that for all$\rho \in \widetilde {G}$one has$\beta =\min _{\{\gamma _1,\gamma _2\}\subset V(X)} tord(\rho (\gamma _1),\rho (\gamma _2))$.

The following proposition was proved first by Alexandre Fernandes [12]. A special case of this is the Arc Criterion of Normal Embedding [11].

Proposition 8.3.13

Let $(X,0)$ and $(Y,0)$ be surface germs. A semialgebraic homeomorphism $\varPhi :(X,0)\to (Y,0)$ preserving the distance to the origin is bi-Lipschitz if, and only if, for any two arcs $\gamma _1,\gamma _2 \in V(X)$ one has

$$\displaystyle \begin{aligned} {} tord(\gamma_1,\gamma_2)=tord(\varPhi(\gamma_1),\varPhi(\gamma_2)). \end{aligned} $$

(8.1)

A special case of Pancake Decomposition for surface germs can be stated as follows:

Theorem 8.3.14

Let $(X,0)$ be a semialgebraic surface germ. Then there exists a decomposition of $(X,0)$ into the germs $(X_i,0)$ such that

• 1. $\cup X_i= X$.

• 2. Each $X_i$ is a LNE $\beta _i$ -Hölder triangle.

• 3. For$i\ne j$, the intersection$X_i \cap X_j$is either the origin or a common boundary arc of$X_i$and$X_j$.

Definition 8.3.15

A pancake decomposition of a surface germ is minimal if the union of any two adjacent Hölder triangles $X_i$ and $X_j$ is not normally embedded. Two pancake decompositions are combinatorially equivalent if they are combinatorially equivalent as Hölder Complexes.

The answer to a natural question “Are any two minimal pancake decompositions of the same surface germ combinatorially equivalent?” is negative (see Sect. 8.5).

8.4 Pizza Decomposition of the Germ of a Semialgebraic Function

This section is related to the outer Lipschitz Geometry of a special kind of a surface germ: The union of a Lipschitz Normally Embedded (LNE) Hölder triangle and the graph of a semialgebraic Lipschitz function defined on it.

Definition 8.4.1

Given a semialgebraic Lipschitz function f defined on a $\beta$-Hölder triangle T, let

$$\displaystyle \begin{aligned} {} Q_{f}(T)=\bigcup_{\gamma\in V(T)}ord_{\gamma} f. \end{aligned} $$

(8.2)

It was shown in [9] that $Q_f(T)$ is either a point or a closed interval in $\mathbb Q\cup \{\infty \}$.

Definition 8.4.2

A Hölder triangle T is elementary with respect to a Lipschitz function f if, for any $q\in Q_f(T)$ and any two arcs $\gamma$ and $\gamma '$ in T such that $ord_{\gamma }f=ord_{\gamma '}f=q$, the order of f is q on any arc in the Hölder triangle $T(\gamma ,\gamma ')\subseteq T$ bounded by the arcs $\gamma$ and $\gamma '$.

Definition 8.4.3

Let T be a Hölder triangle and f a semialgebraic Lipschitz function defined on T. For each arc $\gamma \subset T$, the width$\mu _T(\gamma ,f)$ of the arc $\gamma$ with respect to f is the infimum of exponents of Hölder triangles $T'\subset T$ containing $\gamma$ such that $Q_f(T')$ is a point. For $q\in Q_f(T)$ let $\mu _{T,f}(q)$ be the set of exponents $\mu _T(\gamma ,f)$, where $\gamma$ is any arc in T such that $ord_{\gamma }f=q$. It was shown in [9] that, for each $q\in Q_f(T)$, the set $\mu _{T,f}(q)$ is finite. This defines a multivalued width function$\mu _{T,f}: Q_f(T)\to \mathbb Q\cup \{\infty \}$. If T is elementary with respect to f, then the function $\mu _{T,f}$ is single valued. When f is fixed, we write $\mu _T(\gamma )$ and $\mu _T$ instead of $\mu _T(\gamma ,f)$ and $\mu _{T,f}$.

Definition 8.4.4

Let T be a Hölder triangle and f a semialgebraic Lipschitz function defined on T. We say that T is a pizza slice associated with f if it is elementary with respect to f and, unless $Q_f(T)$ is a point, $\mu _{T,f}(q)=aq+b$ is an affine function on $Q_f(T)$. If T is a pizza slice such that $Q_f(T)$ is not a point, then the supporting arc$\tilde \gamma$ of T with respect to f is the boundary arc of T such that $\mu _T(\tilde \gamma ,f)=\max _{q\in Q_f(T)}\mu _{T,f}(q)$. In that case, $\mu _T(\gamma ,f)=tord(\gamma ,\tilde \gamma )$ for any arc $\gamma \subset T$ such that $tord(\gamma ,\tilde \gamma )\le \mu _T(\tilde \gamma ,f)$.

Definition 8.4.5 (See [9, Definition 2.13])

Let f be a non-negative semialgebraic Lipschitz function defined on a $\beta$-Hölder triangle $T=T(\gamma _1,\gamma _2)$ oriented from $\gamma _1$ to $\gamma _2$. A pizza on T associated with f is a decomposition $\{T_\ell \}_{\ell =1}^p$ of T into $\beta _\ell$-Hölder triangles $T_\ell =T(\lambda _{\ell -1},\lambda _\ell )$ ordered according to the orientation of T, such that $\lambda _0=\gamma _1$ and $\lambda _p=\gamma _2$ are the boundary arcs of T, $T_\ell \cap T_{\ell +1}=\lambda _\ell$ for $0<\ell < p$, and each triangle $T_\ell$ is a pizza slice associated with f.

A pizza $\{T_\ell \}$ on T is minimal if $T_{\ell -1}\cup T_\ell$ is not a pizza slice for any $\ell >1$.

Definition 8.4.6 (See [9, Definition 2.12])

An abstract pizza is a finite ordered sequence $\{q_\ell \}_{\ell =0}^p$, where $q_\ell \in \mathbb Q_{\ge 1}\cup \{\infty \}$, and a finite collection $\{\beta _\ell ,Q_\ell ,\mu _\ell \}_{\ell =1}^p$, where $\beta _\ell \in \mathbb Q_{\ge 1}\cup \{\infty \}$, $Q_\ell =[q_{\ell -1},q_\ell ]\subset \mathbb Q_{\ge 1}\cup \{\infty \}$ is either a point or a closed interval, $\mu _\ell :Q_\ell \to \mathbb Q\cup \{\infty \}$ is an affine function, non-constant when $Q_\ell$ is not a point, such that $\mu _\ell (q)\le q$ for all $q\in Q_\ell$ and $\min _{q\in Q_\ell }\mu _\ell (q)=\beta _\ell$.

Definition 8.4.7

Two pizzas are combinatorially equivalent if the corresponding abstract pizzas are the same.

Theorem 8.4.8 (See [9, Theorem 4.9])

Two non-negative semialgebraic Lipschitz functions f and g defined on a Hölder triangle T are contact Lipschitz equivalent if, and only if, minimal pizzas on T associated with f and g are combinatorially equivalent.

Let $T=T(\gamma _1,\gamma _2)$ and $T'=T(\gamma ^{\prime }_1,\gamma ^{\prime }_2)$ be two normally embedded $\beta$-Hölder triangles. We say that $(T,T')$ is a normal pair if

$$\displaystyle \begin{aligned} {} \begin{aligned} tord(\gamma_1,T')&=tord(\gamma_1,\gamma^{\prime}_1)=tord(\gamma^{\prime}_1,T),\\ {} tord(\gamma_2,T')&=tord(\gamma_2,\gamma^{\prime}_2)=tord(\gamma^{\prime}_2,T). \end{aligned} \end{aligned} $$

(8.3)

For example, a pair $(T, Graph(f))$ considered in this section satisfies this condition. The following question is natural: Let $T=T(\gamma _1,\gamma _2)$ and $T'=T(\gamma ^{\prime }_1,\gamma ^{\prime }_2)$ be a normal pair of semialgebraic $\beta$-Hölder triangles. Is it true that the union $T\cup T'$ is outer Lipschitz equivalent to the union $T\cup Graph(f)$, where f is the distance function $f(x)=dist(x,T')$ defined on T? In the paper [3] the authors give examples when this is not true. This is true, however, when T is elementary with respect to f.

8.5 Outer Lipschitz Geometry, Snakes

Definition 8.5.1

Let $(X,0)$ be a surface germ. An arc $\gamma$ of X is Lipschitz non-singular if there exists a normally embedded Hölder triangle $T \subset X$ such that $\gamma$ is an interior arc of T and $\gamma \not \subset \overline {X\setminus T}$. Otherwise, $\gamma$ is Lipschitz singular. It follows from the pancake decomposition that a surface germ X contains finitely many Lipschitz singular arcs. The union of all Lipschitz singular arcs in X is denoted by $Lsing(X)$. A Hölder triangle $T\subset X$ is non-singular if all interior arcs of T are Lipschitz non-singular.

Definition 8.5.2

If $T=T(\gamma _1,\gamma _2)$ is a non-singular $\beta$-Hölder triangle, an arc $\gamma$ of T is generic if $itord(\gamma _1,\gamma ) = itord(\gamma ,\gamma _2) = \beta$. The set of generic arcs of T is denoted $G(T)$.

Definition 8.5.3

An arc $\gamma$ of a Lipschitz non-singular $\beta$-Hölder triangle T is abnormal if there are two normally embedded Hölder triangles $T'\subset T$ and $T''\subset T$ such that $T'\cap T'' = \gamma$ and $T\cup T'$ is not normally embedded. Otherwise $\gamma$ is normal. The set $Abn(T)$ of abnormal arcs of T is outer Lipschitz invariant.

Definition 8.5.4

A non-singular $\beta$-Hölder triangle T is called a $\beta$-snake if $Abn(T)=G(T)$.

The following important property of snakes can be interpreted as “separation of scales” in outer Lipschitz Geometry.

Lemma 8.5.5

Let T be a $\beta$ -snake, and let $\{T_k\}_{k=1}^p$ be a minimal pancake decomposition of T. Then each $T_k$ is a $\beta$ -Hölder triangle.

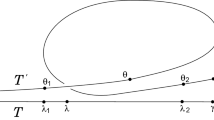
Remark 8.5.6

Minimal pancake decompositions of a snake may be combinatorially non-equivalent, as shown in Fig. 8.3. We use a planar plot to represent the link of a snake. The points in Fig. 8.3 correspond to arcs of the snake. The points with smaller Euclidean distance inside the shaded disks correspond to arcs with the tangency order higher than their inner tangency order $\beta$. Black dots indicate the boundary arcs of pancakes.

Fig. 8.3

Two combinatorially non-equivalent minimal pancake decompositions of a snake. Black dots indicate the boundary arcs of pancakes

Definition 8.5.7

A $\beta$-Hölder triangle T is weakly normally embedded if, for any two arcs $\gamma$ and $\gamma '$ of T such that $tord(\gamma , \gamma ') > itord(\gamma , \gamma ')$, we have $itord(\gamma , \gamma ')=\beta$.

Proposition 8.5.8

Let T be a $\beta$ -snake. Then T is weakly normally embedded.

8.6 Tangent Cones

Definition 8.6.1

The tangent cone$C_0 X$ of a semialgebraic set X at 0 is defined as follows:

$$\displaystyle \begin{aligned} C_0 X=Cone\left(\lim_{\epsilon\to 0}\,\frac 1\epsilon\,\big(X \cap\{|x|=\epsilon\}\big)\right),\end{aligned}$$

where the limit here means the Hausdorff limit.

Remark 8.6.2

There are several equivalent definitions of the tangent cone of a semialgebraic set. In particular, the tangent cone $C_0 X$ can be defined as the set of tangent vectors at the origin to all arcs in X. The tangent cone of a semialgebraic set is semialgebraic.

The tangent cone is Lipschitz invariant:

Theorem 8.6.3 (See [18])

If two germs $(X,0)$ and $(Y,0)$ are outer (resp. ambient) Lipschitz equivalent, then the corresponding tangent cones $C_0 X$ and $C_0 Y$ are outer (resp. ambient) Lipschitz equivalent.

The result is important in Theory of Metric Knots (see [2, 5, 6]) for the proof of Universality Theorem below. This result was also used to prove that, if a complex analytic set is a Lipschitz nonsingular submanifold of ${\mathbb C}^n$, then it is a smooth submanifold [8]. Moreover, the result was used in the recent study of the Zariski Multiplicity Conjecture (see the paper of Fernandes and Sampaio in the present volume).

8.7 Ambient Equivalence: Metric Knots

Definition 8.7.1

Two germs of semialgebraic sets $(X,0)$ and $(Y,0)$ in ${\mathbb R}^n$ are outer Lipschitz equivalent if there exists a homeomorphism $h: (X,0)\to (Y,0)$ bi-Lipschitz with respect to the outer metric. The germs are semialgebraic outer Lipschitz equivalent if the map h can be chosen to be semialgebraic. The germs are ambient Lipschitz equivalent if there exists an orientation preserving bi-Lipschitz homeomorphism $H: ({\mathbb R}^n,0) \to ({\mathbb R}^n,0)$, such that $H(X)=Y$. The germs are semialgebraic ambient Lipschitz equivalent if the map H can be chosen to be semialgebraic.

Definition 8.7.2

The link at the origin$L_X$ of a germ $(X,0)$ in ${\mathbb R}^n$ is the equivalence class of the sets $X\cap S^{n-1}_{0,\varepsilon }$ for small positive $\varepsilon$ with respect to the ambient Lipschitz equivalence. The tangent link of X is the link at the origin of the tangent cone of X.

Remark 8.7.3

By the finiteness theorems of Mostowski, Parusinski and Valette (see [15, 16, 20]) the link at the origin is well defined. We write “the link at the origin” speaking of this notion of the link from Singularity Theory, reserving the word “link” for the notion of the link in Knot Theory. If $n=4$ and X has an isolated singularity at the origin, then each connected component of $L_X$ is a knot in $S^3$.

Definition 8.7.4

A metric knot is an ambient Lipschitz equivalence class of a surface germ $(X,0)$ in ${\mathbb R}^4$ with an isolated singularity and connected link. In particular, the link at the origin of the germ X is an isotopy class of an ordinary topological knot in $S^3$.

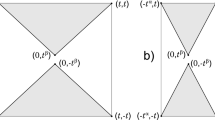
The following result (so called Universality Theorem for metric knots) shows the difference between outer and ambient Lipschitz Geometry of surface germs in ${\mathbb R}^4$:

Theorem 8.7.5 (Universality Theorem)

One can associate to each knot K in $S^3$ a semialgebraic surface germ $(X_K,0)$ in ${\mathbb R}^4$ so that:

• 1. The link at the origin of each germ $X_K$ is a trivial knot;

• 2. All germs $X_K$ are outer Lipschitz equivalent;

• 3. Two germs $X_{K_1}$ and $X_{K_2}$ are ambient semialgebraic Lipschitz equivalent only if the knots $K_1$ and $K_2$ are isotopic.

The idea of a proof is illustrated in Fig. 8.4, representing the link at the origin of a surface germ $X_K$. A detailed explanation can be found in [6].

Fig. 8.4

The proof of Theorem 8.7.5

The following result is a more complicated version of Universality Theorem:

Theorem 8.7.6

For any two knots K and L in $S^3$ , one can associate a semialgebraic surface germ $\tilde X_{KL}$ so that:

• 1. The link at the origin of $\tilde X_{KL}$ is isotopic to L.

• 2. The tangent link of $\tilde X_{KL}$ is isotopic to K.

• 3. All surface germs $\tilde X_{KL}$ are outer bi-Lipschitz equivalent.

The theorem implies, for example, that for a given tangent cone one can find infinitely many outer Lipschitz equivalent, but not ambient Lipschitz equivalent surface germs.