Abstract
We study strong versions of round-optimal MPC. A recent work of Benhamouda and Lin (TCC ’20) identified a version of secure multiparty computation (MPC), termed Multiparty reusable Non-Interactive Secure Computation (MrNISC), that combines at the same time several fundamental aspects of secure computation with standard simulation security into one primitive: round-optimality, succinctness, concurrency, and adaptivity. In more detail, MrNISC is essentially a two-round MPC protocol where the first round of messages serves as a reusable commitment to the private inputs of participating parties. Using these commitments, any subset of parties can later compute any function of their choice on their respective inputs by broadcasting one message each. Anyone who sees these parties’ commitments and evaluation messages (even an outside observer) can learn the function output and nothing else. Importantly, the input commitments can be computed without knowing anything about other participating parties (neither their identities nor their number) and they are reusable across any number of computations.
By now, there are several known MrNISC protocols from either (bilinear) group-based assumptions or from LWE. They all satisfy semi-malicious security (in the plain model) and require trusted setup assumptions in order to get malicious security. We are interested in maliciously secure MrNISC protocols in the plain model, without trusted setup. Since the standard notion of polynomial simulation is un-achievable in less than four rounds, we focus on security with super-polynomial-time simulation (SPS).
Our main result is the first maliciously secure SPS MrNISC in the plain model. The result is obtained by generically compiling any semi-malicious MrNISC and the security of our compiler relies on several well-studied assumptions of an indistinguishability obfuscator, DDH over \({\mathbb Z} ^*_{p}\) and asymmetric pairing groups, and a time-lock puzzle (all of which need to be sub-exponentially hard). As a special case, we obtain the first 2-round maliciously secure SPS MPC based on well-founded assumptions. This MPC is also concurrently self-composable and its first message is short (i.e., its size is independent of the number of the participating parties) and reusable throughout any number of computations. Prior to our work, for two round maliciously secure MPC, neither concurrent MPC nor reusable MPC nor MPC with first message independent in the number of parties was known from any set of assumptions. Of independent interest is one of our building blocks: the first construction of a one-round non-malleable commitment scheme from well-studied assumptions, avoiding keyless hash functions and non-standard hardness amplification assumptions. The full version of this paper can be found at [26].
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
In this work, we study the round complexity of cryptographic protocols, giving special attention to secure multi-party computation (MPC). MPC allows a group of mutually distrusting parties \(P_1, \dots , P_n\), each with private input \(x_i\), to compute the evaluation of some function \(f(x_1, \dots , x_n)\) without revealing their inputs to each other [12, 21, 30].
Round complexity is a fundamental measure of both the efficiency and power of cryptographic protocols. The importance of this measure is strongly grounded in practice: while the bandwidth of modern networks has constantly been increasing, there is a physical lower bound on their latency, imposed by distance and the speed of light. The round complexity of a protocol can also affect its security properties. One very useful property of fully non-interactive and quasi-non-interactiveFootnote 1 arguments is that proofs can be posted to some public bulletin board, like a blockchain, and then any party can later independently verify its validity, even if the original prover is offline. This enables arguments to be recursively composed, which has been used to achieve fundamental new results in the areas of succinct arguments [15], and also to achieve new space and communication efficient secure multi-party computation protocols [25].
The round complexity of MPC protocols in particular has been well-studied over the last few decades. The original MPC construction of [30] was highly round-inefficient, taking a number of rounds proportional to the depth of the circuit for the functionality being computed. Since then, a long line of work [2, 11, 19, 22, 23, 29, 34, 35, 42] has made dramatic improvements, with recent works finally achieving four rounds [2, 19, 22, 23]. This was shown to be optimal by the works of [29, 34], which showed that achieving secure computation in three rounds within the standard regime of black-box polynomial-time simulation is impossible.
In the classical definition of simulation security for MPC protocols, the parties are assumed to run the protocol in an isolated environment, separate from other parties and other executions of protocols. While this definition is simple and elegant, the ubiquity of the internet means that this assumption is not very realistic. The notion of concurrent security fixes this by allowing an adversary to spawn an arbitrary number of parties and executions of a protocol. Unfortunately, the work of [8] showed that concurrent security is impossible in any number of rounds within the standard regime of black-box polynomial-time simulation.
The exciting work of [40] introduced a very useful relaxation of standard polynomial-time simulation, called super-polynomial-time simulation (SPS). In this new definition, the simulator is allowed to run for slightly longer than polynomial-time. This has been used, among other things, to achieve concurrent security for MPC protocols by the works of [20, 28, 37], sidestepping the impossibility result of [8]. In 2017, the work of [7] constructed a concurrent MPC protocol in three rounds, thus bypassing both the lower bounds of [29, 34] and [8] at once. For several years, this has been the state of the art in terms of the round complexity of both MPC and concurrent-secure MPC in the plain model. A very recent work [1] partially advanced the state of the art in terms of round complexity, giving a two-round standalone-secure MPC protocol in the plain model. However, their security proof relies on ad-hoc (exponentially strong) assumptions that are novel to their work, and they do not achieve concurrent security.Footnote 2
An important question, then, is whether concurrent-secure MPC, or even standalone MPC, can be achieved in two rounds in the plain model, without setup, relying on well-studied assumptions. In this work, we study this question.
MrNISC. Going one step further, it is natural to ask whether MPC can be done in one round, with each party sending a single simultaneous message. However, one can very easily show that this is impossible, via the following argument, commonly referred to as the residual function attack. Consider the case of two parties \(P_1\) and \(P_2\), and say that \(P_1\) sends its message \(m_1\). Then \(P_2\) should be able to compute and send her message \(m_2\), so that both parties learn \(f(x_1, x_2)\). However, this means that \(P_2\) can compute \(m_2'\) for any other \(x_2'\) in her head, and learn \(f(x_1, x_2)\) as well. She can do this for arbitrarily many \(x_2'\). This means that parties are able to learn much more than is allowed by a secure MPC protocol. This simple argument also extends to the case of protocols with trusted setup, showing that one-round protocols are also impossible in this case.
This raises the question, how close can we get to a non-interactive protocol without running into this impossibility? We study this question via a recent new strong version of MPC, identified by a recent work by Benhamouda and Lin [14] and termed Multiparty reusable Non-Interactive Secure Computation (MrNISC). MrNISC requires the following general structure:
-
1.
Input encoding: at any time, a party can publish an encoding of its input noninteractively, independent of the number of parties.
-
2.
Computation encoding: At any time, any subset I of parties can jointly compute a function f on their inputs \(x_I = \{x_i\}_{i \in I}\) by broadcasting a single public message. Each party’s message is only dependent on the input encodings of the parties in I.
Parties are allowed to join the system at any time by publishing their input encoding, even after an arbitrary number of computation sessions have occurred.
In this way, MrNISC achieves essentially the best-possible form of non-interactivity for MPC protocols without running into the aforementioned impossibility: once parties have committed to their input, any subset of parties can compute an arbitrary function on their committed inputs via a single round. Note that MrNISC is a strict generalization of two-round concurrent-secure MPC.
Several MrNISC protocols have been constructed in the semi-malicious regime, where security only holds for adversaries who follow the protocol specification.Footnote 3 Benhamouda and Lin [14] constructed such a protocol for all efficiently computable functionalities relying on the DDH assumption in asymmetric bilinear groups. In two concurrent follow-up works, Ananth et al. [3] and Benhamouda et al. [13] obtained MrNISC protocols relying on Learning With Errors (LWE). However, it was unknown whether it is possible to construct MrNISC in the plain model which satisfies the full malicious version of security, where adversaries can deviate arbitrarily from the protocol specification.
1.1 Our Results
In this paper, we give the first affirmative answer to the above question. Specifically, relying on commonly-used, well-established assumptions, we obtain a maliciously secure SPS MrNISC in the plain model, without any trusted setup. In particular, this implies a concurrently secure SPS MPC in two rounds from the same assumptions. We state our (informal) theorem below.
Theorem 1.1
(Main Result, informal). Assume the existence of an indistinguishability obfuscation (iO) scheme which is subexponentially-secure, subexponential DDH (over both asymmetric pairing groupsFootnote 4 and \({\mathbb Z} ^*_{p}\)), and subexponential time-lock puzzles. Then there exists a malicious-secure MrNISC in the plain model, with a super-polynomial simulator.
Key ideas. Our result is obtained via a generic compiler which takes any subexponentially-secure semi-malicious secure MrNISC and upgrades it to malicious security. As mentioned above, the work of [14] showed that such a semi-malicious-secure MrNISC exists assuming subexponential DDH over asymmetric pairing groups. Our transformation relies heavily on the idea of multiple axes of hardness [38], where there are multiple ways to measure the hardness of a problem, such as circuit size and circuit depth. This allows one to define pairs of problems (A, B) where A is simultaneously harder than B (with respect to one axis) and easier than B (with respect to the other). Time-lock puzzles are a well-known way to achieve such scenarios based on circuit size and depth.
Implications for (Classical) MPC. As mentioned, it is possible to view an MrNISC as a standard MPC. Specifically, we get the following:
-
Our MrNISC implies the first concurrent two-round maliciously secure SPS MPC. Indeed, at any point in time, parties can join the protocol by publishing their input encodings and even start evaluation phases. This could happen even after some of the other parties published their input encodings and participated in several evaluation phases. The only previously known malicious (SPS) concurrent MPC required three rounds [7].
-
Our MrNISC implies the first 2-round maliciously secure SPS MPC with a short and reusable first message, based on any assumption. Namely, the first round message is not only independent of the function to be computed (which is necessary for reusability), but it is actually generated independently of the number of participating parties. All prior MPC protocols with this property only satisfy semi-malicious security in the plain model [3, 9, 10, 13, 14].
-
Our MrNISC implies the first 2-round maliciously secure SPS MPC based on well-studied, falsifiable assumptions.
Notable Building Blocks
In the course of obtaining our main result, we achieve two intermediate results, in the areas of zero-knowledge and non-malleable commitments.
First, we give a new definition of two-round zero knowledge, called reusable statistical zero-knowledge with sometimes-statistical soundness. This new type of argument that satisfies both statistical zero knowledge and a weakened form of statistical soundness. (Note that it is well-known that achieving both statistical zero knowledge and full statistical soundness is impossible for all statements in NP unless the polynomial-time hierarchy collapses [41].) We also require a strong form of reusability. We show the following:
Theorem 1.2
(Informal). Assume the existence of a subexponentially-secure indistinguishability obfuscation (iO) scheme, subexponential DDH (over both \({\mathbb Z} ^*_p\) and assymetric pairing groups), and subexponential time-lock puzzles. Then there exists a reusable statistical ZK argument with sometimes-statistical soundness as defined in Definition 5.4.
Second, we give a new one-round non-malleable commitment in the simultaneous-message model under better assumptions than were previously known. This commitment satisfies a strong definition of security called CCA-non-malleability. We prove the following theorem:
Theorem 1.3
(Informal). Assume the existence of a subexponentially-secure indistinguishability obfuscation (iO) scheme, subexponential SXDH, and subexponential time-lock puzzles. Then, there exists a subexponentially-secure one-round CCA commitment scheme supporting a super-polynomial number of tags.
Non-interactive non-malleable commitments were first constructed by the work of [39], using very strong and non-standard assumptions. In particular, their assumption incorporates a strong form of non-malleability into it. The works of [18, 27] were able to obtain constructions based on different assumptions, including (among other things) a rather new assumption called keyless multi-collision-resistant hash functions [16]. This assumption, which is described in more detail below, is still somewhat strong as we do not have any instantiation of it besides using cryptographic hash functions. In contrast, our commitment scheme relies solely on well-established assumptions which have a long history of study.
Our construction is based heavily on and improves upon the work of [36], which achieves a weakened version of one-round non-malleable commitments. In order to achieve our main result, we need full CCA-non-malleable commitments which work in one round, so the construction of [36] will not suffice as-is. We elaborate on this in Sect. 2.
Putting Things Together
Our compiler makes use of these two new tools in order to upgrade security of a semi-malicious MrNISC scheme. Informally, we achieve the following:
Theorem 1.4
(The Compiler, Informal).
Assume the existence of subexponential variants of the following:
-
a reusable two-round statistical zero knowledge argument with sometimes-statistical soundness,
-
a one-round non-malleable commitment,
-
a non-interactive perfectly-binding commitment,
-
a pseudorandom function,
-
a witness encryption scheme for NP,
-
and finally, a semi-malicious MrNISC scheme.
Then, there exists a malicious-secure MrNISC scheme in the plain model, with super-polynomial simulation.
1.2 On the Necessity of iO
We make use of an obfuscation scheme when constructing both our zero knowledge scheme as well as our non-malleable commitment scheme. Also, it is directly used to get the witness encryption scheme. We do not know if iO can be avoided in constructing MrNISC in the plain model.
As mentioned above, constructions of one-round non-malleable commitments exist from other assumptions than iO [18, 39], however these constructions rely on assumptions that are problematic for various reasons. The only known route to avoid these assumptions is via iO [36] but even then previous work failed to achieve one-round protocols.
We now discuss the need in a witness encryption scheme. Intuitively, it seems that some sort of witness encryption for a specific language is required when upgrading security for a semi-malicious MrNISC scheme in the plain model, for the following reason. Since one-round zero knowledge is impossible without setup [31], honest parties are forced to send their second-round semi-malicious MrNISC messages without knowing whether the first round is honest. Sending these messages in the clear would violate security, so the parties must somehow send a “locked” version of their second-round such that they are only revealed conditioned on the first round being honest. Since these messages must be publicly unlockable, this means that the second round is some form of witness encryption. We explain this in more detail in Sect. 2. It is an interesting open question whether it is possible to build a witness encryption scheme for this specific type of statement without relying on iO.
1.3 Related Work
A recent work of Agarwal, Bartusek, Goyal, Khurana, and Malavolta [1] gave the first two-round standalone maliciously secure MPC in the plain model. Although an exciting first step, the result is nonstandard in several ways. First, they require the existence of several primitives (including semi-malicious MPC) which are exponentially secure in the number of parties. Their construction also requires a special type of non-interactive non-malleable commitment. Notably, neither the non-interactive commitments of [18, 32] nor the weakly non-interactive commitments of [36], nor our new one-round non-malleable commitment scheme can be used to instantiate this (because they strongly rely on exponential full security and non-interactivity). The authors of [1] propose two instantiations which work for their construction. One instantiation relies on factoring-based adaptive one-way functions [39],Footnote 5 a strong assumption that incorporates a strong non-malleability flavor. Another instantiation relies on an exponential variant of the “hardness amplifiability” assumption of [18], along with keyless multi-collision resistant hash functions [17]. Both of these assumptions are still highly non-standard:
-
1.
A keyless multi-collision resistant hash function is a single publicly known function for which (roughly) collisions are “incompressible”, namely, it is impossible to encode significantly more than k collisions using only k bits of information. While keyless hash functions are formally a plain-model assumption, there is no known plain-model instantiation based on standard assumptions. The only known instantiation is either in the random oracle model, or by heuristically assuming that some cryptographic hash function, like SHA-256, is such.
-
2.
Hardness amplification assumptions postulate (roughly) that the XOR of independently committed random bits cannot be predicted with sufficiently large advantage. There are concrete (contrived) counter examples for this type of assumptions showing that they are generically false [24], although they certainly might hold for specific constructions.
The specific variant used by Agarwal et al. is novel to their work. It assumes exponential hardness amplification against PPT adversaries, i.e., that there exists a constant \(\delta >0\) such that for large enough \(\ell \), the XOR of \(\ell \) independently committed random bits cannot be predicted by a PPT adversary with advantage better than \(2^{-\ell \delta }\). This assumption (similarly to [39]’s adaptive one-way functions) also incorporates a non-malleability flavor.
Because of this, there is no way to instantiate the protocol of [1] relying on any well-studied assumptions, or even on assumptions not specifically formulated in order to achieve non-malleable commitments. These drawbacks unfortunately seem inherent in the techniques used by [1]. Our work uses a completely different approach from their work, and is thus able to achieve a strictly stronger result, without using ad-hoc assumptions.
2 Technical Overview
In this section, we give an overview of our constructions and the main ideas needed to prove their security. We start by reviewing the syntax of MrNISC, as defined by Benhamouda and Lin [14].
Model and syntax. A MrNISC consists of an input encoding phase done without coordination with other parties in the system (i.e., without even knowing they exist), and an evaluation phase in which only relevant parties participate by publishing exactly one message each. In other words, MrNISC is a strict generalization of 2-round MPC with the following properties:
-
there is no bound on the number of parties;
-
multiple evaluation phases can take place with the same input encodings;
-
parties can join at any point in time and publish their input encoding, even after multiple evaluation phases occurred.
We assume all parties have access to a broadcast channel that parties use to transmit messages to all other parties. The formal syntax of an MrNISC consists of three polynomial-time algorithms \((\textsf{Encode}, \textsf{Eval}, \textsf{Output})\), where \(\textsf{Encode}\) and \(\textsf{Eval}\) are probabilistic, and \(\textsf{Output}\) is deterministic. The allowed operations for a party \(P_i\) are:
-
Input Encoding phase: each party \(P_i\) computes \( m_{i, 1},\sigma _{i,1} \leftarrow \textsf{Encode}(1^\lambda ,x_i)\), where \(x_i\) is \(P_i\)’s private input, \(m_{i,1}\) is \(P_i\)’s round 1 message, and \(\sigma _{i,1}\) is \(P_i\)’s round 1 private state. It broadcasts \(m_{i, 1}\) to all other parties.
-
Function Evaluation phase: any set of parties I can compute an arity-\(|I |\) function f on their respective inputs as follows. Each party \(P_i\) for \(i\in I\) computes \(m_{i,2} \leftarrow \textsf{Eval}(f, \sigma _{i,1}, I, \{m_{j,1}\}_{j\in I})\), where f is the function to compute, \(x_i\) is \(P_i\)’s private input, \(\sigma _{i,1}\) is the private state of \(P_i\)’s input encoding, \(\{m_{j,1}\}_{j\in I}\) are the input encodings of all parties in I, and the output \(m_{i,2}\) is \(P_i\)’s round 2 message. It broadcasts \(m_{i,2}\) to all parties in I
-
Output phase: upon completion of the evaluation phase by each of the participating parties, anyone can compute \(y\leftarrow \textsf{Output}(\{m_{i,1},m_{i,2}\}_{i\in I})\) which should be equal to \(f(\{x_j\}_{j\in I})\).
Security. For security, we require that an attacker does not learn any information beyond what is absolutely necessary, which is the outputs of the computations. Formally, for every “real-world” adversary that corrupts the evaluator and a subset of parties, we design an “ideal world” adversary (called a simulator) that can simulate the view of the real-world adversary using just the outputs of the computations. As in all previous works on MrNISC (including [3, 13, 14]), we assume static corruptions, namely that the adversary commits on the corrupted set of parties at the very beginning of the game. However, all previous works only achieved semi-malicious security (unless trusted setup assumptions are introduced). This notion of security, introduced by Asharov et al. [4], only considers corrupted parties that follow the protocol specification, except letting them choose their inputs and randomness arbitrarily. In contrast, we consider the much stronger and more standard notion of malicious security, which allows the attacker to deviate from the specification of the protocol arbitrarily.
More precisely, in malicious security, the adversary can behave arbitrarily in the name of the corrupted parties. Specifically, after the adversary commits on the corrupted set of parties, it can send an arbitrary round 1 message for a corrupted party, ask for a round 1 message of any honest party (with associated private input), ask an honest party to send the round 2 message corresponding to an evaluation of an arbitrary function on the round 1 message of an arbitrary set of parties, and send an arbitrary round 2 message of a malicious party corresponding to an evaluation of an arbitrary function on the round 1 message of an arbitrary set of parties. The simulator needs to simulate the adversary’s view with the assistance of an ideal functionality that can provide only the outputs of the computations that are being performed throughout the adversary’s interaction.
Typically, protocols are called maliciously secure if for every polynomial-time adversary, there is a polynomial-time simulator for which the real-world experiment and the ideal-world experiment from above are indistinguishable. However, as mentioned, it is impossible to achieve such a notion of malicious security for MPC (let alone MrNISC) in merely two rounds unless trusted setup assumptions are introduced. Therefore, we settle for super-polynomial time simulation (SPS), which means that the simulator can run in super-polynomial time. In contrast, the adversary is still assumed to run in polynomial time.
We refer to Sect. 4 for the precise definition.
Terminology. For the sake of brevity, we will sometimes refer to the input encoding phase as round 1, and the function evaluation phase as round 2.
2.1 The MrNISC Protocol
To obtain our main result, we will start with a semi-malicious-secure MrNISC protocol [13, 14] and introduce modifications to achieve malicious security. Recall that semi-malicious security only guarantees security when the adversary follows the honest protocol specification exactly, except that it can arbitrarily choose corrupted parties’ randomness. We would like to use the following high-level approach used by many classical MPC protocols. During the input encoding phase, we require each party to commit to its input and randomness in addition to publishing a semi-malicious input encoding, and then to prove using zero-knowledge that all of its semi-malicious MrNISC messages were generated by following the prescribed protocol using that committed input and randomness. However, a problem arises when using this strategy with 2-round protocols. (Note that MrNISC requires that evaluation can be carried out in two rounds; in this way, it is a strict generalization of 2-round MPC.) This problem comes from the fact that zero-knowledge in the plain model requires at least two rounds. Assuming we use such a 2-round ZK scheme, honest parties would need to send their second-round MrNISC messages before finding out whether the first-round MrNISC messages were honest. This completely breaks security—if any party publishes semi-malicious messages based on a non-honest transcript, the semi-malicious protocol can make no security guarantees about these messages.
We need some way of overcoming this problem. That is, we need a way to publish second-round messages so that they are only revealed if the first round is honest. To this end, we are going to use witness encryption as a locking mechanism: we “lock” the round 2 message of the underlying (semi-malicious) MrNISC and make sure that it can be unlocked only if all involved parties’ proofs verify. More precisely, party i does:
-
1.
Round 1 message: Commit to its input and randomness and publish a round 1 message using the underlying MrNISC with the committed input/randomness pair. At the same time, generate a verifier’s first-round ZK message for the other parties.
-
2.
Round 2 message: Compute a round 2 message using the underlying MrNISC with randomness derived from the secret state. Generate a zero-knowledge proof that this was done correctly. Publish a witness encryption hiding the aforementioned round 2 message that could be recovered by supplying valid proofs that all other parties’ first-round messages were created correctly.
With this template in mind, even before starting to think about what a security proof will look, it is already evident that there are significant challenges in realizing the building blocks. Here are the three main challenges.
Challenge 1: The ZK argument system. The first challenge arises from trying to use ZK arguments as witnesses for the witness encryption scheme. Recall that witness encryption allows an encryptor to encrypt a message with respect to some statement \(\varPhi \), and only if \(\varPhi \) is false, then the message is hidden. Witness encryption (WE) crucially only can provide security when \(\varPhi \) is false; in particular, if \(\varPhi \) is true, even if it is computationally hard to find a witness for \(\varPhi \), no guarantees are made about the encrypted message being hidden. Thus, it seems like we would need a statistically-sound ZK argument, i.e., a ZK proof: if the verifier’s first-round message is honest, with high probability, there should not exist an accepting second-round ZK message.
It is well-known that to achieve ZK in two rounds, it is necessary to have a simulator that runs in super-polynomial time (i.e., an SPS simulator). In every such known two-round ZK, the simulator works by brute-forcing some trapdoor provided in round 1, and giving proof that “either the statement is true or I found the trapdoor.” Because of the existence of this trapdoor, it would be impossible to make any such ZK argument statistically sound: an unbounded-time machine can always find the trapdoor and prove false statements. So it seems like the ZK scheme needs to satisfy two contradictory requirements: be statistically sound, and be a two-round scheme (which appears to preclude statistical soundness).
Challenge 2: Non-malleability attacks. Since the security of the underlying semi-malicious MrNISC holds only if the adversary knows some randomness for its messages, we need all parties to prove that they know the input and randomness corresponding to their messages. We are aiming for a protocol that can be evaluated in two rounds, so this necessitates using a non-malleable commitment (to prevent an attacker from, say copying the round 1 message of some other party). Unfortunately, non-interactive non-malleable commitments without setup are only known from very strong non-standard assumptions, such as adaptive one-way functions [39], hardness amplifiability [1, 18], and/or keyless hash functions [17, 18, 38]. These are very strong and non-standard assumptions, for some of which we have no plain-model instantiation, except heuristic ones. Thus, we want to achieve a secure MrNISC protocol (in the plain model) without such strong assumptions.
Challenge 3: Adaptive reusability of the primitives. We emphasize that we are building an MrNISC protocol, which significantly strengthens standalone two-round MPC. Because of this, our ZK argument and commitment schemes must satisfy strong forms of reusability. There are several challenges in ensuring both the ZK argument and non-malleable commitment scheme satisfy the types of reusability that we need, and we introduce several new ideas to solve these challenges. We will elaborate on this challenge below after we describe our ideas for solving challenges 1 and 2.
Solving Challenge 1: How Do We Get a “statistically-Sound” SPS ZK?
We now discuss how to achieve the seemingly contradictory requirements of getting a 2-round SPS ZK argument which has a statistical soundness property that would allow it to be a witness for the WE scheme. Our key idea is to relax the notion of statistical soundness to one that is obtainable in two rounds but still sufficient to use with WE.
Imagine we have a WE scheme where the distinguishing advantage of an adversary is tiny (say, subexponential in \(\lambda \)). It would then suffice to have a ZK protocol that is statistically sound a negligible fraction of the time, as long as it is quite a bit larger than the distinguishing advantage of the WE. In more detail, consider a hypothetical zero-knowledge protocol with the following properties:
-
The first round between a computationally-bounded verifier and a prover fully specifies one of the two possible “modes”: a statistical ZK mode and a perfectly sound mode.
-
The perfectly sound mode occurs with some negligible probability \(\epsilon \), and in this mode, no accepting round 2 message exists for any false statement
-
In the statistical ZK mode (which occurs with overwhelming probability \(1-\epsilon \)), the second message is simulatable by an SPS machine and a simulated transcript is statistically indistinguishable from a normal transcript.
-
Furthermore, it is computationally difficult for a malicious prover to distinguish between the two modes.
If we had such a ZK protocol, it would enable us to argue hiding of the witness encryption scheme whenever the first round of the protocol is not honest. The idea of this argument is as follows. Suppose an adversary could learn something about the second-round messages from their witness encryptions in some world where the first round was not honest. In that case, it should also be able to do so even in the perfectly-sound mode (otherwise, it would distinguish the modes). But in this mode, proofs for false statements do not exist; thus, the witness encryption provides full security. Even though this mode happens with negligible probability, it is still enough to contradict witness encryption security, whose advantage is much smaller.
To construct this new ZK scheme, we use ideas that are inspired by the extractable commitment scheme of Kalai, Khurana, and Sahai [33]. This commitment scheme has the property that it is extractable with some negligible tunable probability but is also statistically hiding. This commitment was used in the works of [6] to get a two-round statistical zero-knowledge argument with super-polynomial simulation. To instantiate our new “sometimes perfectly-sound” ZK argument, we use the protocol of [6] as a starting point, but we will need to make significant modifications. Namely, to force a well-defined perfect soundness mode, we will make the first round of this protocol a “simultaneous-message” round, where both the prover and the verifier send a message. We elaborate further on this and other key ideas used in our construction in the full version of the paper [26].
We note an important subtlety in this new definition and our construction. Namely, the statistical ZK and perfect soundness properties only hold with respect to the second round. If the verifier is unbounded-time, then after seeing a first-round prover’s message, it can send a first-round verifier’s message that forces perfect soundness all the time and thus disallows any prover from giving a simulated proof. On the other hand, if the prover is unbounded-time, then after seeing a first-round verifier’s message, it can send a first-round prover’s message, which causes the probability \(\epsilon \) of the perfect soundness mode to be 0. Thus the frequency of perfect soundness mode and the ability of the simulator to give a simulated proof depend on the first round being generated by computationally bounded machines.
Solving Challenge 2: How Do We Avoid Non-interactive Non-malleability?
To solve challenge two, we must somehow get a non-malleable commitment (NMC) scheme which can be executed in the first round without using strong assumptions such as keyless hash functions, hardness amlifiability, or adaptive one-way functions. Recall that unfortunately, all known instantiations of non-interactive NMCs (for a super-polynomial number of tags) currently require the use of (some combination of) these strong assumptions, so it seems at first glance that avoiding them would require making substantial progress on the difficult and well-studied question of non-interactive NMCs.
Our approach to solving this problem is inspired by the exciting work of Khurana [36], which builds a new type of commitment that works as follows. The commitment phase is similar to a non-interactive commitment in that the only communication from the committer is a first-round message C. The role of the receiver is slightly different: The receiver chooses a random string \(\tau \) internally, and it is both C and \(\tau \) together that truly defines the commitment (and, correspondingly, the underlying value being committed to). Consequently, to compute an opening, the committer must receive a \(\tau \) from the receiver. Non-malleability (and binding) hinges upon the fact that the \(\tau \) chosen by the receiver is chosen after seeing the commitment. (See the left diagram below for an illustration of this scheme.) Crucially, this commitment can be constructed from well-founded assumptions (indistinguishability obfuscation, time-lock puzzles, and OWPs), bypassing the need for the strong assumptions discussed earlier (Fig. 1).
The diagram on the left depicts the communication pattern of Khurana’s [36] commitment scheme, whereas the diagram on the right depicts ours. The key difference is that in our scheme, the receiver’s message and the sender’s messages can be sent simultaneously, while in [36] the receiver’s message must be sent after the sender’s message.
We would like to use this commitment scheme in our protocol. There are two main issues that arise.
-
First, to use this scheme, we would need the commitment phase to happen entirely in the first round. Namely, the receiver must publish \(\tau \) simultaneously while the committer is publishing C. (See the right-hand diagram above.) In particular, in the security proof, we need to handle the case of malicious committers who publish C after seeing the round-1 \(\tau \).
-
Second, our goal is to have every party use this commitment to commit to their input and randomness for the protocol. Recall that in the scheme of [36], a well-defined commitment \((C_j, \tau _i)\) consists of both the committer’s message \(C_j\) and the receiver’s random string \(\tau _i\). Although honest parties \(P_j\) will always provide commitments \(C_j\) which are consistent across all \(\tau _i\), it is perfectly plausible for a corrupted party to publish some \(C_j\) where different \(\tau _i\) yield commitments \((C_j, \tau _i)\) to different values.
Solving the first issue involves identifying some technical challenges in the security proof of [36] and making changes to the protocol to avoid these issues. Because of this issue, the non-malleable commitment of [36] is really a two round commitment scheme. In this paper, relying on the axis of hardness given by a time-lock puzzle that we additionally use as an assumption, we construct a truly one round non-malleable commitment scheme, in the simultaneous message model. For the second issue, we use a surprisingly simple idea of adding a standard (potentially malleable) perfectly biding commitment scheme (e.g., Blum’s commitment) at the MrNISC protocol level, we can use this NMC scheme even though it does not satisfy the standard notion of binding. A more detailed technical overview of the non-malleable commitment scheme, as well as the formal construction, can be found in the full version of the paper [26].
Solving Challenge 3: How Do We Get Reusability?
We now describe the challenges which arise when trying to get the type of reusability required by MrNISC. The main problem is to ensure that all of the building blocks we use (i.e., the ZK scheme and the NMC scheme) support the reuse of their first-round message. It turns out that the non-malleable commitment we described in the previous section can be adapted to this reusable setting without much modification. However, several challenges arise when adapting the sometimes-statistically-sound ZK scheme, which we discussed earlier, to the reusable setting. We focus on these challenges here.
Recall that the ZK scheme is a simultaneous message protocol, so a transcript consists of three messages of the form \((\textsf{zk}_{1,P}, \textsf{zk}_{1,V}, \textsf{zk}_{2,P})\), a round-1 message of the prover and the verifier, and a round-2 message of the prover. What we need is for any prover to be able to publish a single \(\textsf{zk}_{1,P}\) in round 1, which can be used in many different sessions with respect to many different \(\textsf{zk}_{1,V}\) messages. In addition, we require a very strong form of reusability: even if a malicious verifier sees an entire transcript \((\textsf{zk}_{1,P}, \textsf{zk}_{1,V}, \textsf{zk}_{2,P})\), and then chooses a new verifier’s first-round message \(\textsf{zk}_{1,V}'\), zero-knowledge should still hold when the prover publishes a proof with respect to \(\textsf{zk}_{1,V}'\) and the prover’s original message \(\textsf{zk}_{1,P}\). Similarly, a verifier should be able to publish a single \(\textsf{zk}_{1,V}\) which can be used in many different sessions with respect to many different \(\textsf{zk}_{1,P}\) messages, and the soundness properties of the ZK scheme should still hold.
Note that it is not immediately clear whether this reusability for ZK arguments are implied by a corresponding non-reusable version of ZK arguments. This turns out not to be the case. To satisfy reusability, we end up having to make several changes to our (non-reusable) sometimes-perfectly-sound ZK scheme. We again describe this in more detail in the full version of the paper [26].
Putting Things Together
We now have the main pieces that we will use to construct a malicious-secure MrNISC: the two-round sometimes-statistically-sound ZK, receiver-assisted one-round CCA-secure commitment, and the underlying semi-malicious MrNISC. Significant challenges arise when attempting to combine these pieces in the way described earlier to get a malicious MrNISC protocol. To see this, it will be convenient to briefly mention the approach we take for the security proof.
A simplified version of the sequence of hybrids we use is as follows. First, we extract the value underlying the commitments and check if anyone acted dishonestly. If so, we switch the honest parties’ witness encryptions to encrypt 0 rather than the actual round 2 messages (this is hybrid 1). Second, we simulate the ZK proof (this is hybrid 2). Third, we switch the underlying value in the commitment to 0 (this is hybrid 3). Once the commitments are independent of the true input, we can use the simulator of the underlying MrNISC (this is hybrid 4). The last hybrid is identical to our simulator.
To make the transitions between the hybrids possible, we need to set the hardness of every primitive carefully. Each hybrid indistinguishability induces some hardness inequality for the involved primitives. Unfortunately, the inequalities seem to be in contradiction to each other. Observe that for the first indistinguishability (between hybrid 0 and hybrid 1), we need our ZK argument’s soundness properties to hold against adversaries who can run the CCA extractor. That is,
For the transition between hybrid 2 to 3, we need to guarantee that the security of the commitment scheme holds even against an adversary that can run the ZK simulator. That is,
Together, the above two inequalities imply that it is necessary to have \(T_\textsf{ZKSim} \ll T_{\textsf{sound}}\). But this is impossible, at least using the techniques we use in constructing the ZK argument. Our simulator works by brute-forcing the verifier’s \(\textsf{zk}_{1, V}\) message to obtain some secret and produces proofs with this knowledge. In other words, whoever has the secret can produce accepting proofs without knowing a witness—this is essentially an upper bound on the soundness of the scheme, i.e., \(T_{\textsf{sound}} \ll T_\textsf{ZKSim}\), which means that our inequalities cannot be satisfied at the same time.
To solve this problem, we introduce another axis of hardness, namely, circuit depth. In particular, assume that it is possible to run the ZK simulator in some super-polynomial depth d. To do this, we would have to construct a ZK argument where the secret embedded in \(\textsf{zk}_{1,V}\) is extractable in depth d. Further, assume that in polynomial depth, it is extremely hard to extract the secret from \(\textsf{zk}_{1,V}\) (much harder than size d). We can use such a ZK argument to solve the problem above. Namely, we can restrict the reduction for hybrids 0 and 1 to run in polynomial depth, and in this complexity class, it holds that \( T_{\textsf{extractor}} \ll T_{\textsf{sound}}\). For the reduction for hybrids 2 and 3, we will allow the depth to be d, in which case the inequality \( T_{\textsf{ZKSim}} \ll T_{\textsf{extractor}}\) is satisfied.
So we have reduced this problem to constructing a ZK argument which is simulatable in some super-polynomial depth d and whose soundness holds against size much larger than d as long as the depth is restricted to be polynomial. It turns out that it is possible to modify our original ZK argument to satisfy this property. We describe how to do this in the full version [26].
Several more minor technical issues arise when putting things together. One such problem is that of “simulation soundness,” that is, we need to guarantee that the adversary cannot give valid ZK arguments for false statements even if it sees simulated arguments from the honest parties. We solve this issue using techniques from the work of [7]. At a very high level, if we use a ZK argument where the simulated proofs are indistinguishable from normal proofs even to an adversary who is powerful enough to run the simulator itself, and if we commit to the witnesses using a non-malleable commitment, it is possible to design a sequence of hybrids that guarantees simulation soundness.
This and other minor technical details result in a construction and sequence of hybrids that are slightly more involved than the simplified version presented in this overview. We refer the reader to Sect. 6 for details.
3 Preliminaries
For any distribution \(\mathcal {X}\), we denote by \(x \leftarrow \mathcal {X}\) the process of sampling a value x from the distribution \(\mathcal {X}\). For a set X we denote by \(x \leftarrow X\) the process of sampling x from the uniform distribution over X. For an integer \(n \in \mathbb {N}\) we denote by [n] the set \(\{1,..,n\}\). A function \(\textsf{negl}: \mathbb {N} \rightarrow \mathbb {R}\) is negligible if for every constant \(c >0\) there exists an integer \(N_c\) such that  for all
for all  . Throughout, when we refer to polynomials in security parameter, we mean constant degree polynomials that take positive value on non-negative inputs. We denote by
. Throughout, when we refer to polynomials in security parameter, we mean constant degree polynomials that take positive value on non-negative inputs. We denote by  an arbitrary polynomial in
an arbitrary polynomial in  satisfying the above requirements of non-negativity.
satisfying the above requirements of non-negativity.
Throughout this paper, all machines are assumed to be non-uniform. We will use \(\lambda \) to denote the security. We will use PPT as an acronym for “probabilistic (non-uniform) polynomial-time”. In addition, we use the notation \(T_1 \ll T_2\) (or \(T_2 \gg T_1\)) if for all polynomials p, \(p(T_1) < T_2\) asymptotically.
The statistical distance between two distributions X and Y over a discrete domain \(\varOmega \) is defined as \(\varDelta (X,Y) = (1/2)\cdot \sum _{\omega \in \varOmega } |\Pr [X=\omega ] - \Pr [Y=\omega ]|\).
\((\mathcal {C},\epsilon )\)-indistinguishability. By \(\mathcal {C}\) we denote an abstract class of adversaries, where each adversary \(\mathcal {A}\in \mathcal {C}\) grows in some complexity measure (i.e. size, depth, etc.) based on the security parameter \(\lambda \). Security definitions will always hold with respect to some class of adversaries which we will specify.
Definition 3.1
( \((\mathcal {C},\epsilon )\)-Indistinguishability). Let \(\epsilon : \mathbb {N}\rightarrow (0,1)\) be a function. We say that two distribution ensembles \({\mathcal X} = \{{\mathcal X} _\lambda \}_{\lambda \in \mathbb {N}}\) and \({\mathcal Y} = \{{\mathcal Y} _\lambda \}_{\lambda \in \mathbb {N}}\) are \((\mathcal {C}, \epsilon )\)-indistinguishable if for any adversary \({\mathcal A} \in \mathcal {C}\), for any polynomial \(\textsf{poly} \), and any \(\lambda \in \mathbb N\),

We use the shorthand \({\mathcal X} \approx _{(\mathcal {C},\epsilon )}{\mathcal Y} \) to denote this. If \({\mathcal A} \) is unbounded time then we say that \({\mathcal Y} \) and \({\mathcal X} \) are statistically indistinguishable and we write \({\mathcal X} \approx _{(\infty ,\epsilon )}{\mathcal Y} \), or alternately \(\varDelta ({\mathcal X}, {\mathcal Y}) \le \epsilon \). (This corresponds to the standard definition of statistical distance.)
4 MrNISC Syntax and Security
We define the syntax of MrNISC and formalize security notions for malicious adversaries as well as semi-malicious adversaries, following the general framework given by Benhamouda and Lin [14].
We assume all parties have access to a broadcast channel, which any party can transmit a message to all other parties. We consider protocols given in the form of three polynomial-time algorithms \((\textsf{Encode}, \textsf{Eval}, \textsf{Output})\), where \(\textsf{Encode}\) and \(\textsf{Eval}\) are probabilistic, and \(\textsf{Output}\) is deterministic, for which we define the syntax as follows:
-
Input Encoding phase: each party \(P_i\) computes \( m_{i, 1} \leftarrow \textsf{Encode}(1^\lambda ,x_i; r_{i,1})\), where \(x_i\) is \(P_i\)’s private input, and the output \(m_{i,1}\) is \(P_i\)’s round 1 message.
-
Function Evaluation phase: any set of parties I can compute an arity-\(|I |\) function f on their respective inputs as follows. Each party \(P_i\) for \(i\in I\) computes \(m_{i,2} \leftarrow \textsf{Eval}(f, x_i, r_{i,1}, I, \{m_{i,1}\}_{i\in I}; r_{i,2})\), where f is the function to compute, \(x_i\) is \(P_i\)’s private input, \(r_{i,1}\) is the randomness which \(P_i\) used to generate its input encoding, \(\{m_{i,1}\}_{i\in I}\) are the input encodings of all parties in I, and the output \(m_{i,2}\) is \(P_i\)’s round 2 message.
-
Output phase: Anyone can compute \(y\leftarrow \textsf{Output}(\{m_{i,1},m_{i,2}\}_{i\in I})\).
Malicious Security. We follow the standard real/ideal paradigm in the following definition. An MrNISC scheme is malicious-secure for every PPT adversary \({\mathcal A} \) in the real world there exists an ideal-world adversary \({\mathcal S} \) (the “simulator”) such that the outputs of the following two experiments \(\textsf{Expt}^{\textsf{Real}}_{{\mathcal A}} (\lambda )\) and \(\textsf{Expt}^{\textsf{Ideal}}_{\mathcal {A}, \mathcal {S}} (\lambda )\) are indistinguishable.
In the following, for ease of exposition, we assume that each party sends at most one computation encoding for any (f, I) pair, and that parties ignore any subsequent computation encodings.
Real Experiment \(\textsf{Expt}^{\textsf{Real}}_{{\mathcal A}}(\lambda , z)\).The experiment initializes the adversary \({\mathcal A} \) with security parameter \(1^\lambda \) and auxiliary input z. In addition, the experiment initializes an empty list \(\mathsf {honest\_outputs}\). \({\mathcal A} \) chooses the number of parties M and the set of honest parties \(H \subseteq [M]\). \({\mathcal A} \) then submits queries to the experiment in an arbitrary number of iterations until it terminates. In every iteration k, it can submit one query of one of the following four types.
-
Corrupt Input Encoding: The adversary \({\mathcal A} \) can corrupt a party \(i\notin H\) and send an arbitrary first message \(m_{i,1}^*\) on its behalf.
-
Honest Input Encoding: The adversary \({\mathcal A} \) can choose an input \(x_i\) for honest party i and ask a party \(i\in H\) to send its first message by running \(m_{i,1}^* \leftarrow \textsf{Encode}(1^\lambda ,x_i; r_{i,1})\), where \(r_{i,1}\) is freshly chosen randomness. This \(m_{i,1}^*\) is sent to the adversary.
-
Honest Computation Encoding: The adversary \({\mathcal A} \) can ask an honest party \(i\in H\) to evaluate a function f on the inputs of parties I. If all first messages of parties in I are already published, party i computes and publishes \(m_{i, 2}^* \leftarrow \textsf{Eval}(f, x_i, I, r_{i,1}, \{m^*_{i,1}\}_{i\in I}; r_{i,2})\). Otherwise, the party instead publishes \(\bot \).
-
Corrupt Computation Encoding: The adversary can send an arbitrary function evaluation encoding \(m^*_{i,2}\) to the honest parties on behalf of some corrupted party \(i \notin H\) with respect to some function f and set I. If all parties in I have sent their \(\textsf{Eval}\) messages for (f, I), the experiment adds the honest parties’ output \((f,I,\textsf{Output}(\{m^*_{i,1}, m^*_{i,2}\}_{i \in I}))\) to the list \(\mathsf {honest\_outputs}\).
The output of the real experiment is defined to be \((\textsf{view}_\mathcal {A}, \tau , \mathsf {honest\_outputs})\), where \(\textsf{view}_\mathcal {A}\) is the output of \(\mathcal {A}\) at the end of the computation, i.e. an arbitrary function of its view, \(\tau \) is the transcript of queries sent by \(\mathcal {A}\) along with the experiment’s responses, and \(\mathsf {honest\_outputs}\) is the list defined above.
Ideal Experiment \(\textsf{Expt}^{\textsf{Ideal}}_{{\mathcal A}, \mathcal {S}}(\lambda ,z)\). The ideal experiment initializes \(\mathcal {A}\) with security parameter \(1^\lambda \) and auxiliary input z. After \(\mathcal {A}\) chooses the number of parties M and the set \(H \subsetneq [M]\), the experiment initializes \(\mathcal {S}\) with \(1^\lambda \), M, and H. In addition, the experiment initializes an empty list \(\mathsf {honest\_outputs}\). Subsequently, the adversary can make the same queries as in the real world, which are handled as follows:
-
Corrupt Input Encoding: When \(\mathcal {A}\) sends a first message \(m_{i,1}^*\) on behalf of some party \(i \notin H\), the experiment forwards this encoding to \(\mathcal {S}\), who responds with an extracted input \(x_i\). \(\mathcal {S}\) also has the option to declare that \(P_i\)’s input is \(\bot \), which means that \(\mathcal {S}\) was not able to extract an input from \(m_{i,1}^*\) (for example, if the adversary sends a bogus string as its message). The experiment then sends \(x_i\) (if it is not \(\bot \)) to the ideal functionality to be used as the input for party i.
-
Honest Input Encoding: When the adversary \({\mathcal A} \) chooses honest input \(x_i\) and asks party \(i\in H\) to send its first message, the experiment sends \(x_i\) to the ideal functionality to be used as the input for party i. The experiment then sends the index i (but not \(x_i\)) to the simulator \(\mathcal {S}\), who generates a simulated honest input encoding \(\tilde{m}_{i,1}\). This encoding is forwarded back to \(\mathcal {A}\).
-
Honest Computation Encoding: When the adversary \({\mathcal A} \) asks an honest party \(i\in H\) for a function evaluation encoding with respect to function f and parties I, assuming all parties in I have published input encodings, the experiment forwards this request to \(\mathcal {S}\). If this is the last honest computation encoding generated with respect to f and I, and all corrupted parties in \(j \in I \setminus H\) have sent first messages \(m_{j,1}^*\) from which non-\(\bot \) inputs have been extracted, then the experiment queries the ideal functionality on (f, I) to obtain the output y, which it forwards to the simulator as well. The simulator must then generate a simulated function evaluation encoding \(\tilde{m}_{i,2}\) on behalf of party i, regardless of whether it receives y or not. This encoding is forwarded to \(\mathcal {A}\).
-
Corrupt Computation Encoding: When the adversary sends a function evaluation encoding \(m^*_{i,2}\) on behalf of some corrupted party corresponding to some (f, I), the experiment forwards \((f, I, i, m^*_{i,2})\) to the simulator. If all parties have sent computation encodings, the simulator chooses whether to allow the honest parties to learn the output corresponding to (f, I). If so, the experiment adds (f, I, y) to the list \(\mathsf {honest\_outputs}\); otherwise, the experiment adds \((f, I, \bot )\) to \(\mathsf {honest\_outputs}\).
The output of the ideal experiment is defined to be \((\widehat{\textsf{view}}, \tau , \mathsf {honest\_outputs})\), where \(\widehat{\textsf{view}}\) is the output of \(\mathcal {A}\) at the end of the experiment, \(\tau \) is the transcript of queries made by \(\mathcal {A}\) along with the experiment’s responses, and \(\mathsf {honest\_outputs}\) is the list defined above. In addition, at any point in the experiment, \(\mathcal {S}\) may choose to abort; in this case, the output of the experiment is whatever \(\mathcal {S}\) outputs at that point.
Definition 4.1
(\((\mathcal {C}_{\textsf{adv}}, \mathcal {C}_{\textsf{sim}},\epsilon )\)-Maliciously Secure MrNISC). We say that an MrNISC protocol \(\varPi \) is \((\mathcal {C}_{\textsf{adv}}, \mathcal {C}_{\textsf{sim}},\epsilon )\)-maliciously secure if for every \(\mathcal {C}_\textsf{adv}\) adversary \((\mathcal {A}, \mathcal {D})\) there exists a \(\mathcal {C}_\textsf{sim}\) ideal-world adversary \(\mathcal {S}\) (i.e., the simulator) such that for every string z,
The standard notion of security requires for every polynomial \(p(\cdot )\) the existence of a polynomial \(q(\cdot )\) for which the protocol is \((p, q, \epsilon )\)-maliciously secure, where \(\epsilon (\cdot )\) is a negligible function. However, since we are interested in two-round protocols, it is known that the standard polynomial notion of security is impossible. Therefore, we focus on the relaxed notion of super-polynomial security (SPS): there is a sub-exponential function \(q(\cdot )\) such that for all polynomials \(p(\cdot )\), the protocol is \((p, q,\epsilon )\)-maliciously secure.
The Semi-malicious Case. We define a variant of the above security definition, which closely mirrors the definition of semi-malicious secure multiparty computation [5]. A semi-malicious MrNISC adversary is modeled as an algorithm which, whenever it sends a corrupted input or computation encoding on behalf of some party \(P_j\), must also output some pair (x, r) which explains its behavior. More specifically, all of the protocol messages sent by the adversary on behalf of \(P_j\) up to that point, including the message just sent, must exactly match the honest protocol specification for \(P_j\) when executed with input x and randomness r. Note that the witnesses given in different rounds need not be consistent. We also allow the adversary to “abort” a function evaluation in two different scenarios. First, instead of sending a Corrupt Input Encoding message for \(P_j\), the adversary can send \((j, \bot )\) to the experiment. In this case, the experiment will respond with \(\bot \) for all Honest Computation Encoding requests for (f, I), and when all parties in I have been queried, it will add \((f, I, \bot )\) to \(\mathsf {honest\_outputs}\). Second, instead of sending a Corrupt Computation Encoding message on behalf of \(P_j\) the adversary can again send \((j, f, I, \bot )\). Again, after receiving such a query, the experiment will respond with \(\bot \) for all Honest Computation Encoding requests for (f, I), and when all parties in I have been queried, it will add \((f, I, \bot )\) to \(\mathsf {honest\_outputs}\).
I have published computation encodings for (f, I). In this sense, the adversary may abort any individual function evaluation. Whenever an adversary aborts a Corrupt Input Encoding message on behalf of party \(P_j\), it must abort any subsequent Corrupt Computation Encoding messages for \(P_j\).
Definition 4.2
( \((\mathcal {C}_{\textsf{adv}}, \mathcal {C}_{\textsf{sim}},\epsilon )\)-Semi-Malicious Secure MrNISC). We say that an MrNISC protocol \(\varPi \) is \((\mathcal {C}_{\textsf{adv}}, \mathcal {C}_{\textsf{sim}},\epsilon )\)-semi-malicious secure if for every \(\mathcal {C}_\textsf{adv}\) semi-malicious adversary \((\mathcal {A}, \mathcal {D})\) there exists \(\mathcal {C}_\textsf{sim}\) ideal-world adversary \(\mathcal {S}\) (i.e., the simulator) such that for every string z,
5 Main Building Blocks
In this section, we give formal definitions for our new notion of reusable sometimes-statistically-sound zero-knowledge arguments along with the receiver-assisted one-round CCA-secure commitments, both of which we make use of in our MrNISC protocol.
5.1 Reusable Statistical ZK Arguments with Sometimes-Statistical Soundness
We define statistical zero-knowledge arguments with a specific communication pattern. The protocol that we need has a “simultaneous message” first round, where both the prover and verifier will simultaneously send a message. The syntax is the following:
-
1.
The (honest) prover \(P = (\textsf{ZKProve}_1,\textsf{ZKProve}_2)\) and verifier \(V=(\textsf{ZKVerify}_1,\textsf{ZKVerify}_2)\) are each composed of two uniform PPT algorithms.
-
2.
\(\textsf{ZKProve}_1\) and \(\textsf{ZKVerify}_1\) get as input only the security parameter \(\lambda \). \(\textsf{ZKProve}_1\) outputs a message \(\textsf{zk}_{1,P}\) and a state \(\sigma _P\). \(\textsf{ZKVerify}_1\) outputs a message \(\textsf{zk}_{1,V}\) and a state \(\sigma _V\). The first round transcript is denoted \(\tau _1=(\textsf{zk}_{1,P}, \textsf{zk}_{1,V})\).
-
3.
\(\textsf{ZKProve}_2\) gets \(\sigma _P\), \(\textsf{zk}_{1,V}\), the instance x, and a witness w. It outputs a message \(\textsf{zk}_{2,P}\).
-
4.
\(\textsf{ZKVerify}_2\) gets the instance x and \(\tau = (\tau _1,\textsf{zk}_{2,P})\), and outputs 0/1.
Looking ahead, we shall consider two-round ZK protocols as above with super-polynomial simulation (SPS), i.e., the simulator can run longer than the soundness bound. Further, we will also require that for a given prover and a verifier, the first message is reusable for proving multiple statements. We denote  the output of the interaction between P and V, where P gets as input the witness w, and both P and V receive the instance x as a common input.
the output of the interaction between P and V, where P gets as input the witness w, and both P and V receive the instance x as a common input.
Definition 5.1
(Reusable Statistical Zero-Knowledge Arguments with Sometimes-Statistical Soundness). Let L be a language in \(\textsf{NP}\) with a polynomial-time computable relation \(R_L\). A protocol between P and V is a \((\mathcal {C}_\textsf{sound}, \mathcal {C}_{\mathcal {S}}, \mathcal {C}_{\textsf{zk}}, \epsilon _{\textsf{sound},1},\epsilon _{\textsf{sound},2}, \epsilon _{\mathcal {S}})\)-reusable statistical zero-knowledge argument with sometimes-statistical soundness if it satisfies Definitions 5.2 to 5.4 below.
Definition 5.2
(Perfect Completeness). Let L be a language in \(\textsf{NP}\) with a polynomial-time computable relation \(R_L\). A protocol between P and V satisfies perfect completeness if for every security parameter  and \((x,w) \in R_L\), it holds that
and \((x,w) \in R_L\), it holds that 
where the probability is over the random coins of P and V.
Additionally, we need a refined soundness property, defined next.
Definition 5.3
(\((\mathcal {C}_\textsf{sound}, \epsilon _{\textsf{sound},1},\epsilon _{\textsf{sound},2})\)-statistical soundness). Consider any prover \(P^*\in \mathcal {C}_{\textsf{sound}}\) and a polynomial \(p(\cdot )\), where on input the security parameter  , \(P^*\) outputs an instance \(x\in \{0,1\}^p \setminus L\). We require that there exists a “soundness mode indicator” machine \(\mathcal {E}\) that on input \((\tau _1, \textsf{state}_V)\) outputs either 0 or 1 such that the following properties hold.
, \(P^*\) outputs an instance \(x\in \{0,1\}^p \setminus L\). We require that there exists a “soundness mode indicator” machine \(\mathcal {E}\) that on input \((\tau _1, \textsf{state}_V)\) outputs either 0 or 1 such that the following properties hold.
-
Frequency of Soundness Mode. For every prover \(P^* \in \mathcal {C}_{\textsf{sound}}\),
 where the probability is over the coins of the prover and the verifier in round 1.
where the probability is over the coins of the prover and the verifier in round 1. -
Perfect Soundness Holds During Soundness Mode. For every prover \(P^*\in \mathcal {C}_{\textsf{sound}}\) and every round-1 state \((\tau _1, \textsf{state}_{P^*}, \textsf{state}_V)\) of the protocol, if \(\mathcal {E}(\tau _1, \textsf{state}_V) = 1\) then for all second-round messages \(\textsf{zk}_{2,P}\) sent by the prover corresponding to some false statement \(x \not \in L\), the verifier rejects on input \((x, \tau _1, \textsf{zk}_{2,P}, \textsf{state}_V)\).
-
Indistinguishability of Soundness Mode. For every prover \(P^*\in \mathcal {C}_{\textsf{sound}}\), it holds that
$$\{(\tau _1, \textsf{state}_{P^*}) \mid \mathcal {E}(\tau _1, \textsf{state}_V)=1\}$$$$\approx _{(\mathcal {C}_{\textsf{sound}}, \epsilon _{\textsf{sound},2})}$$$$\{(\tau _1, \textsf{state}_{P^*}) \mid \mathcal {E}(\tau _1, \textsf{state}_V)=0\}.$$
The full MrNISC protocol needs a powerful version of zero knowledge, as follows:
Definition 5.4
(\((\mathcal {C}_{\mathcal {S}}, \mathcal {C}_{\textsf{zk}}, \epsilon _{\mathcal {S}})\)-Adaptive Reusable Statistical Zero-Knowledge). We say a zero knowledge scheme satisfies \((\mathcal {C}_{\mathcal {S}}, \mathcal {C}_{\textsf{zk}}, \epsilon _{\mathcal {S},1}, \epsilon _{\mathcal {S},2})\)-adaptive reusable statistical zero-Knowledge if there exists a (uniform) simulator \(\textsf{ZKSim}\in \mathcal {C}_{\mathcal {S}}\) which takes as input the round-one transcript \(\tau _1\), the honest prover’s state \(\sigma _P\), and a statement x such that the following holds. Consider an adversary \(V^* \in \mathcal {C}_{\textsf{zk}}\) that takes as input  and an honestly generated prover’s first round message \(\textsf{zk}_{1,P}\), and plays the following game \(\textsf{expt}^b_{V^*, \textsf{zk}}\):
and an honestly generated prover’s first round message \(\textsf{zk}_{1,P}\), and plays the following game \(\textsf{expt}^b_{V^*, \textsf{zk}}\):
-
1.
\(V^*\) may adaptively issue queries of the form \((x,w, \textsf{zk}_{1,V}^*)\). The challenger responds as follows:
-
f \((x,w) \notin R_L\), the challenger responds with \(\bot \).
-
If \((x,w) \in R_L\) and \(b = 0\), the challenger responds with the honest prover’s second message \(\textsf{ZKProve}_2(\sigma _p, \textsf{zk}_{1,V}^*, x, w)\).
-
If \((x,w) \in R_L\) and \(b = 1\), the challenger responds with the simulated prover’s message \(\textsf{ZKSim}(\sigma _p, \textsf{zk}_{1,V}^*, x)\).
-
-
2.
At the end of the game, \(V^*\) outputs an arbitrary function of its view, which is used as the output of the experiment.
It must hold that \(\textsf{expt}^{0}_{V^*,\textsf{zk}} \approx _{(\infty , \epsilon _\mathcal {S})} \textsf{expt}^{1}_{V^*,\textsf{zk}}.\)
An overview and complete details of our construction of the reusable SZK argument with sometimes-statistical soundness can be found in the full version of the paper [26].
5.2 One-Round Simultaneous-Message CCA-Non-malleable Commitments
In the following, we define the syntax and required security properties of the commitment scheme which we use in the main MrNISc construction in Sect. 6. This commitment is a simultaneous-message one-round commitment, where both committer and receiver send a message during the single round. The receiver’s message is a uniform random string \(\tau \), and the committer’s message is some obfuscated program \(\textsf{P}\). The committed value is only fixed when both \(\textsf{P}\) and \(\tau \) are fixed. To reflect this, in the definition of syntax below, \(\textsf{ComputeOpening}\), \(\textsf{VerifyOpening}\), and \(\textsf{CCAVal}\) take both the committer’s message \(\textsf{P}\) and the receiver’s message \(\tau \) as input.
Let  be the tag space which is
be the tag space which is  , where
, where  . The modified syntax is as follows.
. The modified syntax is as follows.
Definition 5.5
(Syntax of one-round simultaneous-message CCA-non-malleable commitments). With respect to the tag space \(\mathcal {T}\), the NMC consists of the following algorithms.
-
 The probabilistic polynomial time commitment algorithm takes as input the security parameter
The probabilistic polynomial time commitment algorithm takes as input the security parameter  , a tag
, a tag  , and a message \(m\in \{0,1\}^*\), and outputs a commitment \(\textsf{P}\).
, and a message \(m\in \{0,1\}^*\), and outputs a commitment \(\textsf{P}\). -
\(\textsf{ComputeOpening}(\tau ,\textsf{tag},\textsf{P},m,r):\) The polynomial time deterministic algorithm \(\textsf{ComputeOpening}\) takes as input a string \(\tau \in \{0,1\}^{\ell _{t}}\), a tag
 , a commitment \(\textsf{P}\), a message \(m\in \{0,1\}^*\), and the randomness r used to commit. It outputs an opening \(\sigma \in \{0,1\}^*\). Above
, a commitment \(\textsf{P}\), a message \(m\in \{0,1\}^*\), and the randomness r used to commit. It outputs an opening \(\sigma \in \{0,1\}^*\). Above  is a polynomial associated with the scheme.
is a polynomial associated with the scheme. -
\(\textsf{VerifyOpening}(\tau ,\textsf{tag},\textsf{P},m,\sigma ):\) The polynomial-time deterministic algorithm \(\textsf{VerifyOpening}\) takes a string \(\tau \in \{0,1\}^{\ell _{t}}\), a tag
 , a commitment \(\textsf{P}\), a message \(m\in \{0,1\}^*\), and an opening \(\sigma \). It outputs a value in \(\{0,1\}\).
, a commitment \(\textsf{P}\), a message \(m\in \{0,1\}^*\), and an opening \(\sigma \). It outputs a value in \(\{0,1\}\).
Such a scheme is said to be a one-round simultaneous-message CCA-non-malleable commitment if it satisfies the following properties:
Definition 5.6
(Correctness of Opening). Let  be the security parameter, and consider any
be the security parameter, and consider any  , any message \(m \in \{0,1\}^*\), any \(\tau \in \{0,1\}^{\ell _{t}}\), any
, any message \(m \in \{0,1\}^*\), any \(\tau \in \{0,1\}^{\ell _{t}}\), any  . Then, \(\Pr [\textsf{VerifyOpening}(\tau , \textsf{tag},\textsf{P},m,\sigma )=1]=1,\)
. Then, \(\Pr [\textsf{VerifyOpening}(\tau , \textsf{tag},\textsf{P},m,\sigma )=1]=1,\)
where \(\sigma =\textsf{ComputeOpening}(\tau ,\textsf{tag},\textsf{P},m,r)\).
Definition 5.7
(Extraction). There exists an (inefficient) algorithm \(\textsf{CCAVal}\) with the following properties. For any  and any message \(m\in \{0,1\}^*\), tag
and any message \(m\in \{0,1\}^*\), tag  , commitment \(\textsf{P}\), and
, commitment \(\textsf{P}\), and  , it holds that
, it holds that
In addition, \(\textsf{CCAVal}\) runs in time  for some fixed polynomial \(\textsf{poly} \).
for some fixed polynomial \(\textsf{poly} \).
We now specify the CCA security property.
Definition 5.8
(\((\mathcal {C},\epsilon )\text{- }\textsf{CCA}\) security). We define the following security game played between the adversary \(\mathcal {A}\in \mathcal {C}\) and the challenger. We denote it by  :
:
-
1.
The challenger manages a list L that is initially empty. The contents of the list are visible to the adversary at all stages.
-
2.
The adversary sends a challenge tag
 .
. -
3.
The adversary submits queries of the following kind in an adaptive manner:
-
(a)
Adversary can ask for arbitrary polynomially many \(\tau \text{- }\)queries. Challenger samples \(\tau ' \leftarrow \{0,1\}^{\ell _{t}}\) and appends \(\tau '\) to L.
-
(b)
Adversary can ask for an arbitrary polynomially many \((\tau ,\textsf{tag},\textsf{P})\)-queries for any \(\tau \in L\), any \(\textsf{tag}\ne \textsf{tag}^*\), and any commitment \(\textsf{P}\). The challenger computes \(\textsf{CCAVal}(\tau ,\textsf{tag},\textsf{P})\) and sends the result to the adversary.
-
(a)
-
4.
The adversary submits two messages
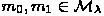 . The challenger samples \(b\leftarrow \{0,1\}\), and computes \(\textsf{P}^* \leftarrow \textsf{CCACommit}(1^{\lambda } ,\textsf{tag}^*,m_b)\). The adversary gets \(\textsf{P}^*\) from the challenger.
. The challenger samples \(b\leftarrow \{0,1\}\), and computes \(\textsf{P}^* \leftarrow \textsf{CCACommit}(1^{\lambda } ,\textsf{tag}^*,m_b)\). The adversary gets \(\textsf{P}^*\) from the challenger. -
5.
The adversary repeats Step 3.
-
6.
Finally, the adversary outputs a guess \(b'\in \{0,1\}\). The experiment outputs 1 if \(b' = b\) and 0 otherwise.
The one-round (simultaneous-message) \(\textsf{CCA}\)-secure commitment scheme \(\textsf{CCA}\) scheme satisfies \((\mathcal {C},\epsilon )\text{- }\textsf{CCA}\) security if for all adversaries \(\mathcal {A}\in \mathcal {C}\):

Our NMC construction is an extension of [36]. It takes the same form as that of [36], namely, the committer publishes a message P, and the receiver publishes a random \(\tau \). We change the internals of the construction, though, to allow the receiver to publish \(\tau \) during the first round, simultaneously while the committer is publishing P. We show that with our modifications, even a rushing committer who chooses P based on \(\tau \) cannot break security. Thus we achieve a (simultaneous-message) one-round NMC which satisfies the full CCA security definition given above, relying on iO and other standard assumptions. We refer to the full version of the paper [26] for details.
6 Malicious-Secure MrNISC
In this section, we give the formal construction and proof of security for our MrNISC protocol.
Required Primitives and Parameters. We make use of the following primitives in our construction.
-
Commitment: A non-interactive perfectly binding commitment (\(\textsf{NICommit}\)).
-
Pseudo-Random Function A pseudo-random function (PRF).
-
Witness Encryption: We use witness encryption We use circuit SAT as our \(\textsf{NP}\) language.
-
Reusable Statistical ZK Arguments with Sometimes-Statistical Soundness: We use a SPS ZK argument \((\textsf{ZKProve}_1, \textsf{ZKVerify}_1, \textsf{ZKProve}_2, \textsf{ZKVerify}_2)\) satisfying Definitions 5.1, 5.3 and 5.4.
-
One-round CCA commitments: We use one-round (simultaneous-message) CCA commitments as in Definitions 5.5 to 5.8.
-
Semi-malicious MrNISC: We use an underlying semi-malicious MrNISC protocol \((\textsf{SM}.\textsf{Encode}, \textsf{SM}.\textsf{Eval}, \textsf{SM}.\textsf{Output})\), satisfying the security notion given in Definition 4.2.
Complexity Hierarchy. In order to argue security, we require that the primitives we use are secure against adversaries of varying complexities. In particular, we require the following complexity hierarchy to hold with respect to the primitives. Let \(T_1, T_2, T_3, T_4, T_5\) be functions over \(\lambda \), such that
where \(T \ll T'\) means that \(p(T) < T'\) asymptotically for all polynomials p. We require the following:
-
The ZK argument scheme satisfies \((\mathcal {C}_\mathcal {S}, \mathcal {C}_\textsf{zk}, \epsilon _\mathcal {S})\)-adaptive reusable statistical zero knowledge (Definition 5.4) where \(\mathcal {C}_\mathcal {S}\) is the class of circuits of size \(\textsf{poly} (T_1)\) and depth \(T_1\) (i.e. the simulator runs in size \(\textsf{poly} (T_1)\) and depth \(T_1\)), and \(\mathcal {C}_\textsf{zk}\) is the class of circuits of size \(p(T_3)\) for all polynomials p, and \(\epsilon _\mathcal {S}\) is any negligible function (i.e. statistical zero knowledge holds as long as the verifier’s first-round message is generated by a machine in \(\mathcal {C}_\textsf{zk}\).
-
The CCA non-malleable commitment scheme satisfies \((\mathcal {C}, \epsilon )\)-CCA security, where \(\mathcal {C}\) is the class of circuits of size \(p(T_1)\) for all polynomials p, and \(\epsilon \) is any negligible function.
-
The CCA non-malleable commitment scheme’s extractor \(\textsf{CCAVal}\) is a circuit of size \(T_2\) and polynomial depth.
-
The perfectly-binding commitment scheme is hiding against adversaries of size \(p(T_2)\) for all polynomials p, and is extractable by a circuit of size \(T_3\).
-
The ZK argument scheme satisfies \((\mathcal {C}_\textsf{sound}, \epsilon _{\textsf{sound},1}, \epsilon _{\textsf{sound},2})\)-statistical soundness, where \(\mathcal {C}_\textsf{sound}\) is the class of circuits of size \(p(T_5)\) and polynomial depth for all polynomials p (refer to Definition 5.3 for details on the meaning of \(\mathcal {C}_\textsf{sound}\)), and \(\epsilon _{\textsf{sound},1} = 1/T_4\), and \(\epsilon _{\textsf{sound},2}\) is any negligible function.
-
The witness encryption scheme satisfies \((\mathcal {C},\epsilon )\)-security, where \(\mathcal {C}\) is the class of circuits of size \(p(T_5)\) for all polynomials p, and \(\epsilon = 1/T_5\).
-
The pseudo-random function is secure against adversaries of size \(p(T_5)\) for all polynomials p.
-
The semi-malicious MrNISC protocol is secure against adversaries of size \(p(T_5)\) for all polynomials p.


Protocol. We give the protocol below, described in terms of the behavior of party \(P_i\) during the input encoding phase, the evaluation phase, and the output computation phase. In particular, we give this behavior by implementing the \(\textsf{Encode}\), \(\textsf{Eval}\) and \(\textsf{Output}\) algorithms defined in Section 4. Assume that each party \(P_i\) has input \(x_i\) and a public identity denoted by  . Note that the \(\textsf{Output}\) algorithm is public and can be performed without \(P_i\)’s private input or state. Throughout the protocol description, we deal with PPT algorithms as follows. If a PPT algorithm P is invoked on some input x without any randomness explicitly given (i.e., we write P(x)), we implicitly assume that it is supplied with freshly chosen randomness. In some cases we will need to explicitly manipulate the randomness of algorithms, in which case we will write P(x; r).
. Note that the \(\textsf{Output}\) algorithm is public and can be performed without \(P_i\)’s private input or state. Throughout the protocol description, we deal with PPT algorithms as follows. If a PPT algorithm P is invoked on some input x without any randomness explicitly given (i.e., we write P(x)), we implicitly assume that it is supplied with freshly chosen randomness. In some cases we will need to explicitly manipulate the randomness of algorithms, in which case we will write P(x; r).
-
Input Encoding \(\textsf{Encode}(1^\lambda , \textsf{tag}_i, x_i)\): The input encoding algorithm takes as input \(1^\lambda \), where \(\lambda \) is the security parameter, along with \(P_i\)’s tag \(\textsf{tag}_i\) and private input \(x_i\), and does the following.
-
1.
Compute the input encoding
 from the semi-malicious protocol, where \(r_{i, \textsf{SM}, 1} \xleftarrow {\$}\{0,1\}^*\) is freshly chosen randomness.
from the semi-malicious protocol, where \(r_{i, \textsf{SM}, 1} \xleftarrow {\$}\{0,1\}^*\) is freshly chosen randomness. -
2.
Choose a PRF key \(K_i\).
-
3.
Compute a perfectly binding commitment
$$\textsf{com}_{i} \leftarrow \textsf{NICommit}(1^\lambda , (x_i,r_{i,\textsf{SM},1}, K_i);r_{i,\textsf{com}})$$of the input and the semi-malicious encoding randomness, where \(r_{i,\textsf{com}} \xleftarrow {\$}\{0,1\}^*\) is freshly chosen randomness.
-
4.
Compute a CCA-non-malleable commitment

of the same values committed to in the perfectly binding commitment, along with the randomness used for generating the perfectly binding commitment, where \(r_{i,\textsf{CCA}} \xleftarrow {\$}\{0,1\}^*\) is freshly chosen randomness.
-
5.
Compute a random string \(\tau _i \xleftarrow {\$}\{0,1\}^\ell \).
-
6.
Compute the first round verifier’s message and state
$$(\sigma _{\textsf{zk},1,i,V}, \textsf{zk}_{1, i, V}) \leftarrow \textsf{ZKVerify}_1(1^\lambda )$$and the first round prover message and state
$$(\sigma _{\textsf{zk},1,i,P}, \textsf{zk}_{1, i, P}) \leftarrow \textsf{ZKProve}_1(1^\lambda ).$$ -
7.
Output \(m_{i,1}=(\hat{m}_{i,1},\textsf{com}_i,\textsf{nmc}_i, \tau _i,\textsf{zk}_{1,i,V},\textsf{zk}_{1,i,P})\).
-
1.
-
Function Evaluation \(\textsf{Eval}(f, \textsf{tag}_i, x_i, r_{i,1}, I, \rho _1)\): The function evaluation algorithm takes as input the function f to be evaluated, the set I of participating parties, \(P_i\)’s private input \(x_i\), the randomness \(r_{i,1}\) which \(P_i\) used to generate its input encoding, and the input encoding transcript \(\rho _1\), and does the following:
-
1.
Parse \(\rho _1=\left\{ \hat{m}_{k,1}, \textsf{com}_k, \textsf{nmc}_k, \tau _k, \textsf{zk}_{1,k,V}, \textsf{zk}_{1,k,P} \right\} _{k\in [n]}\) to obtain \((r_{i,\textsf{SM},1}, r_{i,\textsf{com}},r_{i,\textsf{CCA}},\sigma _{\textsf{zk},1,i,V}, \sigma _{\textsf{zk},1,i,P})\) from \(r_{i,1}\).
-
2.
Compute the semi-malicious function evaluation encoding
$$\hat{m}_{i,2} \leftarrow \textsf{SM}.\textsf{Eval}(f, x_i, r_{i,\textsf{SM},1}, I, \rho _{\textsf{sm,1}}; PRF_{K_i}(f, I, 1))$$of the underlying semi-malicious protocol, using the transcript \(\rho _{\textsf{sm,1}} = \{ \hat{m}_{k,1} \}_{k \in I}\) of the semi-malicious input encodings of all parties from I, where the randomness is chosen using the PRF key committed to during the input encoding phase.
-
3.
Compute a commitment \(\textsf{com}_{i,\hat{m}_{i,2}} \leftarrow \textsf{NICommit}(\hat{m}_{i,2}; PRF_{K_i}(f, I, 2))\) of the encoding \(\hat{m}_{i,2}\) using randomness derived from the PRF key committed to during the input encoding phase.
-
4.
For each \(P_j\), \(j \in I \setminus \{i\}\):
-
Compute an opening
$$\sigma _{i,j, \textsf{CCA}} \leftarrow \textsf{ComputeOpening}(\tau _j, \textsf{tag}_i, \textsf{nmc}_i, (x_i,r_{i,\textsf{SM},1}, K_i, r_{i,\textsf{com}}), r_{i,\textsf{CCA}})$$for the non-malleable-commitment \(\textsf{nmc}_i\) with respect to \(\tau _j\).
-
Compute a round two ZK prover’s message \(\textsf{zk}_{2, i \rightarrow j, P} \leftarrow \textsf{ZKProve}_2(\varPhi _{\textsf{zk},i,j}, W_{\textsf{zk},i}, \sigma _{\textsf{zk},1,i,P}, \textsf{zk}_{1, j, V})\), where \(\varPhi _{\textsf{zk},i,j}\) is the circuit SAT instance defined on page 6. Here \(W_{\textsf{zk},i}=(x_i,r_{i,\textsf{SM},1},K_i, r_{i,\textsf{com}},\sigma _{i,j, \textsf{CCA}},\hat{m}_{i,2})\) is the witness for generating this prover message.
-
-
5.
Compute a witness encryption \(\textsf{WE}_i \leftarrow \textsf{WE}.\textsf{Encrypt}(1^\lambda , \varPhi _{\textsf{WE},i}, r_{\textsf{com}, i, \hat{m}_{i,2}})\) where the circuit \(\varPhi _{\textsf{WE},i}\) is described on page 26, and the plaintext \(r_{\textsf{com}, i, \hat{m}_{i,2}} = PRF_{K_i}(f, I, 2)\) is the opening for \(\textsf{com}_{i,\hat{m}_{i,2}}\).
-
6.
Return \(m_{i,2} = (\textsf{com}_{i, \hat{m}_{i,2}}, \{\textsf{zk}_{2, i \rightarrow j, P}\}_{j \in I \setminus \{i\}}, \textsf{WE}_i )\).
-
1.
-
Output Computation \(\textsf{Output}(\{ m_{j,1}, m_{j,2} \}_{j \in I})\): The output computation algorithm takes as input the input encoding \(m_{j,1}\) and the function evaluation encoding \(m_{j,2}\) of every party \(P_j\) for \(j \in I\) and does the following:
-
1.
Parse
$$m_{j,1}=(\hat{m}_{j,1},\textsf{com}_j,\textsf{nmc}_j, \tau _j,\textsf{zk}_{1,j,v},\textsf{zk}_{1,j,p})$$and
$$m_{j,2} = (\textsf{com}_{j, \hat{m}_{j,2}}, \{\textsf{zk}_{2, j \rightarrow k, P}\}_{k \in I \setminus \{j\}}, \textsf{WE}_j )$$for each \(j \in I\).
-
2.
For each \(j, k \in I, j \ne k\):
-
Run \(\textsf{ZKVerify}_2(\varPhi _{\textsf{zk},j,k}, \textsf{zk}_{1,k,v}, \textsf{zk}_{1,j,p}, \textsf{zk}_{2,j\rightarrow k,p})\), where \(\varPhi _{\textsf{zk},j,k}\) is described on page 25. If the verification fails, abort and output \(\bot \).
-
-
3.
For each \(j \in I\):
-
Compute the decryption \(r_{\textsf{com},j,\hat{m}_{j,2}} \leftarrow \textsf{WE}.\textsf{Decrypt}(\textsf{WE}_j, W_{\textsf{WE},j})\) of the opening \(r_{\textsf{com},j,\hat{m}_{j,2}}\) to the commitment \(\textsf{com}_{j, \hat{m}_{j,2}}\), using the witness \(W_{\textsf{WE},j} = (\{\textsf{zk}_{2, k \rightarrow j, P}, \textsf{com}_{j, \hat{m}_{j,2}} \}_{k \ne j}).\) If the decryption fails, abort and output \(\bot \).
-
Open \(\textsf{com}_{j,\hat{m}_{j,2}}\) to \(P_j\)’s semi-malicious function evaluation encoding \(\hat{m}_{j,2}\) using \(r_{\textsf{com},j, \hat{m}_{j,2}}\).
-
-
4.
Compute the output \(y \leftarrow \textsf{Output}( \{ \hat{m}_{j,1}, \hat{m}_{j,2} \}_{j \in I} )\) using the values \(\hat{m}_{j,2}\) obtained from decrypting the witness encryptions along with the semi-malicious input encodings \(\hat{m}_{j,2}\).
-
5.
Output y.
-
1.
Correctness. Correctness of the protocol follows directly from correctness of the underlying primitives.
We refer to the full version [26] for the proof of security.
Notes
- 1.
By quasi-non-interactive we refer to “non-interactive” protocols that require a trusted setup such as a common reference string.
- 2.
We discuss this work further in Sect. 1.3.
- 3.
Semi-malicious security allows the adversary to choose arbitrary randomness for the parties, but otherwise requires honest behavior.
- 4.
DDH assumption over asymmetric pairing groups is also referred to as the SXDH assumption. We will interchangeably use SXDH wherever we specifically require DDH over assymetric pairing groups.
- 5.
An adaptive one-way function is a non-falsifiable hardness assumption postulating the existence of a one-way function f that is hard to invert on a random point \(y = f(x)\) even if you get access to an inversion oracle that inverts it on every other point \(y'\ne y\).
References
Agarwal, A., Bartusek, J.,Goyal, V., Khurana, D., Malavolta, G.: Two-round maliciously secure computation with super-polynomial simulation. In: TCC, pp. 654–685 (2021)
Ananth, P., Choudhuri, A.R., Jain, A.: A new approach to round-optimal secure multiparty computation. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 468–499. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_16
Ananth, P., Jain, A., Jin, Z., Malavolta, G.: Unbounded multi-party computation from learning with errors. In: Canteaut, A., Standaert, F.-X. (eds.) EUROCRYPT 2021. LNCS, vol. 12697, pp. 754–781. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-77886-6_26
Asharov, G., Jain, A., López-Alt, A., Tromer, E., Vaikuntanathan, V., Wichs, D.: Multiparty computation with low communication, computation and interaction via threshold FHE. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 483–501. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_29
Asharov, G., Jain, A., Wichs, D.: Multiparty computation with low communication, computation and interaction via threshold FHE. Cryptology ePrint Archive, Report 2011/613 (2011). https://eprint.iacr.org/2011/613
Badrinarayanan, S., Fernando, R., Jain, A., Khurana, D., Sahai, A.: Statistical ZAP arguments. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020. LNCS, vol. 12107, pp. 642–667. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45727-3_22
Badrinarayanan, S., Goyal, V., Jain, A., Khurana, D., Sahai, A.: Round optimal concurrent MPC via strong simulation. In: TCC, pp. 743–775 (2017)
Barak, B., Prabhakaran, M., Sahai, A.: Concurrent non-malleable zero knowledge. In: FOCS, pp. 345–354 (2006)
Bartusek, J., Garg, S., Masny, D., Mukherjee, P.: Reusable two-round MPC from DDH. In: TCC, pp. 320–348 (2020)
Bartusek, J., Garg, S., Srinivasan, A., Zhang, Y.: Reusable two-round MPC from LPN. In: PKC, pp. 165–193 (2022)
Beaver, D., Micali, S., Rogaway, P.: The round complexity of secure protocols (extended abstract). In: STOC, pp. 503–513. ACM Press (1990)
Ben-Or, M., Goldwasser, S., Wigderson, A.: Completeness theorems for non-cryptographic fault-tolerant distributed computation (extended abstract). In: STOC, pp. 1–10 (1988)
Benhamouda, F., Jain, A., Komargodski, I., Lin, H.: Multiparty reusable non-interactive secure computation from LWE. In: Canteaut, A., Standaert, F.-X. (eds.) EUROCRYPT 2021. LNCS, vol. 12697, pp. 724–753. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-77886-6_25
Benhamouda, F., Lin, H.: Mr NISC: multiparty reusable non-interactive secure computation. In: TCC, pp. 349–378 (2020)
Bitansky, N., Canetti, R., Chiesa, A., Tromer, E.: Recursive composition and bootstrapping for SNARKS and proof-carrying data. In: STOC, pp. 111–120 (2013)
Bitansky, N., Kalai, Y.T., Paneth, O.: Multi-collision resistance: a paradigm for keyless hash functions. In: STOC, pp. 671–684, June 2018
Bitansky, N., Y., Kalai, T., Paneth, O.: Multi-collision resistance: a paradigm for keyless hash functions. In: STOC, pp. 671–684 (2018)
Bitansky, N., Lin, H.: One-message zero knowledge and non-malleable commitments. In: TCC, pp. 209–234 (2018)
Brakerski, Z., Halevi, S., Polychroniadou, A.: Four round secure computation without setup. In: TCC, pp. 645–677 (2017)
Canetti, R., Lin, H., Pass, R.: Adaptive hardness and composable security in the plain model from standard assumptions, pp. 541–550. IEEE Computer Society Press (2010)
Chaum, D., Crépeau, C., Damgård, I.: Multiparty unconditionally secure protocols (extended abstract). In: STOC, pp. 11–19 (1988)
Choudhuri, A.R., Ciampi, M., Goyal, V., Jain, A., Ostrovsky, R.: Round optimal secure multiparty computation from minimal assumptions. In: TCC, pp. 291–319 (2020)
Ciampi, M., Ostrovsky, R., Siniscalchi, L., Visconti, I.: Round-optimal secure two-party computation from trapdoor permutations. In: TCC, pp. 678–710 (2017)
Dodis, Y., Jain, A., Moran, T., Wichs, D.: Counterexamples to hardness amplification beyond negligible. In: TCC, pp. 476–493 (2012)
Fernando, R., Gelles, Y., Komargodski, I., Shi, E.: Maliciously secure massively parallel computation for all-but-one corruptions. In: Dodis, Y., Shrimpton, T. (eds.) Advances in Cryptology–CRYPTO 2022. CRYPTO 2022. Lecture Notes in Computer Science, vol. 13507, pp. 688-718. Springer, Cham (2022). https://doi.org/10.1007/978-3-031-15802-5_24
Fernando, R., Jain, A., Komargodski, I.: Maliciously-secure MrNISC in the plain model. Cryptology ePrint Archive, Report 2021/1319 (2021). https://eprint.iacr.org/2021/1319
Garg, R., Khurana, D., Lu, G., Waters, B.: Black-box non-interactive non-malleable commitments. In: Canteaut, A., Standaert, F.-X. (eds.) EUROCRYPT 2021. LNCS, vol. 12698, pp. 159–185. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-77883-5_6
Garg, S., Goyal, V., Jain, A., Sahai, A.: Concurrently secure computation in constant rounds. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 99–116. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_8
Garg, S., Mukherjee, P., Pandey, O., Polychroniadou, A.: The exact round complexity of secure computation. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 448–476. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_16
Goldreich, O., Micali, S., Wigderson, A.: How to play any mental game or A completeness theorem for protocols with honest majority. In: STOC, pp. 218–229 (1987)
Goldreich, O., Oren, Y.: Definitions and properties of zero-knowledge proof systems. J. Cryptol. 7(1), 1–32 (1994). https://doi.org/10.1007/BF00195207
Kalai, Y.T., Khurana, D.: Non-interactive non-malleability from quantum supremacy. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11694, pp. 552–582. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26954-8_18
Kalai, Y.T., Khurana, D., Sahai, A.: Statistical witness indistinguishability (and more) in two messages. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10822, pp. 34–65. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78372-7_2
Katz, J., Ostrovsky, R.: Round-optimal secure two-party computation. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 335–354. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_21
Katz, J., Ostrovsky, R., Smith, A.: Round efficiency of multi-party computation with a dishonest majority. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 578–595. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-39200-9_36
Khurana, D.: Non-interactive distributional indistinguishability (NIDI) and non-malleable commitments. In: Canteaut, A., Standaert, F.-X. (eds.) EUROCRYPT 2021. LNCS, vol. 12698, pp. 186–215. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-77883-5_7
Kiyoshima, S., Manabe, Y., Okamoto, T.: Constant-round black-box construction of composable multi-party computation protocol. In: TCC, pp. 343–367 (2014)
Lin, H., Pass, R., Soni, P.: Two-round and non-interactive concurrent non-malleable commitments from time-lock puzzles. In: FOCS, pp. 576–587 (2017)
Pandey, O., Pass, R., Vaikuntanathan, V.: Adaptive one-way functions and applications. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 57–74. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_4
Pass, R.: Simulation in quasi-polynomial time, and its application to protocol composition. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 160–176. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-39200-9_10
Sahai, A., Vadhan, S.P.: A complete promise problem for statistical zero-knowledge. In: FOCS, pp. 448–457 (1997)
Wee, H.: Black-box, round-efficient secure computation via non-malleability amplification. In: FOCS, pp. 531–540 (2010)
Acknowledgement
Rex Fernando is supported in part by a Simons Investigator Award, DARPA SIEVE award, NTT Research, NSF Frontier Award 1413955, BSF grant 2012378, a Xerox Faculty Research Award, a Google Faculty Research Award, and an Okawa Foundation Research Grant. This material is based upon work supported by the Defense Advanced Research Projects Agency through Award HR00112020024. Ilan Komargodski is the incumbent of the Harry & Abe Sherman Senior Lectureship at the School of Computer Science and Engineering at the Hebrew University, supported in part by an Alon Young Faculty Fellowship, by a grant from the Israel Science Foundation (ISF Grant No. 1774/20), and by a grant from the US-Israel Binational Science Foundation and the US National Science Foundation (BSF-NSF Grant No. 2020643).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 International Association for Cryptologic Research
About this paper
Cite this paper
Fernando, R., Jain, A., Komargodski, I. (2023). Maliciously-Secure MrNISC in the Plain Model. In: Hazay, C., Stam, M. (eds) Advances in Cryptology – EUROCRYPT 2023. EUROCRYPT 2023. Lecture Notes in Computer Science, vol 14005. Springer, Cham. https://doi.org/10.1007/978-3-031-30617-4_4
Download citation
DOI: https://doi.org/10.1007/978-3-031-30617-4_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-30616-7
Online ISBN: 978-3-031-30617-4
eBook Packages: Computer ScienceComputer Science (R0)






 where the probability is over the coins of the prover and the verifier in round 1.
where the probability is over the coins of the prover and the verifier in round 1. The probabilistic polynomial time commitment algorithm takes as input the security parameter
The probabilistic polynomial time commitment algorithm takes as input the security parameter  , a tag
, a tag  , and a message
, and a message  , a commitment
, a commitment  is a polynomial associated with the scheme.
is a polynomial associated with the scheme. , a commitment
, a commitment  .
.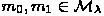 . The challenger samples
. The challenger samples  from the semi-malicious protocol, where
from the semi-malicious protocol, where 
