Keywords

1 Introduction

The study of the oscillatory flow of a viscous and viscoelastic fluid in a flat and rectangular channel under the action of harmonic oscillations of the fluid flow rate can be used in biological mechanics, in particular, for the operation of a microchip system [1]. These systems are designed to diagnose the functioning of various human organs, as well as targeted delivery of drugs to them. In addition, in order to ensure a constant flow of liquid, pneumatic micro pumps with periodic displacement of liquid from free volumes are often used in biomedical installations [2]. In such systems, it can be economical to install with a pulsating flow. In addition, when transporting high-viscosity and heavy oil and oil products over long distances and circulating drilling fluids in a well, one of the important tasks is to develop an effective method for reducing the hydraulic flow resistance [3,4,5]. In all the industries listed above, the liquid used, both drugs and oil products or drilling fluids, treated with high-molecular polymers can be classified as viscoelastic liquids [3,4,5]. As the authors know, at present there is no information on the effect of flow rate pulsations on fluctuations in the coefficients of hydraulic resistance and friction resistance. However, these studies are very important for calculating the pressure gradient and other hydrodynamic characteristics, which have a special place in some biomedical and other technological studies [1, 2]. Thus, the study of shear stress on the wall during oscillatory flow of a viscous and viscoelastic fluid, together with other flow parameters, is of great importance.

The most simplified approach to the theoretical study of the oscillatory flow of a viscous fluid is based on the assumption that a viscous fluid, incompressible, moves laminar in an infinitely long cylindrical tube of circular cross section under the action of a pressure gradient that changes harmonically in time. Investigated in the works of B.C. Gromeka [6, 7], pulsating flows of viscous incompressible fluids in rigid and elastic pipes. In them, he determined the propagation velocities of the pressure pulse wave and their attenuation. Then the oscillatory flow of a viscous fluid in a pipe was studied in the work of I.B. Krendala [8].

Solving the problems of the oscillatory flow of a viscous fluid in a round endless pipe, derived formulas for the velocity profile, fluid flow and impedance during the propagation of a sinusoidal pressure wave. A few years later, P. Lambosia published his findings of the same velocity profile in [9] and, in addition, calculated the viscous drag. J.R. Womersley in [10] re-deduced P. Lambosia’s solution. His distinctive qualitative results were that it was found: firstly, a phase shift between the pressure fluctuations and the cross-sectional average velocity and, secondly, the formation of a non-monotonic distribution of velocity profiles. For the first time, the effect of superimposed oscillations of the cross-sectional average velocity in a laminar flow in a pipe was published in an experimental work [11]. The so-called “annular effect” of Richardson was obtained at relatively high oscillation frequencies, which appears as a maximum on the profile of the oscillating component of the longitudinal velocity in a narrow near-wall layer, the thickness of which decreases with increasing oscillation frequency. In the rest of the pipe, the liquid oscillates as a whole in accordance with the fluctuation of the average velocity over the section. In [12], experiments were also carried out on pipes with an internal diameter of 40 mm, in which the piston creates harmonic changes in the fluid flow rate near zero. The graph shows points obtained from oscillograms, on which local velocities were recorded using an electrothermoanimometer at various points in the pipe section. It can be seen from the graphs that the local velocities have the maximum values near the wall. These experimental results are in good agreement with the results of [11]. Theoretically, the problem of a laminar pulsating fluid flow in a pipe was solved in [12]. In [13], the solution of this problem was carried out similarly to [12], but under the condition that not the harmonic oscillation of the average velocity over the cross section, but the oscillation of the pressure gradient was specified. From the analytical solution of the equation of motion for a pulsating flow, it follows that at certain Reynolds numbers of the time-averaged flow and relatively high frequencies and amplitudes of oscillations, there is a zone of return (reverse) flows near the wall, when the local velocity is directed against the average flow. The presence of these zones was confirmed experimentally in [14] with very good agreement between theory and experiment. In [15], I will carry out a similar solution to the problem of a pulsating flow in a flat channel and in a cylindrical pipe. It is noted that the patterns of fluctuations of hydrodynamic quantities for the flow in a flat channel and in a round cylindrical pipe qualitatively coincide.

Unsteady pulsating flows of a viscous fluid in a round cylindrical pipe of infinite length under the action of a harmonic changing pressure gradient were studied in [16]. By solving the problem, calculation formulas for the distribution of velocity and fluid flow are obtained. Numerical calculations have shown that in a pulsating flow at lower values of the dimensionless oscillation frequency, the velocity, flow rate, and other hydrodynamic parameters from the zero initial state are established slowly, relatively at high oscillation frequencies, and are close to the parameters of a non-pulsating flow. In an oscillating flow at high oscillation frequencies, these parameters are set almost instantly. Pulsating flows of a viscous incompressible fluid were studied in [17] in a rectangular channel.

The problem is solved by the finite difference method. The optimal parameters of the difference scheme are determined, and data are obtained on the amplitude and phase of oscillations of the longitudinal velocity, the coefficient of hydraulic resistance, and other flow parameters. At low vibration frequencies, it is shown that all hydrodynamic parameters fluctuate according to the laws of the average velocity over the cross section. For rectangular channels with different cross-sectional shapes (flat, rectangular, and round cylindrical) in high-frequency oscillations, the dependences of the hydrodynamic quantities on the dimensionless oscillation frequency are of the same nature. The authors also obtained an analytical solution for a developed oscillating flow in triangular [18] and toroidal [19] channels.

Of interest is the study of the pulsating flow of a viscoelastic fluid in a flat channel and in a cylindrical pipe under the influence of harmonic oscillations of the pressure gradient or when harmonic oscillations of the flow rate are superimposed on the flow. In [20], the motion of a viscoelastic fluid along a long pipe under the action of an oscillatory pressure gradient was studied. Laminar oscillatory flows of Maxwell and Oldroyd-B viscoelastic fluids were studied in [21]. Where many interesting features are demonstrated that are absent in Newtonian fluid flows. The results of the study [24] show that in the inertialess mode, when \({\text{Re}} \ll 1\) the properties of the flow depend on three characteristic lengths.

Wavelength \({\lambda }_{0}\) and attenuation length of viscoelastic shear waves \(x_{0} = (\frac{2\nu }{{\omega_{0} }})^{1/2}\), Where is the \(\nu\) -kinematic viscosity; \({\omega }_{0}\)-oscillation frequency, as well as the characteristic transverse size of the system \(a\). In this regard, according to the length, they are divided into three scales and three independent dimensionless groups: \(\frac{{t_{\vartheta } }}{\lambda }\) (viscosity to relaxation time), \(De\) (relaxation time to oscillation period) and (viscosity factor). At the same time, the oscillatory flow regions are divided into two systems corresponding to the “wide” (\(\frac{a}{{x_{0} }} > 1\)) «narrow» (\(\frac{a}{{x_{0} }} < 1\)) system. In wide systems, oscillations are limited by near-wall flows, and in the central core by a no viscous one. In narrow systems, transverse waves cross the entire system and cross its center too, which ultimately leads to constructive resonances that lead to a sharp increase in the amplitude of the velocity profile. In [22], unsteady flows of a viscoelastic fluid were analyzed using the Oldroyd-B model in a round infinite cylindrical tube under the action of a time-dependent pressure gradient in the following cases: (a) the pressure gradient changes with time in accordance with exponential laws; b) the pressure gradient changes according to harmonic laws; c) the pressure gradient is constant. In all cases, formulas have been obtained for the distribution of velocity, fluid flow, and other hydrodynamic quantities in a pulsating flow. Based on the Maxwell model, the problem of unsteady oscillatory flow of a viscoelastic fluid in a round cylindrical pipe was considered in [23]. Formulas for determining dynamic and frequency characteristics are obtained. With the help of numerical experiments, the influence of the oscillation frequency and the relaxation properties of the liquid on the tangential shear stress on the wall is studied. It is shown that the viscoelastic properties of the fluid, as well as its acceleration, are the limiting factors for using the quasi-stationary approach.

In recent decades, electro kinetic phenomena, including electro osmosis, flow potential, electrophoresis, and sedimentation potential, have attracted much attention and provided many applications in micro and Nano channels. In this connection, the authors of [24] studied the electro kinetic flow of viscoelastic fluids in a flat channel under the influence of an oscillatory pressure gradient. It is assumed that the movement of the fluid occurs laminar and unidirectional, in this regard, the movement of the fluid is in a linear mode. Surface potentials are considered small, so the Poisson-Boltzmann equation is linearized. Resonant behavior appears in the flow when the elastic property of the Maxwell fluid dominates. The resonant phenomenon enhances the electro kinetic effect, and at the same time, the efficiency of electro kinetic energy conversion is enhanced.

In the works listed above, the field of fluid velocities is mainly studied for various modes of change in the pressure gradient. The change in shear and normal stress that occurs during motion has been studied relatively little. In most cases, in hydrodynamic models of unsteady flows, liquids were replaced by a sequence of flows with a quasi-stationary distribution of hydrodynamic quantities. However, the structure of unsteady flows differs from the structure of stationary flows, and in such cases such a replacement should be justified in each particular case. At present, the question of the legitimacy of studying quasi-stationary characteristics for determining the field of shear stresses in non-stationary flows of viscous and viscoelastic fluids is far from being resolved. Naturally, under such conditions, it becomes necessary to use hydrodynamic models of non-stationary processes that take into account the change in the hydrodynamic characteristics of the flow depending on time. It should be noted that in the general case, the hydrodynamic characteristic in pipeline transport cannot be determined from the characteristics that correspond to stationary flow conditions.

In this paper, we study the oscillatory flow of a viscoelastic fluid using the Maxwell model in a flat channel when harmonic oscillations of the fluid flow rate are superimposed on the flow. The transfer function of the amplitude-phase frequency characteristics (APFC) is determined. This function is used to study the dependence of the nonstationary shear shear stress on the wall on the dimensionless oscillation frequency, acceleration, and relaxation properties of the fluid.

2 Statement of the Problem and Solution Method

Let us consider the problems of a slow oscillatory flow of a viscoelastic incompressible fluid between two fixed parallel planes extending in both directions to infinity Let us denote the distance between the walls through 2h. Axis \(0x\) runs horizontally in the middle of the channel along the flow. Axis \(0y\) directed perpendicular to the axis \(0x\). The flow of a viscoelastic fluid occurs symmetrically along the channel axis. The differential equation of motion of a viscoelastic incompressible fluid in stress has the following form [25].

$$\rho \frac{{{ }\partial u}}{\partial t} = - \frac{\partial p}{{\partial x}} - \frac{\partial \tau }{{\partial y}}.$$
(1)

where \(u\) - longitudinal speed; \(p\) -pressure; \(\rho\) -density; \(\mu\) -dynamic viscosity; \(\tau\) -tangential stress; \(t\) -time. The rheological equation of the state of the liquid is taken in the form of the Maxwell equation

$$\left( {1 + \lambda \frac{\partial }{{\partial t}}} \right)\tau \left( {y,t} \right) = - \mu \frac{{\partial u}}{{\partial y}}.$$
(2)

where \(\lambda\) -relaxation time. In (2) at \(\lambda =0\) we obtain Newton’s law of viscous friction. Substituting (2) into the equation of motion for the fluid velocity (1), we obtain

$$\rho \left( {1 + \lambda \frac{\partial }{\partial t}} \right)\frac{\partial u}{{\partial t}} = - \left( {1 + \lambda \frac{\partial }{\partial t}} \right)\frac{\partial p}{{\partial x}} + \mu \frac{{\partial^{2} u}}{{\partial y^{2} }}.$$
(3)

We consider that the oscillatory flow of a viscoelastic fluid occurs due to a given harmonic oscillation of the fluid flow rate or the longitudinal velocity averaged over the channel section.

$$Q = a_{Q} cos\omega t = {{Re}} (a_{Q} e^{i\omega t} ).$$
(4)
$${<}u{>}\,= a_{u} cos\omega t = {{Re}} (a_{u} e^{i\omega t} )$$

where \({a}_{Q}\) and \({a}_{u}\)- the amplitude of the liquid flow rate and the amplitude of the longitudinal velocity averaged over the channel section. In this case, the flow occurs symmetrically along the channel axis, and the no-slip conditions are satisfied for the channel wall, i.e. the longitudinal velocity on the channel wall is zero. Then the boundary conditions will be:

$$u = 0\,{\text{at}}\,y = h$$
$$\frac{\partial u}{{\partial y}} = 0\,{\text{at}}\,y = 0$$
(4a)

The linearity of Eq. (3) and the given harmonic fluctuation of the fluid flow or the longitudinal velocity averaged over the channel section in the form (4), it is possible to write the longitudinal velocity, pressure, shear stress on the wall in the following way

$$\begin{gathered} u\left( {y,t} \right) = {{Re}} (u_{1} \left( y \right)e^{i\omega t} ) \hfill \\ p\left( {x,t} \right) = {{Re}} (p_{1} \left( x \right)e^{i\omega t} ) \hfill \\ \tau \left( t \right) = {{Re}} (\tau_{1} e^{i\omega t} ) \hfill \\ \end{gathered}$$
(5)

Substituting expressions (5) into Eq. (3), we obtain

$$\frac{{\partial ^{2} u_{1} \left( y \right)}}{{\partial y^{2} }} - \frac{{\rho i\omega \eta^{2} \left( {i\omega } \right)}}{\mu }u_{1} \left( y \right) = \frac{{\eta^{2} \left( {i\omega } \right)}}{\mu }\frac{{\partial p_{1} \left( x \right)}}{\partial x}.$$
(6)

Here \(\eta^{2} \left( {i\omega } \right) = \left( {1 + i\omega \lambda } \right)\).

The fundamental solutions of Eq. (6), without the right side are the functions \(cos (\frac{{i^{3/2} \alpha_{0} }}{h}\eta \left( {i\omega } \right)y)\,{\text{and}}\, sin (\frac{{i^{3/2} \alpha_{0} }}{h}\eta \left( {i\omega } \right)y)\).

and the solutions of the inhomogeneous part have constants

$$\frac{1}{\rho i\omega }\left( { - \frac{{\partial p_{1} \left( x \right)}}{\partial x}} \right)$$

Thus, the general solution of Eq. (6) has the form.

$$u_{1} \left( y \right) = C_{1} cos \left( {i^{\frac{3}{2}} \alpha_{0} \eta \left( {i\omega } \right)\frac{y}{h}} \right) + C_{2} sin \left( {i^{\frac{3}{2}} \alpha_{0} \eta \left( {i\omega } \right)\frac{y}{h}} \right) + \frac{1}{\rho i\omega }\left( { - \frac{{\partial p_{1} \left( x \right)}}{\partial x}} \right).$$
(7)

To determine constant coefficients \({C}_{1}\) and \({C}_{2}\) we use boundary conditions (4a)

$$\begin{gathered} \frac{{\partial u_{1} \left( y \right)}}{\partial y} = - C_{1} \frac{{i^{3/2} \alpha_{0} }}{h}\eta \left( {i\omega } \right) sin (i^{3/2} \alpha_{0} \eta \left( {i\omega } \right)\frac{y}{h})\\ + \,C_{2} \frac{{i^{3/2} \alpha_{0} }}{h}\eta \left( {i\omega } \right) cos (i^{3/2} \alpha_{0} \eta \left( {i\omega } \right)\frac{y}{h}){ } \hfill \\ \end{gathered}$$
(8)

for has \(y=0\) (8) the form

$$0 = C_{2} \frac{{i^{3/2} \alpha_{0} }}{h}\eta \left( {i\omega } \right)$$

From here it’s easy to find   

$$C_{2} = 0$$

from (7) we determine \({C}_{1}\) on condition, what \({\text{u}}_{{1}} = 0\) at

$$C_{1} = - \frac{1}{\rho i\omega }\left( { - \frac{{\partial p_{1} \left( x \right)}}{\partial x}} \right)\frac{1}{{ cos \left( {i^{\frac{3}{2}} \alpha_{0} \eta \left( {i\omega } \right)} \right)}}$$

As a result of this, to determine the speed, we will have:

$$u_{1} \left( y \right) = \frac{1}{\rho i\omega }\left( { - \frac{{\partial p_{1} \left( x \right)}}{\partial x}} \right)\left( {1 - \frac{{ cos \left( {i^{\frac{3}{2}} \alpha_{0} \eta \left( {i\omega } \right)\frac{y}{h}} \right)}}{{ cos \left( {i^{\frac{3}{2}} \alpha_{0} \eta \left( {i\omega } \right)} \right)}}} \right)$$
(9)

where \(\alpha_{0} - \sqrt {\frac{\omega }{\nu }} h\) -vibration Womersley number (dimensionless oscillation frequency).

Using the equation

$$\tau_{1} = - \frac{\mu }{{\eta^{2} \left( {i\omega } \right)}}\frac{{\partial u_{1} \left( y \right)}}{\partial y}\left| {y = h} \right..$$
(10)

find the tangential shear stress on the wall

$$\tau _{1} = - h\left( { - \frac{{\partial P}}{{\partial x}}} \right)\frac{1}{{i\alpha _{0}^{2} }}\left( {\frac{{i^{{\frac{3}{2}}} \alpha _{0} sin \left( {i^{{\frac{3}{2}}} \alpha _{0} \eta \left( {i\omega } \right)} \right)}}{{\eta \left( {i\omega } \right) cos \left( {i^{{\frac{3}{2}}} \alpha _{0} \eta \left( {i\omega } \right)} \right)}}} \right)$$
(11)

Now we will integrate both parts of formula (9) over a variable ranging from \(-h\) to \(h\), find formulas for fluid flow.

$$Q_{1} = 2h\left[ {\frac{1}{\rho i\omega }\left( { - \frac{{\partial p_{1} \left( x \right)}}{\partial x}} \right)\left( {1 - \frac{{ sin \left( {i^{\frac{3}{2}} \alpha_{0} \eta \left( {i\omega } \right)} \right)}}{{\left( {i^{\frac{3}{2}} \alpha_{0} \eta \left( {i\omega } \right)} \right) cos \left( {i^{\frac{3}{2}} \alpha_{0} \eta \left( {i\omega } \right)} \right)}}} \right)} \right].$$
(12)

Given the formula (12) \({Q}_{1}=2h<{u}_{1}>,\) we find the longitudinal velocity averaged over the channel section.

$${<}{u_{1} }{>} = \frac{{h^{2} }}{{\mu i\alpha_{0}^{2} }}\left( { - \frac{{\partial p_{1} \left( x \right)}}{\partial x}} \right)\left( {1 - \frac{{ sin \left( {i^{\frac{3}{2}} \alpha_{0} \eta \left( {i\omega } \right)} \right)}}{{\left( {i^{\frac{3}{2}} \alpha_{0} \eta \left( {i\omega } \right)} \right) cos \left( {i^{\frac{3}{2}} \alpha_{0} \eta \left( {i\omega } \right)} \right)}}} \right).$$
(13)

Here \(\rho i\omega\) can be written in the form

$$\rho i\omega = i\frac{\omega }{\nu }h^{2} \cdot \frac{\mu }{{h^{2} }} = i\alpha_{0}^{2} \frac{\mu }{{h^{2} }}$$

Then formula (13) takes the form:

$${<}{u_{1} }{>} = - \frac{h}{3\mu }\tau_{1} \cdot \frac{{3\left( {i^{\frac{3}{2}} \alpha_{0} \eta \left( {i\omega } \right) cos (i^{\frac{3}{2}} \alpha_{0} \eta \left( {i\omega } \right)} \right) - sin (i^{\frac{3}{2}} \alpha_{0} \eta \left( {i\omega } \right)))}}{{\left( {i^{\frac{3}{2}} \alpha_{0} )^{2} sin (i^{\frac{3}{2}} \alpha_{0} \eta \left( {i\omega } \right)} \right)}}.$$
(14)

Using formula (14) we determine the transfer function \({W}_{\tau ,u}\left(i\omega \right)\) for shear stress on the walls, as

$$W_{{\tau_{1} ,u_{1} }} \left( {i\omega } \right) = \frac{{\tau_{1} \left( {i\omega } \right)}}{{u_{1} \left( {i\omega } \right)}}$$
(15)

from Eq. (14) we obtain

$$W_{{\tau _{1} ,u_{1} }} \left( {i\omega } \right) = \frac{h}{{3\mu }}\frac{{\tau _{1} \left( {i\omega } \right)}}{{{<}{u_{1} \left( {i\omega } \right)} {>}}} = - \frac{{\left( {i^{{\frac{3}{2}}} \alpha _{0} )^{2} sin (i^{{\frac{3}{2}}} \alpha _{0} \eta \left( {i\omega } \right)} \right)}}{{3\left( {i^{{\frac{3}{2}}} \alpha _{0} \eta \left( {i\omega } \right) cos (i^{{\frac{3}{2}}} \alpha _{0} \eta \left( {i\omega } \right)} \right) - sin (i^{{\frac{3}{2}}} \alpha _{0} \eta \left( {i\omega } \right)))}}.$$
(16)

The transfer function (16) is sometimes called the amplitude-phase frequency response (APFR). This function allows you to determine the dependence of the shear stress on the channel wall on time for a given law of change in the longitudinal velocity averaged over the channel section. As is known, in most cases, when solving non-stationary problems, shear stress on the wall is used, obtained in the quasi-stationary regime of fluid flow. In real cases, such assumptions are valid when the distribution of local velocities over the flow section has a parabolic distribution law. In this case, the tangential shear stress on the channel wall fluctuates in one phase with the fluctuation of the average longitudinal velocity over the channel section.

In this case, the value \(\tau_{0,kc}\) can be calculated using the formula

$$\tau_{0,kc} = \frac{3\mu }{h}< {u_{1} } >$$
(17)

And instead of a quasi-stationary flow of tangential shear stress on the wall \(\tau_{o,kc}\), can be accepted

$$\tau _{{0,kc}} = \tau _{{{\text{HC}}}}$$
(18)

Thus, relation (18) makes it possible to replace the quantity \(\tau_{{{\text{HC}}}}\) on the value \(\tau_{0,kc}\), only under the condition that the actual distribution of local velocities over the flow cross section differs little from the quasi-stationary one. However, in many cases, in a non-stationary flow, the law of distribution of local velocities differs significantly from the quasi-stationary one. In most works [9,10,11,12, 17, 21] it was shown that in the case of oscillatory laminar flow in a cylindrical pipe, the change in local velocities in the adjacent layers is ahead of the change in local velocities in time than in the central layers. The oscillatory flow due to a change in the law of distribution of local velocities over the channel cross section of the value \(\tau_{{{\text{HC}}}}\) actually differs significantly from \(\tau_{{{0}\kappa {\text{C}}}}\).The linear model of unsteady flow is the most complete representation of the dependence \(\tau_{{{\text{HC}}}}\) OT \({<}{u_{1} }{>}\) can be obtained using the transfer function (16).

3 Calculation Results and Analysis

In an unsteady flow, to determine the dependence of the shear stress on the channel wall between the longitudinal velocity averaged over the channel section, we use the transfer function (16). In this regard, we take into account the law of change of the longitudinal velocity averaged over the channel section

$$<{u_{1} }>\,= a_{{u_{1} }} cos \omega t.$$
(19)

where \({\text{a}}_{{{\text{u}}_{1} }}\)-amplitude of the longitudinal velocity averaged over the channel section. Using formulas (19), it is possible to determine the dependence of the shear stress on the wall between the longitudinal velocity averaged over the channel section. Due to the Eqs. (19) used to find the shear stress on the channel wall, its value will also be harmonic, but in the general case, shifted in phase with respect to \(<{u}_{1}>\).

Thus, the change in shear stress on the wall is determined as follows:

$$\tau_{1} = a_{{\tau_{1} }} cos (\omega t + \phi_{{\tau_{1} }} ).$$
(20)

where \(a_{{\tau_{1} }}\) - shear stress amplitude on the channel wall; \(\upphi_{{\tau_{1} }}\) - phase between magnitude \({\uptau }_{1}\) and \({<}{u_{1} }{>}\)

Using the relation

$$cos (\omega t + \phi_{{\tau_{1} }} ) = cos \omega t cos \phi_{{\tau_{1} }} - \sin \omega t sin \phi_{{\tau_{1} }}$$

And given that

$$\frac{{\partial < {u_{1} } > }}{\partial t} = - a_{{u_{1} }} \omega sin \omega t$$

we reduce Eq. (19) to the form

$${\uptau }_{1} = \left( {\frac{{{\text{a}}_{{{\uptau }_{1} }} }}{{{\text{a}}_{{{\text{u}}_{1} }} }}\cos \upphi_{{{\uptau }_{1} }} } \right)< {{\text{u}}_{1} } > + \left( {\frac{{{\text{a}}_{{{\uptau }_{1} }} }}{{{\text{a}}_{{{\text{u}}_{1} }} }} \sin \upphi_{{{\uptau }_{1} }} } \right)\frac{1}{{\upomega }}\frac{{\partial < {{\text{u}}_{1} } > }}{{\partial {\text{t}}}}.$$
(21)

Quantities \((\frac{{{{a}}_{{{{\tau }}_{1} }} }}{{{\text{a}}_{{{\text{u}}_{1} }} }}\cos \phi _{{\tau _{1} }} )\,{\text{and}}\,\frac{{{\text{a}}_{{{{\tau }}_{1} }} }}{{{\text{a}}_{{{\text{u}}_{1} }} }}\sin \phi _{{\tau _{1} }}\) are respectively the real and imaginary parts of the transfer function (16), so from (16) we obtain

$$\begin{gathered} W_{{\tau_{1} ,u_{1} }} = - \frac{1}{3}\left( {\frac{{ - i\alpha_{0}^{2} sin (i^{3/2} \alpha_{0} \left( {1 + iDe\alpha_{0}^{2} )^{1/2} } \right)}}{{i^{3/2} \alpha_{0} (1 + iDe\alpha_{0}^{2} )^{1/2} cos (i^{3/2} \alpha_{0} \left( {1 + iDe\alpha_{0}^{2} )^{1/2} } \right) - sin (i^{3/2} \alpha_{0} \left( {1 + iDe\alpha_{0}^{2} )^{1/2} } \right)}}} \right) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \chi + \beta i \hfill \\ \end{gathered}$$
(22)

Here \(De = \frac{\nu \lambda }{{h^{2} }}\) - elastic Debory number characterizes the elastic properties of a fluid,

$$\chi = \left( {\frac{{a_{{\tau_{1} }} }}{{a_{{u_{1} }} }} cos \phi_{{\tau_{1} }} } \right),\,\beta = \frac{{a_{{\tau_{1} }} }}{{a_{{u_{1} }} }}\sin \phi_{{\tau_{1} }}$$

Then (21) the formula takes the form.

$$\frac{h}{3\mu }\frac{{\tau_{1} }}{{< {u_{1} } > }} = W\tau_{1} ,u_{1} = \chi + \beta \frac{1}{\omega }K_{{\text{H}}}$$
(23)

Here \({\rm K}_{{\text{H}}} = \frac{{\partial < {{\text{u}}_{{1}} } > }}{{< {{\text{u}}_{{1}} } > \partial_{{\text{t}}} }}\) - parameter characterizes the fluid acceleration, \(\chi\) and \(\upbeta\)- dimensionless quantities, \(t\) dimensional values, so it needs to be converted to a dimensionless form, using the transformation

$$t = \frac{{h^{2} \rho }}{3\mu }t^{*}$$

Taking into account (17) and (23) on (22) we obtain the calculation formulas

$$\frac{{\tau_{{{\text{HC}}}} }}{{\tau_{{0\kappa {\text{C}}}} }} = \chi + \frac{3\beta }{{\alpha_{0}^{2} }}K_{{\text{H}}}$$
(24)

Here \(\tau_{{0\kappa {\text{C}}}} = \frac{3\mu }{h}< {u_{1} } > \,{\text{and}}\,\tau_{1} = \tau_{{{\text{HC}}}}\).

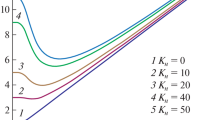
Using formula (24), graphs in Fig. 1 are constructed showing the change in the relative shear stress on the wall in an unsteady flow depending on the dimensionless oscillation frequency when the Debory number is equal to zero.

Fig. 1.
figure 1

Change in the ratio of the non-stationary shear stress on the wall to the quasi-stationary shear stress depending on the dimensionless oscillation frequency, for different values of the liquid acceleration parameter \(K_{H}\)

Full size image

The constructed graph in Fig. 1 shows that when \(K_{{\text{H}}} = 0\) relations \(\frac{{\tau_{{{\text{HC}}}} }}{{\tau_{{0\kappa {\text{C}}}} }}\) close to unity while \(\alpha_{0}^{2}\) less than units. If a \(\alpha_{0}^{2}\) takes on values greater than unity, then even if \(K_{{\text{H}}} = 0\) relations \(\frac{{\tau_{{{\text{HC}}}} }}{{\tau_{{0\kappa {\text{C}}}} }}\) becomes greater than unity and increases with an increase in the dimensionless oscillation frequency. This suggests that shear stresses on the channel wall during unsteady fluid flow can exceed their quasi-stationary values even at those times when the fluid acceleration is zero. Attitude \(\frac{{\tau_{{{\text{HC}}}} }}{{\tau_{{0\kappa {\text{C}}}} }}\) increases with increasing parameter \(K_{{\text{H}}}\) which is explained by a change in the shear stress on the wall, occurs with a phase advance compared to the average speed over the cross section.

Fig. 2.
figure 2

Change in the ratio of the non-stationary shear stress on the wall to the quasi-stationary shear stress depending on the oscillation frequency, for different values of the liquid acceleration parameter \(K_{H}\) and the elastic Debory number 0.01

Full size image
Fig. 3.
figure 3

Change in the ratio of the non-stationary shear stress on the wall to the quasi-stationary shear stress depending on the oscillation frequency, for different values of the liquid acceleration parameter \(K_{H}\) and the elastic Debory number 0.05.

Full size image
Fig. 4.
figure 4

Change in the ratio of the non-stationary shear stress on the wall to the quasi-stationary shear stress depending on the oscillation frequency, for different values of the liquid acceleration parameter \(K_{H}\) and the elastic Debory number 0.1

Full size image

The flow of a viscoelastic fluid in a flat channel shows a significant change in the shear stress on the wall at low vibration frequencies depending on the elastic Debory number. In [21], an oscillatory flow of a viscoelastic fluid in a flat channel and in a cylindrical pipe was studied, where the flow region is divided into two classes, of which \(\alpha_{0} > 1\) belongs to the “broad” class, and the other \(\alpha_{0} < 1\) to “narrow”. In the “wide” classes, the oscillatory fluid flows are limited near the wall flows, and in the central part of the inviscid. In “narrow” systems, shear waves cross the entire flow area, which ultimately leads to a sharp increase in the amplitude of the velocity profile and other hydrodynamic parameters, such as shear stress on the wall, fluid flow, depending on the elastic Debory number. Based on formula (24), graphs are plotted in Figs. 2, 3 and 4 showing the change in shear stress during an oscillatory flow of a viscoelastic fluid in a flat channel depending on the oscillation frequency and the Debory number, respectively \(De = 0.01;0.05;0.1\) It should be noted that all graphs for the flow of a viscoelastic fluid in a flat channel are of an oscillatory nature.

Figure 2 presents, for the case \(De = 0.01\) change in the ratio of the non-stationary shear stress on the channel wall to the quasi-stationary shear stress depending on the dimensionless oscillation frequency. It should be noted that in this case, in contrast to the Newtonian flow, an increase in shear stress is observed in the region near the zero value of the oscillation frequency, depending on the acceleration of the liquid. Then there is a gradual decrease for \(K_{{\text{H}}} = 10;{ }50;100\) and for \(K_{{\text{H}}} = 0;1\) increase to value \(\frac{{\tau_{{{\text{HC}}}} }}{{\tau_{{0\kappa {\text{C}}}} }} = 3\) at high oscillation frequencies. For the case De = 0.05 the change in the ratio of the non-stationary shear stress on the channel wall to the quasi-stationary shear stress depending on the dimensionless oscillation frequency is shown in Fig. 3. In this case, near the zero value of the oscillation frequency, a decrease in shear stress is observed depending on the acceleration of the liquid, and then there is an increase to a maximum in the region \(2 < \alpha_{0} < 4\), then gradually asymptotically decreasing to the value\(\frac{{\tau_{{{\text{HC}}}} }}{{\tau_{{0\kappa {\text{C}}}} }} = 1.5\).

We note the features, for the case \(De = 0.1\) in which, close to zero, the oscillation frequency, a sharp decrease occurs in all cases, except \(K_{{\text{H}}} = 0\) case.

This means that at large values of the relaxation time, reverse flows of the liquid can occur at low oscillation frequencies. Then, with an increase in the oscillation frequency, all curves showing a change in the ratio of the non-stationary shear stress on the channel wall, with oscillation asymptotically approaches, to the value \(\frac{{\tau_{{{\text{HC}}}} }}{{\tau_{{0\kappa {\text{C}}}} }} = 1\) depending on the acceleration of the fluid.

Then the phase advance decreases with increasing frequency of the oscillation and approaches asymptotically to the value of the quasi-stationary flow with oscillation. Thus, the considered features in changes in the shear stress on the wall for a given harmonic fluctuation of the flow rate are caused by the violation of the parabolic law of the distribution of local velocities over the channel section. Calculations show that in the near-surface layer the velocities change in phase with the change in shear stress on the wall along the channel, while in the central part of the flow they remain in phase with the phase of shear stress on the wall. Therefore, the viscoelastic properties of the fluid, as well as its acceleration, are limiting factors for using the quasi-stationary approach. In addition, the found formulas (21) and (22) for determining the transfer function during the flow of a viscoelastic fluid in a non-stationary flow allow, to determine the dissipation of mechanical energy in a non-stationary flow of the medium, which are of greater importance when calculating the regulation of hydraulic and pneumatic systems.

4 Conclusion

The problems of the oscillatory flow of a viscoelastic incompressible fluid in a flat channel are solved for a given harmonic oscillation of the fluid flow rate. The transfer function of the amplitude-phase frequency response is determined. Using this function, the influence of the oscillation frequency, acceleration, and relaxation properties of the liquid on the ratio of the tangential shear stress on the channel wall to the average velocity over the channel section is determined. Calculations show that the non-stationary shear stress on the channel wall during the flow of a viscoelastic fluid increases no monotonically with the acceleration of the fluid particle, at low oscillation frequencies.

Reaching the maximum value, then decreasing with increasing dimensionless oscillation frequency and asymptotically approaching the values without accelerated flow with oscillation. Then the phase advance decreases with increasing frequency of the oscillation and approaches asymptotically to the value of the quasi-stationary flow with oscillation. It is shown that the viscoelastic properties of the fluid, as well as its acceleration, are the limiting factors for using the quasi-stationary approach.

Formulas are found for determining the transfer function for a viscoelastic fluid flow in an unsteady flow, which are of no small importance in calculating the regulation of hydraulic and pneumatic systems.